Scaling Rules at Constant Frequency for Resonant Inductive Power Transfer Systems for Electric Vehicles
Abstract
1. Introduction
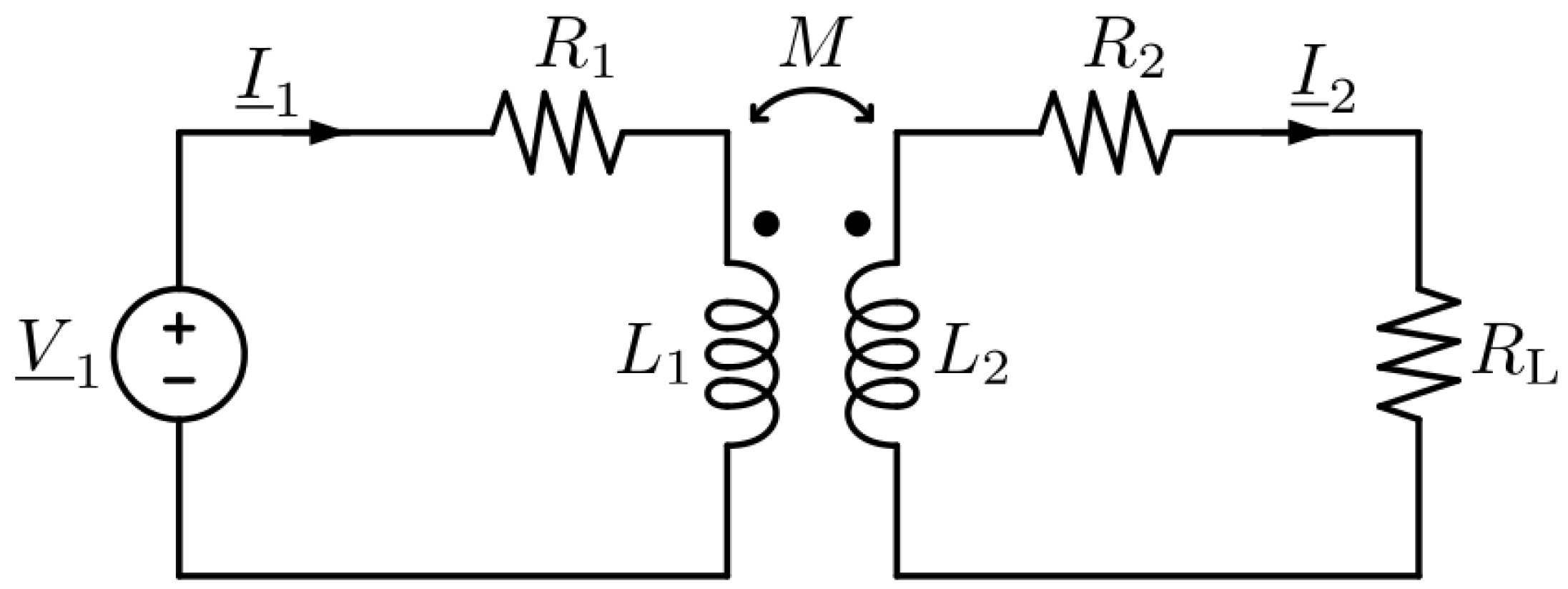
2. Circuit Model of Inductive Power Transfer System
3. Derivation of Scaling Rules
- The working frequency and the current density remain constant in the scaling process. This assumption allows for considering the same exploitation of the conductors material. Moreover, keeping the frequency fixed allows for operating with similar characteristics of the power electronics drivers and control.
- The number of turns of transmitter and receiver coils does not change in the scaling process. This assumption guarantees that the re-sized structure changes only in the dimensions while the constructive characteristics are left unchanged.
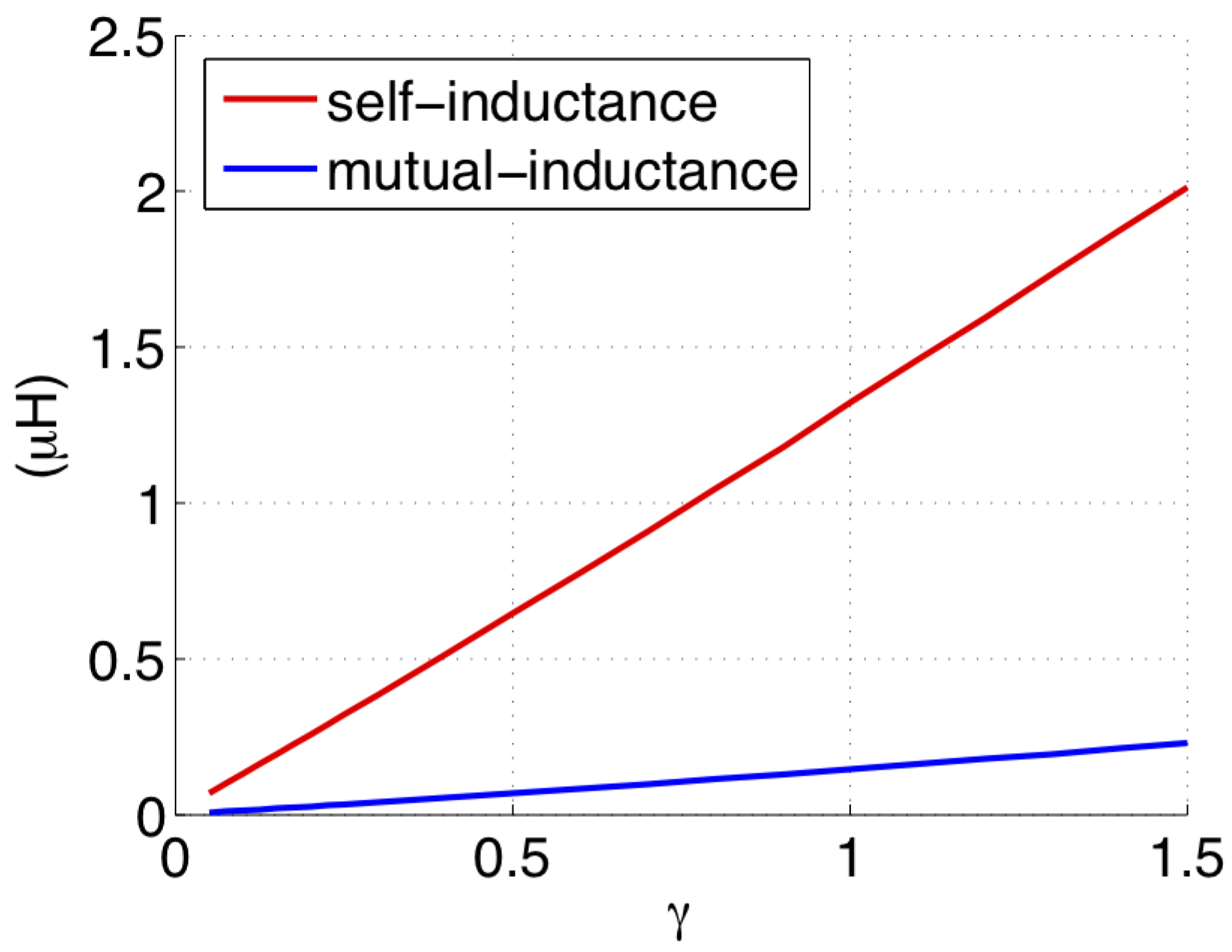
3.1. Scaling of Self and Mutual Inductance
3.2. Scaling of Currents, Voltages and Power
3.3. Scaling of the Compensation Capacitances
4. Scaling-Rules’ Limits of Validity
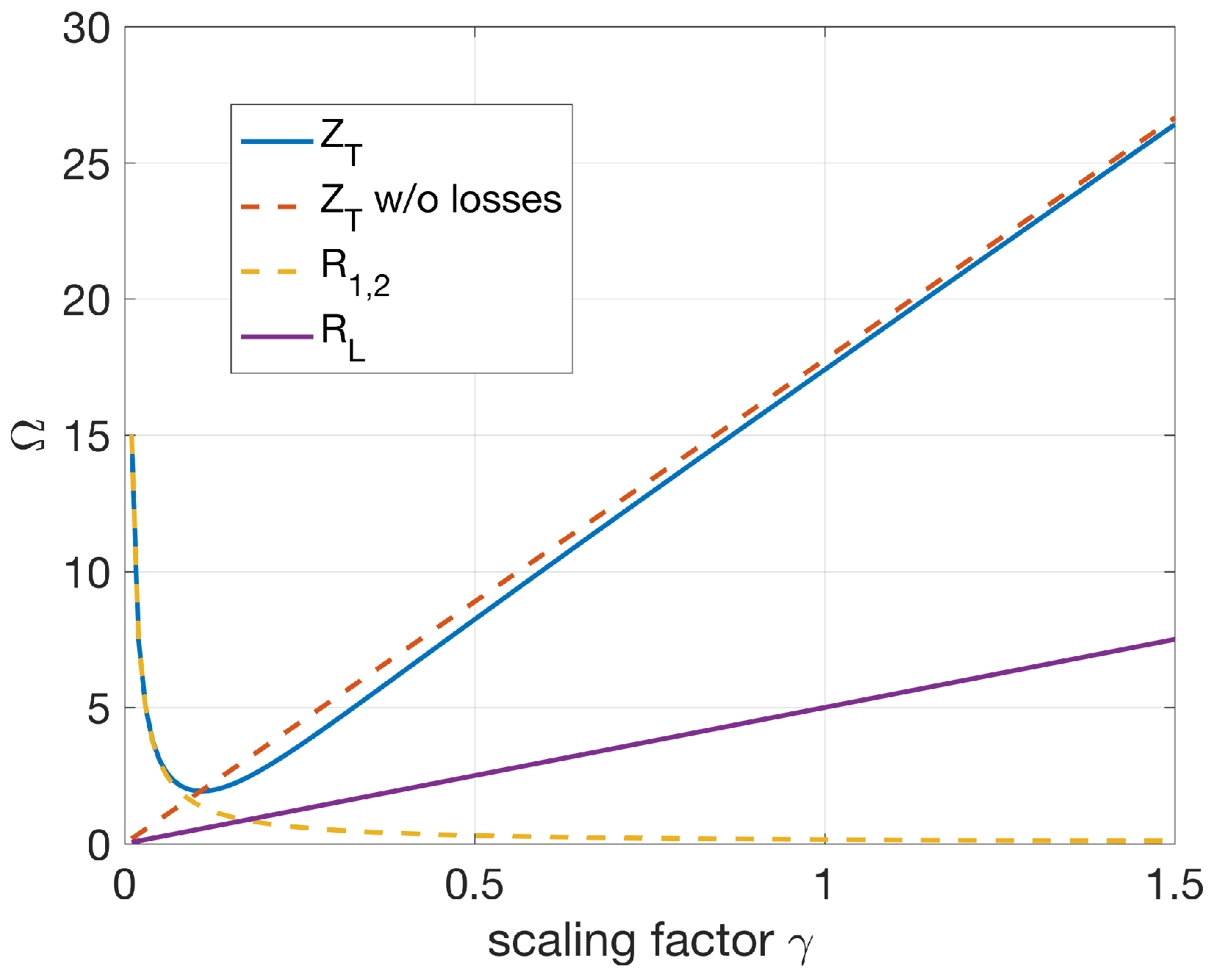
4.1. Coil Resistances
4.2. Capacitors’ ESR
5. Power Losses and Efficiency
6. Experimental Validation
6.1. Power and Losses
6.2. Compensation Capacitors’ Technology
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Scaling of Inductances in Complex Environment



| Parameter | Value |
|---|---|
| Transmitter radius | |
| Transmitter wire diameter | |
| Receiver radius | |
| Receiver wire diameter | |
| Coils distance | |
| Ferrite plate inner rad. | |
| Ferrite plate outer rad. | |
| Ferrite plate thickness | |
| Aluminium plate radius | |
| Aluminium plate thickness | |
| Aluminium-Ferrite plates dist. | |
| Ferrite magnetic permeability | 2000 |
| Ferrite conductivity | |
| Aluminium conductivity |

References
- Lu, Y.; Ma, D.B. Wireless power transfer system architectures for portable or implantable applications. Energies 2016, 9, 1087. [Google Scholar] [CrossRef]
- Park, S.; Kim, H.; Cho, J.; Kim, E.; Jung, S. Wireless power transmission characteristics for implantable devices inside a human body. In Proceedings of the 2014 International Symposium on Electromagnetic Compatibility (EMC Europe), Gothenburg, Sweden, 1–4 September 2014; pp. 1190–1194. [Google Scholar]
- Green, A.W.; Boys, J.T. An inductively coupled high frequency power system for material handling applications. In Proceedings of the IPEC Conference, Singapore, 18–19 March 1993; Volume 2, pp. 821–826. [Google Scholar]
- Tampubolon, M.; Pamungkas, L.; Chiu, H.J.; Liu, Y.C.; Hsieh, Y.C. Dynamic Wireless Power Transfer for Logistic Robots. Energies 2018, 11, 527. [Google Scholar] [CrossRef]
- Radecki, A.; Chung, H.; Yoshida, Y.; Miura, N.; Shidei, T.; Ishikuro, H.; Kuroda, T. 6 W/25 mm2 inductive power transfer for non-contact wafer-level testing. In Proceedings of the 2011 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 20–24 February 2011; pp. 230–232. [Google Scholar]
- Cheng, Z.; Lei, Y.; Song, K.; Zhu, C. Design and loss analysis of loosely coupled transformer for an underwater high-power inductive power transfer system. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar]
- Waffenschmidt, E. Wireless power for mobile devices. In Proceedings of the 2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), Amsterdam, The Netherlands, 9–13 October 2011; pp. 1–9. [Google Scholar]
- Uchida, A.; Shimokawa, S.; Kawano, H.; Ozaki, K.; Matsui, K.; Taguchi, M. Phase and intensity control of multiple coil currents in mid-range wireless power transfer. IET Microw. Antennas Propag. 2014, 8, 498–505. [Google Scholar] [CrossRef]
- Raval, P.; Kacprzak, D.; Hu, A.P. A wireless power transfer system for low power electronics charging applications. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications (ICIEA), Beijing, China, 21–23 June 2011; pp. 520–525. [Google Scholar]
- Jonah, O.; Georgakopoulos, S.V.; Tentzeris, M.M. Wireless power transfer to mobile wearable device via resonance magnetic. In Proceedings of the 2013 IEEE 14th Annual Wireless and Microwave Technology Conference (WAMICON), Orlando, FL, USA, 7–9 April 2013; pp. 1–3. [Google Scholar]
- Bi, Z.; Kan, T.; Mi, C.C.; Zhang, Y.; Zhao, Z.; Keoleian, G.A. A review of wireless power transfer for electric vehicles: Prospects to enhance sustainable mobility. Appl. Energy 2016, 179, 413–425. [Google Scholar] [CrossRef]
- Bosshard, R.; Iruretagoyena, U.; Kolar, J.W. Comprehensive Evaluation of Rectangular and Double-D Coil Geometry for 50 kW/85 kHz IPT System. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 406–1415. [Google Scholar] [CrossRef]
- Zhang, W.; White, J.C.; Abraham, A.M.; Mi, C.C. Loosely Coupled Transformer Structure and Interoperability Study for EV Wireless Charging Systems. IEEE Trans. Power Electron. 2011, 30, 6356–6367. [Google Scholar] [CrossRef]
- Budhia, M.; Covic, G.A.; Boys, J.T. Design and Optimization of Circular Magnetic Structures for Lumped Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2011, 26, 3096–3108. [Google Scholar] [CrossRef]
- Liu, J.; Chan, K.W.; Chung, C.Y.; Chan, N.H.L.; Liu, M.; Xu, W. Single-Stage Wireless-Power-Transfer Resonant Converter with Boost Bridgeless Power-Factor-Correction Rectifier. IEEE Trans. Ind. Electron. 2018, 65, 2145–2155. [Google Scholar] [CrossRef]
- Geng, Y.; Li, B.; Yang, Z.; Lin, F.; Sun, H. A high efficiency charging strategy for a supercapacitor using a wireless power transfer system based on inductor/capacitor/capacitor (LCC) compensation topology. Energies 2017, 10, 135. [Google Scholar] [CrossRef]
- Li, M.; Chen, Q.; Hou, J.; Chen, W.; Ruan, X. 8-Type contactless transformer applied in railway inductive power transfer system. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 2233–2238. [Google Scholar]
- Zakrzewski, K.; Tomczuk, B.; Waindok, A. Nonlinear scaled models in 3D calculation of transformer magnetic circuits. Int. J. Comput. Math. Electr. Electron. Eng. 2006, 25, 91–101. [Google Scholar] [CrossRef]
- Stipetic, S.; Zarko, D.; Popescu, M. Scaling laws for synchronous permanent magnet machines. In Proceedings of the 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 31 March–2 April 2015; pp. 1–7. [Google Scholar]
- Reichert, T.; Nussbaumer, T.; Kolar, J.W. Torque scaling laws for interior and exterior rotor permanent magnet machines. In Proceedings of the IEEE International Magnetics Conference 2009 (INTERMAG 2009), Sacramento, CA, USA, 4–8 May 2009; p. 3. [Google Scholar]
- De Simone, S.; Adragna, C.; Spini, C.; Gattavari, G. Design-oriented steady-state analysis of LLC resonant converters based on FHA. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM 2006), Taormina, Italy, 23–26 May 2006; pp. 200–207. [Google Scholar]
- Hua, C.C.; Fang, Y.H.; Lin, C.W. LLC resonant converter for electric vehicle battery chargers. IET Power Electron. 2016, 9, 2369–2376. [Google Scholar] [CrossRef]
- Huh, J.; Lee, S.W.; Lee, W.Y.; Cho, G.H.; Rim, C.T. Narrow-width inductive power transfer system for online electrical vehicles. IEEE Trans. Power Electron. 2011, 26, 3666–3679. [Google Scholar] [CrossRef]
- Del Toro García, X.; Vázquez, J.; Roncero-Sánchez, P. Design implementation issues and performance of an inductive power transfer system for electric vehicle chargers with series-series compensation. IET Power Electron. 2015, 8, 1920–1930. [Google Scholar] [CrossRef]
- Wojda, R.P.; Kazimierczuk, M.K. Winding resistance of litz-wire and multi-strand inductors. IET Power Electron. 2012, 5, 257–268. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Deng, J.; Nguyen, T.D.; Mi, C.C. A double-sided LCC compensation network and its tuning method for wireless power transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Villa, J.L.; Sallan, J.; Osorio, J.F.S.; Llombart, A. High-misalignment tolerant compensation topology for ICPT systems. IEEE Trans. Ind. Electron. 2012, 59, 945–951. [Google Scholar] [CrossRef]
- Wang, C.S.; Covic, G.A.; Stielau, O.H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems. IEEE Trans. Ind. Electron. 2004, 51, 148–157. [Google Scholar] [CrossRef]
- Paul, C.R. Inductance: Loop and Partial; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 9780470461884. [Google Scholar]
- Ibrahim, M.; Pichon, L.; Bernard, L.; Razek, A.; Houivet, J.; Cayol, O. Advanced modeling of a 2-kW series-series resonating inductive charger for real electric vehicle. IEEE Trans. Veh. Technol. 2015, 64, 421–430. [Google Scholar] [CrossRef]
- Bavastro, D.; Canova, A.; Cirimele, V.; Freschi, F.; Giaccone, L.; Guglielmi, P.; Repetto, M. Design of wireless power transmission for a charge while driving system. IEEE Trans. Magn. 2014, 50, 965–968. [Google Scholar] [CrossRef]
- Shin, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Cho, D.H. Design and Implementation of Shaped Magnetic-Resonance-Based Wireless Power Transfer System for Roadway-Powered Moving Electric Vehicles. IEEE Trans. Ind. Electron. 2014, 61, 1179–1192. [Google Scholar] [CrossRef]
- Pevere, A.; Petrella, R.; Mi, C.C.; Zhou, S. Design of a high efficiency 22 kW wireless power transfer system for EVs fast contactless charging stations. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–7. [Google Scholar]
- Spyker, R.L.; Nelms, R.M. Classical equivalent circuit parameters for a double-layer capacitor. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 829–836. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the law of hysteresis. Trans. Am. Inst. Electr. Eng. 1892, 9, 1–64. [Google Scholar] [CrossRef]
- Reinert, J.; Brockmeyer, A.; De Doncker, R.W. Calculation of losses in ferro- and ferromagnetic materials based on the modified Steinmetz equation. IEEE Trans. Ind. Appl. 2001, 37, 1055–1061. [Google Scholar] [CrossRef]
- Venkatachalam, K.; Sullivan, C.R.; Abdallah, T.; Tacca, H. Accurate prediction of ferrite core loss with nonsinusoidal waveforms using only Steinmetz parameters. In Proceedings of the IEEE Workshop on Computers in Power Electronics, Mayaguez, PR, USA, 3–4 June 2002; pp. 36–41. [Google Scholar]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: An engineering approach. IEEE Trans. Magn. 2003, 39, 981–989. [Google Scholar] [CrossRef]
- Kim, Y.T.; Cho, G.W.; Kim, G.T. The estimation method comparison of iron loss coefficients through the iron loss calculation. J. Electr. Eng. Technol. 2013, 8, 1409–1414. [Google Scholar] [CrossRef]
- Sallan, J.; Villa, J.L.; Llombart, A.; Sanz, J.F. Optimal design of ICPT systems applied to electric vehicle battery charge. IEEE Trans. Ind. Electron. 2009, 56, 2140–2149. [Google Scholar] [CrossRef]
- Meeker, D.C. Finite Element Method Magnetics, Version 4.2. Available online: http://www.femm.info (accessed on 2 July 2018).
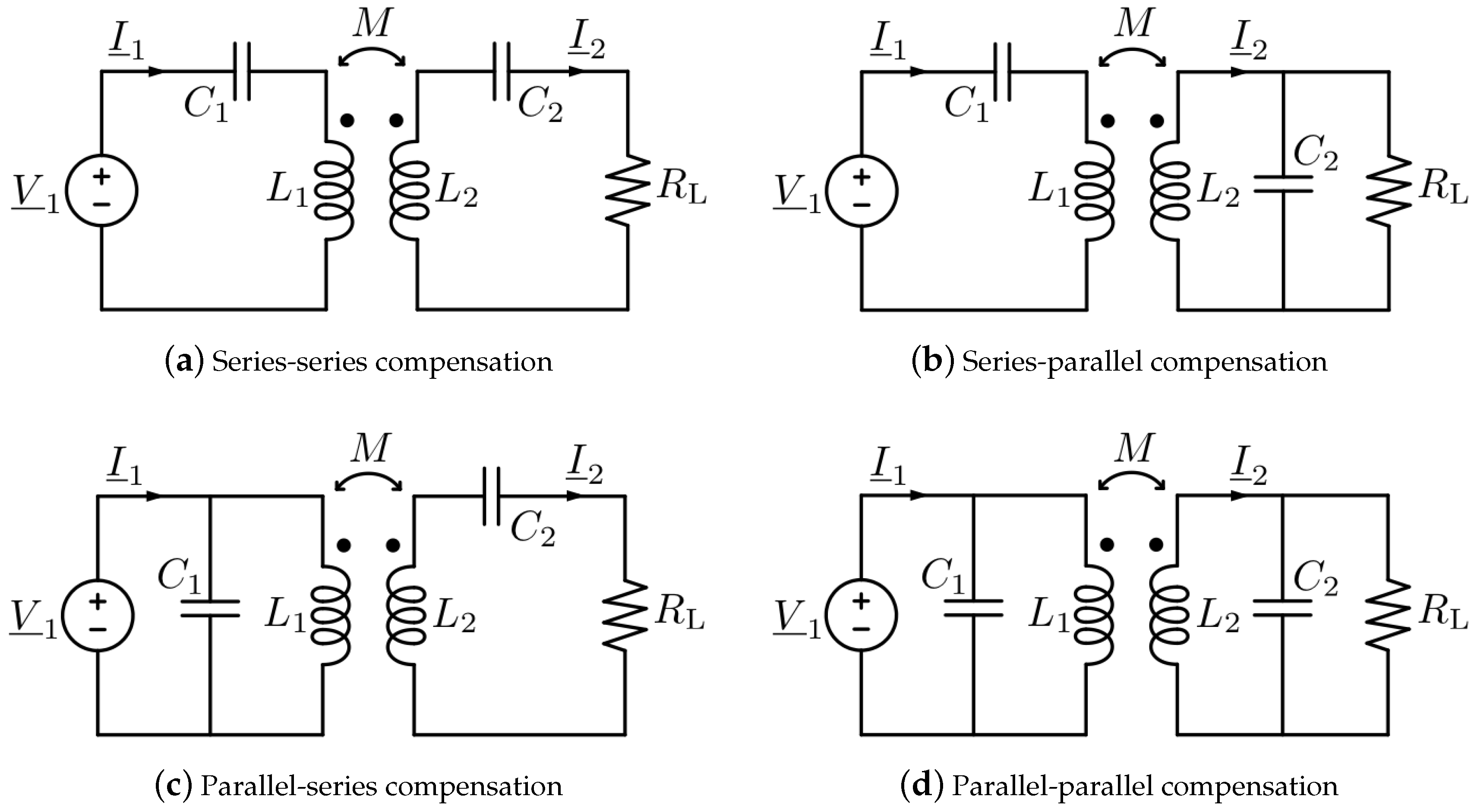


| Compensation Topology | Capacitor |
|---|---|
| series-series | |
| series-parallel | |
| parallel-series | |
| parallel-parallel |
| Parameter | Dimension |
|---|---|
| Coils inner width | |
| Coils inner length | |
| Coils distance | |
| Number of turns | 9 |
| Litz wire diameter | |
| Single ferrite bar | |
| Ferrite core |
| Parameter | Original System | Down-Scaled System | Reference Rule | Expected Scaling Ratio | Measured Scaling Ratio |
|---|---|---|---|---|---|
| Equation (16) | 0.5 | 0.48 | |||
| Equation (16) | 0.5 | 0.48 | |||
| M | Equation (16) | 0.5 | 0.53 | ||
| Equation (23) | 0.5 | 0.52 |
| Parameter | Original System | Down-Scaled System | Reference Rule | Expected Scaling Ratio | Measured Scaling Ratio |
|---|---|---|---|---|---|
| 28.7 | Equation (20) | 0.125 | 0.123 | ||
| Equation (17) | 0.25 | 0.27 | |||
| Equation (17) | 0.25 | 0.23 |
| Parameter | Original System | Down-Scaled System | Reference Rule | Expected Scaling Ratio | Measured Scaling Ratio |
|---|---|---|---|---|---|
| 29.12 | Equation (19) | 0.0312 | 0.0309 | ||
| Equation (24) | 0.125 | 0.101 | |||
| Equation (31) | 0.0191 | 0.0232 |
| Efficiency | Original | Down-Scaled |
|---|---|---|
| IPT System | Technology | Capacitance | ESR |
|---|---|---|---|
| Original | Film | ||
| Down-scaled | Ceramic |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cirimele, V.; Freschi, F.; Guglielmi, P. Scaling Rules at Constant Frequency for Resonant Inductive Power Transfer Systems for Electric Vehicles. Energies 2018, 11, 1754. https://doi.org/10.3390/en11071754
Cirimele V, Freschi F, Guglielmi P. Scaling Rules at Constant Frequency for Resonant Inductive Power Transfer Systems for Electric Vehicles. Energies. 2018; 11(7):1754. https://doi.org/10.3390/en11071754
Chicago/Turabian StyleCirimele, Vincenzo, Fabio Freschi, and Paolo Guglielmi. 2018. "Scaling Rules at Constant Frequency for Resonant Inductive Power Transfer Systems for Electric Vehicles" Energies 11, no. 7: 1754. https://doi.org/10.3390/en11071754
APA StyleCirimele, V., Freschi, F., & Guglielmi, P. (2018). Scaling Rules at Constant Frequency for Resonant Inductive Power Transfer Systems for Electric Vehicles. Energies, 11(7), 1754. https://doi.org/10.3390/en11071754






