Decentralized Circulating Currents Suppression for Paralleled Inverters in Microgrids Using Adaptive Virtual Inductances
Abstract
1. Introduction
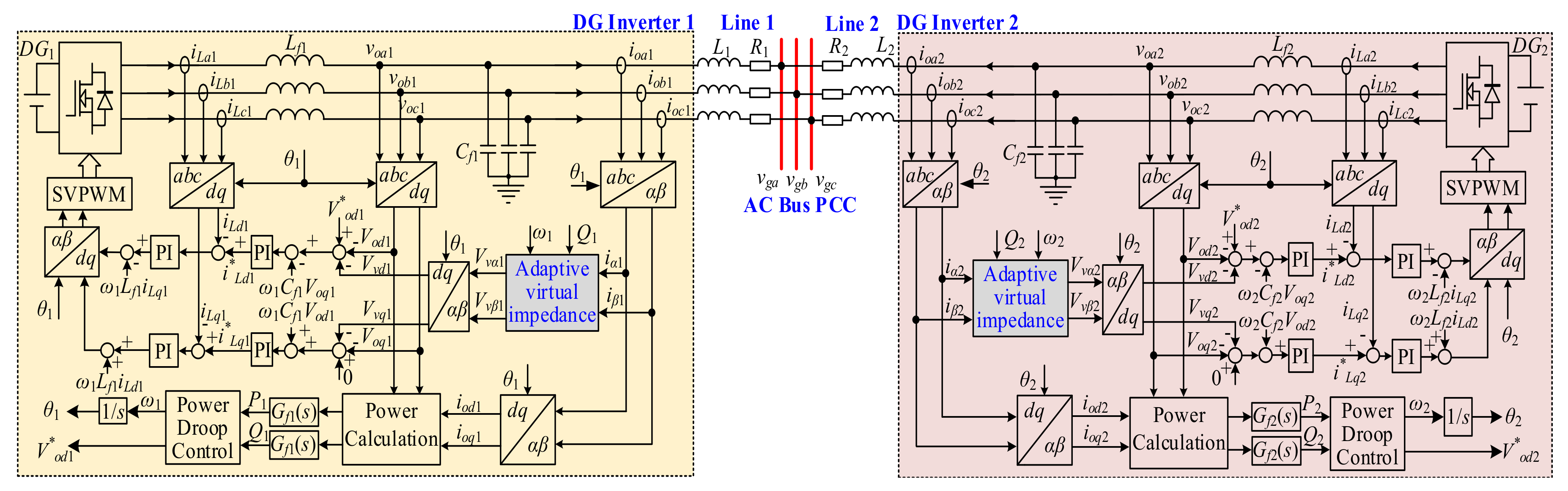
2. Paralleled Inverters with Conventional Droop Control
2.1. Conventional Droop Control
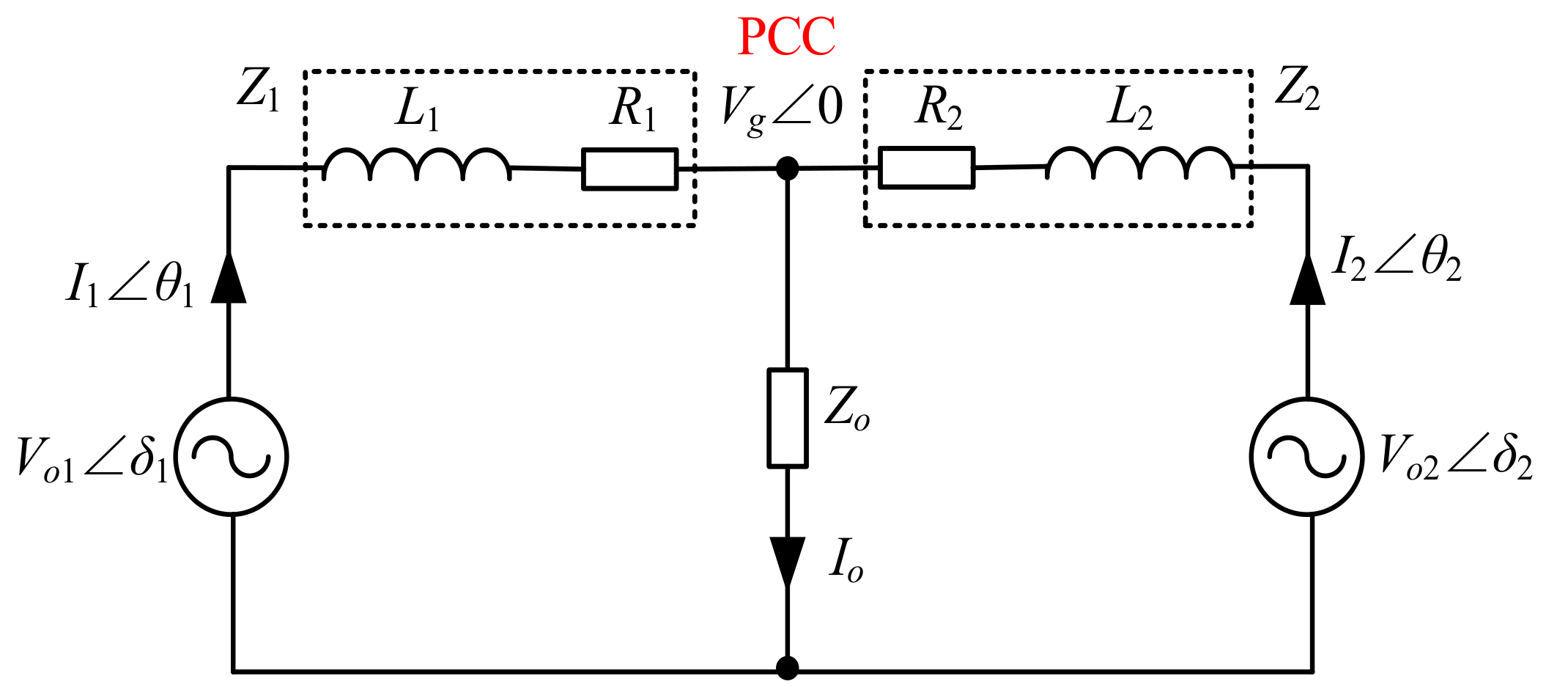
2.2. Generating of Circulating Current
3. Adaptive Virtual Inductance Control Method
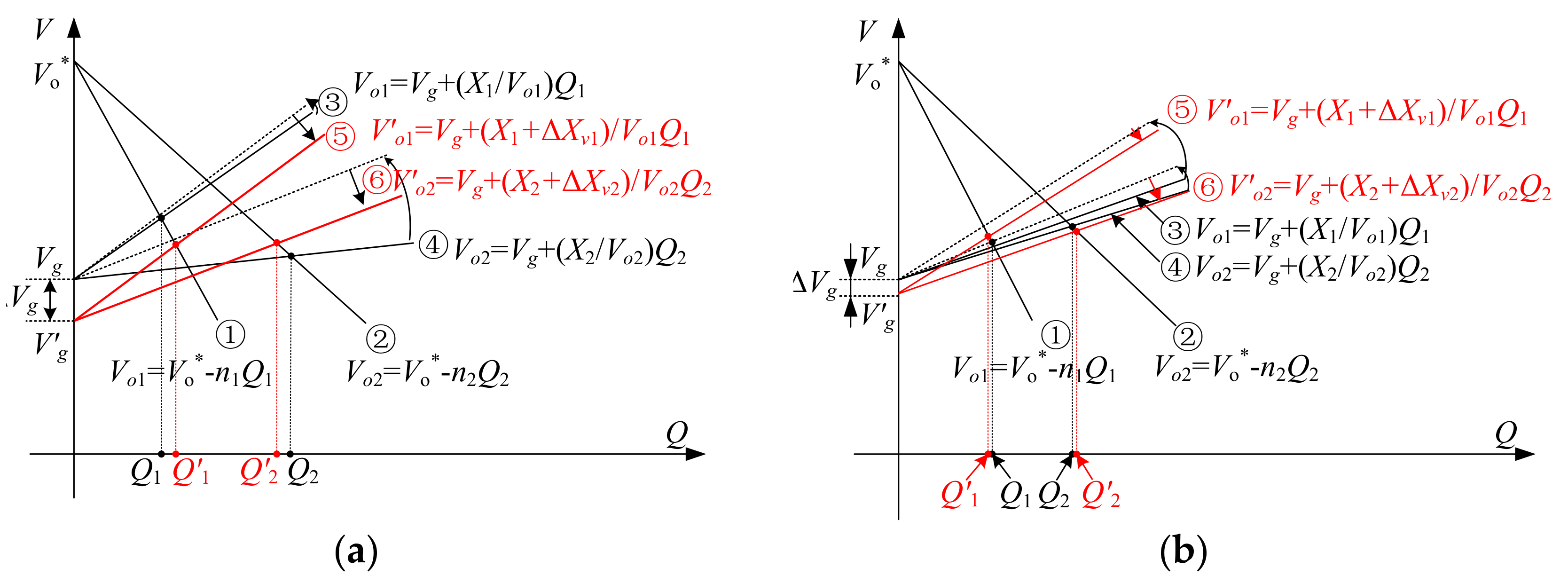
3.1. Operational Principle of the Virtual Inductance Control Method
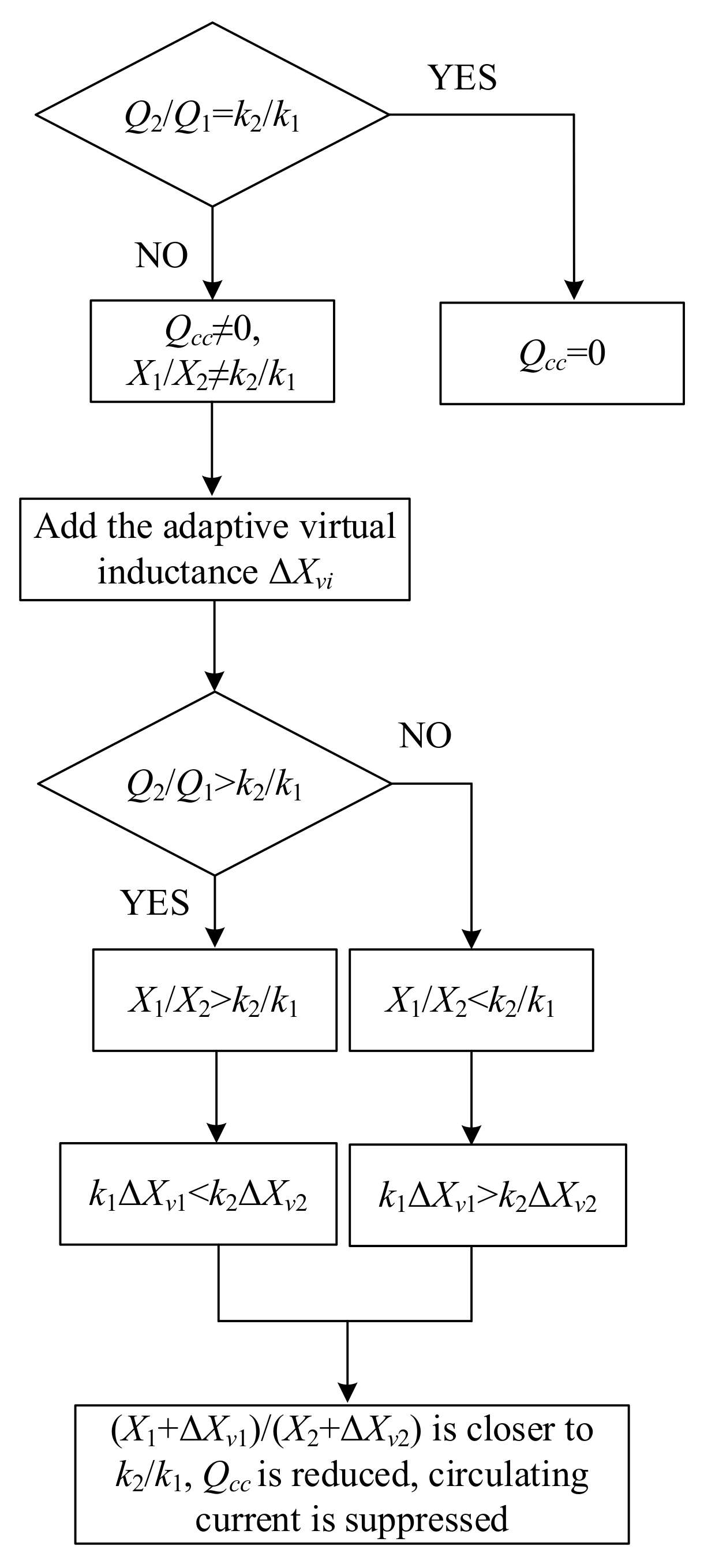
3.2. Realization of the Adaptive Virtual Inductance
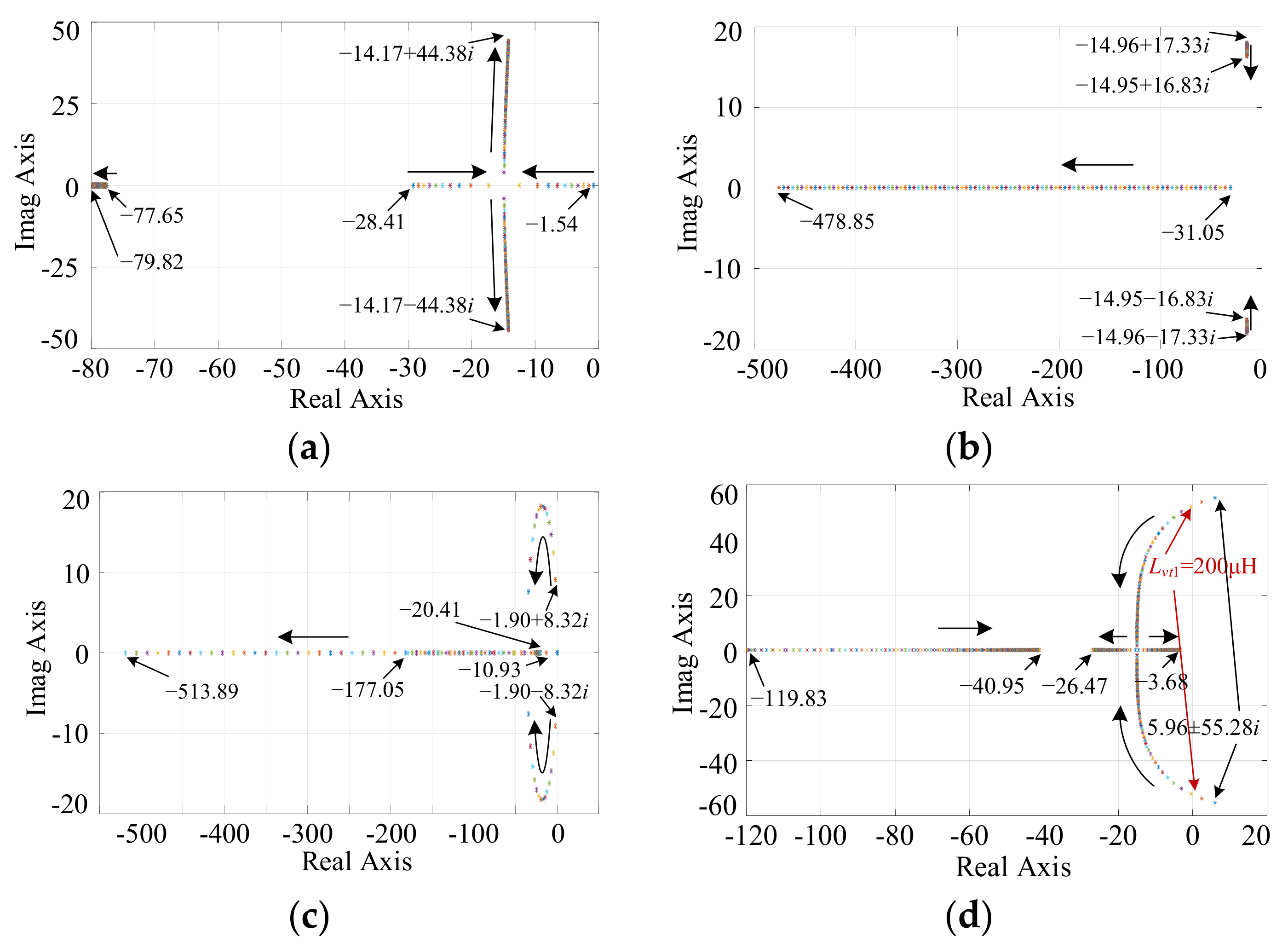
3.3. Stability Analysis
- Case 1:
- n1 = 5 × 10−3 V/Var, Lvt1 = 2 mH, ωf1 = 30 rad/s, m1 is varying from 1 × 10−5 to 1 × 10−3 rad/(s·W);
- Case 2:
- m1 = 2.5 × 10−4 rad/(s·W), Lvt1 = 2 mH, ωf1 = 30, n1 is varying from 1 × 10−4 to 5 × 10−2 V/Var;
- Case 3:
- m1 = 2.5 × 10−4 rad/(s·W), n1 = 5 × 10−3 V/Var, Lvt1 = 2 mH, ωf1 is varying from 0 to 150 rad/s;
- Case 4:
- m1 = 2.5 × 10−4 rad/(s·W), n1 = 5 × 10−3 V/Var, ωf1 = 30, Lvt1 is varying from 100 μH to 10 mH.
3.4. Design of the Key Parameters
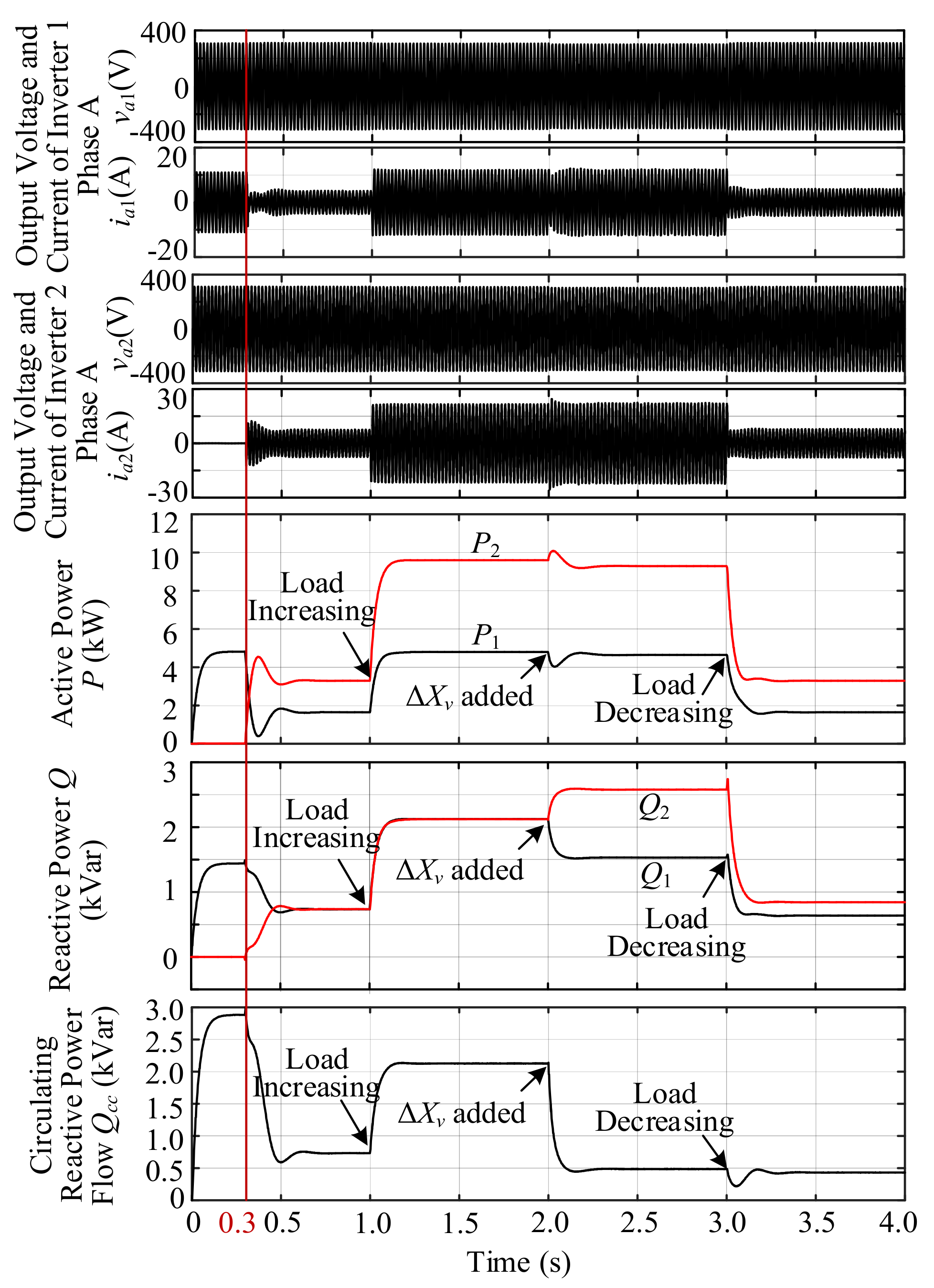
4. Simulation and Experimental Verification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| DGs | distributed generators |
| PCC | the point of common coupling |
| LPF | low-pass filter |
| PLL | phase-locked loop |
| Voi, V*o, Vg | output voltage, nominal output voltage, voltage at PCC |
| δi, θi | power angle, impedance angle |
| Pi, Qi, Qcc | output active power, output reactive power, circulating reactive power flow |
| ωi, ω*, ωfi | system frequency, nominal frequency, corner frequency of the LPF |
| mi, ni | droop coefficients of active and reactive power |
| ki | capacity ratio of each inverter |
| Xvi, XLi | initially added constant virtual output inductance, line inductance |
| Xi, ΔXvi | equivalent output inductance, adaptive virtual inductance |
| Xset, Qset | pre-set inductance and reactive power for the reference DG inverter |
| kv | adaptive coefficient |
| Vvα, Vvβ | the α and β components of the voltage across virtual inductance |
| iα, iβ | the α and β components of output current |
| QN | the rated power of the whole system |
| Xvtimin, Xvtimax | the minimum and maximum total virtual inductance |
| a | constant within (5)–(10) |
References
- Zhong, Q.C. Power-electronics-enabled autonomous power systems: Architecture and technical routes. IEEE Trans. Ind. Electron. 2017, 64, 5907–5918. [Google Scholar] [CrossRef]
- Xu, Q.; Hu, X.; Wang, P.; Xiao, J.; Tu, P.; Wen, C.; Lee, M.Y. A decentralized dynamic power sharing strategy for hybrid energy storage system in autonomous DC microgrid. IEEE Trans. Ind. Electron. 2017, 64, 5930–5941. [Google Scholar] [CrossRef]
- Bacha, S.; Picault, D.; Burger, B.; Otadui, I.E.; Martins, J. Photovoltaics in microgrids: An overview of grid integration and energy management aspects. IEEE Ind. Electron. Mag. 2015, 9, 33–46. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Rahman, M.S.U.; Sunni, F.M.A.L. Review of microgrid architectures—A system of systems perspective. IET Renew. Power Gen. 2015, 9, 1064–1078. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Joint investment and operation of microgrid. IEEE Trans. Smart Grid 2017, 8, 833–845. [Google Scholar] [CrossRef]
- Xie, H.; Zheng, S.; Ni, M. Microgrid development in China: A method for renewable energy and energy storage capacity configuration in a megawatt-level isolated microgrid. IEEE Electrif. Mag. 2017, 5, 28–35. [Google Scholar] [CrossRef]
- Smith, M.; Ton, D. Key connections: The U.S. Department of Energy’s microgrid initiative. IEEE Power Energy Mag. 2013, 11, 22–27. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; Valeri, S.; de Santis, M. Sensitivity-Based Model of Low Voltage Distribution Systems with Distributed Energy Resources. Energies 2016, 9, 801. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Zeng, Y. Universal droop control of inverters with different types of output impedance. IEEE Access 2016, 4, 702–712. [Google Scholar] [CrossRef]
- Sun, Y.; Hou, X.; Yang, J.; Han, H.; Su, M.; Guerrero, J.M. New perspectives on droop control in AC microgrids. IEEE. Trans. Ind. Electron. 2017, 64, 5741–5745. [Google Scholar] [CrossRef]
- Augustine, S.; Lakshminarasamma, N.; Mishra, M.K. Control of photovoltaic-based low-voltage dc microgrid system for power sharing with modified droop algorithm. IET Power Electron. 2016, 9, 1132–1143. [Google Scholar] [CrossRef]
- Marwali, M.; Jung, J.W.; Keyhani, A. Control of distributed generation systems-Part II: Load sharing control. IEEE Trans. Power Electron. 2004, 19, 1551–1561. [Google Scholar] [CrossRef]
- Li, Y.W.; Kao, C.N. An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid. IEEE Trans. Power Electron. 2009, 24, 2977–2988. [Google Scholar]
- Zhong, Q.C. Robust droop controller for accurate proportional load sharing among inverters operated in parallel. IEEE Trans. Ind. Electron. 2013, 60, 1281–1290. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Blaabjerg, F. An Accurate Autonomous Islanding Microgrid Reactive Power, Imbalance Power and Harmonic Power Sharing Scheme. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 1337–1343. [Google Scholar]
- Mahmood, H.; Michaelson, D.; Jiang, J. Accurate reactive power sharing in an islanded microgrid using adaptive virtual impedances. IEEE Trans. Power Electron. 2015, 30, 1605–1617. [Google Scholar] [CrossRef]
- Fan, Y.; Hu, G.; Egerstedt, M. Distributed reactive power sharing control for microgrids with event-triggered communication. IEEE Trans. Control Syst. Technol. 2017, 25, 118–128. [Google Scholar] [CrossRef]
- Lee, C.T.; Chu, C.C.; Cheng, P.T. A new droop control method for autonomous operation of distributed energy resource interface converters. IEEE Trans. Power Electron. 2013, 28, 1980–1993. [Google Scholar] [CrossRef]
- Gu, H.; Wang, D.; Shen, H.; Zhao, W.; Guo, X. New power sharing control for inverter-dominated microgrid based on impedance match concept. Sci. World J. 2013, 2013, 816525. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Blaabjerg, F.; Chen, Z. An Improved Design of Virtual Output Impedance Loop for Droop-Controlled Parallel Three-Phase Voltage Source Inverters. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 2466–2473. [Google Scholar]
- Guerrero, J.M.; de Vicuña, L.G.; Matas, J.; Castilla, M.; Miret, J. Output impedance design of parallel-connected UPS inverters with wireless load-sharing control. IEEE Trans. Ind. Electron. 2005, 52, 1126–1135. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; Valeri, S.; de Santis, M. Linear method for steady-state analysis of radial distribution systems. Int. J. Electr. Power Energy Syst. 2018, 99, 744–755. [Google Scholar] [CrossRef]
- Guerrero, J.M.; de Vicuña, L.G.; Matas, J.; Castilla, M.; Miret, J. A Wireless Controller to Enhance Dynamic Performance of Parallel Inverters in Distributed Generation Systems. IEEE Trans. Power Electron. 2004, 19, 1205–1213. [Google Scholar] [CrossRef]
- Tran, T.V.; Chun, T.W.; Lee, H.H.; Kin, H.G.; Nho, E.C. PLL-based seamless transfer control between grid-connected and islanding modes in grid-connected inverters. IEEE Trans. Power Electron. 2014, 29, 5218–5228. [Google Scholar] [CrossRef]



| System Parameter | Inverter 1 | Inverter 2 |
|---|---|---|
| DC link voltage | 720 V DC | 720 V DC |
| Nominal AC bus voltage | 380 V | 380 V |
| Nominal frequency | 50 Hz | 50 Hz |
| Nominal output power | 5 kW, 1.5 kVar | 10 kW, 3 kVar |
| Filter inductance | 1 mH | 1.5 mH |
| Filter capacitance | 30 μF | 50 μF |
| Line impedance | 0.22 Ω, 100 μH | 0.235 Ω, 110 μH |
| Initial constant virtual inductance | 2.1 mH | 2.3 mH |
| P-ω droop coefficient | 2.5 × 10−4 rad/(s·W) | 1.25 × 10−4 rad/s·W |
| Q-V droop coefficient | 2 × 10−3 V/Var | 1 × 10−3 V/Var |
| Voltage regulator | kpvd1 = 0.1, kivd1 = 50 kpvq1 = 0.1, kivq1 = 50 | kpvd2 = 0.15, kivd2 = 50 kpvq2 = 0.15, kivq2 = 50 |
| Current regulator | kpid1 = 10, kiid1 = 1000 kpiq1 = 10, kiiq1 = 1000 | kpid2 = 10, kiid2 = 1500 kpiq2 = 10, kiiq2 = 1500 |
| Corner frequency of the LPF ωf | 30 rad/s | 30 rad/s |
| Set value of the adaptive virtual inductance Xset | 2 mH | 2 mH |
| Coefficient kv | 4 × 10−6 | 4 × 10−6 |
| Set value of the reactive power Qset | 1.5 kVar | 1.5 kVar |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Hou, S.; Li, X. Decentralized Circulating Currents Suppression for Paralleled Inverters in Microgrids Using Adaptive Virtual Inductances. Energies 2018, 11, 1725. https://doi.org/10.3390/en11071725
Chen J, Hou S, Li X. Decentralized Circulating Currents Suppression for Paralleled Inverters in Microgrids Using Adaptive Virtual Inductances. Energies. 2018; 11(7):1725. https://doi.org/10.3390/en11071725
Chicago/Turabian StyleChen, Jiawei, Shuaicheng Hou, and Xiang Li. 2018. "Decentralized Circulating Currents Suppression for Paralleled Inverters in Microgrids Using Adaptive Virtual Inductances" Energies 11, no. 7: 1725. https://doi.org/10.3390/en11071725
APA StyleChen, J., Hou, S., & Li, X. (2018). Decentralized Circulating Currents Suppression for Paralleled Inverters in Microgrids Using Adaptive Virtual Inductances. Energies, 11(7), 1725. https://doi.org/10.3390/en11071725





