Heat and Mass Transfer Behavior Prediction and Thermal Performance Analysis of Earth-to-Air Heat Exchanger by Finite Volume Method

Abstract

A comprehensive numerical study on coupled heat and mass transfer in an earth-to-air heat exchanger (EAHE) is conducted by self-complied program based on the finite volume method. The soil thermal and moisture coupled characteristics in the vicinity of the pipe and the thermal performance of the EAHE are evaluated by a two-dimensional simulation model. The model of the EAHE is verified by the experimental data, which achieved a good agreement with each other. The numerical results show that there is an obvious moisture peak in the radial direction, and the peak position radially moves away from the wall of the pipe over time. It is also found that the thermal performance of the heat and mass transfer model in soil is better than the pure heat conduction model.

1. Introduction

Nowadays, the energy consumption is growing rapidly. Furthermore, in last decades, a large amount of energy consumption comes from non-renewable fossil fuels such as coal, oil, and natural gas. With the increasingly global energy crisis and the deterioration of the environment, developing and exploiting new green energy have been received worldwide attention. Obviously, solar energy is exactly the ideal type which is inexhaustible and pollution-free. A large amount of solar radiation is stored at superficial layers of the ground and it decreases rapidly with the increasing depth of the soil. As a result, the soil temperature under 4 m is nearly constant [1]. Utilizing the geothermal as a heat source and sink, the EAHE can heat and cool the ambient air for reducing the energy consumption of buildings. The use of EAHE for cooling and heating agricultural greenhouses and buildings has gained much achievement in the past several years [2,3].

A widely used physical model for studying coupled heat and mass transfer in a porous medium was presented by Philip [4] and De Vries [5,6]. In a porous material, the differential equations for the coupled heat and mass transfer process have been based on temperature and moisture concentration gradients as driving potentials, which means that the moisture movement in the porous material is driven by the temperature gradient. Simultaneously, the moisture will trend to redistribute itself under the created moisture gradient. The total moisture flux was divided into two components: liquid water and water vapor. An alternative model was given by Eckert et al. [7,8] in 1979. Jahangir [9] developed the new coupled differential equations for heat, mass and air transfer process in porous medium based on the above alternative model, which could result in a better accuracy and significantly reduce the simulation time by concentrating the computational effort in the vicinity of the soil-pipe. Shah et al. [10] found that liquid moisture moved from the cold end to the warm end while water vapor migrated in the opposite direction. They concluded that the primary cause of liquid water migration was the moisture concentration gradient, while the water vapor migration was predominantly due to the difference in the soil temperature.

Through the experiment in summer, Balghouthi et al. [11] studied the thermal and moisture characteristics of dry and wet soil which are heated by buried capillary plaits under three different operational conditions: heating at 70 $℃$, heating at 40 $℃$ and without heating. It was concluded that the surface temperature amplitude in moist soil was superior to dry soil. In order to determine the thermal and mass diffusion coefficients for two different types of soils, Shah et al. [10] conducted a 1-D steady state soil column experiment. They found that the ratio of the thermal diffusion coefficient to the moisture diffusion coefficient monotonically increases with increasing the moisture concentration, and then gradually decrease after reaching a peak value. To measure the primary and cross-coupling transport coefficients, Jury [12] conducted a two-column experiment through sand for the coupled and simultaneous heat and moisture transfer process.

In order to determine the optimal design of a closed loop EAHE for greenhouse heating, an exergo-economics analysis was conducted by Ozgener et al. [13,14,15,16,17]. Thanu et al. [18] conducted an experimental study of an EAHE system in single pass mode at Guomohar farmhouse. They established the correlations between outlet air and inlet air temperature, indicating the high effectiveness of the EAHE system in summer. With the application of an artificial neural network concept Kumar et al. [19] proposed two models, deterministic and intelligent, that can help the designers evaluate the heating and cooling potential of an EAHE. Furthermore, they found that the deterministic model with an accuracy of 75.3%, while the intelligent model accuracy was 72.6%. Kumar et al. [20] presented a transient model that can evaluate thermal performance and dynamic performance of building and the energy conservation potential of an EAHE by using MATLAB (R2015b, MathWorks, Natick, MA, USA) and the finite difference method. In [21], the thermal performance of the EAHE was experimentally investigated in Brazil. They found that such a system could achieve about 48% of cooling or heating demands. A transient analytical model of an EAHE connecting to a wind tower was presented by Benhammou et al. [22]. The results showed that the thermal performance of the wind tower coupled to EAHE was superior than the conventional cooling tower. In the article [23], Kaushal et al. utilized a commercial CFD to predict the thermal performance of hybrid EAHE and RSM (response surface methodology) to optimize the process parameters. The results revealed that the thermal performance of hybrid EAHE was better than individual EAHE. To evaluate the thermal performance of EAHE under transient operational conditions, Bansal et al. [24] proposed a new concept of derating factor, which is determined by the EAHE air temperature drops in both transient condition and steady state condition. The results indicated that, in transient state, the thermal performance of EAHE gradually deteriorates under the continuous operation.

To present an investigation of the soil thermal and moisture coupled characteristics in the vicinity of the pipe under warming conditions and the thermal performance of the EAHE in transient condition, a transient bi-dimensional model is established in this paper. In addition, a comparative research is carried out for investigating the influence of different heat transfer models, which focuses on the thermal performance parameters of EAHE as follows: the daily mean efficiency, the difference between suction air temperature and delivery air temperature, the daily cooling potential, and derating factor in transient condition.

2. Physical and Mathematical Modeling

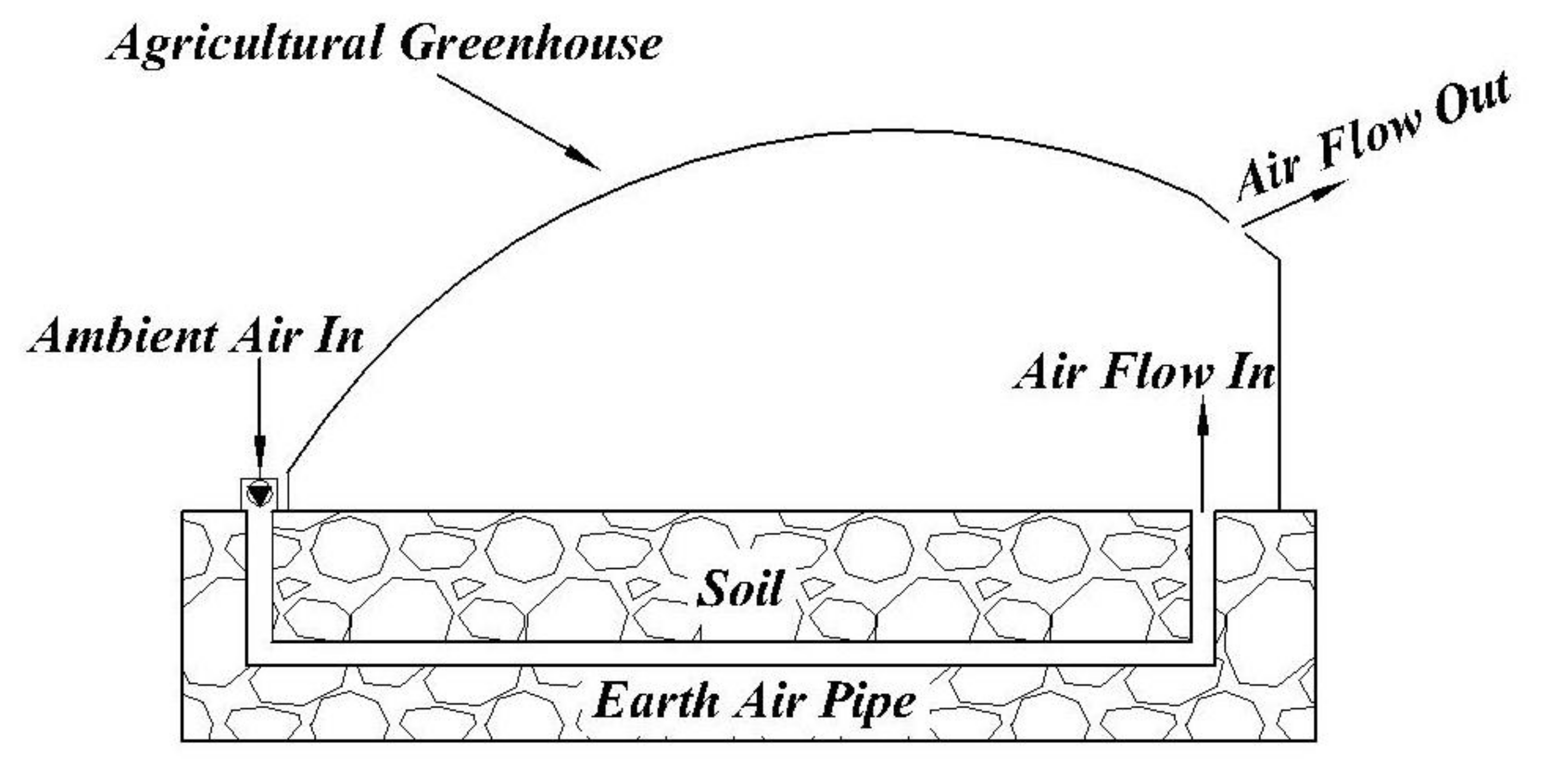
2.1. Description of the System

The major component of the EAHE (Figure 1) is a buried PVC (poly vinyl chloride) pipe in the soil. The length and the interior diameter of the buried pipe is L and D, respectively. As shown in the figure, during the operation of the system, the outlet of the pipe is connected to an agricultural greenhouse while the inlet is combined with ambient air.

At an adequate depth, the soil temperature is comparatively constant during the whole year due to the delayed thermal response of soil, and it is higher than the ambient air temperature in winter but lower in summer. Accordingly, passing through the buried pipes, the ambient air will be heated in winter and cooled in summer. After being injected into the agricultural greenhouse and mixed with the indoor air, the ambient air can make the air temperature and humidity of the agricultural greenhouse meet the basic needs of the crop growth.

2.2. Description of the System

A widely used formulation for heat and mass transfer in porous material is written as follow, in which the key assumptions are adopted [25]:

• The total system pressure is approximated by air pressure
• The vapor-liquid interface is a function of temperature only
• The total pressure is constant during the transfer process
• Heat transfer by radiation is negligible
• The air is incompressible and the property of air is constant

The conservation equations for energy and mass within the soil in 2D cylindrical coordinates can be stated as follows:

$$C\frac{\partial T}{\partial t}=div\left[\left(\lambda +l_g{\rho }_w{D}_{T,vap}\right)gradT\right]+l_g{\rho }_w{D}_{\theta ,vap}grad\theta +{\rho }_w{c}_{p,w}\left[\left(D_{\theta ,w}grad\theta +D_{T,w}gradT\right)gradT\right]+{\rho }_w{c}_{p,vap}\left[\left(D_{\theta ,vap}grad\theta +D_{T,vap}gradT\right)gradT\right]$$

(1)

$$\frac{\partial \theta }{\partial t}=div\left(D_{\theta }grad\theta \right)+div\left(D_{T}gradT\right)$$

(2)

where the coefficient of the above equations are summarized in

Table 1. Physical and thermal properties of medium for simulation.

Materials	Density $\mathit{\rho }$ kg/m3	Volumetric Heat Capacity C J/(m3 K)	Thermal Conductivity $\mathit{\lambda }$ W/(m K)
air	1.165	1171.99	0.0267
soil	${\rho }_b+1000\theta$	$850{\rho }_b+4.189E+06\theta$	$0.234+0.393+1.534{\theta }^{0.5}$
	Hydraulic conductivity hc m/s	Potential $\varphi$ m	Porosity $\xi$ m3/m3
air	-	-	-
soil	$h_{cs}{\mathsf{\Theta }}^{\frac{1}{2}}{[1-{(1-{\mathsf{\Theta }}^{\frac{1}{m}})}^m]}^2$	$-\frac{{({\mathsf{\Theta }}^{-\frac{1}{m}}-1)}^{1-m}}{\alpha }$	0.37
	Thermal liquid diffusivity DT,w m2/(s K)	Thermal vapor Diffusivity DT,vap m2/(s K)	Thermal moisture diffusivity DT m2/(s K)
air	-	-	-
soil	$h_c\gamma \varphi$	$\frac{D_{atm}\nu a\delta \phi \beta }{{\rho }_w}$	$h_c\gamma \varphi +\frac{D_{atm}\nu a\delta \phi \beta }{{\rho }_w}$
	Isohermal liquid diffusivity $D_{\theta ,w}$ m2/s	Isohermal vapor diffusivity $D_{\theta ,vap}$ m2/s	Isohermal moisture diffusivity $D_{\theta }$ m2/s
air	-	-	-
soil	$h_c\frac{\partial \varphi }{\partial \theta }$	$\frac{D_{atm}\nu a\delta g{\rho }_{vap}}{{\rho }_{w}RT}\frac{\partial \varphi }{\partial \theta }$	$\frac{D_{atm}\nu a\delta g{\rho }_{vap}}{{\rho }_{w}RT}\frac{\partial \varphi }{\partial \theta }+h_c\frac{\partial \varphi }{\partial \theta }$

.

The governing transport equations for air in the pipe in 2D cylindrical coordinates are given below:

Continuity equation:

$$\frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho u\right)}{\partial x}+\frac{1}{r}\frac{\partial \left(\rho rv\right)}{\partial r}=0$$

(3)

Momentum equations:

$$\frac{\partial (\rho u)}{\partial t}+div\left(\rho \overrightarrow{u}u\right)=-\frac{\partial p}{\partial x}+div\left[\left(\eta +{\eta }_t\right)gradu\right]+\frac{\partial }{\partial x}\left[\left(\eta +{\eta }_t\right)\frac{\partial u}{\partial x}\right]+\frac{1}{r}\frac{\partial }{\partial r}\left[r\left(\eta +{\eta }_t\right)\frac{\partial v}{\partial x}\right]$$

(4)

$$\frac{\partial (\rho v)}{\partial t}+div\left(\rho \overrightarrow{u}v\right)=-\frac{\partial p}{\partial r}+div\left[\left(\eta +{\eta }_t\right)gradv\right]+\frac{\partial }{\partial x}\left[\left(\eta +{\eta }_t\right)\frac{\partial u}{\partial r}\right]+\frac{1}{r}\frac{\partial }{\partial r}\left[r\left(\eta +{\eta }_t\right)\frac{\partial v}{\partial r}\right]-\frac{2\left(\eta +{\eta }_t\right)}{r^2}v$$

(5)

Energy equation:

$$\frac{\partial \left({\rho }^{*}T\right)}{\partial t}+div({\rho }^{*}\overrightarrow{u}T)=div\left[\left(\lambda +c_p·{\eta }_t/{\sigma }_t\right)gradT\right]$$

(6)

Transport equations for the k-$\epsilon$ model:

$$\frac{\partial \left(\rho k\right)}{\partial t}+div(\rho \overrightarrow{u}k)=div\left[\left(\eta +{\eta }_t/{\sigma }_k\right)gradk\right]+\rho G_k-\rho \epsilon$$

(7)

$$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+div(\rho \overrightarrow{u}\epsilon )=div\left[\left(\eta +{\eta }_t/{\sigma }_{\epsilon }\right)grad\epsilon \right]+\frac{\epsilon }{k}\left(c_1\rho G_k-c_2\rho \epsilon \right)$$

(8)

where $G_k=\frac{{\eta }_t}{\rho }\left\{2\left[{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial r}\right)}^2+{\left(\frac{v}{r}\right)}^2\right]+{\left(\frac{\partial u}{\partial r}+\frac{\partial v}{\partial x}\right)}^2\right\}$, c1 = 1.4, c2 = 1.92, ${\sigma }_k$ = 1.0, ${\sigma }_{\epsilon }$ = 1.3, ${\sigma }_t$ = 0.9.

The boundary conditions of the computational domain are:

$$\begin{array}{ll}x=0,0\le r\le R_{pi}：& \\ & u(r,0,t)=u_0,v(r,0,t)=\theta (r,0,t)=0,T(r,0,t)=T_{amb},k(r,0,t)=(0.5\%~1.5\%)\cdot u_0{}^2\\ & \epsilon (r,0,t)=\frac{c_{\mu }\rho k^2}{{\eta }_t},\mathrm{where},\frac{\rho \eta D}{{\eta }_t}=100~1000，c_{\mu }=0.09\\ x=0,R_{pi}\text{<}r\le R_L：& \\ & \theta (r,0,t)=\theta (r),T(r,0,t)=T_s(r),u(r,0,t)=v(r,0,t)=k(r,0,t)=\epsilon (r,0,t)=0.\\ 0\le x\le L,r=0：& \\ & v(0,x,t)=\theta (0,x,t)=0,\frac{\partial u(0,x,t)}{\partial r}=\frac{\partial T(0,x,t)}{\partial r}=\frac{\partial k(0,x,t)}{\partial r}=\frac{\partial \epsilon (0,x,t)}{\partial r}=0.\\ 0\le x\le L,r=R_L：& \\ & u(R_L,x,t)=v(R_L,x,t)=k(R_L,x,t)=\epsilon (R_L,x,t)=0,\\ & \theta (R_L,x,t)=\theta \left(R_L\right),T(R_L,x,t)=T_s(R_L).\\ x=L,R_{pi}<r\le R_l：& \\ & \theta (r,L,t)=\theta \left(r\right),T(r,L,t)=T_s(r),u(r,L,t)=v(r,L,t)=k(r,L,t)=\epsilon (r,L,t)=0\\ x=L,0\le r\le R_{pi}：& \\ & \frac{\partial v(0,x,t)}{\partial r}=\frac{\partial T(0,x,t)}{\partial r}=\frac{\partial k(0,x,t)}{\partial r}=\frac{\partial \epsilon (0,x,t)}{\partial r}=0,\theta (0,x,t)=0.\end{array}$$

(9)

Furthermore, the outlet air velocity in the axial direction must satisfy total mass conservation laws.

The initial conditions of the computational domain are:

$$\begin{array}{ll}0<x<L,0\text{<}r<R_{pi}：& \\ & u(r,x,0)=u_0,v(r,x,0)=\theta (r,x,0)=0,k(r,x,0)=(0.5\%~1.5\%)\cdot u_0{}^2\\ & T(r,x,0)=T_{amb},\epsilon (r,x,0)=\frac{c_{\mu }\rho k^2}{{\eta }_t},\mathrm{where},\frac{\rho \eta D}{{\eta }_t}=100~1000\\ 0<x<L,R_{pi}\le r<R_L：& \\ & \theta (r,x,0)=\theta \left(r\right),\mathrm{T}(r,x,0)={\mathrm{T}}_s\left(r\right),u(r,x,0)=v(r,x,0)=k(r,x,0)=\epsilon (r,x,0)=0\end{array}$$

(10)

3. Numerical Solution

3.1. General Remarks

The aforementioned conservation equations are discretized by the finite volume method on a staggered grid system [26,27]. The QUICK (Quadratic Upstream Interpolation for Convection Kinetics) scheme and central difference scheme are used to discretize the convection term and the diffusion term, respectively, and an efficient segregated algorithm, SIMPLER (Semi-Implicit Method for Pressure Linked Equations Revised), is applied to the pressure-velocity solution. The algebraic equations for the whole computational domain can be solved by the TDMA (tridiagonal matrix algorithm) +ADI (alternating direction implicit) method. The linearization method is used to deal with the source terms of the governing equations above. The full-field computation method is adopted to solve the fluid-solid coupling heat transfer process. Accordingly, the dependent variables of soil and air region are solved simultaneously. In order to guarantee the continuity of the heat flux at the soil-pipe interface, $\rho c_p$ is regarded as a general density in the energy equation [28]. In the soil region, by adopting a very large value of physical viscosity in the momentum equations, for example 10³⁰, the zero velocity of soil area can be gained. To ensure the convergence of iteration, under-relaxation of the dependent variables and pressure can be incorporated into the solution process of the algebraic equations. According to the upwards treating processes, a 2-D program has been developed to solve the model.

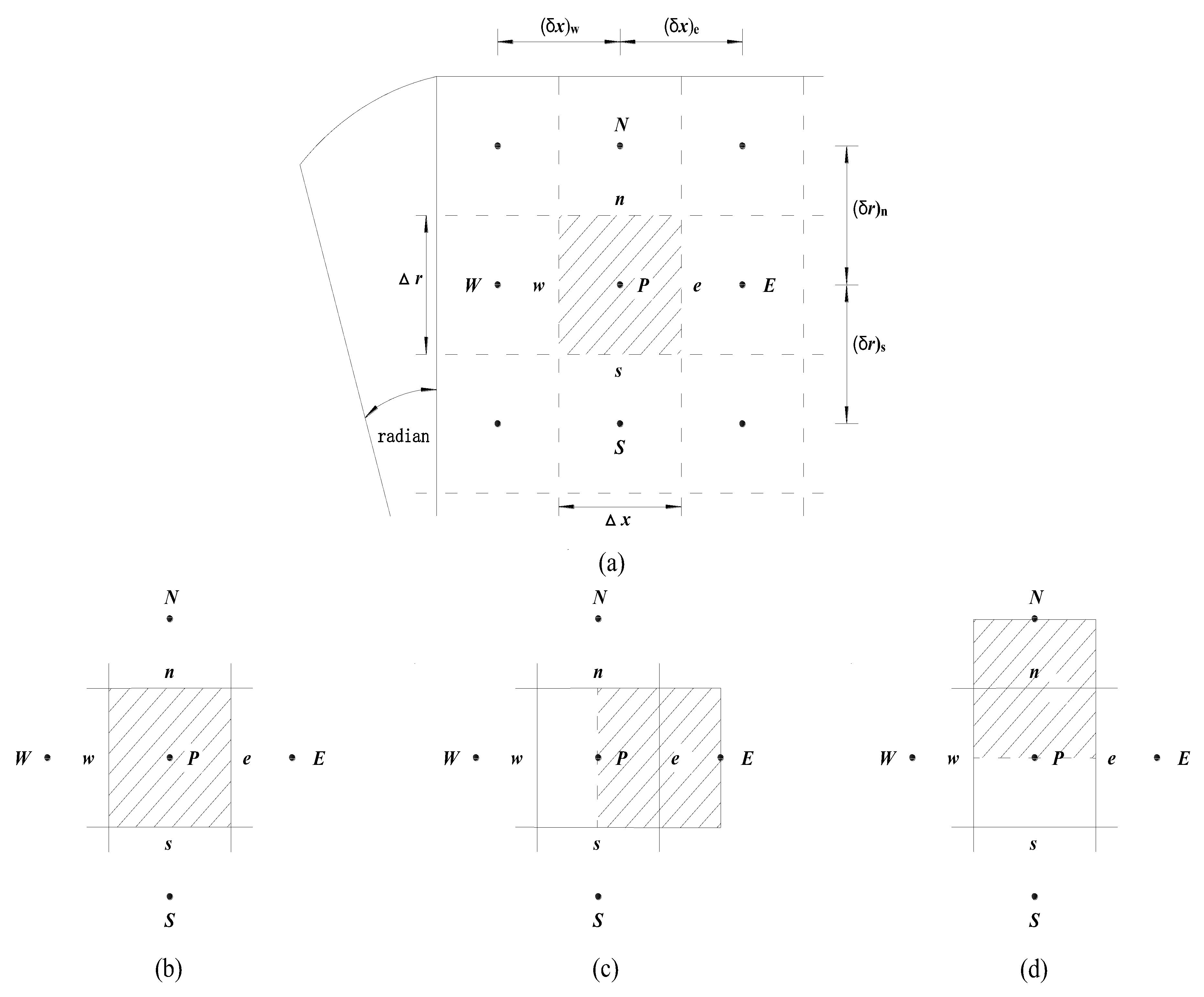
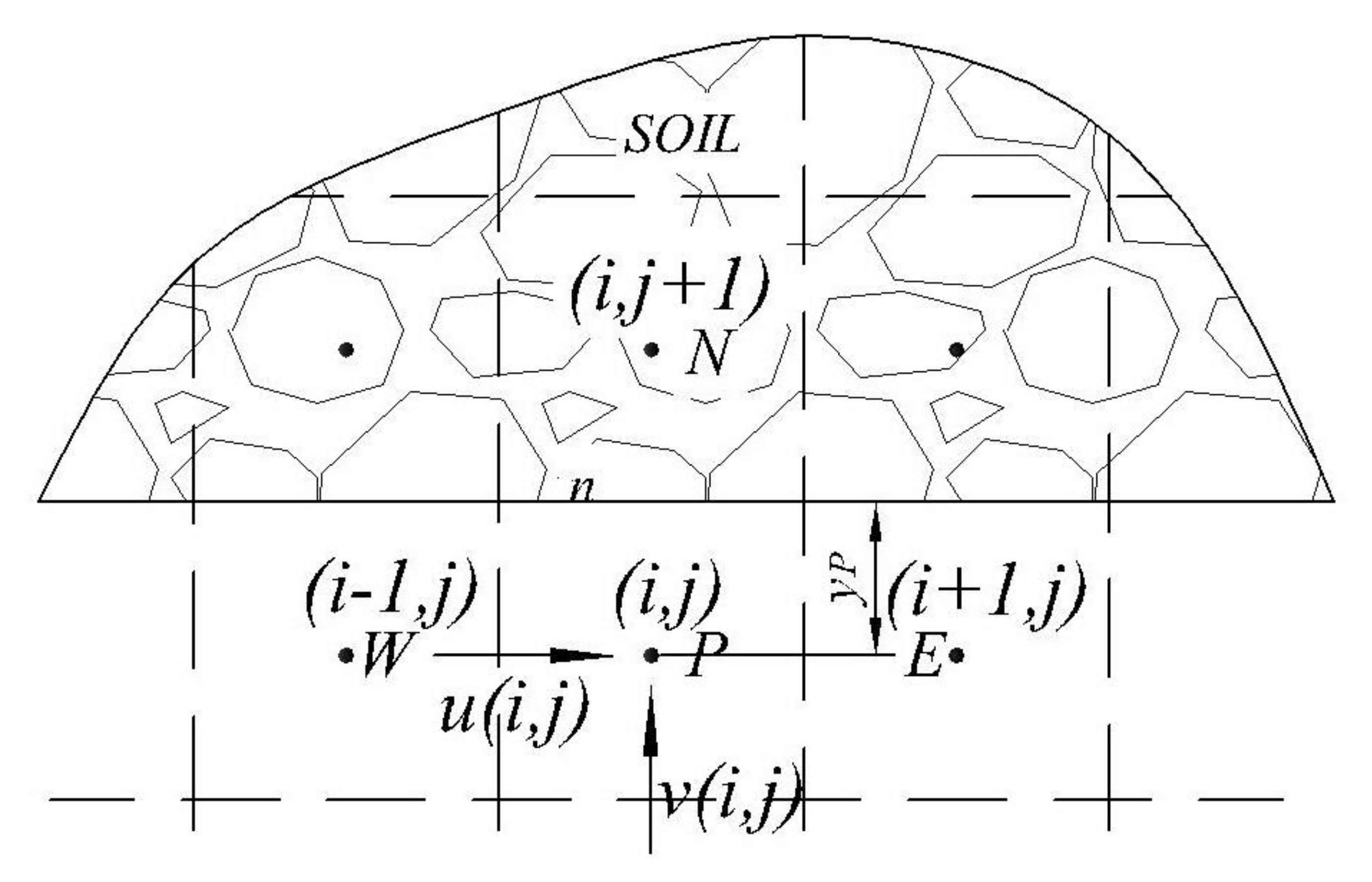
3.2. The Discretization of Governing Equation

A general expression for the afore mentioned governing equations can be written as:

$$\frac{\partial \left(\rho \Phi \right)}{\partial t}=div(\rho \overrightarrow{u}\Phi )=div\left({\Gamma }_{\Phi }grad\Phi \right)+S_{\Phi }$$

(11)

where ${\Gamma }_{\Phi }$ is the nominal diffusion coefficient and $S_{\Phi }$ is the source for the general variable $\Phi$. Equation (11) is discretized by the finite volume method on a staggered grid system as shown in Figure 2.

To enhance the convergence rate, the source term $S_{\Phi }$ is linearized as follows:

$$S_{\Phi }=S_C+S_P{\Phi }_P$$

(12)

where $S_P\le 0$, which guarantees the requirement of diagonal dominant.

For two-dimensional problems, after integration over the control volume, the discretized equation can be obtained as follows:

$$\begin{gathered} F_e{\Phi }_e-F_w{\Phi }_w+F_n{\Phi }_n-F_s{\Phi }_s=S_{\Phi }\mathsf{\Delta }V+D_e\left({\Phi }_E-{\Phi }_P\right)-D_w\left({\Phi }_W-{\Phi }_P\right) \\ +D_n\left({\Phi }_N-{\Phi }_P\right)-D_s\left({\Phi }_S-{\Phi }_P\right) \end{gathered}$$

(13)

The variables ${\Phi }_{n,e,w,s}$ at the control interfaces can be determined using an interpolation or extrapolation involving the values of the neighboring grid points. $F_{n,e,w,s}$ are the flow rate at the interfaces. $D_{n,e,w,s}$ are diffusive conductance. $\Delta V$ is the volume of the control volume.

Using Patankar’s notation [26], Equation (13) can be written in the form:

$$\begin{gathered} a_P{\Phi }_P=a_E{\Phi }_E+a_W{\Phi }_W+a_N{\Phi }_N+a_S{\Phi }_S+b \\ {a}_P=a_E+a_W+a_N+a_S+a_P^0-S_P\mathsf{\Delta }V a_P^0=\frac{{\rho }_P\mathsf{\Delta }V}{\mathsf{\Delta }t} b=S_C\mathsf{\Delta }V \end{gathered}$$

(14)

$$\begin{gathered} a_E=D_e+\left[\left|-F_e,0\right|\right] a_W=D_w+\left[\left|-F_w,0\right|\right] \\ {a}_N=D_n+\left[\left|-F_n,0\right|\right] a_S=D_s+\left[\left|-F_s,0\right|\right] \end{gathered}$$

(15)

where $a_P$, $a_P^0$ and $a_{N,W,E,S}$ are coefficients of the discretized equation. b is constant term in the discretized equation.

Underrelaxation of the dependent variable is incorporated into the solution process of the algebraic equations, Equation (14) becomes:

$$\frac{a_P}{\chi }{\Phi }_P=a_E{\Phi }_E+a_W{\Phi }_W+a_N{\Phi }_N+a_S{\Phi }_S+b+\frac{1-\mathsf{\chi }}{\chi }{a}_P{\Phi }_P^0$$

(16)

where $\chi$ is the underrelaxation factor. ${\Phi }_P^0$ is the value of general variable $\Phi$ of the previous time level.

3.3. Treatments of Near Wall Nodes

The correct processing method of the near wall nodes is an important step for the programming calculation. In this paper, the wall function method is applied to establish the fluid-solid interface boundary conditions. As shown in Figure 3, some variables of the first inner node P can be stated as follows:

• The equivalent viscosity conductivity between the first inner node and the wall is, ${\eta }_t(i,j)=\frac{y_P{}^{+}\eta }{ln(E{y}_P{}^{+})/K}$
• The equivalent thermal conductivity between the first node and the wall is, ${\lambda }_t(i,j)=\frac{y_p{}^{+}\eta c_p}{{\sigma }_T[ln(E{y}_P{}^{+})+P]}$
• By adopting large coefficient method, the dissipation rate of the first inner P is taken the given value ${\epsilon }_P(i,j)=\frac{c_{\mu }{}^{\frac{3}{4}}{k}_P{}^{\frac{3}{4}}}{K{y}_P}$
• The first order normal derivatives of velocity normal to wall and the turbulence kinetic energy equal to zero.

where $y_P{}^{+}=\frac{\rho y_P{c}_{\mu }{}^{\frac{1}{4}}{k}_P{}^{\frac{1}{2}}}{\eta },K=0.4~0.42,E=7.4~10,\mathrm{and}P=9.$

3.4. Calculation of Some Thermal Performance Variables

3.4.1. Cooling Potential

The cooling potential of EAHE for a period of time $\tau$ can be calculated by the following equation:

$$\begin{array}{l}{Q}_{cool}=\dot{m}{c}_{p,a}{\displaystyle {\int }_0^{\tau }(T_a{}^{(in)}-T_a{}^{(out)})}dt\end{array}$$

(17)

where $T_a{}^{(in)}=\frac{{\displaystyle {\sum }_{j\in A_{in}}[T_a{}^{(in)}(j)\cdot u_{in}(j)\cdot A_{in}(j)]}}{{\displaystyle {\sum }_{j\in A_{in}}[T_a{}^{(in)}(j)\cdot A_{in}(j)]}}$

$$T_a{}^{(in)}=\frac{{\displaystyle {\sum }_{j\in A_{out}}[T_a{}^{(out)}(j)\cdot u_{out}(j)\cdot A_{out}(j)]}}{{\displaystyle {\sum }_{j\in A_{out}}[T_a{}^{(out)}(j)\cdot A_{out}(j)]}}$$

(18)

$T_a{}^{(in)}(j)$ and $T_a{}^{(out)}(j)$ are the air temperature of each grid point at inlet and outlet surface of the pipe respectively. $u_{in}(j)$ and $u_{out}(j)$ denote the air velocity of each grid point at inlet and outlet surface of the pipe, respectively.

3.4.2. Average Nusselt Number of the Wall

The equivalent average Nusselt number of the wall can be calculated according to the following correlations:

$$N_{u,ave}=\frac{h\cdot {\lambda }_a}{D}$$

(19)

$$\mathrm{where},h=\frac{Q_{cool}}{[\frac{T_a{}^{(in)}+T_a{}^{(out)}}{2}-T_{sw}]\cdot S_{surface}}$$

(20)

The temperature of n-interface in Figure 2 can be calculated by the interpolation from neighboring grid points according to the heat flux equilibrium.

$$T_n=T(in)=\frac{{\lambda }_s(N)ln\frac{R_N}{R_n}}{{\lambda }_s(N)ln\frac{R_N}{R_n}+{\lambda }_a(P)ln\frac{R_n}{R_P}}{T}_N+\frac{{\lambda }_a(P)ln\frac{R_n}{R_P}}{{\lambda }_s(N)ln\frac{R_N}{R_n}+{\lambda }_a(P)ln\frac{R_n}{R_P}}{T}_P$$

(21)

$T_{sw}$ is the average soil temperature at the soil-pipe interface.

$$T_{sw}=\frac{1}{S_{surface}}{\displaystyle {\sum }_{i\in surface}[A(i)\cdot T(i)]}$$

(22)

$S_{surface}$ is the area of the soil-pipe interface. The $R_N$ and $R_P$ are radial distance of N point and P point, respectively.

3.4.3. Mean Efficiency

The mean efficiency of EAHE for a Period $\tau$ is calculated by the following relation,

$${\eta }_{mean}=\frac{{\displaystyle {\int }_0^{\tau }(T_a{}^{(in)}-T_a{}^{(out)})dt}}{{\displaystyle {\int }_0^{\tau }(T_a{}^{(in)}-T_s)dt}}$$

(23)

$T_a^{\left(in\right)}$ and $T_a^{\left(out\right)}$ are the average air temperature at inlet and outlet surface of the pipe respectively. $T_s$ is soil temperature.

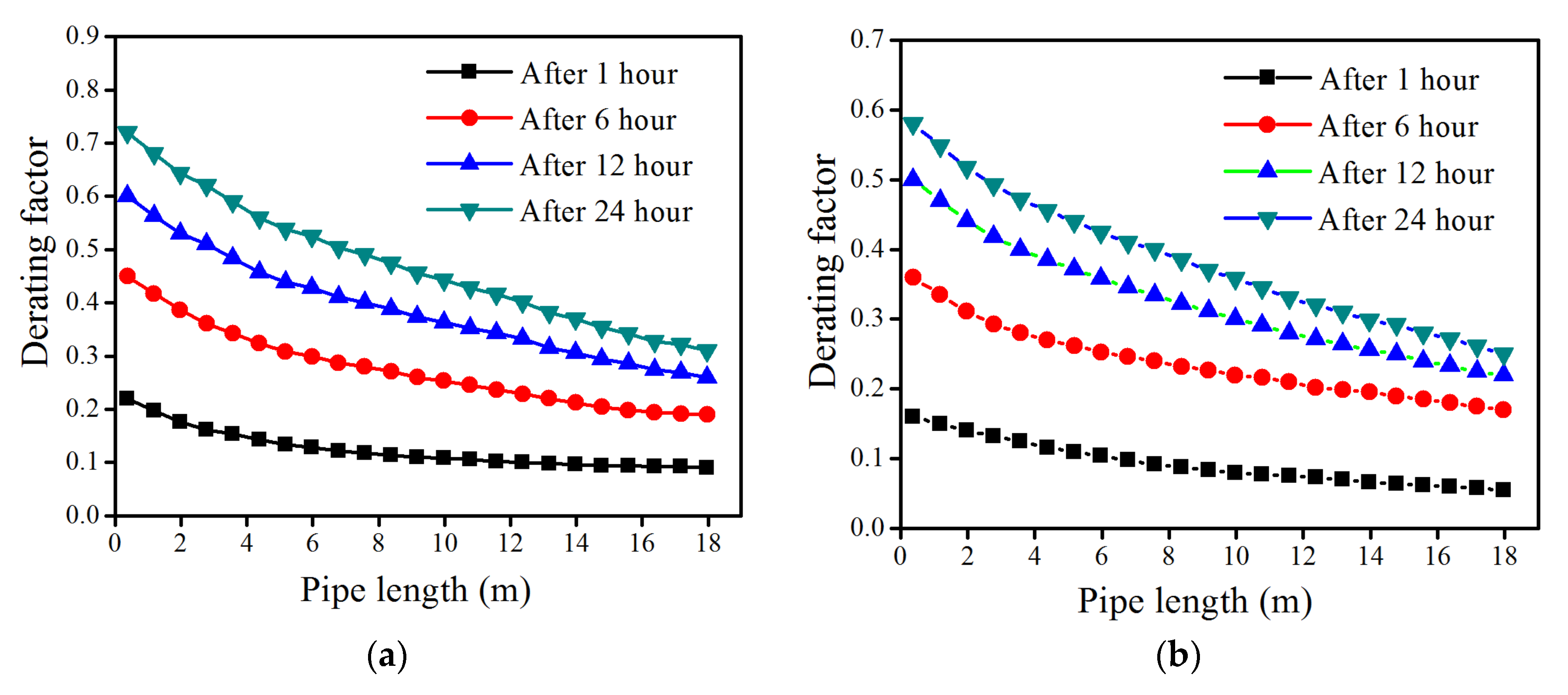
3.4.4. Derating Factor

Temperature drops gained by EAHE in steady state condition and transient condition are used to determine the derating factor which is defined as follows:

$$D{F}_{l,t}=1-\frac{{(T_a{}^{(in)}-T_a{}^{(l)})}_{transient}}{{(T_a{}^{(in)}-T_a{}^{(l)})}_{steady}}$$

(24)

$D{F}_{l,t}$: derating factor at a distance of ‘l’ from EAHE inlet, after time ‘t’. $T_a{}^{(l)}$ is the air temperature at length of ‘l’ m from the pipe inlet.

3.5. Converge Criteria

In our previously numerical simulation about heat and moisture transfer in soil by looking into the process of convergence, it has been verified that when the two convergence criterion as follows are satisfied at the same time, the convergent solution can be well obtained:

$$R_{max}/\dot{m}\le {10}^{-6},\mathrm{and},\left|\left(N_{u,ave}{}^{q+200}-N_{u,ave}{}^q\right)/N_{u,ave}{}^{q+200}\right|\le {10}^{-6}$$

(25)

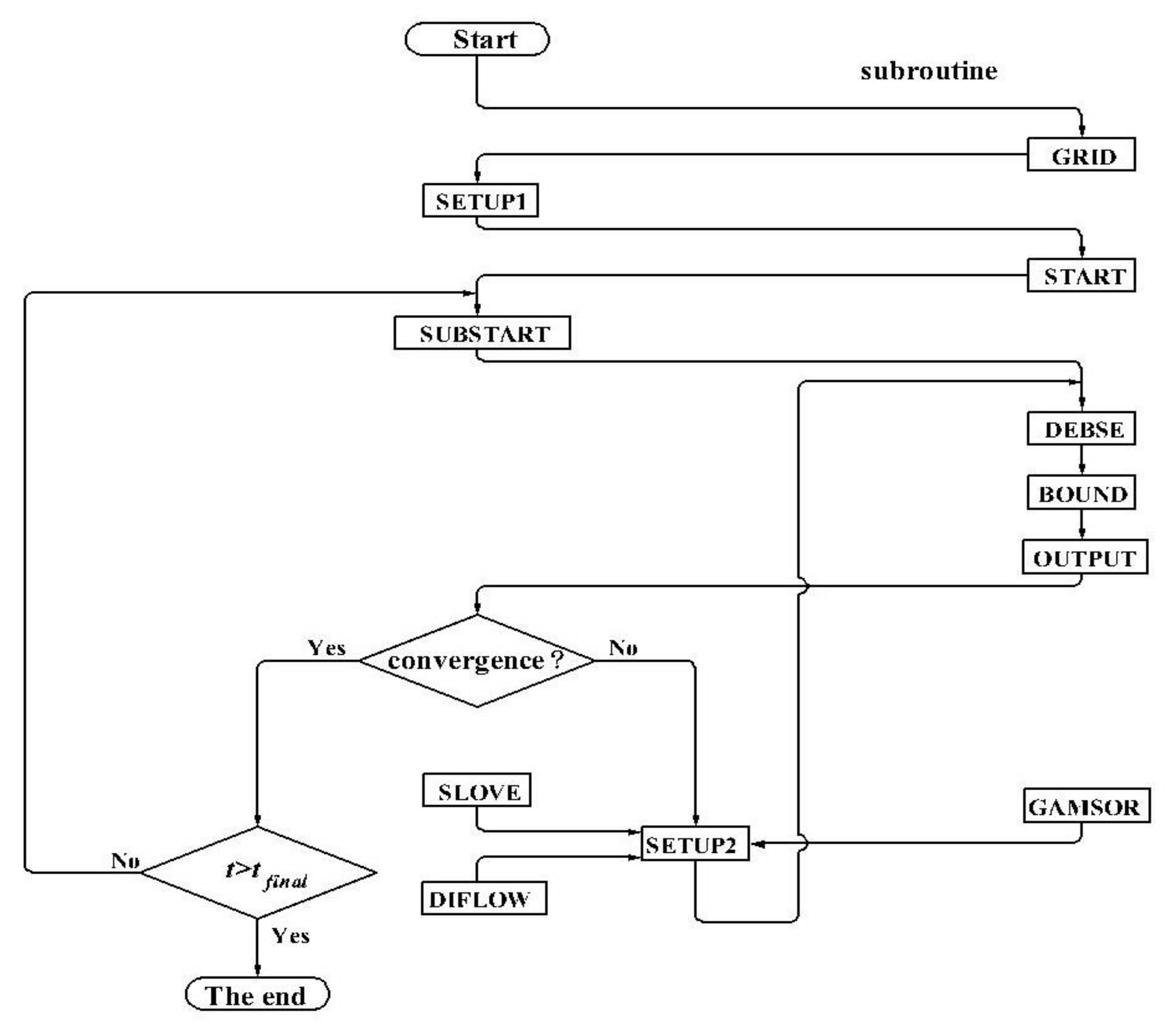
3.6. The Structure of Computation Program

The numerical simulation program of heat and moisture transfer in soil is divided into two parts: main program and user subroutine. The main program determines the flow of the entire numerical simulation and the operation and termination of the program. The calculation conditions and contents are completed by different subroutine modules. The flowchart of the computation program is shown in Figure 4. The functions of each subroutine module in the diagram are as follows:

• SETUP1: Set structure parameters;
• GRID: Divide the computational domain into control volumes;
• START: Set initial conditions;
• SUBSTART: Store the solutions of the previous time level;
• DENSE: Set density field;
• BOUND: Set boundary conditions;
• OUTPUT: Output the solutions of the variables of the previous iteration level and observe its convergence;
• SETUP2: Solve the variables and call subroutine SOLVE, subroutine DIFLOW and subroutine GAMSOR;
• SOLVE: Solve algebraic equations;
• DIFLOW: Solve the coefficients of discrete scheme; and
• GAMSOR: Set source terms of the governing equations and diffusion coefficients.

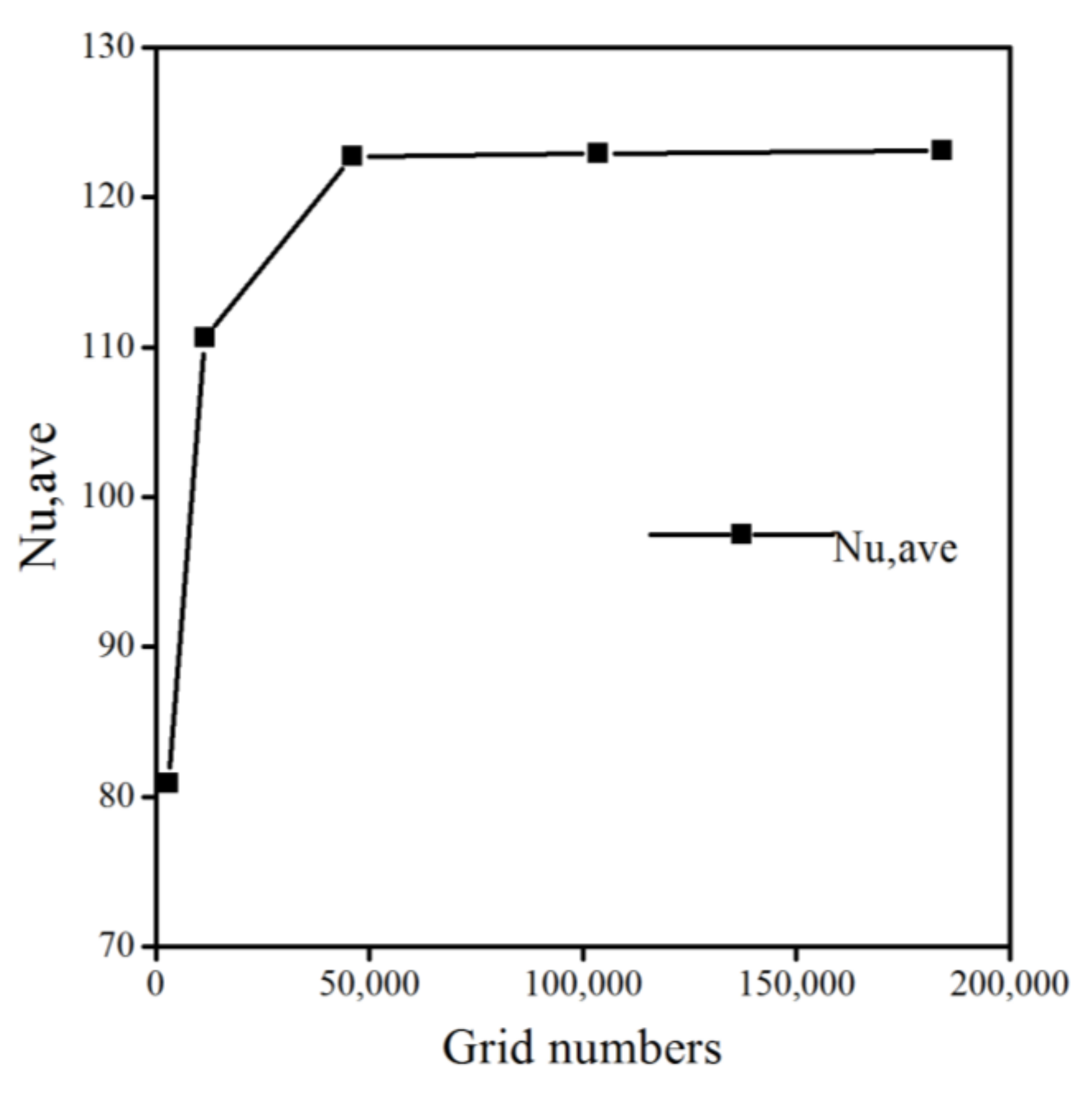
3.7. Grid-Independence Test

In this paper, five sizes of grid were established to determine the accuracy of the average Nusselt number of the wall (32 × 90, 64 × 180, 128 × 360, 192 × 540, and 256 × 720), and the results are shown in Figure 5. The value of the average Nusselt number of the wall changes no more than 2%, when the total grid number increases from 4.6 × 10⁴ to 1.8 × 10⁵, which indicates a great stability of the grid. In order to save computation time and guarantee the accuracy of the simulation, the optimum grid size, 128 × 360, is adopted in the following simulation.

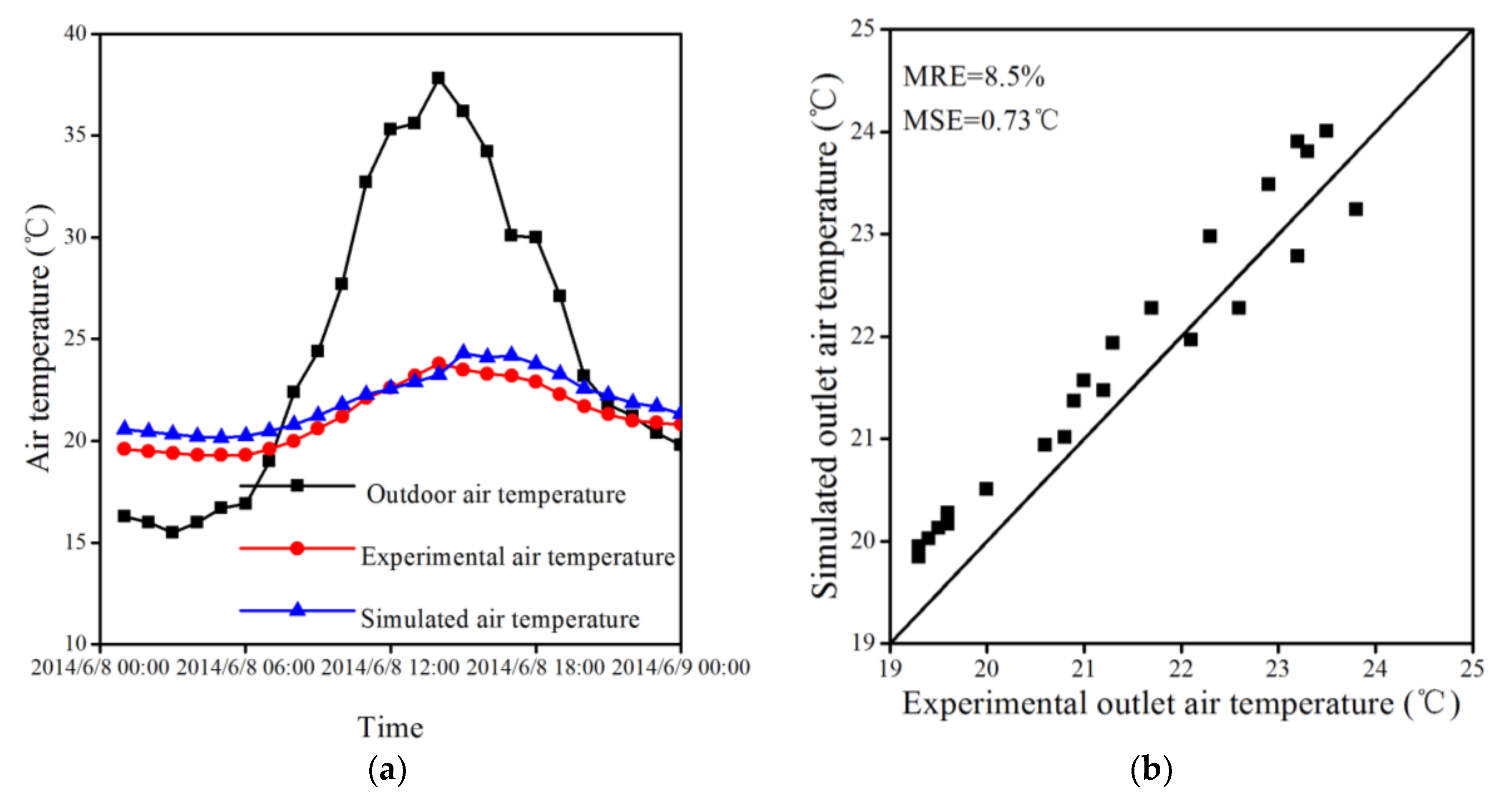
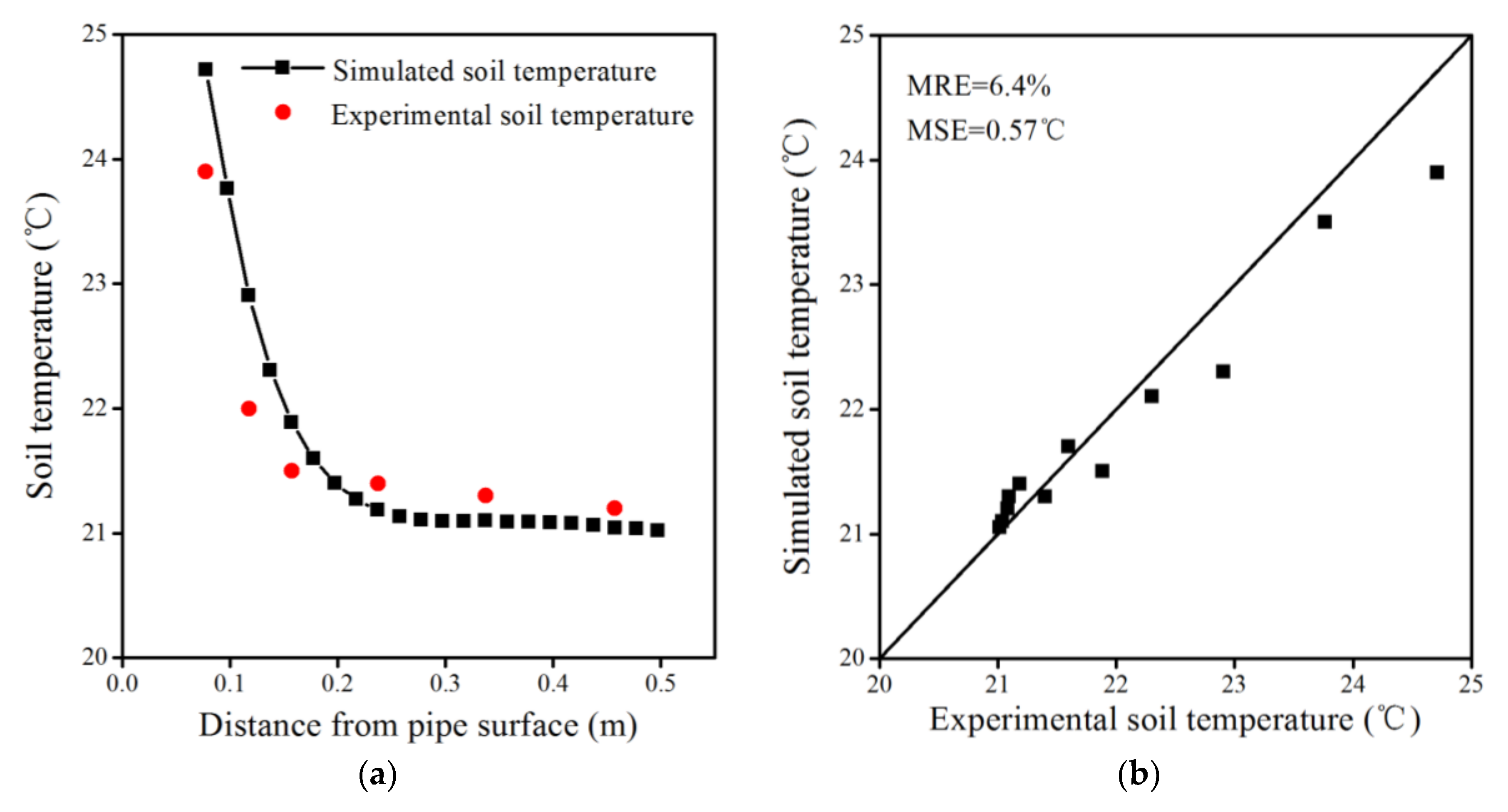
3.8. Self-Complied Program Examination

The accuracy and feasibility of self-complied program was verified through experimental data. A long-term experimental test was carried out by Liu [29] from 25 April 2014 to 27 August 2014 using the existing facility which contains an 18 m heat exchanger pipe, the diameter of which is 110 mm, and the pipe is buried under the ground of the agricultural greenhouse for the depth of 1 m. The inlet velocity of the air was 4.5 m/s. The temperature of soil at different depth were measured. In addition, the schematic diagram of this experimental platform is shown in Figure 6.

In order to clearly compare the measured data with simulated results concluded from the self-complied program, a whole day’s experimental data of 8 June 2014 was adopted to verify the model. The comparative results are presented in Figure 7a and Figure 8a, and the error analysis of model estimation was shown in Figure 7b and Figure 8b. Figure 7a illustrates the variation of the measured outdoor air temperature, outlet air temperature and simulated outlet air temperature with time, indicating the simulated outlet air temperature is in good agreement with the experimental data. Furthermore, Figure 7b demonstrates the matching level of testing and simulated data, which indicates the mean square error (MSE) is 0.73 $℃$ and the mean relative error (MRE) is 8.5%. The comparison of the soil temperature along the radial direction between the testing and simulated data is shown in Figure 8a, which indicates that the two sets of data match very well. As shown in Figure 8b, the MSE is only 0.57 $℃$ and the MRE is 6.4%. The error can satisfy the needs of the engineering practice. According to the comparison and error analysis of testing and simulated data, the self-complied program used in this paper can reliably and precisely deal with the 2D coupled heat and mass transfer in soil.

4. Results and Discussion

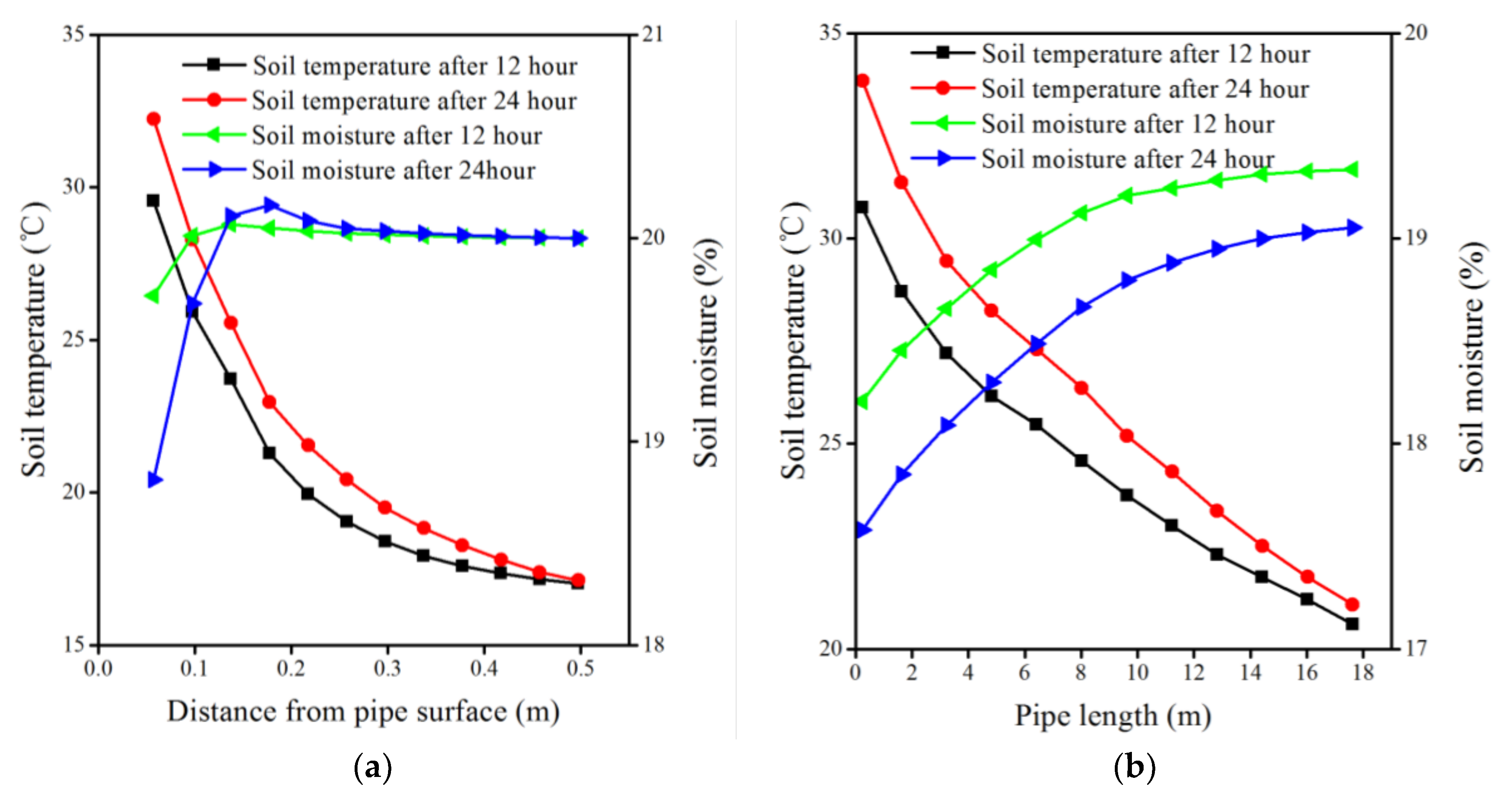
4.1. Soil Temperature and Moisture Concentration Analysis in Radial and Axial Directions

The soil temperature and moisture concentration profiles from 0 m to 0.5 m away from the soil-pipe interface are simulated and plotted in Figure 9a. The initial soil moisture concentration is assumed to be 20%, and the air flow rate and inlet air temperature are set as 154 m³/h and 38 $℃$, respectively.

As shown in Figure 9a, after 24 h continuous operation, the soil moisture concentration monotonically first increases, and then gradually drops to initial state after reaching the moisture peak value. As a result, the moisture concentration curve at the end of 24 h can be separated into three regions: temperature driven section, common driven section, and undisturbed section.

In the first region, moisture migrates under temperature gradient from the higher temperature regions to lower temperature regions, while simultaneously tending to redistribute itself in reverse under the created soil moisture concentration gradient. The main cause of soil moisture migration is temperature gradient in this region. Accordingly, the soil moisture concentration drops from 20% to 18.81% at the soil-pipe interface and has been below initial value in the first 0.13 m of the first region. The soil moisture concentration increases monotonically from the soil-pipe interface and exceeds the initial value about 20% at the last part of the first region due to the accumulation of moisture concentration. Finally, the soil moisture concentration peaks at 20.16% when the temperature gradient and the created moisture gradient reach a temporary equilibrium at 0.18m away from the soil-pipe interface.

In the second region, soil moisture concentration gradually decreases from the peak value to the initial value. Differing from the first region, the moisture migration direction caused by the temperature gradient is same as the moisture migration direction caused by the moisture gradient. The moisture radially migrates outwards the soil-pipe interface under both moisture gradient and temperature gradient. Accordingly, this region is called common drive section.

The third region is radially away from the soil-pipe interface from 0.37 m to 0.5 m. In this undisturbed region, moisture concentration remains nearly constant. From Figure 7a it can be seen that soil moisture concentration reaches the peak value of 20.07% at the radial distance of 0.13 m after 12 h of continuous operation. As a result, it is concluded that the peak value increases and the peak position moves radially outwards with time, and the area of the undisturbed region decreases gradually with time.

Although the soil temperature decreases gradually along the radial direction from the soil-pipe interface, the decreasing rate drops with the increase of the distance away from the soil-pipe interface. Noticing the soil temperature increases with the continuous operation of the system. From Figure 9a, the penetration of heat at the entrance region is not beyond four times of the pipe diameter at the end of 24 h. As a result, the computational domain extends to five times of the pipe diameter in this paper.

Figure 9b represents the change of the soil temperature and moisture concentration away from the soil-pipe interface about 0.05 m along with the pipe length. It is easy to find that the soil temperature gradually decreases along the length of the pipe, and the moisture concentration increases rapidly near the air entrance region and then gradually slows down. Meanwhile, the soil moisture concentration becomes smaller with time.

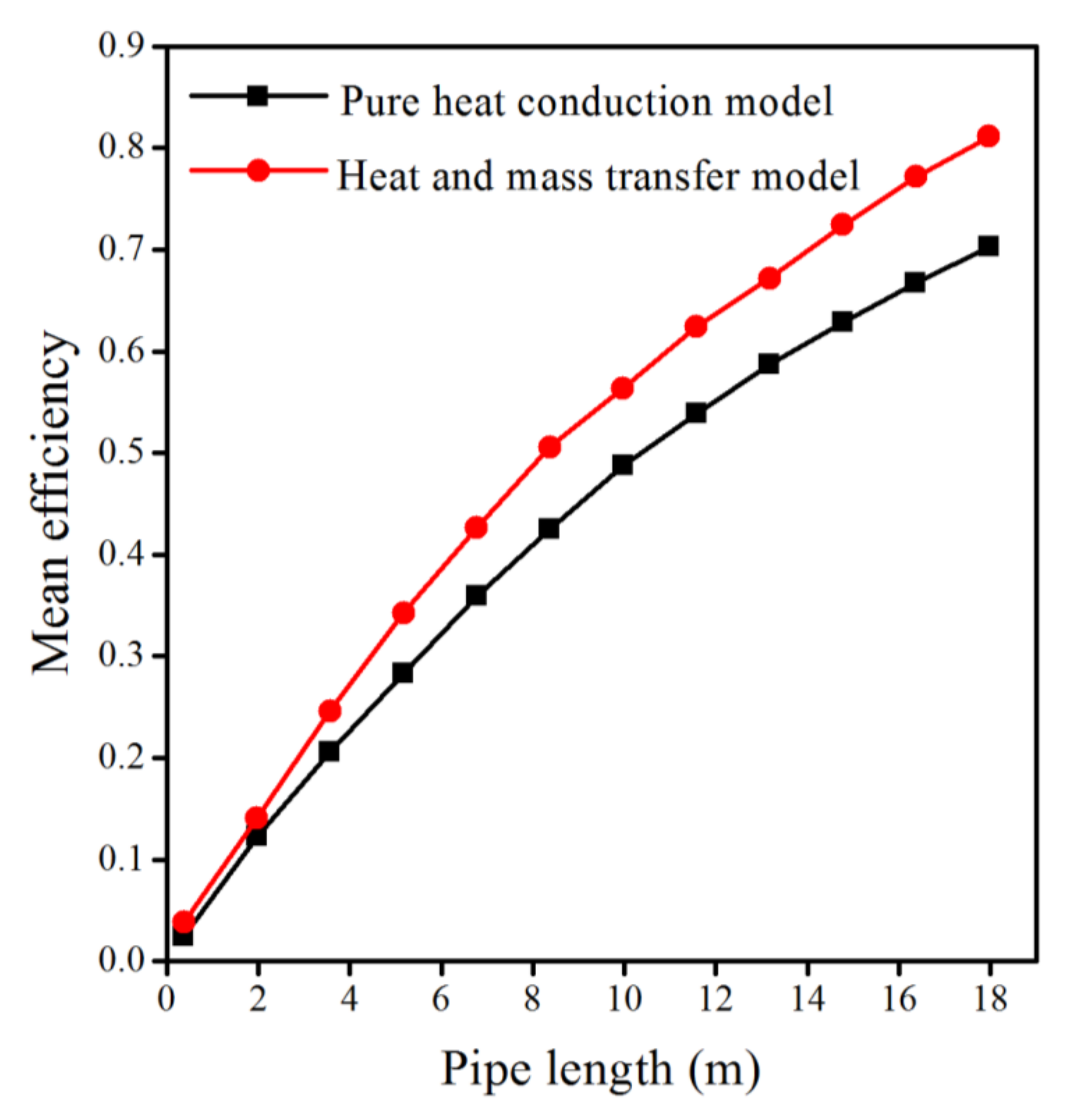
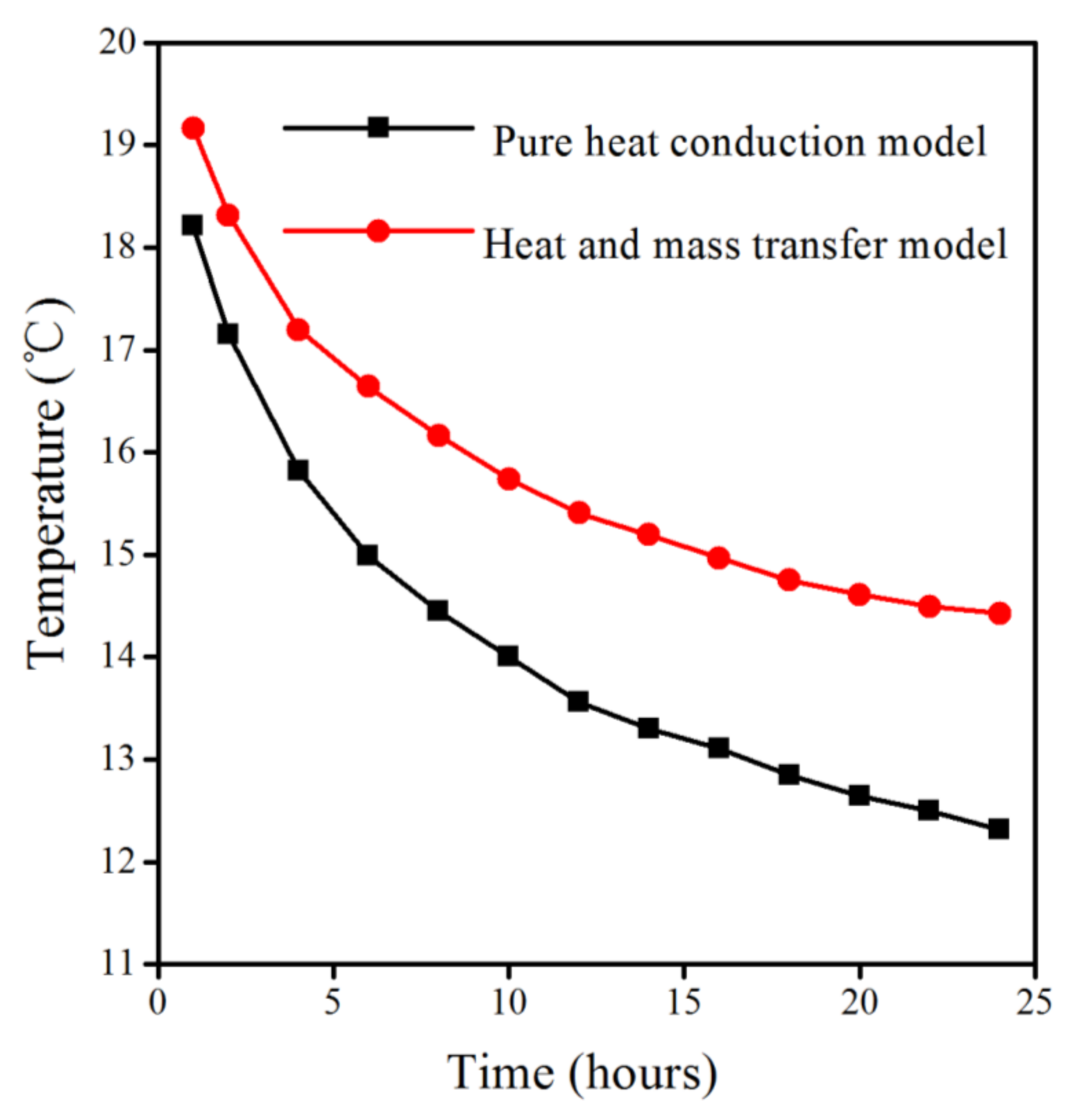
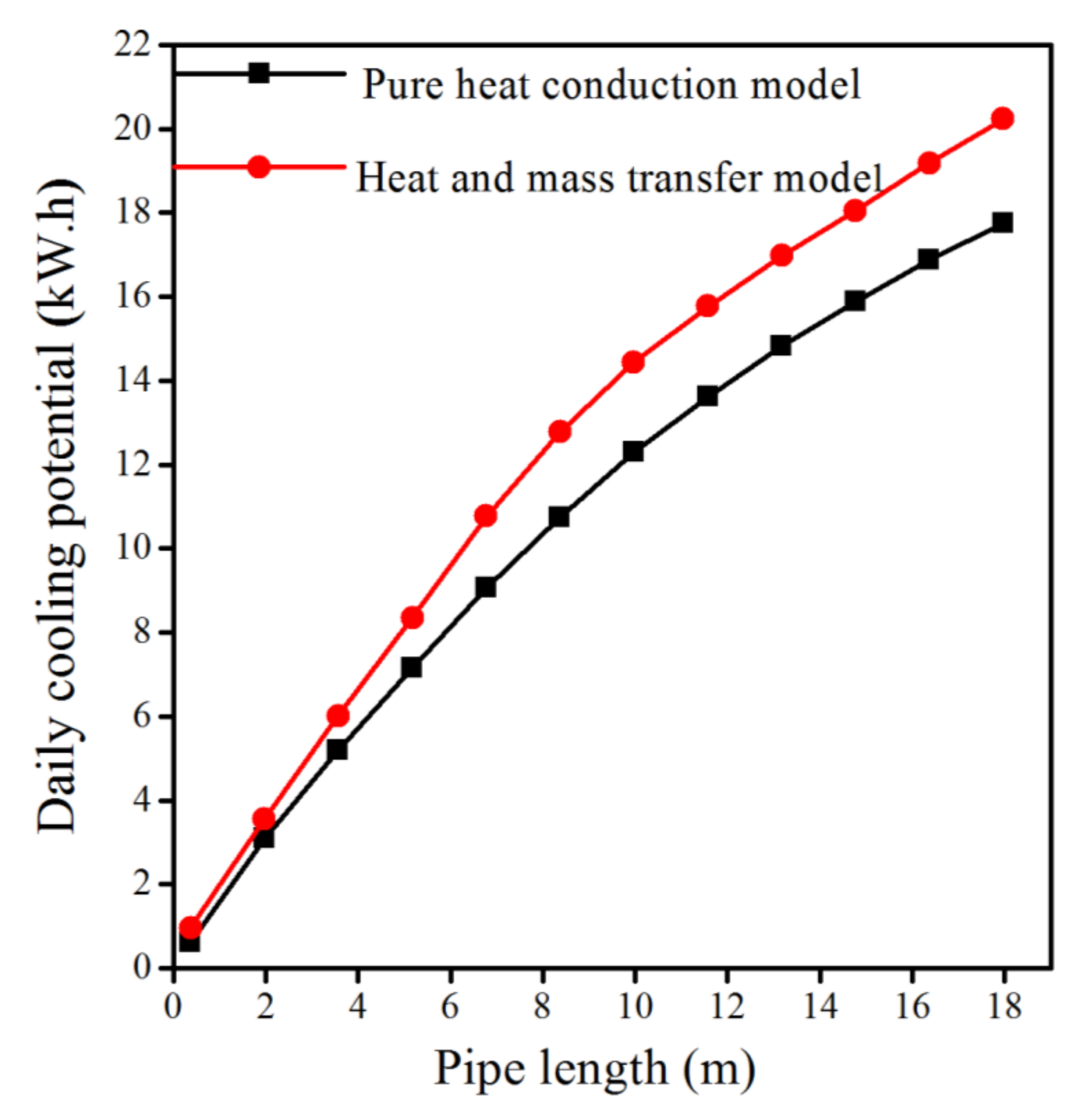
4.2. Thermal Performance Evaluation under Different Heat Transfer Models

The effect of the pipe length on the daily mean efficiency is illustrated in the Figure 10. It is found that the daily mean efficiency increases with the increasing of the pipe length for different heat transfer models. For a change in the pipe length from 5 to 15 m, there is an obvious increase in daily mean efficiency of heat and mass transfer model from 34.2% to 72.5% and a variation gained from pure heat conduction model from 28.3% to 62.8%. As a result, it has been proved that the heat and mass transfer model can yield the best daily mean efficiency is compared to the pure heat conduction model.

Figure 11 shows the evolution of difference between temperature of inlet air and outlet air as function of operating duration. The value of air temperature difference between inlet and outlet varies between 15.3 $℃$ and 13.8 $℃$ for heat and mass transfer model and pure heat conduction model after 12 h of continuous operation. The value of the same is 14.4 $℃$ and 12.2 $℃$ when EAHE runs continuously for 24 h. According to the graph, the air temperature difference between inlet and outlet drops for the long period of continuous operation. However, the temperature difference between two heat transfer models becomes bigger with time. This can be explained by the fact that moisture migration leads to the soil temperature in the vicinity of buried pipe of heat and mass transfer model is lower than the pure heat conduction model during the running process of the system. Accordingly, the outlet air temperature of heat and mass transfer model is lower than the pure heat conduction model.

Figure 12 represents the variation of the daily cooling potential along with the pipe length for different heat transfer models. It is shown that the daily cooling potential increases as function of pipe length for two heat transfer models. For which, it is observed a rise from 8.4 to 18.1 kW h corresponds to variation of pipe length from 5 to 15 m for heat and mass transfer model. For the same change in the pipe length, it is observed a rise from 7.2 to 15.9 kW h for pure heat conduction model. And, the difference of the daily cooling potential of two heat transfer models becomes bigger according to the pipe length. Additionally, it is true that increasing the pipe length has a positive effect of increasing the daily cooling potential, but the increasing rate drops according to the pipe.

In Figure 13, the evolution of the derating factors at different lengths of pipe after different times of continuous operation under transient conditions for two heat transfer models is shown. It is mentioned that the derating factor decreases as function of pipe length. The derating factor drops from 0.22 to 0.1 and 0.72–0.31 after 1 and 24 h of continuous operation of EAHE, respectively, for pure heat conduction model. The value of the same for heat and mass transfer model is 0.06–0.16 and 0.25–0.58. The value of the derating factor at a distance of 6 m from the pipe inlet for continuous operating duration of 24 h varies between 0.11 and 0.43, 0.13 and 0.52 for the heat and mass transfer model and the pure heat conduction model, respectively. Therefore, it is concluded that thermal performance deteriorates with the duration of continuous operation. Larger values of the derating factor mean greater deterioration in the thermal performance of EAHE under transient conditions. As shown in Figure 13, the value of the derating factor of pure heat conduction model is greater than heat and mass transfer model for an equal period of time. Furthermore, curves of the derating factor for pure heat conduction model are much steeper than the corresponding curves for heat and mass transfer model. According to the above analysis, deterioration in thermal performance of EAHE for pure heat conduction model is larger and more rapid than the heat and mass transfer model.

5. Conclusions

In this paper, a numerical study conducted on an EAHE integrated with an agricultural greenhouse is presented. The thermal performance of EAHE under different heat transfer models and soil temperature and moisture behaviors are discussed in detail. Some main conclusions are summarized as follow:

• There is an obvious moisture peak in the radial direction, which has an important effect on the heat and mass transfer process. Furthermore, the location of peak will move radially outwards and the peak value becomes bigger with time.
• Compared with the pure heat conduction model, the lower outlet air temperature and soil temperature can be obtained for the heat and mass transfer model for an equal period of continuous operation duration.
• Heat and mass transfer model can yield best mean efficiency, daily cooling potential and thermal performance of EAHE in transient conditions are compered to pure heat conduction model.
• Thermal performance of EAHE deteriorates with duration of operation. Accordingly, understanding the soil thermal saturation and recovery of an EAHE system under different types of operation (intermittent or continuous) is very important.