Three-Dimensional Peridynamic Model for Predicting Fracture Evolution during the Lithiation Process
Abstract
1. Introduction
2. Coupled Diffusion-Mechanical Deformation Formulation
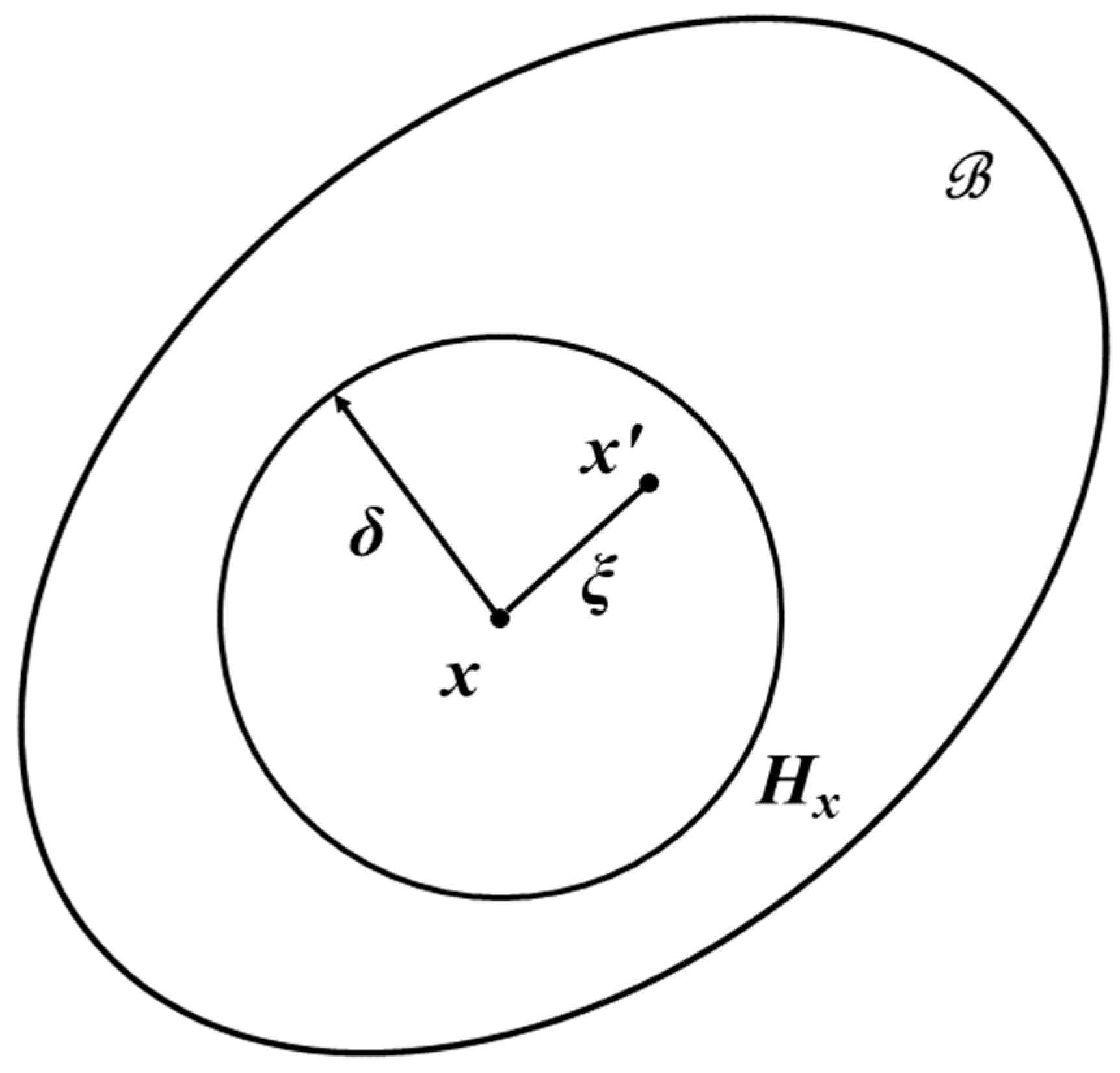
3. Peridynamic Theory
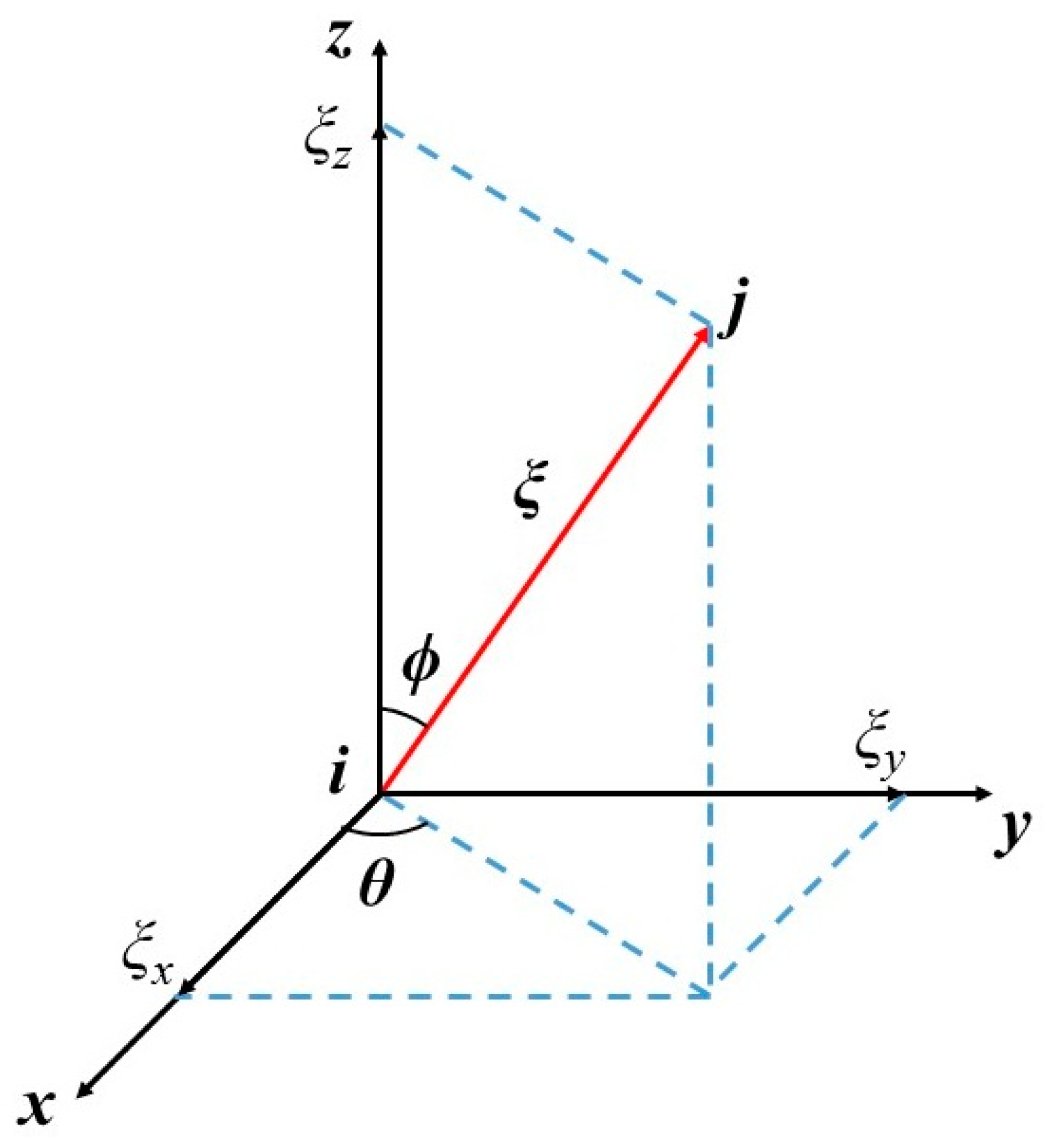
4. Peridynamic Differential Operator Approach
5. Numerical Studies
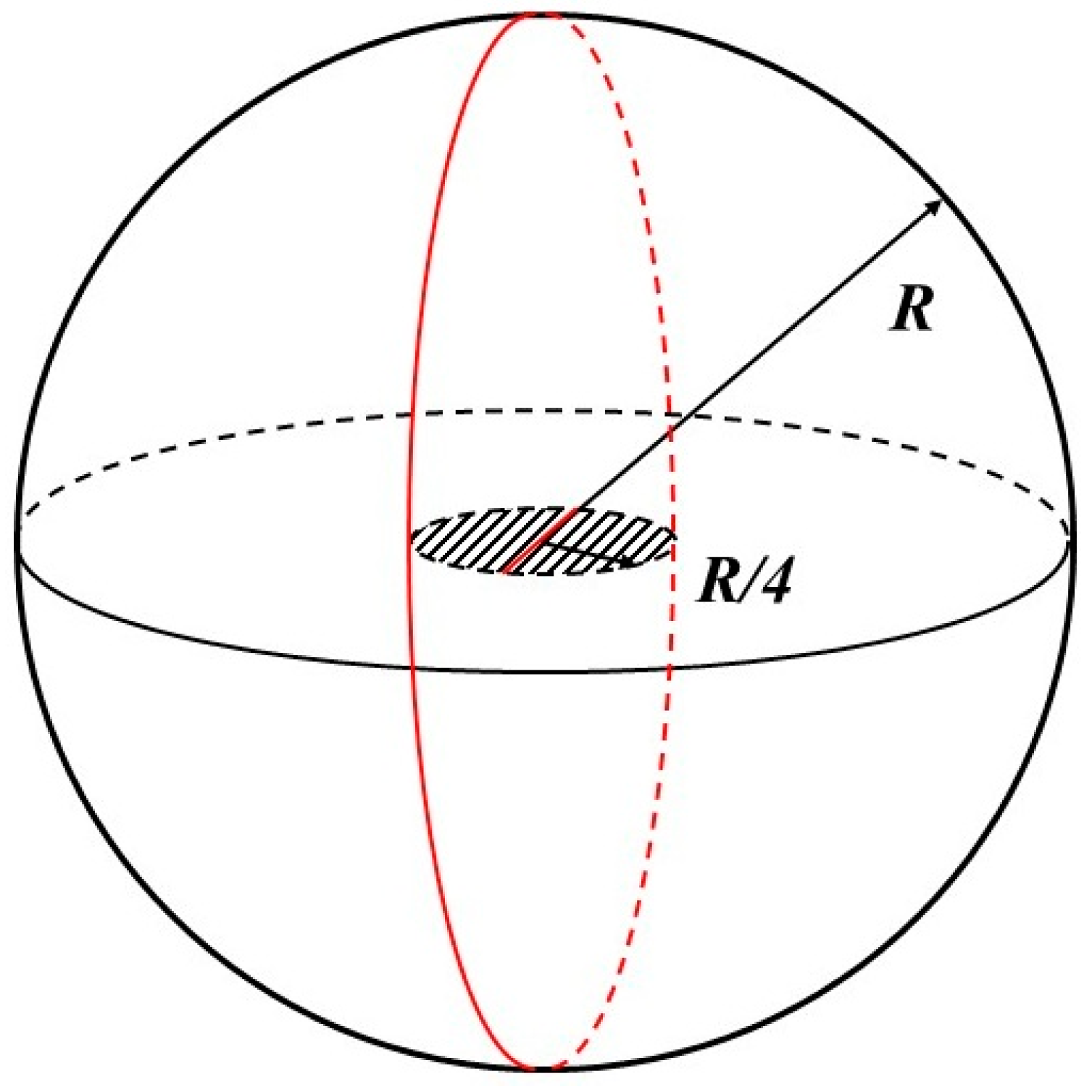
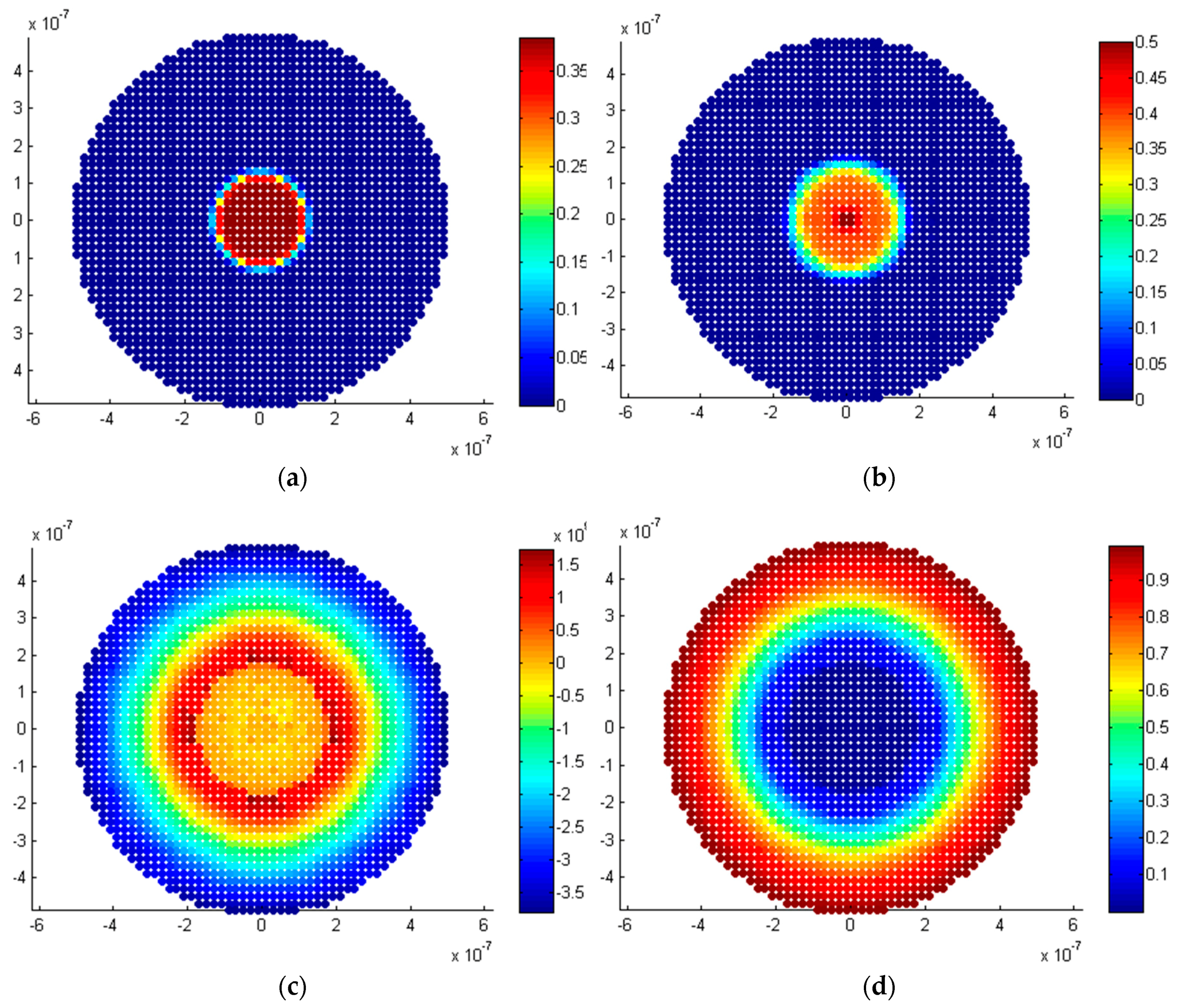
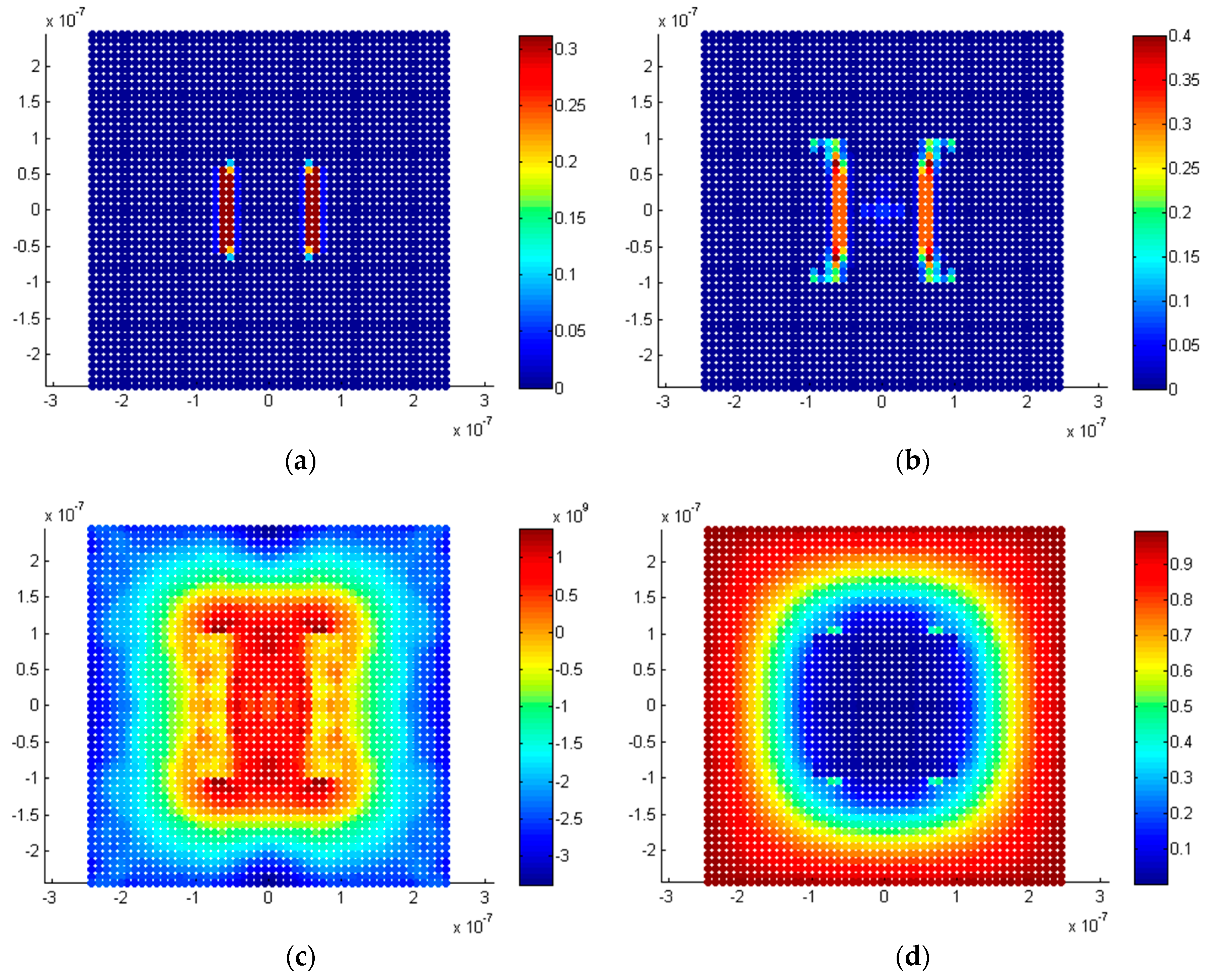
5.1. Spherical Model
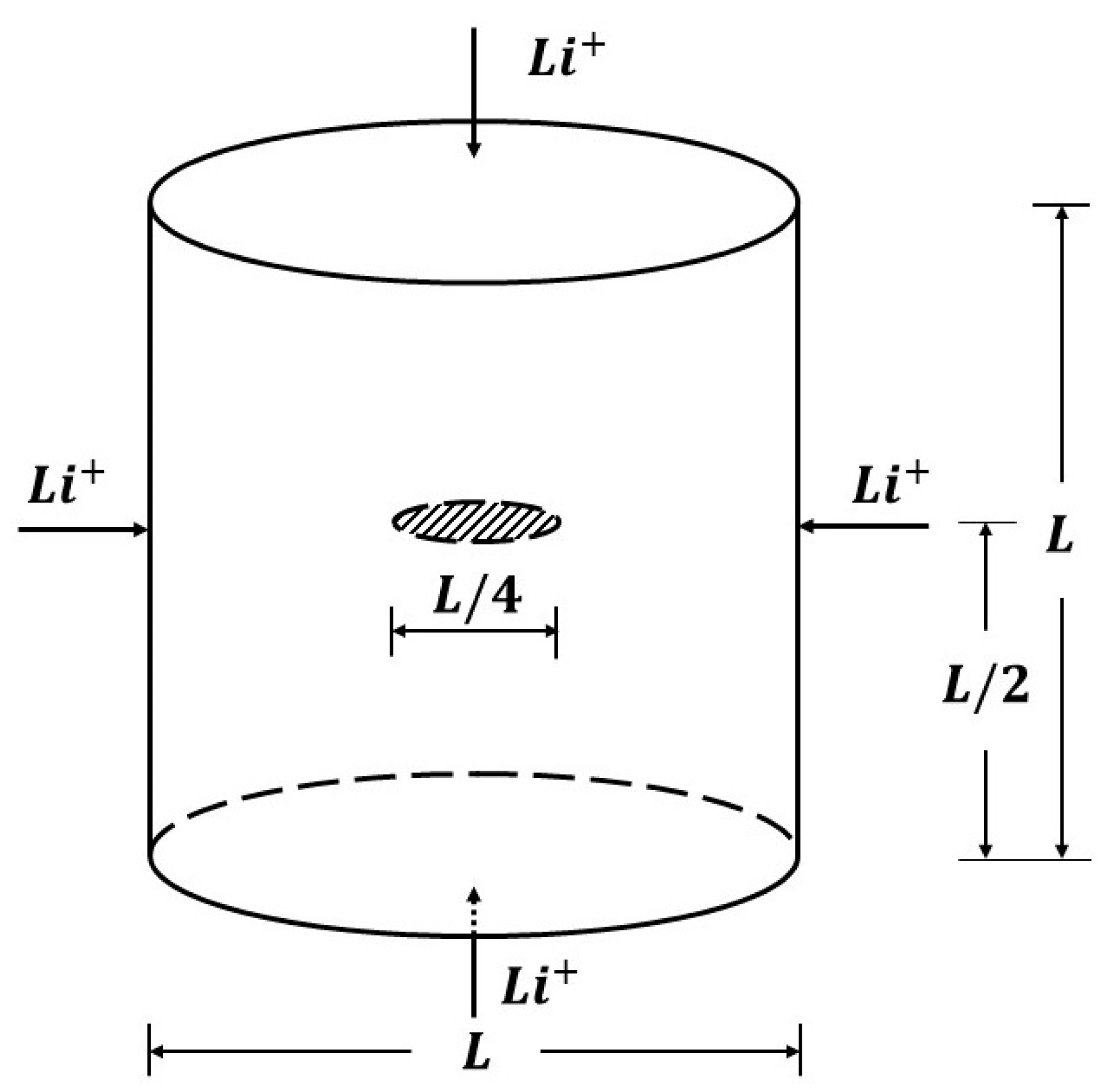
5.2. Cylindrical Model
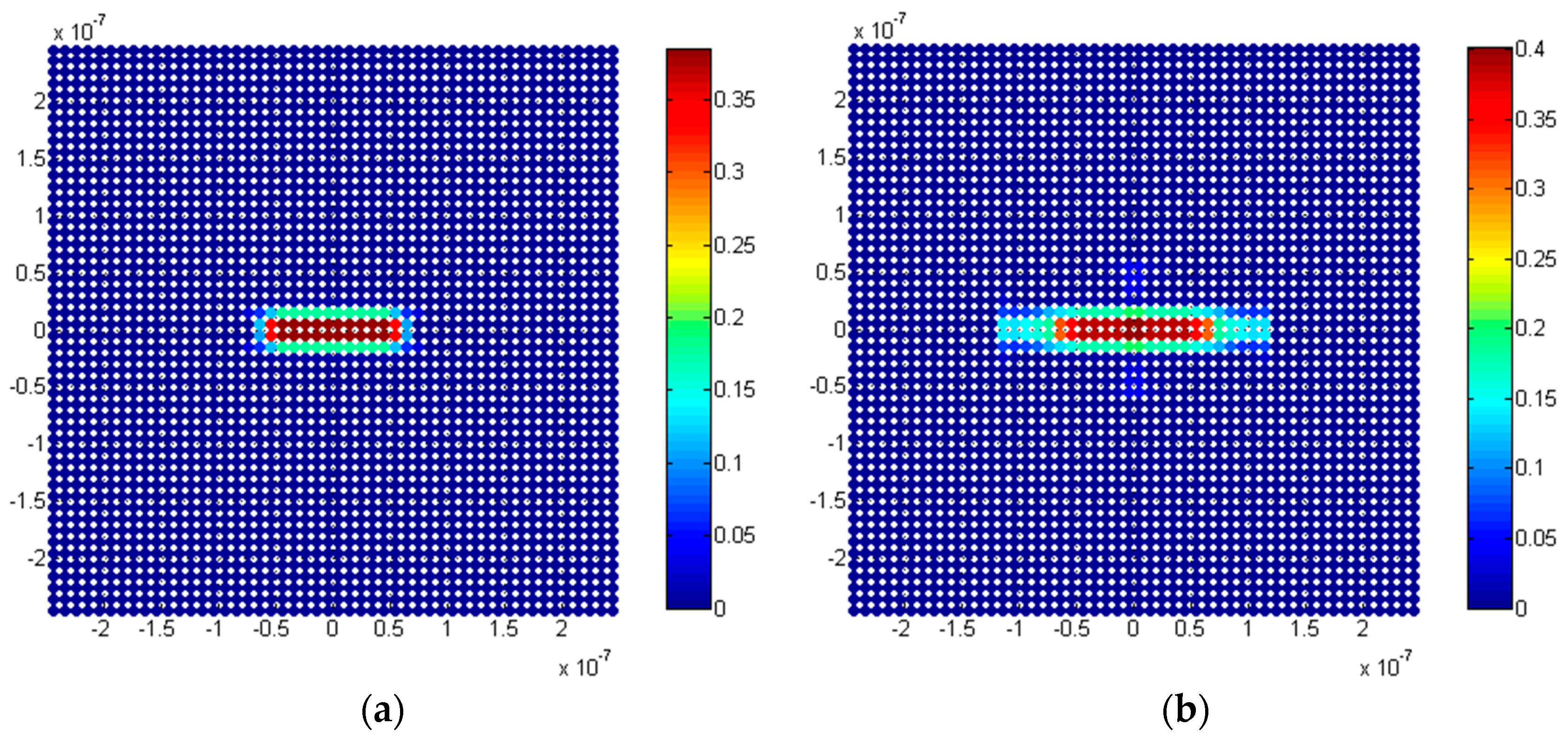
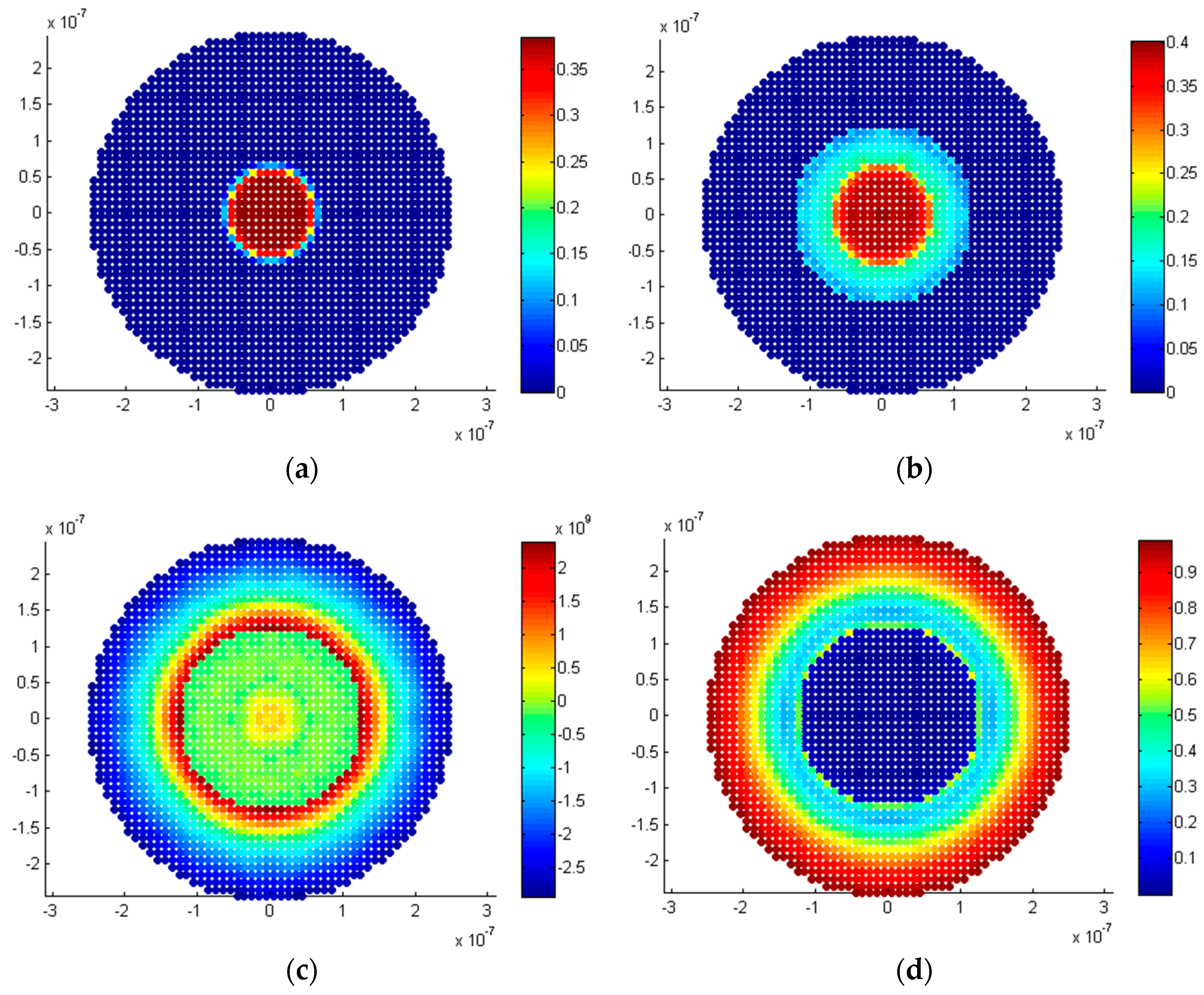
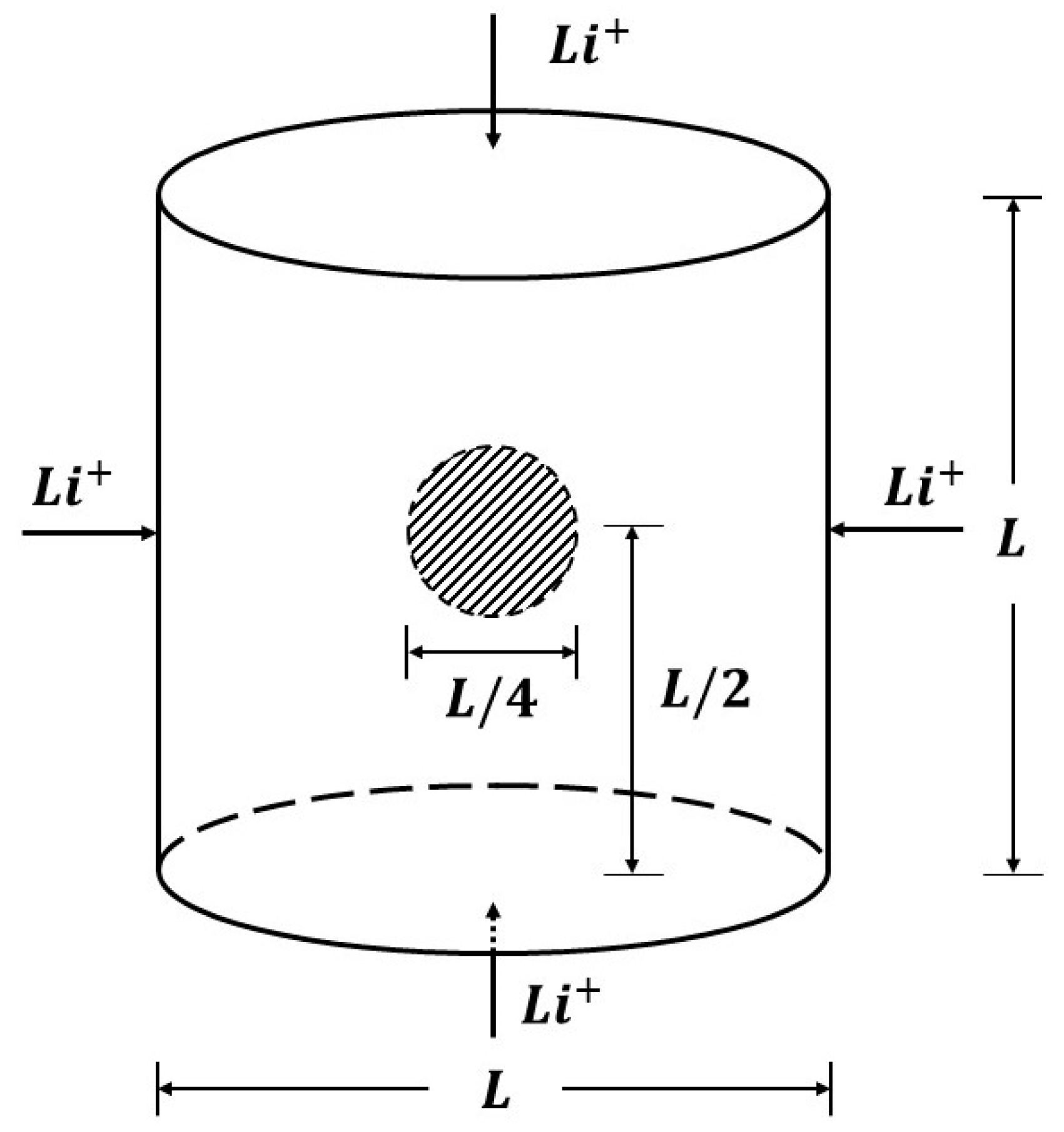
5.2.1. Penny-Shaped Crack along the Horizontal Plane
5.2.2. Penny-Shaped Crack along the Vertical Plane
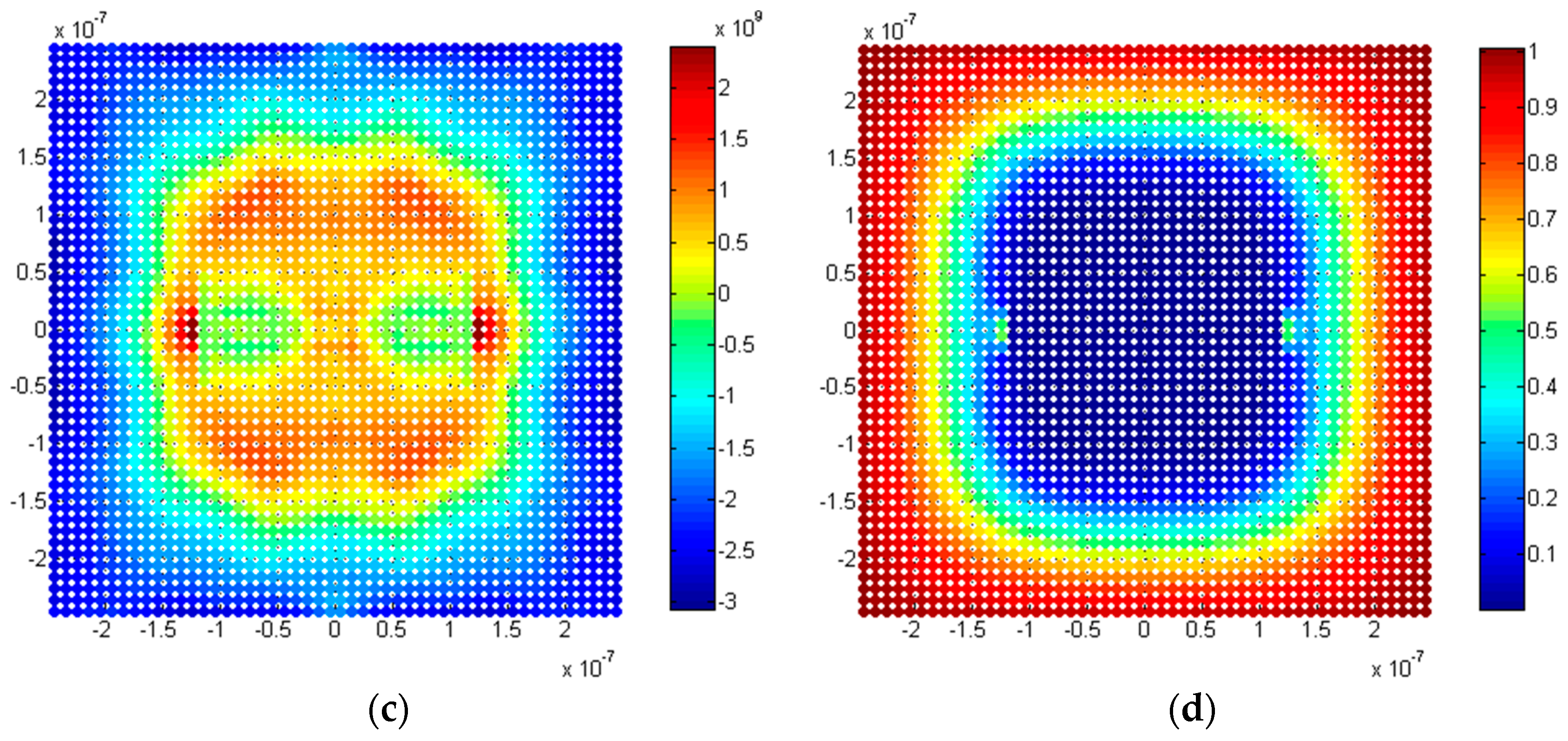
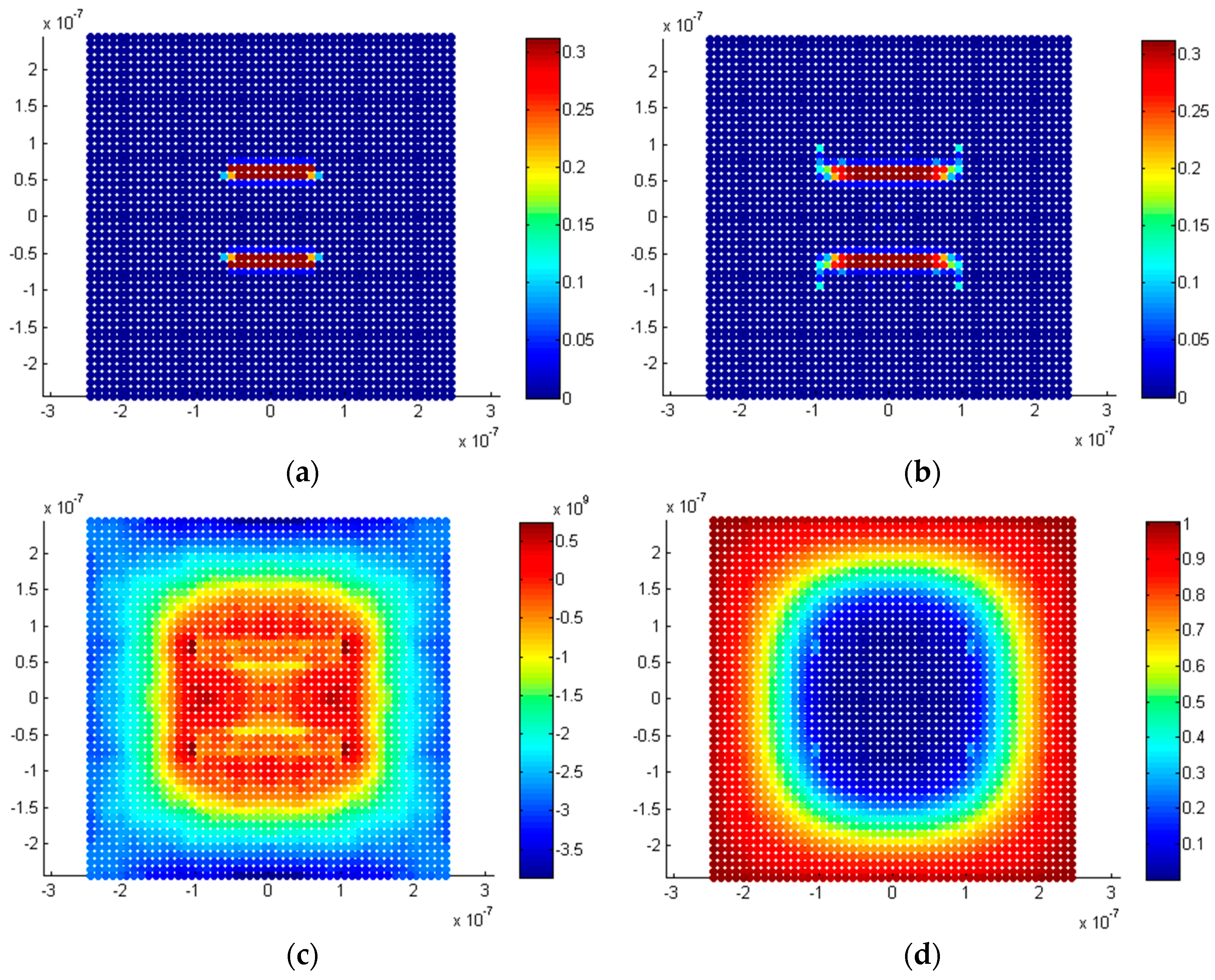
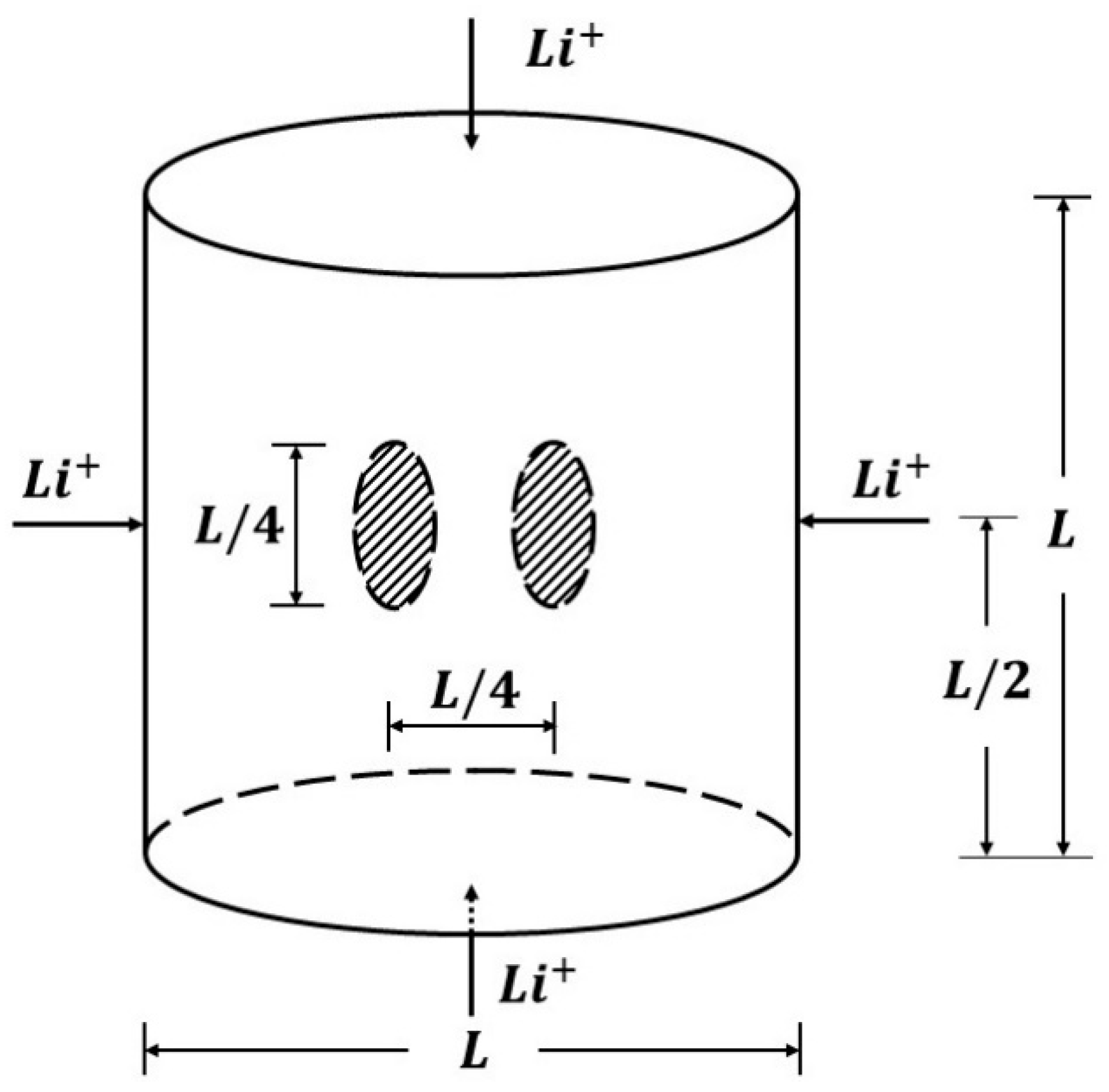
5.2.3. Twin Penny-Shaped Cracks along Horizontal Planes
5.2.4. Twin Penny Shape Cracks along Vertical Planes
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Annex, V.I. Regulations for the Prevention of Air Pollution from Ships and NOx Technical Code; MARPOL 73/78; International Maritime Organization (IMO): London, UK, 1998. [Google Scholar]
- Rosenkranz, C. Deep-cycle batteries for plug-in hybrid application. In Proceedings of the EVS20 Plug-In Hybrid Vehicle Workshop, Long Beach, CA, USA, 15–19 November 2003. [Google Scholar]
- Chung, S.Y.; Bloking, J.T.; Chiang, Y.M. Electronically conductive phospho-olivines as lithium storage electrodes. Nat. Mater. 2002, 1, 123–128. [Google Scholar] [CrossRef] [PubMed]
- De las Casas, C.; Li, W. A review of application of carbon nanotubes for lithium ion battery anode material. J. Power Sources 2012, 208, 74–85. [Google Scholar] [CrossRef]
- Zhang, W.J. A review of the electrochemical performance of alloy anodes for lithium-ion batteries. J. Power Sources 2011, 196, 13–24. [Google Scholar] [CrossRef]
- Nadimpalli, S.P.V.; Tripuraneni, R.; Sethuraman, V.A. Real-time stress measurements in germanium thin film electrodes during electrochemical Lithiation/Delithiation cycling. J. Electrochem. Soc. 2015, 162, A2840–A2846. [Google Scholar] [CrossRef]
- Chan, C.K.; Peng, H.; Liu, G.; McIlwrath, K.; Zhang, X.F.; Huggins, R.A.; Cui, Y. High-performance lithium battery anodes using silicon nanowires. Nat. Nanotechnol. 2008, 4, 31–35. [Google Scholar] [CrossRef] [PubMed]
- Ryu, I.; Choi, J.W.; Cui, Y.; Nix, W.D. Size-dependent fracture of Si nanowire battery anodes. J. Mech. Phys. Solids 2011, 4, 1717–1730. [Google Scholar] [CrossRef]
- Ren, J.G.; Wu, Q.H.; Tang, H.; Hong, G.; Zhang, W.; Lee, S.T. Germanium–graphene composite anode for high-energy lithium batteries with long cycle life. J. Mater. Chem. A 2013, 4, 1821–1826. [Google Scholar] [CrossRef]
- Winter, M.; Besenhard, J.O.; Spahr, M.E.; Novak, P. Insertion electrode materials for rechargeable lithium batteries. Adv. Mater. 1998, 4, 725–763. [Google Scholar] [CrossRef]
- Gao, B.; Kleinhammes, A.; Tang, X.P.; Bower, C.; Fleming, L.; Wu, Y.; Zhou, O. Electrochemical intercalation of single-walled carbon nanotubes with lithium. Chem. Phys. Lett. 1999, 307, 153–157. [Google Scholar] [CrossRef]
- Lee, J.H.; Kong, B.S.; Yang, S.B.; Jung, H.T. Fabrication of single-walled carbon nanotube/tin nanoparticle composites by electrochemical reduction combined with vacuum filtration and hybrid co-filtration for high-performance lithium battery electrodes. J. Power Sources 2009, 4, 520–525. [Google Scholar] [CrossRef]
- Yan, J.; Song, H.; Yang, S.; Yan, J.; Chen, X. Preparation and electrochemical properties of composites of carbon nanotubes loaded with Ag and TiO2 nanoparticle for use as anode material in lithium-ion batteries. Electrochim. Acta 2008, 4, 6351–6355. [Google Scholar] [CrossRef]
- Liu, P.; Sridhar, N.; Zhang, Y.W. Lithiation-induced tensile stress and surface cracking in silicon thin film anode for rechargeable lithium battery. J. Appl. Phys. 2012, 112, 093507. [Google Scholar] [CrossRef]
- Wang, X.; Shen, W.; Huang, X.; Zang, J.; Zhao, Y. Estimating the thickness of diffusive solid electrolyte interface. Sci. China Phys. Mech. Astron. 2017, 60, 064612. [Google Scholar] [CrossRef]
- Grantab, R.; Shenoy, V.B. Pressure-gradient dependent diffusion and crack propagation in lithiated silicon nanowires. J. Electrochem. Soc. 2012, 4, A584–A591. [Google Scholar] [CrossRef]
- Zuo, P.; Zhao, Y.P. A phase field model coupling lithium diffusion and stress evolution with crack propagation and application in lithium ion batteries. Phys. Chem. Chem. Phys. 2015, 4, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.F.; Zhou, M. Coupled mechano-diffusional driving forces for fracture in electrode materials. J. Power Sources 2013, 230, 176–193. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 4, 175–209. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Cai, Y.; Rabczuk, T. Dual-horizon peridynamics. Int. J. Numer. Methods Eng. 2016, 108, 1451–1476. [Google Scholar] [CrossRef]
- Amani, J.; Oterkus, E.; Areias, P.; Zi, G.; Nguyen-Thoi, T.; Rabczuk, T. A non-ordinary state-based peridynamics formulation for thermoplastic fracture. Int. J. Impact Eng. 2016, 87, 83–94. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Rabczuk, T. Dual-horizon peridynamics: A stable solution to varying horizons. Comput. Methods Appl. Mech. Eng. 2017, 318, 762–782. [Google Scholar] [CrossRef]
- Diyaroglu, C.; Oterkus, E.; Madenci, E.; Rabczuk, T.; Siddiq, A. Peridynamic modeling of composite laminates under explosive loading. Compos. Struct. 2016, 144, 14–23. [Google Scholar] [CrossRef]
- Diyaroglu, C.; Oterkus, E.; Oterkus, S.; Madenci, E. Peridynamics for bending of beams and plates with transverse shear deformation. Int. J. Solids Struct. 2015, 69, 152–168. [Google Scholar] [CrossRef]
- Oterkus, E.; Madenci, E. Peridynamics for failure prediction in composites. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; p. 1692. [Google Scholar]
- Wang, H.; Oterkus, E.; Oterkus, S. Peridynamic modelling of fracture in marine lithium-ion batteries. Ocean Eng. 2018, 151, 257–267. [Google Scholar] [CrossRef]
- Wang, H.; Oterkus, E.; Oterkus, S. Predicting fracture evolution during lithiation process using peridynamics. Eng. Fract. Mech. 2018, 192, 176–191. [Google Scholar] [CrossRef]
- Fick, A. On liquid diffusion. J. Membr. Sci. 1995, 4, 33–38. [Google Scholar] [CrossRef]
- Zhang, X.; Lee, S.W.; Lee, H.W.; Cui, Y.; Linder, C. A reaction-controlled diffusion model for the lithiation of silicon in lithium-ion batteries. Extrem. Mech. Lett. 2015, 4, 61–75. [Google Scholar] [CrossRef]
- Shenoy, V.B.; Johari, P.; Qi, Y. Elastic softening of amorphous and crystalline Li–Si phases with increasing Li concentration: A first-principles study. J. Power Sources 2010, 4, 6825–6830. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; McGraw-Hill: London, UK, 1977; Volume 3. [Google Scholar]
- Brebbia, C.A.; Telles, J.C.F.; Wrobel, L.C. Boundary Element Techniques: Theory and Applications in Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 4, 813–833. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 4, 1526–1535. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic states and constitutive modeling. J. Elast. 2007, 4, 151–184. [Google Scholar] [CrossRef]
- Oterkus, S.; Madenci, E.; Oterkus, E.; Hwang, Y.; Bae, J.; Han, S. Hygro-thermo-mechanical analysis and failure prediction in electronic packages by using peridynamics. In Proceedings of the 2014 IEEE 64th Electronic Components and Technology Conference (ECTC), Lake Buena Vista, FL, USA, 27–30 May 2014; pp. 973–982. [Google Scholar]
- Rabczuk, T.; Belytschko, T. A three dimensional large deformation meshfree method for arbitrary evolving cracks. Comput. Methods Appl. Mech. Eng. 2007, 196, 2777–2799. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Methods Eng. 2004, 4, 2316–2343. [Google Scholar] [CrossRef]
- Malvern, L.E. Introduction to the Mechanics of a Continuous Medium; Prentice-Hall: Hertfordshire, UK, 1969. [Google Scholar]
- Madenci, E. Peridynamic integrals for strain invariants of homogeneous deformation. ZAMM J. Appl. Math. Mech./Z. Angew. Math. Mech. 2017, 4, 1236–1251. [Google Scholar] [CrossRef]
- Madenci, E.; Barut, A.; Futch, M. Peridynamic differential operator and its applications. Comput. Methods Appl. Mech. Eng. 2016, 304, 408–451. [Google Scholar] [CrossRef]



| R | Radius of spherical particle | 0.5 μm |
| L | Longitudinal length of cylindrical nanowire | 0.5 μm |
| Elastic constant of pure silicon | 80 GPa | |
| Elastic constant of lithiated silicon, Li15Si4 | 41 GPa | |
| Poisson’s ratio of pure silicon | 0.22 | |
| Poisson’s ratio of lithiated silicon, Li15Si4 | 0.24 | |
| Ω | Partial molar volume | 8.5 × 10−6 m3 mol−1 |
| M | Molecular mobility | 500 m2 J−1 s−1 |
| Boltzmann constant | 1.38 × 10−23 J·K−1 | |
| T | Absolute temperature | 300 K |
| NA | Avogadro’s constant | 6.02 × 1023 mol−1 |
| Maximum concentration | 1.18 × 104 mol m−3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Oterkus, E.; Oterkus, S. Three-Dimensional Peridynamic Model for Predicting Fracture Evolution during the Lithiation Process. Energies 2018, 11, 1461. https://doi.org/10.3390/en11061461
Wang H, Oterkus E, Oterkus S. Three-Dimensional Peridynamic Model for Predicting Fracture Evolution during the Lithiation Process. Energies. 2018; 11(6):1461. https://doi.org/10.3390/en11061461
Chicago/Turabian StyleWang, Hanlin, Erkan Oterkus, and Selda Oterkus. 2018. "Three-Dimensional Peridynamic Model for Predicting Fracture Evolution during the Lithiation Process" Energies 11, no. 6: 1461. https://doi.org/10.3390/en11061461
APA StyleWang, H., Oterkus, E., & Oterkus, S. (2018). Three-Dimensional Peridynamic Model for Predicting Fracture Evolution during the Lithiation Process. Energies, 11(6), 1461. https://doi.org/10.3390/en11061461






