Design and Control of Small DC-Link Capacitor-Based Three-Level Inverter with Neutral-Point Voltage Balancing

Abstract

This paper presents a method to improve the quality of input-output currents in a three-level neutral-point clamped (NPC) inverter with small direct current-link (DC-link) capacitor systems. The inverter systems with the small DC-link capacitors have several advantages in terms of cost, volume, life-time, and reliability when compared to inverters that use large DC-link capacitors. However, there are problems with respect to the deterioration of the input current quality and a severe ripple of neutral-point voltage (NPV), which can cause an aggravated output current. To mitigate these issues, an additional circuit is applied for the input current shaping and a compensation algorithm is applied to reduce the ripple voltage of NPV. The effectiveness of the proposed design and control method is verified with various simulation and experimental results.

1. Introduction

Three-level neutral-point clamped (NPC) inverters have been widely used in medium-voltage power conversion systems. Three-level NPC inverters have several advantages over conventional two-level inverters, such as reduced stress of the power device and enhanced output quality [1,2].

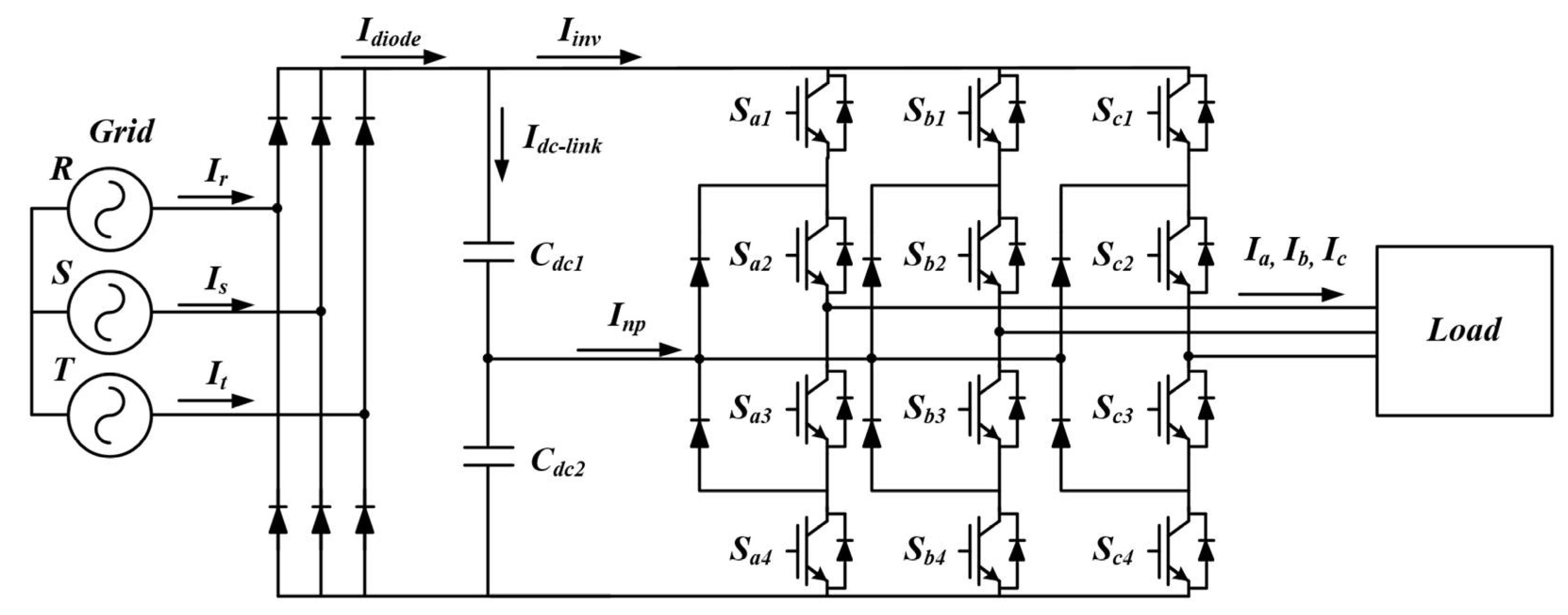
The conventional rectifier system for an inverter is shown in Figure 1. Diode rectifier systems generally utilize capacitors with large capacitances to stabilize the operation of the inverter system. The purpose of the DC-link capacitor is to perform DC-link voltage regulation and to absorb the switching ripple current. Therefore, the DC-link of an NPC inverter is mainly composed of an electrolytic capacitor with a large capacitance. Moreover, the electrolytic capacitor occupies a lot of the space in the whole system. Furthermore, as electrolytic capacitors have a short life time. There is a decreased reliability of power-conversion systems [3,4,5].

Therefore, many studies have focused on replacing electrolytic capacitors with film capacitors to reduce the volume of the system. While film capacitors have a much higher reliability, they have a much less capacitance per unit than that of electrolytic capacitors. A small film capacitor improves the reliability of the system and eliminates the initial charging circuit, thus reducing the overall system volume and cost [6,7,8,9].

In addition, film capacitors can store less energy than electrolytic capacitors. Therefore, film capacitors are unable to compensate for the input–output power difference. Small-capacity inverter systems are beneficial in applications such as fans, pumps, and compressors, where the load variation is not significant [10,11,12].

To improve the quality of the input current caused by small capacitors, many researchers have studied various control techniques, including the use of the pulse-power injection method, output-current compensation technique, and harmonic injection technique [3,4,6,7,8,9,10,11,12,13,14,15]. In the case of [8], the output-current compensation method distorted the output current in order to improve the input current. In [11], there is a disadvantage in realizing high efficiency, as there is a need for a microprocessor that operates at high speed.

By increasing the demand in terms of small current distortion, low dv/dt stress and high efficiency, the three-level inverter is widely applied in various applications. However, the previous studies for the small DC-link system fed by the diode rectifier is based on the two-level inverters and there are considerable issues when the three-level inverter is applied in the small DC-link system. As shown in Figure 1, the DC-link of the NPC inverter is divided into two voltage sources to generate three different output voltage levels; i.e., −V_dc/2, 0, and +V_dc/2. However, for the DC-link capacitors used in the three-level inverter, there is a difference between V_dc1 and V_dc2 owing to differences in manufacturing tolerances, mismatches in the switch characteristics, and the grid unbalance. The unbalance of the DC-link voltage includes alternating current (AC) unbalance and DC unbalance. The occurrence of a DC unbalance implies that two DC-link capacitors have different voltages, and the voltage difference does not change with time. The DC unbalance can cause the distortion of the output currents. The solution for the DC unbalance problem is to choose an appropriate switching-modulation method. The AC unbalance is an AC-ripple of V_dc1 and V_dc2, which change with time. The frequency of the AC ripple is three times the output fundamental frequency and the DC-link capacitor value. A large AC unbalance causes the output currents to contain the ripple frequency, which causes the distortion. Furthermore, a large AC unbalance imposes stress on converter devices. These problems from the AC unbalance become severe when the small capacitors are applied for the DC-link. In order to restrict the neutral-point AC ripple voltage, a neutral-point voltage stabilization method using DPWM and the offset injection method are used [5,16,17,18,19,20,21,22,23,24].

This paper focuses on the design and its control algorithm to improve the quality of the input–output currents generated by the three-level NPC inverter based small DC-link system. An applied DC-link shunt compensator (DSC) circuit solves the input current deterioration caused by the small DC-link capacitor. In addition, the output current quality is improved using the AC ripple-reduction algorithm. Finally, the performance and feasibility of the proposed method are verified using simulation and experimental results.

2. Description of Grid Current Improvement Technique

Generally, the DC-link capacitor in a three-level inverter compensates the power difference between the diode output power and the inverter input power through the charge-discharge operation of the capacitor. However, it is difficult to compensate for the instantaneous difference power owing to the decrease in the capacitance of the DC-link capacitor. In this section, the design method for the three-level inverter with the small DC-link capacitors is presented to shaping the rectified grid current [10]. The rectified input current, I_diode can be expressed as the sum of the inverter current that is consumed by the load and the charging current for the DC-link capacitor voltage, as shown in Figure 1.

$$I_{diode}=I_{inv}+I_{dc-link}$$

(1)

Assuming that the DC-link capacitance is very small, the DC-link current may be negligible. In this case, the quality of I_diode is decided according to the inverter current, I_inv.

$$I_{didode}\approx I_{inv}$$

(2)

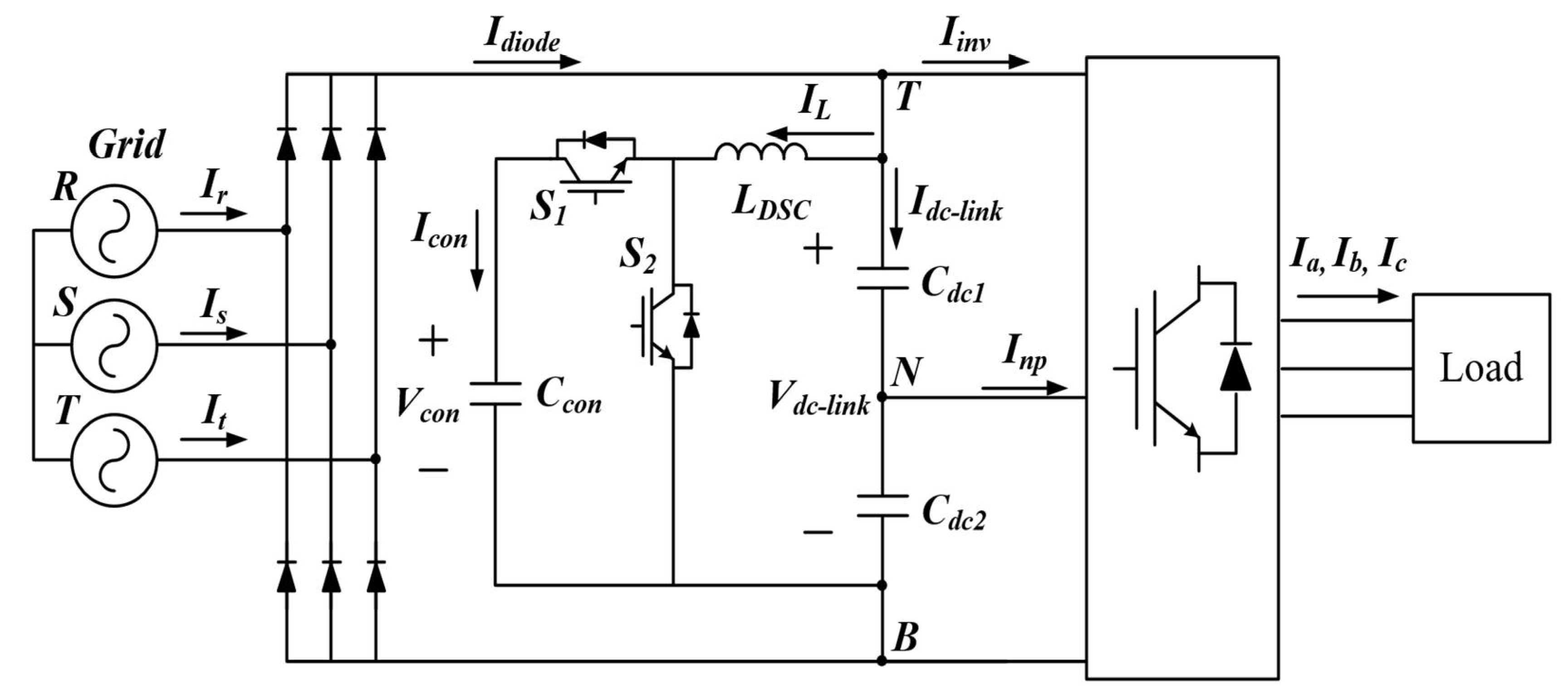
Therefore, in order to improve the quality of the rectified input current I_diode, it is necessary to change the inverter current I_inv or add a compensation value to change the input current I_diode. The three-level inverter with an additional circuit is shown in Figure 2. The additional circuit is called a DSC, which is used to improve the input current quality.

The proposed three-level NPC inverter consists of the small film capacitors that replace the large electrolytic capacitors and a DC-DC buck-boost converter. The inverter applying the large capacitors for the DC-link, the I_diode, flows for the period to charge the capacitors, and the period is relatively short because the capacitors have a large capacity. In case small capacitors are applied, most of the electric charge from the input grid is delivered to the load directly. Therefore, the I_diode flows consistently and its shape contains the six-order harmonic ideally because the three-phase grid currents are rectified by the diode rectifier. The proposed design method equips the DSC circuit to shape the I_diode into the six-order sinusoidal waveforms.

Assuming that the inverter uses small capacitors, I_diode can be expressed as follows:

$$I_{diode}\approx I_{inv}+I_L$$

(3)

The inverter current I_inv can be derived as:

$$\begin{array}{ccc}{I}_{inv}& =& \frac{P_{inv}}{V_{dc-link}}=\frac{P_{inv}}{V_{dc0}+V_{6th}}=\frac{P_{inv}(V_{dc0}-V_{6th})}{(V_{dc0}+V_{6th})(V_{dc0}-V_{6th})}\hfill \\ & =& \frac{P_{inv}{V}_{dc0}-P_{inv}{V}_{6th}}{V_{dc0}^2-V_{6th}^2}\approx \frac{P_{inv}}{V_{dc0}}-\frac{P_{inv}{V}_{6th}}{V_{dc0}^2}(where,V_{dc0}^2>>V_{6th}^2)\end{array}$$

(4)

where P_inv is the inverter power, V_dc0 is the average value of V_dc-link, and V_6th is the 6th-order harmonic of the DC-link voltage. By substituting (4) into (3), the rectified input current is given as:

$$I_{diode}\approx \frac{P_{inv}}{V_{dc0}}-\frac{P_{inv}\cdot V_{6th}}{V_{dc0}^2}+I_L$$

(5)

Assuming that there is a constant-power load in the inverter, the first term of (5) will have a DC value. However, because the second term is the 6th-order harmonic component of the DC-link voltage, it causes the degradation of the input current quality. Therefore, the compensation value is added to the current I_L, which flows in the DSC circuit, to improve the input current quality. The I_L with the added compensation value I_comp is as follows:

$$I_L=I_{con}+\alpha \frac{P_{inv}\cdot V_{6th}}{V_{dc0}^2}$$

(6)

where I_con is capacitor current of C_con and α is a weighting factor that adjusts the injected value of the compensative current. Finally, the input current Equation is given in (7). The input current can be improved by controlling the DSC circuit.

$$I_{diode}\approx \frac{P_{inv}}{V_{dc0}}+\left(\alpha -1\right)\frac{P_{inv}\cdot V_{6th}}{V_{dc0}^2}+I_{con}$$

(7)

As recognizable by (7), if α is 1, I_diode is constant value (P_inv/V_dc0 + I_con) and the input grid currents form square waveforms. By increasing the value of α, the shape of I_diode contains the six-order harmonic that become similar with I_diode when the large DC-link capacitors are applied [10,25]. Therefore, the input grid currents also acquire the shape of sinusoidal waveforms by adjusting α.

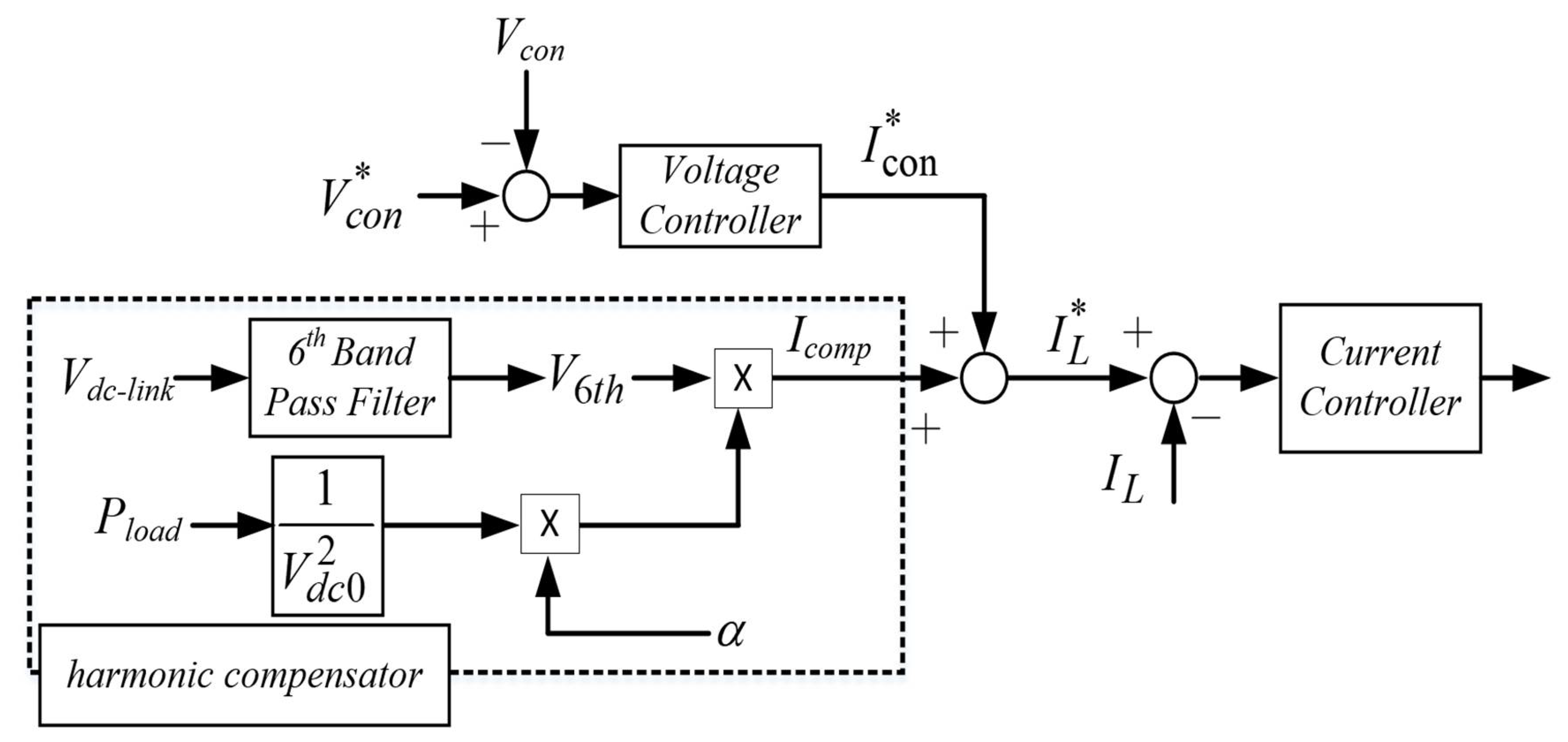
The control block diagram of the DSC is as shown in Figure 3. The DSC controller consists of a voltage controller, harmonics compensator, and current controller. The voltage controller controls V_con, which is the output voltage of DSC. The harmonic compensator extracts the 6th-order harmonic of the DC-link voltage using the band-pass filter (BPF), and the 6th-order harmonic is used to calculate the compensative current I_comp. The current controller controls I_L, which flows through the DSC inductor L_DSC. To compensate for the 6th-order harmonic, I_comp is added to the reference signal I_L*. I_comp consists of the product of the weighting factor alpha and V_6th, which is filtered by BPF. The bandwidth of BPF extracts the 6th-order harmonic of the DC-link voltage, V_dc-link(V_dc1 + V_dc2).

3. AC Ripple-Reduction Algorithm for the Output Current

The quality of the input current can be improved by applying the DSC. However, because the DSC only improves the input current, a separate control technique is needed to improve the output current quality. For three-level NPC inverters, there is an AC ripple in the DC-link. The charge-discharge of the capacitor voltage is determined according to the switching state and the direction of the neutral-point current, I_np, which flows through the neutral-point, N. In addition, the values of V_dc1 and V_dc2 are not the same and fluctuated. Therefore, the three-level inverter also generates the distorted pole voltages under the large AC ripple condition of the capacitor voltages. The distorted output pole voltage degrades the quality of the output current. Hence, V_dc1 and V_dc2 should be controlled with the same value to realize the improved output current quality.

The three-phase voltage references are expressed as:

$$\begin{array}{l}{v}_{u,ref}=v_m\sin \omega t\\ v_{v,ref}=v_m\sin \left(\omega t-{120}^{\circ }\right)\\ v_{w,ref}=v_m\sin \left(\omega t+{120}^{\circ }\right)\end{array}$$

(8)

where v_m is the magnitude of the phase voltage.

The reconfigured on-time ratio of the three-level NPC inverter is as follows:

$$\begin{array}{l}{r}_{u,ref}=\frac{2\cdot v_{u,ref}}{V_{dc-link}}=\frac{2\cdot v_m}{V_{dc-link}}\sin \omega t\\ r_{v,ref}=\frac{2\cdot v_{v,ref}}{V_{dc-link}}=\frac{2\cdot v_m}{V_{dc-link}}\sin \left(\omega t-{120}^{\circ }\right)\\ r_{w,ref}=\frac{2\cdot v_{w,ref}}{V_{dc-link}}=\frac{2\cdot v_m}{V_{dc-link}}\sin \left(\omega t+{120}^{\circ }\right)\end{array}$$

(9)

where r_x,ref is within the range of $[-1,1]$. For every switching cycle, the on-time ratios can be classified as r_max, r_mid, and r_min, which represent the maximum, middle, and minimum values of the three-phase on-time ratios, respectively.

$$\begin{array}{l}{r}_{max}=max\left(r_{u,ref},r_{v,ref},r_{w,ref}\right)\\ r_{mid}=mid\left(r_{u,ref},r_{v,ref},r_{w,ref}\right)\\ r_{min}=min\left(r_{u,ref},r_{v,ref},r_{w,ref}\right)\end{array}$$

(10)

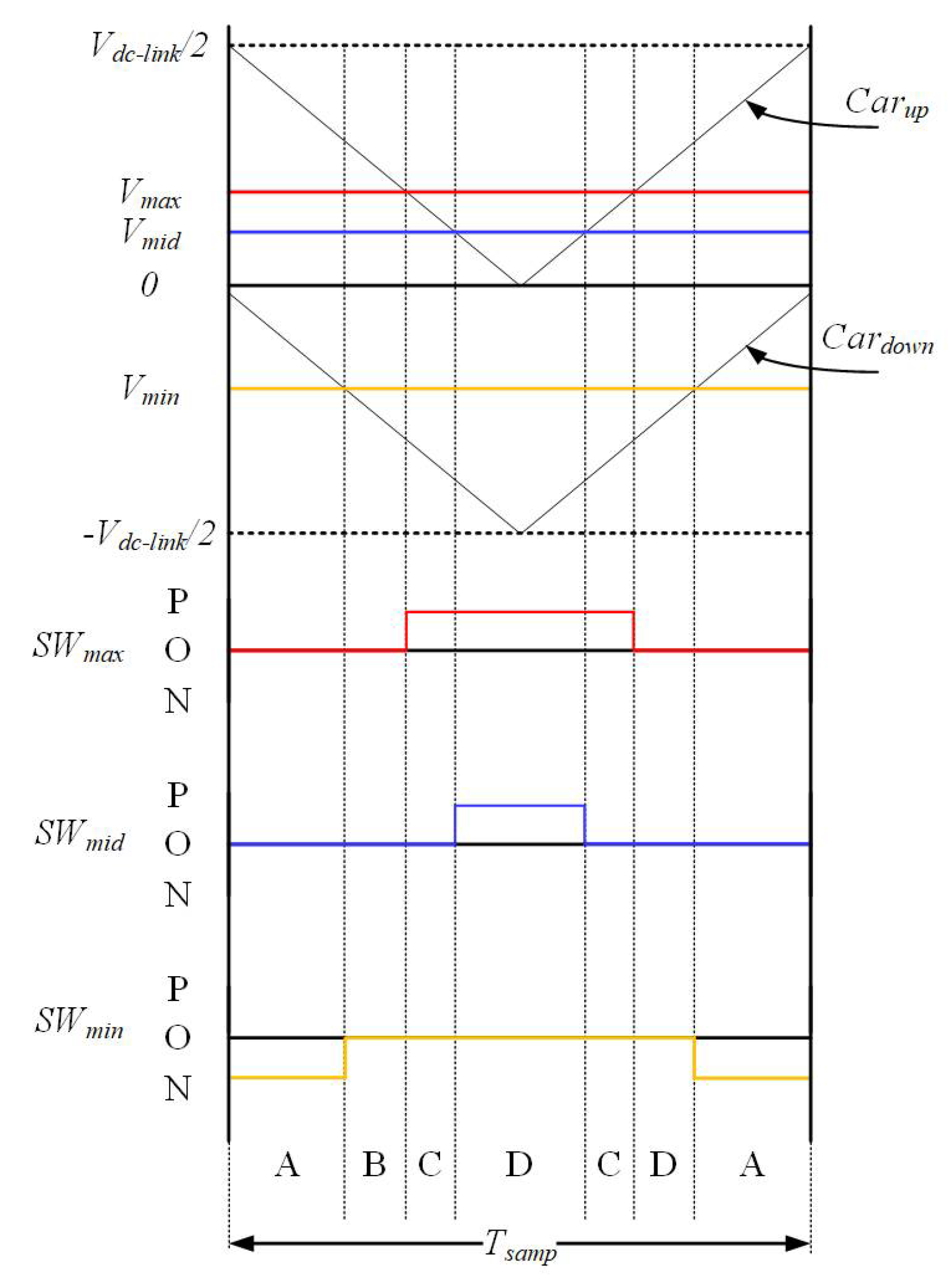
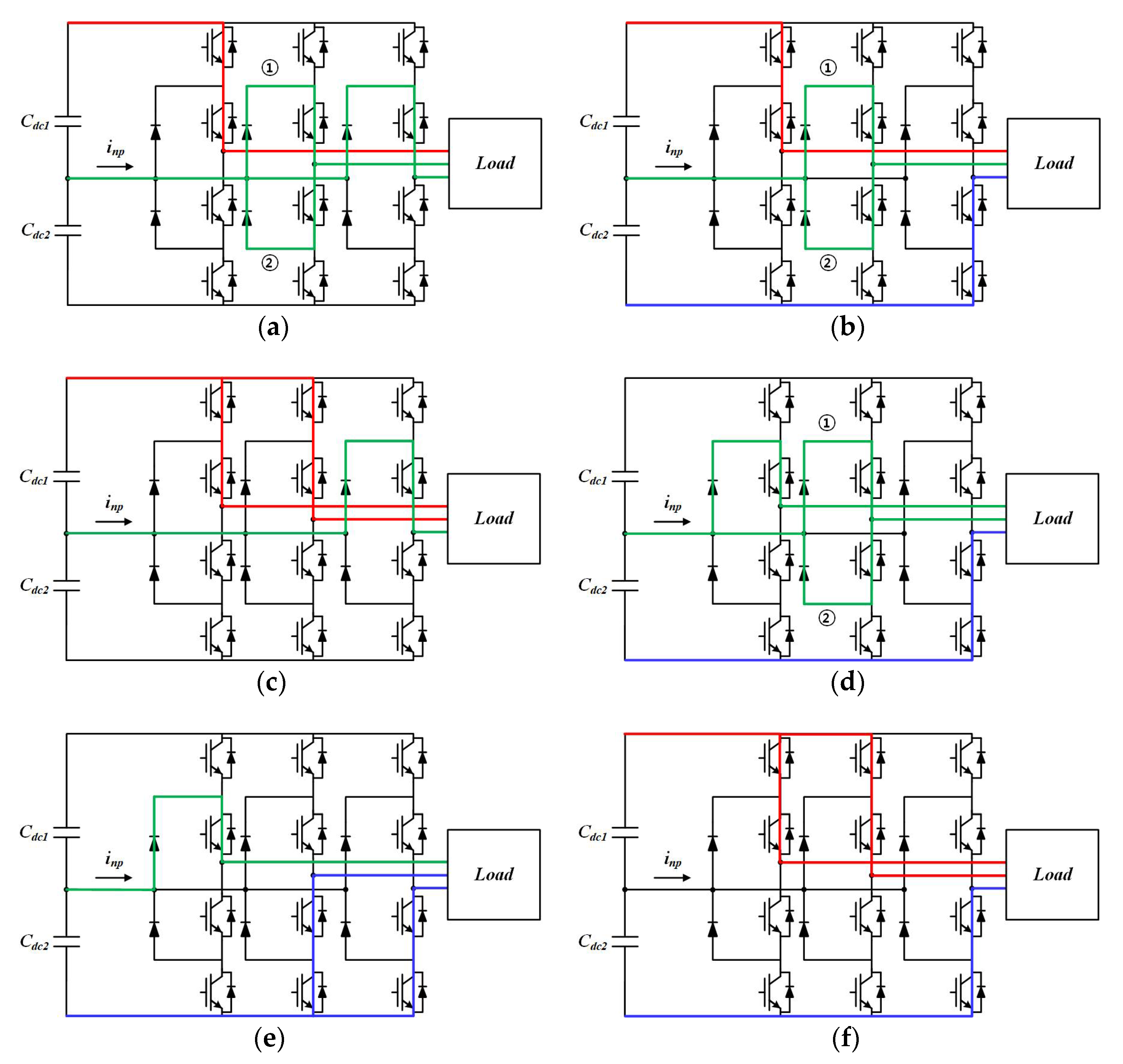
For the carrier-based PWM (CB-PWM), the switching state is as shown in Figure 4. During the control period, the switching state changes six times. In sector A, the min-phase is in the N state; therefore, all of the switching states become [OON]. In sector B, the min-phase changed to the O state and all of the switching states become [OOO]. In sector C, the max-phase changed to the P state and the switching state becomes [POO]. Similarly, in sector D, the max-phase and min-phase hold the switching state, and the state of the mid-phase changes to the P state. Therefore, the switching state is changed [PPO]. During the control period, the switching state changes as follows: A→B→C→D→C→B→A. The variation of neutral-point voltage according to the switching state is given in

Table 1. Neutral-point voltage fluctuation according to the switching state.

Switching State			Neutral-Point Current	Neutral-Point Voltage
Max	Mid	Min
P	O	O	−Imax	Increase
	O	N	Imid	Imid > 0	Decrease
				Imid < 0	Increase
	P	O	Imin	Increase
O	O	N	−Imin	Decrease
	N	N	Imax	Decrease
PPN, PNN, OOO			None	Constant

.

The neutral-point voltage (V_dc2 − V_dc1) varies depending on the switching state and the direction of the neutral-point current I_np. Figure 5a shows the [POO] switching state. The max-phase switch is the P clamping state. In this case, the neutral-point is connected to mid- and min-phases. Therefore, the neutral-point current equals −I_max. In addition, the upper capacitor, C_dc1 is discharged. As a result, the neutral-point voltage will decrease. Figure 5b shows the [PON] switching state. The max-phase switch is in the P clamping state and the min-phase switch is in the N clamping state. In this case, the neutral-point is connected to the mid-phase. Therefore, the neutral-point current is equal to I_mid. However, because the current in the mid-phase has either a positive or a negative value, the direction of the current has two cases. Assuming that I_mid is larger than zero, the neutral-point current flows to current path ① in Figure 5b and the voltage of the lower capacitor is discharged. Therefore, the neutral-point voltage increases.

Figure 5c shows the [PPO] switching state. In this case, the neutral-point is connected to the min-phase. Therefore, the neutral-point current is equal to I_min. Then, the V_dc2 voltage increases, resulting in an increased neutral-point voltage. For the [OON] switching state, the neutral-point is connected to the max-phase and mid-phase. The neutral-point current is equal to −I_min. I_min, which is always a negative value. Therefore, in the [OON] state, the neutral-point voltage decreases because the neutral-point current is a negative value. Similarly, for the [ONN] switching state, the neutral-point is connected to the max-phase, and the neutral-point current is equal to I_max, as shown in Figure 5e. Because the value of I_max is always positive, the neutral-point voltage decreases. Finally, the [PPN] and [PNN] states are disconnected from the neutral-point. Therefore, the neutral-point voltage is constant.

It can therefore be confirmed that the variation of the neutral-point voltage fluctuates with the neutral-point current [26]. The v_max phase is always connected to point T, at during the product r_max and the T_samp. The v_min phase is always connected to point B, during the product |r_min| and T_samp. However, the pole of a phase with the middle value is connected to T or B when r_mid is positive or negative during the product |r_mid| and T_samp. In addition, assuming that the three-phase output current, DC-link voltage, and the reference signal do not change during one control period, the current at the neutral-point, which is expressed in [27], can be given as:

$${\langle I_{np}\rangle }_{Ts}=-{\langle I_{max}\cdot \left|r_{max}\right|+I_{mid}\cdot \left|r_{mid}\right|+I_{min}\cdot \left|r_{min}\right|\rangle }_{Ts}$$

(11)

where I_max, I_mid, and I_min are output currents that flow during each turn-on period of r_max, r_mid, and r_min, respectively. <x>_Ts represents the average value during one control period.

In the switching waveforms shown in Figure 4, additional switching should be injected to minimize the neutral-point voltage for the ripple minimization in the neutral-point voltage. Therefore, the offset is added to the reference signal to minimize I_np. The mean value of I_np, which is added to the reference signal by the offset, is as follows:

$${\langle I_{np}\rangle }_{Ts,off}=-{\langle I_{max}\cdot \left|r_{max}+r_{off}\right|+I_{mid}\cdot \left|r_{mid}+r_{off}\right|+I_{min}\cdot \left|r_{min}+r_{off}\right|\rangle }_{Ts}$$

(12)

In (12), r_max is always positive and r_min is always negative. However, r_mid and r_off can have either a positive or negative value. In addition, r_off should be lower than r_max and higher than r_min.

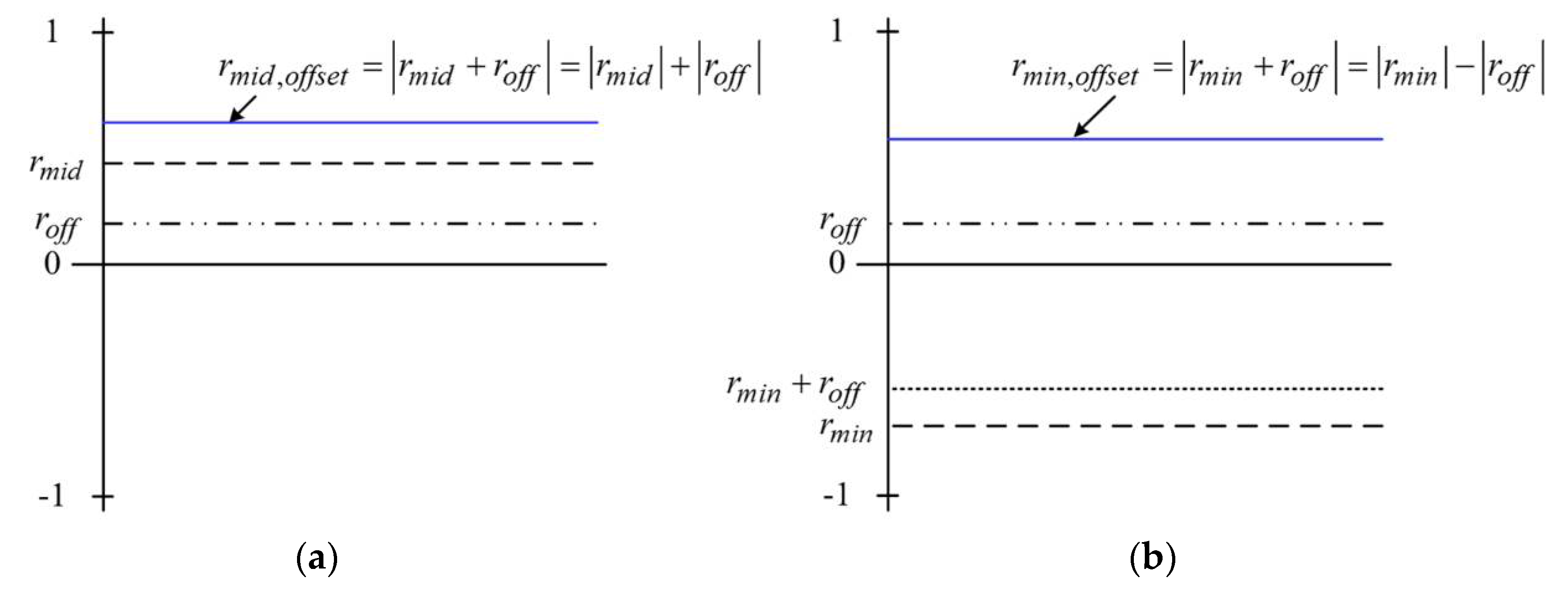
Case 1 (r_mid > 0 and r_off > 0): Assuming that r_mid > 0, as shown in Figure 6, r_min,offset, which is added to r_off, is subtracted from the absolute value of r_min to the absolute value of r_off. Then, using (11), the neutral-point current is added to the compensation value as follows:

$${\langle I_{np}\rangle }_{Ts,off,case1}^{}={\langle I_{np}\rangle }_{Ts}-{\langle I_{max}\cdot \left|r_{off}\right|+I_{mid}\cdot \left|r_{off}\right|-I_{min}\cdot \left|r_{off}\right|\rangle }_{Ts}$$

(13)

From (13), r_off, which causes <I_np>_Ts* to be zero, is derived as follows:

$$\left|r_{off}\right|=\frac{I_{np}}{I_{max}+I_{mid}-I_{min}}$$

(14)

Because the denominator should have a positive value, r_off can be expressed as:

$$r_{off}=\frac{I_{np}}{I_{max}+I_{mid}-I_{min}},I_{np}>0$$

(15)

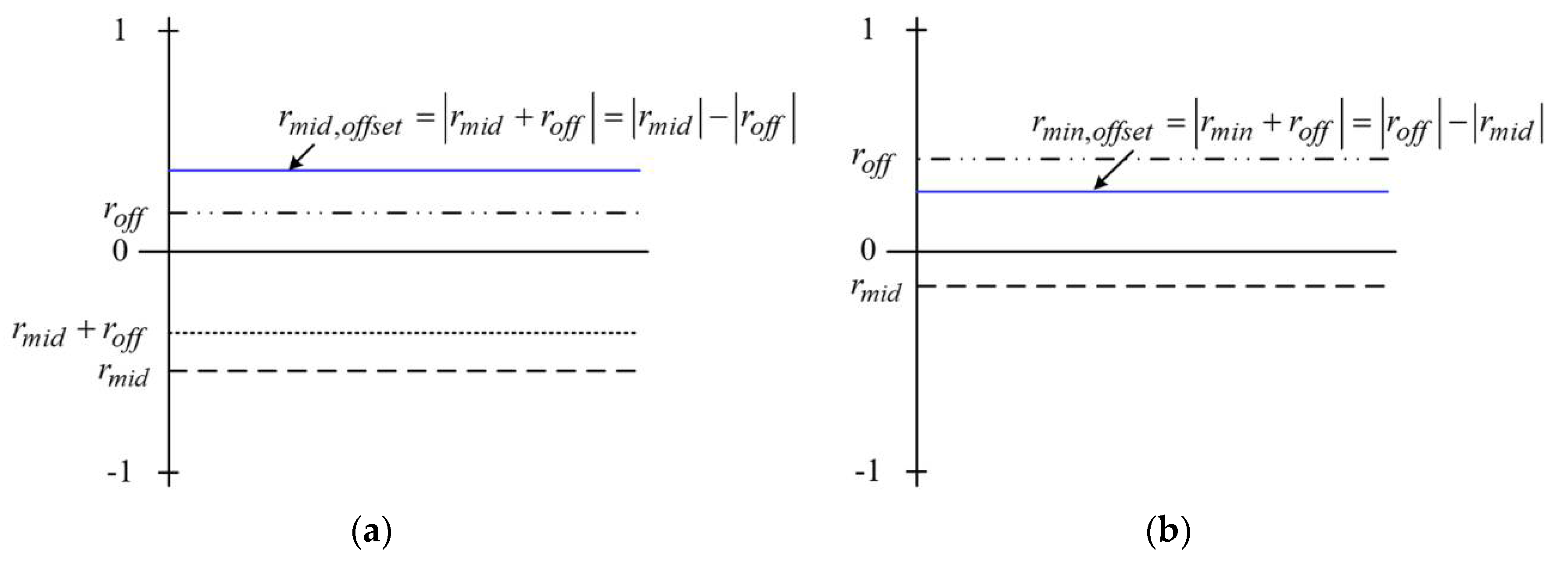
Case 2 (r_mid < 0 and r_off > 0): In this case, <I_mid∙|r_mid+r_off|>_Ts has two cases, as shown in Figure 7.

In case 2, the two values were compared to calculate two each value. First, in case 2-1, assuming that |r_mid| > |r_off|, the neutral-point current is as follows:

$${\langle I_{np}\rangle }_{Ts,off,case2-1}^{}={\langle I_{np}\rangle }_{Ts}-{\langle I_{max}\cdot \left|r_{off}\right|-I_{mid}\cdot \left|r_{off}\right|-I_{min}\cdot \left|r_{off}\right|\rangle }_{Ts}$$

(16)

Similar to case 1, the value for making the neutral current equal to zero is derived as:

$$r_{off}=\frac{I_{np}}{I_{max}-I_{mid}-I_{min}},I_{np}>0$$

(17)

In the second case 2-2, assuming that |r_mid| < |r_off|, the neutral-point current can be estimated as:

$$\begin{array}{ccc}{\langle I_{np}\rangle }_{Ts,off,case2-2}^{}& =& -{\langle \begin{array}{l}{I}_{max}\cdot \left|r_{max}+r_{off}\right|+I_{mid}\cdot \left(\left|r_{off}\right|-\left|r_{mid}\right|+\left|r_{mid}\right|-\left|r_{mid}\right|\right)+\\ I_{min}\cdot \left|r_{min}+r_{off}\right|\end{array}\rangle }_{Ts}\hfill \\ & =& {\langle I_{np}\rangle }_{Ts}-{\langle I_{max}\cdot \left|r_{off}\right|-I_{mid}\cdot \left(\left|r_{off}\right|-2\left|r_{mid}\right|\right)-I_{min}\cdot \left|r_{off}\right|\rangle }_{Ts}\hfill \end{array}$$

(18)

The offset value required to make the neutral current equal zero is as follows:

$$\left|r_{off}\right|=\frac{I_{np}+2\left|r_{off}\right|\cdot I_{mid}}{I_{max}+I_{mid}-I_{min}}$$

(19)

In this case, the denominator term is over zero, and r_off > 0. Therefore, r_off can be expressed as:

$$r_{off}=\frac{I_{np}+2\left|r_{off}\right|\cdot I_{mid}}{I_{max}+I_{mid}-I_{min}},I_{np}+2\left|r_{off}\right|\cdot I_{mid}>0$$

(20)

Case 1 and case 2 were calculated when r_off is positive. On the contrary, case 3 and case 4 calculate the offset value when r_off is a negative value.

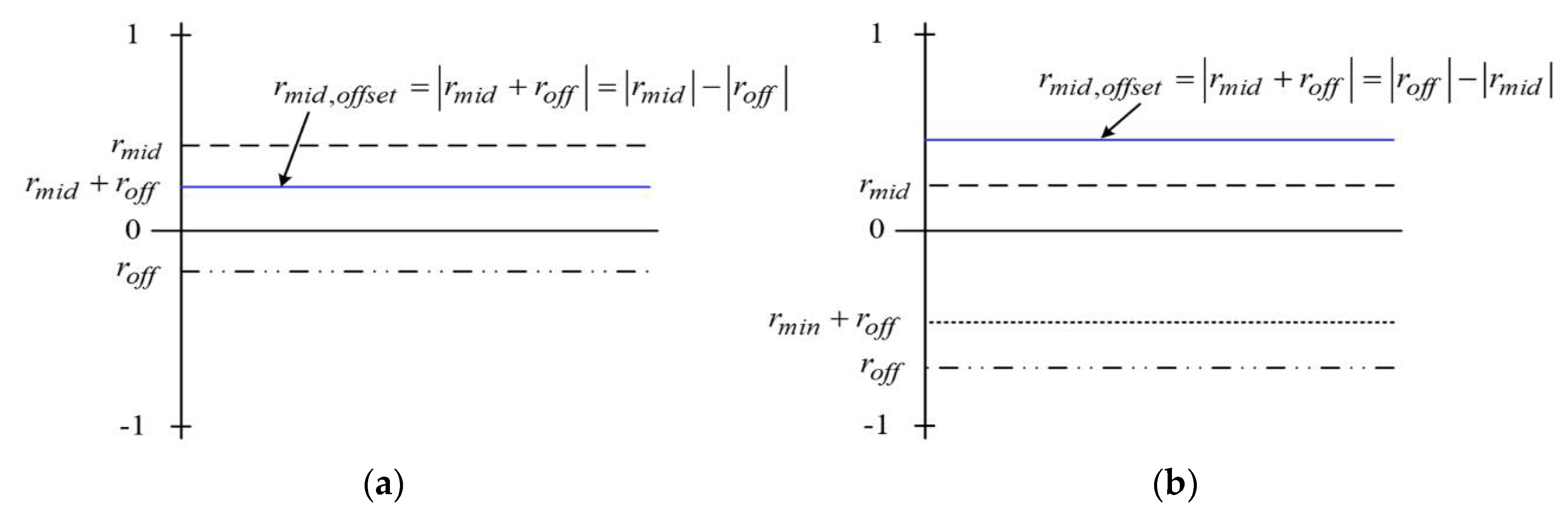
Case 3 (r_mid > 0 and r_off < 0): This case is similar to case 2 because the absolute value of r_off may be different from the absolute value of r_mid. Therefore, for case 3, there are two ways to calculate the offset value, which is shown in Figure 8.

In case 3-1, assume that |r_mid| > |r_off|; then, the neutral-point current is derived as:

$${\langle I_{np}\rangle }_{Ts,off,case3-1}^{}={\langle I_{np}\rangle }_{Ts}-{\langle I_{max}\cdot \left|r_{off}\right|-I_{mid}\cdot \left|r_{off}\right|-I_{min}\cdot \left|r_{off}\right|\rangle }_{Ts}$$

(21)

The offset value is used to compensate the neutral-point current equal to zero as:

$$\left|r_{off}\right|=\frac{I_{np}}{-I_{max}-I_{mid}+I_{min}}$$

(22)

In this case, because the denominator is less than zero, I_np must be negative. By using the condition that I_np and r_off are less than zero, the offset value can be expressed as:

$$r_{off}=\frac{I_{np}}{I_{max}+I_{mid}-I_{min}},I_{np}<0$$

(23)

For case 3-2, |r_mid| < |r_off|. Similar to case 2-2, the offset to make the neutral-point current equal to zero is given as:

$$r_{off}=\frac{I_{np}+2\left|r_{mid}\right|\cdot I_{mid}}{I_{max}-I_{mid}-I_{min}},I_{np}<0$$

(24)

Case 4 (r_mid < 0 and r_off < 0): In this case, the compensation value can be obtained similarly to case 1. Finally, the offset is used to make the neutral-point current equal to zero.

$$r_{off}=\frac{I_{np}}{I_{max}-I_{mid}-I_{min}},I_{np}<0$$

(25)

Based on the calculation for cases 1 to 4, r_off can be summarized as shown in

Table 2. Compensation value of AC ripple-reduction algorithm.

Requirement		roff
Inp > 0	rmid > 0	$r_{off}=\frac{I_{np}}{I_{max}+I_{mid}-I_{min}}$
	rmid < 0	$\left|r_{mid}\right|>\left|r_{off}\right|$	$r_{off}=\frac{I_{np}}{I_{max}-I_{mid}-I_{min}}$
		$\left|r_{mid}\right|<\left|r_{off}\right|$	$r_{off}=\frac{I_{np}+2\left|r_{off}\right|\cdot I_{mid}}{I_{max}+I_{mid}-I_{min}}$
Inp < 0	rmid > 0	$\left|r_{mid}\right|>\left|r_{off}\right|$	$r_{off}=\frac{I_{np}}{I_{max}+I_{mid}-I_{min}}$
		$\left|r_{mid}\right|<\left|r_{off}\right|$	$r_{off}=\frac{I_{np}+2\left|r_{mid}\right|\cdot I_{mid}}{I_{max}-I_{mid}-I_{min}}$
	rmid < 0	$r_{off}=\frac{I_{np}}{I_{max}-I_{mid}-I_{min}}$

.

However, in all regions, the sum of r_off and r_x.ref should be maintained within the range $[-1,1]$. Therefore, the range of each on-time ratio is determined as follows:

$$-1+\left|r_{min}\right|\le r_{off}\le 1-\left|r_{max}\right|$$

(26)

The final on-time ratio and the injected r_off can be derived as:

$$\begin{array}{l}{r}_{u,ref}^{*}=\frac{2\cdot v_m}{V_{dc-link}}\sin \omega t+r_{off}\\ r_{v,ref}^{*}=\frac{2\cdot v_m}{V_{dc-link}}\sin \left(\omega t-{120}^{\circ }\right)+r_{off}\\ r_{w,ref}^{*}=\frac{2\cdot v_m}{V_{dc-link}}\sin \left(\omega t+{120}^{\circ }\right)+r_{off}\end{array}$$

(27)

The reconfigured reference voltage obtained using the proposed method makes the average value of the neutral-point current for a switching period (<I_np>_Ts) equal to zero, thus suppressing the ac ripple in the neutral-point of the DC-link.

4. Simulation Results

Simulations were performed to verify the effectiveness of the proposed method using the tool PSIM. The simulation circuit of the drive system is given in Figure 2. The simulation parameters are indicated in

Table 3. Simulation parameters.

Parameter	Value
Vrms-line	220 (V)
Cdc-link	10 (μF)
Rload	10 (Ω)
Lload	1.6 (mH)
CDSC	15 (μF)
LDSC	1.5 (mH)

. The output fundamental frequency is 60 Hz and the output MI is 0.75. C_dc-link is the series value of C_dc1 and C_dc2.

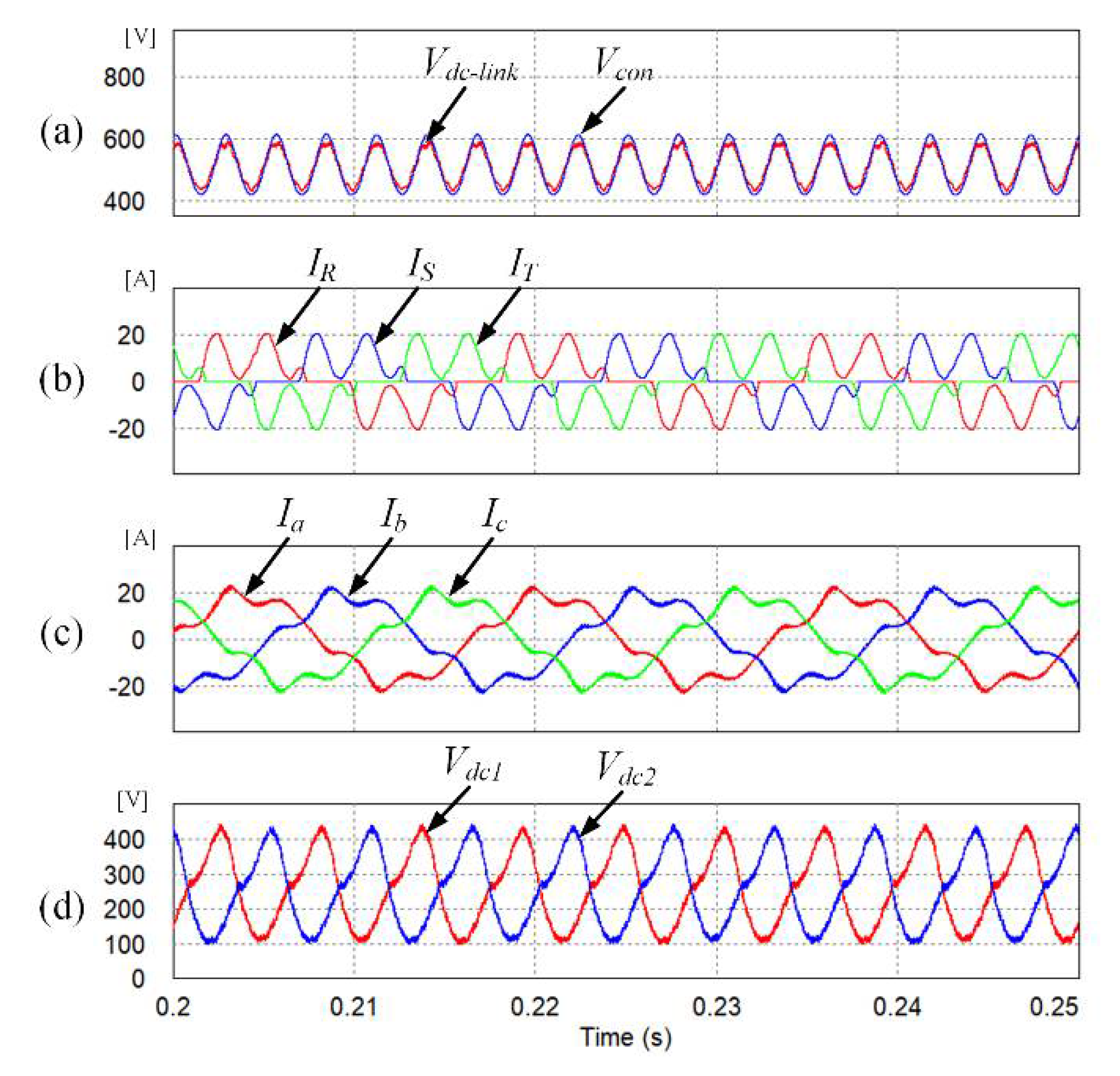
Figure 9 shows the simulation results of the three-level inverter without any proposed control scheme. The input current total harmonic distortion (THD) is 68.76%, which is not suitable for the limits of the THD specified by IEC 61000, which is the international standard for input current. In addition, Figure 9d shows the DC-link voltage of the three-level inverter. The neutral-point voltage ripple is very large when the algorithm is not applied. As a result, the output current THD is 17.78%, as shown in Figure 9c.

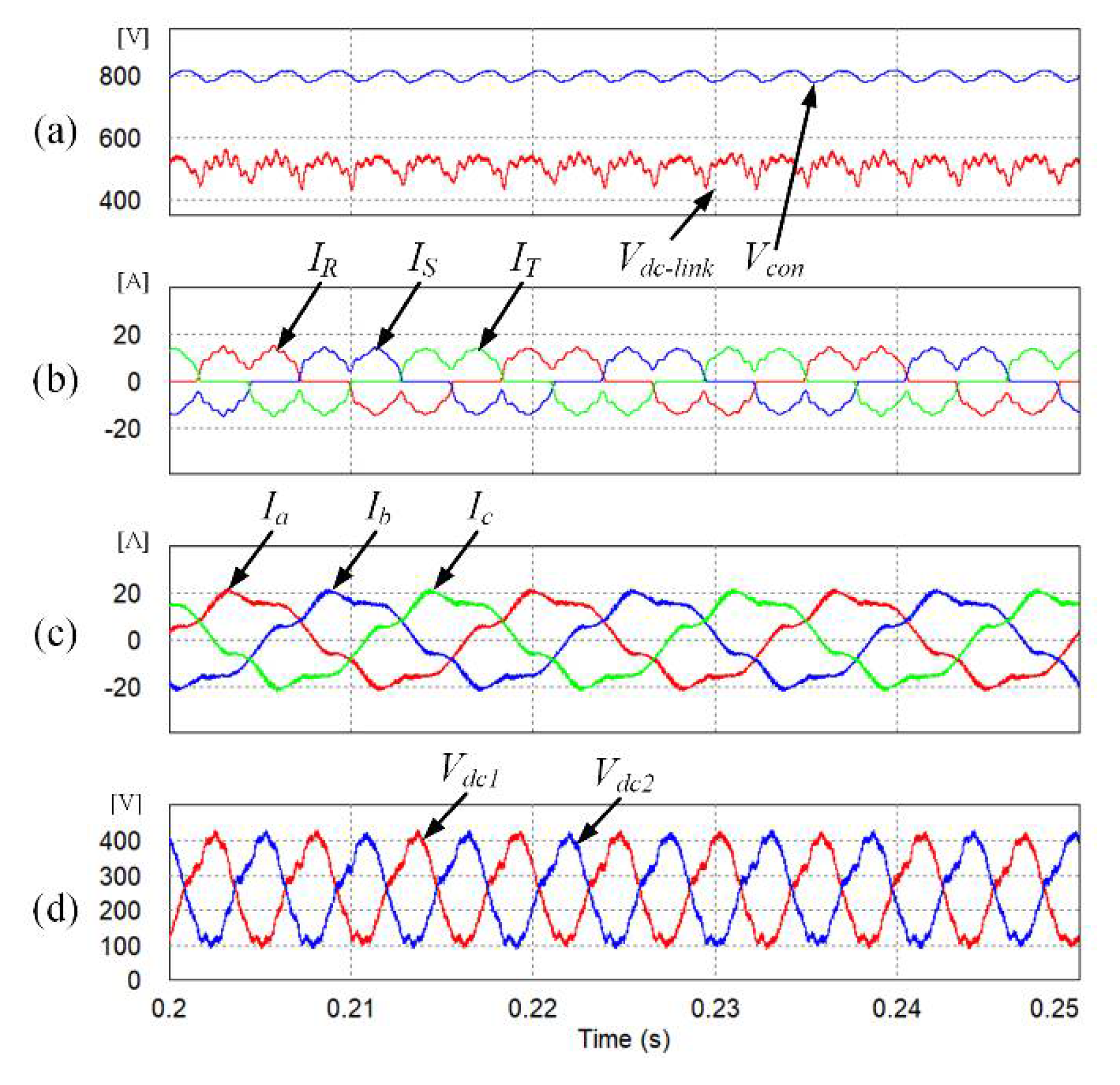
Figure 10a shows the DC-link voltage and the voltage V_con. V_con was set to 800 V using DSC control. Therefore, the quality of the input currents is improved and the THD becomes 37.57%. However, because the ripple of the neutral-point voltage was not reduced, the quality of the output currents was slightly improved. As a result, there is no improvement in the THD of the output currents, which is 14.44%.

However, because the ripple of the neutral-point voltage was not reduced, the quality of the output currents was slightly improved. As a result, there is no improvement in the THD of the output currents, which is 14.44%.

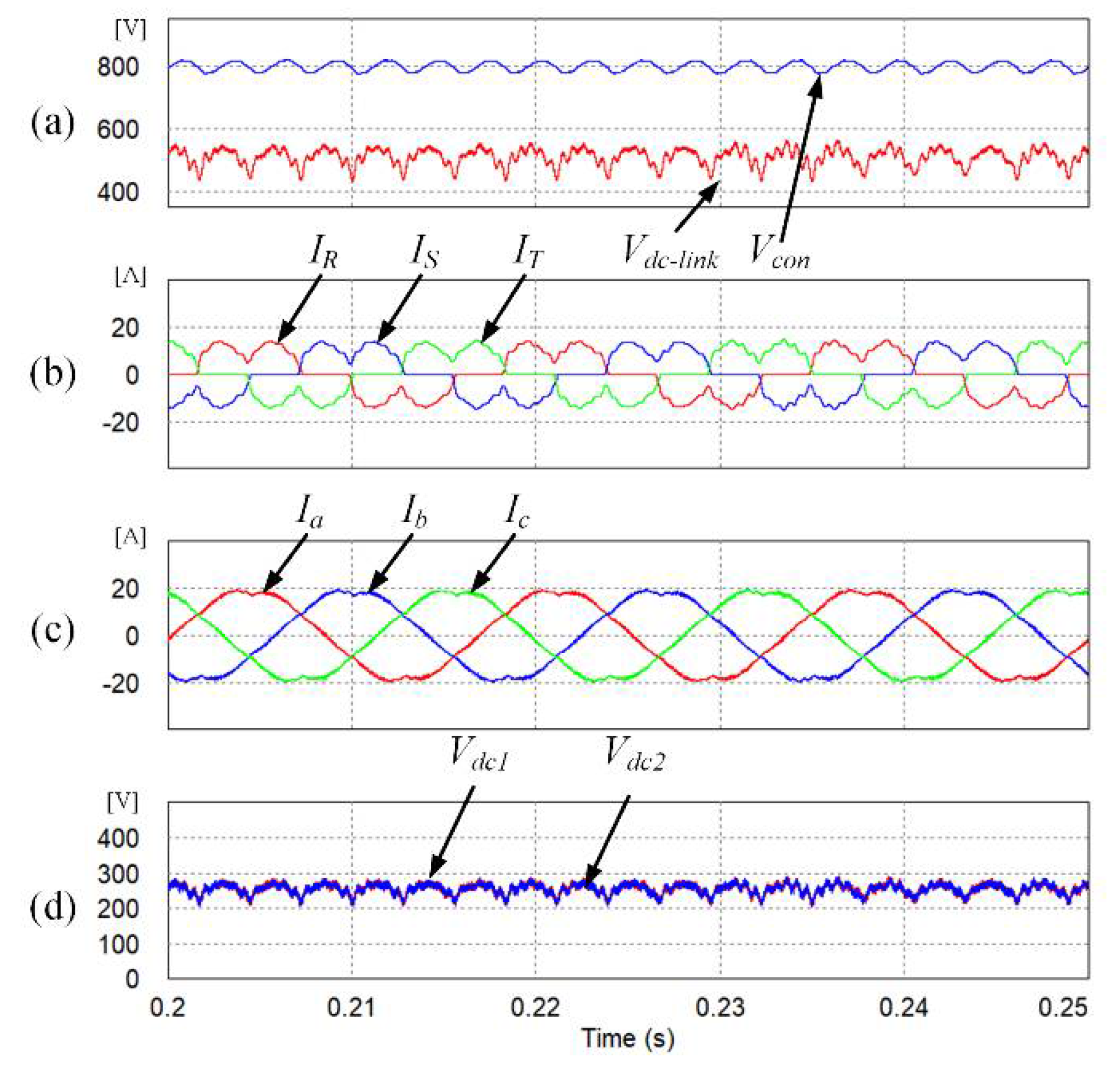
Figure 11 shows the simulation results obtained for the proposed algorithm, DSC, and the AC ripple-reduction. The DC-link voltage of the three-level inverter is shown in Figure 11d. The AC ripple-reduction algorithm reduces the neutral-point voltage. Finally, the THD of the input current is 36.42% and the output current is 5.14%.

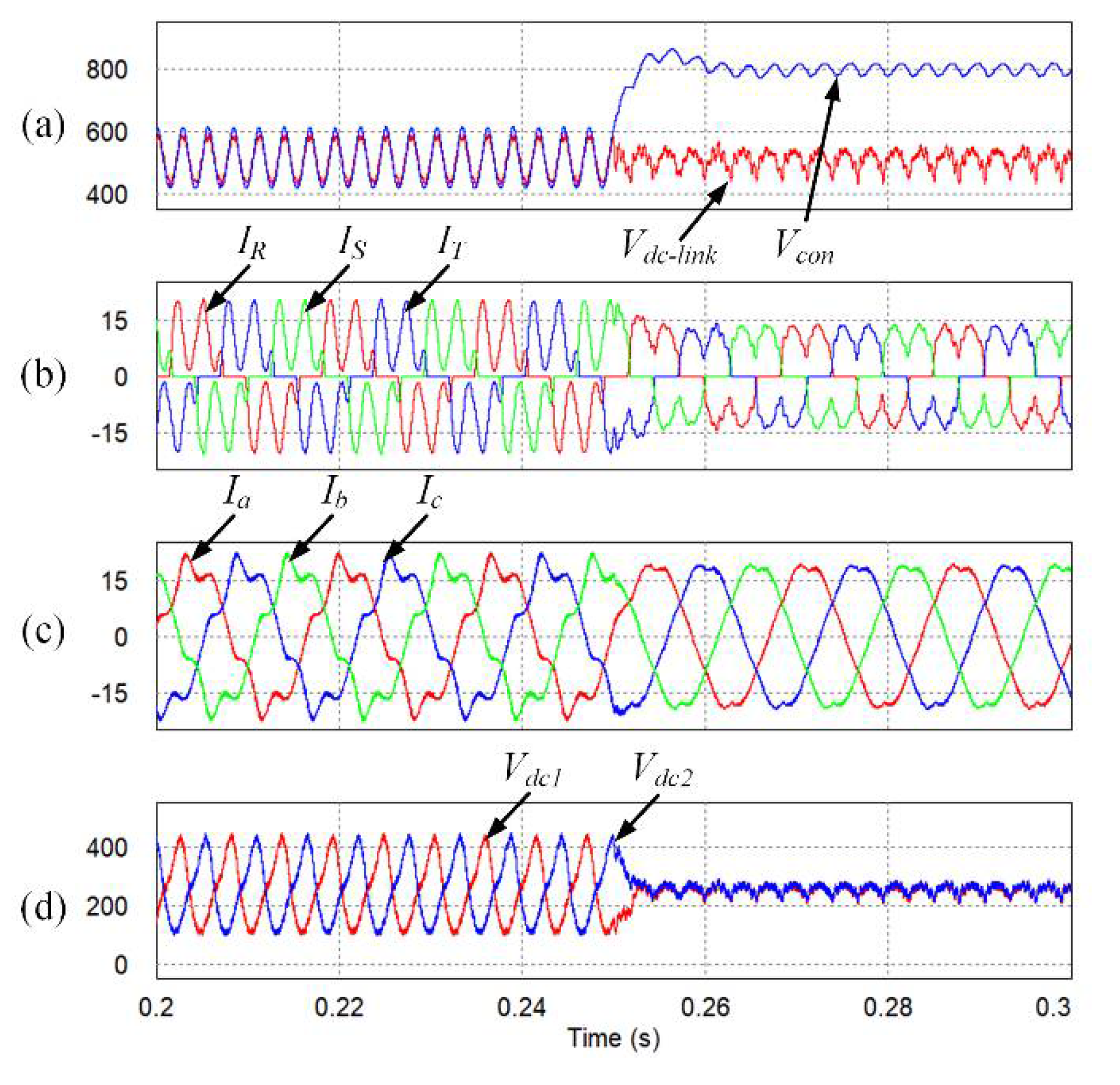
The simulation results of the transition operations are shown in Figure 12. The proposed algorithm is applied at 0.25 s. As the control scheme changes, the input–output currents are well controlled. Owing to the control scheme change, the quality of the input–output currents is improved and the ac ripple of the neutral-point voltage is reduced.

Finally, the THD of the input currents is improved from 67.50% to 36.51% by using the DSC. Furthermore, the THD of the output currents is improved from to 16.44% to 4.46% by using the ac ripple-reduction algorithm.

5. Experimental Results

The experimental results are presented to verify the feasibility of the proposed design and control method in actual implementation. Figure 13 shows the hardware set-up including a control board, NPC inverter and three-phase diode rectifier. The control board consists of a digital signal processor (DSP) TMS320F2833 (Texas Instruments Co., Dallas, TX, USA) and other peripherals. The parameters of the experiment are the same as the simulation, as indicated in Table 3.

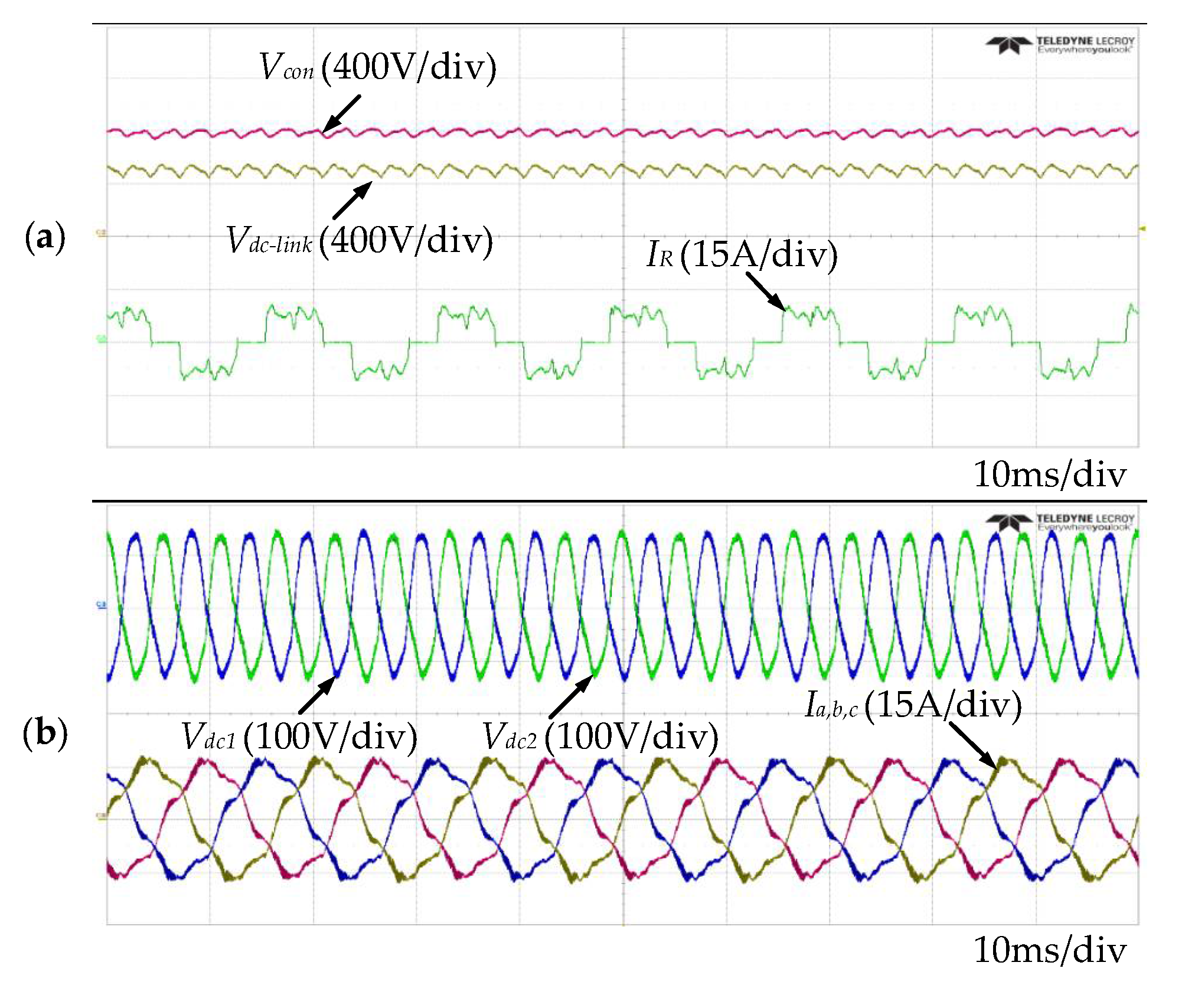
Figure 14 shows the experimental results obtained for the case using the conventional sinusoidal pulse-width modulation (SPWM). The DC-link voltage fluctuates at 538 V owing to the presence of the diode rectifier. Because the DSC controls are not performed, V_con has the same magnitude as V_dc-link. Therefore, the input current quality is very low and the THD is 59.07%. Figure 14b shows the capacitor voltage in the DC-link and the output current. In the three-level NPC inverter, the output pole voltage is not constant because of the fluctuating neutral-point voltage, so the output current is distorted. V_dc1 and V_dc2 have voltage ripples of about 250 V, and the THD of the output current is 13.2%.

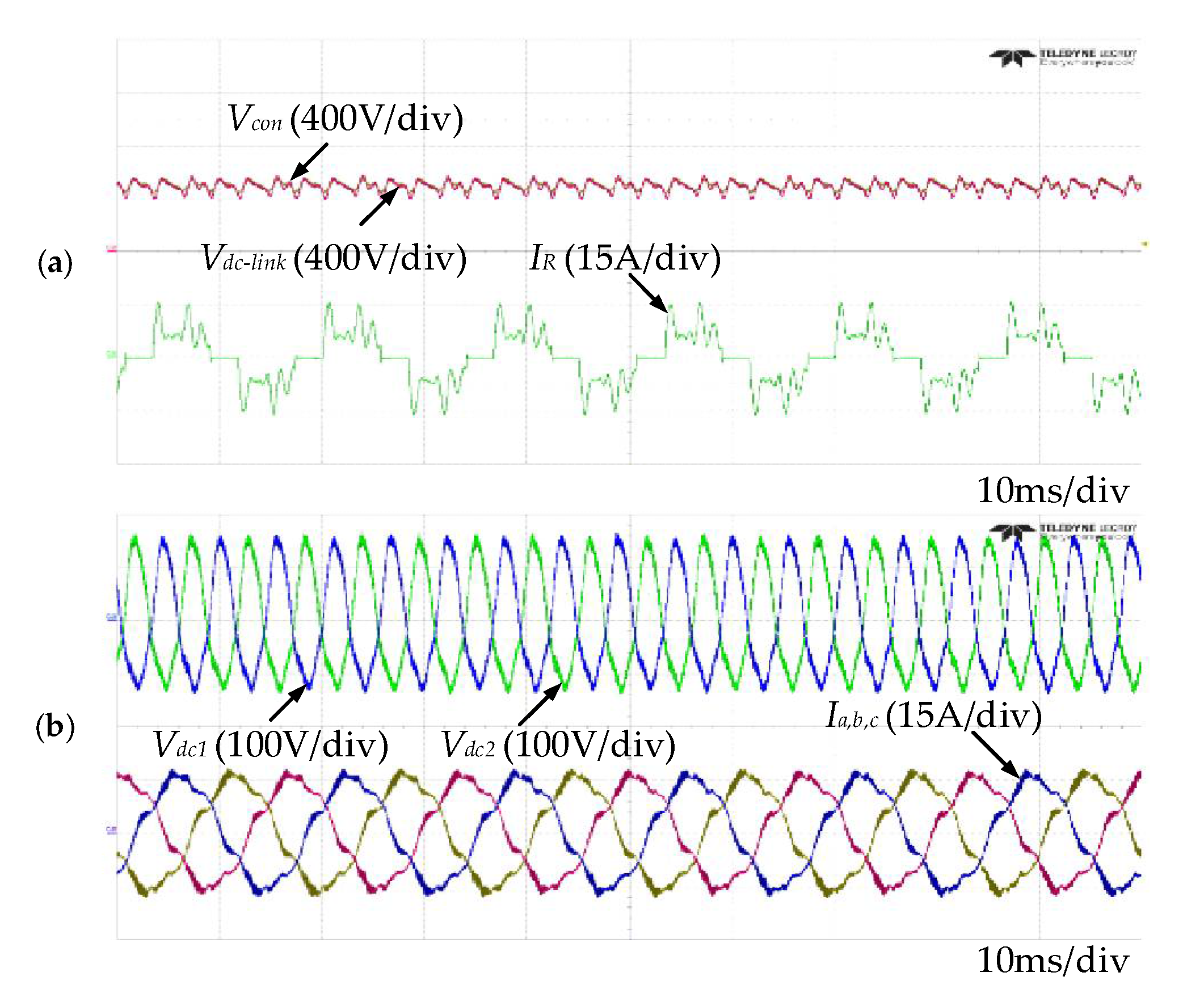
Figure 15 shows the experimental waveforms for the DSC control. Figure 15a shows the DC-link voltage and the input current. Because the DSC in not applied, the THD of the input current is equal to 53.18%. Figure 15b shows the waveform after the ac ripple-reduction algorithm is applied.

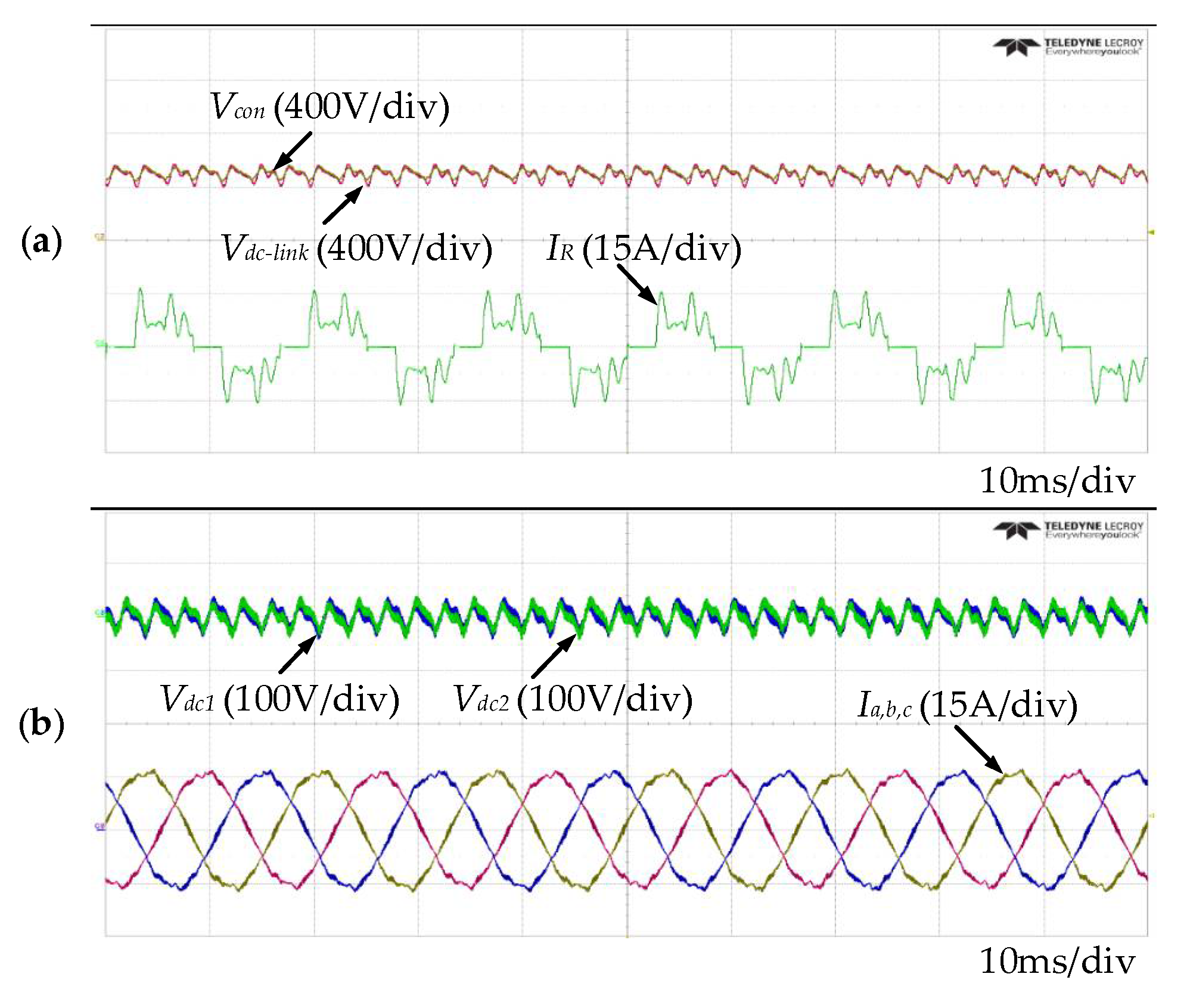
Figure 16 shows the experimental waveforms obtained when only the ac ripple-reduction control is applied. Figure 16a shows the DC-link voltage and the input current. The DC-link voltage fluctuates at 538 V because of the diode rectifier, as shown in Figure 14a. V_con was set to 800 V. DSC control improves the quality of the input currents, and the THD is improved to 35.68%. Moreover, the magnitude of the AC ripple in the neutral-point voltage was reduced to 50 V. As a result, the output pole voltage becomes more constant and the quality of the output currents is improved. In this case, the THD of the output currents is decreased to 2.13%.

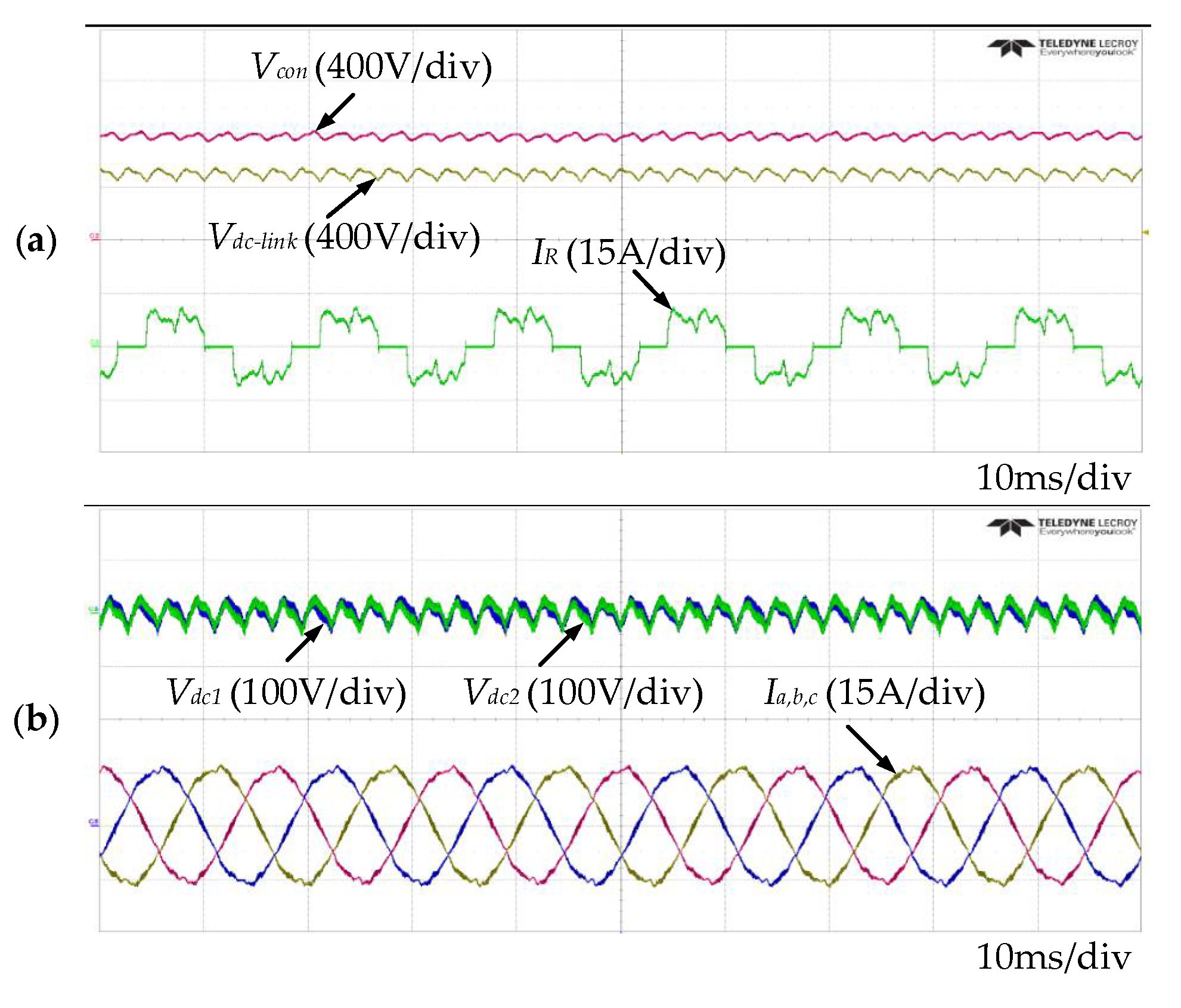
Figure 17 shows the output waveform of the proposed algorithm. The DSC circuit improves the quality of the input current. In addition, the ac ripple-reduction of the neutral-point voltage algorithm improves the quality of the output current. As shown in Figure 17a, the voltage of V_con was maintained at 800 V. In this case, the THD of the input current is 35.78%. Figure 17b shows the voltages V_dc1 and V_dc2 after applying the ac ripple-reduction algorithm, and the distortion of the output current was reduced. The output current THD is equal to 1.75%.

6. Conclusions

In this paper, a method to improve the input–output currents quality for a three-level NPC inverter was proposed. It is desirable to replace a high-capacity electrolytic capacitor with a small-capacity film capacitor because of problems with the former with respect to life-time, reliability, and system volume. To reduce the capacitance and volume of the capacitors, the electrolytic capacitors were replaced by film capacitors. Small-capacity inverter systems are beneficial for applications such as fans, pumps, and compressors, where the load variation is not significant. Two control methods were applied to solve the problem caused by small capacitance values. The proposed method calculates the compensation value to reduce the neutral-point voltage ripple. This value is added to the reference signal considering the current section of the reference voltage. As a result, the output current THD was improved from 13.2% to 1.75%. In addition, the DSC circuit was used in this paper. The input current THD was improved from 59.07% to 35.78% in order to satisfy the 4th grade of IEC 61,000. The feasibility of the proposed system was demonstrated by performing both simulations and experiment.