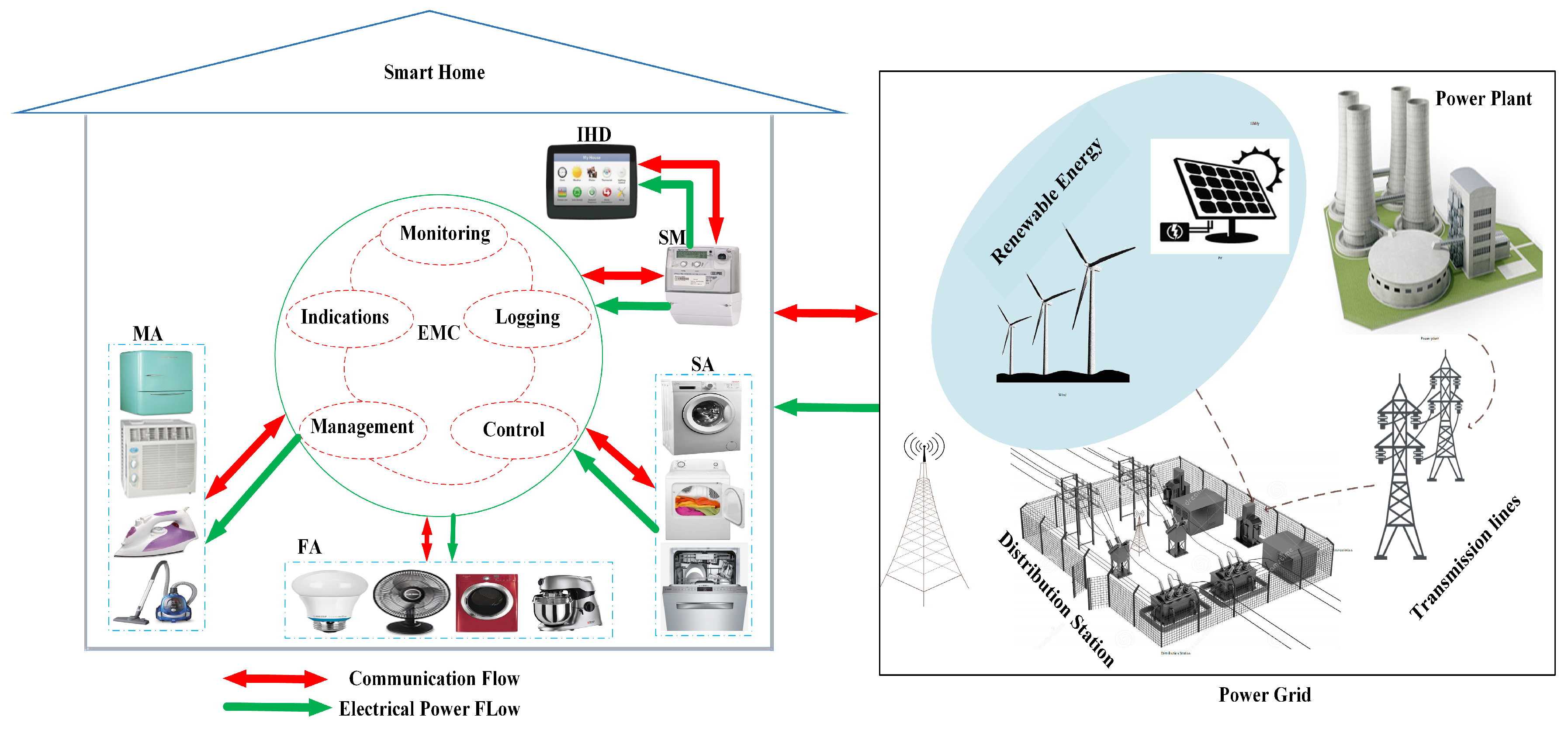
1. Introduction
The gap between energy demand and generation is increasing rapidly which affects the reliability and stability of existing power systems [
1]. Although peak generators which operate on fossil fuels or natural gases fulfill the energy demand during peak hours and avoid blackouts [
2], emission of green house gases and expensive cost of electricity, generated by these generators, generates the need of smart grids with integration of information and communication technologies. The use of information communication technology plays a very important role in making smart grids stable and reliable [
3]. The smart grid enables the bi-directional communication in traditional power grids. Demand response (DR) programs are used to match the supply and demand between the electricity consumer and the utility. In residential and commercial buildings, more than 60% of electricity consumption can be saved by efficiently integrating DR programs [
4]. A home energy management system (HEMS) performs a vital role in enhancing the effectiveness of the smart grid. The successful integration of HEMS with electricity tariffs and a DR program is favorable for the utility as well as for the end consumers. Thus, this results in optimal load shaping and electricity bill reduction.
The smart grid has two main elements: DR and demand side management (DSM). Many utility companies are adopting different DSM strategies to encourage the consumers to efficiently use electricity. Moreover, to motivate the electricity consumers for minimize the wastage of electricity, various incentives are introduced by utility companies. This enables the consumers to voluntarily alter the electricity usage patterns in an optimal fashion to minimize the electricity bill. These strategies provide an equilibrium between electricity load demand and supply from the utility. Numerous benefits are provided by DR programs to electricity consumers [
5]. These programs persuade the consumers to change their life style i.e., change electricity utilization patterns according to dynamic electricity rates. The end consumers minimize the electricity expenses along with peak to average ratio (PAR) by efficiently managing the electricity utilization profiles. Around the globe, utility companies also establish numerous electricity tariffs: real time pricing (RTP) schemes, critical peak pricing (CPP) schemes, etc. to help the end consumers. In residential sector, major objectives considered for efficient load management are: reduction in PAR, minimization of electrical bills and greenhouse gas emissions to smart grids. In recent years, a lot of heuristic techniques and DSM schemes have been presented to cope with these aforementioned challenges. Moreover, other techniques such as linear programming, mixed integer linear programming, mixed integer non-linear programming, etc. are also used to reduce the electricity utilization cost and efficiently schedule of household load. Though, in literature, a number of popular heuristic and non-heuristic techniques are available such as particle swarm optimization, mixed integer non-linear programming, elephant herding optimization (EHO), adaptive cuckoo search (ACS) etc., to cope with the aforesaid challenges.
In this study, a hybrid optimization algorithm is proposed based on the distinctive qualities of EHO and ACO. The EHO has an effective global search capabilities with inherent restrains of high execution time [
6]. Whereas, ACS has an efficient searching process with precise searching capabilities [
7]. Both algorithms have some advantages. In order to fully utilize the capabilities of both techniques, a hybrid technique (HEAC) is proposed. This technique globally explores the search space by using updating operator of EHO and searches locally by using ACS operators. A balance is maintained between exploration and exploitation. Hence, it achieves optimal results in less computational time.
This study is the extension of [
8], a HEM scheme is presented which is a hybrid of: ACS and EHO algorithms and named, hybrid elephant adaptive cuckoo (HEAC). Moreover, we also calculate the consumer satisfaction (comfort) level. Dynamic programming (DP) and cooperative game theory (GT) are used to enable the coordination among electrical devices. The knapsack problem is solved by DP to obtain an efficient schedule of electrical devices, whereas, a GT-based coordination system is also introduced which uses shapley values to assign the time interval to the electrical devices [
9]. The electricity pricing scheme ToU is implemented for electricity utilization cost calculation. Furthermore, simulations are carried out for two case studies: hot and cold regions. The control parameters remain the same for all three heuristic techniques. However, the living habits of consumers and power ratings of all electrical devices are different in both regions.
The focus of this study is to maximize the participation of the consumers to reduce the gap between energy demand and supply. Moreover, an efficient management of electricity utilization and to achieve minimum electricity cost along with the PAR reduction are also the objectives of this study. The main contributions are given below:
A hybrid technique is designed which provides an optimal solution with minimum execution time via effectively exploring and exploiting the search space.
We also introduce coordination among electrical devices.
The smart electrical devices are able to coordinate with each other in order to reduce electricity cost and minimize PAR.
The performance analysis is also provided for cold and hot regions on the basis of numerous performance parameters.
The organization of the remaining paper is as follow: literature work is presented in
Section 2.
Section 3 explains the problem description. In
Section 4, we present the system model and proposed techniques are uncovered. Simulation results are depicted in
Section 5. At the end, the paper is concluded in
Section 6.
2. Related Work
Due to the increase in demand with increasing populations and scarce energy generation resources, the power system is suffering from numerous challenges, for instance, management of electricity load, cost reduction of energy utilization and increasing consumer comfort. Research efforts have been made to address the aforementioned issues, an optimal scheduling of load is one of the solutions. Therefore, a number of heuristic techniques have been proposed and implemented in recent years to schedule the electricity load.
Wen et al. in [
4] proposed a novel scheme for managing energy for small commercial and residential buildings. This scheme used reinforcement learning to formulate the rescheduling problem. Additionally, for job scheduling, the reinforcement learning does not need the modeling of consumer’s dissatisfaction. Thus, the energy management system (EMS) can initiate task execution which results in flexible requests from the consumers.
In [
10], Shirazi and Jadid presents an algorithm for managing energy resources. This scheme uses dynamic pricing for scheduling electrical devices which are controllable in off-peak hours and ensure efficient electricity utilization. Mixed integer non-linear programming is used for modeling the energy management based on dynamic pricing mechanism. The authors divided the time period of 24 h into forty eight slots each of which is of 30 min. In addition, thermal power sources are adopted in peak hours to reduce the cost of electricity.
To control and manage the electrical devices [
11], a consumer preference based algorithm is proposed. To evaluate the performance of the algorithm, different scenarios are taken into consideration and implemented by assigning priorities to electric devices. Results show that the proposed model efficiently manages the load resulting in minimum cost and PAR. However, comfort is compromised.
Ahmad et al. in [
12] proposed an algorithm which integrates the energy storage system and renewable energy source with residential domains. The multiple knapsack problem is used to formulate constraint optimization problems and is implemented by using GA, wind driven optimization, binary particle swarm optimization, and bacterial foraging optimization (BFO). Authors also proposed a hybrid technique named hybrid genetic particle swarm optimization. The hybrid genetic particle swarm optimization based HEM system achieved
% decrease in electricity cost and
% reduction in PAR. In addition, integration of renewable energy sources and energy storage systems minimizes the electricity bill by
% and PAR by
%. The PAR minimization ensures the reliable and stable power grid operations.
Samadi et al. in [
13] proposed a game theory based scheme to model the interaction of consumers with excessive amount of electricity generation. Further, this local generation enables the stability of the utility by reducing the load. The extensive simulation results illustrate the superiority of the proposed algorithm in terms of reduction in electricity bill.
An HEM model is proposed in [
14], to optimally balance the load in peak hours based on day ahead RTP scheme. They also proposed a hybrid scheduling technique and incorporate coordination which enables the consumers to make changes in schedules at run-time for reducing waiting time. Moreover, a study is provided which evaluates the scheme based on pricing schemes; RTP, ToU, and CPP. Results illustrate the significant minimization in aggregated electricity bills. However, a trade-off exists between consumer comfort and the electricity bill.
In [
15], the authors proposed a multi-layer ant colony optimization (EMS-MACO) algorithm to reduce electricity production cost by finding the optimum micro-source operation. Moreover, to analyze the performance of the algorithm, technical and economic time dependent constraints are taken into consideration. Additionally, the effectiveness of MACO was checked by modifying particle swarm optimization and conventional EMS. The electric cost is considerably reduced as compared to MCEMS and particle swarm optimization.
Ma et al. in [
16] formulated the scheduling problem to attain minimum electricity cost and maximum consumer comfort. Two classes of consumer electrical devices are considered in this article. Delay tolerant electrical devices are included in the first and second classes, throttle-able devices are considered. This scheme showed that the ability to schedule electrical devices flexibly provides a balance between the electricity cost and consumer comfort.
An intelligent framework for energy management is presented in [
17]. In this scheme, through energy storage and electrical device scheduling, consumers gain benefits in terms of less electricity cost during heavy load in off-peak hours. Further, consumers buy electricity from the grid when prices are low and use storage devices when prices are high because of high load in peak hours. Integration of storage devices helps in reducing the PAR and makes the power system stable.
An effective approach for the load allocation problem is proposed in [
18]. In this scheme, four parameters (price, fairness, demand, and priority) are used to assign electricity resources to the consumers. Based on the computed priority, the electrical devices can execute its operation without any interruption. Then, the energy sources are assigned to remaining electrical devices for reducing the peak load.
In [
19], an efficient HEM scheme is proposed using three heuristic algorithms: GA, the crow search algorithm, and cuckoo search optimization algorithm. The efficient load management for electricity cost minimization along with maximum consumer comfort is the objective of this study. Additionally, they also integrate the energy storage system with HEMS to minimize the load. Furthermore, two case studies: single home and multiple homes are done to check the scalability of the proposed scheme based on RTP and CPP pricing signals. Experimental results show the effectiveness of the scheme for cost and PAR minimization for both scenarios (single and multiple homes). However, a trade-off between consumer comfort (waiting time) and electricity bill is observed.
From extensive literature analysis, it is observed that generally researchers focused on various conflicting multi-objective problems. Moreover, for minimizing electricity cost and PAR, consumer comfort is compromised (high waiting time). Further, some of the existing literature focuses on the maximization of consumer comfort along with the minimization of electricity bill and PAR.
3. Problem Description
In smart grid, maximization of consumer’s comfort level, reduction of energy utilization cost and PAR are some of the major challenges. However, a trade-off always exists between these performance parameters. The consumer’s comfort is usually sacrificed to minimize the electricity cost and PAR. The above mentioned issues are addressed by numerous techniques.
Authors proposed a HEM model in [
14], to optimally stabilize the load during off peak and on peak hours based on day ahead RTP scheme. They also proposed a hybrid scheduling technique and incorporate coordination which enables the consumers to make changes in scheduler at run-time. Moreover, the performance of the proposed work is evaluated based on three pricing schemes: ToU, RTP, and CPP. Simulation results illustrate the significant minimization in electricity bills. However, a trade-off exists between the consumer satisfaction and aggregated electricity utilization cost. In [
15], a generic model of EMS, incorporated with home area network (HAN) is proposed. Additionally, an effective scheduling strategy is also introduced for home electricity utilization. They use a well known heuristic technique GA to solve optimization problems on the basis of merged RTP and inclined block rate (IBR) pricing signals to manage the operations of all electrical devices in an efficient way. Simulation results illustrate that a significant reduction in electricity bill and PAR is achieved. However, there is no mechanism to facilitate the consumer preferences. Adika et al. in [
18], classify electrical devices into two classes: (i) electrical device decides that can bear delay and (ii) low power tolerant electrical devices. An equilibrium between the discomfort level of the consumers and electricity utilization cost is effectively achieved in their work. However, the computational complexity and processing time of their work are very high. In [
20], the authors proposed an approach for heterogeneous electrical devices to efficiently allocate the electricity resources on the basis of fairness, demand, price, and priority. The higher priority electrical devices complete their operation even in peak hours. The electricity resources are then allocated to as many electrical devices as possible in the remaining time. Additionally, the energy storage systems are also integrated to store electricity in low-price hours for emergency usage. However, the cost of installation and maintenance of energy storage systems is not considered.
4. Proposed System Model
Major objectives of this work are: (i) efficient management of load; (ii) minimization of PAR and electricity utilization cost. Additionally, the consumer comfort (waiting time) is also considered.
Figure 1 illustrates the proposed system model. In this work, a smart home with multiple electrical devices is considered with different length of operation time (LoTs) and power rates (PRs) which are taken in advance from the end consumers. This information is stored in centralized units where the embedded system based EMC schedules the electrical devices according to the consumer defined LoTs. To provide cost-effective communication in HAN, Zigbee, Zwave, and wifi are widely adopted communication protocols. Furthermore, we also incorporate the coordination among the electrical devices for the real time load demand which makes the system adaptable.
Three meta-heuristic techniques (EHO, ACS, and HEAC) are used to schedule electrical devices with the aim of minimizing the electricity utilization cost and PAR for the end consumers. The coordination among electrical devices is established to facilitate the consumer and avoid the wastage of electricity. The optimization problem is formulated through knapsack problem to integrate the coordination at run-time. This gives the consumers authority to alter the schedule of the energy management controller for efficient power consumption. Consumers can ON/OFF electrical devices at execution times with respect to their need. A new schedule for electrical devices is generated including consumer emergency electrical devices, without affecting the scheduled load of other electrical devices.
The LoTs of the emergency electrical devices are in minutes instead of hours like other manageable electrical devices. The scheduler stops all scheduling operations of electrical devices as the interruption is generated by the consumer. Additionally, it checks for running manageable electrical devices in that particular time-slot. Immediately, after finding a running manageable electrical device, operations of that particular manageable electrical devices are terminated as this electrical device is no longer required. The scheduler calculates the remaining time in that specific interval and assign it to the consumer’s emergency electrical device. This helps in efficiently managing the electrical devices in order to facilitate the consumer comfort level. Approaches like DP and cooperative GT are implemented to handle this complex scheduling problem, as they are highly suitable for tackling the coalition and decision making problems.
4.1. Scenarios
The living habits of consumers are considered in two regions: hot and cold. These habits include: the consumers’ occupancy, status of the electrical devices (either ON or OFF) and their energy consumption patterns [
21]. Moreover, the coordination among the electrical devices and scheduler is introduced. Let us say that,
be a set of manageable electrical devices and
be a set of consumer’s emergency electrical devices. If a consumer wants to use an emergency electrical device, the proposed model enables the consumer to generate an interrupt signal at run-time. Consequently, the scheduler immediately halt the working of any running manageable electrical device in the specific time interval. Thus, calculate the remaining time and then allocate the remaining slot to consumer’s emergency electrical device at run-time without affecting other running electrical devices. The Knapsack problem is a combinatorial optimization problem having a set of items, each with a specific weight and a particular value [
22]. As coordination is based on the knapsack problem, in the proposed scenario, the set of items is referred to electrical devices, the capacity is mapped via power ratings and prices are encoded to represent the values in the peak and off peak hours.
Note that, PRs and consumers preferred electrical devices are different in hot and cold regions. For the comparative performance analysis, all the electrical devices for scheduling are considered the same for all the aforesaid techniques in both regions.
In this study, the main focus is to minimize the electricity bill for the end consumers by optimally managing the power utilization throughout a day. This also improves the power grid stability by limiting the use of peak diesel generators, consequently reducing the emissions of greenhouse gases, causing significant threats to the environment. However, in [
23], the peak diesel generators are considered which are powered through natural gas and help in making the environment greener than a potential coal powered baseline plants. DSM controls the electricity utilization and manages the demand side activities for the end consumer. It motivates the consumer to schedule the heavy load in off peak hours, resulting in low peaks by efficiently managing the load throughout the day. This adaptation in the system also helps in reducing the greenhouse gas emission due to the peak generators. Different incentive based electricity pricing tariffs are established by energy generation companies such as time-based ToU and dynamically based (CPP, RTP, DAP, IBR) etc. Due to the tentative behavior of optimization algorithms, we considered both hot and cold regions. Both regions have different off-peak and on-peak hours. In a hot region, on weekdays, the peak hours are from 11 a.m. to 5 p.m. Whereas, in cold region, 7 a.m.–8 a.m., 5 p.m.–7 p.m. are the peak hours on weekdays [
24].
4.2. Proposed Scheme
In the literature, a lot of optimization schemes have been presented to schedule electrical devices optimally. In case of EHO, it has distinguished local search abilities [
6], whereas, ACS proves to be efficient in finding optimal results in less computational time [
25]. In order to enable parallel interpolation and extrapolation, a dire need for an algorithm emerges which can maximize the benefits of scheduling. Therefore, by combining ACS and EHO, an efficient algorithm is proposed which exploits both local and global search spaces simultaneously. Additional, to evaluate the effectiveness of a hybrid approach HEAC, a comparative analysis is carried out based on performance parameters. In the coming subsection, all three implemented heuristic techniques are discussed in detail.
4.2.1. EHO
On land, elephants are one of the largest animals. They are social animals and prefer to live in a family composed of several groups under the leadership of a matriarch, often the oldest female elephant [
6]. Females prefer to live together, while male elephants tend to live in isolation and they can stay in touch with their clan through very low-frequency vibrations.
The EHO is encoded in our proposed work to tackle the problem of global optimization during the scheduling of electrical devices. The two operators of EHO named update and separate are used to ensure the optimal scheduling of all the devices. The former is used to update the schedule of the electrical devices while in the latter, electrical devices with high consumption cost are separated from the solution [
26]. Three basic rules are defined to solve the optimization problem: (i) The population of electrical devices (elephants) based on class of the device i.e., manageable and shiftable electrical device, fixed number of electrical devices are assigned in each class (clan of elephants); (ii) In each generation (iteration for scheduling the electrical devices), fixed number of manageable electrical devices with worst fitness values are discarded and the remaining electrical devices are scheduled to reduce the load at specific time intervals; (iii) Whereas, the matriarch is mapped as the solution which has less consumption cost and helping in avoiding the peak creation.
Solution updating operator: In this step, a new population is generated and the position of every electrical device (elephant) is influenced by the best solution in each iteration.
is the aggregated number of electrical devices (elephant clans) and
q represents the number of electrical devices in each class. The current position of all devices is updated as [
6]:
where,
and
are newly updated and old positions for electrical device (elephant)
q in class (elephant clan)
. A scale factor
determines the influence of the best solution. The
represents the best position of the solution
.
r is the random number in the range of [0, 1]. The fittest electrical device is updated as [
6]:
where, the influence of the
on
is determined by a factor
. The new individual
in Equation (
2) is generated by the information obtained from each electrical device in the class. Where,
is the centre of solution
[
6]:
where,
illustrates the
d-th dimension, and the total dimension is represented by
D. The solution updating operator can be calculated on the basis of herding behaviour of elephant.
Separating operator: The electrical devices with the worst fitness value are excluded from the solution and this is known as the process of separation. The separating process is modelled into separating operator to solve optimization problems. At each generation, the electrical devices with worst fitness value leave the solution as shown in Equation (
4) [
6].
where,
and
represents the maximum and minimum bound of each electrical device position, respectively. In solution,
,
represents the worst individual electrical device.
is a type of uniform and stochastic distribution in the range of [0, 1]. The sequential steps of EHO are given in Algorithm 1.
| Algorithm 1: EHO |
- 1:
Initialization - 2:
Initialize , , , set = 2, , = , = - 3:
whiledo - 4:
Sort all the electrical devices based on their fitness. - 5:
for do - 6:
for do - 7:
Update and generate using Equation ( 1). - 8:
if then - 9:
Update and generate using Equation ( 2). - 10:
end if - 11:
end for - 12:
end for - 13:
for do - 14:
Replace the worst value of electrical device in solution using Equation ( 4). - 15:
end for - 16:
Evaluate fitness of population by the newly update positions. - 17:
. - 18:
end while
|
4.2.2. ACS
The ACS algorithm is a heuristic technique and inspired by the thinking of cuckoo bird, which usually explores the search space by using the Levy step [
23]. The Levy step used is taken from the Levy distribution proposed by Mantegna algorithm [
25]. The authors assimilate a step size proportional to the fitness of a nest in search space. The step size is designed as [
25]:
where,
t is the generation of the ACS; the fitness value of nest
i in
t-th generation is
;
is the best fitness value; the worst fitness value in the generation
t is
. Initially the step size is high and its value decreases as the generation increases. This indicates that when the algorithm reaches the optimal solution, the step size is very small leading to higher precision. Equation (
5), shows that in nature the step size is adaptive and uses the fitness value to decide the next step size. It is modeled as [
25]:
Equation (
6) provides the new search space from current solution to the ACS algorithm. The other advantage of ACS is that there is no need for defining the initial parameter [
25]. It is faster than the cuckoo search algorithm. Assume that, the step size is proportional to the global best solution, then Equation (
6) is designed as [
25]:
where,
is the global best solution among all
for i (for i = 1, 2, …, N) at time
t. Algorithm 2 shows the working ACS.
| Algorithm 2: ACS |
- 1:
begin - 2:
Generate initial pop. q of nest , - 3:
Define min. step size - 4:
Define max. step size - 5:
for all do - 6:
Evaluate the fitness of function = - 7:
end for - 8:
while () or (stopping criteria) do - 9:
Calculate the average fitness value of each the host nest - 10:
Find the min. fitness value between all the host nest - 11:
for all the host nest do - 12:
Current position - 13:
if falls outside the limits then - 14:
Replace with - 15:
end if - 16:
Again evaluate the fitness function = - 17:
if () then - 18:
Replace with - 19:
Replace with - 20:
end if - 21:
end for - 22:
Abandon a fraction of the worst nest - 23:
Randomly generate new nest to replace worst nest - 24:
Calculate the fitness of new nest - 25:
end while - 26:
end
|
4.2.3. HEAC
Here, we are going to discuss our proposed algorithm named as HEAC which is a hybrid algorithm and follows the steps of both EHO and ACS. These techniques are very effective and promising for solving optimization problems. EHO obtains the best global solution for a particular problem, whereas, its execution time is high. On the other hand, ACS has global as well as local search abilities which makes it efficient and suitable for most of the optimization problems. The structure of ACS is easy, as no initial parameters are required for an optimization problem. This quality makes it ideal for its integration with different algorithms to improve performance. The step size in ACS is of great importance; it has an inverse relation with generation size because as generation size increases it becomes smaller. This increase in step size enhances the efficiency of the ACS algorithm and when the algorithm reaches the best global solution in search space, the step size becomes very small which means high precision. Moreover, the step size is directly proportional to the fitness of each nest preset in the search space, so the step size is adaptively determined by the fitness value. This makes it different from traditional cuckoo search algorithms, where the step size is fixed for every iteration. The proposed HEAC follows the initial steps of EHO, and then updates the solution using steps of ACS. In Algorithm 3, the working procedure of HEAC is elaborated for a better understanding. Further, the tuning of parameters in the proposed algorithm is flexible and depends on the problem to be solved.
| Algorithm 3: HEAC |
- 1:
Initialization - 2:
Initialize , , , , - 3:
Define min. step size value - 4:
Define max. step size value - 5:
while () do - 6:
Sort all the elephants based on their fitness. - 7:
for do - 8:
for do - 9:
Current position - 10:
if falls outside the limits then - 11:
Replace with - 12:
end if - 13:
Calculate the fitness function = - 14:
if () then - 15:
Replace with - 16:
Replace with - 17:
end if - 18:
end for - 19:
end for - 20:
Evaluate the fitness of new nest - 21:
for do - 22:
Replace the elephant with worst value in clan . - 23:
end for - 24:
Evaluate population by the newly update positions. - 25:
. - 26:
end while
|
4.3. Coordination
The coordination in the proposed work is defined as the mechanism of exchanging information among the electrical devices to enable dynamic scheduling in the system. This enables the system to efficiently manage the manageable electrical devices throughout the day. Moreover, it also facilitates the consumer to dynamically schedule the electrical devices at run-time. In this work, cooperative GT and DP approaches are exploited to incorporate the mechanism of coordination among the electrical devices. The former also known as combinatorial theory and is used to establish coordination among the players which is replaced with electrical devices in the proposed work [
27]. In this work, the electrical devices coordinate with each other and work together to achieve a common goal. Initially, the scheduler maps the electrical devices as players working together to uniformly distribute the load in 24 h with minimum wastage of time. Then, only the manageable electrical devices coordinate with each other and with the consumer emergency electrical devices; they form a coalition to reduce the energy consumption cost and waiting time.
The latter is used for coordination among the electrical devices based on [0, 1] knapsack problem using DP [
28]. This enables the consumers to ON/OFF electrical devices according to need. A new schedule for electrical devices is generated including consumer emergency electrical devices. The LoTs of the consumer’s emergency electrical devices are in minutes instead of hours. If a consumer generates an interrupt and wants to switch-on an emergency electrical device, the scheduler stops all the scheduling operations of electrical devices and looks for manageable electrical devices in that particular time-slot. Immediately, after finding the running manageable electrical device, the operations of that particular device are terminated as this electrical device is no longer required. The scheduler calculates the remaining time in that particular time interval and assigns it to the emergency electrical devices. This helps in efficiently managing the electrical devices to facilitate the consumers. Thus, we can conclude that DP and cooperative GT are implemented to handle this complex scheduling problem, as they are highly suitable for tackling the coalition and decision making problems.
5. Simulations and Results
In this work, we evaluate the performance of our proposed hybrid HEAC technique on the basis of the results obtained from extensive simulations. The results obtained from the simulations are then compared with other implemented techniques such as EHO and ACS. Region-based ToU pricing signals are used to relatively analyze the electricity usage patterns of the end consumers. The utility companies readily establish the hourly ToU price rate for the consumers. For simulation purposes, a home is considered with a set of electrical devices. These electrical devices are categorized into three categories: (i) fixed electrical devices; (ii) shiftable electrical devices; and (iii) manageable electrical devices, respectively.
The set of fixed electrical devices include; light, fan, oven, and blender. The category of shiftable electrical device include washing machine, clothes dryer, and dishwasher. Moreover, AC, refrigerator, iron, and vacuum cleaner are enclosed in manageable electrical devices.
Table 1 and
Table 2, represents the input parameters including electrical devices, their LOT, and PR, respectively. Additionally, two approaches namely; (i) cooperative GT approach and (ii) DP approach are incorporated with the heuristic schemes to establish coalition, and coordination among electrical devices. In cooperative GT approach, shapley values are used to introduce cooperation among electrical devices, whereas, the DP approach breaks the problem into sub-parts and then solves these sub parts. The final results are stored in memory and this step in known as memorization. The coordination facilitates the end consumers to optimally manage the load and reduce the electricity utilization bill. Additionally, it also enables the end consumer to interrupt the running schedule of electrical devices at run-time and generates a call to run the desired electrical device in that particular instance of time. Consumer defined emergency electrical devices, their PR, and LoTs are shown in
Table 3.
The time horizon is divided into twenty-four equal time segments. This assumes that each electrical device can operate for at least one hour, if an electrical device does not need a complete hour or the consumer sends an interrupt in the run-time. The remaining time in that specific time-slot will be wasted, the coordination provide an effective solution for the aforementioned problem.
5.1. Hot Region with and without Coordination
Online data for ToU pricing signals [
24] is considered for electricity cost calculation. The consumers have a choice to take desired action while keeping in mind electricity utilization cost and the satisfaction (comfort) level. The consumers’ electricity utilization patterns for three cases: (i) without coordination; (ii) coordination with DP; and (iii) coordination with GT are shown in
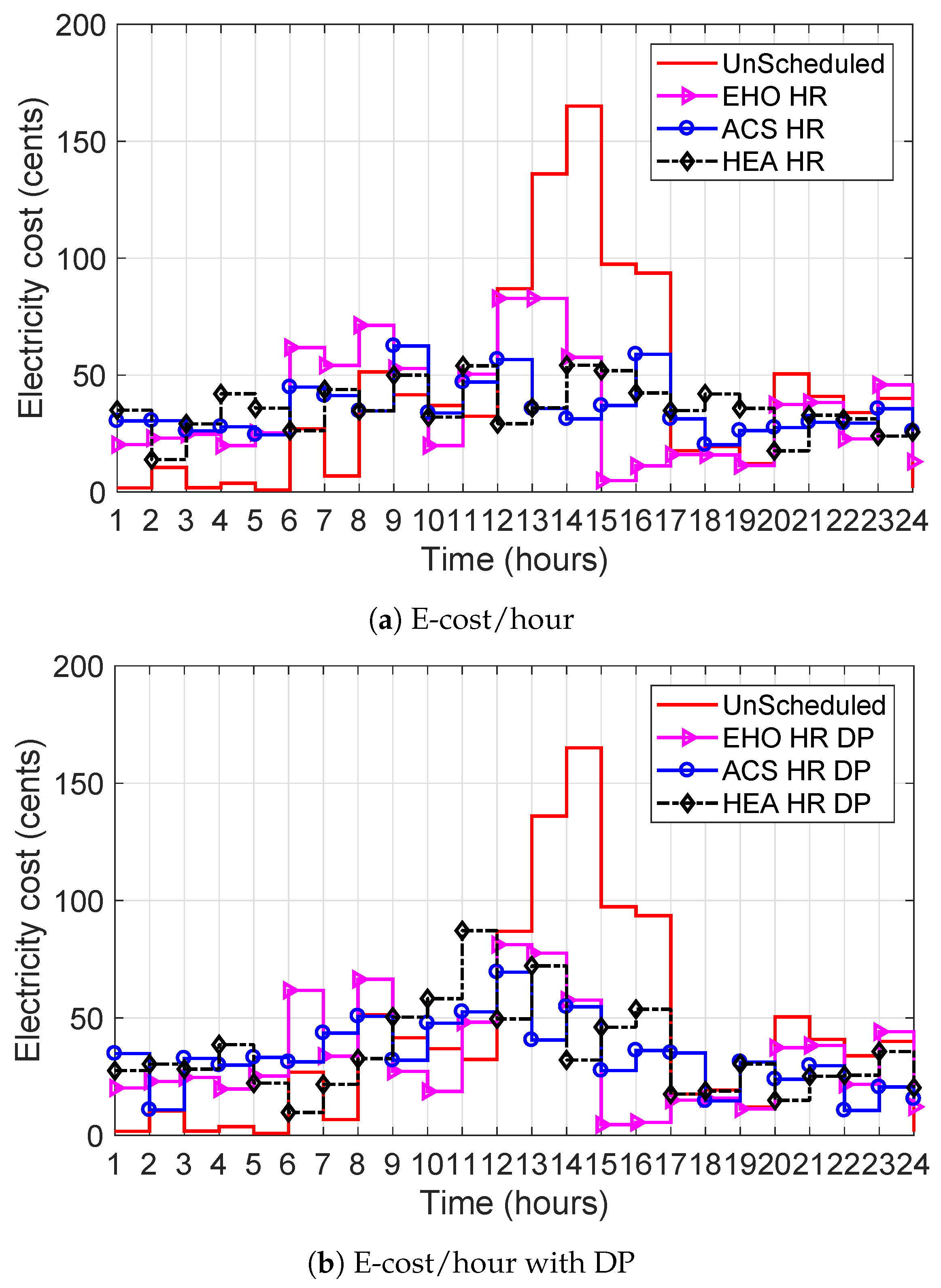
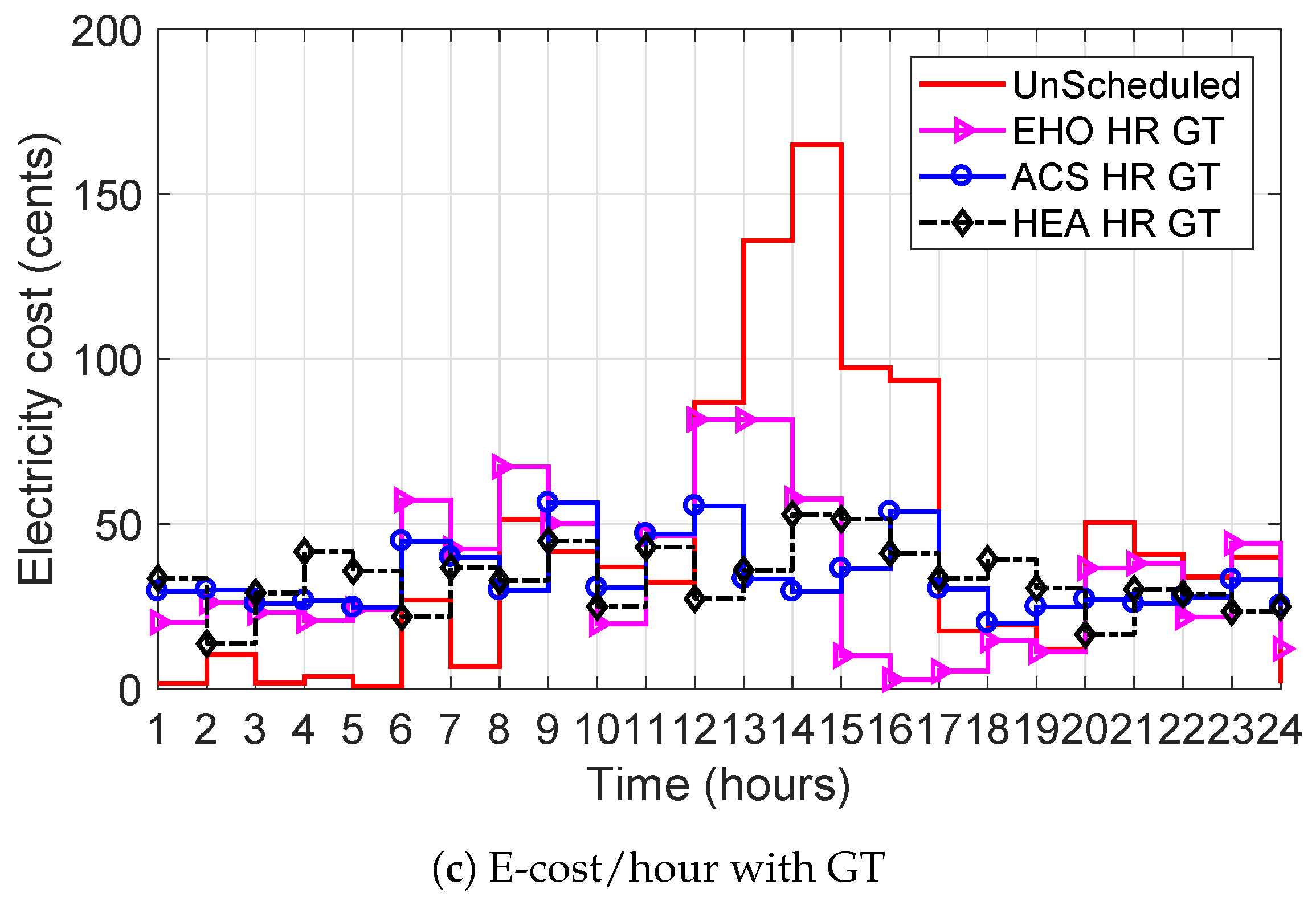
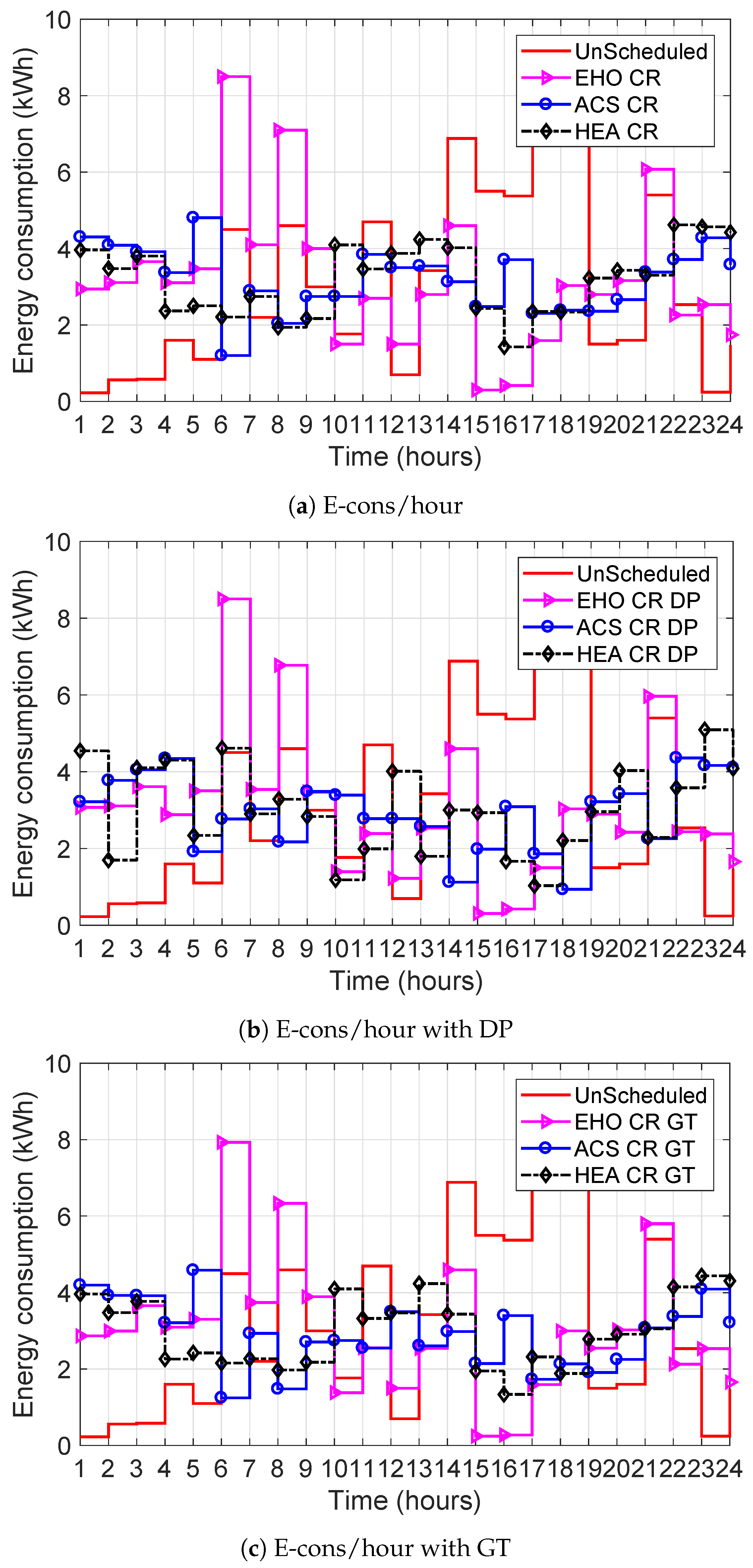
Figure 2a–c, respectively. In all cases, the three implemented algorithms efficiently manage and reduce the load utilization for the end consumers.
Figure 3a–c illustrate the hourly electricity utilization cost patterns for the three cases: (i) without coordination; (ii) coordination with DP; and (iii) coordination with GT, respectively. It is clearly observed from the figure that the utilization of electricity is relatively low during the hours where prices are high. This reduction is achieved by limitizing the consumers’ on-requests in peak hours for all aforementioned cases. Moreover, the bar plots in
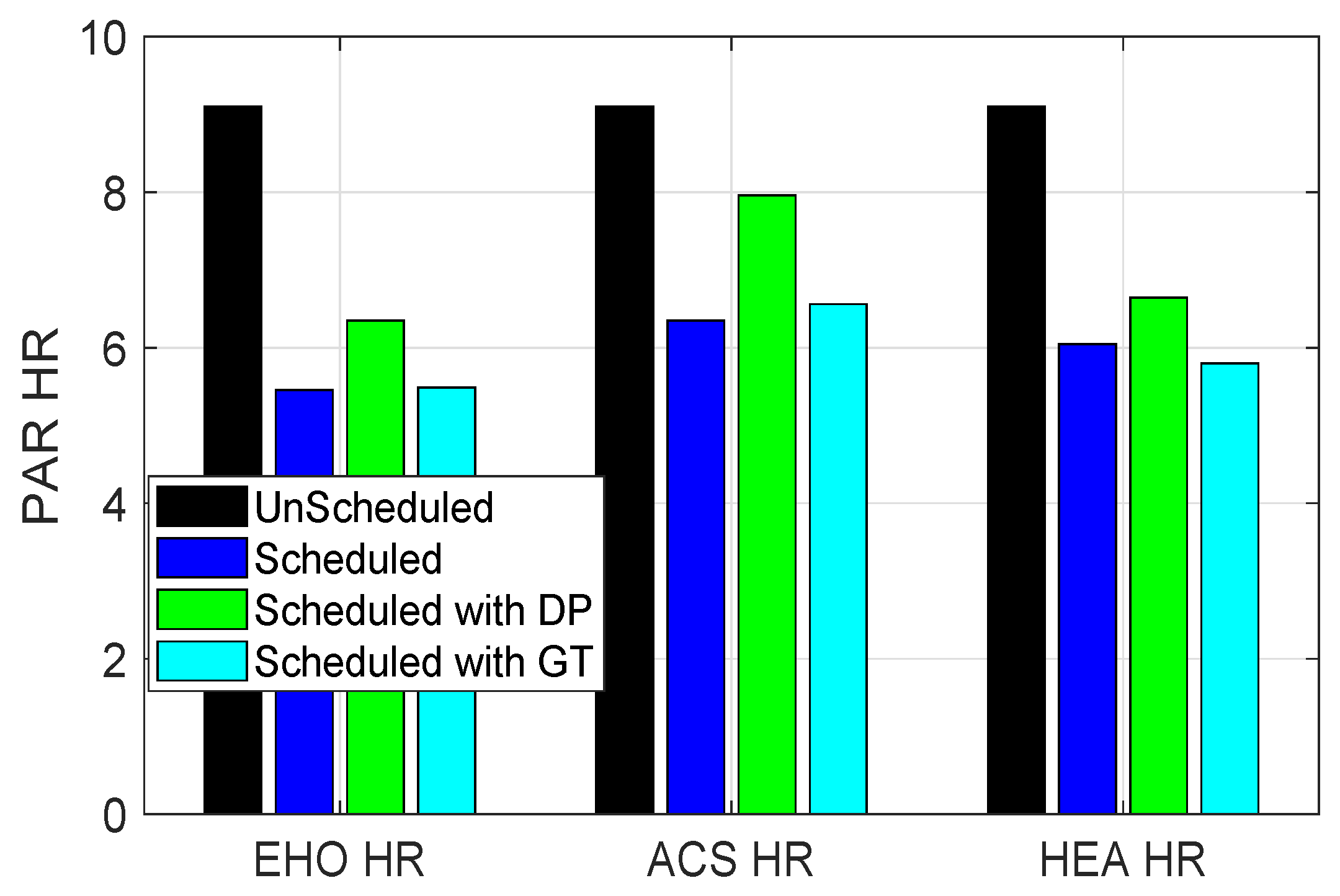
Figure 4 shows the effect of scheduling on PAR, before and after the coordination is incorporated in the system. The heuristic algorithms used for scheduling show significant reduction in PAR as compared to unscheduled case. The proposed model tuned with heuristic algorithms (EHO, ACS, and HEAC) efficiently reduces PAR upto
%,
%, and
%, respectively. The integration of coordination with DP achieves
%,
%, and
%, whereas, GT approach achieves
%,
%, and
% reduction in PAR. Peak formations are one of the major problems in smart grids. The electricity providing companies use fossil fuel and natural gas generator to fulfill the energy demand in peak hours. The system designed in this work efficiently tackle the problem of peak formations.
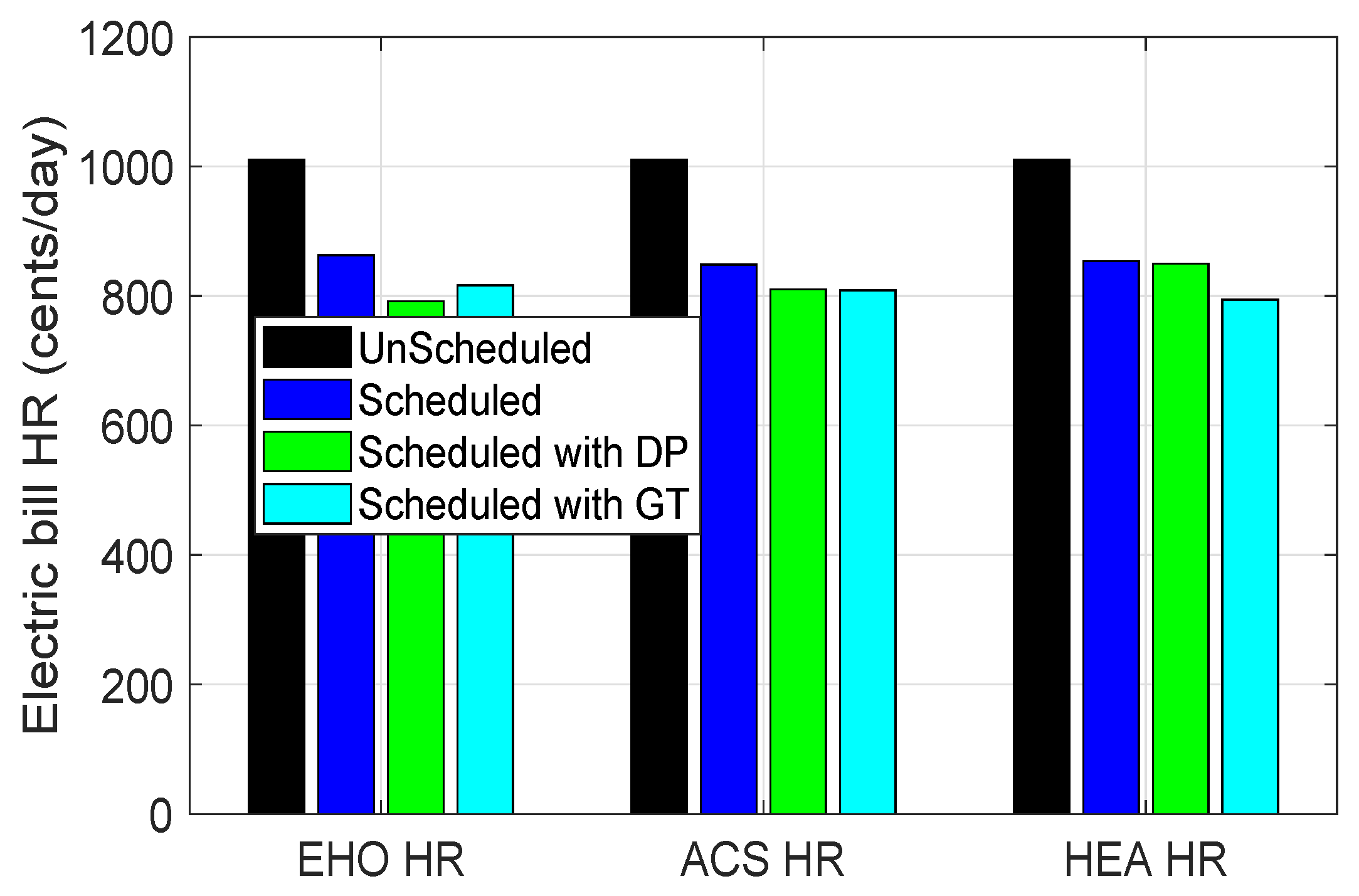
Figure 5 represent the aggregated electricity bill for the end consumer with and without coordination. Bar plots show
%,
%, and
% reduction in cost using EHO, ACS, and HEAC, respectively, without coordination. After the coordination is incorporated using DP approach bar plots show
%,
%, and
% reduction in electricity bill, whereas, using GT approach, it shows
%,
%, and
% minimization in the electricity bill is achieved using EHO, ACS, and HEAC, respectively.
The coordination between electrical devices using DP and GT approaches incorporated with the heuristic algorithms make the proposed system efficient and consumer friendly. This enables the consumers to set the priority of any two emergency electrical devices. The LoTs of these electrical devices vary randomly as per the needs of the consumer. At run-time, the consumer can generate an interrupt signal in running schedule of electrical devices. The scheduler halts the operations of running manageable electrical devices in that specific time-slot and assigns the remaining time to the consumer’s emergency electrical device without affecting the operations of other electrical devices. Hence, reducing the overall load as well as electricity bill for the end consumer. The statistics for extensive simulations in hot region when the number of homes increases from 1 to 20–200 are presented in
Table 4,
Table 5 and
Table 6.
5.2. Cold Region with and without Coordination
The electricity usage profile before and after coordination with DP, GT approaches are represented in
Figure 6a–c. Results of the simulations show that the electricity utilization of all electrical devices is efficiently distributed within 24 h.
Figure 6a shows the maximum energy utilization limited to
(kWh),
(kWh),
(kWh) for EHO, ACS, and HEAC, respectively.
Figure 6b illustrates that the maximum electricity utilization limits for EHO, ACS, and HEAC with the coordination using DP are
(kWh),
(kWh), and
(kWh), respectively. Moreover,
Figure 6c represents the result for coordination based on GT approach, maximum energy utilization limits to
(kWh),
(kWh), and
(kWh), respectively.
For the three aforementioned cases, the hourly electricity usage cost profile using the heuristic algorithms (EHO, ACS, HEAC) is also shown in
Figure 7a–c. The minimization in electricity utilization cost is attained by optimal scheduling the load from high price hours to low price hours.
The PAR is shown in
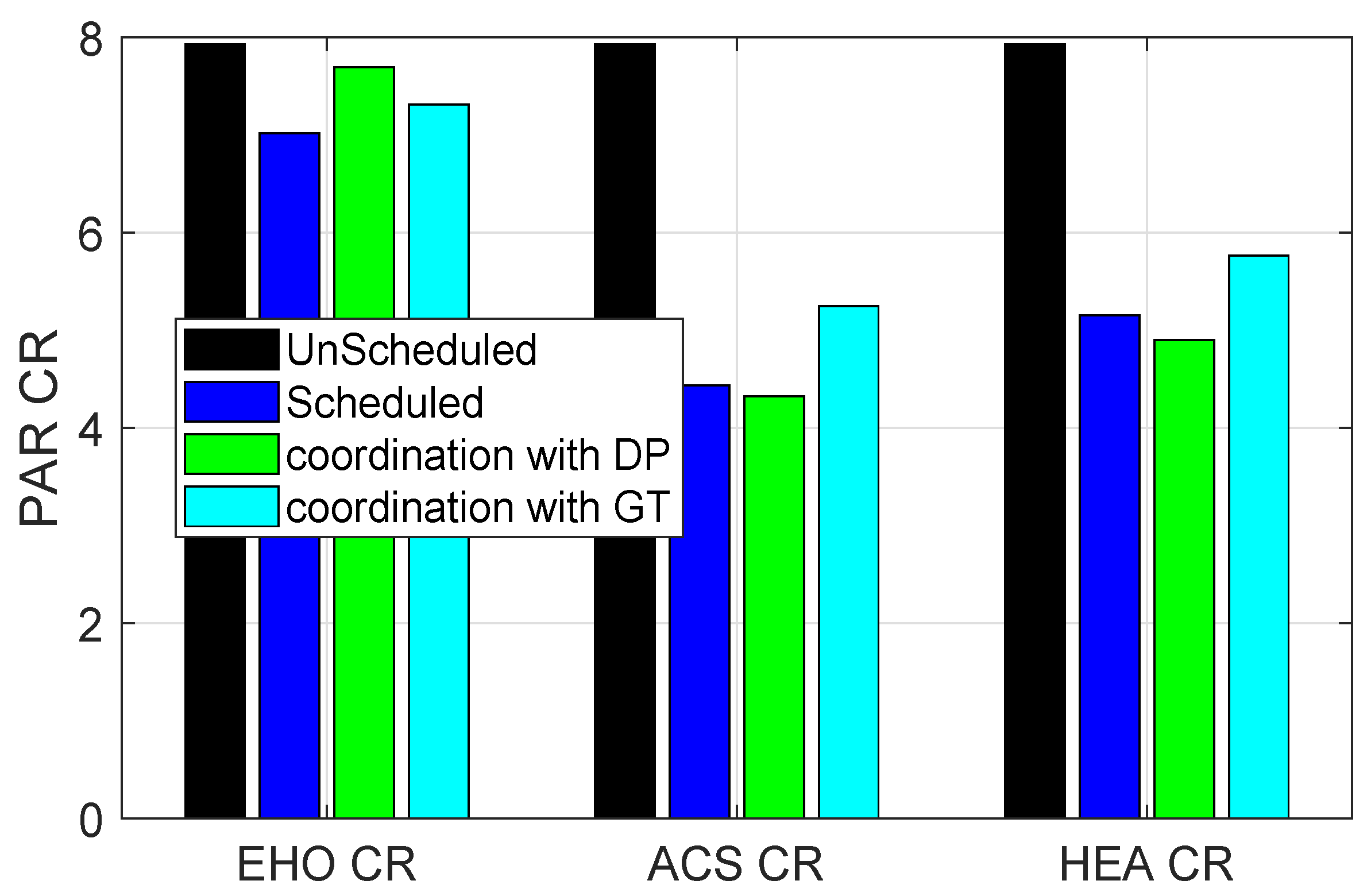
Figure 8 and bar plots show the reduction in PAR when we compare with unscheduled case. EHO, ACS, and HEAC techniques efficiently minimize PAR up to
%,
%, and
% without coordination. In case of coordination with DP,
%,
%, and
% reduction is achieved using EHO, ACS, and HEAC, respectively. Moreover, in the case of coordination with GT approach plot shows
%,
%, and
% reduction in PAR by EHO, ACS, and HEAC, respectively.
Per day total cost is depicted in
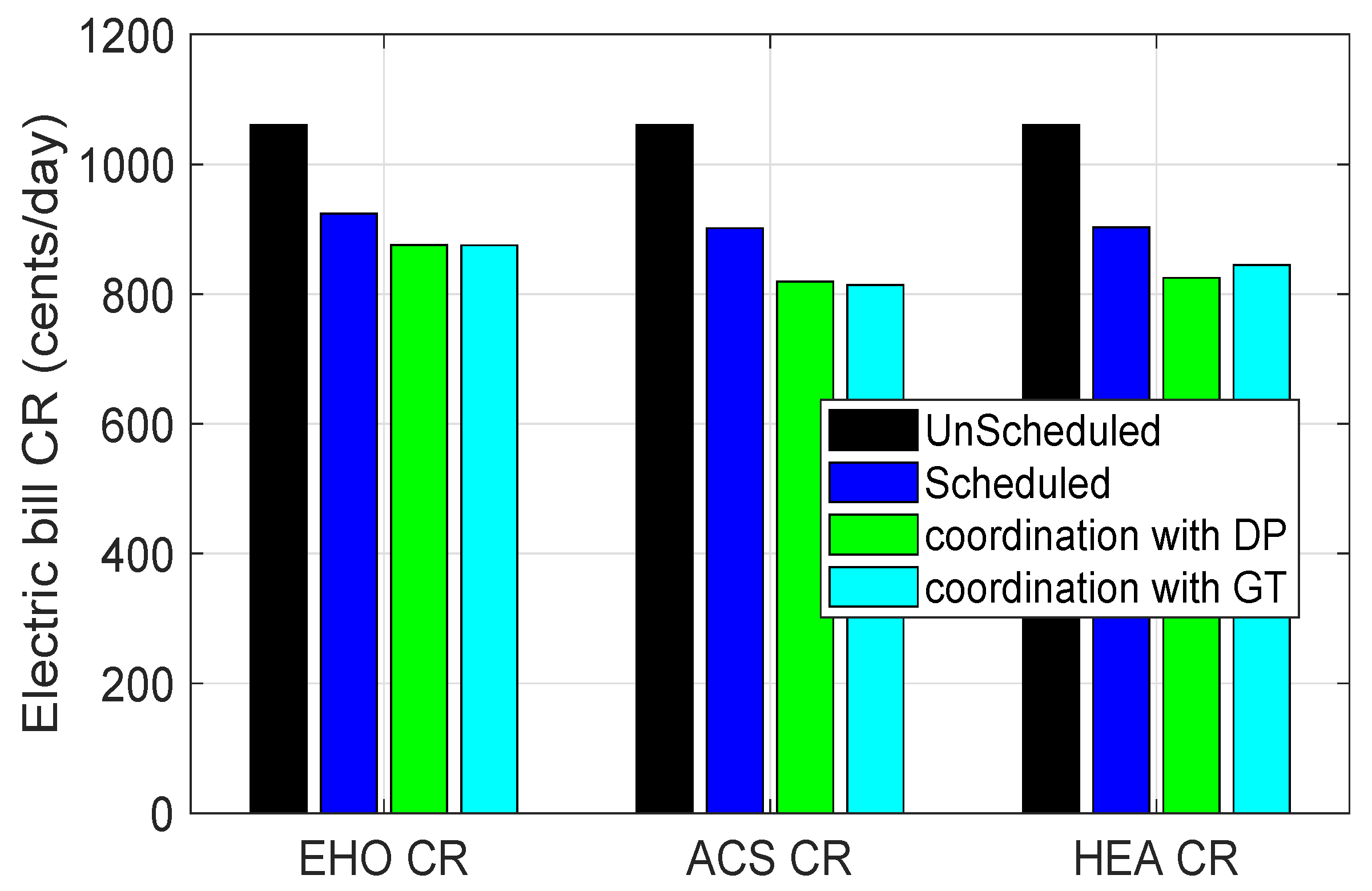
Figure 9 with and without coordination. Before coordination, results show
%,
%, and
% minimization in total cost for a day using EHO, ACS, and HEAC, respectively. As coordination is incorporated with aforementioned heuristic techniques using DP method, the total cost of a day minimizes by EHO, ACS, and HEAC is up to
%,
%, and
%, respectively. On the other hand with GT,
%,
%, and
% minimization in total electricity cost is achieved by EHO, ACS, and HEAC, respectively, for a day, as shown in
Figure 9. The difference in cost with and without coordination is there for all implemented techniques because, in coordination, two electrical devices are set as emergency electrical devices by the consumers. These electrical devices have LoTs in minutes which this reduces the aggregated load after coordination and consequently reduces the consumer’s electricity bill per day. The HEAC algorithm in each scenario, (with and without coordination) outperformed EHO and ACS. The statistics for extensive simulations in cold region are presented in
Table 7,
Table 8 and
Table 9, when the number of homes increases from 1 to 20–200.
Extensive simulations are performed to validate the suitability of the proposed scheme in both hot and cold regions. Moreover, it is evident from the results that the implemented algorithms are capable of efficiently scheduling electrical devices in both hot and cold regions. Additionally, the proposed scheme is successful in achieving minimum electricity consumption cost in both regions. Furthermore, the incorporation of coordination and cooperation among electrical devices through the proposed scheme, the scheduler enables the consumers to independently schedule the electrical devices resulting in more flexible, efficient and consumer friendly system. Thus, it reduces the electricity cost and minimizes the PAR.
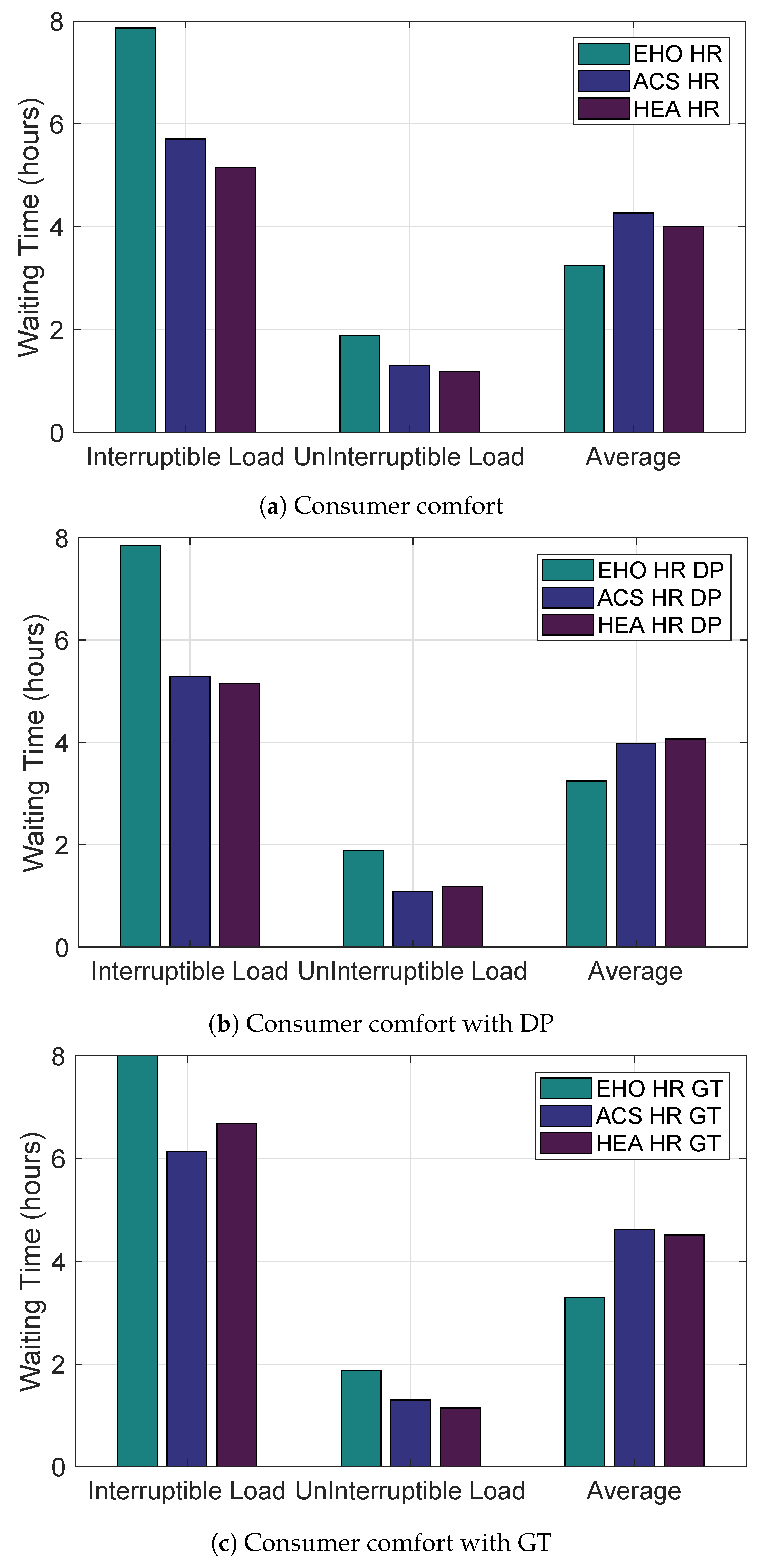
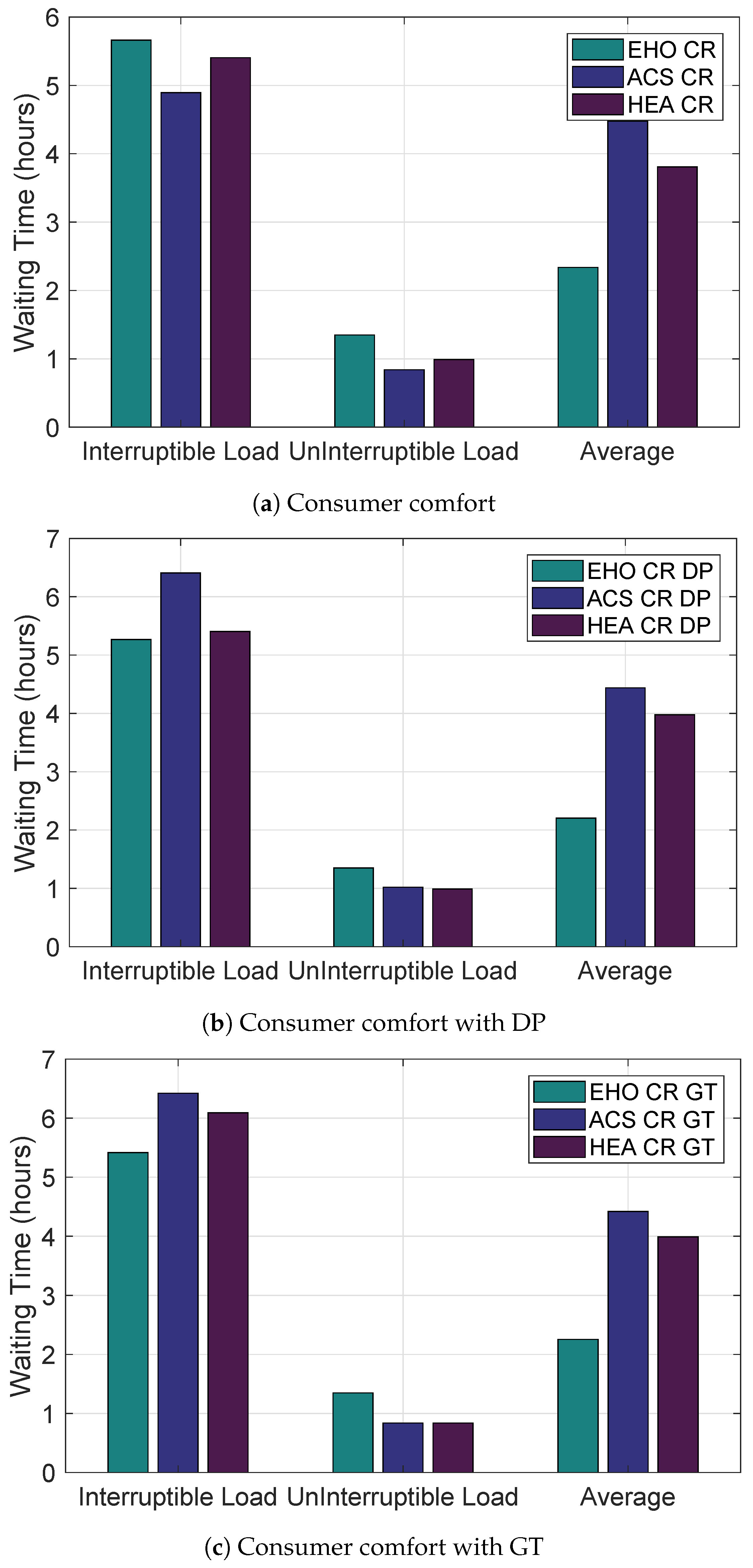
5.3. Consumer Comfort
In this study, we have also considered consumer comfort which is computed in terms of electricity bill and waiting time of an electrical device. In order to reduce energy utilization cost, load is shifted from high peak hours to low peak hours which results in an increased waiting time of electrical devices. So there exists a trade-off between energy utilization cost and electrical device waiting time. To reduce the trade-off, we have introduced the coordination and the result is evident from
Figure 10a–c. These figures depict that electrical devices without coordination have longer waiting times than with the coordination scenario. As coordination of electrical devices enables a consumer to generate an interruption and operate the electrical device according to its needs by ignoring the scheduled set by the DSM system for that electrical devices, it reduces the waiting time of electrical devices, and hence, increases the consumer’s comfort as shown in
Figure 10b,c.
Figure 11a–c show the average waiting time of electrical devices for both with and without coordination scenarios. The heuristic algorithms EHO and HEAC show a minimum waiting time as compared to ACS with coordination scenario. Moreover, EHO has a minimum waiting time in both scenarios.
5.4. Performance Trade-Offs by Scheduling Techniques
Figure 4 and
Figure 5 and
Figure 8 and
Figure 9, clearly illustrate the trade-offs between PAR and electricity utilization cost of the whole day in hot and cold regions, respectively. Moreover,
Figure 10 and
Figure 11 show the consumer satisfaction (comfort) level in terms of waiting time for both hot and cold regions. It is clearly seen from the figures that there exists a trade-off between the electricity utilization cost and consumer comfort.
6. Conclusions and Future Work
A residential DSM scheme is proposed to alter the energy utilization patterns of consumers in order to utilize the available energy efficiently. In this work, electrical devices are scheduled using three heuristic algorithms, namely: EHO, ACS, and a hybrid HEAC. The performance of these algorithms is evaluated on the basis of three performance parameters: PAR, electricity utilization cost, and consumer comfort. The cost of energy utilization is computed using regional-based ToU tariffs. For a fair comparison of these algorithms, control parameters and categorization of electrical devices are kept the same, whereas, the power rating of electrical devices and their types varies according to the regions and needs of the end consumers. The coordination between electrical devices has a great importance in terms of electricity cost reduction and consumers’ comfort maximization, so we have incorporated this concept using GT and DP. Two scenarios are designed to check the effectiveness of our proposed scheme, one with coordination and the other without coordination. Results from extensive simulations show that the scenario with coordination of electrical devices has better results as compared to the scenario without coordination. It can be observed from the results that our proposed heuristic algorithm HEAC manages the load efficiently. However, a trade-off is also there, as we cannot achieve the best values for all three performance parameters simultaneously.
In future, we are planning to integrate the paradigm of cloud computing for realtime load balancing and reduction in consumption cost. The data processing will enable the consumers to expect the pattern of electricity prices from the utility. Moreover, the realtime processing and permanent storage of the data will allow the utility to manage the problem of power dispatch. Additionally, the concept of fog computing will also be utilized to minimize the delay in the processing of consumer requests. Furthermore, the fog paradigm also provides the features of location awareness and efficient wireless access. Thus, these features will be used to incorporate coordination among electrical devices in a very short time with more freedom in the management of load and this will help in minimizing the consumption cost at the consumer side. Moreover, it will enable the utility to reduce the random losses based on the available information by making expectations regarding the consumer behaviour in different time slots.