Optimal Efficiency Tracking Control Scheme Based on Power Stabilization for a Wireless Power Transfer System with Multiple Receivers
Abstract
1. Introduction
2. System Structure and Theoretical Analysis
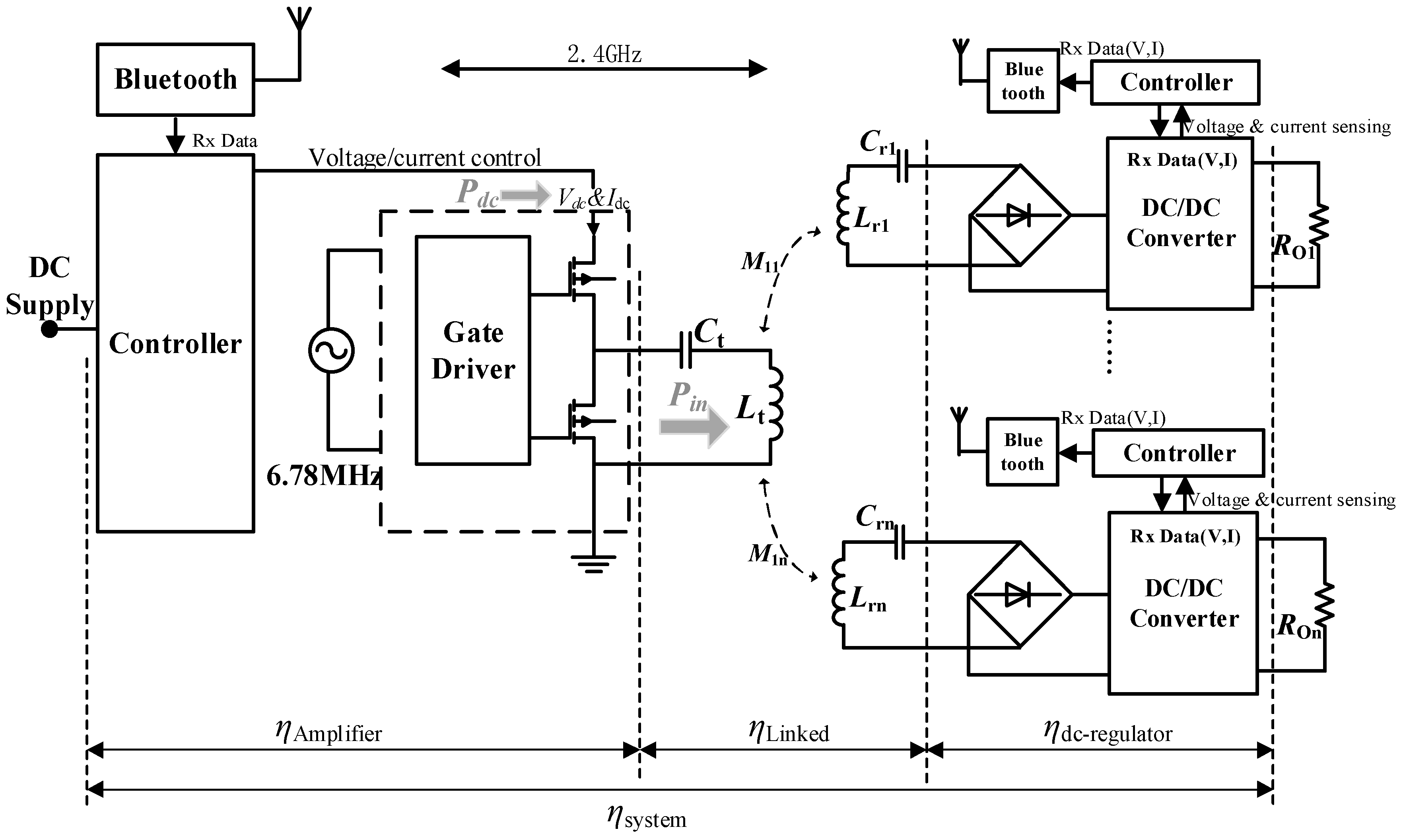
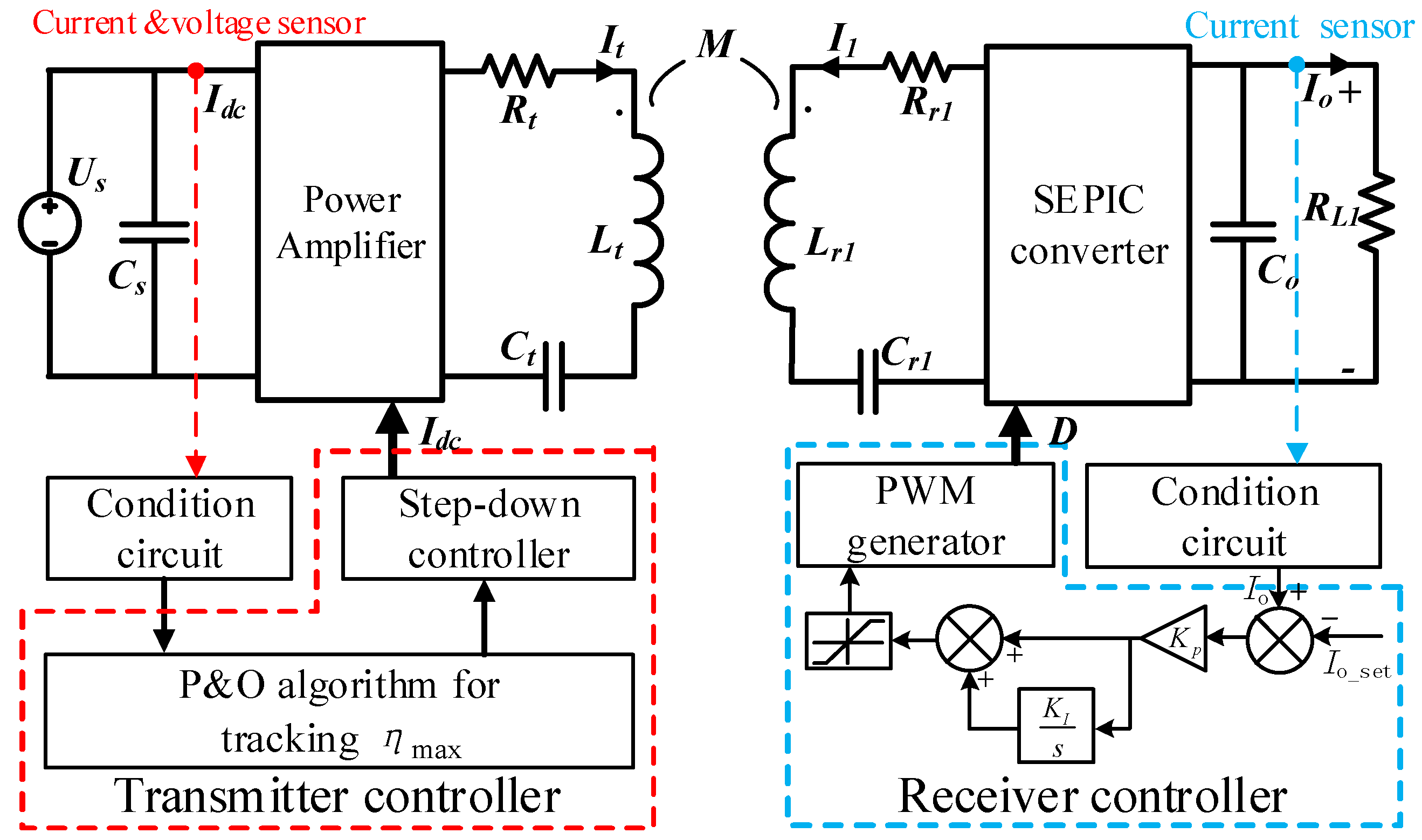
2.1. System Structure
2.2. Optimal Load Condition for Reflected Impedance Match
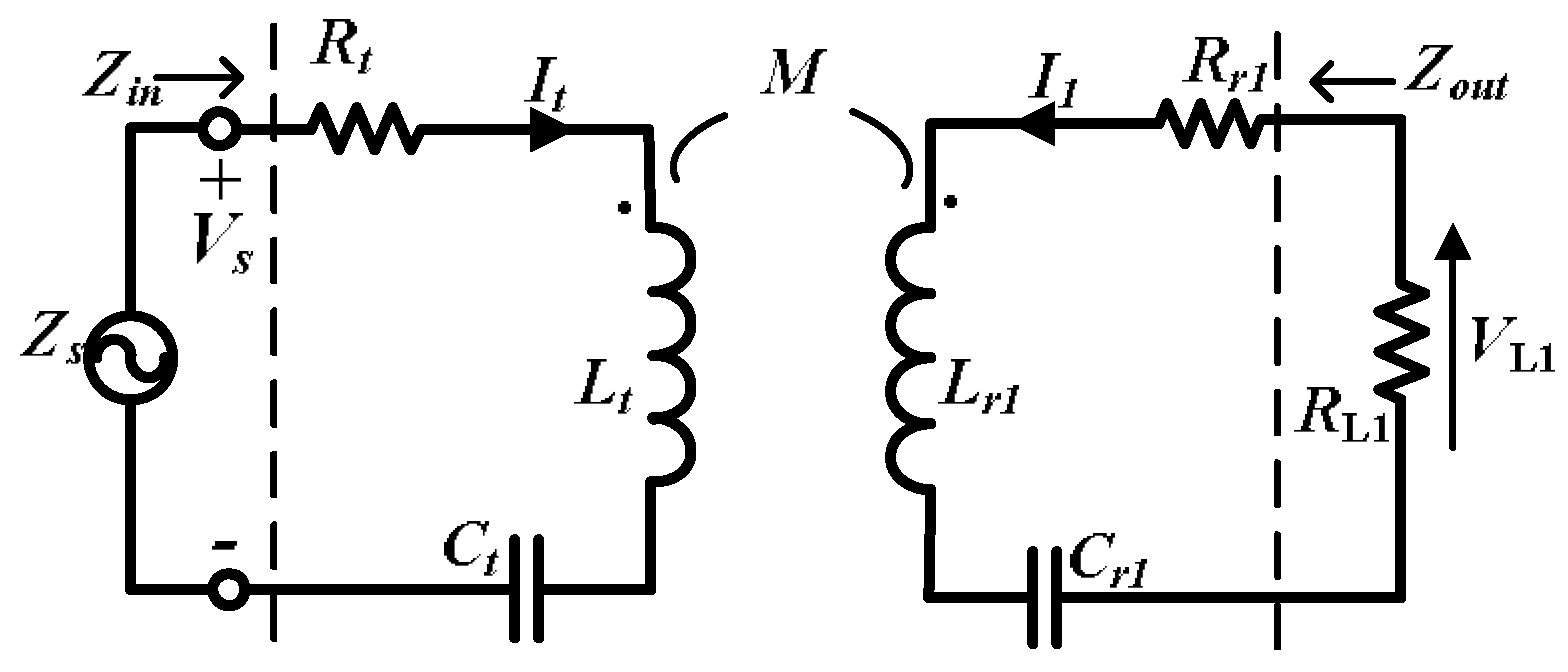
2.2.1. System with Single Receiver
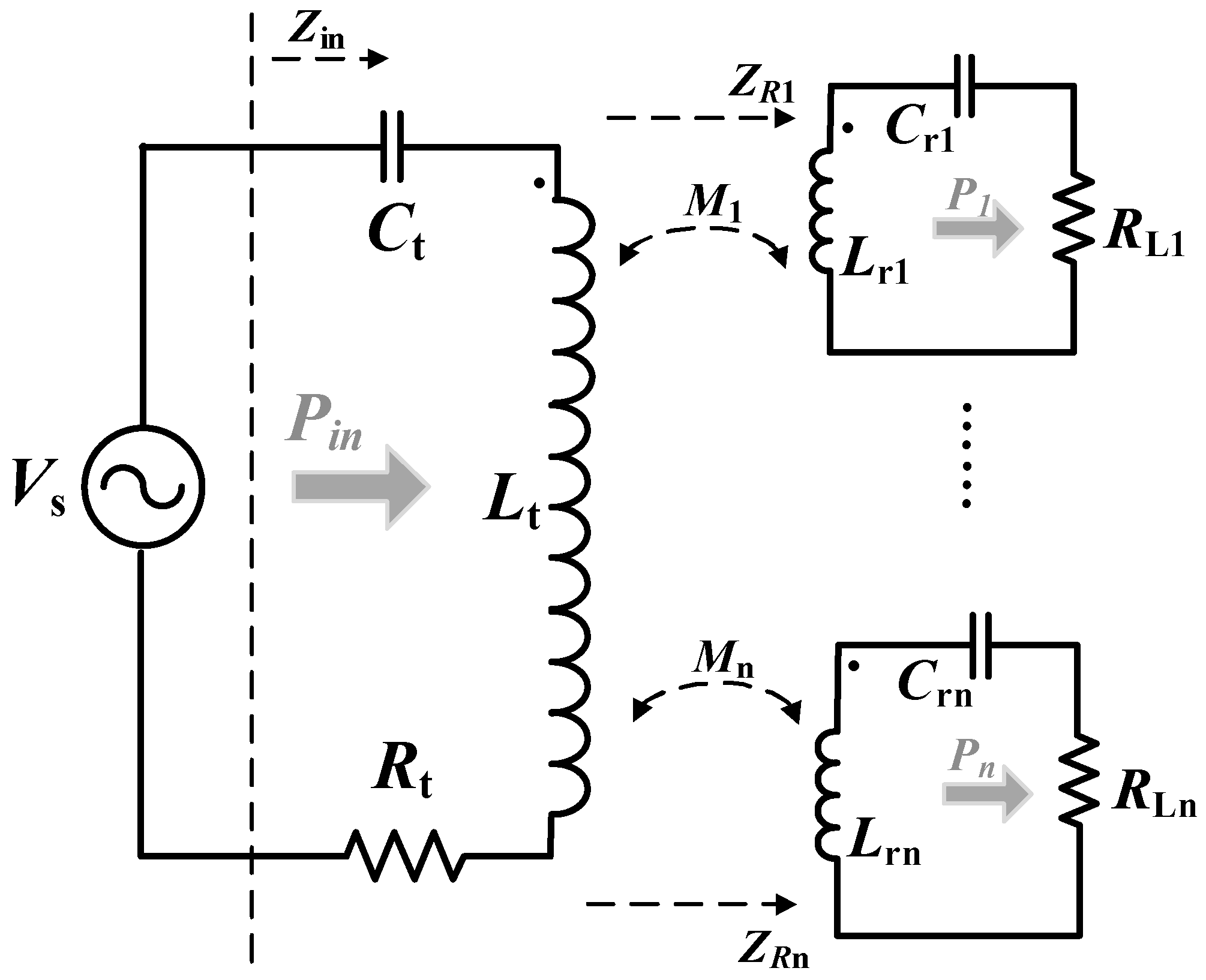
2.2.2. System with Multiple Receivers
2.3. Analysis of Load Transformation
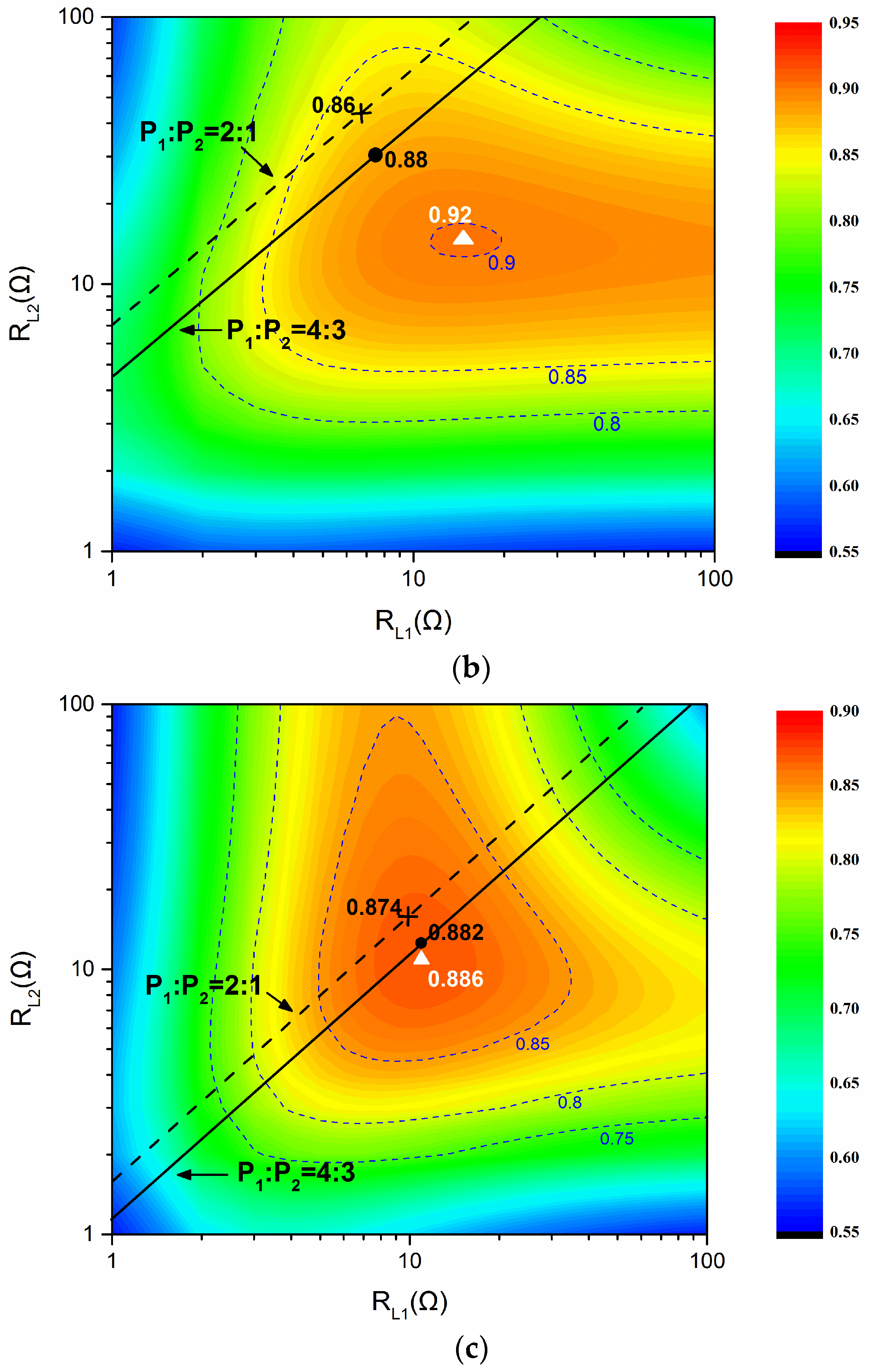
3. Analysis of the Power Division and Efficiency Evaluation Method
4. Analysis of the Proposed Control Scheme
4.1. Structure of Proposed Control Scheme
4.2. Operating Principle Analysis
- In the initialization phase, the initial output power of the transmitter is determined by the number of loads and power requirements. The duty cycle D is adjusted by the PI controlled DC-DC converter so that the current Io at the receiving end reaches the required current.
- The input power Pdc of the transmitter is recorded after initialization and the corresponding change of the input power is calculated in real time by increasing or decreasing the DC input current Idc of the power amplifier. When the change of Idc is ΔIdc, the new value of Idc is expressed as Idc1 = Idc0 − ΔIdc or Idc1 = Idc0 + ΔIdc. The new value of the input power is expressed as Pdc1 = Pdc0 + ΔPdc or Pdc1 = Pdc0 + ΔPdc. As the transmitter’s power varies, the output current Io of the receiver will also change due to the variation in power received by the load.
- After storing the new current Idc1 and input power Pdc1 of the transmitter, the receiver adjusts D again to restore the output current Io to the set value.
- Finally, the new input power Pdc1 obtained by adjusting the Idc is compared with the Pdc. If the Pdc1 is less than the Pdc, the current Idc should continue to be adjusted in the forward direction, and steps 2 and 3 repeated until the Pdc1 increases. Otherwise, if Pdc1 is greater than Pdc, the adjustment direction of Idc should be reversed and steps 2 and 3 repeated until the Pdc1 no longer decreases. At this point, the maximum efficiency of the system is tracked.
5. Experimental Verification
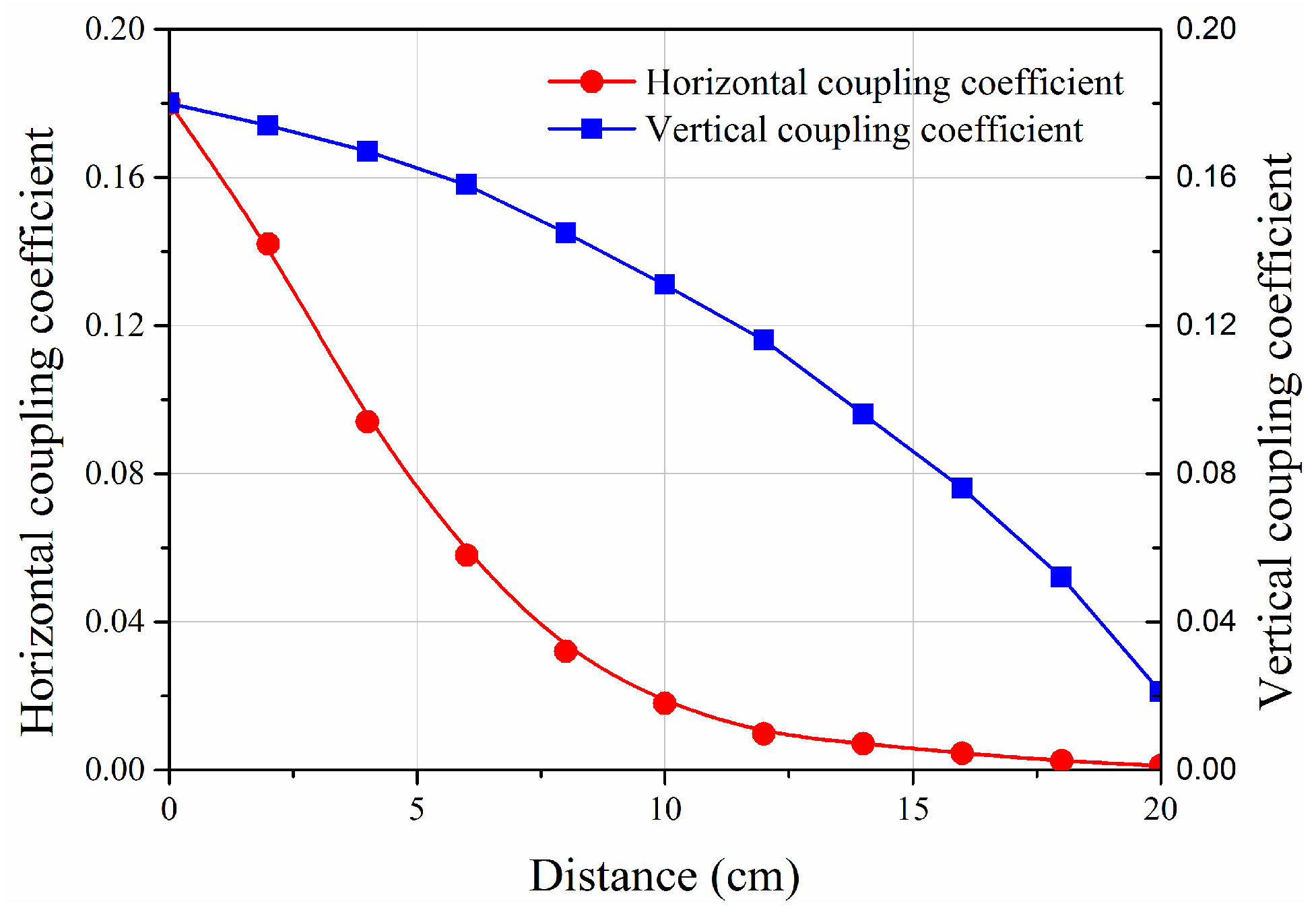
5.1. Experimental Setup
5.2. Experiment Results of the Proposed Control Method
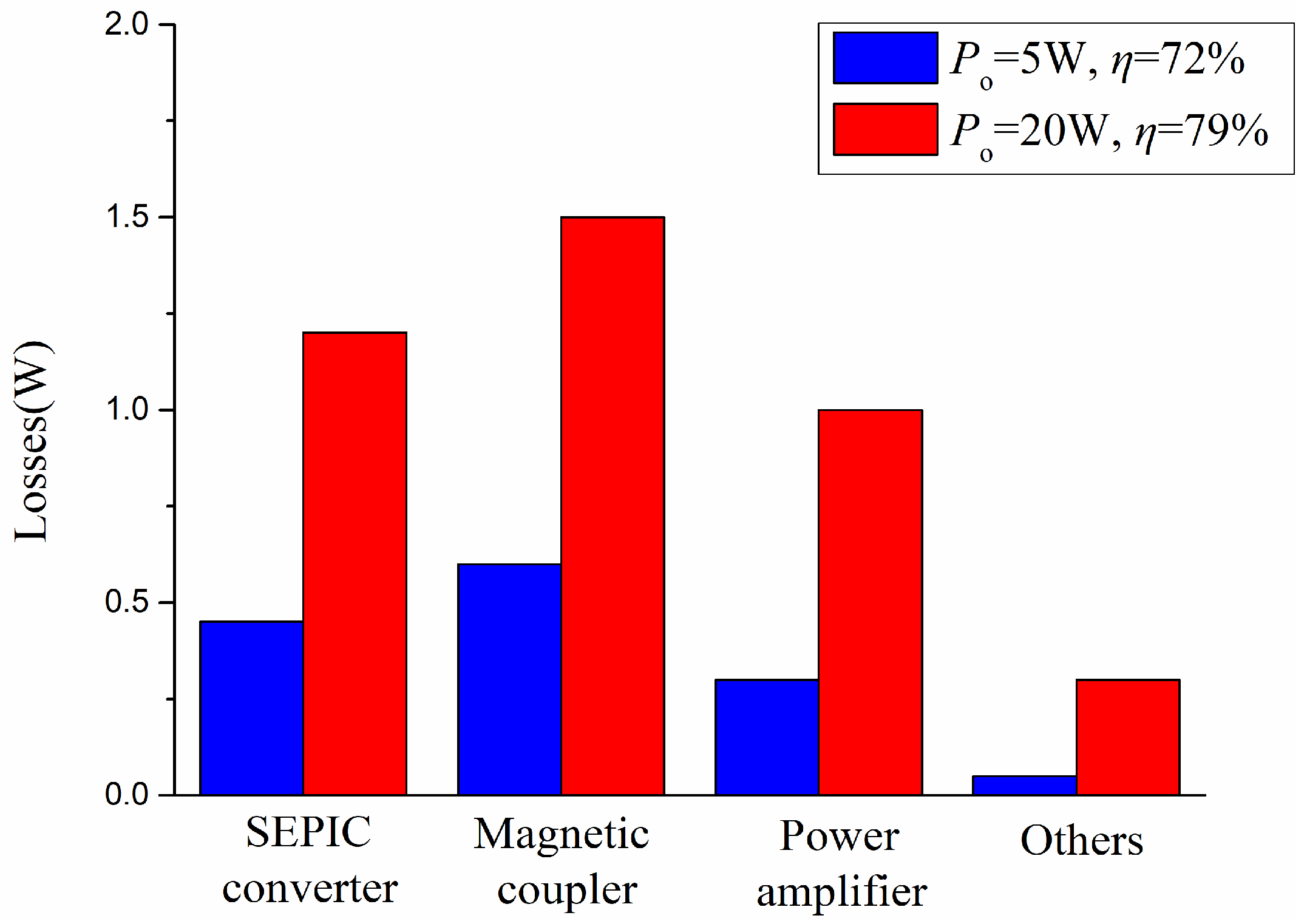
5.3. Discussion of System Loss
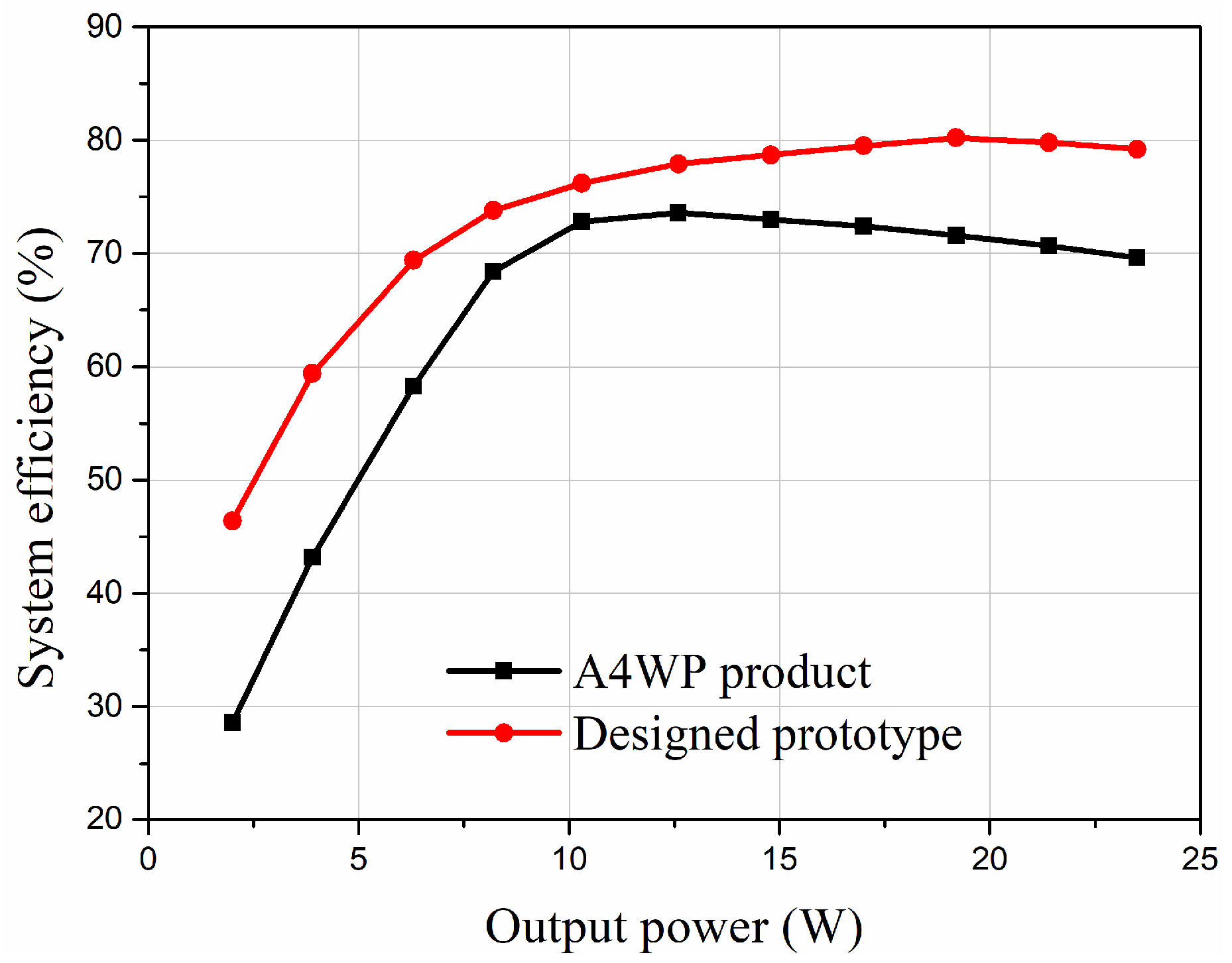
5.4. Comparison to Previous Methods
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, J.; Kim, D.; Choi, J.; Kim, K.; Park, Y. Free-Positioning Wireless Charging System for Small Electronic Devices Using a Bowl-Shaped Transmitting Coil. IEEE Trans. Microw. Theory Tech. 2015, 63, 791–800. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Modern trends in inductive power transfer for transportation applications. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 1, 28–41. [Google Scholar] [CrossRef]
- Chen, C.-J.; Chu, T.H.; Lin, C.L.; Jou, Z.C. A study of loosely coupled coils for wireless power transfer. IEEE Trans. Circuits Syst. II Exp. Briefs 2010, 57, 536–540. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; Palandrani, F.; de Santis, V.; Hirata, A.; Feliziani, M. Wireless Power Transfer Charging System for AIMDs and Pacemakers. IEEE Trans. Microw. Theory Tech. 2016, 64, 633–642. [Google Scholar] [CrossRef]
- Montgomery, K.L.; Yeh, A.J.; Ho, J.S.; Tsao, V.; Iyer, S.M.; Grosenick, L.; Ferenczi, E.A.; Tanabe, Y.; Deisseroth, K.; Delp, S.L.; et al. Wirelessly powered, fully internal optogenetics for brain, spinal, and peripheral circuits in mice. Nat. Med. 2015, 12, 969–974. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, D.R.; Tanabe, Y.; Weng, D.; Hsu, A.S.; Liao, S.-Y.; Zhen, Z.; Zhu, Z.-Y.; Sun, C.; Dong, Z.; Yang, F.; et al. Conformal phased surfaces for wireless powering of bioelectronic microdevices. Nat. Biomed. Eng. 2017. [Google Scholar] [CrossRef] [PubMed]
- Tanaba, Y.; Ho, J.S.; Liu, J.; Liao, S.-Y.; Zhen, Z.; Hsu, S.; Shuto, C.; Zhu, Z.-Y.; Ma, A.; Vassos, C.; et al. High-performance wireless powering for peripheral nerve neuromodulation systems. PLoS ONE 2017, 12, e0186698. [Google Scholar] [CrossRef] [PubMed]
- Sample, A.P.; Meyer, D.A.; Smith, J.R. Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer. IEEE Trans. Ind. Electron. 2011, 58, 544–554. [Google Scholar] [CrossRef]
- Kurs, A.; Moffatt, R.; Soljacic, M. Simultaneous mid-range power transfer to multiple devices. Appl. Phys. Lett. 2010, 96. [Google Scholar] [CrossRef]
- Kim, J.W.; Son, C.; Kim, D.H.; Kim, K.H.; Park, Y.J. Analysis of wireless energy transfer to multiple devices using CMT. In Proceedings of the Asia Pacific Microwave Conference Proceedings, Yokohama, Japan, 7–10 December 2010. [Google Scholar]
- Cannon, B.L.; Hoburg, J.F.; Stancil, D.D.; Goldstein, S.C. Magnetic Resonant Coupling As a Potential Means for Wireless Power Transfer to Multiple Small Receivers. IEEE Trans. Power Eletcron. 2009, 24, 1819–1825. [Google Scholar] [CrossRef]
- Koh, K.E.; Beh, T.C.; Imura, T.; Hori, Y. Impedance Matching and Power Division Using Impedance Inverter for Wireless Power Transfer via Magnetic Resonant Coupling. IEEE Trans. Ind. Appl. 2014, 50, 2061–2070. [Google Scholar] [CrossRef]
- Fu, M.; Yin, H.; Ma, C. Megahertz Multiple-Receiver Wireless Power Transfer Systems with Power Flow Management and Maximum Efficiency Point Tracking. IEEE Trans. Microw. Theory Tech. 2017, 65, 4285–4293. [Google Scholar] [CrossRef]
- Yin, H.; Fu, M.; Liu, M.; Song, J.; Ma, C. Autonomous Power Control in A Reconfigurable 6.78 Megahertz Multiple-receiver Wireless Charging System. IEEE Trans. Ind. Electron. 2018, 65, 6177–6187. [Google Scholar] [CrossRef]
- Fu, M.; Zhang, T.; Ma, C.; Zhu, X. Efficiency and Optimal Loads Analysis for Multiple-Receiver Wireless Power Transfer Systems. IEEE Trans. Microw. Theory Tech. 2015, 63, 801–812. [Google Scholar] [CrossRef]
- Zhu, J.; Luo, B.; Zhang, X.; Hu, Y. Extendible load-isolation wireless charging platform for muti-receiver applications. IET Power Electr. 2017, 10, 134–142. [Google Scholar] [CrossRef]
- Tanabe, Y.; Poon, A.S.Y.; Camarillo, D.B.; Wu, L.C.; Yeh, A. Wearable Impact Measurement Device with Wireless Power and Data Communication. U.S. Utility Patent Application No. 14/256722, 23 October 2014. [Google Scholar]
- Tanabe, Y.; Chang, T.; Yeh, A.J.; Poon, A.S.Y. A small dual-band asymmetric dipole antenna for 13.56 MHz power and 2.45 GHz data transmission. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1120–1123. [Google Scholar] [CrossRef]
- Sallan, J.; Villa, J.L.; Llombart, A.; Sanz, J.F. Optimal Design of ICPT Systems Applied to Electric Vehicle Battery Charge. IEEE Trans. Ind. Electron. 2009, 56, 2140–2149. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, C.; Jiang, J.; Song, K.; Wei, G. A 3-kW Wireless Power Transfer System for Sightseeing Car Supercapacitor Charge. IEEE Trans. Power Electron. 2017, 32, 3301–3316. [Google Scholar] [CrossRef]
- Mai, R.; Liu, Y.; Li, Y.; Yue, P.; Cao, G.; He, Z. An Active-Rectifier-Based Maximum Efficiency Tracking Method Using an Additional Measurement Coil for Wireless Power Transfer. IEEE Trans. Power Electron. 2018, 33, 716–728. [Google Scholar] [CrossRef]
- Low, Z.N.; Chinga, R.A.; Tseng, R.; Lin, J. A loosely coupled planar wireless power transfer system supporting multiple receivers. IEEE Trans. Ind. Electron. 2009, 56, 1801–1812. [Google Scholar] [CrossRef][Green Version]
- Nithya, R.; Sundaramoorthi, R. Design and Implementation of SEPIC Converter with Low Ripple Battery Current for Electric Vehicle Applications. In Proceedings of the 1st International Conference on Emerging Trends in Engineering Technology and Science, Thanjavur, India, 24–26 February 2016. [Google Scholar]
- Hu, J.; Sagneri, A.D.; Rivas, J.M.; Han, Y.; Davis, S.M.; Perreault, D.J. High Frequency Resonant SEPIC Converter With Wide Input and Output Voltage Ranges. IEEE Trans. Power Electr. 2012, 27, 189–200. [Google Scholar] [CrossRef]
- Teng, J.; Huang, W.; Hsu, T.; Wang, C. Novel and Fast Maximum Power Point Tracking for Photovoltaic Generation. IEEE Trans. Ind. Electron. 2016, 63, 4955–4966. [Google Scholar] [CrossRef]
- Tseng, R.; von Novak, B.; Shevde, S.; Grajski, K.A. Introduction to the alliance for wireless power loosely coupled wireless power transfer system specification version 1.0. In Proceedings of the IEEE Wireless Power Transfer, Perugia, Italy, 21–24 May 2013. [Google Scholar]
- Gati, E.; Kampitsis, G.; Manias, S. Variable frequency controller for inductive power transfer in dynamic conditions. IEEE Trans. Power Electron. 2017, 32, 1–13. [Google Scholar] [CrossRef]
- Boztepe, M.; Guinjoan, F.; Velasco-Quesada, G.; Silvestre, S.; Chouder, A.; Karatepe, E. Global MPPT scheme for photovoltaic string inverters based on restricted voltage window search algorithm. IEEE Trans. Ind. Electron. 2014, 61, 3302–3312. [Google Scholar] [CrossRef]

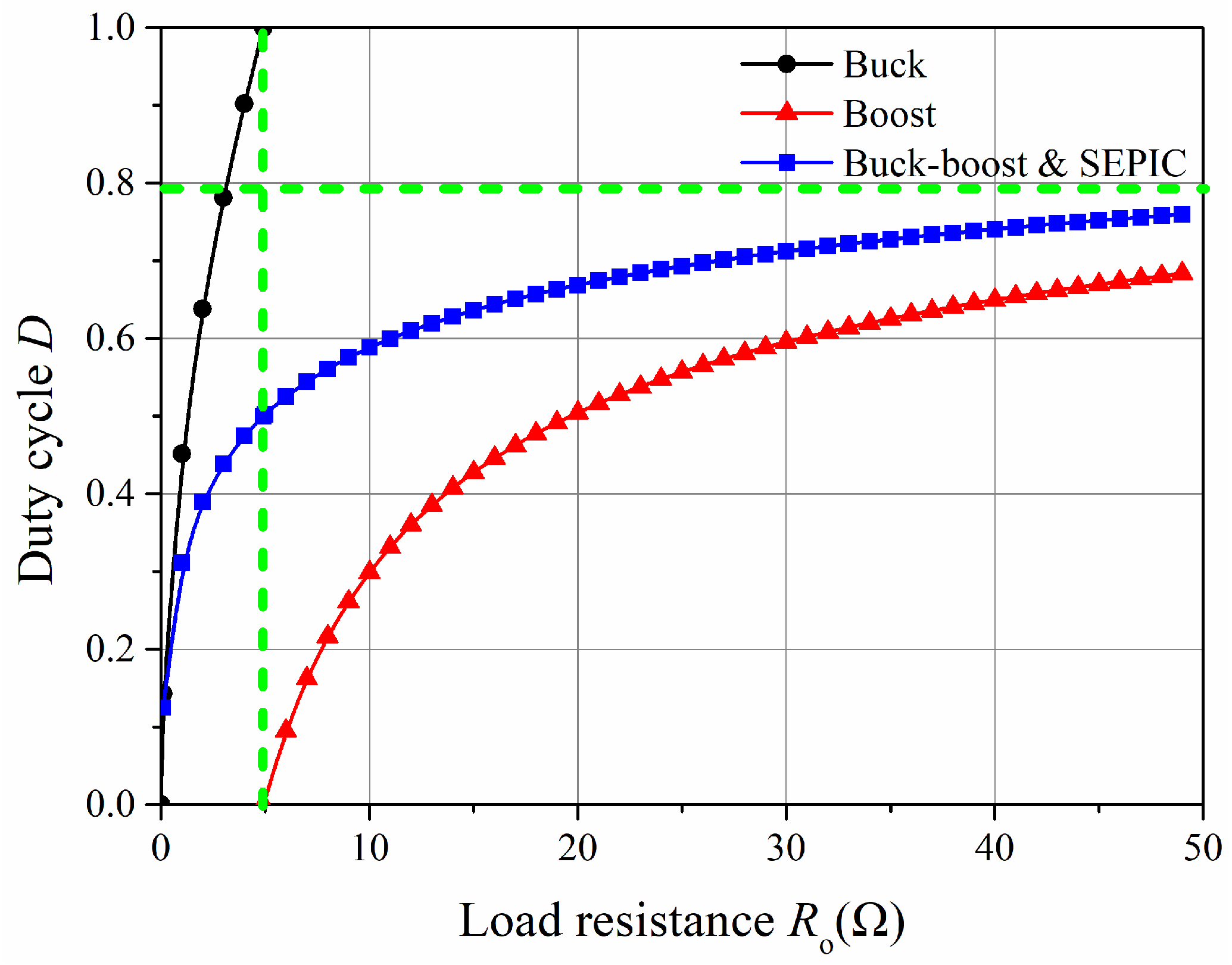




| Converter Type | Voltage Gain (Uout/Uin) | Load Resistance Transformation (RLi/Roi) | The Range of RLi |
|---|---|---|---|
| Boost | 0~Roi | ||
| Buck | Roi~+∞ | ||
| Buck-Boost | 0~+∞ | ||
| Single-Ended Primary Inductance Converter (SEPIC) | 0~+∞ |
| Symbol | Quantity | Value |
|---|---|---|
| Lt | Primary-side coil inductance | 2.13 μH |
| Rt | Primary-side coil resistance | 0.53 Ω |
| Lri | Secondary-side coil inductance | 3.73 μH |
| Rri | Secondary-side coil resistance | 0.76 Ω |
| fs | System operating frequency | 6.78 MHz |
| Ioi | Charging current | 0.1 A~2 A |
| Symbol | (A) Position 1 | (B) Position 2 | (C) Position 3 | |||
|---|---|---|---|---|---|---|
| k1 | 0.089 | 0.048 | 0.051 | |||
| k2 | 0.062 | 0.089 | 0.048 | |||
| M1 | 0.251 | 0.135 | 0.144 | |||
| M2 | 0.175 | 0.251 | 0.135 | |||
| Ƞ_opt | 93% | 92% | 88.6% | |||
| P1:P2 | 2:1 | 4:3 | 2:1 | 4:3 | 2:1 | 4:3 |
| Ƞ%_opt | 92% | 91% | 86% | 88% | 87.4% | 88.2% |
| Ƞmea | 84.3% | 83.5% | 77.8% | 78.2% | 78.6% | 79.4% |
| Symbol | A4WP | Designed Prototype |
|---|---|---|
| P1:P2 | 1:1 | 1:1 |
| k1 | 0.064 | 0.065 |
| k2 | 0.058 | 0.056 |
| M1 | 0.18 | 0.183 |
| M2 | 0.163 | 0.158 |
| Ioi | 0.1 A~2 A | 0.1 A~2 A |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Song, K.; Li, Z.; Jiang, J.; Zhu, C. Optimal Efficiency Tracking Control Scheme Based on Power Stabilization for a Wireless Power Transfer System with Multiple Receivers. Energies 2018, 11, 1232. https://doi.org/10.3390/en11051232
Li Y, Song K, Li Z, Jiang J, Zhu C. Optimal Efficiency Tracking Control Scheme Based on Power Stabilization for a Wireless Power Transfer System with Multiple Receivers. Energies. 2018; 11(5):1232. https://doi.org/10.3390/en11051232
Chicago/Turabian StyleLi, Yang, Kai Song, Zhenjie Li, Jinhai Jiang, and Chunbo Zhu. 2018. "Optimal Efficiency Tracking Control Scheme Based on Power Stabilization for a Wireless Power Transfer System with Multiple Receivers" Energies 11, no. 5: 1232. https://doi.org/10.3390/en11051232
APA StyleLi, Y., Song, K., Li, Z., Jiang, J., & Zhu, C. (2018). Optimal Efficiency Tracking Control Scheme Based on Power Stabilization for a Wireless Power Transfer System with Multiple Receivers. Energies, 11(5), 1232. https://doi.org/10.3390/en11051232






