Determining Time-Varying Drivers of Spot Oil Price in a Dynamic Model Averaging Framework
Abstract
1. Introduction
2. Literature Review
2.1. Models
2.2. Oil Price Drivers
3. Data
4. Methodology
4.1. Model Specification
4.2. Assumptions and Limitations Involved in the DMA Method
4.3. Model Calibration
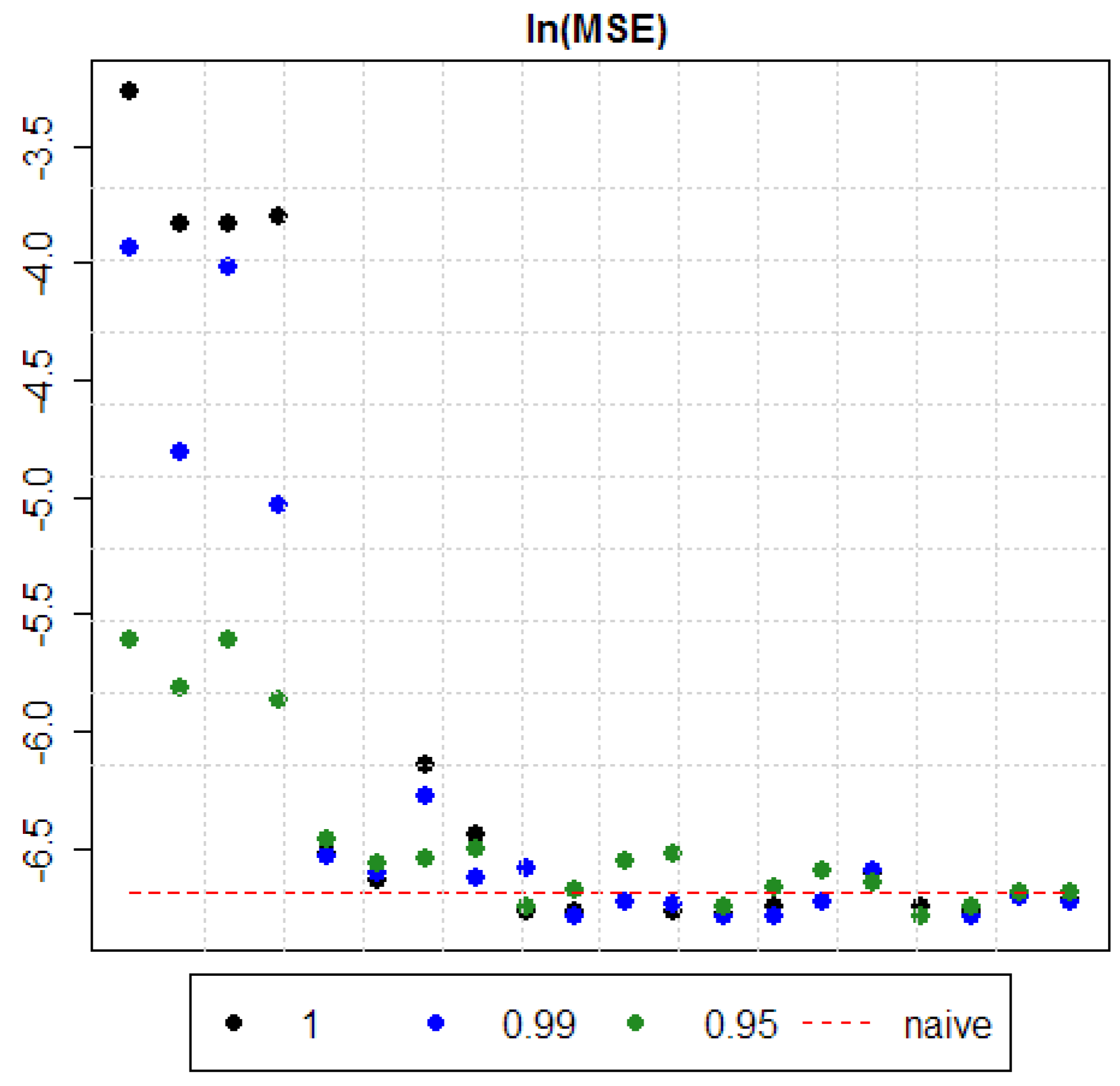
4.3.1. Forgetting Factor
4.3.2. Variance Matrix
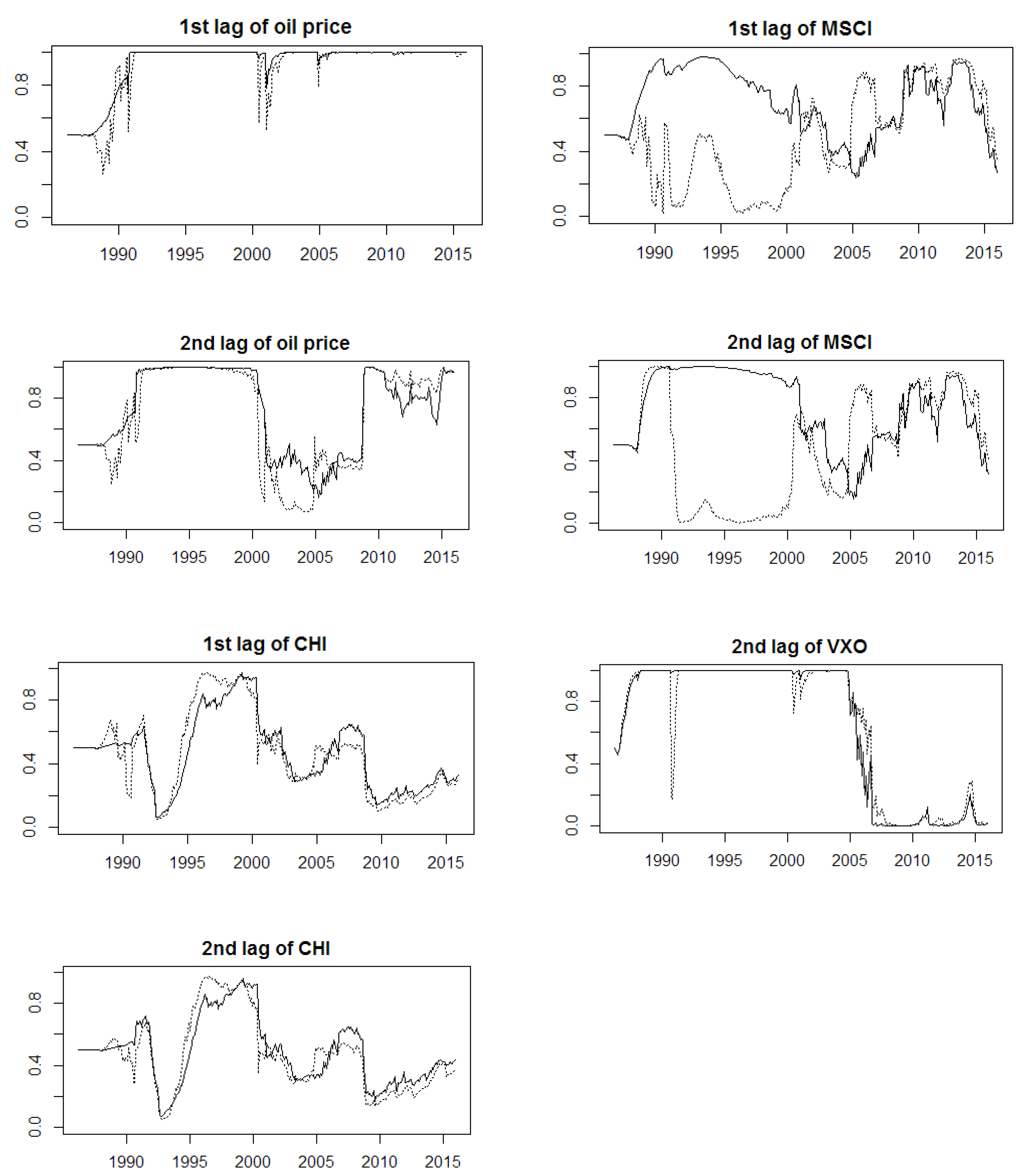
4.4. Time-Varying Parameters Preselection
4.5. Economic Interpretation
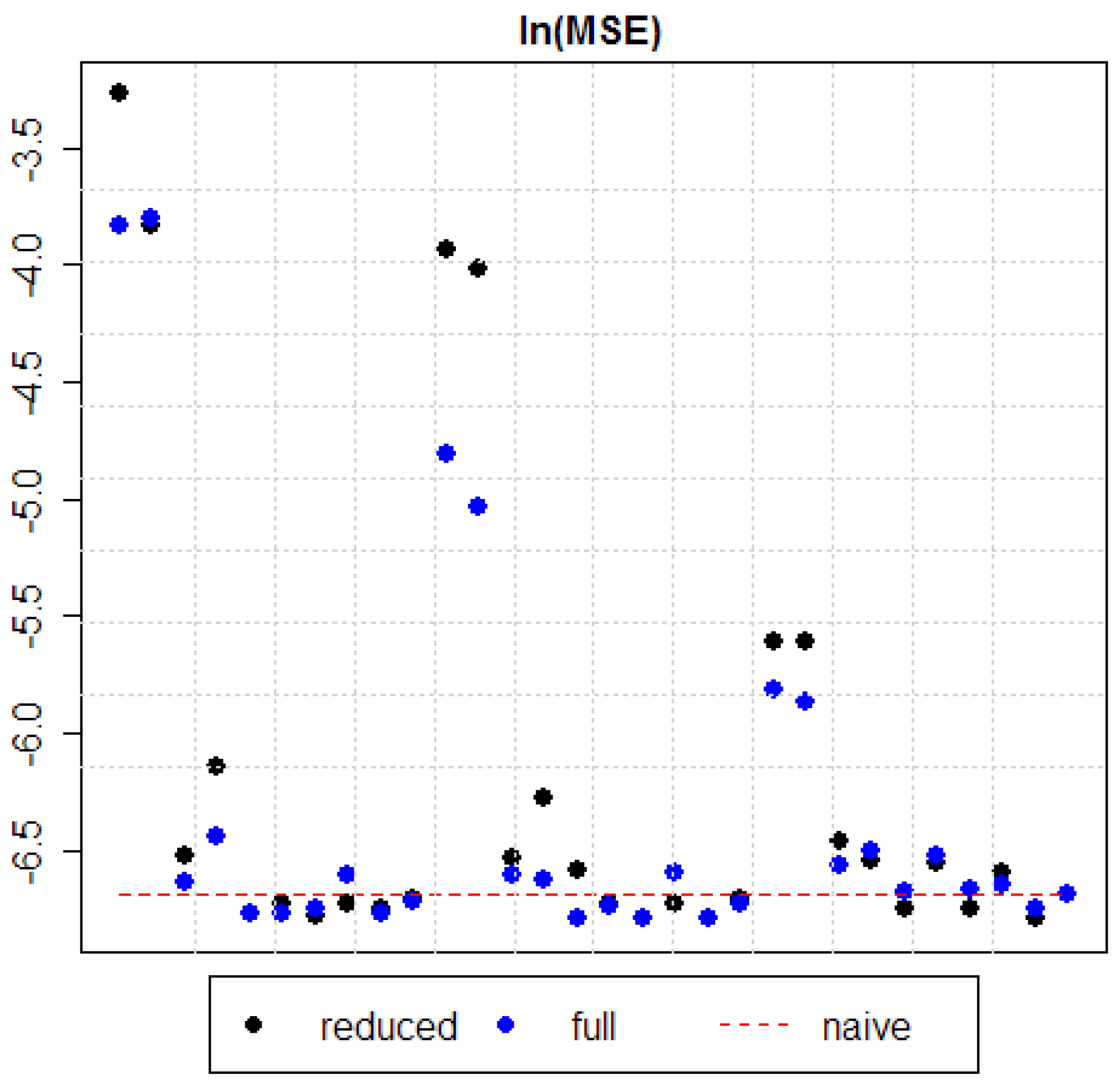
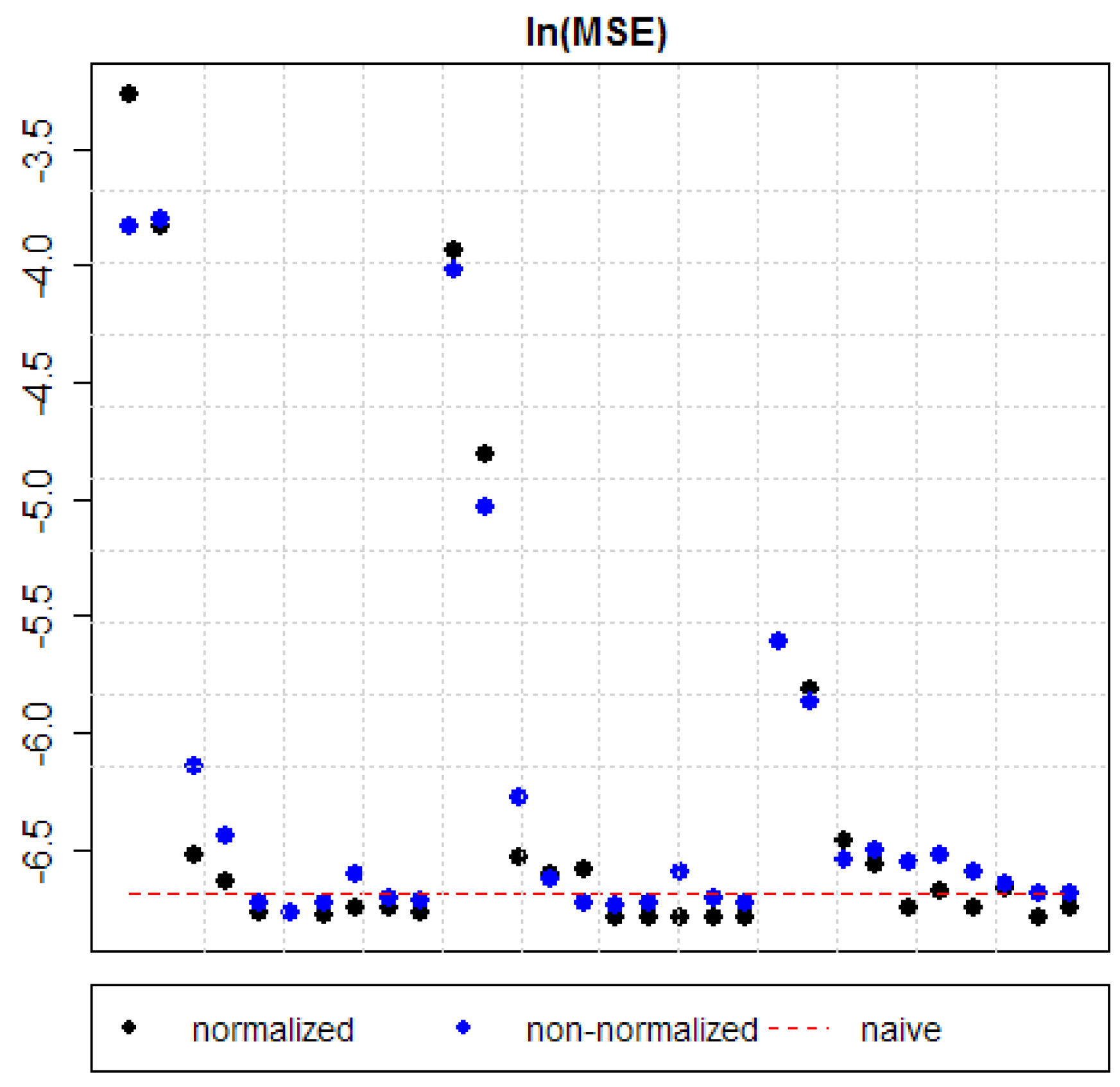
5. Results
6. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Data Sources
- BMA—Bayesian Model Averaging
- DMA—Dynamic Model Averaging
- forgetting factor—described in Section 4.1 and 4.3.1
- “full” model—described in Section 4.4
- futures forecast—a forecast is equal to the current price of 1-month futures price
- MSE—mean squared error, i.e., the average of the squares of differences between the real values of a time-series and the forecasted values of this time-series
- naïve forecast—a forecast is equal to the last observed value
- normalization—defined by Equation (7)
- posterior probability—conditional probability assigned after the relevant evidence is taken into account
- posteriori inclusion probability—defined by Equation (5)
- posteriori predictive probability—defined by Equation (4)
- prior probability—probability expressing the belief about it, before some evidence is taken into account
- “reduced” model—described in Section 4.4
- swing producer—supplier of a commodity, controlling its global deposits, able to change the level of supply at minimal cost, and, therefore, able to influence the price and balance the market
References
- Yang, C.W.; Hwang, M.J.; Huang, B.N. An analysis of factors affecting price volatility of the US oil market. Energy Econ. 2002, 24, 107–119. [Google Scholar] [CrossRef]
- ECB. Forecasting the price of oil. Econ. Bull. 2015, 4, 87–98. [Google Scholar]
- Acharya, V.V.; Lochstoer, L.A.; Ramadorai, T. Limits to arbitrage and hedging: Evidence from commodity markets. J. Financ. Econ. 2013, 109, 441–465. [Google Scholar] [CrossRef]
- Alquist, R.; Kilian, L. What do we learn from the price of crude oil futures? J. Appl. Econom. 2010, 25, 539–573. [Google Scholar] [CrossRef]
- Raftery, A.E.; Karny, M.; Ettler, P. Online prediction under model uncertainty via Dynamic Model Averaging: Application to a cold rolling mill. Technometrics 2010, 52, 52–66. [Google Scholar] [CrossRef] [PubMed]
- Aastveit, K.A.; Bjornland, H.C. What drives oil prices? Emerging versus developed economies. J. Appl. Econom. 2015, 30, 1013–1028. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Wu, G. Does China factor matter? An econometric analysis of international crude oil prices. Energy Policy 2014, 72, 78–86. [Google Scholar]
- Baumeister, C.; Peersman, G. Time-varying effects of oil supply shocks on the US economy. Am. Econ. J. Macroecon. 2013, 5, 1–28. [Google Scholar] [CrossRef]
- Coleman, L. Explaining crude oil prices using fundamental measures. Energy Policy 2012, 40, 318–324. [Google Scholar] [CrossRef]
- Lippi, F.; Nobili, A. Oil and the macroeconomy: A quantitative structural analysis. J. Eur. Econ. Assoc. 2012, 10, 1059–1083. [Google Scholar] [CrossRef]
- Liu, J.; Wei, Y.; Ma, F.; Wahab, M.I.M. Forecasting the realized range-based volatility using dynamic model averaging approach. Econ. Model. 2017, 61, 12–26. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C. Energy prices and exchange rates of the U.S. dollar: Further evidence from linear and nonlinear causality analysis. Econ. Model. 2012, 29, 2289–2297. [Google Scholar] [CrossRef]
- Buncic, D.; Moretto, C. Forecasting copper prices with dynamic averaging and selection models. N. Am. J. Econ. Financ. 2015, 33, 1–38. [Google Scholar] [CrossRef]
- Aye, G.; Gupta, R.; Hammoudeh, S.; Kim, W.J. Forecasting the price of gold using Dynamic Model Averaging. Int. Rev. Financ. Anal. 2015, 41, 257–266. [Google Scholar] [CrossRef]
- Bork, L.; Moller, S.V. Forecasting house prices in the 50 states using Dynamic Model Averaging and Dynamic Model Selection. Int. J. Forecast. 2015, 31, 63–78. [Google Scholar] [CrossRef]
- Baur, D.G.; Beckmann, J.; Czudaj, R. Gold Price Forecasts in a Dynamic Model Averaging Framework—Have the Determinants Changed over Time? Ruhr Economic Papers No. 506; Ruhr-Universitat: Bochum, Germany, 2014; p. 27. [Google Scholar]
- Koop, G.; Korobilis, D. Forecasting inflation using Dynamic Model Averaging. Int. Econ. Rev. 2012, 53, 867–886. [Google Scholar] [CrossRef]
- Naser, H. Estimating and forecasting the real prices of crude oil: A data rich model using a dynamic model averaging (DMA) approach. Energy Econ. 2016, 56, 75–87. [Google Scholar] [CrossRef]
- Xu, C. Forecasting oil prices. Oil Gas J. 2016, 114, 26. [Google Scholar]
- Fan, L.; Li, H. Volatility analysis and forecasting models of crude oil prices: A review. Int. J. Glob. Energy Issues 2015, 38, 5–17. [Google Scholar] [CrossRef]
- Behimri, N.B.; Pires Manso, J.R. Crude oil price forecasting techniques: A comprehensive review of literature. Altern. Invest. Anal. Rev. 2013, 2, 30–49. [Google Scholar]
- Klein, T.; Walther, T. Oil price volatility forecast with mixture memory GARCH. Energy Econ. 2016, 58, 46–58. [Google Scholar] [CrossRef]
- Silva, E.G.; Legey, L.F.L.; Silva, E.A. Forecasting oil price trends using wavelets and hidden Markov models. Energy Econ. 2010, 32, 1507–1519. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Y.; Huang, D. Forecasting crude oil market volatility: Further evidence using GARCH-class models. Energy Econ. 2010, 32, 1477–1484. [Google Scholar] [CrossRef]
- Vo, M.T. Regime-switching stochastic volatility: Evidence from the crude oil market. Energy Econ. 2009, 31, 779–788. [Google Scholar] [CrossRef]
- Nomikos, N.K.; Pouliasis, P.K. Forecasting petroleum futures markets volatility: The role of regimes and market conditions. Energy Econ. 2011, 33, 321–337. [Google Scholar] [CrossRef]
- Agnolucci, P. Volatility in crude oil futures: A comparison of the predictive ability of GARCH and implied volatility models. Energy Econ. 2009, 31, 316–321. [Google Scholar] [CrossRef]
- Coppola, A. Forecasting oil price movements: Exploiting the information in the futures market. J. Futures Mark. 2008, 28, 34–56. [Google Scholar] [CrossRef]
- Sadorsky, P. Modeling and forecasting petroleum futures volatility. Energy Econ. 2006, 28, 467–488. [Google Scholar] [CrossRef]
- Yousefi, S.; Weinreich, I.; Reinarz, D. Wavelet-based prediction of oil prices. Chaos Solitons Fractals 2005, 25, 265–275. [Google Scholar] [CrossRef]
- Kaufmann, R.K.; Dees, S.; Gasteuil, A.; Mann, M. Oil prices: The role of refinery utilization. Futures markets and non-linearities. Energy Econ. 2008, 30, 2609–2622. [Google Scholar] [CrossRef]
- Dees, S.; Karadeloglou, P.; Kaufmann, R.K.; Sanchez, M. Modelling the world oil market: Assessment of a quarterly econometric model. Energy Policy 2007, 35, 178–191. [Google Scholar] [CrossRef]
- Gori, F.; Ludovisi, D.; Cerritelli, P.F. Forecast of oil price and consumption in the short-term under three scenarios: Parabolic, linear and chaotic behavior. Energy Econ. 2007, 32, 1291–1296. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Lai, K.K. A roughset-refined text mining approach for crude oil market tendency forecasting. Int. J. Knowl. Syst. Sci. 2005, 2, 33–46. [Google Scholar]
- Wang, Y.; Wu, C.; Yang, L. Oil price shocks and stock market activities: Evidence from oil-importing and oil-exporting countries. J. Comp. Econ. 2013, 41, 1220–1239. [Google Scholar] [CrossRef]
- Kulkarni, S.; Haidar, I. Forecasting model for crude oil price using artificial neural networks and commodity futures prices. 2009; arXiv:0906.4838. [Google Scholar]
- Yu, L.; Wang, S.; Lai, K.K. Forecasting crude oil price with an EMD-based neural network. Ensemble learning paradigm. Energy Econ. 2008, 30, 2623–2635. [Google Scholar] [CrossRef]
- Shambora, W.; Rossiter, R. Are there exploitable inefficiencies in the futures market for oil? Energy Econ. 2007, 29, 18–27. [Google Scholar] [CrossRef]
- Baumeister, C.; Kilian, L. What central bankers need to know about forecasting oil prices. Int. Econ. Rev. 2014, 55, 869–889. [Google Scholar] [CrossRef]
- Heryan, T. Oil spot prices’ next day volatility: Comparison of European and American short-run forecasts. In Financial Environment and Business Development; Bilgin, M., Danis, H., Demir, E., Can, U., Eds.; Eurasian Studies in Business and Economics 4; Springer: Cham, Switzerland, 2017; pp. 285–296. [Google Scholar]
- McQuarrie, A.D.R.; Tsai, C.-L. Regression and Time Series Model Selection; World Scientific: Singapore, 1998. [Google Scholar]
- Salisu, A.A.; Fasanya, I.O. Modelling oil price volatility with structural breaks. Energy Policy 2013, 52, 554–562. [Google Scholar] [CrossRef]
- Baumeister, C.; Kilian, L.; Lee, T.K. Forecasting the real price of oil in a changing world: A forecast combination approach. Energy Econ. 2015, 46, S33–S43. [Google Scholar] [CrossRef]
- Lammerding, M.; Stephan, P.; Trede, M.; Wilfling, B. Speculative bubbles in recent oil price dynamics: Evidence from a Bayesian Markov-switching state-space approach. Energy Econ. 2013, 36, 491–502. [Google Scholar] [CrossRef]
- Du, X.; Yu, C.L.; Hayes, D.J. Speculation and volatility spillover in the crude oil and agricultural commodity markets: A Bayesian analysis. Energy Econ. 2011, 33, 497–503. [Google Scholar] [CrossRef]
- Zagaglia, P. Macroeconomic factors and oil futures prices: A data-rich model. Energy Econ. 2010, 32, 409–417. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial. Stat. Sci. 1999, 14, 382–401. [Google Scholar]
- Koop, G. Bayesian Econometrics; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Sims, C. Bayesian Methods in Applied Econometrics, or, Why Econometrics Should Always and Everywhere Be Bayesian, Hotelling Lecture, 29 June 2007, Duke University. 2007. Available online: http://sims.princeton.edu/yftp/EmetSoc607/AppliedBayes.pdf (accessed on 3 October 2017).
- Sala-I-Martin, X. I just ran two million regressions. Am. Econ. Rev. 1997, 87, 178–183. [Google Scholar]
- Culka, M. Uncertainty analysis using Bayesian Model Averaging: A case study of input variables to energy models and inference to associated uncertainties of energy scenarios. Energy Sustain. Soc. 2016, 6, 7. [Google Scholar] [CrossRef]
- Breitenfellner, A.; Crespo Cuaresma, J.; Keppel, C. Determinants of crude oil prices: Supply, demand, cartel or speculation? Monetary Policy Econ. 2009, 4, 111–136. [Google Scholar]
- Leamer, E.E. Specification Searches: Ad hoc Inference with Nonexperimental Data; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Clyde, M.; George, E.I. Model uncertainty. Stat. Sci. 2004, 19, 81–94. [Google Scholar]
- Kulhavy, R.; Zarrop, M.B. On a general concept of forgetting. Int. J. Control 1993, 58, 905–924. [Google Scholar] [CrossRef]
- Dedecius, K.; Nagy, I.; Karny, M. Parameter tracking with partial forgetting method. Int. J. Adapt. Control Signal Process. 2012, 26, 1–12. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Stefanski, R. Structural transformation and the oil price. Rev. Econ. Dyn. 2014, 17, 484–504. [Google Scholar] [CrossRef]
- Blanchard, O.J.; Riggi, M. Why are the 2000s so different from the 1970s? A structural interpretation of changes in the macroeconomic effects of oil prices. J. Eur. Econ. Assoc. 2013, 11, 1032–1052. [Google Scholar] [CrossRef]
- Ji, Q. System analysis approach for the identification of factors driving crude oil prices. Comput. Ind. Eng. 2012, 63, 615–625. [Google Scholar] [CrossRef]
- Fattouh, B.; Scaramozzino, P. Uncertainty, expectations, and fundamentals: Whatever happened to long-term oil prices? Oxf. Rev. Econ. Policy 2011, 27, 186–206. [Google Scholar] [CrossRef]
- Fan, Y.; Xu, J.-H. What has driven oil prices since 2000? A structural change perspective. Energy Econ. 2011, 33, 1082–1094. [Google Scholar] [CrossRef]
- Hotelling, H. The economics of exhaustible resources. J. Political Econ. 1931, 39, 137–175. [Google Scholar] [CrossRef]
- Arora, V.; Tanner, M. Do oil prices respond to real interest rates? Energy Econ. 2013, 36, 546–555. [Google Scholar] [CrossRef]
- Byrne, J.P.; Lorusso, M.; Xu, B. Oil Prices and Informational Frictions: The Time-Varying Impact of Fundamentals and Expectations; CEERP Working Paper No. 6; Heriot-Watt University: Edinburgh, UK, 2017. [Google Scholar]
- Bernabe, A.; Martina, E.; Alvarez-Ramirez, J.; Ibarra-Valdez, C. A multi-model approach for describing crude oil price dynamics. Phys. A Stat. Mech. Its Appl. 2004, 338, 567–584. [Google Scholar] [CrossRef]
- Yousefi, A.; Wirjanto, T.S. The empirical role of the exchange rate on the crude-oil price information. Energy Econ. 2004, 26, 783–799. [Google Scholar] [CrossRef]
- Basher, S.A.; Haug, A.A.; Sadorsky, P. Oil prices, exchange rates and emerging stock markets. Energy Econ. 2012, 34, 227–240. [Google Scholar] [CrossRef]
- Du, L.; He, Y. Extreme risk spillovers between crude oil and stock markets. Energy Econ. 2015, 51, 455–465. [Google Scholar] [CrossRef]
- Mensi, W.; Beljid, M.; Boubaker, A.; Managi, S. Correlations and volatility spillovers across commodity and stock markets: Linking energies, food, and gold. Econ. Model. 2013, 32, 15–22. [Google Scholar] [CrossRef]
- Arouri, M.E.H.; Jouini, J.; Nguyen, D.K. Volatility spillovers between oil prices and stock sector returns: Implications for portfolio management. J. Int. Money Financ. 2011, 30, 1387–1405. [Google Scholar] [CrossRef]
- Creti, A.; Joets, M.; Mignon, V. On the links between stock and commodity markets’ volatility. Energy Econ. 2013, 37, 16–28. [Google Scholar] [CrossRef]
- Silvennoinen, A.; Thorp, S. Financialization, crisis and commodity correlation dynamics. J. Int. Financ. Mark. Inst. Money 2013, 24, 42–65. [Google Scholar] [CrossRef]
- Kumar, D. Realized volatility transmission from curde oil to equity sectors: A study with economic significance analysis. Int. Rev. Econ. Financ. 2017, 49, 149–167. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, F.; Wei, Y.; Wu, C. Forecasting realized volatility in changing world: A dynamic model averaging approach. J. Bank. Financ. 2016, 64, 136–149. [Google Scholar] [CrossRef]
- Mollick, A.V.; Assefa, T.A. U.S. stock returns and oil prices: The tale from daily data and the 2008–2009 financial crisis. Energy Econ. 2013, 36, 1–18. [Google Scholar] [CrossRef]
- Fayyad, A.; Daly, K. The impact of oil price shocks on stock market returns: Comparing GCC countries with the UK and USA. Emerg. Mark. Rev. 2011, 12, 61–78. [Google Scholar] [CrossRef]
- Kang, W.; Ratti, R.A.; Yoon, K.H. Time-varying effect of oil market shocks on the stock market. J. Bank. Financ. 2015, 61, S150–S163. [Google Scholar] [CrossRef]
- Aloui, R.; Aissa, M.S.B.; Nguyen, D.K. Conditional dependence structure between oil prices and exchange rates: A copula-GARCH approach. J. Int. Money Financ. 2013, 32, 719–738. [Google Scholar] [CrossRef]
- Akram, Q.F. Commodity prices, interest rates and the dollar. Energy Econ. 2009, 31, 838–851. [Google Scholar] [CrossRef]
- Wang, S.; Yu, L.; Lai, K.K. A novel hybrid AI system framework for crude oil price forecasting. Lect. Notes Comput. Sci. 2004, 3327, 233–242. [Google Scholar]
- Chen, S.-S.; Chen, H.-C. Oil prices and real exchange rates. Energy Econ. 2007, 29, 390–404. [Google Scholar] [CrossRef]
- Bal, D.P.; Rath, B.N. Nonlinear causality between crude oil price and exchange rate: A comparative study of China and India. Energy Econ. 2015, 51, 149–156. [Google Scholar]
- Uddin, G.S.; Tiwari, A.K.; Arouri, M.; Teulon, F. On the relationship between oil price and exchange rates: A wavelet analysis. Econ. Model. 2013, 35, 502–507. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Rivera-Castro, M.A. A wavelet decomposition approach to crude oil price and exchange rate dependence. Econ. Model. 2013, 32, 42–57. [Google Scholar] [CrossRef]
- Turhan, I.; Hacihasanoglu, E.; Soytas, U. Oil prices and emerging market exchange rates. Emerg. Mark. Financ. Trade 2013, 49, 21–36. [Google Scholar] [CrossRef]
- Reboredo, J.C. Modelling oil price and exchange rate co-movements. J. Policy Model. 2012, 34, 419–440. [Google Scholar] [CrossRef]
- Riggi, M.; Venditti, F. The time varying effect of oil price shocks on euro-area exports. J. Econ. Dyn. Control 2015, 59, 75–94. [Google Scholar] [CrossRef]
- Bekiros, S.; Gupta, R.; Paccagnini, A. Oil price forecastability and economic uncertainty. Econ. Lett. 2015, 132, 125–128. [Google Scholar] [CrossRef]
- Andreasson, P.; Bekiros, S.; Nguyen, D.K.; Uddin, G.S. Impact of speculation and economic uncertainty on commodity markets. Int. Rev. Financ. Anal. 2016, 43, 115–127. [Google Scholar] [CrossRef]
- Hamilton, J.D. Causes and consequences of the oil shock of 2007–08. Brook. Pap. Econ. Act. 2009, 40, 215–259. [Google Scholar] [CrossRef]
- Fattouh, B.; Kilian, L.; Mahadeva, L. The role of speculation in oil markets: What have we learned so far? Energy J. 2013, 34, 20–30. [Google Scholar] [CrossRef]
- Carmona, R. Financialization of the commodities markets: A non-technical introduction. In Commodities, Energy and Environmental Finance; Aid, R., Ludkovski, M., Sircar, R., Eds.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Kilian, L.; Murphy, D.P. The role of inventories and speculative trading in the global market for crude oil. J. Appl. Econom. 2014, 29, 454–478. [Google Scholar] [CrossRef]
- Kaufmann, R.K. The role of market fundamentals and speculation in recent price changes for crude oil. Energy Policy 2011, 39, 105–115. [Google Scholar] [CrossRef]
- Pirrong, C. Stochastic fundamental volatility, speculation, and commodity storage. In Commodity Price Dynamics. A Structural Approach; Pirrong, C., Ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Kemp, J. Oil Inventories Lose Their Influence on Prices. Reuters. 2010. Available online: http://blogs.reuters.com/great-debate/2010/03/24/oil-inventories-lose-their-influence-on-prices (accessed on 3 October 2017).
- Killian, L.; Hicks, B. Did unexpectedly strong economic growth cause the oil price shock of 2003–2008? J. Forecast. 2013, 32, 385–394. [Google Scholar] [CrossRef]
- Hamilton, J.D. Oil and the macroeconomy since world war II. J. Political Econ. 1983, 91, 228–248. [Google Scholar] [CrossRef]
- Li, R.; Leung, G.C.K. The integration of China into the world crude oil market since 1998. Energy Policy 2011, 39, 5159–5166. [Google Scholar] [CrossRef]
- Kilian, L. Not all oil price shocks are alike: Disentangling demand and supply shocks in the crude oil market. Am. Econ. Rev. 2009, 99, 1053–1069. [Google Scholar] [CrossRef]
- He, Y.; Wang, S.; Lai, K.K. Global economic activity and crude oil prices: A cointegration analysis. Energy Econ. 2010, 32, 868–876. [Google Scholar] [CrossRef]
- Nguyen, D.K.; Walther, T. Modeling and Forecasting Commodity Market Volatility with Long-Term Economic and Financial Variables; MPRA Paper 84464; University Library of Munich: Munich, Germany, 2018. [Google Scholar]
- Bu, H. Effect of inventory announcements on crude oil price volatility. Energy Econ. 2014, 46, 485–494. [Google Scholar] [CrossRef]
- Karali, B.; Power, G.J. Short- and long-run determinants of commodity price volatility. Am. J. Agric. Econ. 2013, 95, 724–738. [Google Scholar] [CrossRef]
- Kao, C.-W.; Wan, J.-Y. Price discount, inventories and the distortion of WTI benchmark. Energy Econ. 2012, 34, 117–124. [Google Scholar] [CrossRef]
- Alquist, R.; Kilian, L.; Vigfusson, R.J. Forecasting the price of oil. In Handbook of Economic Forecasting; Elliott, G., Timmermann, A., Eds.; Elsevier: New York, NY, USA, 2013. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. 2015. Available online: http://www.R-project.org (accessed on 3 October 2017).
- Trapletti, A.; Hornik, K.; LeBaron, B. Time Series Analysis and Computational Finance. 2015. Available online: http://cran.r-project.org/web/packages/tseries/index.html (accessed on 3 October 2017).
- D’Agostino, A.; Giannone, D. Macroeconomic forecasting and structural change. J. Appl. Econom. 2013, 28, 82–101. [Google Scholar] [CrossRef]
- Karny, M.; Kulhavy, R. Structure determination of regression-type models for adaptive prediction and control. In Bayesian Analysis of Time Series and Dynamic Models; Spall, J.C., Ed.; Marcel Dekker: New York, NY, USA, 1988; pp. 313–345. [Google Scholar]
- Ljung, L. System Identification: Theory for the User; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Clyde, M. Bayesian model averaging and model search strategies. Bayesian Stat. 1999, 6, 157–185. [Google Scholar]
- Garcia, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Karny, M. Algorithms for determining the model structure of a controlled system. Kybernetika 1983, 19, 164–178. [Google Scholar]
- Conigliani, C.; O’Hagan, A. Sensitivity of the fractional Bayes factor to prior distributions. Can. J. Stat. 2000, 28, 343–352. [Google Scholar] [CrossRef]
- Karny, M.; Andrysek, J.; Bodini, A.; Guy, T.V.; Kracik, J.; Ruggeri, F. How to exploit external model of data for parameter estimation? Int. J. Adapt. Control Signal Process. 2006, 20, 41–50. [Google Scholar] [CrossRef]
- Miguel, B.; Koop, G. Model Switching and Model Averaging in Time-Varying Parameter Regression Models; Scottish Institute for Research in Economics Discussion Papers; SIRE: Edinburgh, UK, 2013; p. 34. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 134–144. [Google Scholar]
- Kruse, R.; Wegener, C. Time-varying persistence in real oil prices and its determinant. 2017; unpublished. [Google Scholar]
| Name | Description | Economic Factor Measured by the Driver (and Units) |
|---|---|---|
| dependent variable in regression models | ||
| WTI | WTI spot price | crude oil spot price (in USD) |
| independent variables in regression models (drivers) | ||
| MSCI | MSCI World Index | stocks prices (index) |
| TB3MS | U.S. 3-month treasury bill secondary market rate | interest rate (in percentages) |
| KEI | Kilian’s index of global economy activity [101] | global economic activity (index) |
| TWEXM | trade weighted U.S. dollar index | exchange rate (Mar, 1973 = 100) |
| PROD | U.S. crude oil production | oil supply (in thousand barrels) |
| IMP | daily average of U.S. crude oil import | oil demand (in thousand barrels per day) |
| INV | U.S. total ending stocks of commercial crude oil (excluding SPR) | speculative pressures (in thousand barrels) |
| VXO | implied volatility of S&P 100 | volatility of stocks market (index) |
| CONS | total consumption of petroleum products in OECD | oil demand (in quad BTU) |
| CHI | Shanghai Composite Index merged with Hang Seng Index as a representative of Chinese economy | Chinese economy (rescaled index) |
| other time-series | ||
| NFP | 1-month NYMEX WTI futures prices | alternative forecast of crude oil price (in USD) |
| Model | xt(k) (Drivers Considered in the Model) |
|---|---|
| Model 1 | 1st lag of MSCI, |
| 1st lag of TB3MS, 1st lag of KEI, 1st lag of TWEXM, 1st lag of PROD, 1st lag of IMP,1st lag of INV, | |
| 1st lag of VXO, 1st lag of CONS, 1st lag of CHI | |
| Model 2 | 1st lag of WTI, |
| 1st lag of MSCI, | |
| 1st lag of TB3MS, 1st lag of KEI, 1st lag of TWEXM, 1st lag of PROD, 1st lag of IMP, 1st lag of INV, | |
| 1st lag of VXO, 1st lag of CONS, 1st lag of CHI | |
| Model 3 | 1st lag of WTI, |
| 1st lag of MSCI, | |
| 1st lag of TB3MS, 1st lag of KEI, 1st lag of TWEXM, 1st lag of PROD, 1st lag of IMP, 1st lag of INV, | |
| 1st lag of VXO, 1st lag of CONS, 1st lag of CHI, | |
| 1st lag of NFP | |
| Model 4 | 1st lag of WTI, 2nd lag of WTI, |
| 1st lag of MSCI, 2nd lag of MSCI, | |
| 1st lag of TB3MS, 1st lag of KEI, 1st lag of TWEXM, 1st lag of PROD, 1st lag of IMP, 1st lag of INV, | |
| 1st lag of VXO, 1st lag of CONS, 1st lag of CHI, | |
| Model 5 | 1st lag of WTI, 2nd lag of WTI, 1st lag of MSCI, 2nd lag of MSCI, 1st lag of VXO, 2nd lag of VXO, |
| 1st lag of CHI, 2nd lag of CHI |
| Presence of the Driver in the Model with Normalized Data is Indicated by “x”, and in the Model with Non-Normalized Data by “o”. | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |||||||||||
| α | 1 | 0.99 | 0.95 | 1 | 0.99 | 0.95 | 1 | 0.99 | 0.95 | 1 | 0.99 | 0.95 | 1 | 0.99 | 0.95 |
| 1st lag of WTI | x o | x o | x o | x o | x o | x o | x o | x o | x o | x o | x o | x o | |||
| 2nd lag of WTI | x o | x o | x o | x o | x o | x o | |||||||||
| 1st lag of MSCI | x o | x o | o | o | x o | x o | o | x o | |||||||
| 2nd lag of MSCI | x o | o | x o | ||||||||||||
| 1st lag of TB3MS | x | o | x o | x o | x | x o | x | x o | x o | x | x o | ||||
| 1st lag of KEI | x | x o | x o | x o | x | x o | |||||||||
| 1st lag of TWEXM | x o | x o | x o | x | x o | x | x | x o | x o | x | x o | ||||
| 1st lag of PROD | o | o | x | x o | x | x o | x | x | x o | ||||||
| 1st lag of IMP | x o | o | x | o | x | ||||||||||
| 1st lag of INV | x o | o | x | o | x | ||||||||||
| 1st lag of VXO | x | x o | o | x | o | o | o | o | x o | ||||||
| 2nd lag of VXO | x | x | x | ||||||||||||
| 1st lag of CONS | o | x | x o | x o | x | x o | x | x o | |||||||
| 1st lag of CHI | x | x | o | x | x o | ||||||||||
| 2nd lag of CHI | o | x o | x o | ||||||||||||
| 1st lag of NFP | x o | o | x o | ||||||||||||
| Models | α | |||
|---|---|---|---|---|
| 1 | 0.99 | 0.95 | ||
| Model 1 (normalized) | reduced | 0.03794 | 0.01949 | 0.00365 |
| full | 0.02169 | 0.00817 | 0.00298 | |
| Model 1 (non-normalized) | reduced | 0.02176 | 0.01795 | 0.00365 |
| full | 0.02235 | 0.00654 | 0.00283 | |
| Model 2 (normalized) | reduced | 0.00147 | 0.00145 | 0.00156 |
| full | 0.00131 | 0.00135 | 0.00141 | |
| Model 2 (non-normalized) | reduced | 0.00215 | 0.00187 | 0.00144 |
| full | 0.00159 | 0.00132 | 0.00150 | |
| Model 3 (normalized) | reduced | 0.00115 | 0.00138 | 0.00117 |
| full | 0.00115 | 0.00113 | 0.00126 | |
| Model 3 (non-normalized) | reduced | 0.00120 | 0.00120 | 0.00142 |
| full | 0.00115 | 0.00118 | 0.00147 | |
| Model 4 (normalized) | reduced | 0.00114 | 0.00112 | 0.00117 |
| full | 0.00117 | 0.00112 | 0.00127 | |
| Model 4 (non-normalized) | reduced | 0.00119 | 0.00120 | 0.00136 |
| full | 0.00135 | 0.00136 | 0.00130 | |
| Model 5 (normalized) | reduced | 0.00117 | 0.00113 | 0.00113 |
| full | 0.00115 | 0.00113 | 0.00117 | |
| Model 5 (non-normalized) | reduced | 0.00122 | 0.00122 | 0.00124 |
| full | 0.00121 | 0.00120 | 0.00125 | |
| Benchmarks | ||||
| 1-month futures | 0.00122 | |||
| naïve (i.e., the last period’s actuals are used as this period’s forecast) | 0.00124 | |||
| Equal-Weighted Averaging | 0.02694 | |||
| MSE smaller than those of benchmark forecasts are bolded. | ||||
| Halt: Forecast from the Chosen Model is More Accurate than the Forecast from the … | Stat. | p-val. |
|---|---|---|
| BMA | 0.8676 | 0.1931 |
| Equal-Weighted Averaging | 9.5349 | 0.0000 |
| 1-month futures | 0.7614 | 0.2235 |
| naive | 14.6047 | 0.0000 |
| Model 1 (normalized) | 8.7911 | 0.0000 |
| Model 2 (normalized) | 2.0940 | 0.0185 |
| Model 3 (normalized) | 1.8576 | 0.0320 |
| Model 4 (normalized) | −0.1078 | 0.5429 |
| Strategy | Mean | SD | Sharpe Ratio |
|---|---|---|---|
| DMA | 0.0069 | 0.0614 | 0.1131 |
| “Hold oil” | 0.0066 | 0.0848 | 0.0778 |
| Based on futures | −0.0010 | 0.0688 | −0.0141 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drachal, K. Determining Time-Varying Drivers of Spot Oil Price in a Dynamic Model Averaging Framework. Energies 2018, 11, 1207. https://doi.org/10.3390/en11051207
Drachal K. Determining Time-Varying Drivers of Spot Oil Price in a Dynamic Model Averaging Framework. Energies. 2018; 11(5):1207. https://doi.org/10.3390/en11051207
Chicago/Turabian StyleDrachal, Krzysztof. 2018. "Determining Time-Varying Drivers of Spot Oil Price in a Dynamic Model Averaging Framework" Energies 11, no. 5: 1207. https://doi.org/10.3390/en11051207
APA StyleDrachal, K. (2018). Determining Time-Varying Drivers of Spot Oil Price in a Dynamic Model Averaging Framework. Energies, 11(5), 1207. https://doi.org/10.3390/en11051207




