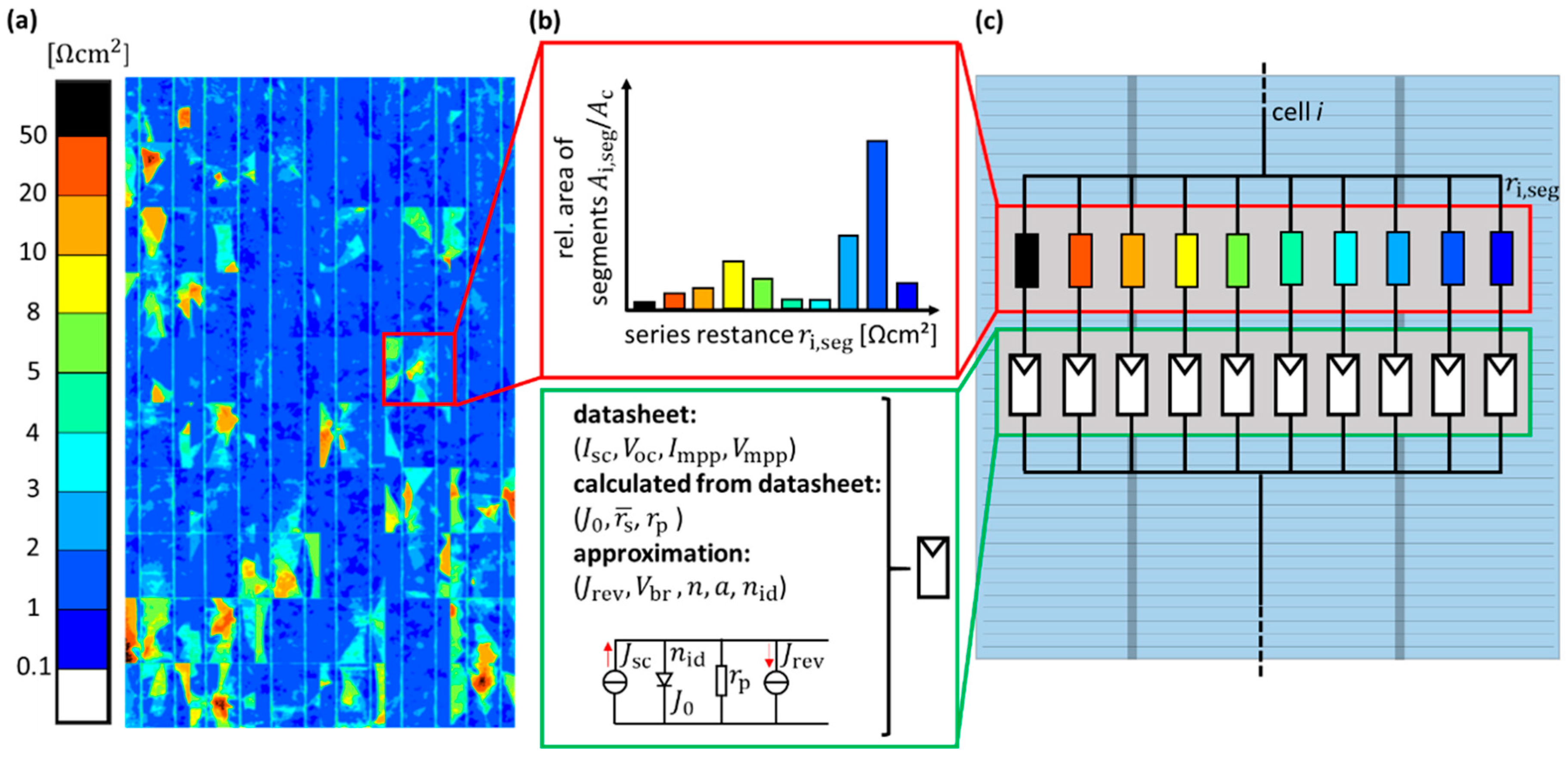
2.2.1. Series Resistance Mapping from EL Images
The simplest and most common approach for describing the electrical properties of solar cells and even total PV modules is the evaluation of the one-diode model.
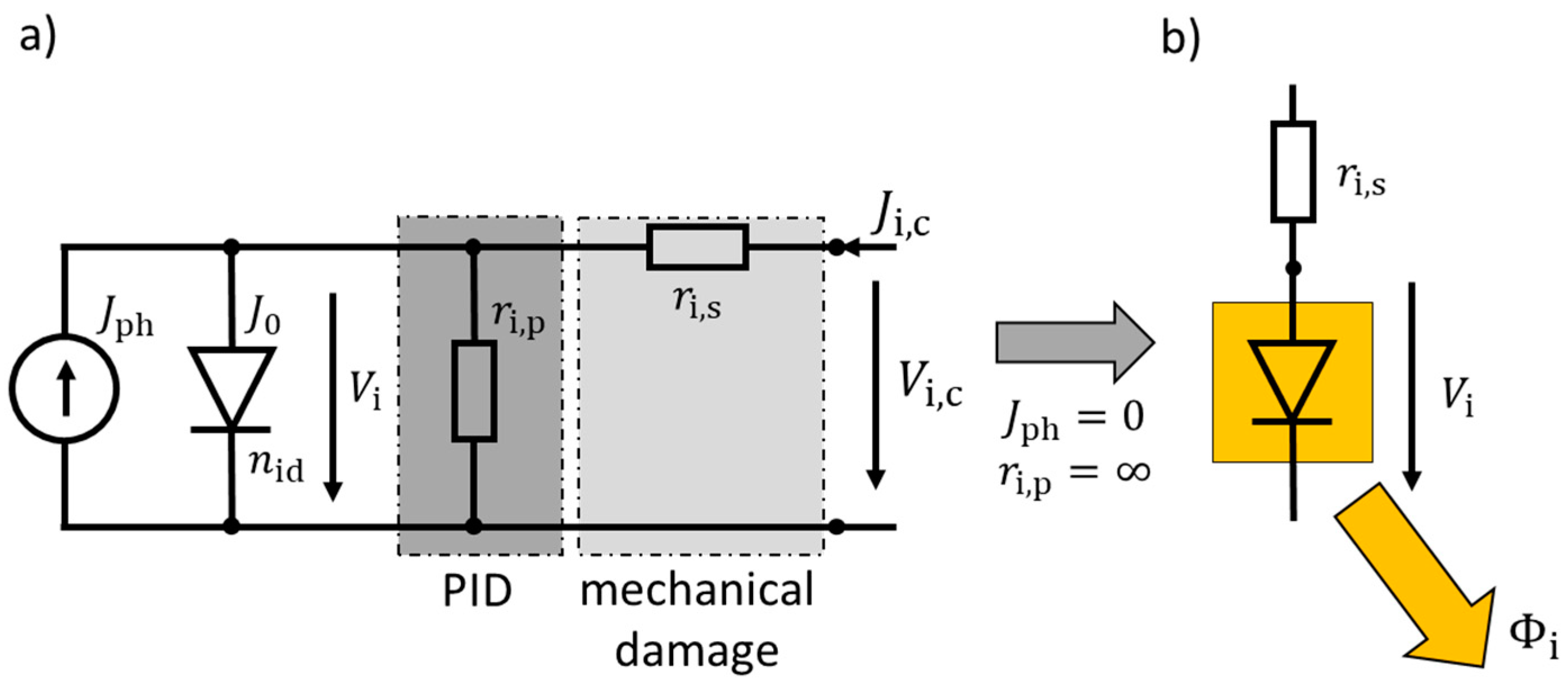
Figure 1a shows the equivalent circuit of the one-diode model, with the photo current source providing the photo generated current density
, series resistance
, the diode parameters with the ideality factor
and saturation current density
as well as the parallel resistance
, which reproduces the current(
I)/voltage(
V) curve of each solar cell with cell index i in a module with a total number
N of solar cells. Further simplified for a module in the dark (
0),
Figure 1b shows the simplified equivalent circuit in the case of an idealized parallel resistance
. The junction voltage
generates the luminescence intensity
Specific defects such as mechanically damaged and cracked solar cells only change the local series resistance , i.e., the equivalent connecting resistance of partially separated segments. The diode parameters ( and ) are assumed to be unchanged and still the same as for the originally defect free solar cells. In contrast, defects like PID, in the simplest approximation, only change the parallel resistance of a cell.
These assumptions allow us to calculate the change in series resistance
or parallel resistance
directly from EL images, which essentially map the local junction voltages
. Each luminescence intensity captured in each pixel of an EL image or even larger segments of approximately the same intensity are described with equivalent circuits, as shown in
Figure 1a,b.
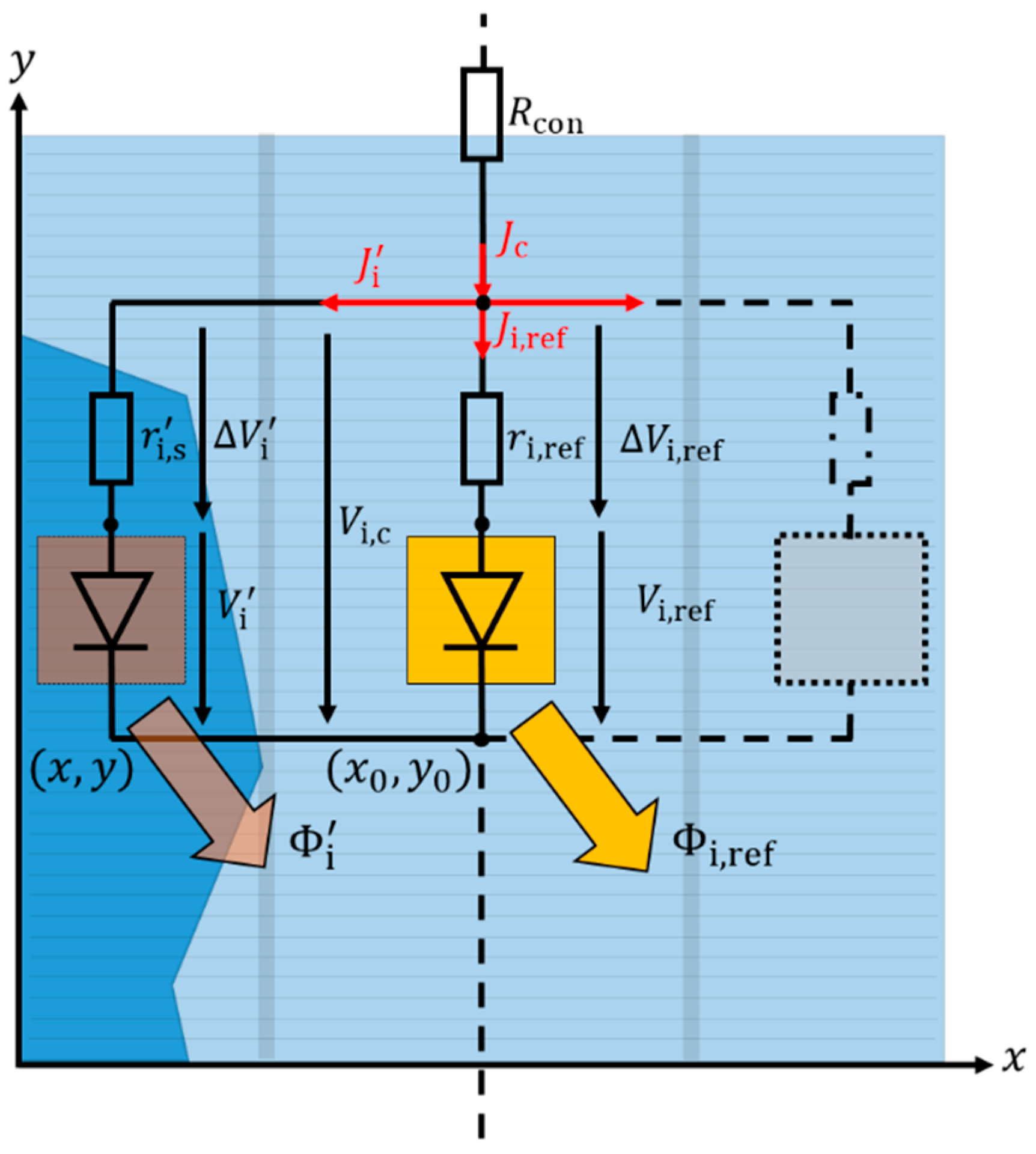
Figure 2 shows the parallel connected spatial distribution of equivalent circuits for evaluating the local luminescence intensities
inside a solar cell i with cell voltage
. The cell current density
is identical for all series connected cells inside the module.
Since the local luminescence intensities,
captured in an EL image depend exponentially on the local junction voltage
of cell i, an increase in local series resistance
decreases the local junction voltage
and therefore also decreases the local luminescence intensity
.
The index i represents the cell number inside the module up to the total number N of cells. Each locally assigned value is indicated by an upper quote throughout this paper. Depending on the spatial resolution of one cell in the EL image, each local value is also mapped by x and y inside each cell i.
Potthoff et al. proposed that in each cell, even with cracks and inactive areas, there is always one spot
with good connection to the bus bars [
3]. As a consequence, the series resistance
at this location is the lowest series resistance. Therefore, this part of the cell shows the highest luminescence intensity
in the EL image. If this EL image is generated with low current density
(approximately
of short circuit density
[
3]), the voltage drops are negligible across the local reference series resistance
as well as connecting resistances
between the cells.
Based on this simplification, Potthoff et al. calculated from the low current EL image the contribution of each cell to the overall module voltage
used for generating the EL signal. Their evaluation of the low current EL image quantitatively connected the local luminescence
(
), measured in arbitrary units, to the local junction voltages
of each cell i in the module with the calibration factor:
calculated with the reference luminescence intensity
(
) of each cell i up to the total number
N of cells, the module voltage
for generating the EL signal and the thermal voltage
[
3].
At this point, we extend Potthoff et al.’s approach. For EL images from higher current injections (30% ), the local series resistance, even at the brightest spot, is no longer negligible. Though, if the series resistance at the brightest spot is well known, all other series resistances can be calculated in relation to the reference series resistance at the brightest spot. Here, we assume that this reference resistance remains unchanged by the structural defect and is therefore directly proportional to the mean series resistance of the cell in the originally produced defect free module (data sheet module).
Our approach calculates the mean series resistance of undamaged and all identical cells from the data sheet of the undamaged PV module. The mean series resistance is derived from a lumped one-diode model with the total module resistance , the cell area and the number of cells N that represents the data sheet information of the module.
The reference series resistance at the brightest spot always represents the minimal series resistance of the cell. This minimal resistance , is calculated taking the statistical deviation from of the mean resistance of the defect free cell into account. For the similar spatial fluctuation of the series resistance of defect free cells, the statistical deviation is assumed to be constant and identical for all cells.
Based on the equivalent circuit of
Figure 2, we evaluate the local luminescence intensities
(
) in each cell i. The influence of parallel resistance is neglected. Therefore, the total local current density
(
) is equal to the total current through the local diode and thereby proportional to the local luminescence
(
).
Using the exponential dependence between the local current density
(
) and the local voltage
(
), the local luminescence intensities
(
) as well as the reference luminescence
(
) are proportional to their local current densities,
at each local region (
) of a cell i and the reference region (
) of the same cell. Therefore, the voltage difference,
is defined with respect to the local luminescence intensities
(
). Combining Equations (3) and (4) results in:
for each region of interest (
) with the local series resistance
(
) in relation to the reference region (
) with the local series resistance
(
). As a result, the local series resistance,
for each individual cell i is calculated combining Equations (3) and (5). The thermal voltage
, the ideality factor
, as well as the saturation current density
are assumed to be identical and constant for all cells and unrelated to the structural defect. Thereby, all local luminescence intensities
(
) from the high current EL image (compare
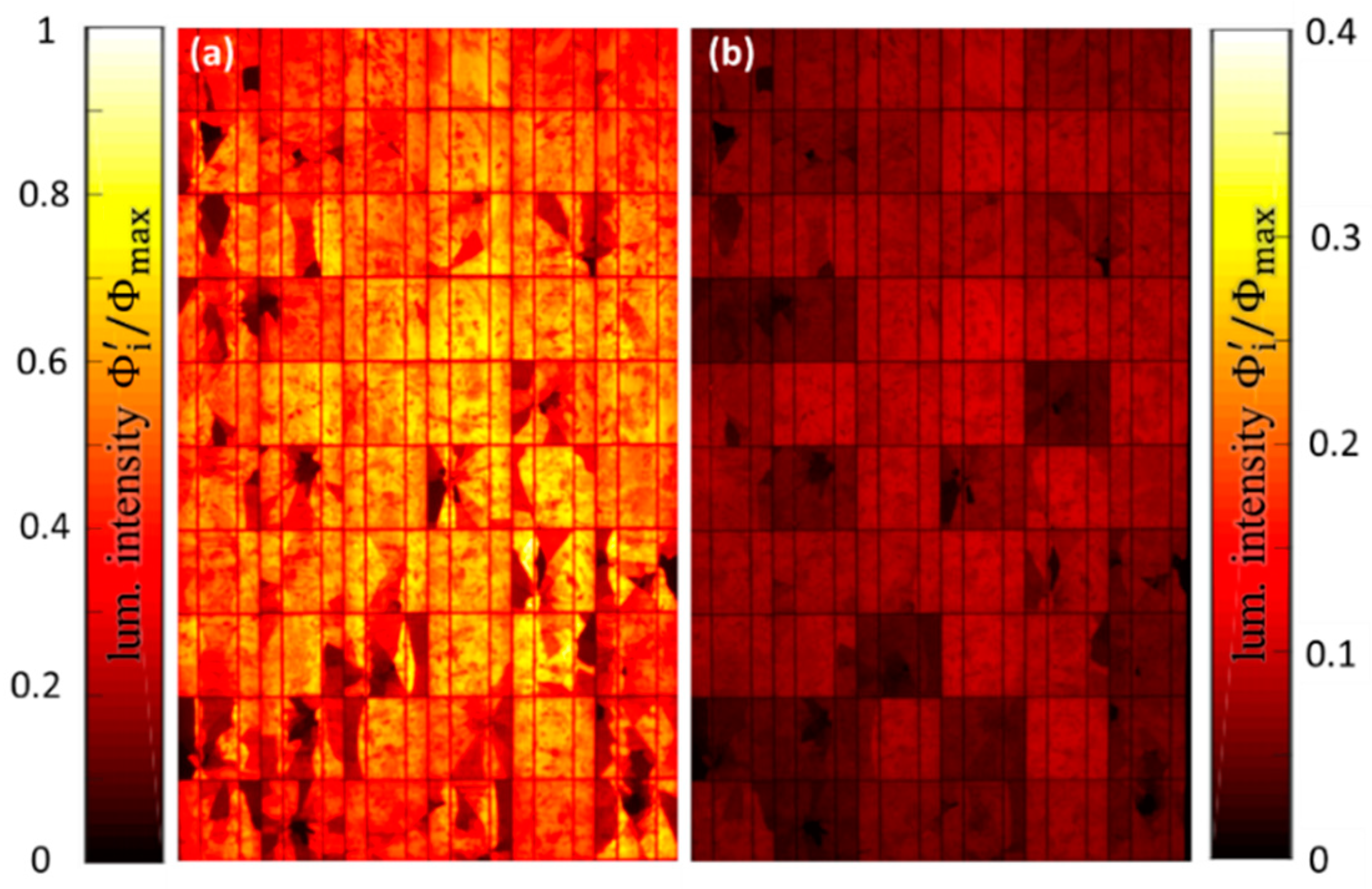
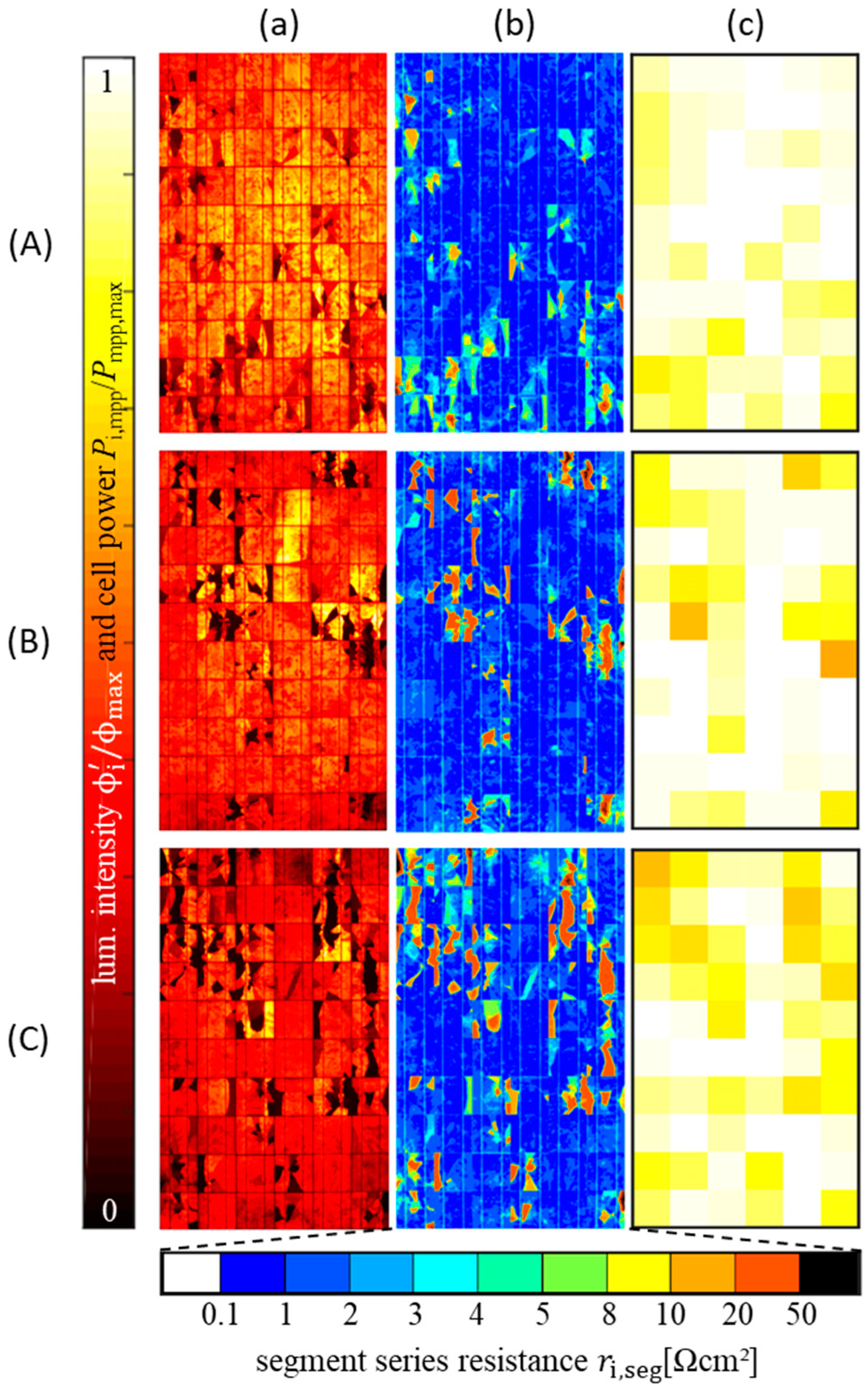
Figure 1a) are transposed into the series resistance mapping
(
) further discussed in
Section 2.3.
Since the statistical deviation of series resistances is at first unknown and itself depends on the calculated series resistance map , we use the bisection method to calculate the factor from Equation (6) iteratively.
We start from a guessed initial statistical deviation
and calculate the module series resistance map
from the high current EL image. Then, we derive the mean series resistance
of one defect free cell
from the sum of all local series resistances
divided by the number of pixels per cell. Using the bisection method, we adjust the statistical deviation
iteratively until the mean series resistance
derived from series resistance map
equals the series resistance
of one defect-free cell derived from the data sheet. This calibration of the series map with respect to the data sheet allows for the transposition of the EL image into a series resistance input for the simulation model, shown in
Section 2.3.
However, the resistance map as well as the mean series resistance derived from the data sheet, depend on the assumed ideality factor . Therefore, all further simulated results need to be evaluated in relation to an ideality factor expectation interval. As a further approximation, the ideality factors of all cells are assumed to be identical. Nevertheless, these approximations already lead to excellent results when comparing simulated and measured I/V curves.
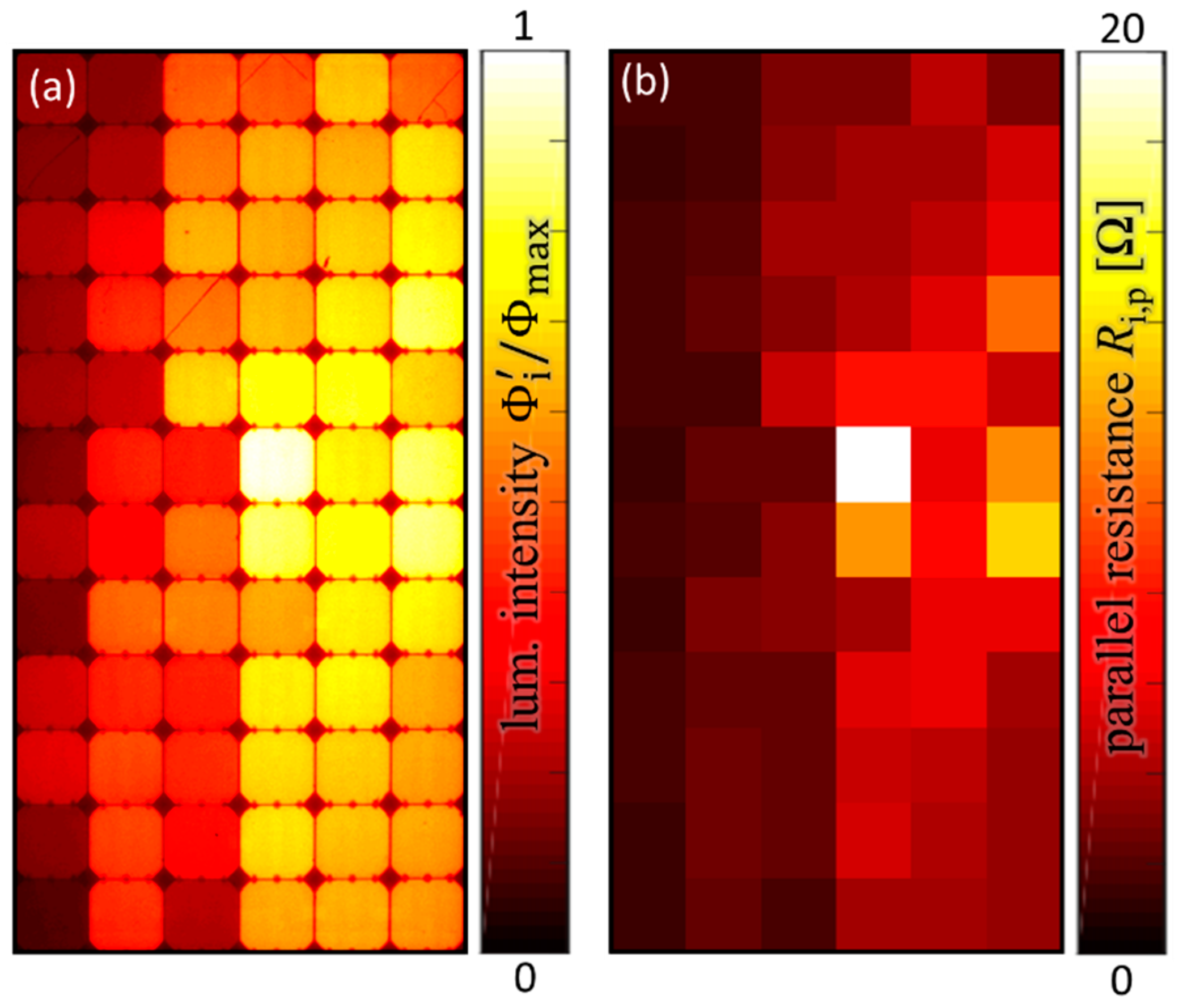
2.2.2. Parallel Resistance Mapping from EL Images
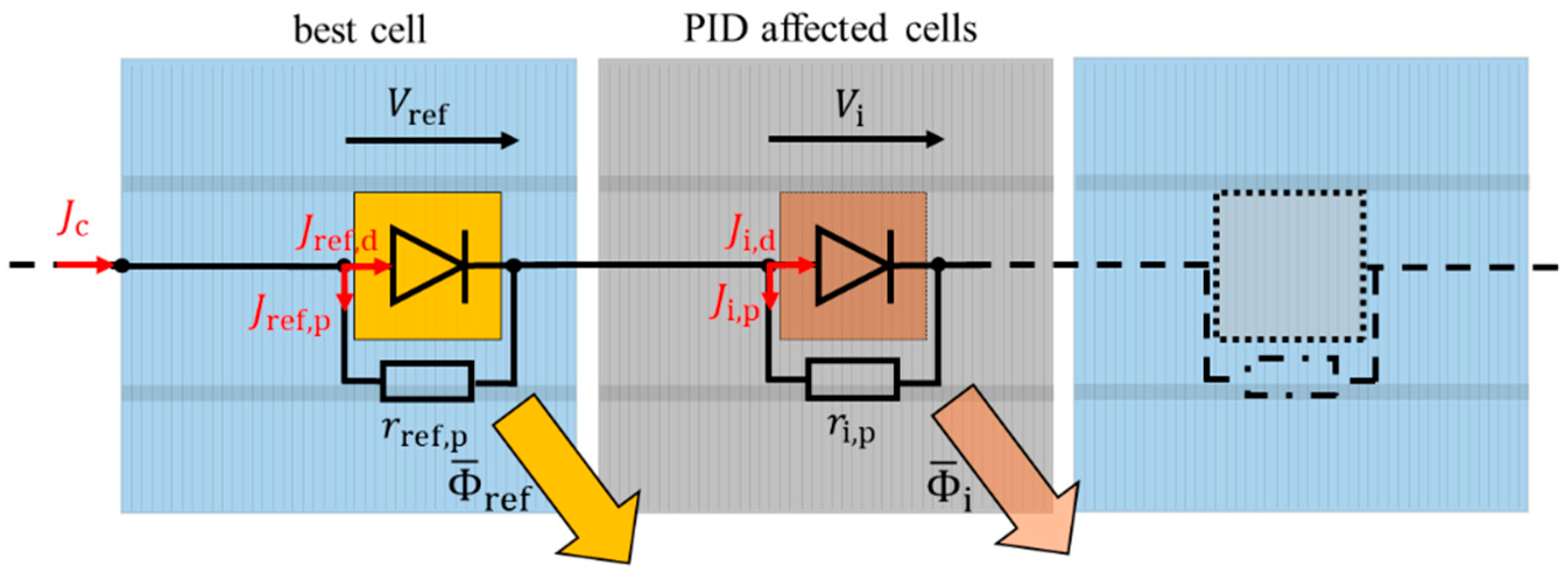
Figure 3 shows the equivalent circuit for evaluating the mean luminescence
of each cell i in relation to the maximal mean luminescence
of all cells. Here, the same principle approach as shown in
Section 2.2.1 evaluates the total parallel resistance
of each cell i. However, this parallel resistance approximation (PRA) only holds true if the evaluated defect type is limited to change in parallel resistance and is not additionally influencing the local series resistance of the cell.
The connecting resistance
between the cells and the local series resistance
is neglected for the cell current density
, used for generating the low current EL image. The cell current
being the same for every in series connected cell, is divided into parallel resistance current density
and local diode current density
. The diode current density
of a cell i is proportional to mean luminescence
, defined analogously by Equation (3). Solving for the parallel resistance current density,
at the reference cell with the maximal mean luminescence
and using Equations (1) and (3) results in the relation,
In this case, taking into account the reference parallel resistance
, the calibration factor,
is calculated by solving Equation (8) with the main branch
of the Lambert-W function. Using Equation (8) analogously for the mean luminescence
of all other cells instead of the reference cell, the parallel resistance,
is calculated for each cell i. The cell current
is well-known, since it needs to be adjusted and measured to generate the low current EL image. The recombination current density
is calculated from the data sheet information of the PV module and only the ideality
remains a scalable parameter. Again, all further simulated results will be evaluated in relation to an ideality factor expectation interval.