The Maximum-Allowable Well Depth While Drilling of Extended-Reach Wells Targeting to Offshore Depleted Reservoirs

Abstract

In depleted offshore reservoirs, pore pressure declines and consequently horizontal in-situ stresses decrease as well. This causes a very limited well depth for extended-reach drilling targeting to offshore depleted reservoirs. In this paper, based on analyzing the safe mud weight window of the depleted offshore reservoirs, a model of predicting the Maximum Allowable Measured Depth (MAMD) for extended-reach drilling targeting to offshore depleted reservoirs is developed. Meanwhile, the numerical method of the model is proposed, and the key affecting factors of the MAMD are also investigated. The results show the pore pressure depletion has obvious effects on the MAMD. With the depletion of pore pressure, the safe mud weight window appears narrower and even disappears, consequently the predicted MAMD becomes shorter. For a normal regime depositional environment in the depleted reservoirs, it may be impossible to drill with conventional drilling method in the nearby directions of the maximum horizontal in-situ stress, while it may be much safer and attain a long MAMD when drilling in the directions near the minimum horizontal in-situ stress. Moreover, the MAMD will decrease with the increase of Poisson’s ratio and Biot’s parameter, and its response to Poisson’s ratio is more obvious. For a specific target depleted reservoir, the extended-reach drilling with a high borehole inclination may have a longer MAMD than that with a low borehole inclination. This paper presents a method for promoting the design of extended-reach drilling targeting to offshore depleted reservoirs.

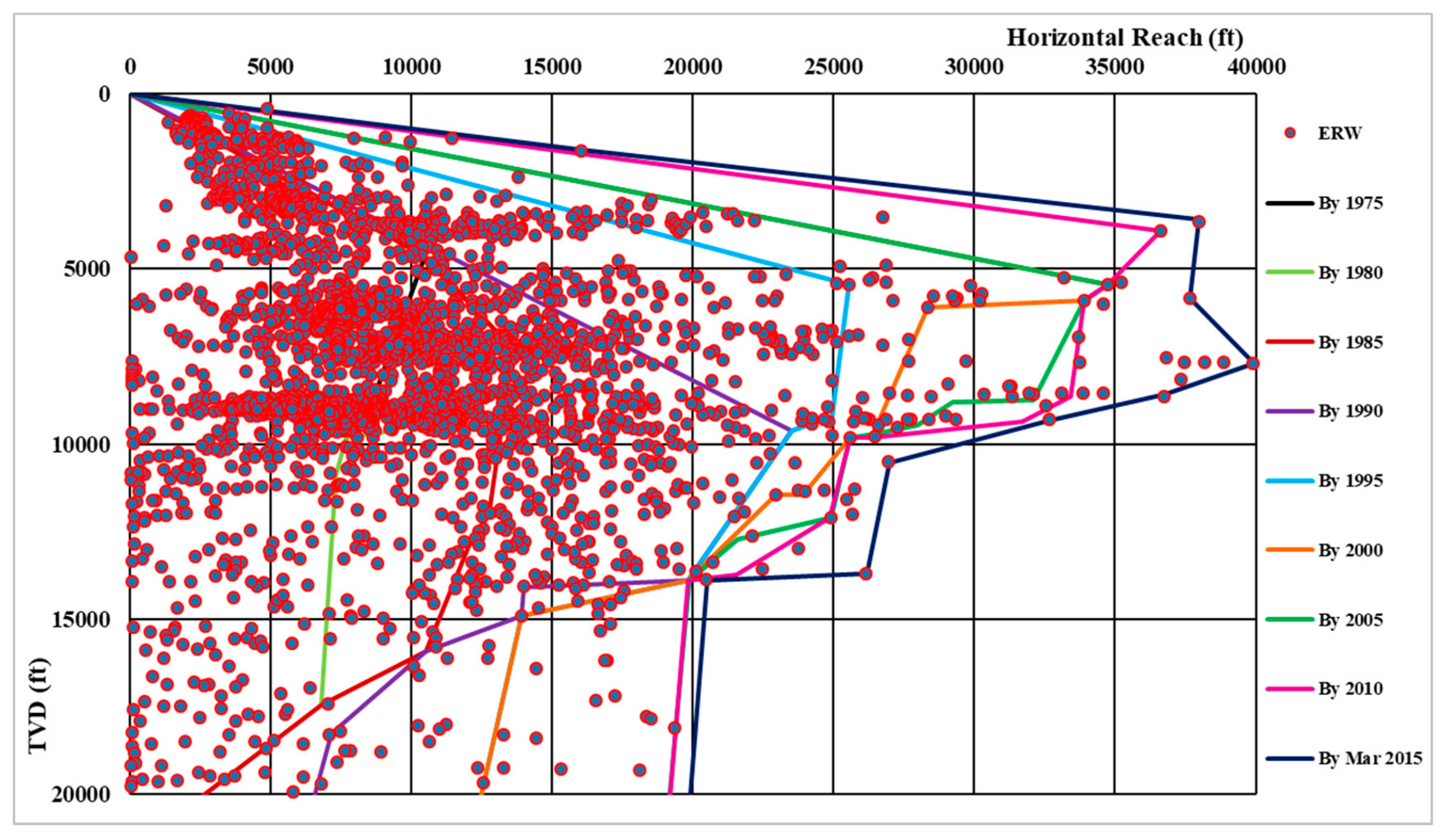
1. Introduction

Wells are considered as extended-reach wells (ERWs) when their horizontal displacement (HD) to true vertical depth (TVD) ratio are higher than 2.0 [1,2]. In recent years, the extended-reach wells envelope is continuously expanded (see Figure 1), and now it is not surprising to drill extended-reach wells with HD to TVD ratio greater than 6.0 or with HD longer than 30,000 ft [3,4,5,6,7]. Recently, the world’s longest well at the Sea of Okhotsk was successfully drilled. The measured depth of the well with horizontal completion is 49,212 ft. This is an ultra-extended-reach well with HD to TVD ratio of 8.0 and HD of 46,355 ft.

ERWs are commonly drilled in offshore projects where large oil and gas reservoirs areas are drained from one or more platforms. This can minimize environmental impacts and field-development costs by reducing drilling sites or offshore platforms [8,9,10]. ERWs can be drilled from one platform to reach reservoirs at a great distance. Although the platform is located in the newly developing reservoirs, some ERWs may target depleted reservoirs which are considered counterproductive with additional platforms. However, there is a Maximum Allowable Measured Depth (MAMD) to allow conventional drilling as the operating window should remain within the safe mud weight window between fracture pressure gradient and pore pressure gradient or collapse pressure gradient [2,11,12]. In extended-reach drilling targeting to depleted reservoirs, the fracture pressure gradient may be significantly reduced and collapse pressure gradient would be increased in some directions [13,14,15]. This may result in a narrow safe mud weight window of the depleted target and a limited measured depth of ERWs (see Figure 2).

In depleted reservoirs, the pore pressure declines. This results in a decrease of the horizontal in-situ stresses in the reservoirs while the overburden stress usually remains constant [16]. Compilation of pore pressure/stress data in depletion reservoirs reveals that the minimum horizontal in-situ stress decrease at 50–80% of the pore pressure depletion rate [17,18]. The obvious decrease of the minimum horizontal in-situ stress will cause a significant decrease of the fracture pressure gradient in some directions. Depletion also increases the stress anisotropy and leads to higher compressive stresses acting on the wellbore, which will result in wellbore breakouts. As reported by Aadnoy and Looyeh (2010) [19] and Addis (1997) [17], the collapse pressure gradient may increase with depletion in inclined or horizontal wellbore. Therefore, the safe-mud-weight window in the depleted target may become narrow, and even zero or negative in some directions, which results in a very limited MAMD of extended-reach drilling and difficulties to reach the target.

The initial concept and model for open hole extension limit of extended-reach drilling was proposed by Gao (2009) [20]. Due to the complexity of the drilled formations and borehole hydraulic conditions, then several models were updated. These models include those presented by Sun (2013) [21], Li (2016) [22] and Chen (2018) [2]. However, few of these models can be applied for predicting the MAMD of extended-reach drilling targeting offshore depleted reservoirs. In this paper, based on analyzing the safe mud weight window of the depleted offshore reservoirs, a model of predicting the Maximum Allowable Measured Depth (MAMD) for extended-reach drilling targeting to offshore depleted reservoirs is developed. Meanwhile the numerical method of the model is proposed, and the key affecting factors of the MAMD are also investigated.

2. Model and Methodology

2.1. Effect of Depletion on In Situ Stresses

Aadnoy and Looyeh (2010) reported that the properties of orthotropic rocks measured from different directions are different, and defined the constitutive relation of orthotropic materials as [19]

$$\left[\epsilon \right]=\frac{1}{E}\left[K\right]\left[\sigma -{\alpha }_p{p}_p\right]$$

(1)

or,

$$\left[\begin{array}{l}{\epsilon }_x\\ {\epsilon }_y\\ {\epsilon }_z\\ {\gamma }_{yz}\\ {\gamma }_{xz}\\ {\gamma }_{xy}\end{array}\right]=\left[\begin{array}{cccccc}\frac{1}{E_x}& -\frac{{\nu }_{yx}}{E_y}& -\frac{{\nu }_{zx}}{E_z}& 0& 0& 0\\ -\frac{{\nu }_{xy}}{E_x}& \frac{1}{E_y}& -\frac{{\nu }_{zy}}{E_z}& 0& 0& 0\\ -\frac{{\nu }_{xz}}{E_x}& -\frac{{\nu }_{yz}}{E_y}& \frac{1}{E_z}& 0& 0& 0\\ 0& 0& 0& \frac{1}{G_{yz}}& 0& 0\\ 0& 0& 0& 0& \frac{1}{G_{xz}}& 0\\ 0& 0& 0& 0& 0& \frac{1}{G_{xy}}\end{array}\right]\left[\begin{array}{l}{\sigma }_x\\ {\sigma }_y\\ {\sigma }_z\\ {\tau }_{yz}\\ {\tau }_{xz}\\ {\tau }_{xy}\end{array}\right]$$

(2)

The properties of laminated rocks are always isotropic in one plane, say the x-y plane. Then, the properties are transversely isotropic and symmetric about z-axis. Then, the alterations of horizontal in-situ stresses due to pore pressure changes can be estimated by

$$\frac{\Delta {\sigma }_h}{\Delta p_p}={\alpha }_p\left(1-\frac{{\nu }_{V\min }+{\nu }_h{\nu }_{V\max }}{1-{\nu }_h^2}\right)$$

(3)

$$\frac{\Delta {\sigma }_H}{\Delta p_p}={\alpha }_p\left(1-\frac{{\nu }_{V\min }{\nu }_h+{\nu }_{V\max }}{1-{\nu }_h^2}\right)$$

(4)

The small difference between Poisson’s ratios in various directions can be neglected [23,24], then we can get the ratio of horizontal in-situ stresses change to pore pressure change

$$A=\frac{\Delta {\sigma }_H}{\Delta p_p}=\frac{\Delta {\sigma }_h}{\Delta p_p}={\alpha }_p\left(\frac{1-2\nu }{1-\nu }\right)$$

(5)

In the above equation, A is the stress path, and indicates the ratio of horizontal in-situ stresses reduction with pore pressure depletion. As reported by Segall and Fitzgerald (1998) [25], Equation (5) is applicable when the ratio of the reservoir lateral extent to its thickness is larger than 10:1.

2.2. Stresses Distribution around an Inclined Wellbore Considering Depletion and Seepage Effects

For a newly drilled borehole, the borehole wall is usually permeable due to the absence of mud cake. The drilling fluid, therefore, flows into the formation and changes the stresses around the wellbore. Therefore, the seepage is an important factor and needs to be considered. The stresses around the borehole under the effects of in-situ stresses and seepage have been reported in the literature (e.g., Chen et al. (2008) and Chen and Gao (2017)) [2,26]

$$\{\begin{array}{l}{\sigma }_r=\left(\frac{{\sigma }_{xx}+{\sigma }_{yy}}{2}\right)\left(1-\frac{r_w^2}{r^2}\right)+\left(\frac{{\sigma }_{xx}-{\sigma }_{yy}}{2}\right)\left(1+\frac{3r_w^4}{r^4}-\frac{4r_w^2}{r^2}\right)\cos 2\theta +{\sigma }_{xy}\left(1+\frac{3r_w^4}{r^4}-\frac{4r_w^2}{r^2}\right)\sin 2\theta \\ +\delta \left[\frac{{\alpha }_p\left(1-2\nu \right)}{2\left(1-\nu \right)}\left(1-\frac{r_w^2}{r}\right)-\varphi \right]\left(p_w-p_{fp}\right)+\frac{r_w^2}{r^2}{p}_w\\ {\sigma }_{\theta }=\left(\frac{{\sigma }_{xx}+{\sigma }_{yy}}{2}\right)\left(1+\frac{r_w^2}{r^2}\right)+\left(\frac{{\sigma }_{xx}-{\sigma }_{yy}}{2}\right)\left(1+\frac{3r_w^4}{r^4}\right)\cos 2\theta +{\sigma }_{xy}\left(1+\frac{3r_w^4}{r^4}\right)\sin 2\theta \\ +\delta \left[\frac{{\alpha }_p\left(1-2\nu \right)}{2\left(1-\nu \right)}\left(1+\frac{r_w^2}{r}\right)-\varphi \right]\left(p_w-p_{fp}\right)-\frac{r_w^2}{r^2}{p}_w\\ {\sigma }_z={\sigma }_{zz}-2\nu \left({\sigma }_{xx}-{\sigma }_{yy}\right)\frac{r_w^2}{r^2}\cos 2\theta -4\nu {\tau }_{xy}\frac{r_w^2}{r^2}\sin 2\theta +\delta \left[\frac{{\alpha }_p\left(1-2\nu \right)}{\left(1-\nu \right)}-\varphi \right]\left(p_w-p_{fp}\right)\\ {\tau }_{r\theta }=\left[\frac{\left({\sigma }_{xx}-{\sigma }_{yy}\right)}{2}\sin 2\theta +{\tau }_{xy}\cos 2\theta \right]\left(1+\frac{2r_w^2}{r^2}-\frac{3r_w^4}{r^4}\right)\\ {\tau }_{rz}=\left[{\tau }_{yz}\sin \theta +{\tau }_{xz}\cos \theta \right]\left(1-\frac{r_w^2}{r^2}\right){\tau }_{\theta z}=\left[-{\tau }_{xz}\sin \theta +{\tau }_{yz}\cos \theta \right]\left(1+\frac{r_w^2}{r^2}\right)\end{array}$$

(6)

The far field stress tensor after depletion is represented by

$$\left[\sigma \right]=\left[\begin{array}{ccc}{\sigma }_H-\Delta {\sigma }_H& 0& 0\\ 0& {\sigma }_h-\Delta {\sigma }_h& 0\\ 0& 0& {\sigma }_{\nu }\end{array}\right]$$

(7)

For an inclined wellbore with inclination α and azimuth β, the following equations can be applied to convert the stresses from the global coordinate (far-field stresses coordinate) to the local coordinate (wellbore coordinate)

$$\left[{\sigma }^{\prime }\right]=\left[\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{zz}\\ {\tau }_{xy}\\ {\tau }_{xz}\\ {\tau }_{yz}\end{array}\right]=\left[Q\right]\left[\begin{array}{ccc}{\sigma }_H-\Delta {\sigma }_H& 0& 0\\ 0& {\sigma }_h-\Delta {\sigma }_h& 0\\ 0& 0& {\sigma }_{\nu }\end{array}\right]\left[Q^T\right]$$

(8)

where

$$\left[Q\right]=\left[\begin{array}{ccc}\cos \alpha \cos \beta & \cos \alpha \sin \beta & \sin \alpha \\ \sin \beta & \cos \beta & 0\\ \sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha \end{array}\right]$$

(9)

2.3. The Model of MAMD While Drilling of ERWs Targeting to Depleted Reservoirs

The stresses on the wellbore wall are determined, then the collapse pressure and fracture pressure can be determined based on proper failure criteria. The shear failure of the wellbore wall is subjected to Mohr–Coulomb failure criterion. For isotropic formation, in terms of effective principal stresses, the criterion can be given in the following form [26]

$${\sigma }_1-{\alpha }_p\left(p_p-\Delta p_p\right)=\left[{\sigma }_3-{\alpha }_p\left(p_p-\Delta p_p\right)\right]\frac{1+\sin \phi }{1-\sin \phi }+2c\frac{\cos \phi }{1-\sin \phi }$$

(10)

However, there may exist a set of parallel planes of weakness in sedimentary rocks [27,28,29,30], commonly referred as bedding planes, which are more susceptible to sliding compared to the intrinsic rock. Jaeger et al. (2009) proposed a slippage criterion for weakness planes [29]. In terms of effective principal stresses, it can be given in analogy to the Mohr–Coulomb criterion as

$$\begin{array}{l}{\sigma }_1-{\alpha }_p\left(p_p-\Delta p_p\right)=\left[{\sigma }_3-{\alpha }_p\left(p_p-\Delta p_p\right)\right]\frac{\sin 2\lambda \cos {\phi }_w-\left(\cos 2\lambda +1\right)\sin {\phi }_w+2\sin {\phi }_w}{\sin 2\lambda \cos {\phi }_w-\left(\cos 2\lambda +1\right)\sin {\phi }_w}\\ +2c_w\frac{\cos {\phi }_w}{\sin 2\lambda \cos {\phi }_w-\left(\cos 2\lambda +1\right)\sin {\phi }_w}\end{array}$$

(11)

where λ is the angle between the normal to the weakness plane and σ₁. The above failure criterion has two asymptotes that occur as $\lambda \to \pi /2$ or as $\lambda \to {\phi }_w={\tan }^{-1}{c}_w$. Therefore, as long as $\lambda <{\phi }_w$, the failure along the plane of weakness is not possible and then the Mohr–Coulomb failure criterion (Equation (10)) can be used for checking shear failure [30].

Wellbore collapse is a phenomenon associated with low wellbore pressures when the radial stress is usually the minimum principal stress. For isotropic formation, the critical borehole pressure causing collapse at a given point, defined by the circumferential angle θ, which ranges from 0° to 360°. can be determined by the following function

$$f_{M-C}(p_{c\theta })=\left({\sigma }_1-{\sigma }_3\right)-\sin \phi \left[{\sigma }_1+{\sigma }_3-2{\alpha }_p\left(p_p-\Delta p_p\right)\right]-2c\cos \phi =0$$

(12)

For a formation with weak plane, the critical borehole pressure causing collapse at a given point can be determined by the following function

$$f_{W-P}(p_{c\theta })=\left({\sigma }_1-{\sigma }_3\right)\left[\sin 2\lambda \cos {\phi }_w-\left(\cos 2\lambda +1\right)\sin {\phi }_w\right]+2\sin {\phi }_w\left[{\alpha }_p\left(p_p-\Delta p_p\right)-{\sigma }_3\right]-2c_w\cos {\phi }_w=0$$

(13)

As stated early, as long as $\lambda <{\phi }_w$, the failure along the plane of weakness is not possible and Equation (12) can be used for determining the critical borehole pressure causing collapse at a given point.

For any given wellbore azimuth and inclination, there is a maximum borehole pressure, named wellbore collapse pressure, to ensure the wellbore stability. It can be estimated as

$$p_c=\max \left\{p_{c\theta }\left(\theta \in \left[0^{\circ },{360}^{\circ }\right]\right)\right\}$$

(14)

The formation will fracture when the minimum effective principal stress reaches the tensile strength of rock

$${\sigma }_3-{\alpha }_p\left(p_p-\Delta p_p\right)=-\left|S_t\right|$$

(15)

Fracturing occurs at high wellbore pressure when the radial stress is usually the maximum principal stress. The critical borehole pressure causing fracture at a given point around the wellbore can be estimated by the following function

$$f_T\left(p_{f\theta }\right)={\sigma }_3-{\alpha }_p\left(p_p-\Delta p_p\right)+\left|S_t\right|$$

(16)

For any given wellbore azimuths and inclination, there is a minimum borehole pressure to avoid wellbore fracture, which is defined as wellbore fracture pressure. It can be estimated as

$$p_f=\min \left\{p_{f\theta }\left(\theta \in \left[0^{\circ },{360}^{\circ }\right]\right)\right\}$$

(17)

Then, the collapse pressure gradient and fracture pressure gradient can be estimated, respectively, by

$${\rho }_c=\frac{p_c}{g\times TV{D}_f}; {\rho }_f=\frac{p_f}{g\times TV{D}_f}$$

(18)

For drilling operation in depleted reservoirs, there is an altered safe mud weight window. Its lower bound is the larger value of the depleted pore pressure gradient and the collapse pressure gradient. Its upper bound is the lowered fracture pressure gradient due to depletion, which is the maximum value of mud weight that will not induce any fracture opening for the wellbore in the depleted reservoirs. Safe mud weight window for drilling in depleted reservoirs is defined as

$$\max \left\{{\rho }_c,{\rho }_p-\Delta {\rho }_p\right\}<{\rho }_s<{\rho }_f$$

(19)

If the value of equivalent circulating density (ECD) of drilling fluid is controlled within the depleted safe mud weight window, no overflow or mud loss will occur, and the wellbore is in a stable condition. When drilling forward, the drill pipe moves slowly, the acceleration pressure drop can be ignored. Then, ECD in the borehole is defined as the sum of the equivalent static density (ESD) of drilling fluid and the equivalent density of friction pressure loss in annulus [31]. It is expressed as

$${\rho }_{\mathrm{ecd}}={\rho }_{esd}+{\rho }_{dp}$$

(20)

In extended reach drilling targeting to offshore depleted reservoirs, the safe mud weight window is narrow, whereas ECD and annulus friction pressure loss are high due to the long measured depth. In the long horizontal section of extended-reach drilling, the equivalent density of drilling fluid friction pressure loss in annulus increases as the length of the horizontal section increases. However, in contrast to drilling vertical wells, the safe mud weight window may be narrow in the target zones of extended-reach drilling because TVD remains almost the same while the pore pressure is reduced greatly in the target zones (see Figure 2). This means the bottom hole is relatively weak while its ECD and annulus friction pressure loss are high over the long horizontal section. This may cause wellbore fracturing as the wellbore extends and ECD increases. When the equivalent density of drilling fluid friction pressure loss in annulus is greater than or equal to the width of safe mud weight window of the formation, it will give great challenges to the options of drilling fluid density and drilling security. Therefore, for a given depleted target zone, when the equivalent density of drilling fluid friction pressure loss in annulus is equal to the width of safe mud weight window, the well is considered to reach its maximum allowable measured depth (MAMD). Therefore, for a specific depleted target zone, the MAMD can be estimated by

$$MAMD=\frac{\left({\rho }_f-\max \left\{{\rho }_c,{\rho }_p-\Delta {\rho }_p\right\}\right)}{{\rho }_{dp}}\times TV{D}_f$$

(21)

The numerical method and flowchart for predicting the MAMD of extended-reach drilling targeting to offshore depleted reservoirs is shown in Figure 3. It first imports data of the designed ERW and the depleted target zone, such as well configuration, rock mechanical properties, the magnitude of pore pressure depletion, porosity properties, strength parameters of weak plane, strength parameters of intact rock matrix, and drilling fluid properties. Then, the critical borehole pressures causing wellbore collapse and fracture can be predicted. For predicting critical borehole pressures causing collapse around the wellbore, isotropic failure criterion is used. For formations with some sets of oriented weakness planes, anisotropic failure criteria should also be investigated. Once the critical borehole pressures causing collapse around the wellbore are determined, the maximum value is selected as the wellbore collapse pressure (see Equation (14)). The same procedure is used to determine the wellbore fracture pressure (see Equation (17)). Then, the wellbore collapse pressure is compared to the depleted pore pressure, and the safe mud weight window of the depleted target zones is determined using Equation (19). Substituting the safe mud weight window of the depleted target and the predicted equivalent density of drilling fluid friction pressure loss in annulus into Equation (21), the MAMD for extended-reach drilling targeting to offshore depleted reservoirs can be obtained.

3. Results and Discussions

For a particular offshore depleted target zone, TVD, pore pressure, and the formation in-situ stresses, porosity and thermal properties have their specific values.

Table 1. Input data for modeling.

Variables	Value
TVD of the target (m)	2500
Overburden pressure (MPa)	52.616
Maximum horizontal in-situ stress (MPa)	46.828
Minimum horizontal in-situ stress (MPa)	37.463
Initial pore pressure (MPa)	25.235
Depleted pore pressure (MPa)	15.141
Angle between the azimuth of borehole and the azimuth of maximum horizontal in-situ stress (°)	70
Well inclination (°)	86
Wellbore radius (m)	0.216
Poisson’s ratio (dimensionless)	0.25
Biot’s parameter (dimensionless)	0.8
Tensile strength (MPa)	2
Cohesion strength (MPa)	7
Young’s modulus (MPa)	6700
Friction angle (°)	25
Coefficient of seepage effect (dimensionless)	1
Porosity (dimensionless)	0.25

defines the properties of the depleted target zone. The stresses around the borehole considering depletion and seepage effects can be predicted, and the collapse pressure gradient and fracture pressure gradient of the depleted target zone can be predicted using Equation (18). The safe mud weight window of the target formation can be determined using Equation (19).

In this case, the initial pore pressure of the formation is normal pressure; after depletion the pore pressure is reduced by 40%. There is no weak plane in the depleted target zone. The TVD of the target is 2500 m. For specific drilling fluid and annular space, the equivalent density of drilling fluid friction pressure loss in annulus (ρ_dp) can be predetermined. Assuming the bottom hole of the designed extended-reach well (ERW) is fractured, the MAMD while drilling can be predicted using Equation (21). Note that the equivalent density of drilling fluid friction pressure loss in annulus is usually considered to be independent of pressure except in high pressure wells [32,33]. TVD of the target zone is not very large, thus the zone has a relative low pressure. Therefore, the effects of pressure on the equivalent density of drilling fluid friction pressure loss which has a direct effect on the MAMD are not further discussed here.

Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show the safe mud weight window of the target zone and the predicted MAMD with different pore pressure depletion. As shown in Figure 4 and Figure 5, without depletion, i.e., pore pressure depletion ratio $\Delta p_p/p_p=0$, safe mud weight window of the target zone is relatively wide and the predicted MAMD is long. In this case with a normal depositional environment, there is an obvious anisotropy for safe mud weight window and the predicted MAMD. In the direction of the maximum horizontal in-situ stress, safe mud weight window is the narrowest, and the predicted MAMD is the shortest. In Figure 6 and Figure 7, with pore pressure depletion $\Delta p_p/p_p=0.2$, the predicted safe mud weight window of the target zone becomes narrower and the predicted MAMD decreases. In Figure 8 and Figure 9, the pore pressure is further depleted with $\Delta p_p/p_p=0.4$, the predicted safe mud weight window of the target zone is even narrower and the predicted MAMD further decreases. In the directions near the maximum horizontal in-situ stress, safe mud weight window even becomes negative, and the predicted MAMD is zero. In Figure 10 and Figure 11, with pore pressure depletion $\Delta p_p/p_p=0.6$, in most directions near the maximum horizontal in-situ stress, the safe mud weight window is very narrow and even negative, and the predicted MAMD is very limited or disappears. It is impossible to drill in these directions with conventional drilling method. However, drilling in the direction of the minimum horizontal in-situ stress is prone to attain a wider safe mud weight window and a longer MAMD than the other directions. Therefore, for extended reach drilling targeting to offshore depleted reservoirs, it may be impossible to drill with conventional drilling method in the nearby directions of the maximum horizontal in-situ stress, while it may be much safer and attain a much longer MAMD in the nearby directions of the minimum horizontal in-situ stress.

As mentioned previously, pore pressure depletion affects the horizontal in-situ stresses, and consequently the safe mud weight window and the MAMD. The stress path is defined as the horizontal in-situ stresses change with pore pressure decline to express the stress-depletion response of the depleted reservoirs. The stress path depends upon Poisson’s ratio and Biot’s parameter, whose effects on the MAMD while performing extended-reach drilling targeting the offshore depleted reservoirs are investigated. As shown in Figure 12, for a given Biot’s coefficient, with the increase of Poisson’s ratio, both stress path and MAMD decrease significantly. As indicated in Figure 13, for a given Poisson’s ratio, the stress path increases linearly with the increase of Biot’s parameter, and the MAMD decreases slowly and linearly with the increase of Biot’s parameter.

With all other parameters kept constant, the effects of horizontal in-situ stresses ratio ${\sigma }_H/{\sigma }_h$ and borehole inclination on the MAMD are also investigated. The results are, respectively, plotted in Figure 14 and Figure 15. Figure 14 reveals that the MAMD decreases with the increase of horizontal in-situ stresses ratio, and the decrease rate increases when ${\sigma }_H/{\sigma }_h\ge 1.5$. As shown in Figure 15, for the investigated case, the effect of bottom hole inclination on the MAMD is not obvious from 0° to 15°, and the MAMD increases slowly. After that, the MAMD increases relatively quickly with the increase of inclination from 15° to 55°. At the inclination near 55°, the predicted MAMD reaches the maximum value. Then, the MAMD decreases with the increase of inclination from 55° to 90°, but the MAMD is still higher than that of extended-reach drilling with a low borehole inclination. This reveals that, for a specific target depleted reservoir, the extended-reach drilling with a high borehole inclination may have a longer MAMD than that with a low borehole inclination.

4. Conclusions

Based on analyzing the safe mud weight window of the depleted offshore reservoirs, a model of predicting the Maximum Allowable Measured Depth (MAMD) for extended-reach drilling targeting to offshore depleted reservoirs is developed. Meanwhile, the numerical method of the model is proposed, and the key affecting factors of the MAMD are also investigated. The results show pore pressure depletion has obvious effects on the MAMD. With the depletion of pore pressure, the safe mud weight window appears narrower and even disappears. As a result, the predicted MAMD becomes shorter and the borehole even becomes impossible to drill with conventional drilling method. For a normal regime depositional environment in the depleted reservoirs, it may be impossible to drill with conventional drilling method in the nearby directions of the maximum horizontal in-situ stress, while it may be much safer to drill in the directions near the minimum horizontal in-situ stress. Moreover, the MAMD will decrease with the increase of Poisson’s ratio and Biot’s parameter, and its response to Poisson’s ratio is more obvious. For a specific target depleted reservoir, the extended-reach drilling with a high borehole inclination may have a longer MAMD than that with a low borehole inclination.