A Bayesian Dynamic Method to Estimate the Thermophysical Properties of Building Elements in All Seasons, Orientations and with Reduced Error
Abstract
1. Introduction
2. Methodology
2.1. Static Model of Heat Transfer: The Average Method
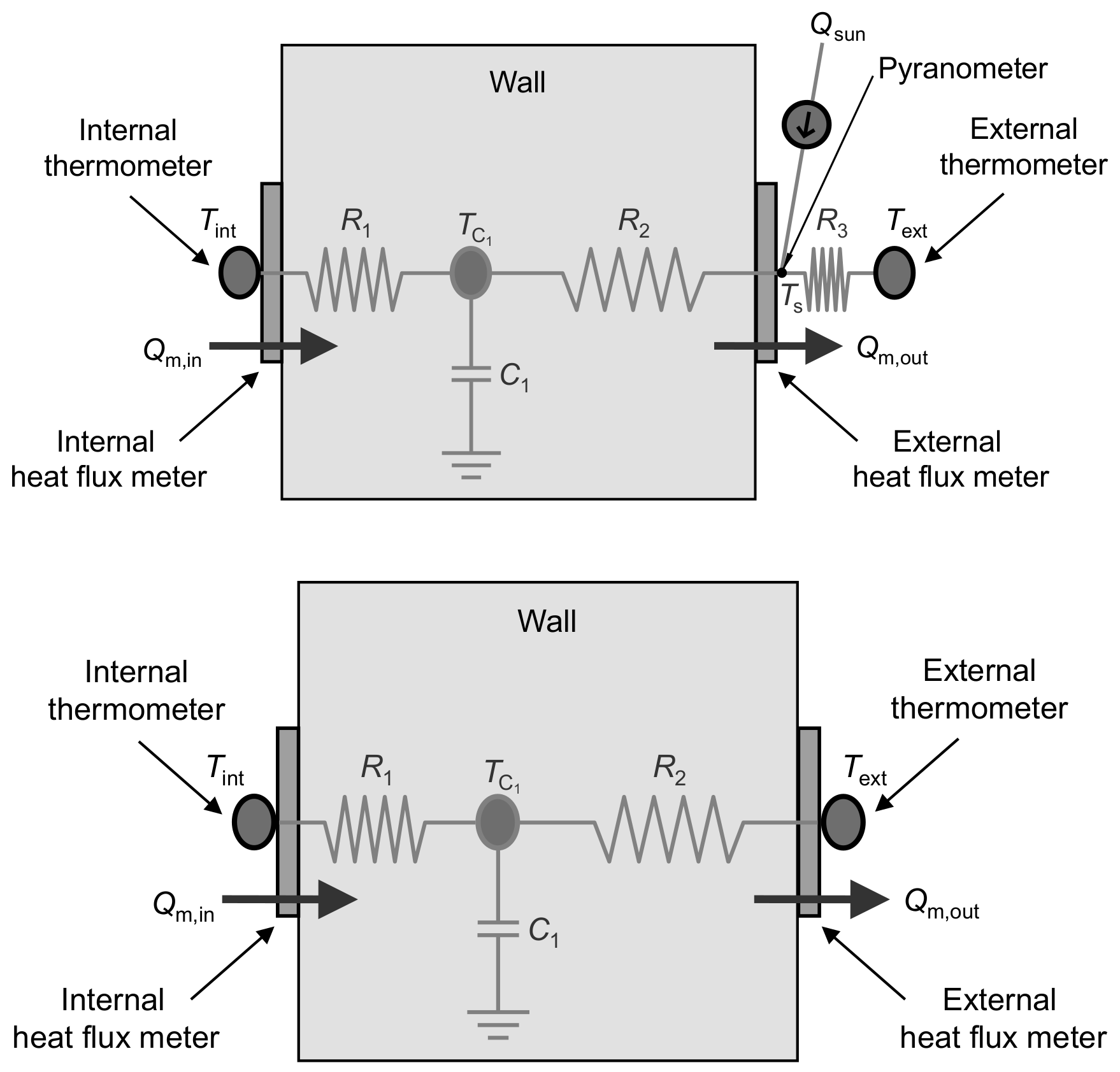
2.2. Dynamic Model: Lumped-Thermal-Mass Models
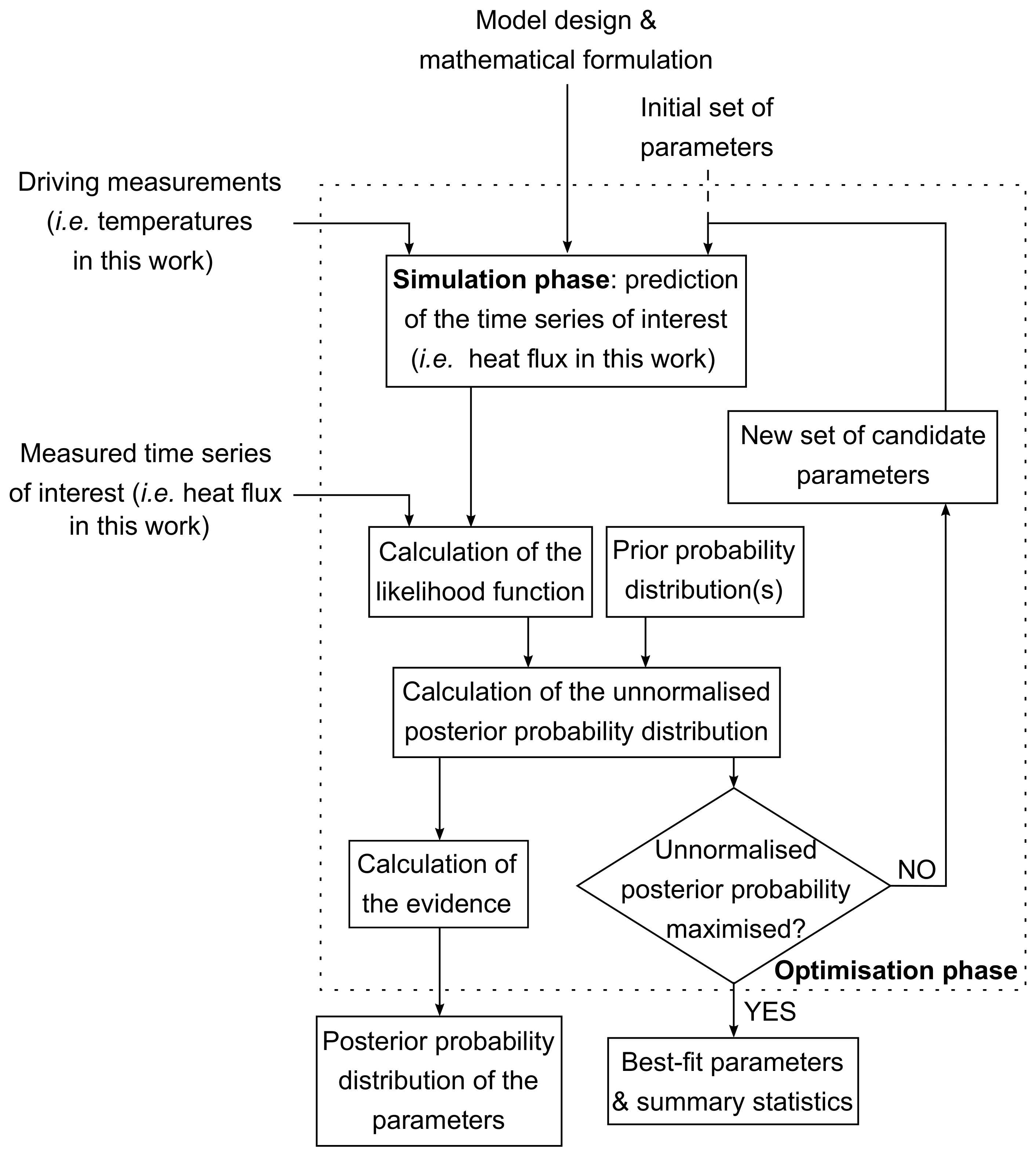
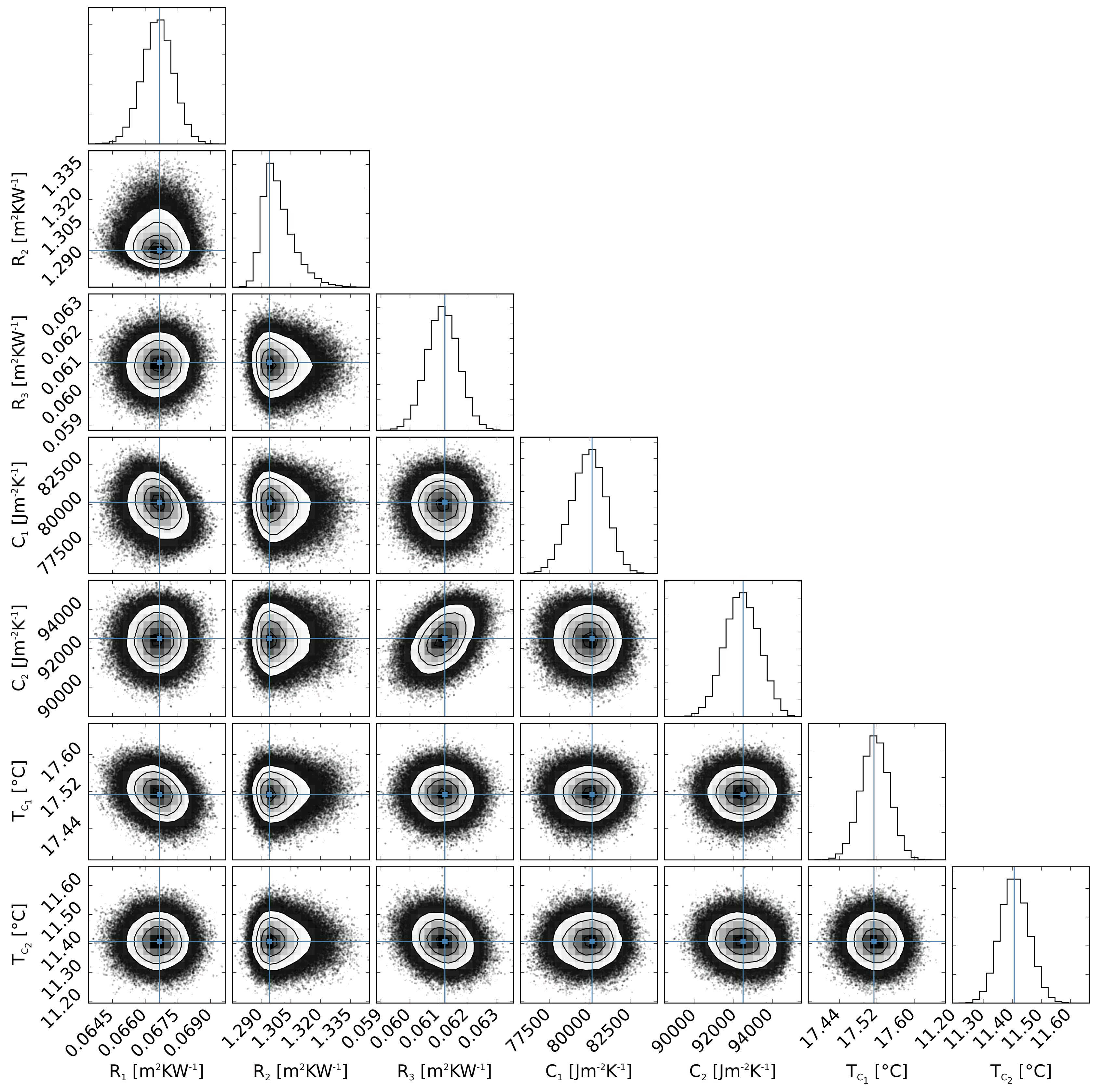
2.3. Bayesian Inference: Optimisation Phase for Thermophysical Parameter Estimation
2.3.1. Likelihood Function
Independent and Identically Distributed Residuals
Discrete Cosine Transform
2.3.2. Prior Probability Distributions on the Parameters of the Model
Uniform Priors
Log-Normal Priors
2.4. Model Selection and Validation
2.4.1. Model Comparison
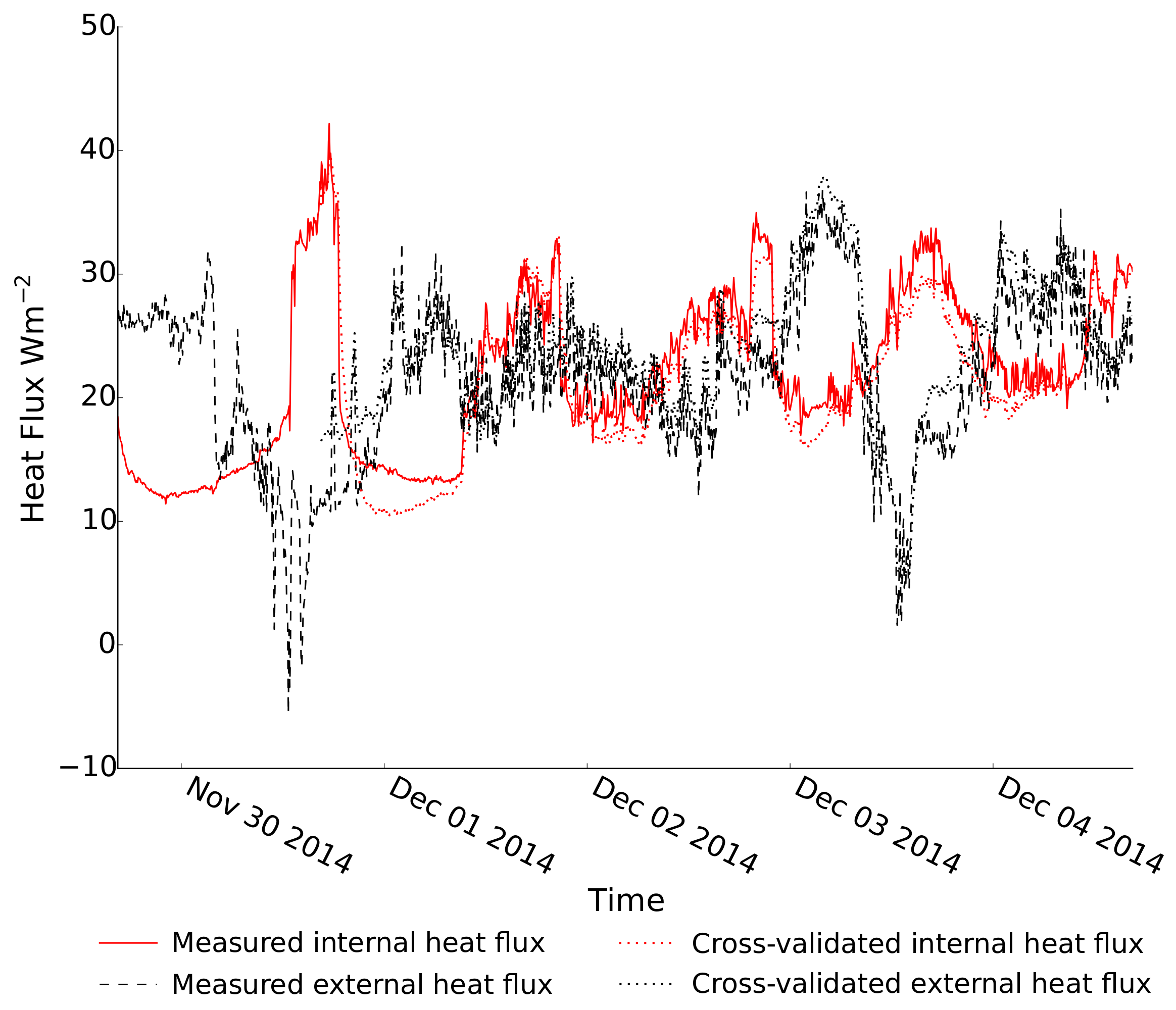
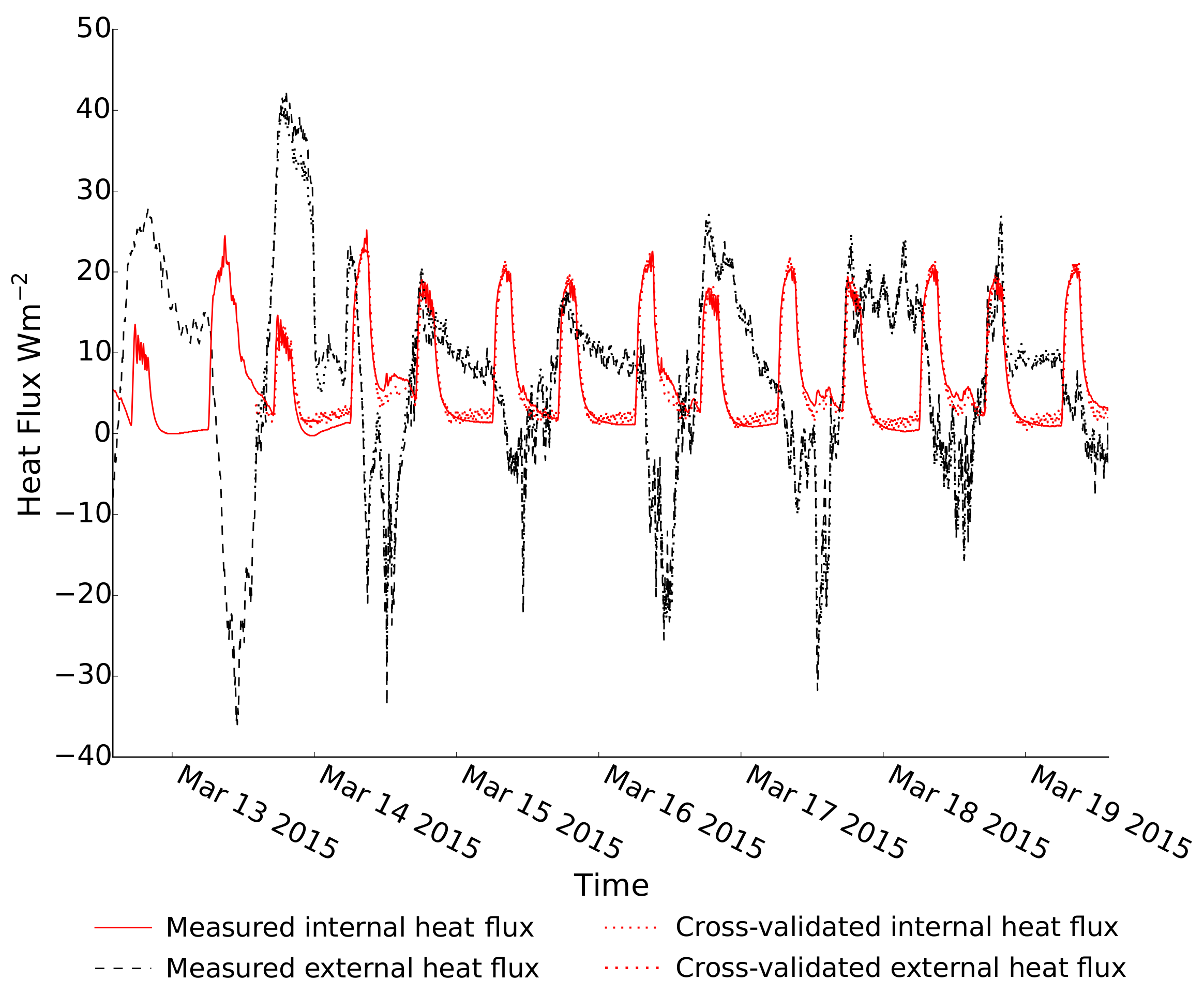
2.4.2. Cross-Validation
3. Experimental Data Collection and Analysis
3.1. Case Studies
3.2. Definition of Priors
Uniform Prior Distributions on the Parameters of the Model
Log-Normal Prior Distributions on the Parameters of the Model
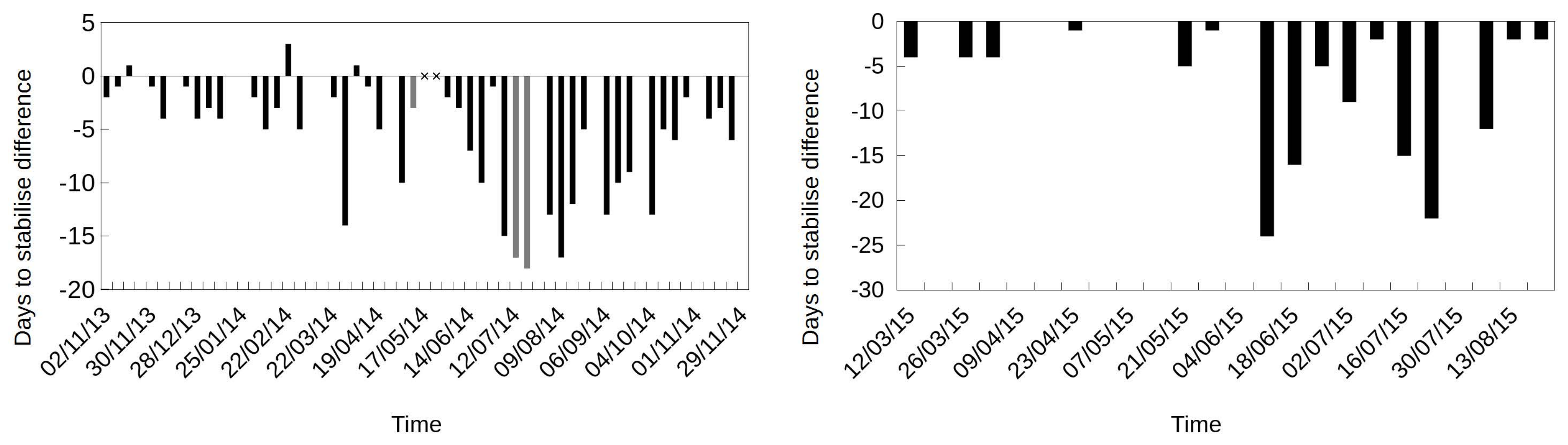
3.3. Stabilisation Criteria and Monitoring Campaign Length
3.4. Quantification of Uncertainties on in-Situ Observations
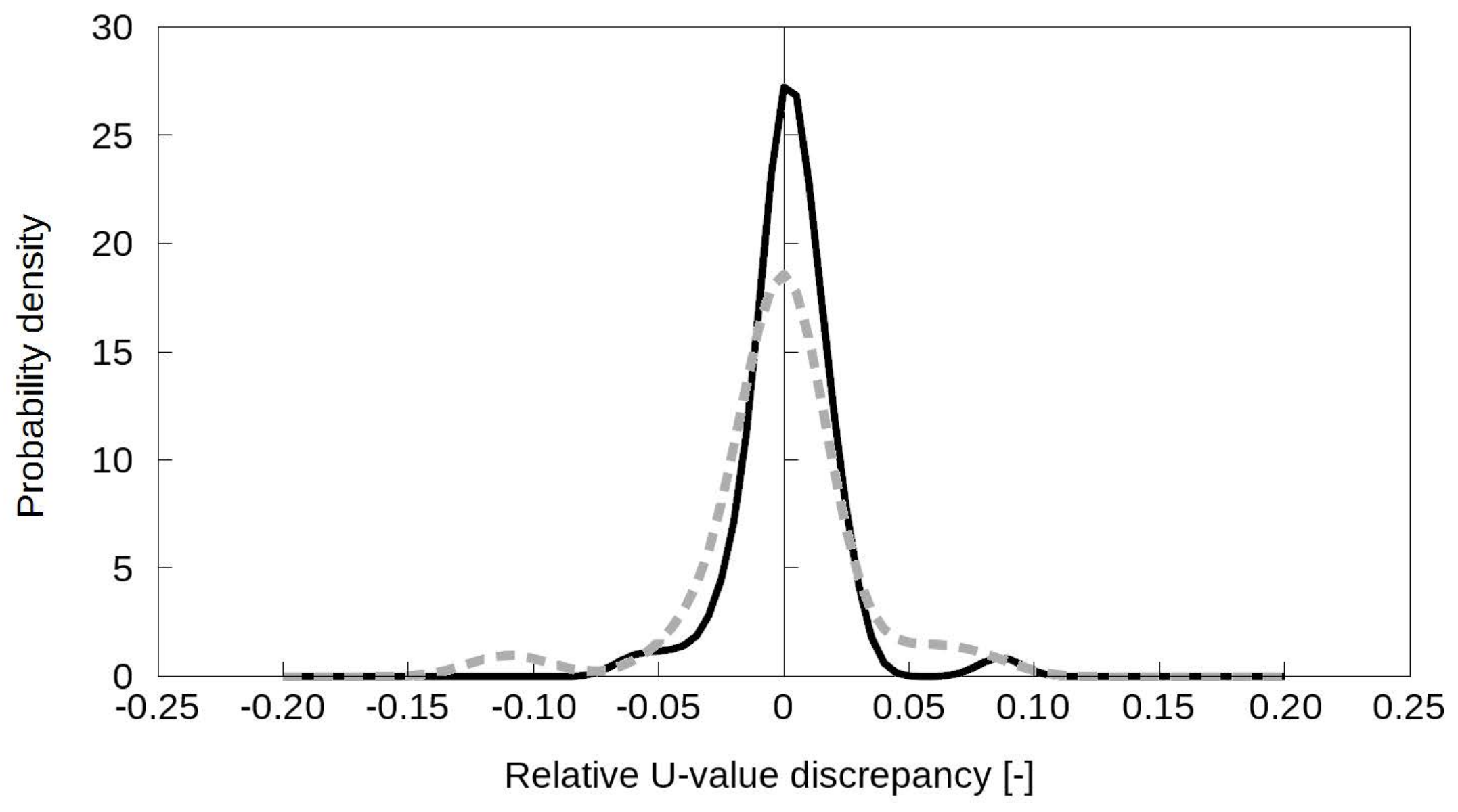
3.5. Quantification of Systematic Measurement Errors
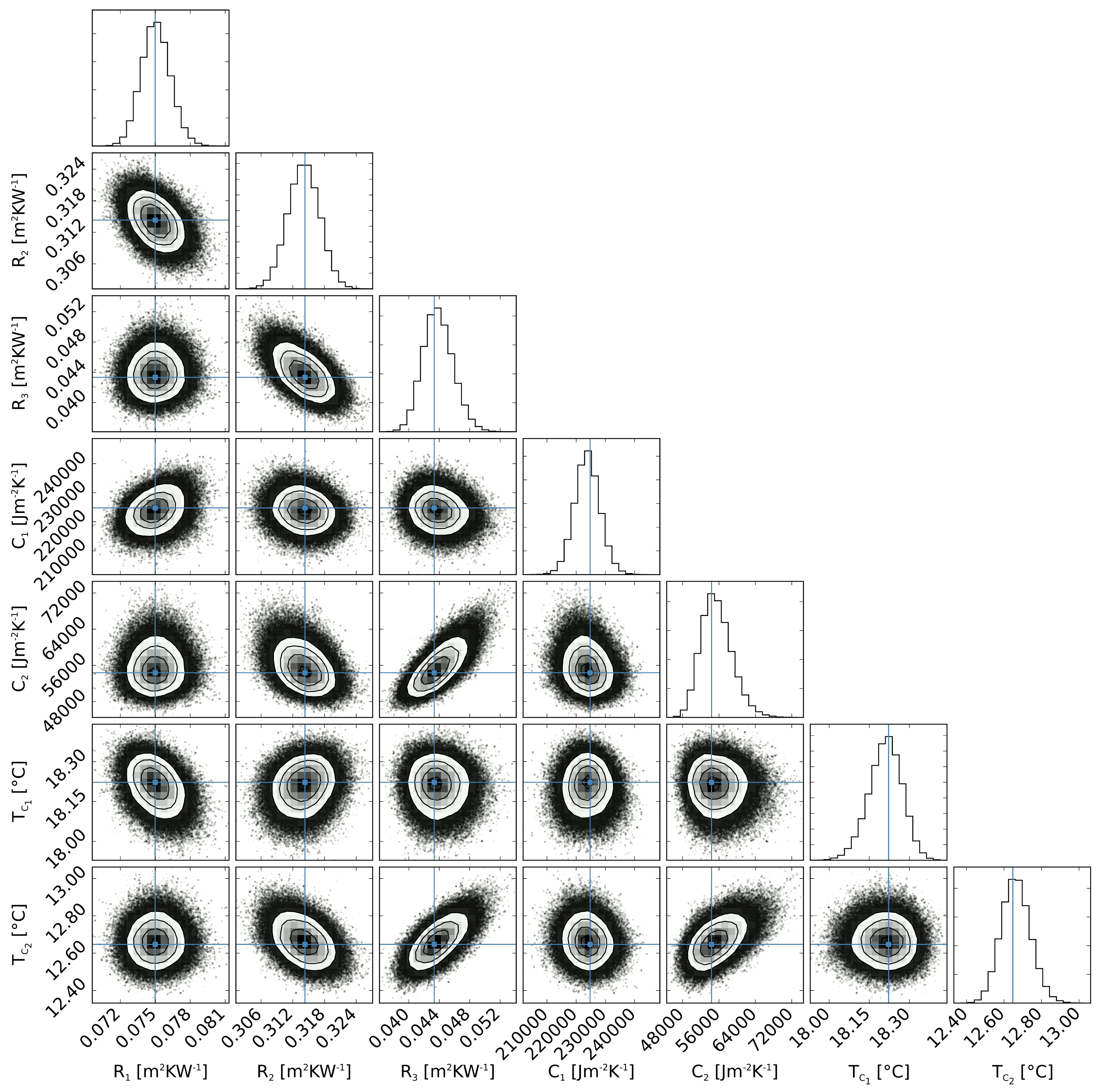
4. Results and Discussion
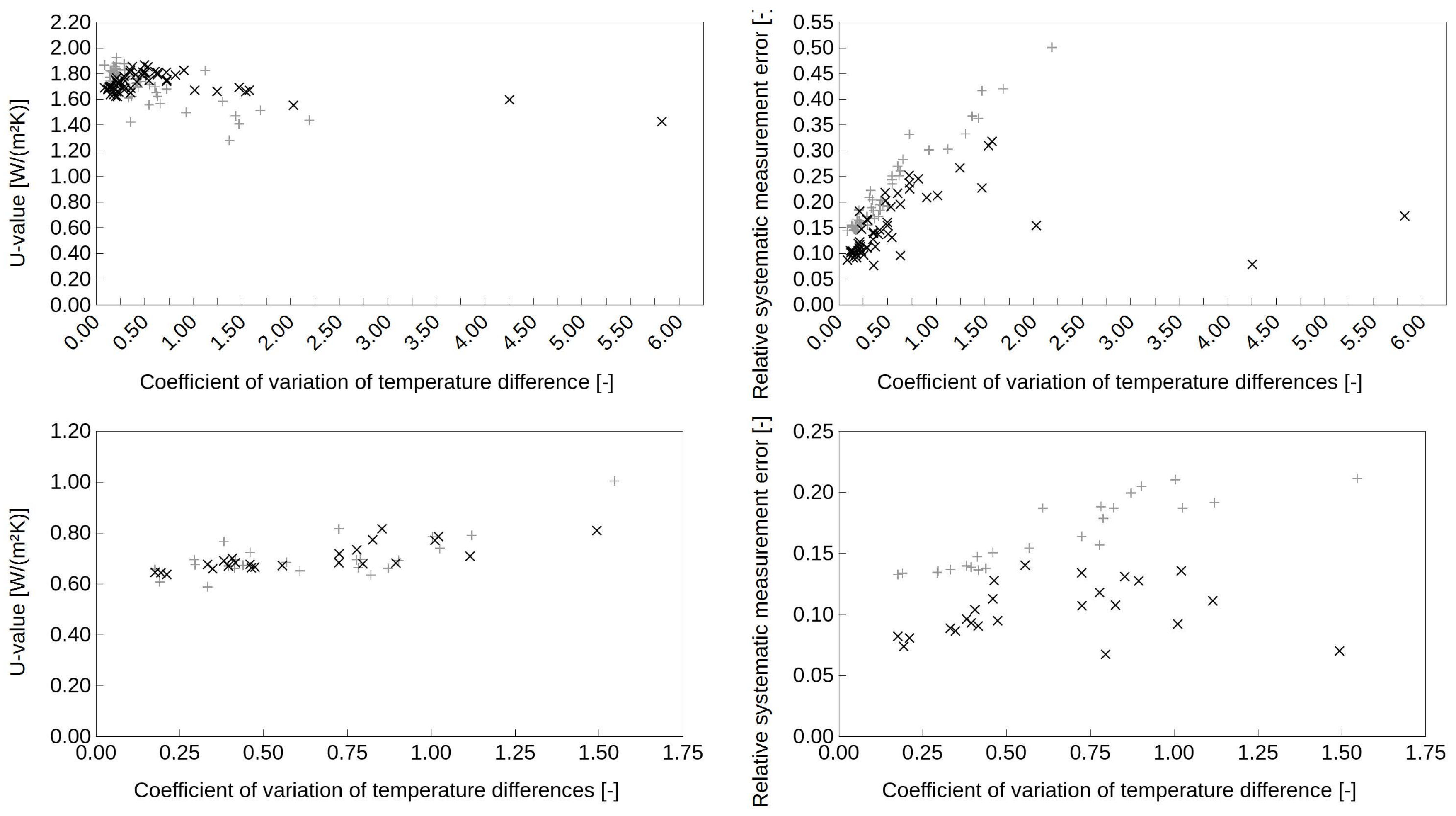
4.1. Thermophysical Performance of North-Facing Walls Exposed to High Temperature Differences
4.1.1. Thermophysical Performance of the Solid Wall
4.1.2. Thermophysical Performance of the Cavity Wall
4.2. Reducing the Required Monitoring Length and Temperature Difference
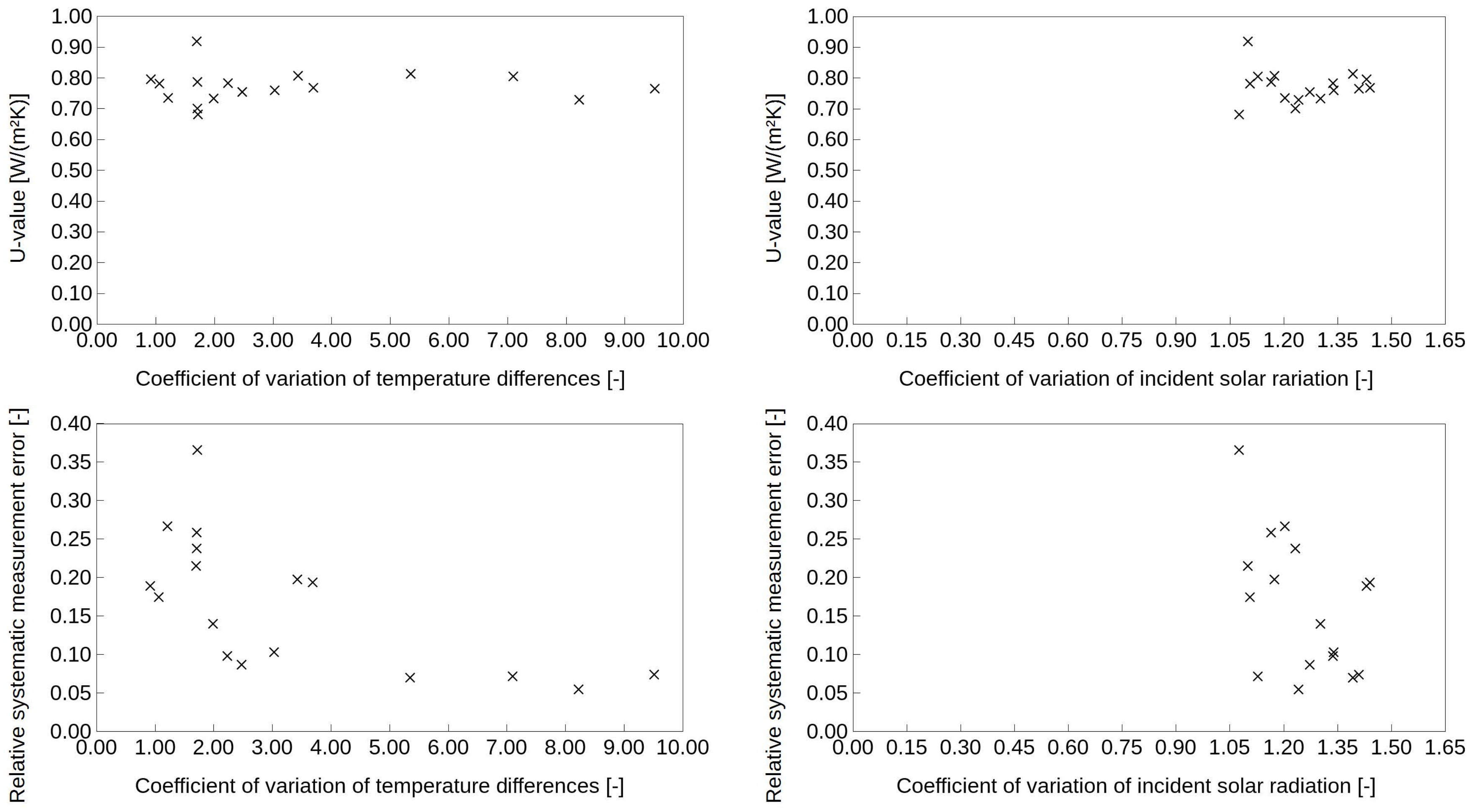
4.3. Thermophysical Performance of an East-Facing Wall
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zero Carbon Hub. Closing the Gap between Design & As-Built Performance. End of Term Report; Technical Report; Zero Carbon Hub: London, UK, 2014. [Google Scholar]
- IEA EBC Annex 58—Reliable Building Energy Performance Characterisation Based on Full Scale Dynamic Measurements. Available online: http://www.iea-ebc.org/projects/project?AnnexID=58 (accessed on 31 January 2018).
- IEA EBC Annex 70—Building Energy Epidemiology: Analysis of Real Building Energy Use at Scale. Available online: http://www.iea-ebc.org/projects/project?AnnexID=70 (accessed on 31 January 2018).
- IEA EBC Annex 71—Energy Performance Assessment Based on in-situ Measurements. Available online: http://www.iea-ebc.org/projects/project?AnnexID=71 (accessed on 31 January 2018).
- Cesaratto, P.G.; De Carli, M. A measuring campaign of thermal conductance in situ and possible impacts on net energy demand in buildings. Energy Build. 2013, 59, 29–36. [Google Scholar] [CrossRef]
- Biddulph, P.; Gori, V.; Elwell, C.A.; Scott, C.; Rye, C.; Lowe, R.; Oreszczyn, T. Inferring the thermal resistance and effective thermal mass of a wall using frequent temperature and heat flux measurements. Energy Build. 2014, 78, 10–16. [Google Scholar] [CrossRef]
- Desogus, G.; Mura, S.; Ricciu, R. Comparing different approaches to in situ measurement of building components thermal resistance. Energy Build. 2011, 43, 2613–2620. [Google Scholar] [CrossRef]
- Ficco, G.; Iannetta, F.; Ianniello, E.; d’Ambrosio Alfano, F.R.; Dell’Isola, M. U-value in situ measurement for energy diagnosis of existing buildings. Energy Build. 2015, 104, 108–121. [Google Scholar] [CrossRef]
- McIntyre, D.A. In situ measurement of U-values. Build. Serv. Eng. Res. Technol. 1985, 6, 1–6. [Google Scholar] [CrossRef]
- Siviour, J. Experimental U-values of some house walls. Build. Serv. Eng. Res. Technol. 1994, 15, 35–36. [Google Scholar] [CrossRef]
- Jiménez, M.J.; Porcar, B.; Heras, M.R. Application of different dynamic analysis approaches to the estimation of the building component U value. Build. Environ. 2009, 44, 361–367. [Google Scholar] [CrossRef]
- Naveros, I.; Bacher, P.; Ruiz, D.P.; Jiménez, M.J.; Madsen, H. Setting up and validating a complex model for a simple homogeneous wall. Energy Build. 2014, 70, 303–317. [Google Scholar] [CrossRef]
- Deconinck, A.H.; Roels, S. A maximum likelihood estimation of the thermal resistance of a cavity wall from on-site measurements. Energy Procedia 2015, 78, 3276–3281. [Google Scholar] [CrossRef]
- Albatici, R.; Tonelli, A.M. Infrared thermovision technique for the assessment of thermal transmittance value of opaque building elements on site. Energy Build. 2010, 42, 2177–2183. [Google Scholar] [CrossRef]
- Nardi, I.; Paoletti, D.; Ambrosini, D.; de Rubeis, T.; Sfarra, S. U-value assessment by infrared thermography: A comparison of different calculation methods in a Guarded Hot Box. Energy Build. 2016, 122, 211–221. [Google Scholar] [CrossRef]
- O’Grady, M.; Lechowska, A.A.; Harte, A.M. Infrared thermography technique as an in-situ method of assessing heat loss through thermal bridging. Energy Build. 2017, 135, 20–32. [Google Scholar] [CrossRef]
- Lehmann, B.; Ghazi Wakili, K.; Frank, T.; Vera Collado, B.; Tanner, C. Effects of individual climatic parameters on the infrared thermography of buildings. Appl. Energy 2013, 110, 29–43. [Google Scholar] [CrossRef]
- International Organization for Standardization. Thermal Insulation—Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance; Part 1: Heat Flow Meter Method; BS ISO 9869-1; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Jiménez, M.J.; Madsen, H. Models for describing the thermal characteristics of building components. Build. Environ. 2008, 43, 152–162. [Google Scholar] [CrossRef]
- Deconinck, A.H.; Roels, S. Comparison of characterisation methods determining the thermal resistance of building components from onsite measurements. Energy Build. 2016, 130, 309–320. [Google Scholar] [CrossRef]
- Hens, H. Building Physics—Heat, Air and Moisture: Fundamentals and Engineering Methods with Examples and Exercises; Ernst & Sohn Verlag für Architektur und technische Wissenschaften GmbH & Co. KG: Berlin, Germany, 2012. [Google Scholar]
- Roulet, C.; Gass, J.; Marcus, I. In-Situ U-Value Measurement: Reliable Results in Shorter Time by Dynamic Interpretation of Measured Data. In Thermal Performance of the Exterior Envelopes of Buildings III; ASHRAE Transactions: Atlanta, GA, USA, 1987; pp. 777–784. [Google Scholar]
- Kristensen, N.R.; Madsen, H.; Jørgensen, S.B. Parameter estimation in stochastic grey-box models. Automatica 2004, 40, 225–237. [Google Scholar] [CrossRef]
- Baker, P.H.; van Dijk, H.A.L. PASLINK and dynamic outdoor testing of building components. Build. Environ. 2008, 43, 143–151. [Google Scholar] [CrossRef]
- Kramer, R.; van Schijndel, J.; Schellen, H. Simplified Thermal and Hygric Building Models: A Literature Review. Front. Archit. Res. 2012, 1, 318–325. [Google Scholar] [CrossRef]
- Dubois, S.; McGregor, F.; Evrard, A.; Heath, A.; Lebeau, F. An inverse modelling approach to estimate the hygric parameters of clay-based masonry during a Moisture Buffer Value test. Build. Environ. 2014, 81, 192–203. [Google Scholar] [CrossRef]
- Berger, J.; Orlande, H.R.; Mendes, N.; Guernouti, S. Bayesian inference for estimating thermal properties of a historic building wall. Build. Environ. 2016, 106, 327–339. [Google Scholar] [CrossRef]
- Rouchier, S.; Busser, T.; Pailha, M.; Piot, A.; Woloszyn, M. Hygric characterization of wood fiber insulation under uncertainty with dynamic measurements and Markov Chain Monte-Carlo algorithm. Build. Environ. 2017, 114, 129–139. [Google Scholar] [CrossRef]
- Gori, V.; Marincioni, V.; Biddulph, P.; Elwell, C. Inferring the thermal resistance and effective thermal mass distribution of a wall from in situ measurements to characterise heat transfer at both the interior and exterior surfaces. Energy Build. 2017, 135, 398–409. [Google Scholar] [CrossRef]
- Gori, V. A Novel Method for the Estimation of Thermophysical Properties Of Walls From Short and Seasonally Independent in-Situ Surveys. Ph.D. Thesis, University College London, London, UK, 2017. [Google Scholar]
- Paschkis, V.; Baker, H. A method for determining unsteady-state heat transfer by means of an electrical analogy. Trans. Am. Soc. Mech. Eng. 1942, 64, 105–112. [Google Scholar]
- Madsen, H.; Holst, J. Estimation of continuous-time models for the heat dynamics of a building. Energy Build. 1995, 22, 67–79. [Google Scholar] [CrossRef]
- Gutschker, O. Parameter identification with the software package LORD. Build. Environ. 2008, 43, 163–169. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Information Theory, Inference and Learning Algorithms, 6th ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Python Language Reference, version 3.0; Python Software Foundation: Wilmington, DE, USA, 2017.
- Wales, D.J.; Doye, J.P. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Madsen, H. Time Series Analysis; Google-Books-ID: 0yFNKoIWdFkC; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Rao, K.R.; Yip, P.C. Discrete Cosine Transform: Algorithms, Advantages, Applications; Academic Press: Boston, MA, USA, 1990. [Google Scholar]
- Sánchez, V.; Garcia, P.; Peinado, A.M.; Segura, J.C.; Rubio, A.J. Diagonalizing properties of the discrete cosine transforms. IEEE Trans. Signal Process. 1995, 43, 2631–2641. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal Distributions across the Sciences: Keys and Clues. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Norlén, U. Determining the thermal resistance from in-situ measurements. In Proceedings of the Workshop on Application of System Identification in Energy Saving In Buildings, Luxembourg City, Luxembourg, 4–7 October 1994; pp. 402–429. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning Data Mining, Inference, and Prediction, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- DiCiccio, T.J.; Kass, R.E.; Raftery, A.; Wasserman, L. Computing Bayes Factors by Combining Simulation and Asymptotic Approximations. J. Am. Stat. Assoc. 1997, 92, 903–915. [Google Scholar] [CrossRef]
- Hukseflux. User Manual HFP01 & HFP03 Heat Flux Plate/Heat Flux Sensor (v1620). Available online: http://www.hukseflux.com/sites/default/files/product_manual/HFP01_HFP03_manual_v1620.pdf (accessed on 3 October 2016).
- Campbell Scientific. CR1000 Measurement and Control Datalogger. Available online: https://www.campbellsci.co.uk/cr1000 (accessed on 28 January 2015).
- Kipp and Zonen. CMP3 Pyranometer. Available online: http://www.kippzonen.com/Product/11/CMP3-Pyranometer (accessed on 29 July 2016).
- Eltek. Squirrel 450/850 Series Data Logger. Available online: http://www.eltekdataloggers.co.uk/450_series.html (accessed on 28 January 2015).
- Eltek. RX250AL Receiver/Logger. Available online: http://www.eltekdataloggers.co.uk/rx250.html (accessed on 15 November 2017).
- Zhao, J.; Plagge, R.; Ramos, N.M.M.; Lurdes Simões, M.; Grunewald, J. Concept for development of stochastic databases for building performance simulation—A material database pilot project. Build. Environ. 2015, 84, 189–203. [Google Scholar] [CrossRef]
- Macdonald, I.A. Quantifying the Effects of Uncertainty in Building Simulation. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2002. [Google Scholar]
- Clarke, J.; Yaneske, P.; Pinney, A. The Harmonisation of Thermal Properties of Building Materials; Technical Report BRE/169/12/1; BRE: Watford, UK, 1990. [Google Scholar]
- Eames, M.E.; Ramallo-Gonzalez, A.P.; Wood, M.J. An update of the UK’s test reference year: The implications of a revised climate on building design. Build. Serv. Eng. Res. Technol. 2016, 37, 316–333. [Google Scholar] [CrossRef]
- Bohm, G.; Zech, G. Introduction to Statistics and Data Analysis for Physicists; DESY: Hamburg, Germany, 2010. [Google Scholar]
- International Organization for Standardization. Thermal Performance of Building Components—Dynamic Thermal Characteristics—Calculation Methods; EN ISO 13786; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Gori, V.; Elwell, C. Estimation of thermophysical properties from in-situ measurements in all seasons: Quantifying and reducing errors using dynamic grey-box methods. Energy Build. 2018, 167, 290–300. [Google Scholar] [CrossRef]
- JCGM. JCGM 200:2012—International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM); Technical Report; Joint Committee for Guides in Metrology (JCGM/WG1): Sèvres Cedex, France, 2012. [Google Scholar]
- Energy Saving Trust. Post-Construction Testing—A Professionals Guide to Testing Housing for Energy Efficiency; CE128/GIR64; Energy Saving Trust: London, UK, 2005. [Google Scholar]
- Gori, V.; Elwell, C. Long-Term in-situ Measurements of Heat Flux and Temperature on a Solid-Brick Wall in an Office Building in the UK; UCL Energy Institute: London, UK, 2018. [Google Scholar] [CrossRef]
- Gori, V.; Elwell, C. Characterization of the thermal structure of different building constructions using in-situ measurements and Bayesian analysis. Energy Procedia 2017, 132, 537–542. [Google Scholar] [CrossRef]
- Gori, V.; Elwell, C. Long-Term in-situ Measurement of Heat Flux and Temperature on a Filled Cavity Wall in a Residential Building in the UK; UCL Energy Institute: London, UK, 2018. [Google Scholar] [CrossRef]
- Gori, V.; Elwell, C. Long-Term in-situ Measurement on an East-Facing Filled Cavity Wall in a Residential Building in the UK; UCL Energy Institute: London, UK, 2018. [Google Scholar]


| Parameters | Literature | AM | 1TM (1 HF) | 1TM (2 HF) | 2TM | Units |
|---|---|---|---|---|---|---|
| R-value | ||||||
| U-value |
| Parameters | Literature | AM | 1TM (1 HF) | 1TM (2 HF) | 2TM | Units |
|---|---|---|---|---|---|---|
| R-value | ||||||
| U-value |
| Method | Min | Max | Mean | St Dev | Units | |
|---|---|---|---|---|---|---|
| SWall | AM | 1.28 | 1.92 | 1.71 | 0.14 | |
| AM error | 14 | 50 | 22 | 8 | % | |
| 2TM | 1.43 | 1.87 | 1.72 | 0.08 | ||
| 2TM error | 8 | 32 | 15 | 6 | % | |
| CWall_N | AM | 0.59 | 1.00 | 0.71 | 0.08 | |
| AM error | 13 | 21 | 16 | 3 | % | |
| 2TM | 0.64 | 0.82 | 0.70 | 0.05 | ||
| 2TM error | 7 | 14 | 10 | 2 | % |
| Model | Min | Max | Mean | St Dev | Units |
|---|---|---|---|---|---|
| 2TM | 0.68 | 0.92 | 0.77 | 0.05 | |
| 2TM error | 5 | 37 | 16 | 9 | % |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gori, V.; Biddulph, P.; Elwell, C.A. A Bayesian Dynamic Method to Estimate the Thermophysical Properties of Building Elements in All Seasons, Orientations and with Reduced Error. Energies 2018, 11, 802. https://doi.org/10.3390/en11040802
Gori V, Biddulph P, Elwell CA. A Bayesian Dynamic Method to Estimate the Thermophysical Properties of Building Elements in All Seasons, Orientations and with Reduced Error. Energies. 2018; 11(4):802. https://doi.org/10.3390/en11040802
Chicago/Turabian StyleGori, Virginia, Phillip Biddulph, and Clifford A. Elwell. 2018. "A Bayesian Dynamic Method to Estimate the Thermophysical Properties of Building Elements in All Seasons, Orientations and with Reduced Error" Energies 11, no. 4: 802. https://doi.org/10.3390/en11040802
APA StyleGori, V., Biddulph, P., & Elwell, C. A. (2018). A Bayesian Dynamic Method to Estimate the Thermophysical Properties of Building Elements in All Seasons, Orientations and with Reduced Error. Energies, 11(4), 802. https://doi.org/10.3390/en11040802







