Symmetric Fuzzy Logic and IBFOA Solutions for Optimal Position and Rating of Capacitors Allocated to Radial Distribution Networks
Abstract
:1. Introduction
2. Related Work
3. The Proposed Methodology for Optimal Placement and Sizing of Capacitor
3.1. Fuzzy-Based Load Flow
3.2. Optimal Placement and Sizing of the Capacitor
3.3. Improved Bacterial Foraging Optimization Algorithm (IBFOA)
- an ability to search food
- self-charging (mobile behavior)
| Algorithm 1 Pseudo code of IBFOA |
| 1: Initialize parameters |
| 2: Optimal placement of capacitor if is greater and if is smaller then calculate VSI, LSF. Evaluate fitness function 1 for each node. |
| 3: Update Elimination and dispersal, reproduction, chemotaxis steps. |
| 4: Perform chemotaxis to find best fitness Calculate Fitness function for every bacterium Substitute the value in Flast Generate random vector Evaluate movement of bacterium Update fitness function If then go to the next bacterium |
| 5: Perform reproduction up to . |
| 6: Perform Elimination and dispersal and Evaluate fitness 2. Perform elimination and dispersal up to |
| 7: Calculate fitness for capacitor size |
| 8: End |
4. Experimental Results
- Operating speed: 2.90 GHz.
- Processor: Intel Pentium@ 2.90 GHz.
- RAM: 4 GB.
- MATLAB Version: R2014a.
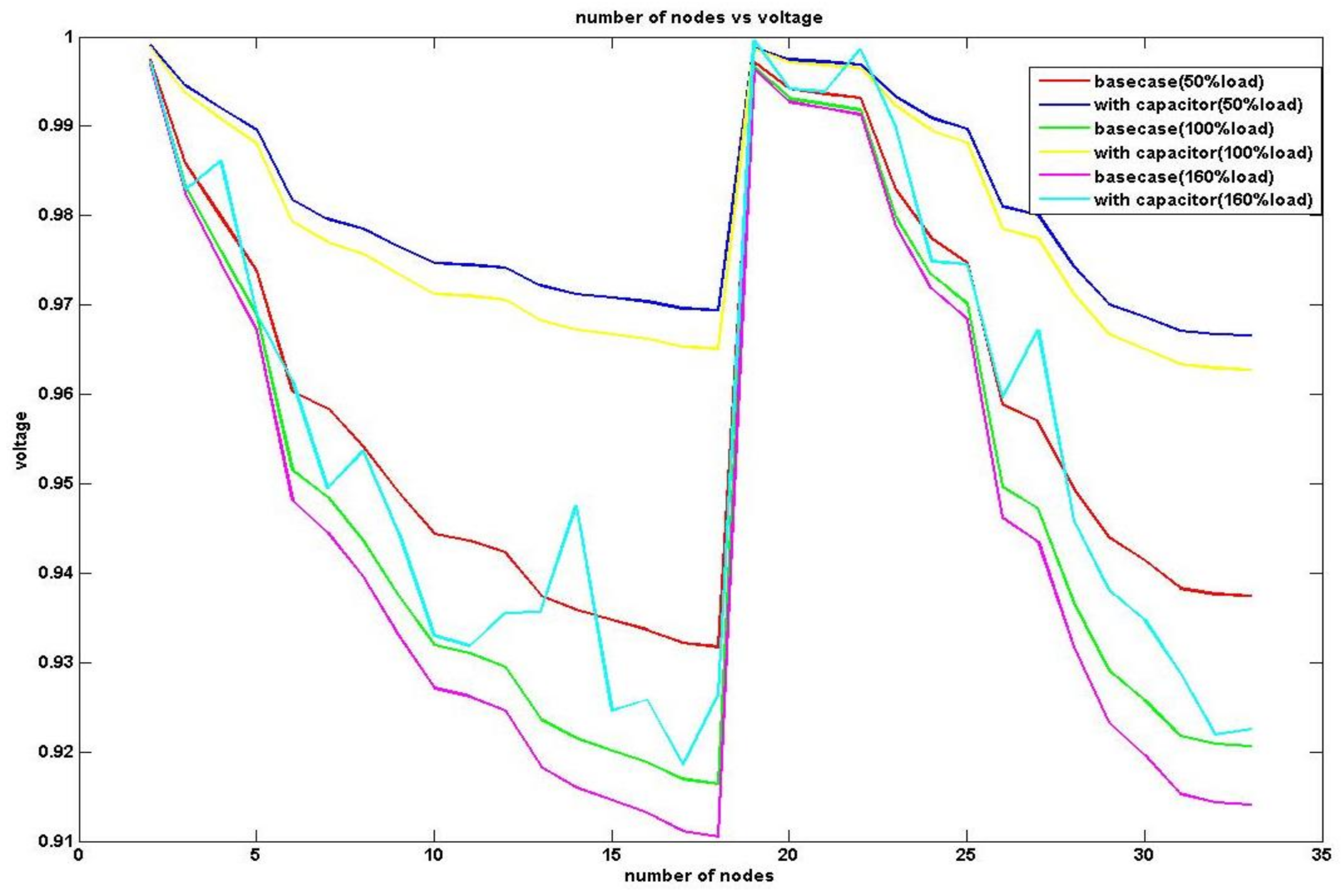
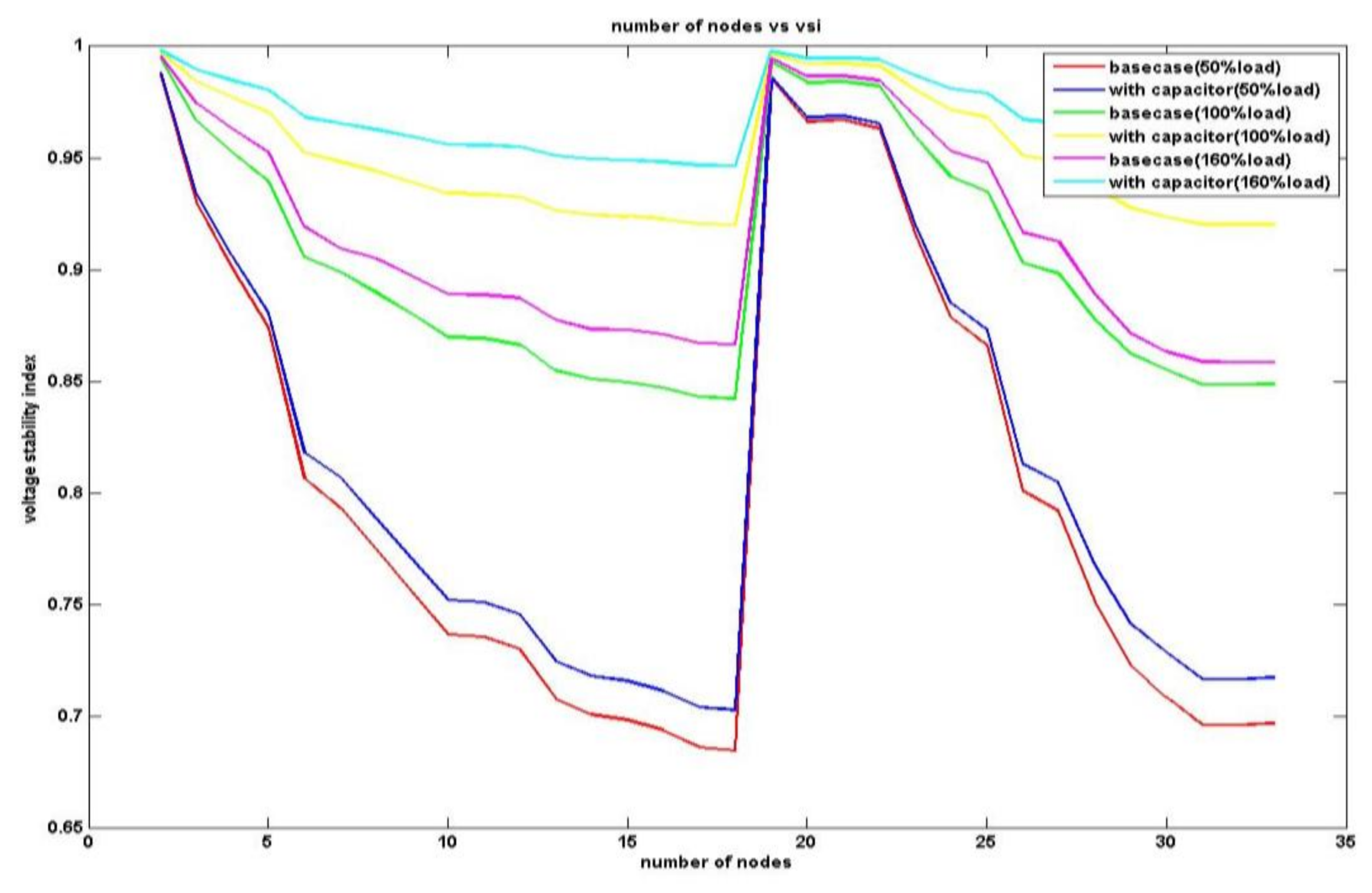
4.1. The 33-Node RDN
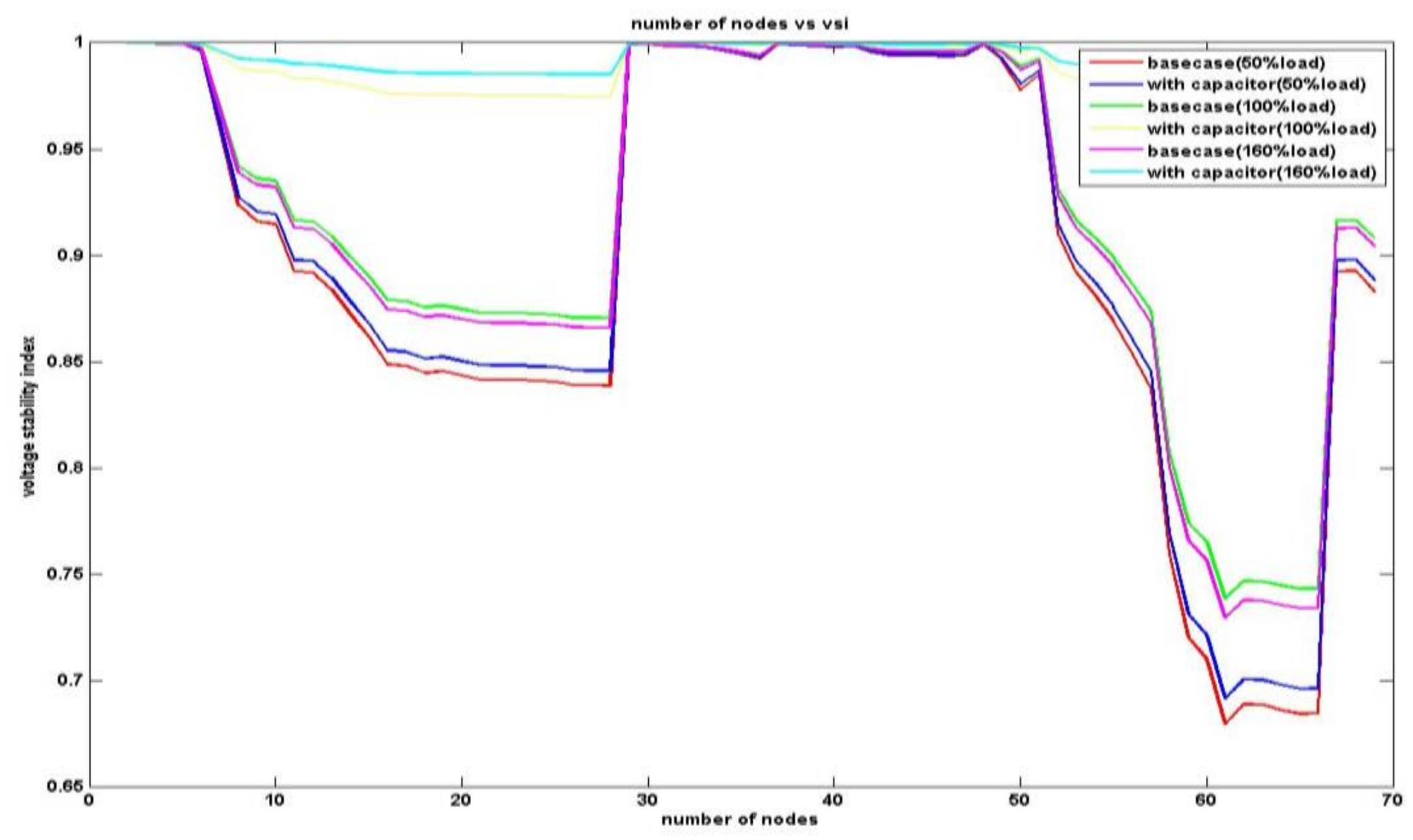
4.2. 69-Node RDN
4.3. 141-Node RDN
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electr. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Viawan, F.; Karlsson, D. Voltage and reactive power control in systems with synchronous machine-based distributed generation. IEEE Trans. Power Deliv. 2008, 23, 1079–1087. [Google Scholar] [CrossRef]
- Barker, P.P.; De Mello, R.W. Determining the impact of distributed generation on power systems. I. Radial distribution systems. IEEE Power Eng. Soc. Summer Meet. 2000, 3, 1645–1656. [Google Scholar] [CrossRef]
- Sonwane, P.M.; Kushare, B.E. Optimal Capacitor Placement and Sizing: An Overview. Int. J. Innov. Res. Adv. Eng. 2015, 2, 103–113. [Google Scholar]
- Naik, S.G.; Khatod, D.K.; Sharma, M.P. Optimal allocation of combined DG and capacitor for real power loss minimization in distribution networks. Int. J. Electr. Power Energy Syst. 2013, 53, 967–973. [Google Scholar] [CrossRef]
- Ng, H.N.; Salama, M.M.A.; Chikhani, A.Y. Classification of capacitor allocation techniques. IEEE Trans. Power Deliv. 2000, 15, 387–392. [Google Scholar] [CrossRef]
- Etemadi, A.H.; Fotuhi-Firuzabad, M. Distribution system reliability enhancement using optimal capacitor placement. IET Gener. Transm. Distrib. 2008, 2, 621–631. [Google Scholar] [CrossRef]
- Carpinelli, G.; Proto, D.; Noce, C.; Russo, A.; Varilone, P. Optimal allocation of capacitors in unbalanced multi-converter distribution systems: A comparison of some fast techniques based on genetic algorithms. Electr. Power Syst. Res. 2010, 80, 642–650. [Google Scholar] [CrossRef]
- Miloševič, B.; Begovič, M. Capacitor placement for conservative voltage reduction on distribution feeders. IEEE Trans. Power Deliv. 2004, 19, 1360–1367. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D.K. Optimal planning of distributed generation systems in distribution system: A review. Renew. Sustain. Energy Rev. 2012, 16, 5146–5165. [Google Scholar] [CrossRef]
- Popović, D.H.; Greatbanks, J.A.; Begović, M.; Pregelj, A. Placement of distributed generators and reclosers for distribution network security and reliability. Int. J. Electr. Power Energy Syst. 2005, 27, 398–408. [Google Scholar] [CrossRef]
- DcDermott, T.E.; Drezga, I.; Broadwater, R.P. A heuristic nonlinear constructive method for distribution system reconfiguration. IEEE Trans. Power Syst. 1999, 14, 478–483. [Google Scholar] [CrossRef]
- Borges, C.L.T.; Falcao, D.M. Optimal distributed generation allocation for reliability, losses, and voltage improvement. Int. J. Electr. Power Energy Syst. 2006, 28, 413–420. [Google Scholar] [CrossRef]
- Peças Lopes, J.A.; Hatziargyriou, N.; Mutale, J.; Djapic, P.; Jenkins, N. Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities. Electr. Power Syst. Res. 2007, 77, 1189–1203. [Google Scholar] [CrossRef]
- Wu, T.; Rothleder, M.; Alaywan, Z.; Papalexopoulos, A.D. Pricing energy and ancillary services in integrated market systems by an optimal power flow. IEEE Trans. Power Syst. 2004, 19, 339–347. [Google Scholar] [CrossRef]
- Valle, Y.D.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Prakash, K.; Sydulu, M. Particle swarm optimization based capacitor placement on radial distribution systems. IEEE Power Energy Soc. Gen. Meet. 2007, 1–5. [Google Scholar] [CrossRef]
- Elsheikh, A.; Helmy, Y.; Abouelseoud, Y.; Elsherif, A. Optimal capacitor placement and sizing in radial electric power systems. Alex. Eng. J. 2014, 53, 809–816. [Google Scholar] [CrossRef]
- Chiou, J.P.; Chang, C.F. Development of a novel algorithm for optimal capacitor placement in distribution systems. Electr. Power Energy Syst. 2015, 73, 684–690. [Google Scholar] [CrossRef]
- Zeinalzadeh, A.; Mohammadi, Y.; Moradi, M.H. Optimal multi objective placement and sizing of multiple DGs and shunt capacitor banks simultaneously considering load uncertainty via MOPSO approach. Electr. Power Energy Syst. 2015, 67, 336–349. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Optimal capacitor placement in radial distribution systems using teaching learning based optimization. Electr. Power Energy Syst. 2014, 54, 387–398. [Google Scholar] [CrossRef]
- Shuaib, Y.; Mohamed, M.; Kalavathi, S.; Christober, C.; Rajan, A. Optimal capacitor placement in radial distribution system using Gravitational Search Algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 384–397. [Google Scholar] [CrossRef]
- Raju, M.R.; Murthy, K.R.; Ravindra, K. Direct search algorithm for capacitive compensation in radial distribution systems. Int. J. Electr. Power Energy Syst. 2012, 42, 24–30. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Ali, E.S.; Abd Elazim, S.M. Optimal sizing and locations of capacitors in radial distribution systems via flower pollination optimization algorithm and power loss index. Eng. Sci. Technol. Int. J. 2016, 19, 610–618. [Google Scholar] [CrossRef]
- Li, J.; Dang, J.; Bu, F.; Wang, J. Analysis and improvement of the bacterial foraging optimization algorithm. J. Comput. Sci. Eng. 2014, 8, 1–10. [Google Scholar] [CrossRef]
- Chakravorty, M.; Das, D. Voltage Stability Analysis of Radial Distribution Networks. Int. J. Electr. Power Energy Syst. 2001, 23, 129–135. [Google Scholar] [CrossRef]
- Ghosh, S.; Das, D. Method for load-flow solution of radial distribution networks. IET Proc. Gener. Transm. Distrib. 1999, 146, 641–648. [Google Scholar] [CrossRef]
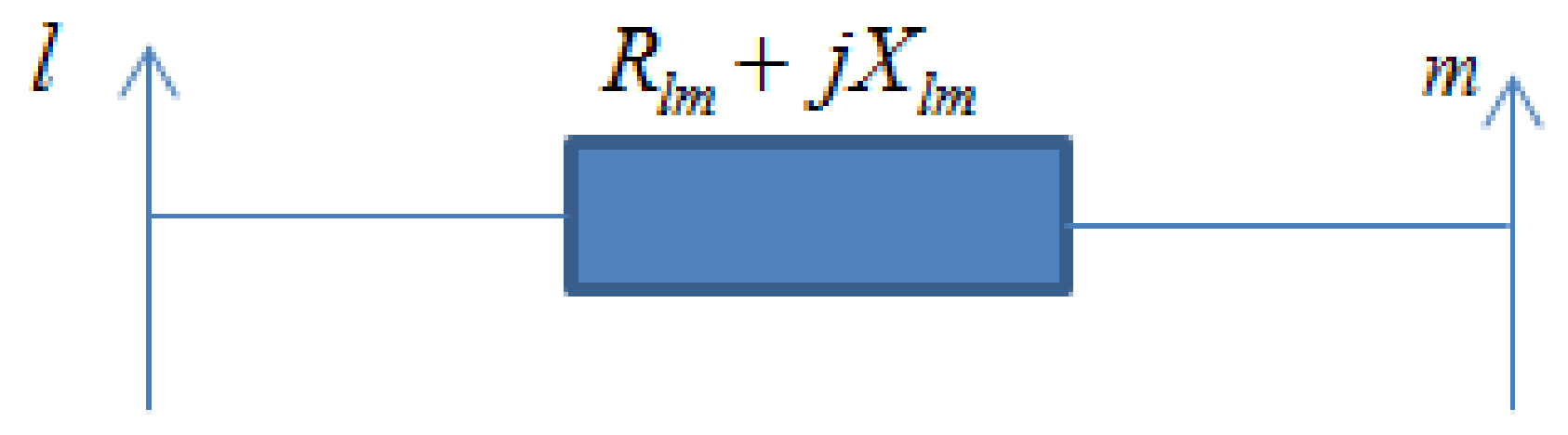


| Parameters | Base Case | Proposed Method |
|---|---|---|
| Light Load (50%) | ||
| Optimal location & size | - | 18 & 698 30 & 280 25 & 360 |
| Vmin (p.u.) & node | 0.9545 & 18 | 0.9731 & 32 |
| VSImin(p.u.) & node | 0.6959 & 18 | 0.7271 & 32 |
| Power loss (kW) | 57.33 | 41.02 |
| Nominal Load (100%) | ||
| Optimal location & size | - | 18 & 695 30 & 850 25 & 525 |
| Vmin (p.u.) & node | 0.9133 & 18 | 0.9699 & 32 |
| VSImin(p.u.) & node | 0.7849 & 18 | 0.8761 & 32 |
| Power loss (kW) | 202.25 | 131.78 |
| Peak Load (160%) | ||
| Optimal location & size | - | 18 & 750 30 & 820 25 & 1066 |
| Vmin (p.u.) & node | 0.8543 & 18 | 0.8871 & 32 |
| VSImin(p.u.) & node | 0.8876 & 18 | 0.9728 & 32 |
| Power loss (kW) | 523.85 | 411.01 |
| Load Type | Cases | Power Loss (kW) | Min. Voltage (p.u.) | Capacitor Location | Capacitor Size (kVAr) |
|---|---|---|---|---|---|
| Normal load (100%) | Proposed Method | 132.56 | 0.9698 (32) | 18, 25, 30 | 695, 525, 850 |
| GSA [22] | 134.5 | 0.9672 | 26, 13, 15 | 350, 450, 800 | |
| SA [22] | 151.75 | 0.9591 | 10, 30, 14 | 450, 350, 900 | |
| IP [24] | 171.78 | 0.9501 | 9, 29, 30 | 450, 800, 900 |
| Parameters | TLBO [21] | Proposed Method | DSA [23] | FPA [24] |
|---|---|---|---|---|
| Light Load (50%) | ||||
| Optimal location & size (kVAr) | 22 & 150 61 & 450 62 & 450 | 65 & 295 60 & 283 10 & 492 | 15 & 300 60 & 300 61 & 450 | - |
| Vmin (p.u.) & node | 0.9662 & 65 | 0.9687 & 65 | 0.9683 & 65 | - |
| VSImin (p.u.) & node | - | 0.7191 & 65 | - | - |
| Power loss (kW) | 34.43 | 33.28 | 35.52 | - |
| Nominal Load (100%) | ||||
| Optimal location & size (kVAr) | 22 & 300 61 & 1050 62 & 300 | 65 & 432 60 & 420 10 & 828 | 15 & 450 60 & 450 61 & 900 | 61 & 1250 21 & 250 |
| Vmin (p.u.) & node | 0.9321 & 65 | 0.9425 & 65 | 0.9318 & 65 | 0.9323 |
| VSImin (p.u.) & node | - | 0.7945 & 65 | - | - |
| Power loss (kW) | 146.80 | 143.97 | 147.00 | 145.78 |
| Peak Load (160%) | ||||
| Optimal location & size (kVAr) | 22 & 300 61 & 1050 62 & 750 | 65 & 1210 60 & 570 10 & 480 | 15 & 900 60 & 900 61 & 1800 | - |
| Vmin (p.u.) & node | 0.8795 & 65 | 0.8823 & 65 | 0.8936 & 65 | - |
| VSImin (p.u.) & node | - | 0.9754 & 65 | - | - |
| Power loss (kW) | 417.28 | 416.01 | 427.3 | - |
| Parameters | TLBO [21] | Proposed Method | GSA (100% Load Only) [22] |
|---|---|---|---|
| Light Load (50%) | |||
| Optimal location & size (kVAr) | 49 & 150 50 & 0 75 & 0 78 & 0 81 & 150 87 & 150 | 52 & 328 32 & 434 80 & 450 42 & 180 43 & 570 116 & 150 | - |
| Vmin (p.u.) & node | 0.9680 & 52 | 0.9699 & 52 | - |
| VSImin & node | - | 0.8598 & 52 | - |
| Power loss (kW) | 13.2511 | 12.18 | - |
| Nominal Load (100%) | |||
| Optimal location & size (kVAr) | 15 & 900 21 & 600 55 & 900 63 & 900 78 & 900 85 & 750 | 52 & 870 32 & 878 80 & 450 42 & 890 43 & 750 116 & 903 | 23 & 150 50 & 350 55 & 350 64 & 150 80 & 150 99 & 150 |
| Vmin (p.u.) & node | 0.9484 & 52 | 0.9508 & 52 | - |
| VSImin & node | - | 0.9281 & 52 | - |
| Power loss (kW) | 44.7311 | 43.00 | 45.74 |
| Peak Load (160%) | |||
| Optimal location & size (kVAr) | 31 & 900 45 & 900 62 & 900 63 & 900 79 & 900 87 & 900 | 52 & 870 32 & 750 80 & 460 42 & 350 43 & 570 116 & 360 | - |
| Vmin (p.u.) & node | 0.9073 & 52 | 0.9228 & 52 | - |
| VSImin & node | - | 0.9456 & 52 | - |
| Power loss (kW) | 129.1649 | 127.25 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kishore, C.; Ghosh, S.; Karar, V. Symmetric Fuzzy Logic and IBFOA Solutions for Optimal Position and Rating of Capacitors Allocated to Radial Distribution Networks. Energies 2018, 11, 766. https://doi.org/10.3390/en11040766
Kishore C, Ghosh S, Karar V. Symmetric Fuzzy Logic and IBFOA Solutions for Optimal Position and Rating of Capacitors Allocated to Radial Distribution Networks. Energies. 2018; 11(4):766. https://doi.org/10.3390/en11040766
Chicago/Turabian StyleKishore, Chandan, Smarajit Ghosh, and Vinod Karar. 2018. "Symmetric Fuzzy Logic and IBFOA Solutions for Optimal Position and Rating of Capacitors Allocated to Radial Distribution Networks" Energies 11, no. 4: 766. https://doi.org/10.3390/en11040766
APA StyleKishore, C., Ghosh, S., & Karar, V. (2018). Symmetric Fuzzy Logic and IBFOA Solutions for Optimal Position and Rating of Capacitors Allocated to Radial Distribution Networks. Energies, 11(4), 766. https://doi.org/10.3390/en11040766




