Rapid Estimation Method for State of Charge of Lithium-Ion Battery Based on Fractional Continual Variable Order Model
Abstract
:1. Introduction
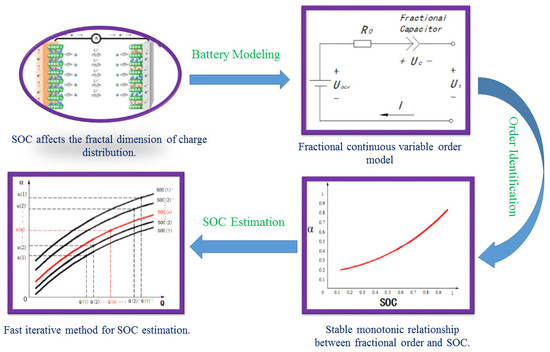
2. Fractional Order Model of Lithium-Ion Batteries
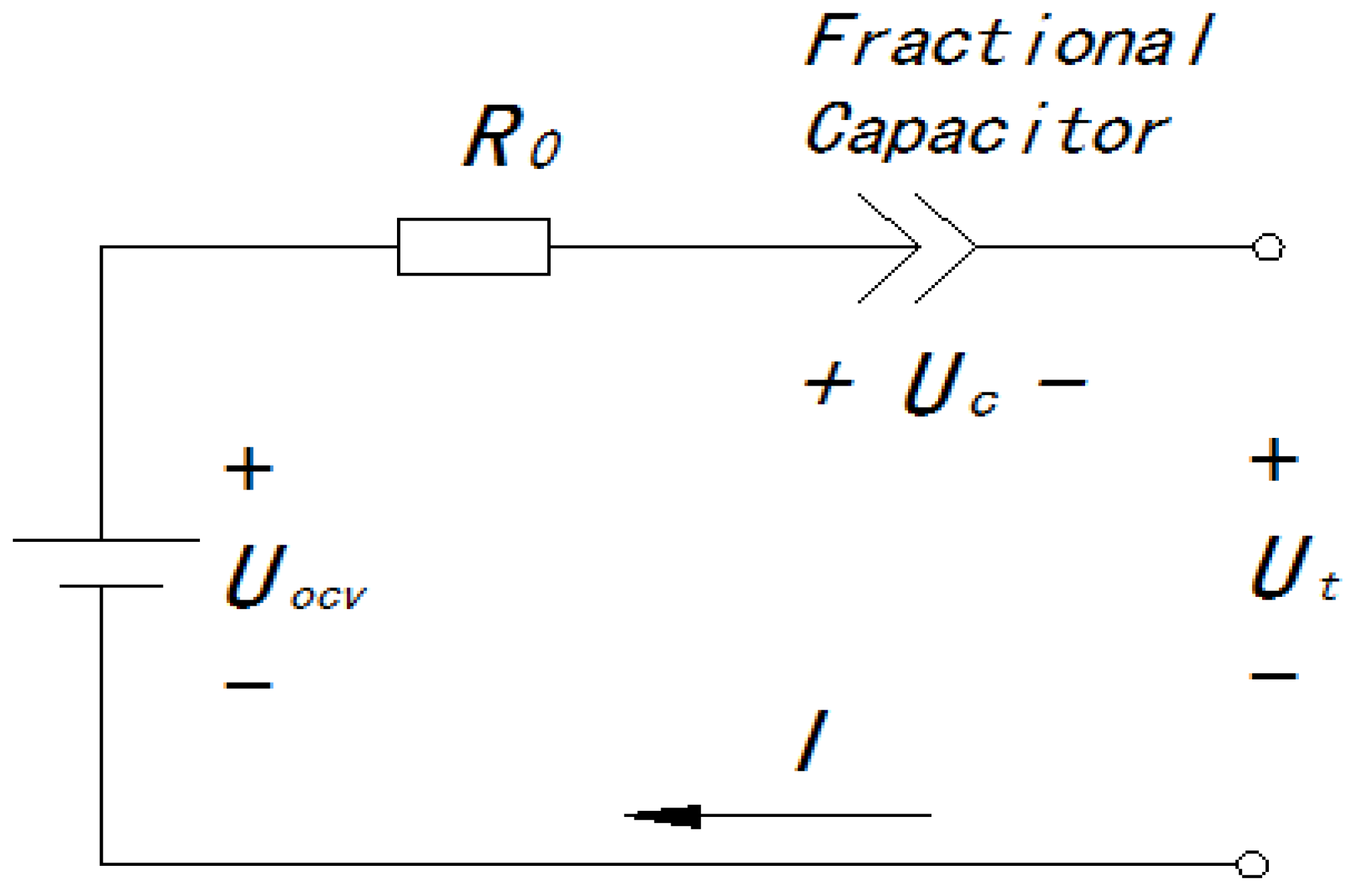
2.1. Battery Modeling
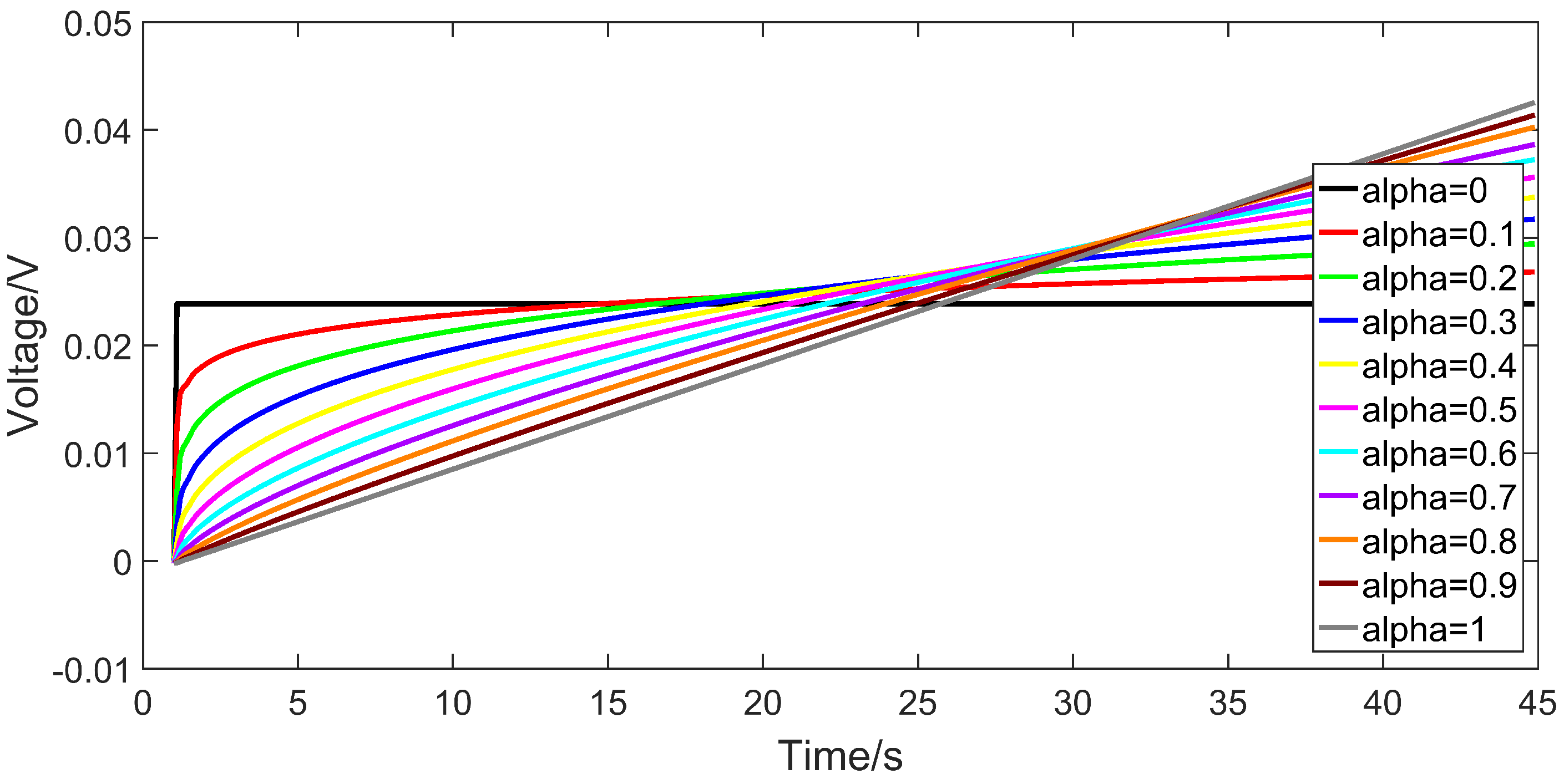
2.2. The Output Dynamic of the Fractional Capacitor
3. Order Identification of Fractional Order Model
3.1. Identification Method
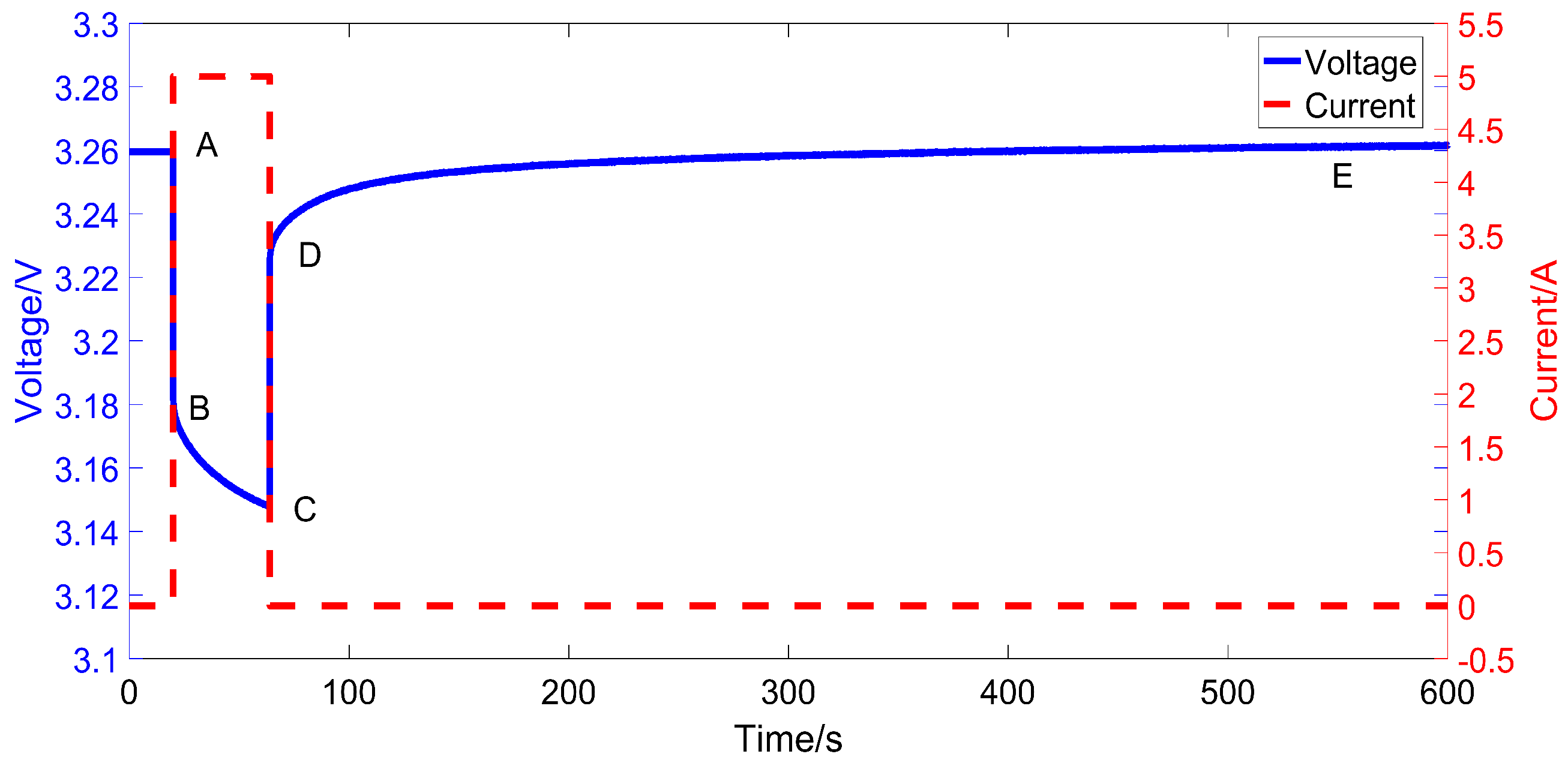
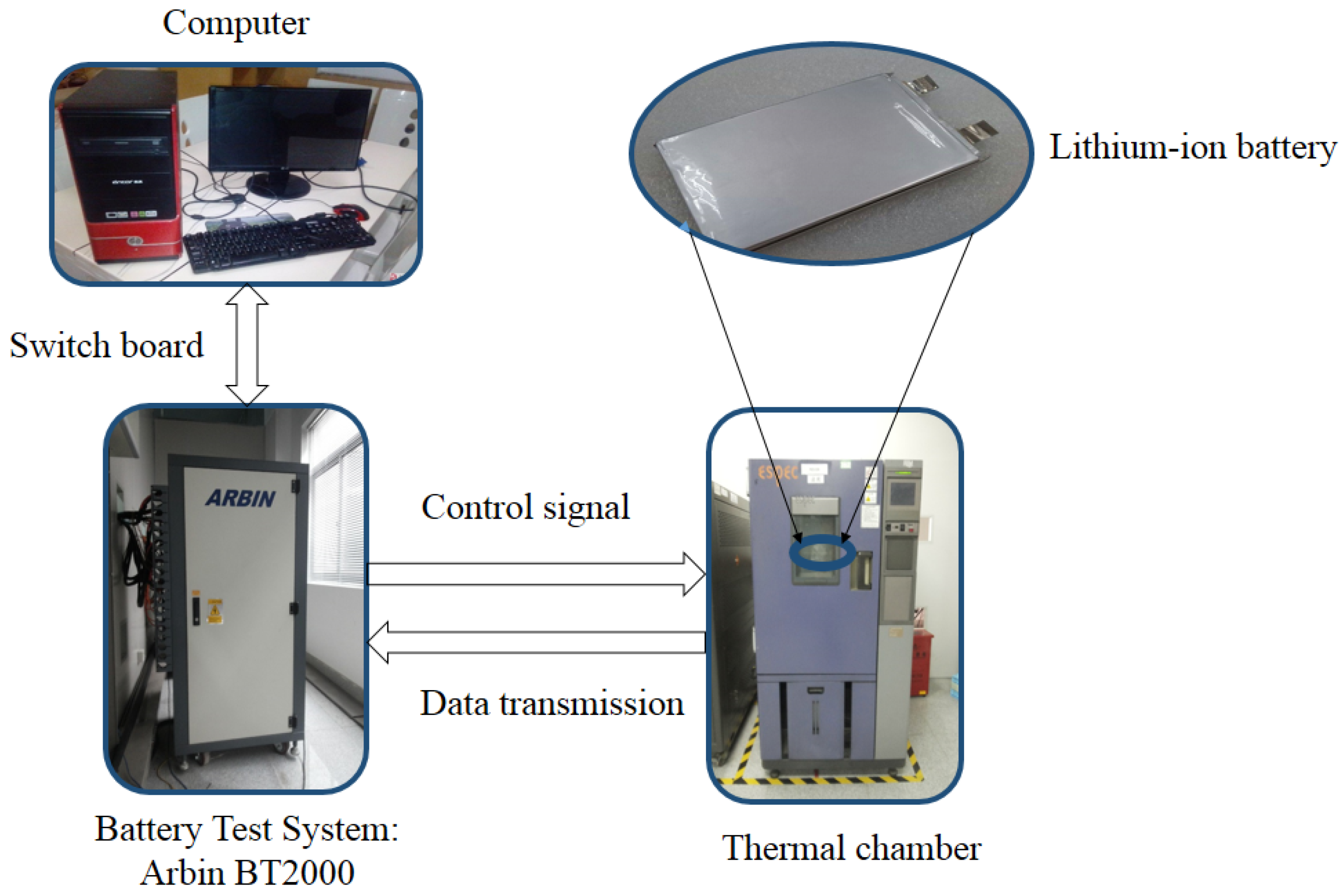
3.2. Experiment Setup
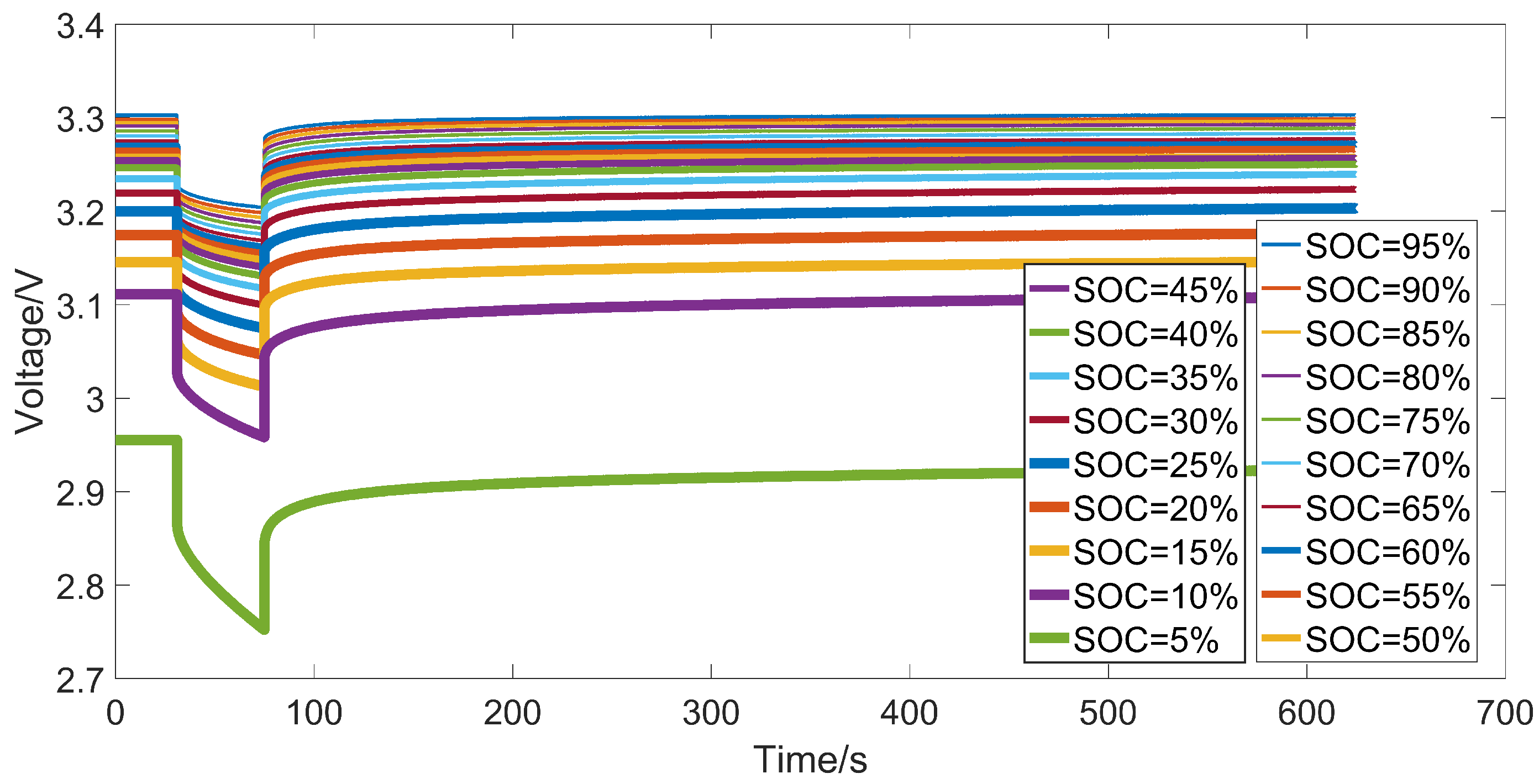
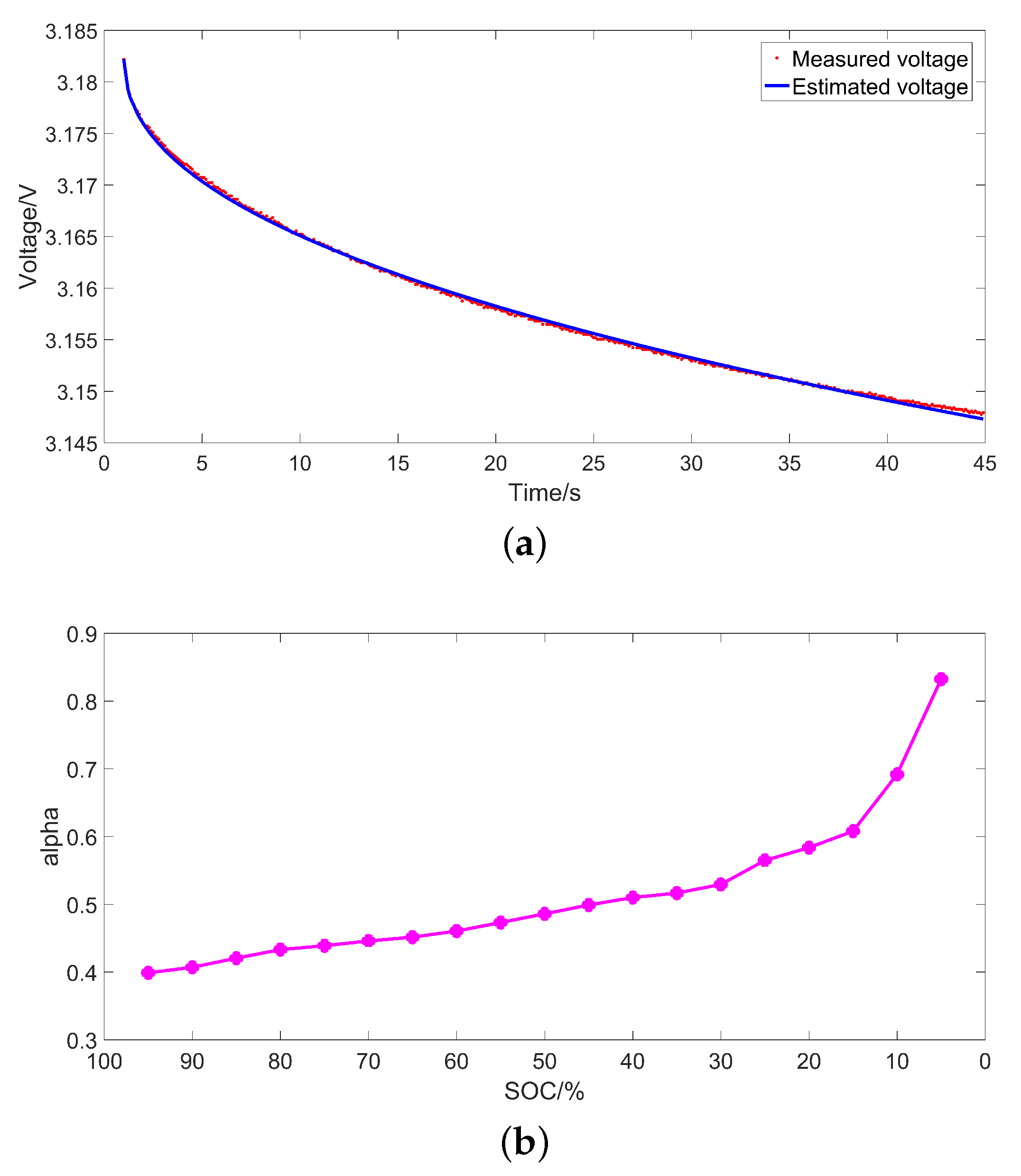
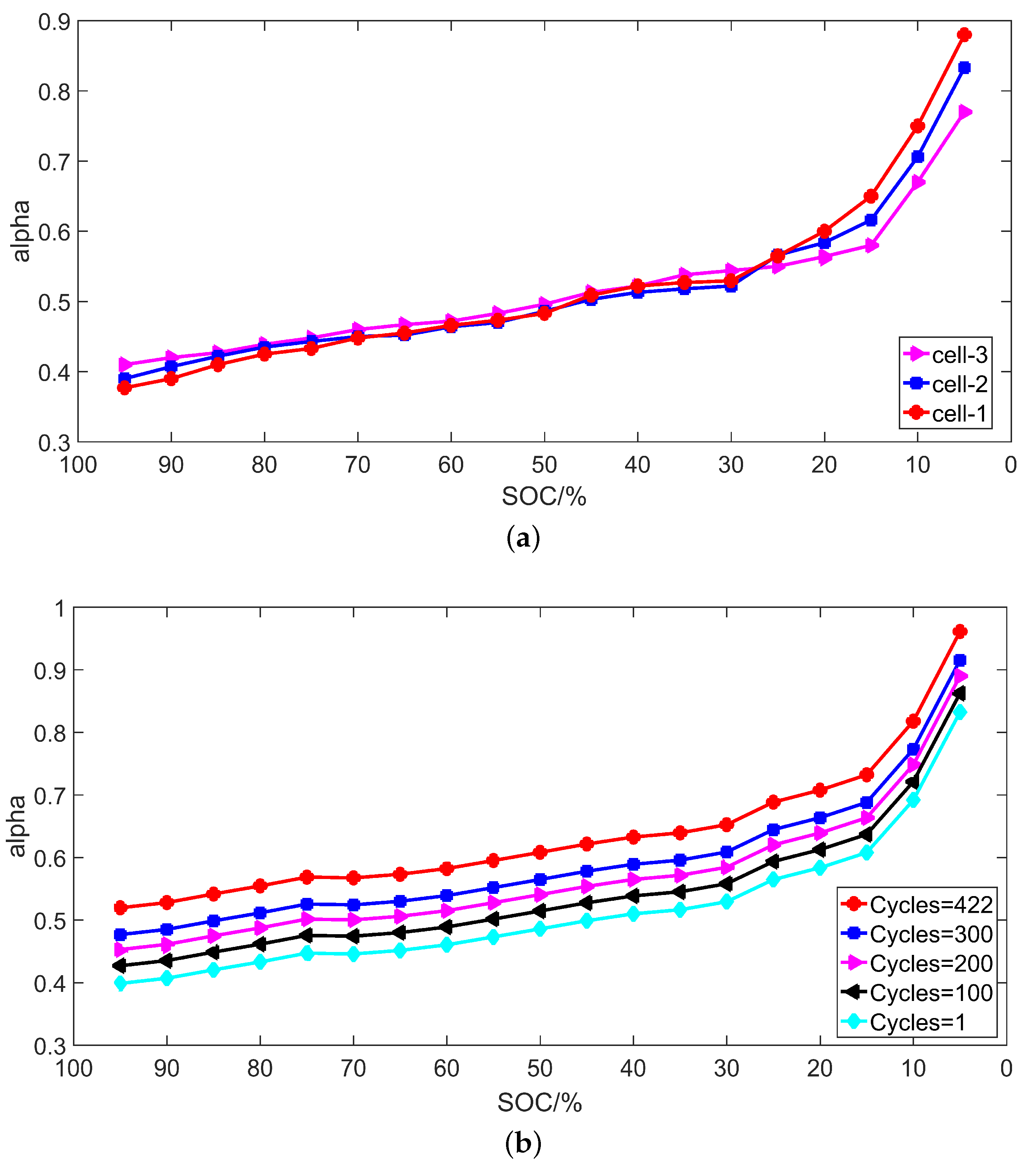
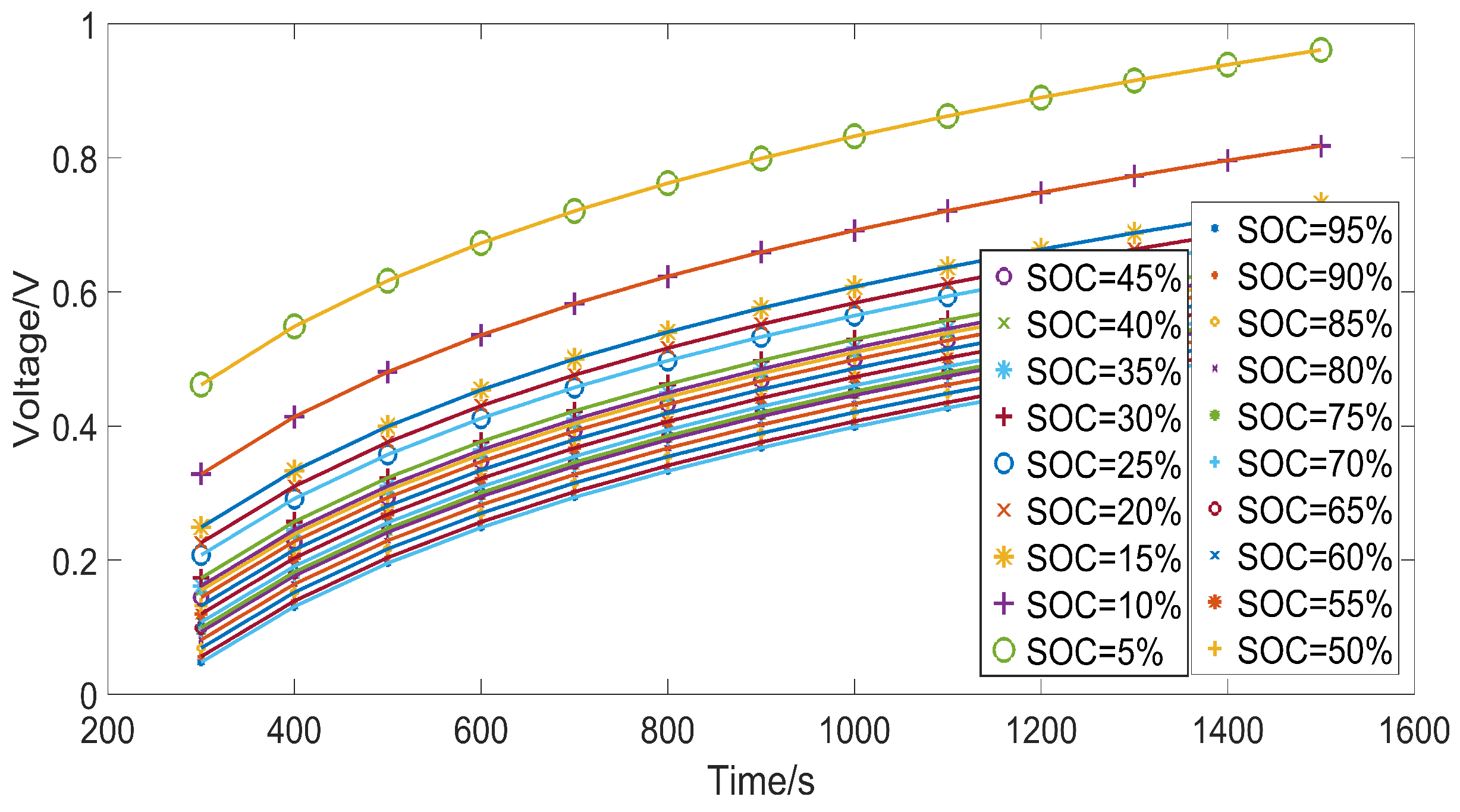
3.3. Identification Results
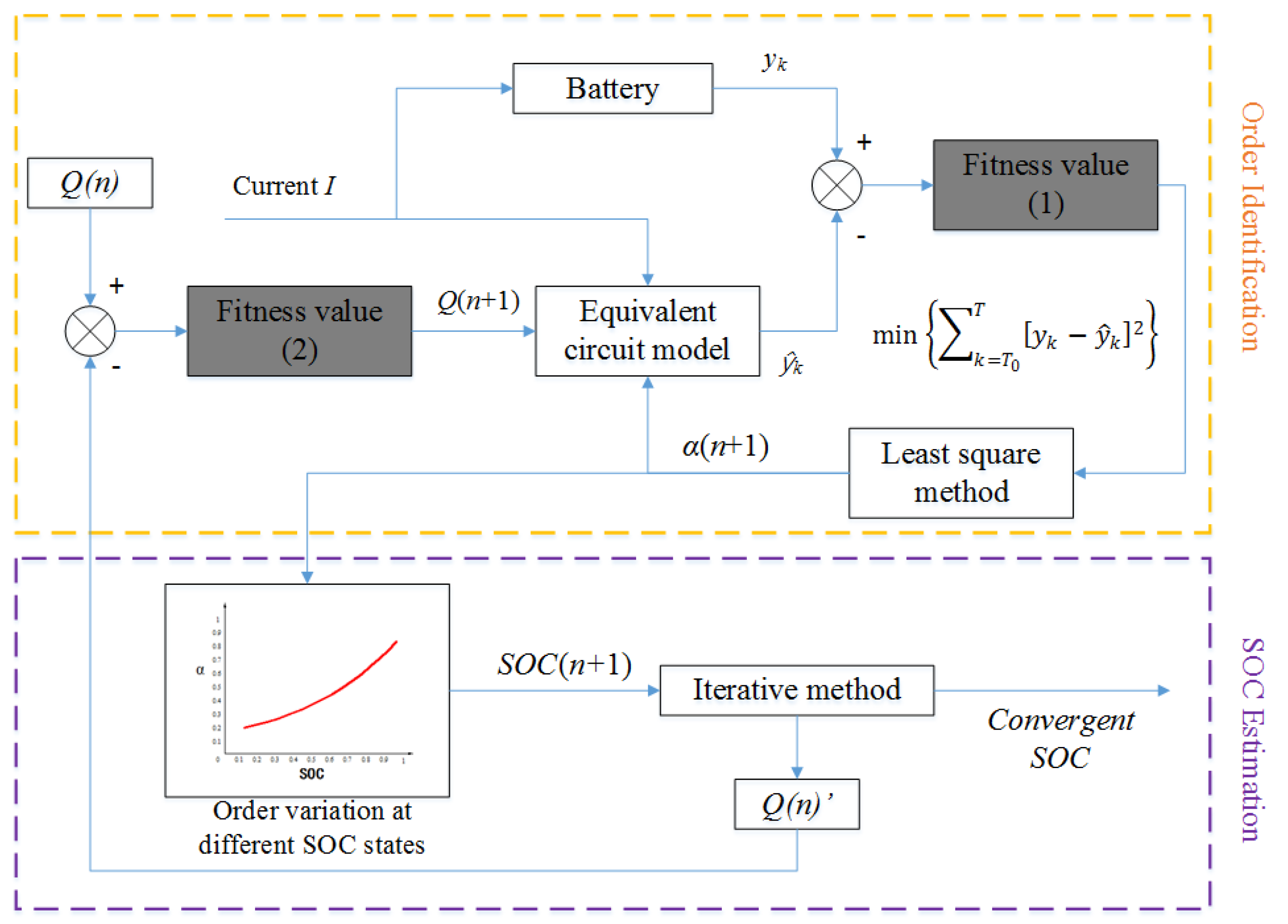
4. SOC Estimation
4.1. The Iterative Method for SOC Estimation
- The initial coefficient is selected in the given variation range which is shown in Table 2. For convenience, the initial coefficient is generally integer in this paper.
- Based on the least square principle, the order is identified when the coefficient is fixed at , and the battery SOC can be obtained from Table 2.
- According to Table 3, the coefficient is searched when the order (n) and the battery SOC are known.
- The coefficient is calculated based on the formula:
- The coefficient is used as the new coefficient, repeat steps 2–4 until the coefficient and the order converge to the fixed value. The framework of SOC estimation based on the iterative method is shown in Figure 10.
4.2. Proof of the Convergence of the SOC
- When the order is fixed, the coefficient Q given by the identification is positive with SOC, and their relationship can be expressed as: SOC;
- When the coefficient Q is fixed, the order given by the identification is inversely proportional to SOC, and their relationship can be expressed as: (1/SOC);
- At the same battery SOC, the coefficient is proportional to the order, and their relationship is expressed as: .
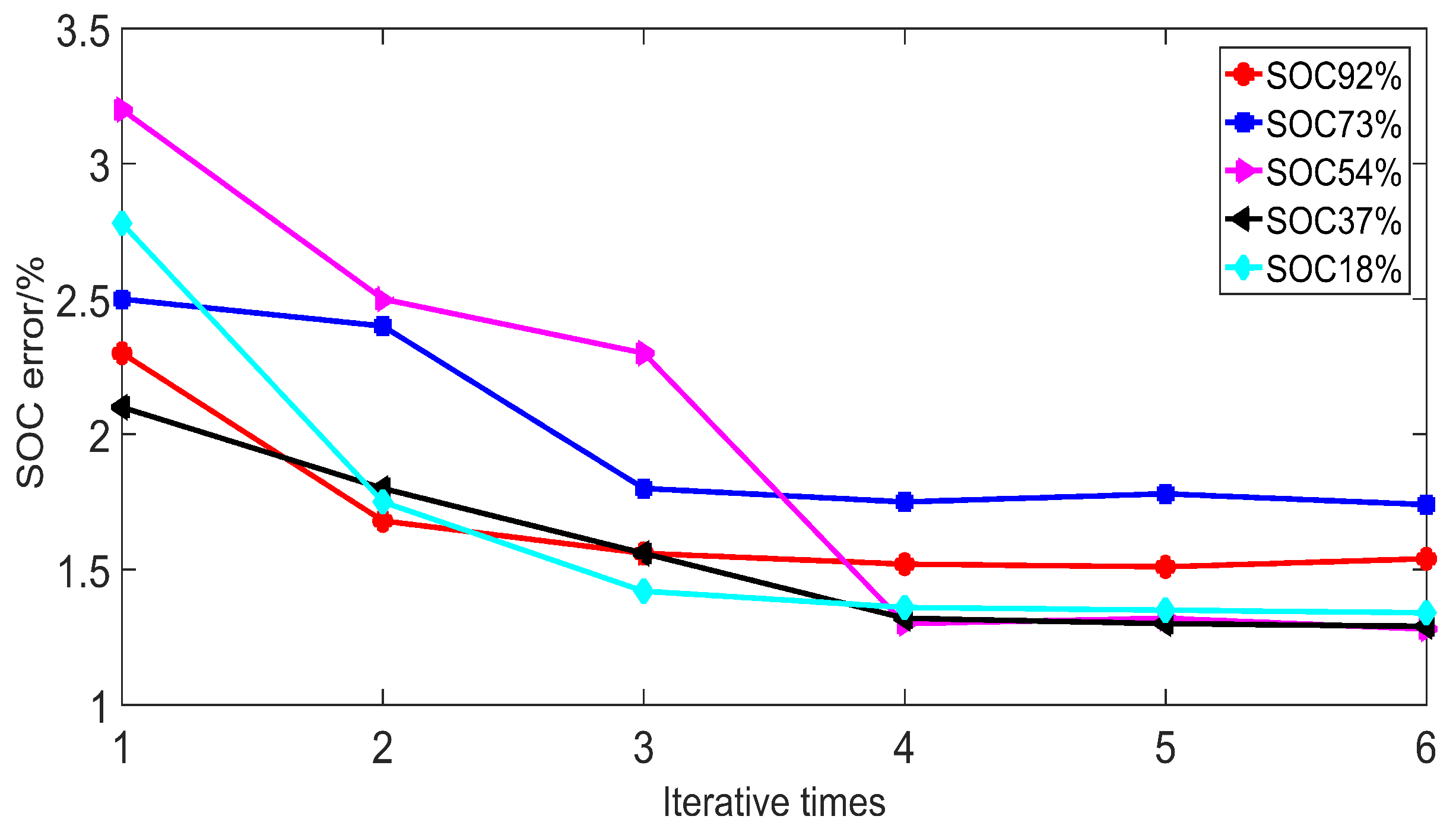
4.3. Experiment Validation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Li, J.; Barillas, J.K.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
- Kong, S.N.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Kang, L.W.; Zhao, X.; Ma, J. A new neural network model for the state-of-charge estimation in the battery degradation process. Appl. Energy 2014, 121, 20–27. [Google Scholar] [CrossRef]
- Yang, F.; Xing, Y.; Wang, D.; Tsui, K.L. A comparative study of three model-based algorithms for estimating state-of-charge of lithium-ion batteries under a new combined dynamic loading profile. Appl. Energy 2016, 164, 387–399. [Google Scholar] [CrossRef]
- Li, D.; Ouyang, J.; Li, H.; Wan, J. State of charge estimation for LiMn2O4, power battery based on strong tracking sigma point Kalman filter. J. Power Sources 2015, 279, 439–449. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Gao, F. Lithium polymer battery state-of-charge estimation based on adaptive unscented Kalman filter and support vector machine. IEEE Trans. Power Electron. 2016, 31, 2226–2238. [Google Scholar] [CrossRef]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint estimation of the electric vehicle power battery state of charge based on the least squares method and the Kalman filter algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, W.; Sharkh, S.M. Estimation of state of charge of lithium-ion batteries used in HEV using robust extended Kalman filtering. Energies 2012, 5, 1098–1115. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Liaw, B.Y.; Zhang, J. Graphical analysis of electrochemical impedance spectroscopy data in Bode and Nyquist representations. J. Power Sources 2016, 309, 82–98. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Ge, H.; Zhang, J. Analytical solution to the impedance of electrode/electrolyte interface in lithium-ion batteries. J. Electrochem. Soc 2015, 162, A7037–A7048. [Google Scholar] [CrossRef]
- Radvanyi, E.; Havenbergh, K.V.; Porcher, W.; Jouanneau, S.; Bridel, J.S. Study and modeling of the solid electrolyte interphase behavior on nano-silicon anodes by electrochemical impedance spectroscopy. Electrochim. Acta 2014, 137, 751–757. [Google Scholar] [CrossRef]
- Zou, Y.; Li, S.E.; Shao, B.; Wang, B. State-space model with non-integer order derivatives for lithium-ion battery. Appl. Energy 2016, 161, 330–336. [Google Scholar] [CrossRef]
- Liu, C.; Liu, W.; Wang, L.; Hu, G.; Ma, L.; Ren, B. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Cao, J. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model. J. Power Sources 2013, 233, 277–284. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, K.; Ravey, A.; Gao, F.; Miraoui, A. Parameter sensitivity analysis for fractional-order modeling of lithium-ion batteries. Energies 2016, 9, 123. [Google Scholar] [CrossRef]
- Oustaloup, A.; Sabatier, J.; Lanusse, P. From fractal robustness to the CRONE control. FCAA 2007, 2, 1–30. [Google Scholar]
- Mastali, M.; Samadani, E.; Farhad, S.; Fraser, R.; Fowler, M. Three-dimensional multi-particle electrochemical model of LiFePO4 Cells based on a resistor network methodology. Electrochim. Acta 2016, 190, 574–587. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.E.; Peng, H.; Liu, Z. Fractional-order modeling and parameter identification for lithium-ion batteries. J. Power Sources 2015, 293, 151–161. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Baronti, F.; Chow, M.Y. Online adaptive parameter identification and state-of-charge coestimation for lithium-polymer battery cells. IEEE Trans. Ind. Electron. 2014, 61, 2053–2061. [Google Scholar] [CrossRef]
- Li, X.; Song, K.; Wei, G.; Lu, R.; Zhu, C. A novel grouping method for lithium iron phosphate batteries based on a fractional joint Kalman filter and a new modified K-means clustering algorithm. Energies 2015, 8, 7703–7728. [Google Scholar] [CrossRef]
- Zhong, F.; Li, H.; Zhong, S.; Zhong, Q.; Yin, C. An SOC estimation approach based on adaptive sliding mode observer and fractional order equivalent circuit model for lithium-ion batteries. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 127–144. [Google Scholar] [CrossRef]
- Xiao, R.; Shen, J.; Li, X.; Yan, W.; Pan, E.; Chen, Z. Comparisons of modeling and state of charge estimation for lithium-ion battery based on fractional order and integral order methods. Energies 2016, 9, 184. [Google Scholar] [CrossRef]
- Riu, D.; Montaru, M.; Bultel, Y. Time domain simulation of Li-ion batteries using non-integer order equivalent electrical circuit. Nonlinear Sci. Numer. Simul. 2013, 18, 1454–1462. [Google Scholar] [CrossRef]
- Deng, Z.; Cao, H.; Li, X.; Jiang, J.; Yang, J.; Qin, Y. Generalized predictive control for fractional order dynamic model of solid oxide fuel cell output power. J. Power Sources 2010, 195, 8097–8103. [Google Scholar] [CrossRef]
- Sabatier, J.; Merveillaut, M.; Francisco, J.M.; Guillemard, F.; Porcelatto, D. Lithium-ion batteries modeling involving fractional differentiation. J. Power Sources 2014, 262, 36–43. [Google Scholar] [CrossRef]
- Unterrieder, C.; Zhang, C.; Lunglmayr, M.; Priewasser, R.; Marsili, S.; Huemer, M. Battery state-of-charge estimation using approximate least squares. J. Power Sources 2015, 278, 274–286. [Google Scholar] [CrossRef]
- Khadhraoui, A.; Jelassi, K.; Trigeassou, J.C.; Melchior, P. Identification of fractional model by least-squares method and instrumental variable. J. Comput. Nonlinear Dyn. 2015, 10, 050801. [Google Scholar] [CrossRef]
- Plubtieng, S.; Punpaeng, R. A new iterative method for equilibrium problems and fixed point problems of nonexpansive mappings and monotone mappings. Appl. Math. Comput. 2008, 197, 548–558. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]



| Battery | Nominal Capacity (Ah) | Nominal Voltage (V) | Max Voltage (V) | Continuous Discharge Rate |
|---|---|---|---|---|
| LiFePO | 10 | 3.2 | 3.65 | 5C |
| Q (SOC) | 1500 | 1400 | 1300 | 1200 | 1100 | 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (95%) | 0.520 | 0.499 | 0.477 | 0.453 | 0.427 | 0.399 | 0.368 | 0.333 | 0.294 | 0.249 | 0.196 | 0.131 | 0.048 |
| (90%) | 0.528 | 0.507 | 0.485 | 0.461 | 0.435 | 0.407 | 0.376 | 0.341 | 0.302 | 0.257 | 0.204 | 0.139 | 0.056 |
| (85%) | 0.542 | 0.521 | 0.499 | 0.475 | 0.449 | 0.421 | 0.389 | 0.354 | 0.315 | 0.270 | 0.217 | 0.152 | 0.069 |
| (80%) | 0.555 | 0.534 | 0.512 | 0.488 | 0.462 | 0.433 | 0.402 | 0.367 | 0.328 | 0.282 | 0.229 | 0.164 | 0.081 |
| (75%) | 0.569 | 0.548 | 0.526 | 0.502 | 0.476 | 0.447 | 0.416 | 0.381 | 0.342 | 0.296 | 0.243 | 0.178 | 0.095 |
| (70%) | 0.568 | 0.547 | 0.524 | 0.500 | 0.474 | 0.446 | 0.415 | 0.380 | 0.340 | 0.295 | 0.242 | 0.177 | 0.093 |
| (65%) | 0.573 | 0.553 | 0.530 | 0.506 | 0.480 | 0.452 | 0.420 | 0.385 | 0.346 | 0.301 | 0.247 | 0.182 | 0.099 |
| (60%) | 0.582 | 0.562 | 0.539 | 0.515 | 0.489 | 0.461 | 0.429 | 0.394 | 0.355 | 0.309 | 0.256 | 0.191 | 0.108 |
| (55%) | 0.595 | 0.574 | 0.552 | 0.528 | 0.502 | 0.473 | 0.442 | 0.407 | 0.367 | 0.322 | 0.268 | 0.203 | 0.120 |
| (50%) | 0.608 | 0.587 | 0.565 | 0.541 | 0.515 | 0.486 | 0.455 | 0.419 | 0.380 | 0.334 | 0.281 | 0.216 | 0.132 |
| (45%) | 0.622 | 0.600 | 0.578 | 0.554 | 0.528 | 0.499 | 0.468 | 0.432 | 0.393 | 0.347 | 0.293 | 0.228 | 0.144 |
| (40%) | 0.633 | 0.612 | 0.589 | 0.565 | 0.539 | 0.510 | 0.478 | 0.443 | 0.404 | 0.358 | 0.304 | 0.239 | 0.155 |
| (35%) | 0.639 | 0.618 | 0.596 | 0.572 | 0.545 | 0.517 | 0.485 | 0.450 | 0.410 | 0.364 | 0.311 | 0.245 | 0.161 |
| (30%) | 0.653 | 0.631 | 0.609 | 0.585 | 0.558 | 0.529 | 0.498 | 0.462 | 0.423 | 0.377 | 0.323 | 0.257 | 0.173 |
| (25%) | 0.689 | 0.667 | 0.645 | 0.620 | 0.594 | 0.565 | 0.533 | 0.498 | 0.458 | 0.412 | 0.358 | 0.292 | 0.208 |
| (20%) | 0.708 | 0.687 | 0.664 | 0.639 | 0.613 | 0.584 | 0.552 | 0.516 | 0.476 | 0.430 | 0.376 | 0.310 | 0.226 |
| (15%) | 0.732 | 0.711 | 0.688 | 0.664 | 0.637 | 0.608 | 0.576 | 0.540 | 0.500 | 0.454 | 0.400 | 0.334 | 0.249 |
| (10%) | 0.818 | 0.796 | 0.773 | 0.748 | 0.721 | 0.692 | 0.659 | 0.623 | 0.583 | 0.536 | 0.481 | 0.414 | 0.328 |
| (5%) | 0.961 | 0.939 | 0.916 | 0.890 | 0.863 | 0.832 | 0.799 | 0.762 | 0.721 | 0.673 | 0.617 | 0.549 | 0.462 |
| (SOC) | 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (95%) | 6764.89 | 4995.59 | 3701.96 | 2677.47 | 1943.05 | 1394.94 | 1004.62 | 724.90 | 523.43 | 379.37 | 277.40 |
| (90%) | 6612.03 | 4933.26 | 3561.10 | 2610.80 | 1883.99 | 1356.18 | 980.79 | 704.82 | 508.37 | 368.16 | 269.10 |
| (85%) | 6354.77 | 4666.28 | 3429.65 | 2476.08 | 1799.93 | 1301.13 | 936.63 | 674.77 | 486.86 | 352.75 | 258.05 |
| (80%) | 6110.80 | 4445.50 | 3282.41 | 2381.90 | 1723.12 | 1247.80 | 898.23 | 646.97 | 466.62 | 337.86 | 247.33 |
| (75%) | 5786.83 | 4289.07 | 3111.35 | 2272.46 | 1642.53 | 1186.48 | 854.41 | 616.02 | 444.06 | 321.68 | 235.17 |
| (70%) | 5805.85 | 4306.70 | 3124.99 | 2282.88 | 1645.93 | 1192.59 | 859.28 | 619.60 | 446.84 | 323.87 | 236.91 |
| (65%) | 5714.46 | 4226.74 | 3065.94 | 2239.94 | 1619.71 | 1170.04 | 842.43 | 607.98 | 438.43 | 317.73 | 232.45 |
| (60%) | 5566.95 | 4103.19 | 2975.21 | 2174.13 | 1571.84 | 1135.62 | 818.47 | 590.71 | 425.68 | 308.45 | 225.65 |
| (55%) | 5313.81 | 3932.67 | 2851.52 | 2084.47 | 1506.80 | 1090.73 | 785.65 | 565.63 | 408.37 | 295.77 | 216.37 |
| (50%) | 5127.95 | 3756.52 | 2731.28 | 1997.65 | 1444.12 | 1043.29 | 753.19 | 542.31 | 391.52 | 283.81 | 207.71 |
| (45%) | 4912.03 | 3603.20 | 2613.90 | 1912.71 | 1382.93 | 999.23 | 721.40 | 519.78 | 375.20 | 271.97 | 199.07 |
| (40%) | 4705.02 | 3482.07 | 2522.65 | 1843.67 | 1333.26 | 963.50 | 695.19 | 501.40 | 361.84 | 262.31 | 192.05 |
| (35%) | 4647.45 | 3396.71 | 2475.85 | 1803.53 | 1301.79 | 942.60 | 680.14 | 490.39 | 353.92 | 256.53 | 187.80 |
| (30%) | 4445.22 | 3251.03 | 2373.97 | 1728.31 | 1248.71 | 904.82 | 652.48 | 470.69 | 339.78 | 246.39 | 180.44 |
| (25%) | 3953.72 | 2894.10 | 2110.81 | 1534.47 | 1112.68 | 804.93 | 580.71 | 418.83 | 302.44 | 219.34 | 160.65 |
| (20%) | 3712.56 | 2720.42 | 1982.60 | 1443.31 | 1045.15 | 755.65 | 545.35 | 393.28 | 283.97 | 205.92 | 150.82 |
| (15%) | 3421.80 | 2509.61 | 1831.04 | 1331.00 | 965.15 | 697.89 | 503.46 | 363.02 | 262.12 | 190.08 | 139.21 |
| (10%) | 2607.84 | 1910.16 | 1395.86 | 1016.16 | 737.65 | 533.88 | 385.96 | 278.84 | 201.70 | 146.56 | 107.57 |
| (5%) | 1662.63 | 1219.92 | 892.37 | 650.39 | 472.720 | 342.75 | 248.09 | 179.50 | 130.06 | 94.68 | 69.63 |
| OCV-SOC Method (%) | Iterative Method (%) | |||||
|---|---|---|---|---|---|---|
| First Iteration | Second Iteration | Third Iteration | Fourth Iteration | Fifth Iteration | Sixth Iteration | |
| 92.00 | 94.08 | 90.44 | 93.36 | 93.38 | 93.38 | 93.38 |
| 73.00 | 71.17 | 71.24 | 74.54 | 74.31 | 74.34 | 74.31 |
| 54.00 | 52.21 | 55.35 | 52.70 | 54.72 | 54.70 | 54.70 |
| 37.00 | 36.22 | 37.66 | 37.59 | 36.52 | 36.51 | 36.51 |
| 18.00 | 17.51 | 17.69 | 17.73 | 18.25 | 18.25 | 18.25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Li, H.; Xu, J.; Chen, S.; Chen, N. Rapid Estimation Method for State of Charge of Lithium-Ion Battery Based on Fractional Continual Variable Order Model. Energies 2018, 11, 714. https://doi.org/10.3390/en11040714
Lu X, Li H, Xu J, Chen S, Chen N. Rapid Estimation Method for State of Charge of Lithium-Ion Battery Based on Fractional Continual Variable Order Model. Energies. 2018; 11(4):714. https://doi.org/10.3390/en11040714
Chicago/Turabian StyleLu, Xin, Hui Li, Jun Xu, Siyuan Chen, and Ning Chen. 2018. "Rapid Estimation Method for State of Charge of Lithium-Ion Battery Based on Fractional Continual Variable Order Model" Energies 11, no. 4: 714. https://doi.org/10.3390/en11040714
APA StyleLu, X., Li, H., Xu, J., Chen, S., & Chen, N. (2018). Rapid Estimation Method for State of Charge of Lithium-Ion Battery Based on Fractional Continual Variable Order Model. Energies, 11(4), 714. https://doi.org/10.3390/en11040714