Simulating Engineering Flows through Complex Porous Media via the Lattice Boltzmann Method

Abstract

In this paper, recent achievements in the application of the lattice Boltzmann method (LBM) to complex fluid flows are reported. More specifically, we focus on flows through reactive porous media, such as the flow through the substrate of a selective catalytic reactor (SCR) for the reduction of gaseous pollutants in the automotive field; pulsed-flow analysis through heterogeneous catalyst architectures; and transport and electro-chemical phenomena in microbial fuel cells (MFC) for novel waste-to-energy applications. To the authors’ knowledge, this is the first known application of LBM modeling to the study of MFCs, which represents by itself a highly innovative and challenging research area. The results discussed here essentially confirm the capabilities of the LBM approach as a flexible and accurate computational tool for the simulation of complex multi-physics phenomena of scientific and technological interest, across physical scales.

1. Introduction

The lattice Boltzmann method (LBM) is a computational framework for the study of fluid mechanics founded on Boltzmann’s kinetic equation: from the evolution of the dynamics of (groups of) molecules, the macroscopic quantities (density, velocity and temperature) fields are retrieved [1]. Due to its discrete nature, LBM allows for investigating complex flows at a mesoscopic level, compared to continuum-based approaches, which are a direct emanation of the Navier-Stokes equations for fluid flows. Together with its intrinsic computational efficiency, this is the main reason why LBM has marked an impressive growth in the last three decades from a niche methodology into a robust and reliable computational tool for a constantly increasing number of technical applications [2,3,4,5,6,7,8].

A special class of engineering problems is represented by flows through porous media, which are often encountered in heat transfer devices [9,10,11,12] as well as chemical reactors [13,14] and different types of fuel cell technologies [15,16]. The detailed modeling of transport phenomena in porous media might be a very demanding task, due to the coexistence of a broad range of physical (sometimes from macro- to nano-) scales across the same global domain [17,18,19]. For that reason, continuum-based Computational Fluid Dynamics (CFD) approaches usually employ simplified models where the actual porous structure is replaced by its general macroscopic properties, such as the volume-averaged permeability, porosity, surface-to-volume ratio, etc. [19]. At the same time, the detailed flow description at a pore-scale level is usually limited to very small domain portions [12], due to the difficulties in reaching a sufficient numerical accuracy at reasonable computational costs.

Generally speaking, LBM is particularly well suited for flow through irregular (porous) media, essentially due to its dual particle-field nature [1] and to additional features such as: (i) the previously mentioned excellent computational performance; and (ii) ease in implementing (complex) porous media geometries. In recent years, a significant number of advanced LBM applications to porous media have emerged in the scientific literature, including: coupled LBM-finite volume methods for fluid-solid heat transfer [20,21,22] and dissolution [23] modeling; simulation of surface catalysis in fractal porous media [24,25]; simulation of gas diffusion layers in fuel cells at a pore level [26]; and heterogenous catalysis modeling in nanoporous structures [27,28,29,30,31]. All such studies essentially confirmed the reliability and versatility of LBM-based methods to deal with complex, multi-scale flows through porous media, thus justifying further research and development in that area.

In the present work, we show some recent implementations of our purposely developed LBM solver, which is based on a simple multi-component formulation and includes a special procedure for the detailed porous media reconstruction, as well as a novel reactive boundary condition to account for surface chemistry at the pore-scale level. The test cases consist of a single-channel Selective Catalytic Reactor (SCR), a nanoporous pulsed-flow reactor and a highly innovative Microbial Fuel Cell (MFC) reactor. The rest of the paper is organized as follows: first, the numerical methodology is described in Section 2; results from the selected test cases are presented and commented on in Section 3, while concluding remarks and suggestions for future developments are given in Section 4.

2. Methodology

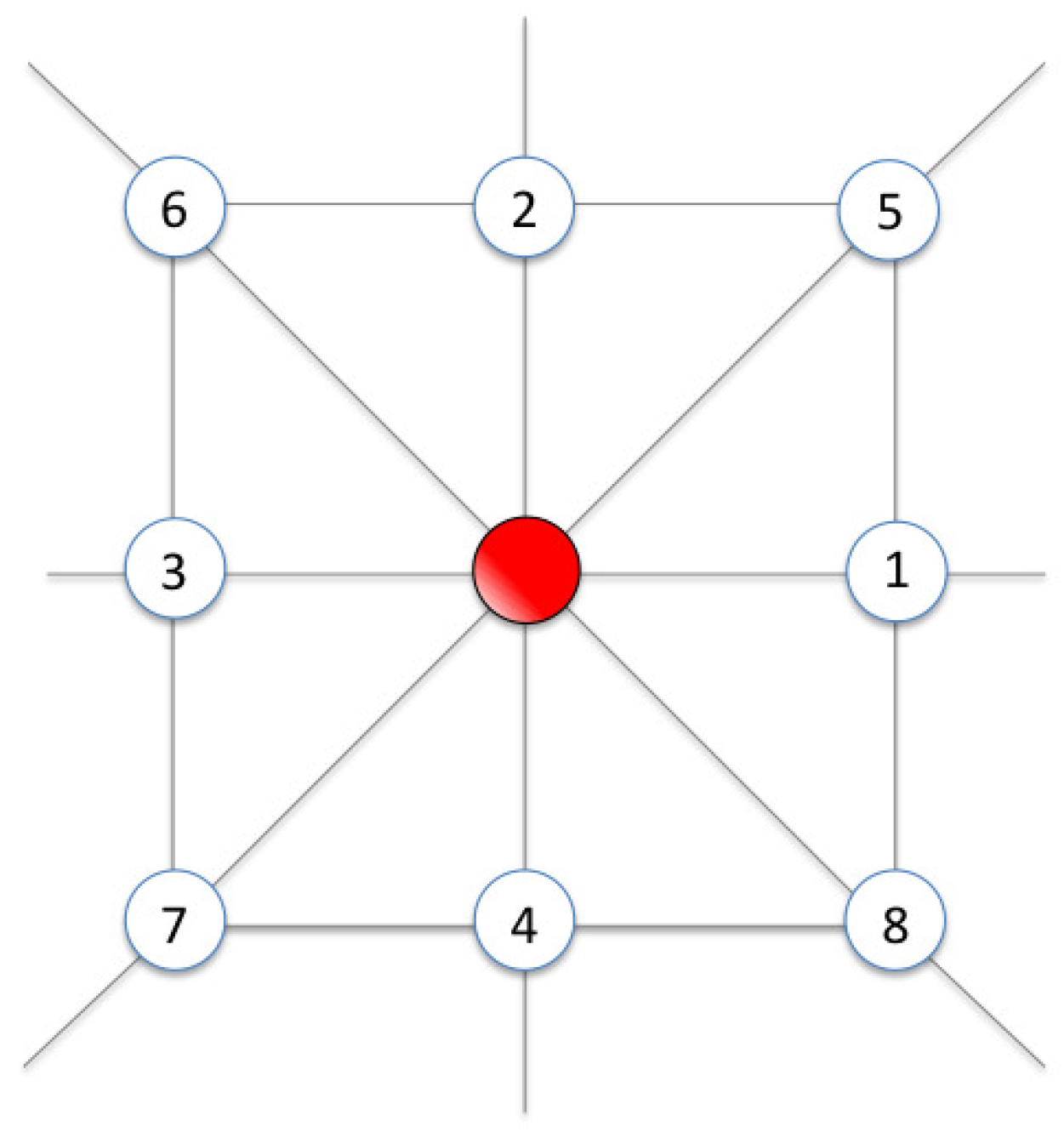
2.1. The Lattice Boltzmann Method

The LBM foundation consists of the so-called generalized Boltzmann Transport Equation (BTE), which for a particle system in the presence of external or internal forces $\mathbf{F}$ yields:

$$\frac{\partial f(\mathbf{x},\mathbf{v},t)}{\partial t}+\mathbf{v}(\mathbf{x},t)·{\nabla }_{\mathbf{x}}f(\mathbf{x},\mathbf{v},t)+\mathbf{a}(\mathbf{x},t)·{\nabla }_{\mathbf{v}}f(\mathbf{x},\mathbf{v},t)=\mathsf{\Omega }+\mathbf{F}(\mathbf{x},t)·\mathbf{v}(\mathbf{x},t),$$

(1)

where $f(\mathbf{x},\mathbf{v},t)$ is the probability density function (PDF) of finding a (group of) molecules at site $\mathbf{x}$, at time t, moving with molecular velocity $\mathbf{v}(\mathbf{x},t)$. The term $\mathsf{\Omega }$ on the right-hand side (RHS)represents the collision operator, a function of $f(\mathbf{x},\mathbf{v},t)$ itself, which makes Equation (1) extremely complex to solve. Compared to Equation (1), two fundamental simplifications lie at the basis of the success of LBM:

• the adoption of a simplified formulation of the collision operator, that is the so-called Bhatnagar-Gross-Krook (BGK) approximation [32]: $\mathsf{\Omega }=\omega =\frac{1}{\tau }$, with $\tau$ the relaxation time towards local equilibrium;
• the (groups of) molecules are forced to move along pre-determined and fixed i directions [33].

The product of such assumptions is the standard lattice Boltzmann Equation (LBE), which can be written as follows:

$$f_i(\mathbf{x}+{\mathbf{c}}_i\Delta t,t+\Delta t)-f_i(\mathbf{x},t)=-\omega \Delta t(f_i(\mathbf{x},t)-f_i^{eq}(\mathbf{x},t)),$$

(2)

where ${\mathbf{c}}_i$ represents the ith discrete velocity of the lattice.

The left-hand side (LHS) of Equation (2) represents the free-streaming part, and the RHS represents the collisional relaxation towards a local thermodynamic equilibrium state, which happens on a time-scale $\tau =1/\omega$. The equilibrium distribution function $f_i^{eq}$ is commonly expressed as a low-Mach, second-order expansion of a local Maxwellian [1], namely:

$$f_i^{eq}=w_i\rho \left(1+\frac{1}{c_s^2}{\mathbf{c}}_{\mathbf{i}}·\mathbf{u}+\frac{1}{2c_s^4}{({\mathbf{c}}_{\mathbf{i}}·\mathbf{u})}^2-\frac{1}{2c_s^2}{\left|\right|\mathbf{u}\left|\right|}^2\right).$$

(3)

In order to guarantee the isotropy of the method, the weights $w_i$ should obey isotropy constraints [33]: ${\sum }_i{w}_i=1$, ${\sum }_i{w}_i{\mathbf{c}}_i=\mathbf{0}$ and ${\sum }_i{w}_i{\mathbf{c}}_i{\mathbf{c}}_i=c_s^2\mathbf{1}$, which ensure that the species density and velocity encoded by the distributions $f_i$ and $f_i^{eq}$ coincide. The kinetic connectivity of the lattice node, with respect to its neighbors, is then fully described by the set of $b+1$ discrete velocities, with b representing the neighbors number. For $b=8$, the standard D2Q9 scheme is recovered [33], as shown in Figure 1.

Since the pioneering work of Gustensen et al. [34], a lot of effort has been spent in the LBM modeling community in order to extend Equation (2) for the simulation of multi-component flows, including single-phase and multi-phase immiscible fluid systems as well as gas mixtures with various levels of complexity [5,6,35,36]. A recent development line is represented by the series of papers from Arcidiacono et al. [37,38], where the concept of fast-slow decomposition of motions near quasi- equilibrium states [39] was applied in order to obtain a thermodynamically consistent LBM model for multi-component mixtures. The same approach was later on extended for the simulation of surface catalytic reactions [40], accounting also for thermal gradient effects [41].

The numerical results presented in this work are based on the LBM approach proposed by Asinari [42,43] for mixture modeling. For the sake of clarity, we briefly report the equations related to the case of binary mixtures, which can be easily modified to incorporate an arbitrary number of species. Considering two species $\alpha$ and $\varsigma$ and neglecting the presence of external forces $\mathbf{F}$, we can recast Equation (1) as follows, [43]:

$$\frac{\partial f^{\alpha }}{\partial t}+\mathbf{v}·\nabla f^{\alpha }={\mathsf{\Omega }}^{\alpha \alpha }+{\mathsf{\Omega }}^{\alpha \varsigma },$$

(4)

where ${\mathsf{\Omega }}^{\alpha \varsigma }={\mathsf{\Omega }}^{\varsigma \alpha }$, with $\alpha \ne \varsigma$, is the cross-collision term for the two species. In the spirit of the BGK approximation, the collision operators at the RHS of Equation (4) can be expressed as:

$${\mathsf{\Omega }}^{\alpha \alpha }=\frac{1}{{\tau }_{\alpha }}(f^{\alpha }-f^{eq,\alpha })\mathrm{and}{\mathsf{\Omega }}^{\alpha \varsigma }=\frac{1}{{\tau }_{\alpha \varsigma }}(f^{\alpha }-f^{eq,\alpha \varsigma }),$$

(5)

with ${\tau }_{\alpha }$ and ${\tau }_{\alpha \varsigma }$ being the two (adjustable) relaxation parameters and the equilibrium distribution functions provided by the following Maxwellians:

$$\begin{array}{ccc}\hfill f^{eq,\alpha }({\rho }_{\alpha },{\mathbf{u}}_{\alpha },T_{\alpha })& =& \frac{{\rho }_{\alpha }}{{\left(2\pi R_{\alpha }{T}_{\alpha }\right)}^{\mathcal{D}/2}}{e}^{-{(\mathbf{v}-{\mathbf{u}}_{\alpha })}^2/\left(2R_{\alpha }{T}_{\alpha }\right)},\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill f^{eq,\alpha \varsigma }({\rho }_{\alpha },{\mathbf{u}}_{\alpha \varsigma },T_{\alpha \varsigma })& =& \frac{{\rho }_{\alpha }}{{\left(2\pi R\alpha T_{\alpha \varsigma }\right)}^{\mathcal{D}/2}}{e}^{-{(\mathbf{v}-{\mathbf{u}}_{\alpha \varsigma })}^2/\left(2R_{\alpha }{T}_{\alpha \varsigma }\right)},\hfill \end{array}$$

(7)

where $\mathcal{D}$ is the space dimension, while $R_{\alpha }$ and $T_{\alpha }$ are the gas constant and the absolute temperature for species $\alpha$, respectively. The BGK collision operators can be then combined as follows:

$${\mathsf{\Omega }}_{\alpha }=-\left(\frac{1}{{\tau }_{\alpha }}+\frac{1}{{\tau }_{\alpha \varsigma }}\right)[f^{\alpha }-f^{eq,\alpha }]-\frac{1}{{\tau }_{\alpha \varsigma }}[f^{eq,\alpha }-f^{eq,\alpha \varsigma }].$$

(8)

By assuming the mixture as isothermal ($T_{\alpha }=T_{\alpha \varsigma }=T$) and discretizing in the velocity space, Equation (4) can be rearranged as, [42,43]:

$$f^{\alpha }(\mathbf{x}+{\mathbf{c}}_i,t+1)-f^{\alpha }(\mathbf{x},t)=\left(\frac{1}{{\tau }_{\alpha }}+\frac{1}{{\tau }_{\alpha \varsigma }}\right)(f_i^{e{q}^{*},\alpha }-f^{\alpha }),$$

(9)

in which the modified equilibirum PDF $f_i^{e{q}^{*},\alpha }$ is given by, [42]

$$f_i^{e{q}^{*},\alpha }=(1-{\sigma }_0)f_i^{eq,\alpha }({\rho }_{\alpha },{\mathbf{u}}_{\alpha },t)+{\sigma }_0{f}_i^{eq,\alpha }({\rho }_{\alpha },\mathbf{u},t),$$

(10)

with ${\sigma }_0={\tau }_{\alpha }/\left({\tau }_{\alpha }{\tau }_{\alpha \varsigma }\right)$ , and

$$f_i^{eq,\alpha }({\rho }_{\alpha },\mathbf{u},t)=w_i\left\{{\rho }_{\alpha }+\frac{{\mathbf{c}}_i·\mathbf{u}}{R_{\alpha }T}+\frac{1}{2}\left[\frac{{({\mathbf{c}}_i·\mathbf{u})}^2}{{\left(R_{\alpha }T\right)}^2}-\frac{\mathbf{u}·\mathbf{u}}{R_{\alpha }T}\right]\right\}.$$

(11)

Since in Equation (11) we consider the barycentric velocity $\mathbf{u}$, the corresponding equilibrium PDF accounts for both self and mutual collision terms; moreover, the formulation in Equation (11) is completely general and accounts for the possible differences in the speed of sounds of the different species under investigation. For the sake of simplicity, for the LBM engineering applications considered in the present work, without lack of generality, we have assumed ${\tau }_{\alpha }$ and $R_{\alpha }$ equal and constant for all the species: the values of $\tau$ are computed according to the chosen Knudsen number, while a single value for the species speed of sound is considered in the following.

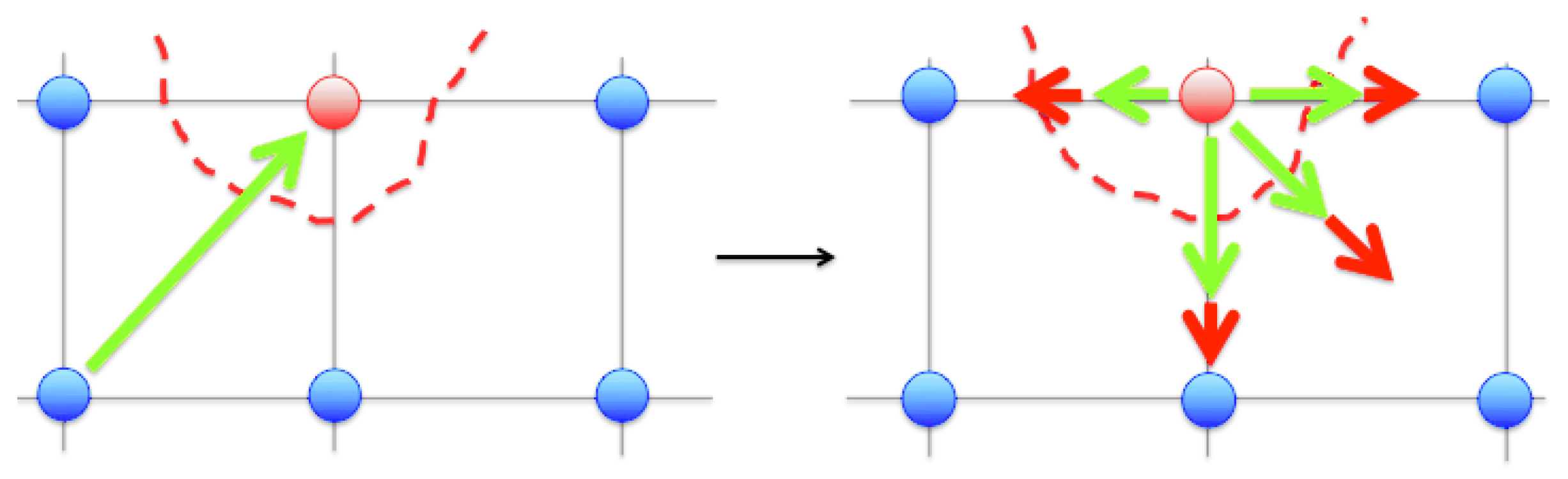
2.2. Reactive Boundary Condition

In the LBM framework, accounting for chemical reactivity comes as a natural adaptation of the basic scheme. In more detail, surface chemistry has been often accounted for through specifically developed boundary conditions [40,41,44], reaching a remarkable accuracy level with relatively straightforward modifications to the baseline methodology.

In the present work, we account for heterogeneous catalysis starting from the generic first-order reaction mechanism expressed by:

$$R\to P,$$

(12)

where R is the reactant species (usually transported by a carrier C) and P is the reaction product. The interaction of R with the surface catalyst is assumed to be an inter-conversion into the product P upon contact with the solid walls, happening at a characteristic time scale that can be considered much smaller (i.e., instantaneous) as compared to the fluid-dynamic time scales represented by the lattice collision step (see, e.g., [44]).

To include the above-mentioned mechanism in our LBM solver, a “sputtering” boundary condition was developed in [29,45]. Each solid node that is adjacent to fluid nodes acts as a catalytic site, as shown in Figure 2. Note that the boundary condition is designed to preserve locally the $R+P$ mass and the modulus of barycentric momentum.

The new populations that emerge from each discrete catalytic site are randomly oriented, thus mimicking the effect of the local wall orientation on the flow dynamics. The model behaves such that, upon colliding with a solid site, the reactant R partially transforms into the product P with a given probability p, which is directly connected to the specific chemical kinetics.

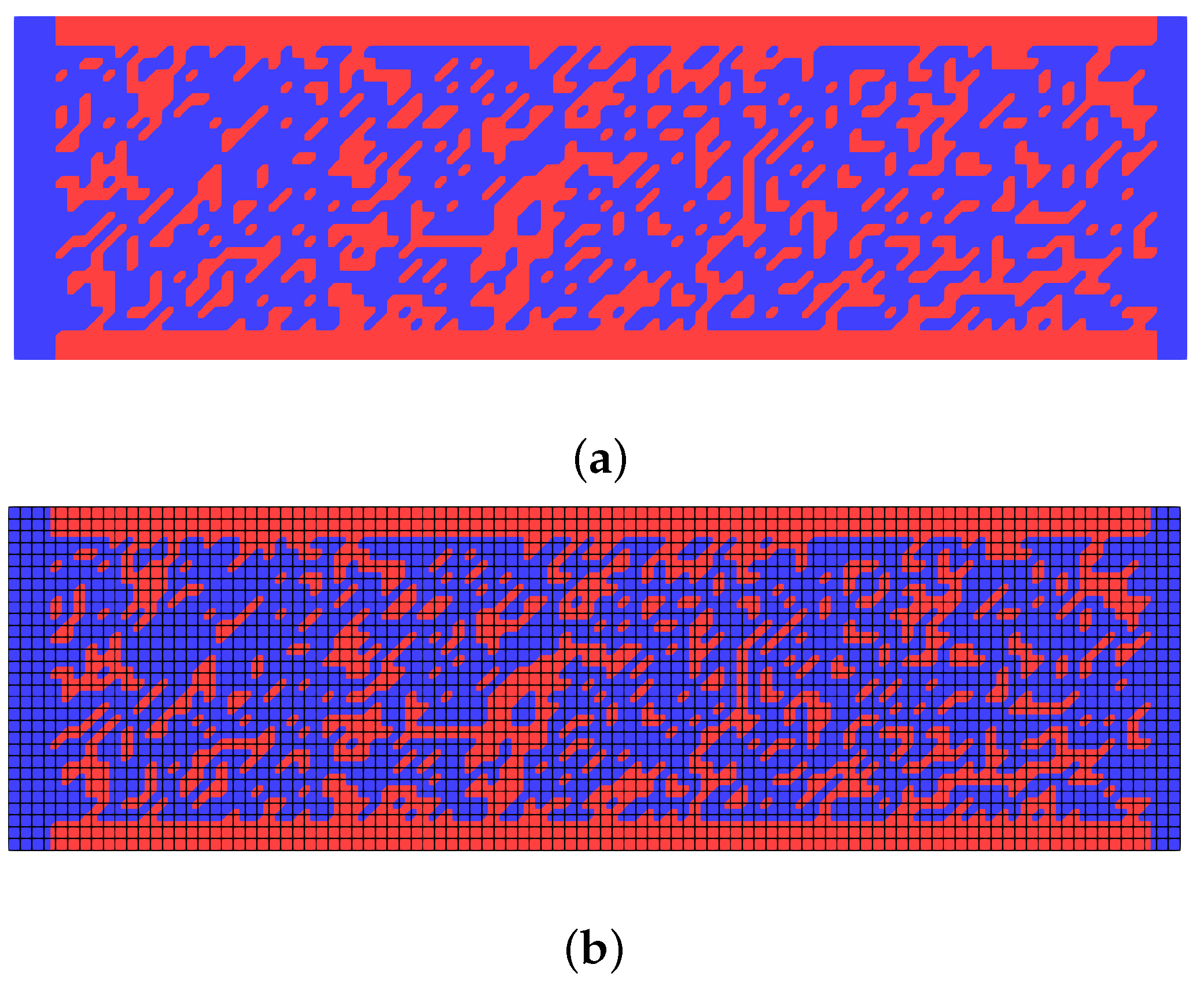
2.3. Porous Domain Reconstruction

The catalytic porous material is reconstructed by adopting a simple and effective procedure. At the beginning of each simulation, the volume occupied by the porous medium is entirely filled with solid nodes (solid is colored in red in Figure 3). Subsequently, a number of sphere seeds is randomly inserted in the solid region and the radii of these spheres are randomly grown between a minimum and a maximum threshold value. The lattice nodes inside the randomly generated spheres are set as fluid (blue in Figure 3): fixing the number of spheres and their maximum radius, it is possible to retrieve the desired structural porosity, defined as $\epsilon =V_f/V_{tot}$, with $V_f$ the empty (fluid) volume and $V_{tot}$ the total occupied volume.

3. Results and Discussion

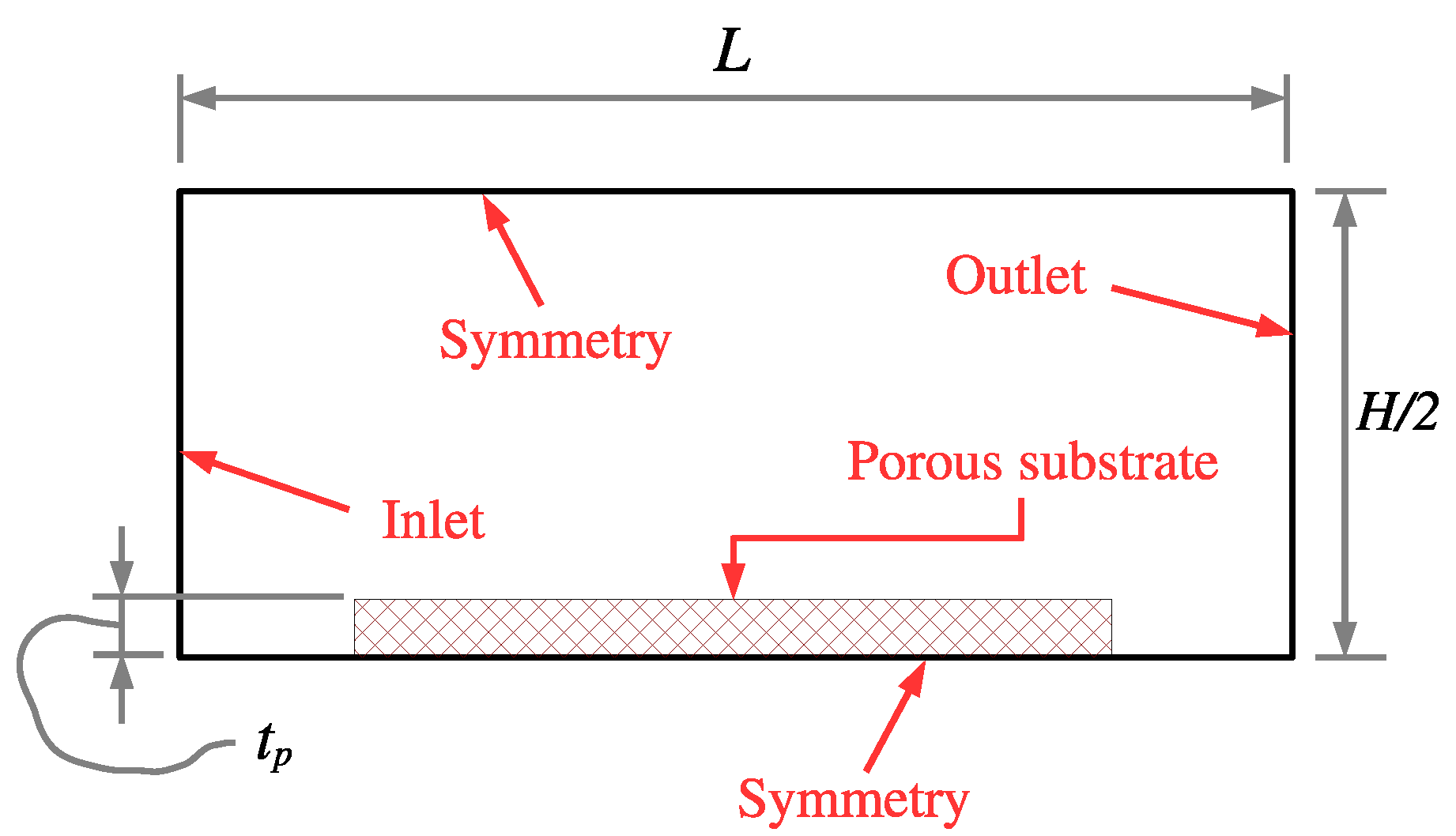
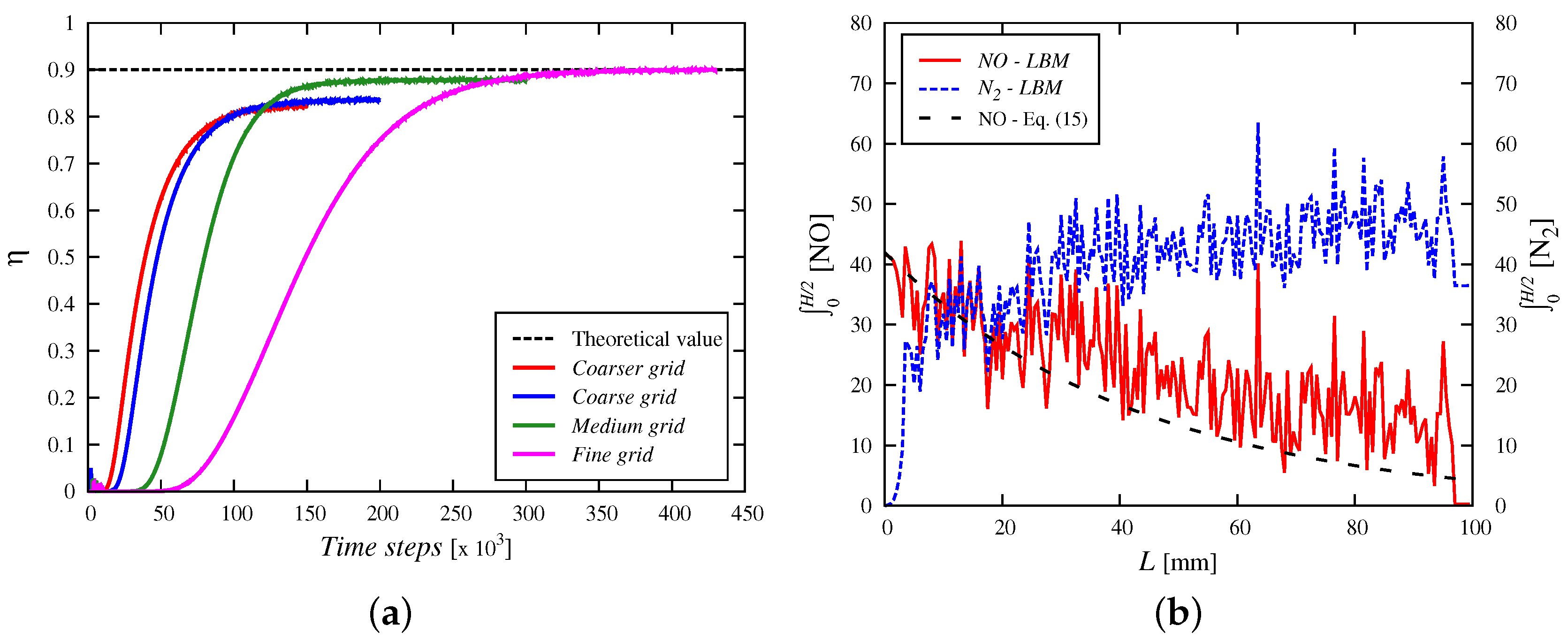
3.1. Selective Catalytic Reduction of NO${}_x$ Emissions

The first application we present is the simulation of a simplified, square-shaped channel of an SCR catalytic device for automotive exhaust gases aftertreatment. The computational domain, which includes the catalytic porous substrate, is sketched in Figure 4, along with the adopted boundary conditions. To account for the NO${}_x$ conversion in the substrate, it has been assumed that the standard NO reduction mechanism dominates among the others, which is usually the case when the NO${}_2$ amount in the total NO${}_x$ emissions is small compared to the NO fraction (see e.g., [46]).

Additionally, the ammonia storage-release and coverage effects have been neglected. This yields the following single-reaction mechanism:

$$4{\mathrm{NH}}_3+4\mathrm{NO}+{\mathrm{O}}_2\to 4{\mathrm{N}}_2+6{\mathrm{H}}_2\mathrm{O},$$

(13)

which fits perfectly in the generic form (12) and be described by a classic Arrhenius-type relation, such as:

$$k=A{e}^{-\frac{E_a}{\mathcal{R}T}},$$

(14)

with A the Arrhenius pre-exponential factor, $E_a$ the activation energy, $\mathcal{R}$ the universal gas constant and T the absolute temperature. In the case of Equation (13), such parameters can be set to A = 8.35 × 10${}^7$ m${}^3$/kg·s, $E_a$ = 8.5 × 10${}^4$ J/mol, $\mathcal{R}$ = 8.314 J/mol·K and T = 623 K, which are likely to provide a NO conversion efficiency typical of production SCR catalytic supports [47]. With the above values, we find k = 6.233 m${}^3$/kg·s.

Once the kinetic parameters are set, with the plug-flow reactor assumption, the evolution of NO concentration can be modeled according to the following expression:

$$C=C_0{e}^{-k^{*}\theta },$$

(15)

where $C_0$ and C are the NO concentration inside the exhaust gases at the inlet and outlet section of the SCR reactor, respectively, $k^{*}$ is the value of k rescaled by the SCR bulk density and $\theta$ is the reactor residence time. For the purposes of the present work, we assume a target conversion efficiency of ∼90%, which means $C/C_0\sim 0.10$. Since the conversion parameter p represents the amount of product species released from the reactor active sites, we fix a $90\%$ reaction rate by posing $p=0.9$. Concerning the substrate structural characteristics, the $\epsilon$ parameter is set to ∼0.7, which is a common value for automotive catalytic supports [13]. Given the substrate geometry, this yields an average pore diameter of $D_p\sim 100\mathsf{\mu }$m. According to these values, an estimate of the substrate permeability can be made through the Carman-Kozeny theoretical relationship [19]:

$$k=\frac{{\epsilon }^3}{\mathcal{K}(1-\epsilon )}{D}_p^2,$$

(16)

where $\mathcal{K}$ is an empirical constant of the order of ${10}^2$. For $\mathcal{K}=150$ [48], Equation (16) delivers a value of $k\sim 7.5\times {10}^{-11}$ m${}^2$, which is in fair agreement with the permeability of the catalytic substrates used in automotive applications [13,48].

Table 1. Main simulation parameters for the SCR channel case.

Parameter	Value
Channel length L (mm)	100
Half-channel height $H/2$ (mm)	6
Substrate thickness $t_p$ (mm)	$1.5$
Chemical species	3
Gas mixture viscosity (m${}^2$/s)	$5.5\times {10}^{-5}$
$\epsilon$ (%)	∼70
$\mathrm{Re}$	∼100
Reaction parameter p	$0.9$
Exhaust gas reference temperature (K)	623

resumes the main parameters adopted for the LBM simulations.

Four preliminary simulations were performed with different grid densities, in order to ensure the grid independence of the numerical results. Increasing the mesh resolution, we have considered computational grids featuring $1000\times 68$ nodes, $1500\times 100$ nodes, $3000\times 200$ and $4000\times 264$ nodes, respectively. We define the conversion efficiency parameter $\eta$ as:

$$\eta =\frac{{\left[{\mathrm{N}}_2\right]}_{outlet}}{{\left[\mathrm{NO}\right]}_{inlet}},$$

(17)

where [NO] is the total concentration of NO at inlet (reactant) and [N${}_2]$ the concentration of N${}_2$ at the outlet (product). We have assumed that the simulations have converged when the conversion efficiency parameter $\eta$ reaches a steady-state value.

Figure 5a shows the trends of the predicted conversion efficiency vs. the time step advancement, compared to the theoretical value computed through Equations (13)–(15). The trends confirm that the third (medium) grid is sufficient to obtain accurate and convergent results after about 200,000 time steps. Note that in this case the physical time step is equal to ∼5 $\times {10}^{-5}$ s.

In Figure 5b, the integral of species concentration (The N${}_2$ concentration should be regarded as a relative increase with respect to the N${}_2$ content at the inlet.) across the channel height is reported, along the reactor axis and together with the equivalent NO content profile returned by the plug-flow reactor assumption. The profiles are consistent with the theoretical expectations, with a progressive decrease of the NO content and a simultaneous increase of N${}_2$. The somewhat “noisy” plots are due to the randomly distributed porous structure, which affects the integral output at each axial coordinate value differently. Note that, once $\epsilon$ and the max/min pore diameter are fixed, changing the initial random distribution of the pore reconstruction spheres is not expected to significantly affect the average species trends along the reactor.

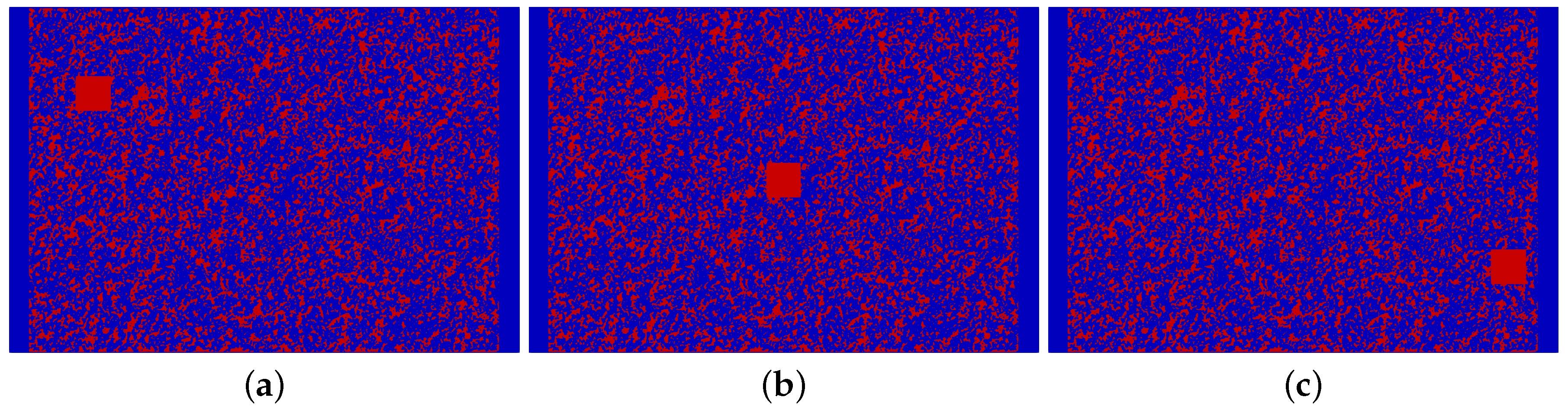
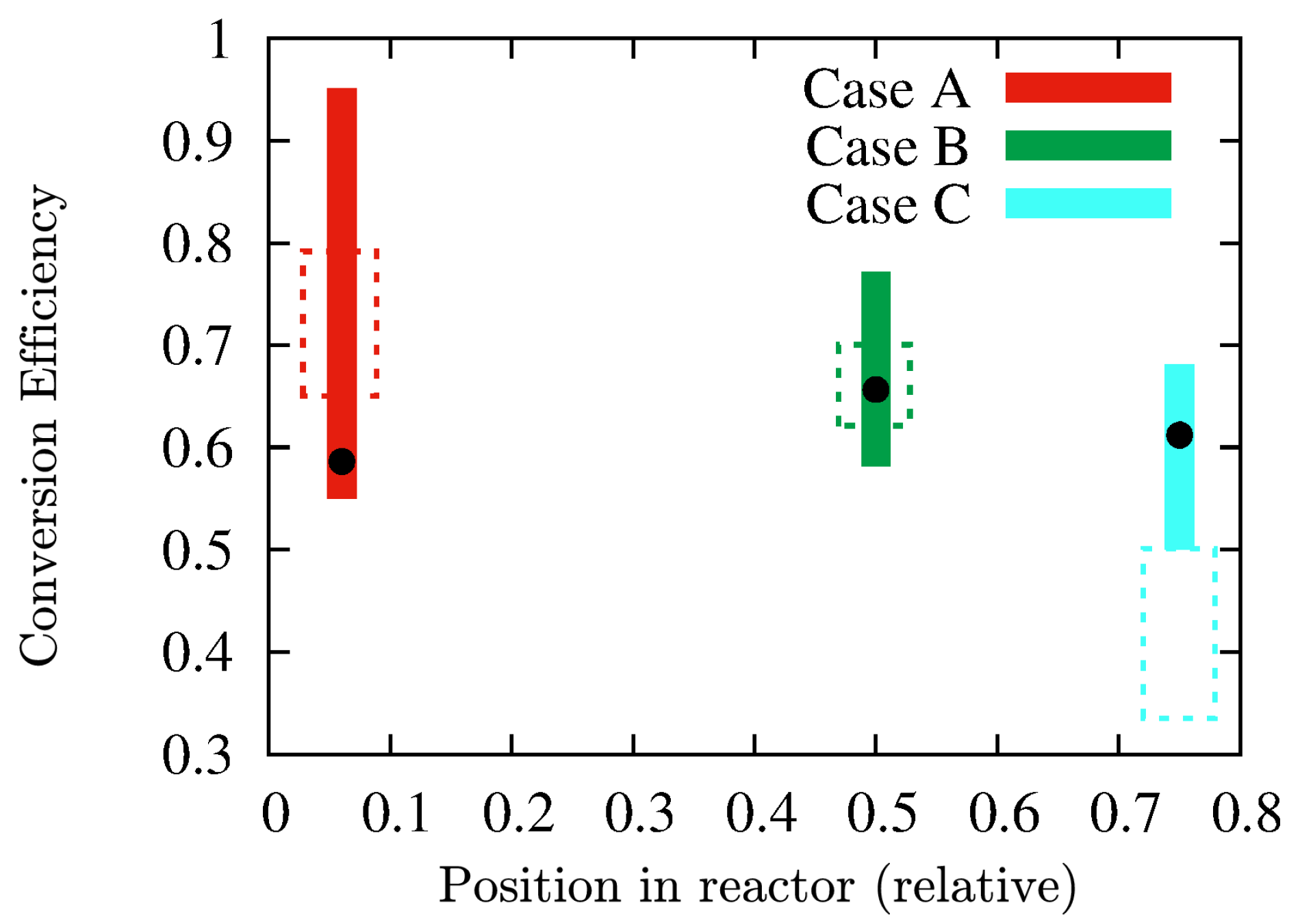
3.2. Heterogeneous Catalysis in Pulsed-Flow Reactors

Unsteady kinetic characterization of catalytic devices is often made through pulse-response methods such as Temporal Analysis of Products (TAP) methods [49,50,51,52] and Unsteady-State Processes in Catalysis (USPC) [53]. These techniques typically apply to high-vacuum conditions, where the molecular mean free path is significant compared to the characteristic size of the device. Instead, the exploration of the non-high-vacuum regime is still an open question, thus leading to a great interest in the development of effective numerical methods to investigate such type of reactive flows.

Although essentially new for these kinds of applications, LBM could represent a game changer in the rarefied gas modeling field due to its intrinsic computational efficiency compared, for instance, to methods such as Direct Simulation Monte Carlo [54]. The mesoscopic nature of LBM should allow, in principle, to properly capture flow dynamics and reaction kinetics for pulsed-flow systems, at least up to the moderate Knudsen number limit ($0.1<Kn<1$).

Here, we present a computational analysis based on the experimental and theoretical work of [51], where TAP-like catalytic conversion was studied by means of an ad hoc developed probabilistic theory, according to three different reactor geometries (Figure 6). The flow considered in the reference experimental measurements is characterized by pure Knudsen-diffusion (i.e., $Kn>1$), with a single reactive species traveling through the test field. The LBM simulations reproduce a more general pulsed-flow regime, with a characteristic Knudsen number $Kn\sim 0.65$. The catalyst consists of a single, square-shaped platinum foil, surrounded by a chemically inert porous media with an average porosity of $\epsilon \sim 70\%$.

As for the SCR case, an initial grid-independence study was performed, founding a resolution of $496\times 336$ (about 10 lattice nodes per pore diameter) as the minimal required for grid independent results. The carrier and reactant species were injected during the first 6000 time steps only, mimicking a single-pulse flow configuration. Subsequently, the injection was switched off, letting the species diffuse across the domain for the remaining part of the simulation. Each run lasted for about ${10}^7$ time steps, considering that the numerical time step corresponds to ∼${10}^{-7}$ s. The catalyst was placed at three different relative locations (see Figure 6) and the conversion parameter $\eta$ was determined as:

$$\eta =\frac{M_{tot,P}}{M_{tot,R}},$$

(18)

where $M_{tot,P}$ and $M_{tot,R}$ represent the total masses of products and reactants, respectively.

As shown in Figure 7, an acceptable agreement is achieved by the LBM simulations compared with the reference experimental and theoretical results. It should be remarked again that the experimental and theoretical results from [51] were obtained in the pure Knudsen-diffusion regime. Additionally, an average over the first ten reactant pulses was considered, in the experiments. In our case, single-pulse simulations were performed and the flow was only marginally in the Knudsen-diffusion regime. Interestingly, both LBM and the theoretical model of [51] deviates from the experimental measurements in Case C: this was found to be related to the deterioration of $\eta$ in the actual experimental conditions, due to the proximity of the catalytic particle to the reactor outlet.

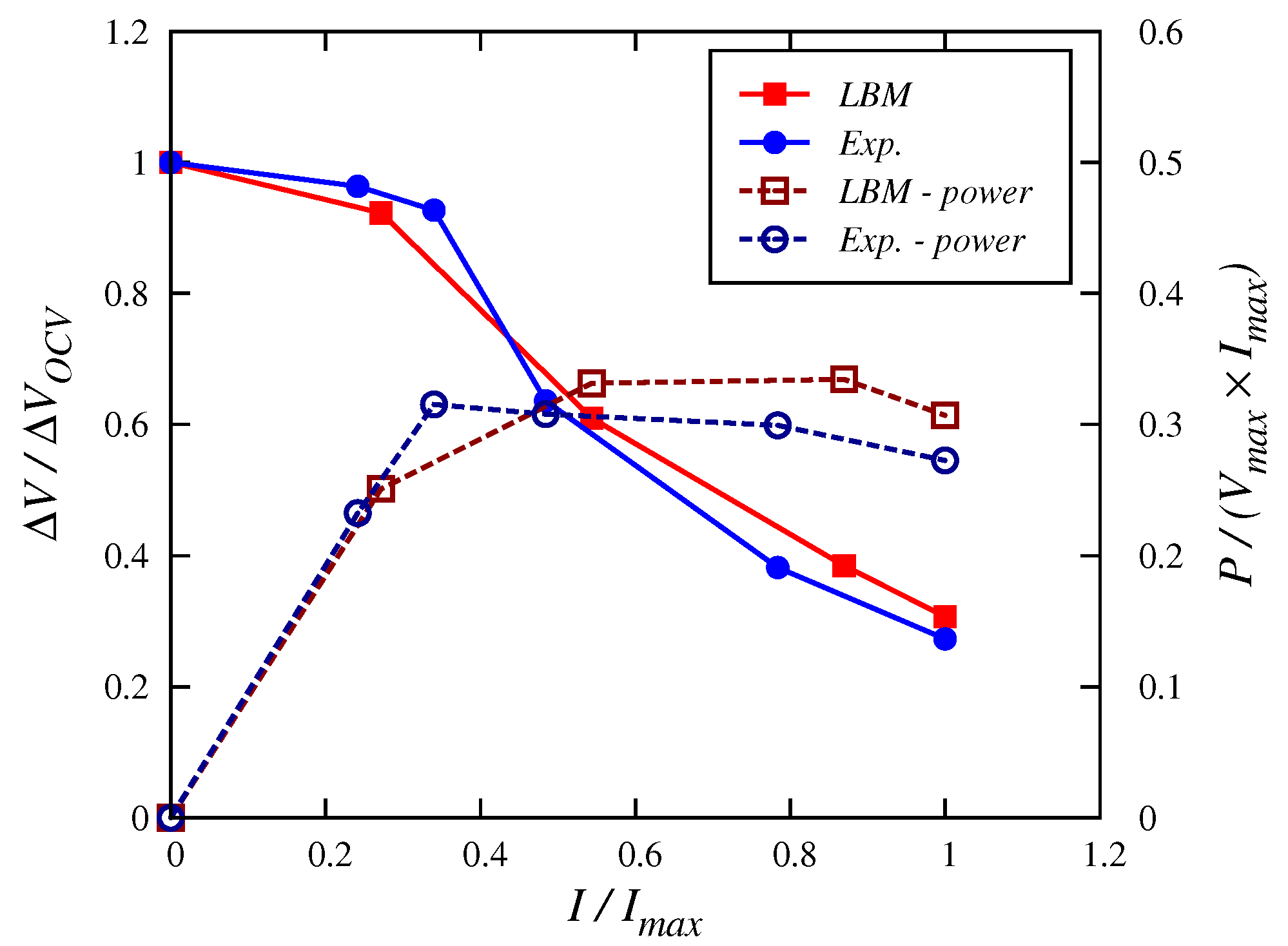
3.3. Microbial Fuel Cells Characterization

In recent years, Microbial Fuel Cells (MFCs) have been the object of considerable research efforts all over the world, due to their interesting potential as direct waste-to-energy converters [16,55,56,57]. Compared to the experimental activity on traditional Fuel Cells (FC), dealing with MFCs entails the management of a wider set of parameters, related to the electro- and bio-chemical processes that take place inside these reactors. In such a complex scenario, the availability of flexible and effective computational tools could be of great help to experiments, in order to accelerate the deployment of MFC-based technology from laboratory-scale to real world, industrial-scale applications.

Here, we present some preliminary LBM results, aimed at the reproduction of the experimental campaign performed at the Energy Lab of the University of Naples “Parthenope” [56,57]. The experimental apparatus featured tubular MFC reactors, made of Falcon test tubes [58] filled with carbon- fiber anode brushes and disk-shaped ceramic porous cathodes (see Figure 8a,b). The organic substrate was prepared from vegetable residuals mixed with water and without any further, specific pre-treatment.

The reconstruction of the MFC reactor is shown in Figure 8c. The anode brush and cathode disk were both treated as sectioned porous media, with $\epsilon$ equal to ∼72% and ∼76%, respectively. Moreover, the anode media was considered as active, with the generation of H${}^{+}$ ions according to the bacteria activity trends, while the cathode was assumed as a passive porous structure. The $N-N$ section represents the Nafion membrane, also included in the experimental setup, which acts as a no-slip wall for water and solid waste species, while it is a permeable boundary for the H${}^{+}$ ions. The motion of ions inside the reactor is due to the presence of diffusion and repulsion between positive ions and the potential difference between the electrodes. The diffusion process is automatically included in the standard LBM scheme, while the repulsive force has been modeled through the following pseudo-potential approach [59]:

$$F=-G{c}_s^2\frac{\nabla {\psi }^2}{2},$$

(19)

where $\psi$ is the pseudo-potential that accounts for the local H${}^{+}$ density and is given by:

$$\psi =1-e^{-\left[{\mathrm{H}}^{+}\right]},$$

(20)

while G represents the strength of the repulsive interaction:

$$G=\frac{q}{c_s^2},$$

(21)

with q being the electrical charge of H${}^{+}$ ions. The potential difference between the two electrodes was fixed as the input parameter for the operation of our MFC model. Note that, in order to ensure that the simulated configuration matches the physical scales of the actual reactor, physical units were converted into lattice units (LU) through the following simple Equation:

$${\Gamma }^{phys}=\Theta {\Gamma }^{lu},$$

(22)

where $\Gamma$ represents any given quantity in the physical or lattice unit space, while $\Theta$ is the quantity-specific conversion factor. Conversion factors for quantities such as the viscosity and length scales are readily obtainable from numerical stability constraints (the former) and from the lattice grid dimension (the latter). The remaining conversion factors are then established as a combination of the known ones.

Table 2. Main physical parameters for the MFC reactor and their LU conversions.

Parameter	${\mathbf{\Gamma }}^{\mathit{phys}}$	${\mathbf{\Gamma }}^{\mathit{lu}}$ [LU]
Length	$0.1$ (m)	400
Kinematic viscosity	$5.5\times {10}^{-5}$ (m${}^2$/s)	1.6667
Density	$1\times {10}^3$ (kg/m${}^3$)	1
H${}^{+}$ concentration	$1.78\times {10}^{-4}$ (mol/L)	$1.78\times {10}^{-7}$
pH	$3.75$	$6.75$
Open-Circuit Voltage (OCV)	$0.5$ (V)	$0.005$

reports the main physical quantities and the corresponding quantities in LU for the reference MFC reactor configuration.

A set of simulations was performed on a $400\times 100$ lattice grid, in order to obtain polarization and power curves as a function of the imposed potential difference $\Delta V$. Figure 9 displays the normalized numerical trends, compared to the experimental data presented in [57]. The agreement between the experiments and and the numerical predictions is remarkable, with the latter being capable of correctly predicting the typical trends of MFCs operation, namely:

• negligible activation losses in the small currents region, due to the slow start-up time of bacterial activity (typically 3–5 days);
• quasi-linear Ohmic-losses region, which represents the majority of the MFC operational range;
• no appreciable concentration-loss phase.

4. Conclusions

In this work, ad hoc developed algorithms for the simulation of reactive flows through micro- and nano-scale porous media via the Lattice Boltzmann Method are presented and discussed. Different technological applications are considered: namely, automotive SCR converters under thermally steady operating conditions; heterogeneous (nano-)porous catalytic systems under non-steady (pulsed) operating conditions; electro-chemical energy conversion systems, even in the presence of complex biological substrates, like in MFC reactors. In all of these heterogeneous environments, the proposed porous media reconstruction procedure and reactive boundary condition have proven to be sufficiently accurate and reliable to correctly describe the flows in study. Of particular significance is the MFC application, due to the high innovation level and challenges related to the investigation of such kinds of devices.

On the computational side, the LBM code was able to achieve ∼1.5 million lattice site updates per second (MLUPS). This is a remarkable result in terms of computing performance, given that three evolving species are tracked simultaneously, which highlights the efficiency of the developed implementation.

To further extend the versatility of the proposed methodology, the future development steps should be focused on: robust 3D implementation; inclusion of non-isothermal effects in the fluid flow and chemistry mechanisms; inclusion of adsorption-desorption modeling over the surface catalytic sites; and extension of the reconstruction algorithm to account for specific porous structural configurations.