Computational Intelligence Approaches for Energy Load Forecasting in Smart Energy Management Grids: State of the Art, Future Challenges, and Research Directions
Abstract
:1. Introduction
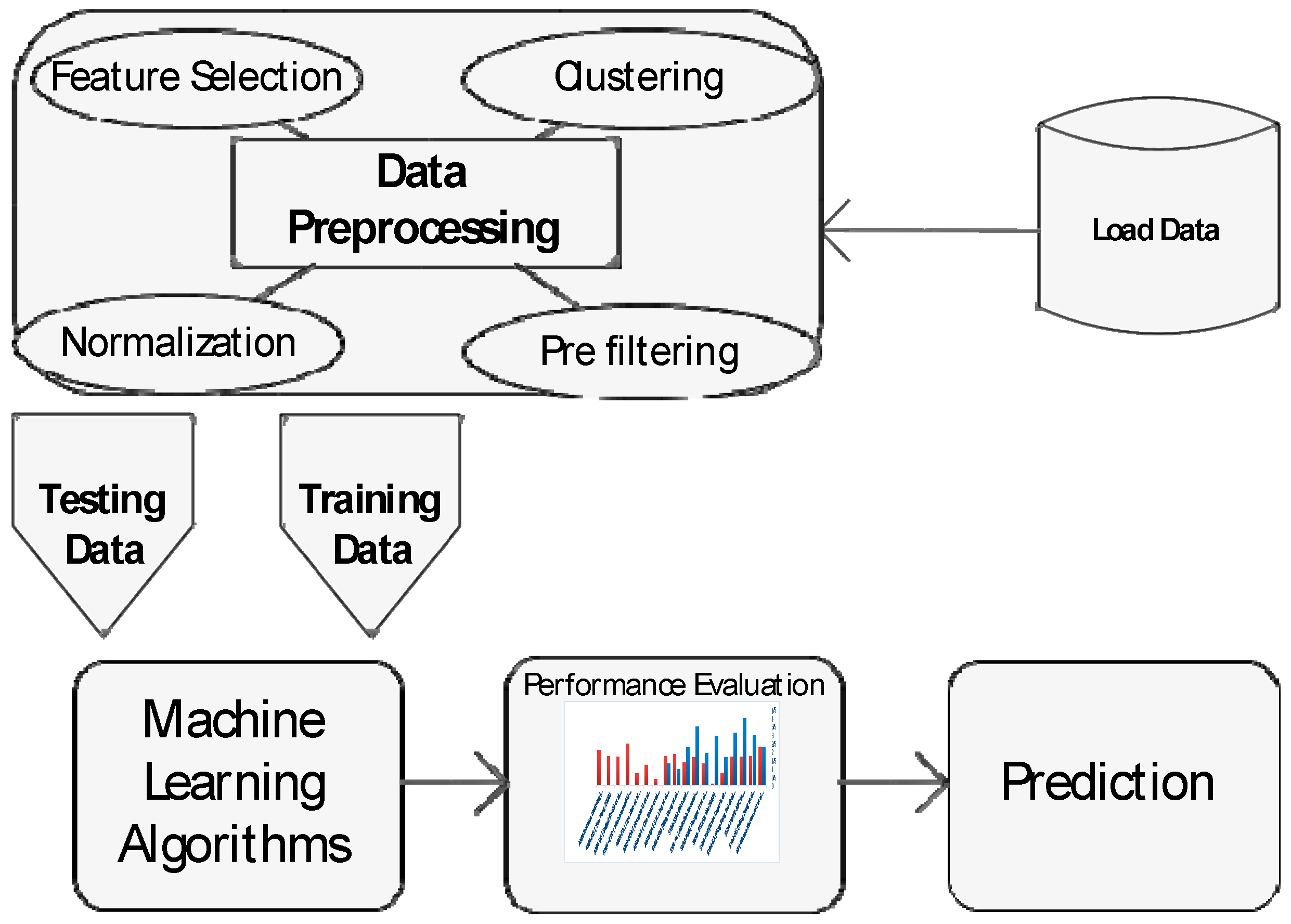
2. Methodology
- Pre-processing stage
- Learning stage
- Performance evaluation stage
3. Datasets Used in CI Approaches for ILF
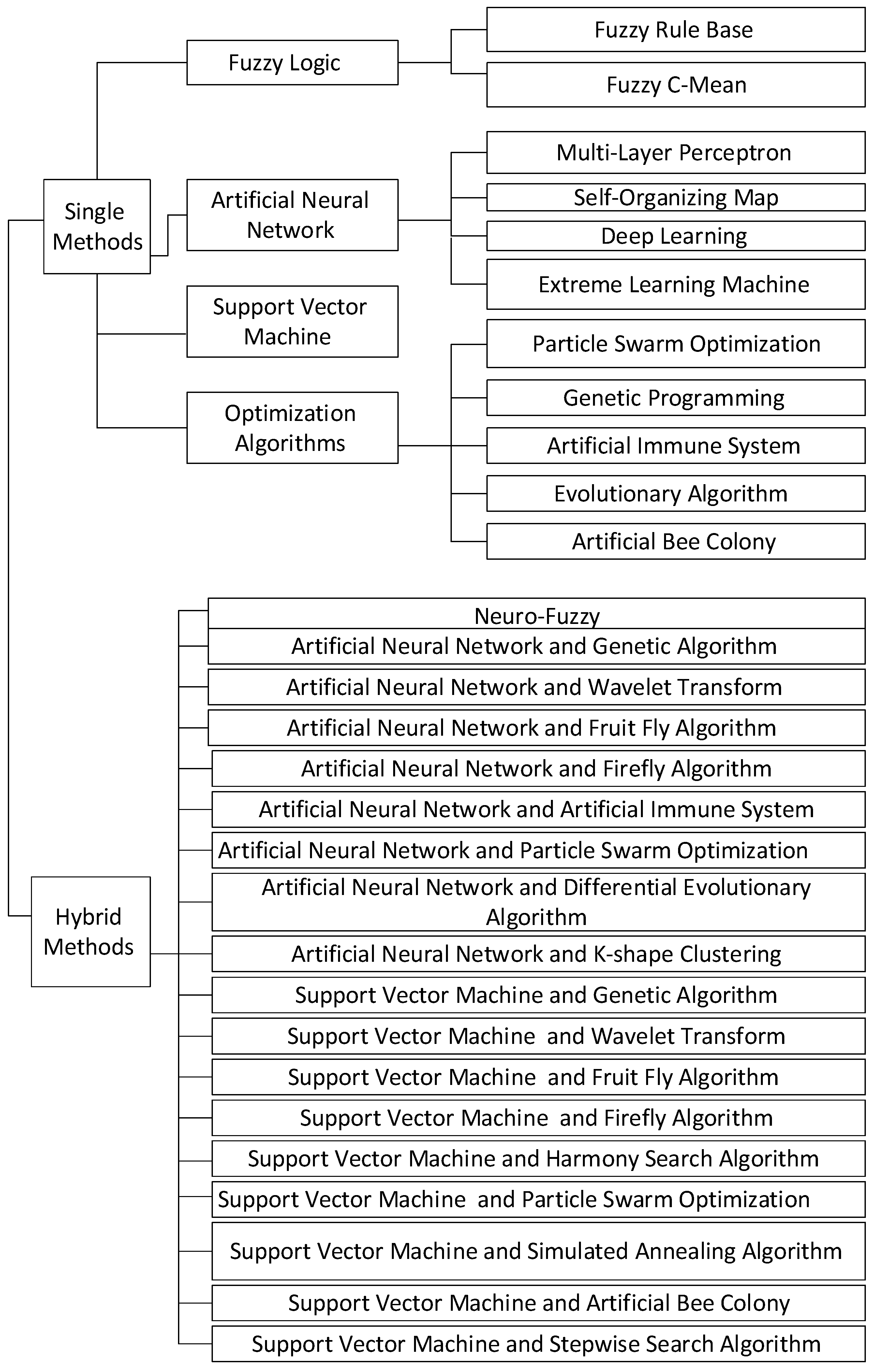
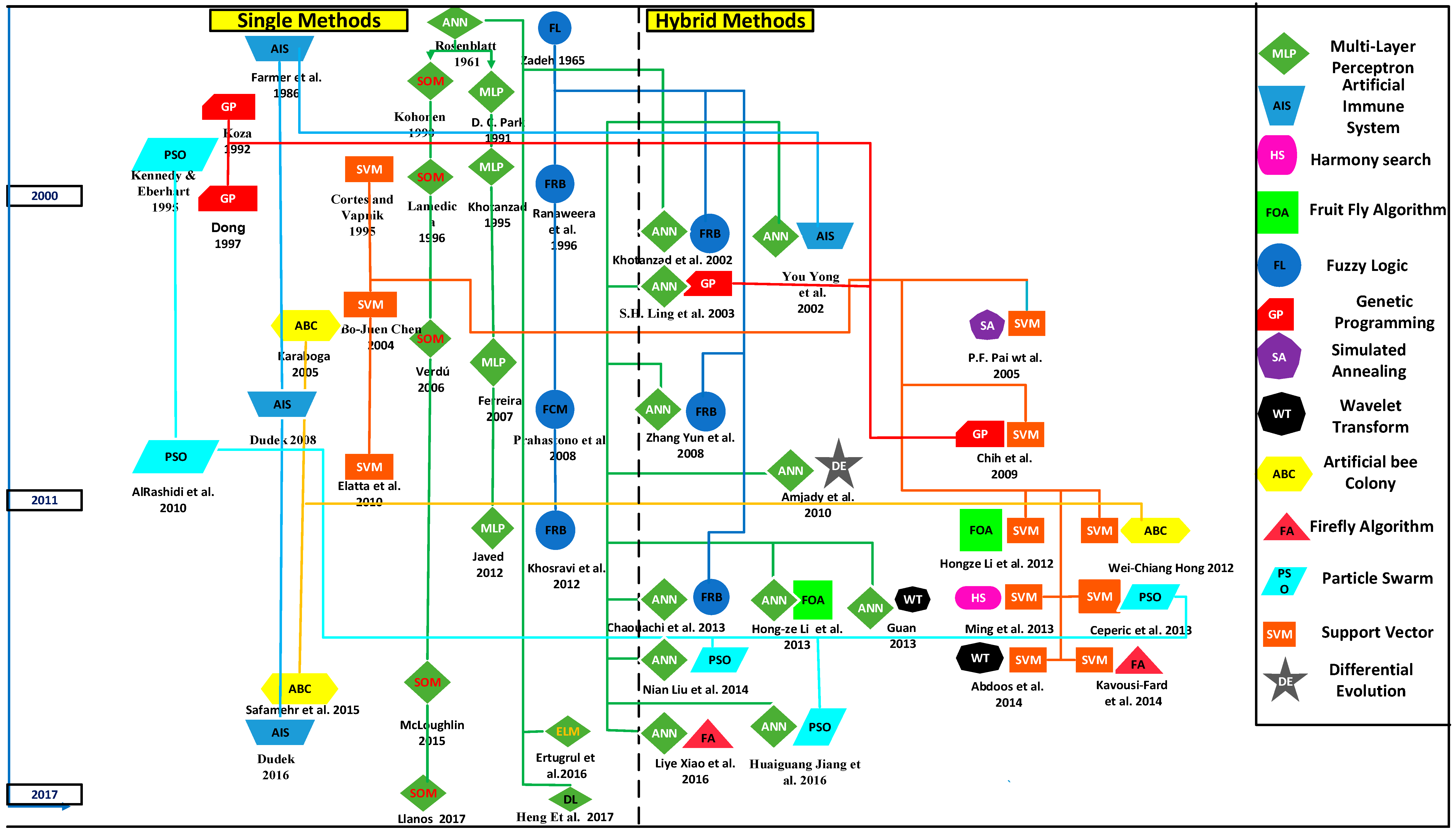
4. State-Of-The-Art of Single and Hybrid CI Techniques Applied for ILF
4.1. Single (Stand-Alone Modeling) Methods
4.1.1. Fuzzy Logic Sets
4.1.2. Artificial Neural Networks (ANN)
4.1.3. Support Vector Machine (SVM)
4.1.4. Clustering Techniques
4.1.5. Genetic Algorithm (GA)
4.1.6. Artificial Bee Algorithm
4.1.7. Artificial Immune System (AIS)
4.1.8. Particle Swarm Optimization (PSO)
4.2. Hybrid Methods
4.2.1. Neuro-Fuzzy (NF)
4.2.2. Artificial Neural Network and Wavelet Transform
4.2.3. Optimization Algorithms Integrated with Artificial Neural Network
Artificial Neural Network and Genetic Algorithm
Artificial Neural Network and Fruit Fly Optimization Algorithm (ANN-FOA)
Artificial Neural Network and Firefly Algorithm (ANN-FA)
Artificial Neural Network and Artificial Immune Systems (ANN-AIS)
Artificial Neural Network and Particle Swarm Optimization (ANN-PSO)
4.2.4. Artificial Neural Network and Clustering Techniques
4.2.5. Optimization Algorithms Integrated with Support Vector Machine
Genetic Algorithm and Support Vector Machine
Support Vector Machine and Simulated Annealing Algorithm (SVM-SA)
Support Vector Machine and Particle Swarm Optimization (SVM-PSO)
Support Vector Machine and Artificial Bee Colony (SVM-ABC)
Support Vector Machine and Harmony Search Algorithm (SVM-HS)
Support Vector Machine and Fruit Fly Optimization Algorithm (SVM-FOA)
Support Vector Regression and Firefly Algorithm (SVR-FA)
5. Criteria Used for Evaluation
6. Method Evaluation
7. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| ABC | Artificial bee colony |
| AIS | Artificial immune system |
| ANN | Artificial neural network |
| CI | Computational intelligence |
| DE | Differential evolutionary algorithm |
| DL | Deep learning |
| ELM | Extreme learning machine |
| FA | Firefly algorithm |
| FANN | Firefly neural network |
| FCM | Fuzzy C-means |
| FL | Fuzzy logic |
| FOA | Fruit fly optimization algorithm |
| FRB | Fuzzy rule base |
| GA | Genetic algorithm |
| GNN | Genetic neural network |
| GP | Genetic programming |
| GSVM | Genetic support vector machine |
| HS | Harmony search algorithm |
| ILF | Intelligent load forecasting |
| LTLF | Long-term load forecasting |
| MLP | Multilayer perceptron |
| MTLF | Medium-term load forecasting |
| NF | Neuro fuzzy |
| NILM | Non-Intrusive Load Management |
| RNNs | recurrent neural networks |
| WT | Wavelet transform |
References
- Mohsenian-Rad, A.-H.; Wong, V.W.S.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Diamantoulakis, D.P.; Kapinas, V.M.; Karagiannidis, G.K. Big data analytics for dynamic energy management in smart grids. Big Data Res. 2015, 2, 94–101. [Google Scholar] [CrossRef]
- Tso, G.K.; Yau, K.K. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Depuru, S.S.S.R.; Wang, L.; Devabhaktuni, V. Smart meters for power grid: Challenges, issues, advantages and status. Renew. Sustain. Energy Rev. 2011, 15, 2736–2742. [Google Scholar] [CrossRef]
- Charytoniuk, W.; Chen, M.; Van Olinda, P. Nonparametric regression based short-term load forecasting. IEEE Trans. Power Syst. 1998, 13, 725–730. [Google Scholar] [CrossRef]
- Momoh, J.; Ma, X.; Tomsovic, K. Overview and literature survey of fuzzy set theory in power systems. IEEE Trans. Power Syst. 1995, 10, 1676–1690. [Google Scholar] [CrossRef]
- Soheilirad, M.; Hizam, H.; Farzan, P.; Hojabri, M.; Fallah, S.N.; Soheilirad, G. Wind farm reactive power optimization by using imperialist competitive algorithm. In Proceedings of the 2013 International Conference on Power, Energy and Control (ICPEC), Sri Rangalatchum Dindigul, India, 6–8 February 2013. [Google Scholar]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Hong, T. Short Term Electric Load Forecasting; North Carolina State University: Raleigh, NC, USA, 2010. [Google Scholar]
- Hong, T.; Wilson, J.; Xie, J. Long term probabilistic load forecasting and normalization with hourly information. IEEE Trans. Smart Grid 2014, 5, 456–462. [Google Scholar] [CrossRef]
- Dudek, G. Artificial immune system with local feature selection for short-term load forecasting. IEEE Trans. Evol. Comput. 2017, 21, 116–130. [Google Scholar] [CrossRef]
- Azadeh, A.; Moghadam, R.T.; Ghaderi, S.F.; Tarverdian, S.; Saberi, M. Integration of artificial neural networks and genetic algorithm to predict electrical energy consumption. Appl. Math. Comput. 2007, 186, 1731–1741. [Google Scholar] [CrossRef]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Zhu, Y.; He, Y. Short-term load forecasting model using fuzzy c means based radial basis function network. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, ISDA’06, Jinan, China, 16–18 October 2006. [Google Scholar]
- Welikala, S.; Dinesh, C.; Ekanayake, M.P.B.; Godaliyadda, R.I.; Ekanayake, J. Incorporating Appliance Usage Patterns for Non-Intrusive Load Monitoring and Load Forecasting. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Srinivasan, D. Interval type-2 fuzzy logic systems for load forecasting: A comparative study. IEEE Trans. Power Syst. 2012, 27, 1274–1282. [Google Scholar] [CrossRef]
- Ferreira, V.H.; da Silva, A.P.A. Toward estimating autonomous neural network-based electric load forecasters. IEEE Trans. Power Syst. 2007, 22, 1554–1562. [Google Scholar] [CrossRef]
- Ding, N.; Benoit, C.; Foggia, G.; Bésanger, Y.; Wurtz, F. Neural network-based model design for short-term load forecast in distribution systems. IEEE Trans. Power Syst. 2016, 31, 72–81. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- López, M.; Valero, S.; Senabre, C.; Aparicio, J.; Gabaldonc, A. Application of SOM neural networks to short-term load forecasting: The Spanish electricity market case study. Electr. Power Syst. Res. 2012, 91, 18–27. [Google Scholar] [CrossRef]
- Llanos, J.; Morales, R.; Núñez, A.; Sáez, D.; Lacalle, M.; Marín, L.G.; Hernández, R.; Lanas, F. Load estimation for microgrid planning based on a self-organizing map methodology. Appl. Soft Comput. 2017, 53, 323–335. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep Learning for Household Load Forecasting—A Novel Pooling Deep RNN. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Hill, D.J.; Luo, F.; Xu, Y. Short-Term Residential Load Forecasting based on Resident Behaviour Learning. IEEE Trans. Power Syst. 2018, 33, 1087–1088. [Google Scholar] [CrossRef]
- Ertugrul, Ö.F. Forecasting electricity load by a novel recurrent extreme learning machines approach. Int. J. Electr. Power Energy Syst. 2016, 78, 429–435. [Google Scholar] [CrossRef]
- Ekici, S. Electric Load Forecasting using Regularized Extreme Learning Machines. Int. J. Ind. Electr. Electr. Eng. 2016, 4, 119–122. [Google Scholar]
- Chen, B.-J.; Chang, M.-W. Load forecasting using support vector machines: A study on EUNITE competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Elattar, E.E.; Goulermas, J.; Wu, Q.H. Electric load forecasting based on locally weighted support vector regression. IEEE Trans. Syst. Man Cybern. Part C 2010, 40, 438–447. [Google Scholar] [CrossRef]
- Alvarez, F.M.; Troncoso, A.; Riquelme, J.C.; Aguilar Ruiz, J.S. Energy time series forecasting based on pattern sequence similarity. IEEE Trans. Knowl. Data Eng. 2011, 23, 1230–1243. [Google Scholar] [CrossRef]
- Safamehr, H.; Rahimi-Kian, A. A cost-efficient and reliable energy management of a micro-grid using intelligent demand-response program. Energy 2015, 91, 283–293. [Google Scholar] [CrossRef]
- AlRashidi, M.; El-Naggar, K. Long term electric load forecasting based on particle swarm optimization. Appl. Energy 2010, 87, 320–326. [Google Scholar] [CrossRef]
- Lee, D.G.; Lee, B.W.; Chang, S.H. Genetic programming model for long-term forecasting of electric power demand. Electr. Power Syst. Res. 1997, 40, 17–22. [Google Scholar] [CrossRef]
- Yun, Z.; Quan, Z.; Caixin, S.; Shaolan, L.; Yuming, L.; Yang, S. RBF neural network and ANFIS-based short-term load forecasting approach in real-time price environment. IEEE Trans. Power Syst. 2008, 23, 853–858. [Google Scholar]
- Chaouachi, A.; Kamel, R.M.; Andoulsi, R.; Nagasaka, K. Multiobjective intelligent energy management for a microgrid. IEEE Trans. Ind. Electr. 2013, 60, 1688–1699. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Goel, L. Short-term load forecasting by wavelet transform and evolutionary extreme learning machine. Electr. Power Syst. Res. 2015, 122, 96–103. [Google Scholar] [CrossRef]
- Guan, C.; Luh, P.B.; Michel, L.D.; Wang, Y.; Friedland, P.B. Very short-term load forecasting: Wavelet neural networks with data pre-filtering. IEEE Trans. Power Syst. 2013, 28, 30–41. [Google Scholar] [CrossRef]
- Ling, S.-H.; Leung, F.H.F.; Lam, H.K.; Lee, Y.-S.; Tam, P.K.S. A novel genetic-algorithm-based neural network for short-term load forecasting. IEEE Trans. Ind. Electr. 2003, 50, 793–799. [Google Scholar] [CrossRef]
- Li, H.-Z.; Guo, S.; Li, C.-J.; Sun, J.-Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl.-Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Hu, R.; Wen, S.; Zeng, Z.; Huang, T. A short-term power load forecasting model based on the generalized regression neural network with decreasing step fruit fly optimization algorithm. Neurocomputing 2017, 221, 24–31. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Liang, T.; Wang, C. A combined model based on multiple seasonal patterns and modified firefly algorithm for electrical load forecasting. Appl. Energy 2016, 167, 135–153. [Google Scholar] [CrossRef]
- Yong, Y.; Sun’an, W.; Wanxing, S. Short-term load forecasting using artificial immune network. In Proceedings of the International Conference on Power System Technology, PowerCon 2002, Kunming, China, 13–17 October 2002. [Google Scholar]
- Mishra, S.; Patra, S.K. Short term load forecasting using a neural network trained by a hybrid artificial immune system. In Proceedings of the IEEE Region 10 and the Third international Conference on Industrial and Information Systems, ICIIS 2008, Kharagpur, India, 8–10 December 2008. [Google Scholar]
- Liu, N.; Tang, Q.; Zhang, J.; Fan, W.; Liu, J. A hybrid forecasting model with parameter optimization for short-term load forecasting of micro-grids. Appl. Energy 2014, 129, 336–345. [Google Scholar] [CrossRef]
- Lee, C.-M.; Ko, C.-N. Time series prediction using RBF neural networks with a nonlinear time-varying evolution PSO algorithm. Neurocomputing 2009, 73, 449–460. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. Short-term load forecast of microgrids by a new bilevel prediction strategy. IEEE Trans. Smart Grid 2010, 1, 286–294. [Google Scholar] [CrossRef]
- Ahmad, A.; Javaid, N.; Guizani, M.; Alrajeh, N.; Khan, Z.A. An accurate and fast converging short-term load forecasting model for industrial applications in a smart grid. IEEE Trans. Ind. Inform. 2017, 13, 2587–2596. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Construction of optimal prediction intervals for load forecasting problems. IEEE Trans. Power Syst. 2010, 25, 1496–1503. [Google Scholar] [CrossRef]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Pérez, F.; Fernández, Á.; Lloret, J. Artificial neural network for short-term load forecasting in distribution systems. Energies 2014, 7, 1576–1598. [Google Scholar] [CrossRef]
- Quilumba, F.L.; Lee, W.-J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using smart meter data to improve the accuracy of intraday load forecasting considering customer behavior similarities. IEEE Trans. Smart Grid 2015, 6, 911–918. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, W.-C. Forecasting regional electricity load based on recurrent support vector machines with genetic algorithms. Electr. Power Syst. Res. 2005, 74, 417–425. [Google Scholar] [CrossRef]
- Wu, C.-H.; Tzeng, G.-H.; Lin, R.-H. A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression. Expert Syst. Appl. 2009, 36, 4725–4735. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, W.-C. Support vector machines with simulated annealing algorithms in electricity load forecasting. Energy Convers. Manag. 2005, 46, 2669–2688. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Y.; Muljadi, E.; Zhang, J.; Gao, W. A short-term and high-resolution distribution system load forecasting approach using support vector regression with hybrid parameters optimization. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Ceperic, E.; Ceperic, V.; Baric, A. A strategy for short-term load forecasting by support vector regression machines. IEEE Trans. Power Syst. 2013, 28, 4356–4364. [Google Scholar] [CrossRef]
- Hong, W.-C. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm. Energy 2011, 36, 5568–5578. [Google Scholar] [CrossRef]
- Daut, M.A.M.; Hassan, M.Y.; Abdullah, H.; Abdul, R.H.; Abdullah, M.P.; Hussin, F. An Improved Building Load Forecasting Method using a combined Least Square Support Vector Machine and modified Artificial Bee Colony. ELEKTRIKA-J. Electr. Eng. 2017, 16, 1–5. [Google Scholar]
- Zeng, M.; Xue, S.; Wang, Z.; Zhu, X.; Zhang, G. Short-term load forecasting of smart grid systems by combination of general regression neural network and least squares-support vector machine algorithm optimized by harmony search algorithm method. Appl. Math. 2013, 7, 291–298. [Google Scholar] [CrossRef]
- Li, H.; Guo, S.; Zhao, H.; Su, C.; Wang, B. Annual electric load forecasting by a least squares support vector machine with a fruit fly optimization algorithm. Energies 2012, 5, 4430–4445. [Google Scholar] [CrossRef]
- Cao, G.; Wu, L. Support vector regression with fruit fly optimization algorithm for seasonal electricity consumption forecasting. Energy 2016, 115, 734–745. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid modified firefly algorithm and support vector regression model for accurate short term load forecasting. Expert Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Abdoos, A.; Hemmati, M.; Abdoos, A.A. Short term load forecasting using a hybrid intelligent method. Knowl.-Based Syst. 2015, 76, 139–147. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Applying support vector machine to predict hourly cooling load in the building. Appl. Energy 2009, 86, 2249–2256. [Google Scholar] [CrossRef]
- Edwards, R.E.; New, J.; Parker, L.E. Predicting future hourly residential electrical consumption: A machine learning case study. Energy Build. 2012, 49, 591–603. [Google Scholar] [CrossRef]
- Jin, C.H.; Pok, G.; Lee, Y.; Park, H.-W.; Kim, K.D.; Yun, U.; Ryu, K.H. A SOM clustering pattern sequence-based next symbol prediction method for day-ahead direct electricity load and price forecasting. Energy Convers. Manag. 2015, 90, 84–92. [Google Scholar] [CrossRef]
- Ghasemi, A.; Shayeghi, H.; Moradzadeh, M.; Nooshyar, M. A novel hybrid algorithm for electricity price and load forecasting in smart grids with demand-side management. Appl. Energy 2016, 177, 40–59. [Google Scholar] [CrossRef]
- Tong, C.; Li, J.; Lang, C.; Kong, F.; Niu, J.; Rodrigues, J.J.P.C. An efficient deep model for day-ahead electricity load forecasting with stacked denoising auto-encoders. J. Parallel Distrib. Comput. 2017. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Economakos, E. Application of fuzzy concepts to power demand forecasting. IEEE Trans. Syst. Man Cybern. 1979, 9, 651–657. [Google Scholar]
- Ali, D.; Yohanna, M.; Puwu, M.I.; Garkida, B.M. Long-term load forecast modelling using a fuzzy logic approach. Pac. Sci. Rev. A 2016, 18, 123–127. [Google Scholar] [CrossRef]
- Chen, C.P.; Zhang, C.-Y. Data-intensive applications, challenges, techniques and technologies: A survey on Big Data. Inf. Sci. 2014, 275, 314–347. [Google Scholar] [CrossRef]
- Rosenblatt, F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms; Cornell Aeronautical Laboratory: Buffalo, NY, USA, 1961; Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/256582.pdf (accessed on 1 March 2018).
- Park, D.C.; El-Sharkawi, M.A.; Marks, R.J.; Atlas, L.E.; Damborg, M.J. Electric load forecasting using an artificial neural network. IEEE Trans. Power Syst. 1991, 6, 442–449. [Google Scholar] [CrossRef]
- Khotanzad, A.; Hwang, R.-C.; Abaye, A.; Maratukulam, D. An adaptive modular artificial neural network hourly load forecaster and its implementation at electric utilities. IEEE Trans. Power Syst. 1995, 10, 1716–1722. [Google Scholar] [CrossRef]
- Khotanzad, A.; Afkhami-Rohani, R.; Lu, T.-L.; Abaye, A.; Davis, M.; Maratukulam, D.J. ANNSTLF-a neural-network-based electric load forecasting system. IEEE Trans. Neural Netw. 1997, 8, 835–846. [Google Scholar] [CrossRef] [PubMed]
- Javed, F.; Arshad, N.; Wallin, F.; Vassileva, I.; Dahlquist, E. Forecasting for demand response in smart grids: An analysis on use of anthropologic and structural data and short term multiple loads forecasting. Appl. Energy 2012, 96, 150–160. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Lamedica, R.; Prudenzi, A.; Sforna, M.; Caciotta, M.; Cencellli, V.O. A neural network based technique for short-term forecasting of anomalous load periods. IEEE Trans. Power Syst. 1996, 11, 1749–1756. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Adamowski, J.F.; Li, Y. Short-term electricity demand forecasting with MARS, SVR and ARIMA models using aggregated demand data in Queensland, Australia. Adv. Eng. Inf. 2018, 35, 1–16. [Google Scholar] [CrossRef]
- Paparrizos, J.; Gravano, L. k-shape: Efficient and accurate clustering of time series. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, Melbourne, VIC, Australia, 31 May–4 June 2015; ACM: New York, NY, USA, 2015. [Google Scholar]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1941, 4, 87–112. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Farmer, J.D.; Packard, N.H.; Perelson, A.S. The immune system, adaptation, and machine learning. Phys. D Nonlinear Phenom. 1986, 22, 187–204. [Google Scholar] [CrossRef]
- De Castro, L.N.; Timmis, J. Artificial Immune Systems: A New Computational Intelligence Approach; Springer Science & Business Media: Berlin, Germany, 2002. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Lin, C.-T.; Lee, C.S.G. Neural-network-based fuzzy logic control and decision system. IEEE Trans. Comput. 1991, 40, 1320–1336. [Google Scholar] [CrossRef]
- Jang, J.-S.; Sun, C.-T. Neuro-fuzzy modeling and control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Li, K.; Su, H.; Chu, J. Forecasting building energy consumption using neural networks and hybrid neuro-fuzzy system: A comparative study. Energy Build. 2011, 43, 2893–2899. [Google Scholar] [CrossRef]
- Khotanzad, A.; Zhou, E.; Elragal, H. A neuro-fuzzy approach to short-term load forecasting in a price-sensitive environment. IEEE Trans. Power Syst. 2002, 17, 1273–1282. [Google Scholar] [CrossRef]
- Jawerth, B.; Sweldens, W. An overview of wavelet based multiresolution analyses. SIAM Rev. 1994, 36, 377–412. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Dong, Z.-Y. An adaptive neural-wavelet model for short term load forecasting. Electr. Power Syst. Res. 2001, 59, 121–129. [Google Scholar] [CrossRef]
- Pan, W.-T. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- El-Telbany, M.; El-Karmi, F. Short-term forecasting of Jordanian electricity demand using particle swarm optimization. Electr. Power Syst. Res. 2008, 78, 425–433. [Google Scholar] [CrossRef]
- Koprinska, I.; Rana, M.; Troncoso, A.; Martinez-Alvarez, F. Combining pattern sequence similarity with neural networks for forecasting electricity demand time series. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013. [Google Scholar]
- Fahiman, F.; Erfani, S.M.; Rajasegarar, S.; Palaniswami, M.; Leckie, C. Improving load forecasting based on deep learning and K-shape clustering. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017. [Google Scholar]
- Shi, Y. Particle swarm optimization: developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001. [Google Scholar]
- Hong, W.-C. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Akay, B. A study on particle swarm optimization and artificial bee colony algorithms for multilevel thresholding. Appl. Soft Comput. 2013, 13, 3066–3091. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspir. Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms, 1st ed.; Elsevier: Waltham, MA, USA, 2014. [Google Scholar]
- Kalogirou, S.A.; Bojic, M. Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy 2000, 25, 479–491. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
| Type Classifier | Author | Title of Paper | Objectives |
|---|---|---|---|
| Single Methods | |||
| FCM | Zhu et al. [16] | Short-term Load Forecasting Model Using Fuzzy C Means Based Radial Basis Function Network | To present application of Fuzzy C-mean to STLF. |
| FRB | Welikala et al. [17] | Incorporating Appliance Usage Patterns for Non-Intrusive Load Monitoring and Load Forecasting | To develop a load monitoring method that can predict the amount of flexible load available at consumer premises. |
| Khosravi et al. [18] | Interval Type-2 Fuzzy Logic Systems for Load Forecasting: A Comparative Study | To examine the application of FRB for STLF. | |
| MLP | Ferreira et al. [19] | Toward Estimating Autonomous Neural Network-Based Electric Load Forecasters | To apply NN-based learning technique for STLF. |
| Ding et al. [20] | Neural Network-Based Model Design for Short-Term Load Forecast in Distribution Systems | To design an ILF model using MLP arrangement. | |
| Kong et al. [21] | Short-Term Residential Load Forecasting based on LSTM Recurrent Neural Network | To develop a short-term residential load forecasting model. | |
| SOM | Lopez et al. [22] | Application of SOM Neural Networks to Short-Term Load Forecasting: The Spanish Electricity Market Case Study | Presents a forecasting model based on SOM algorithm. |
| Llanos et al. [23] | Load Estimation for Microgrid Planning Based on a Self-Organizing Map Methodology | To apply SOM algorithm as a clustering technique for load forecasting in a micro grid. | |
| DL | Shi et al. [24] | Deep Learning for Household Load Forecasting—A Novel Pooling Deep RNN | Exploring the capability of DL algorithm to directly learn uncertainties in load databases. |
| Kong et al. [25] | Short-Term Residential Load Forecasting based on Resident Behavior Learning | Developing an ILF model utilizing appliance load data. | |
| ELM | Ertugrul [26] | Forecasting Electricity Load by a Novel Recurrent Extreme Learning Machines Approach | Presenting an ILF model based on ELM. |
| SAMI EKICI [27] | Electric Load Forecasting Using Regularized Extreme Learning Machines | Investigating the performances of ELM for ILF. | |
| SVM | Chen et al. [28] | Load Forecasting Using Support Vector Machines: A Study on EUNITE Competition 2001 | To forecast the maximum values of daily load demand. |
| Elattar et al. [29] | Electric Load Forecasting Based on Locally Weighted Support Vector Regression | Modifying SVR algorithm to solve the ILF problem. | |
| Clustering techniques | Alvarez et al. [30] | Energy Time Series Forecasting Based on Pattern Sequence Similarity | To predict the load time series using k-shape clustering algorithm to find the similarity of pattern sequences. |
| ABC | Safamehr et al. [31] | A Cost-Efficient and Reliable Energy Management of a Micro-Grid Using Intelligent Demand–Response Program | Developing ABC algorithm to reshape the load profile by reducing the demand peak. |
| AIS | Dudek [13] | Artificial Immune System with Local Feature Selection for Short-Term Load Forecasting | To design an AIS algorithm for STLF. |
| PSO | AlRashidi et al. [32] | Long-Term Electric Load Forecasting Based on Particle Swarm Optimization | Presents a new method for long-term ILF. |
| GP | Lee et al. [33] | Genetic programming model for long-term forecasting of electric power demand | To discuss the application of GP to solve ILF. |
| EA | Logenthiran et al. [2] | Demand-Side Management in Smart Grid Using Heuristic Optimization | Proposing a technique to shift the day ahead peak load. |
| Hybrid Methods | |||
| Neuro-fuzzy | Yun et al. [34] | RBF Neural Network and ANFIS-Based Short-Term Load Forecasting Approach in Real-Time Price Environment | To investigate the feasibility of a neuro-fuzzy based load forecasting model in a real-time price environment. |
| Chaouachi et al. [35] | Multi-Objective Intelligent Energy Management for a Microgrid | Proposed an optimization model to balance the supply-demand in a microgrid. | |
| WT-NN | Li et al. [36] | Short-Term Load Forecasting by Wavelet Transform and Evolutionary Extreme Learning Machine | Proposes a novel STLF method. |
| Guan et al. [37] | Very Short-Term Load Forecasting: Wavelet Neural Networks With Data Pre-Filtering | Develop an ANN algorithm with data pre-filtering for ILF one hour ahead. | |
| GNN | Ling et al. [38] | A Novel Genetic-Algorithm-Based Neural Network for Short-Term Load Forecasting | To propose a GA-based neural network model for STLF. |
| Azadeh et al. [14] | Integration of Artificial Neural Networks and Genetic Algorithm to Predict Electrical Energy Consumption | Evaluation the application of GA-ANN for ILF. | |
| FOA_NN | Li et al. [39] | A Hybrid Annual Power Load Forecasting Model Based on Generalized Regression Neural Network with Fruit Fly Optimization Algorithm | To develop a hybrid annual load forecasting model. |
| Rui Hu et al. [40] | A Short-Term Power Load Forecasting Model Based on the Generalized Regression Neural Network with Decreasing Step Fruit Fly Optimization Algorithm | Proposed a short-term power load forecasting model based on the ANN, optimized by FOA. | |
| FA_NN | Liye Xiao et al. [41] | A Combined Model Based on Multiple Seasonal Patterns and Modified Firefly Algorithm for Electrical Load Forecasting | Improving the forecasting accuracy using combined neural network with FA. |
| AIS-NN | Yong [42] | Short-Term Load Forecasting Using Artificial Immune Network | Presenting a method for STLF in power system. |
| Mishra et al. [43] | Short-Term Load Forecasting Using a Neural Network Trained by a Hybrid Artificial Immune System | To propose a hybrid AIS algorithm for short-term load prediction. | |
| PSO-NN | Nian Liu et al. [44] | A Hybrid Forecasting Model with Parameter Optimization for Short-Term Load Forecasting of Micro-Grids | To propose a hybrid model with parameter optimization for ILF in a micro-grid. |
| Lee et al. [45] | Time Series Prediction Using RBF Neural Networks with a Nonlinear Time-Varying Evolution PSO Algorithm | To integrate PSO algorithm in a neural network load forecasting model to find the optimal model parameters. | |
| DE-NN | Amjady [46] | Short-Term Load Forecast of Microgrids by a New Bi-Level Prediction strategy | To develop a load prediction model by integrating neural network and evolutionary algorithm as feature selection technique and forecast engine. |
| Ahmad et al. [47] | An Accurate and Fast Converging Short-Term Load Forecasting Model for Industrial Applications in a Smart Grid | To propose a combined DE and ANN algorithm to predict the industrial load in smart grid. | |
| SA-NN | Khosravi et al. [48] | Construction of Optimal Prediction Intervals for Load Forecasting Problems | Investigated a model for prediction of load intervals instead of exact load values. |
| K-shape clustering-NN | Hernandez et al. [49] | Artificial Neural Networks for Short-Term Load Forecasting in Microgrids Environment | Presenting a solution for short-term load forecasting (STLF) in microgrids |
| Quilumba [50] | Using Smart Meter Data to Improve the Accuracy of Intraday Load Forecasting Considering Customer Behavior Similarities | To apply the k-shape clustering method to identify the similar energy usage pattern among the users with smart meters before load prediction. | |
| GSVM | Pai et al. [51] | Forecasting Regional Electricity Load Based on Recurrent Support Vector Machines with Genetic Algorithms | To investigate the feasibility of an ILF model tested on annual regional loads in Taiwan. |
| Wu et al. [52] | A Novel Hybrid Genetic Algorithm for Kernel Function and Parameter Optimization in Support Vector Regression | Predicting electrical daily load using SVR with dynamic parameter optimization. | |
| SA-SVM | Pai et al. [53] | Support Vector Machines with Simulated Annealing Algorithms in Electricity Load Forecasting | Elucidates the feasibility of using SVMs to forecast electricity load. |
| PSO-SVM | Jiang et al. [54] | A Short-Term and High-Resolution Distribution System Load Forecasting Approach Using Support Vector Regression with Hybrid Parameters Optimization | Presenting a hybrid PSO-SVM method for predicting load deviation in the distribution system. |
| Ceperic et al. [55] | A Strategy for Short-Term Load Forecasting by Support Vector Regression Machines | Improving an SVR based STLF model using PSO algorithm for hyper-parameter selection. | |
| ABC-SVM | Hong [56] | Electric Load Forecasting by Seasonal Recurrent SVR (Support Vector Regression) with Chaotic Artificial Bee Colony Algorithm | Proposing an ILF model considering seasonal or climate changes and economic activities. |
| Mat Daut et al. [57] | An Improved Building Load Forecasting Method Using a Combined Least Square Support Vector Machine and Modified Artificial Bee Colony | To improve the load forecasting performance by a new combined method. | |
| HS-SVM | Ming Zeng et al. [58] | Short-Term Load Forecasting of Smart Grid Systems by Combination of General Regression Neural Network and Least Squares-Support Vector Machine Algorithm Optimized by Harmony Search Algorithm Method | Developing a heuristic hybrid algorithm used for LS-SVM for short-term load forecasting model. |
| FOA-SVM | Li et al. [59] | Annual Electric Load Forecasting by a Least Squares Support Vector Machine with a Fruit Fly Optimization Algorithm | To examine the feasibility of the LSSVM model to forecast annual electric loads. |
| Cao et al. [60] | Support Vector Regression with Fruit Fly Optimization Algorithm for Seasonal Electricity Consumption Forecasting | Proposed a hybrid method combining SVM with FOA to forecast monthly consumption. | |
| FA-SVM | Fard et al. [61] | A New Hybrid Modified Firefly Algorithm and Support Vector Regression Model for Accurate Short-Term Load Forecasting | To develop a SVR based model for STLF using FA algorithm to adjust the parameters. |
| WT-SVM | Abdoos et al. [62] | Three Short-Term Load Forecasting Using a Hybrid Intelligent Method | Proposed a method for hourly heating load forecast integrating WT theory with ANN. |
| Dataset Type | Description | Total Time Period | Recording Step |
|---|---|---|---|
| Commercial load of an office building in China [63] | outdoor temperature, humidity, and solar radiation were taken from climate database of a typical year in Guangzhou, China, while the hourly Cooling load consumption were simulated by software. | May, June, July, and August of a typical meteorology year. | 2 h |
| Residential energy consumption dataset [64] | This dataset was collected from three different Campbell Creek homes. | the second week of September 2010 | 15 min |
| Historical regional load data varies from 7 to 39 MW in a Microgrid [49] | Database contains raw data collected by several sensor networks (electric, weather, calendar, etc.) from the Spanish utility Iberdrola. | From 1 January 2008 to 31 December 2010 | Hourly |
| Taiwan regional electricity load data [51] | The dataset includes regional electricity load data from 1981 to 2000 in Taiwan. | From 1981 to 2000 | Annual |
| Public hourly electricity load and price time series datasets [65] | Australian energy market operator; 2012. Available at: http://www.nemmco.com.au New York independent system operator; 2012. Available at: http://www.nyiso.com | Daily load of the year 2005 | Hourly |
| The electricity price and demand data [66] | New York independent system operator (NYISO) Electricity Market Data. Available: http://www.nyiso.com/ | From 1 January 2014 to 1 March 2014 | Hourly |
| Heterogeneous data (history electricity load distributions, weather parameters, and season parameters) [67] | Load distributions per hour in four area: Los Angeles, California, New York City, Florida | 15 July 2015 to 10 September 2016. | Hourly |
| Smart metering dataset [50] | Real-world smart meter data for residential customers of two different electric utility companies, from the United States and Ireland. | August 2009 to December 2010. | 30 min |
| Almanac of Minutely Power dataset (AMPds) [25] | Minutely current readings of a Canadian household and its 19 appliances http://ampds.org/. | One year 2013 | Minutely |
| Internet-based load dataset [19] | 1/Hourly load and temperature values, available at: ee.washington.edu/class/555/el-sharkawi/index files/Page3404.html 2/Daily peak load and temperature values available at: http://neuron.tuke.sk/competition 3/Half-hourly load, price, and temperature values available at: www.nemmco.com.au | 1/From 1 January 1985–31 March 1991 2/From 1 January 1997–31 January 1999 3/From 4 December 2001–31 December 2003 | 1/Hourly 2/Daily 3/Half-hourly |
| Main Types | Method | Adv. | Dis. |
|---|---|---|---|
| Single method | FL | Decision making for uncertain information | Drawback of Cognitive uncertainties |
| ANN | Unsupervised Learning | Overfitting | |
| SVM | Structural Risk Minimization | Parameter uncertainty | |
| GP | Optimal Search | Lack of Memory | |
| PSO | Memory storage | local minimization drawback | |
| Hybrid method | NF | Data characterization | Unknown optimal Number of clusters |
| ANN-k-shape clustering | Feature extraction via unsupervised procedure | Unknown optimal Number of clusters | |
| ANN-WT | Input selection | Only frequency resolution | |
| SVM-FOA | Fast searching algorithm | complicated architecture | |
| SVM-HS | Suitable for small sample and faster computational speed | complicated architecture |
| Accuracy | Description |
|---|---|
| Mean Absolute percentage Error: | N: Number of samples : Actual data value : Predicted value |
| Root Mean Square Error: | N: Number of samples : Actual data value : Predicted value |
| Coefficient of Determination: | : Variance of data : Actual data value : Predicted value |
| Mean Bias Error: | N: Number of samples : Actual data value : Predicted value |
| Method | Reference | MAPE |
|---|---|---|
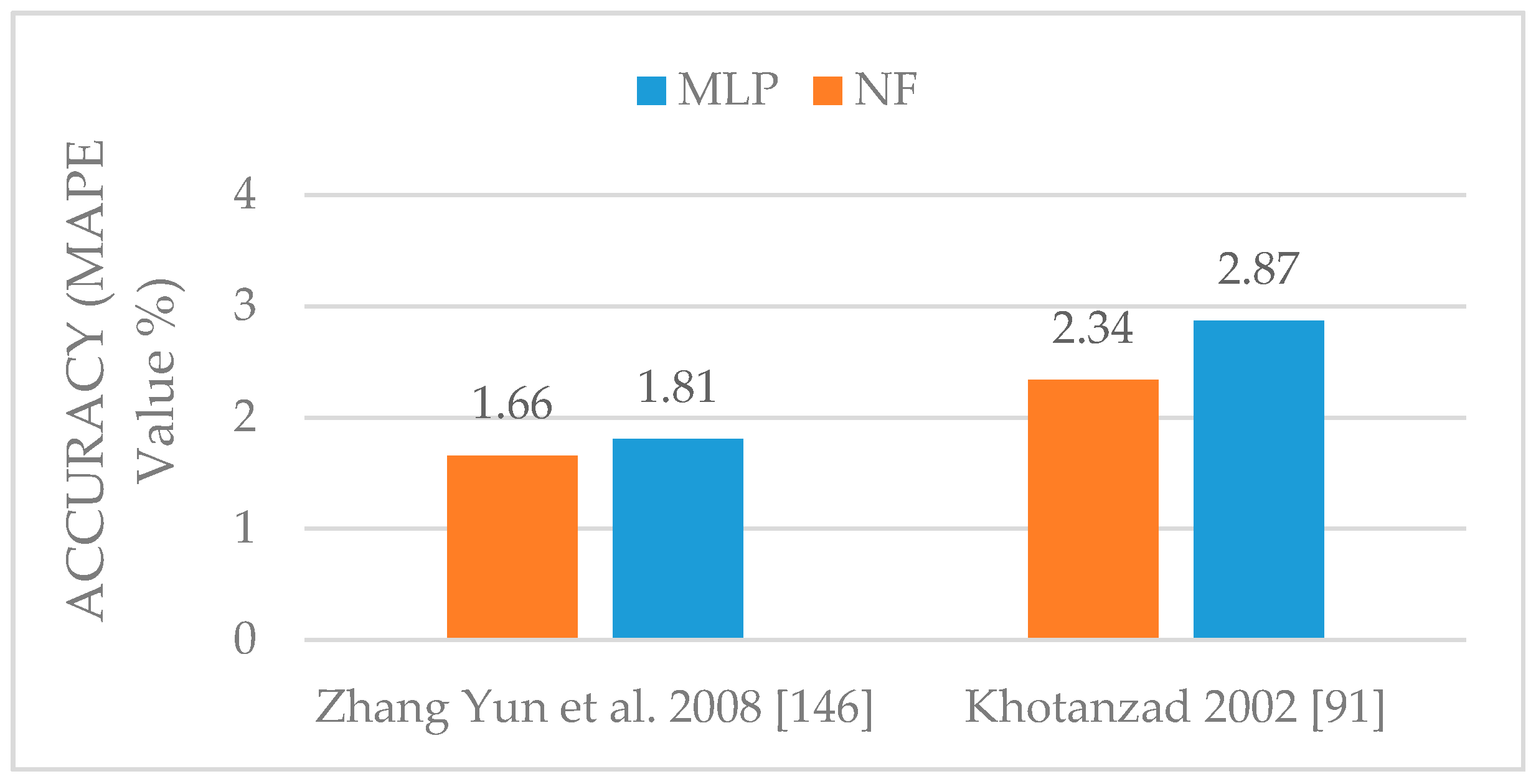
| MLP | Khotanzad 2002 [91] | 2.87% |
| MLP | Zhang Yun et al., 2008 [34] | 1.81% |
| NF | Khotanzad 2002 [91] | 2.34% |
| NF | Zhang Yun et al., 2008 [34] | 1.66% |
| Method | Reference | MAPE |
|---|---|---|
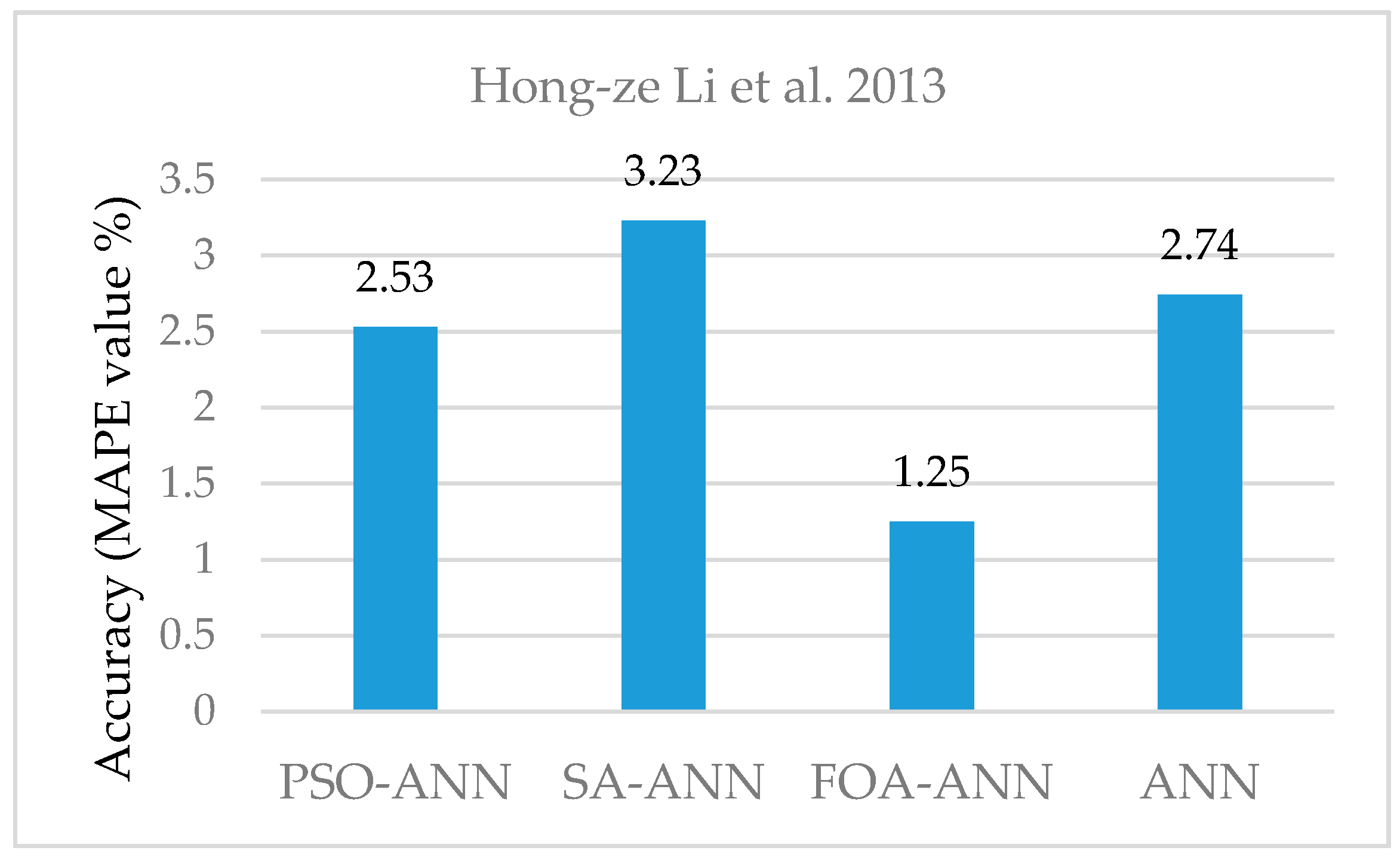
| ANN | Hong-ze Li et al., 2013 [39] | 2.74% |
| FOA-ANN | Hong-ze Li et al., 2013 [39] | 1.25% |
| PSO-ANN | Hong-ze Li et al., 2013 [38] | 2.53% |
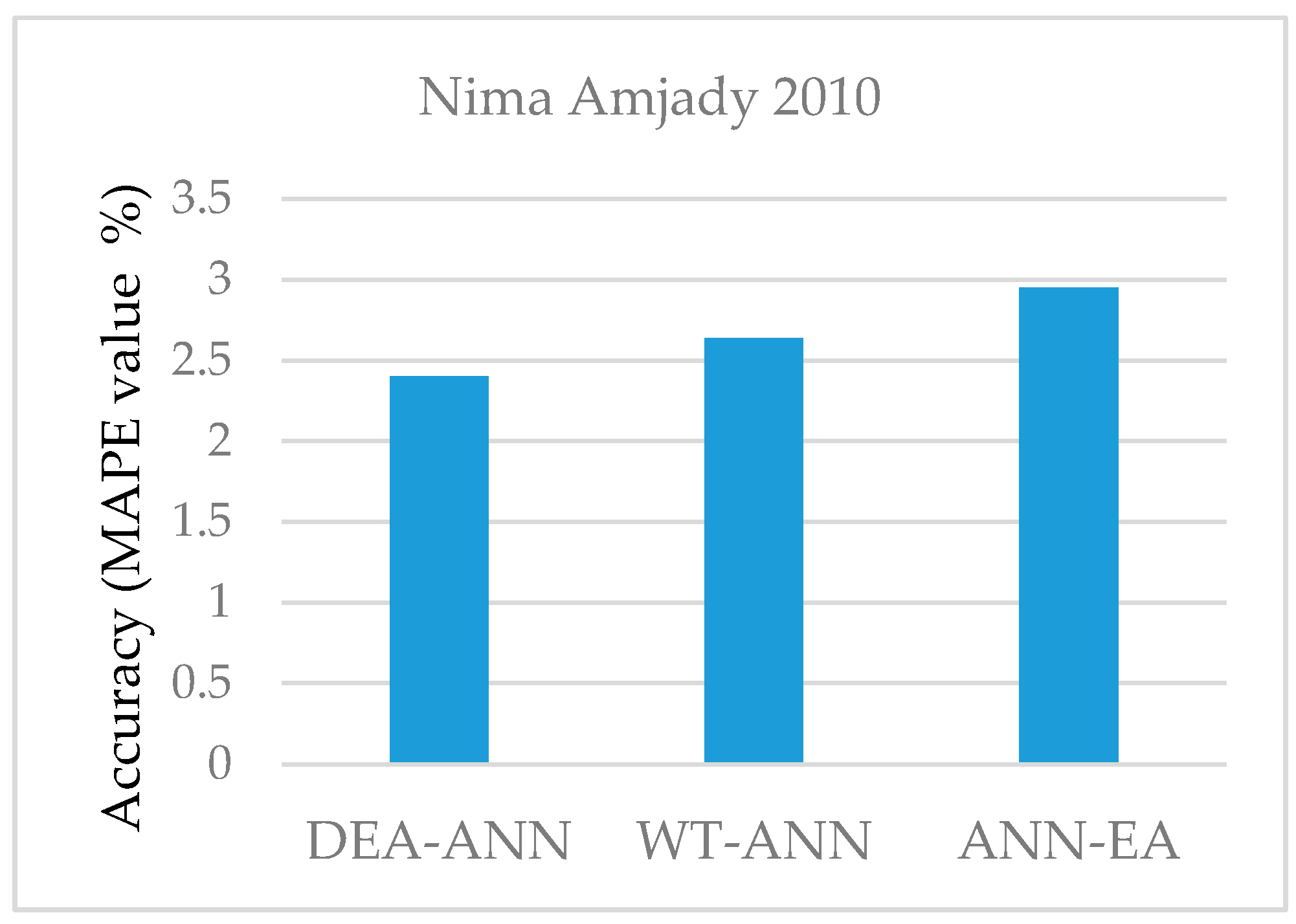
| EA-ANN | Nima Amjady 2010 [46] | 2.95% |
| WT-ANN | Nima Amjady 2010 [46] | 2.64% |
| DE-ANN | Nima Amjady 2010 [46] | 2.4% |
| Method | References | MAPE |
|---|---|---|
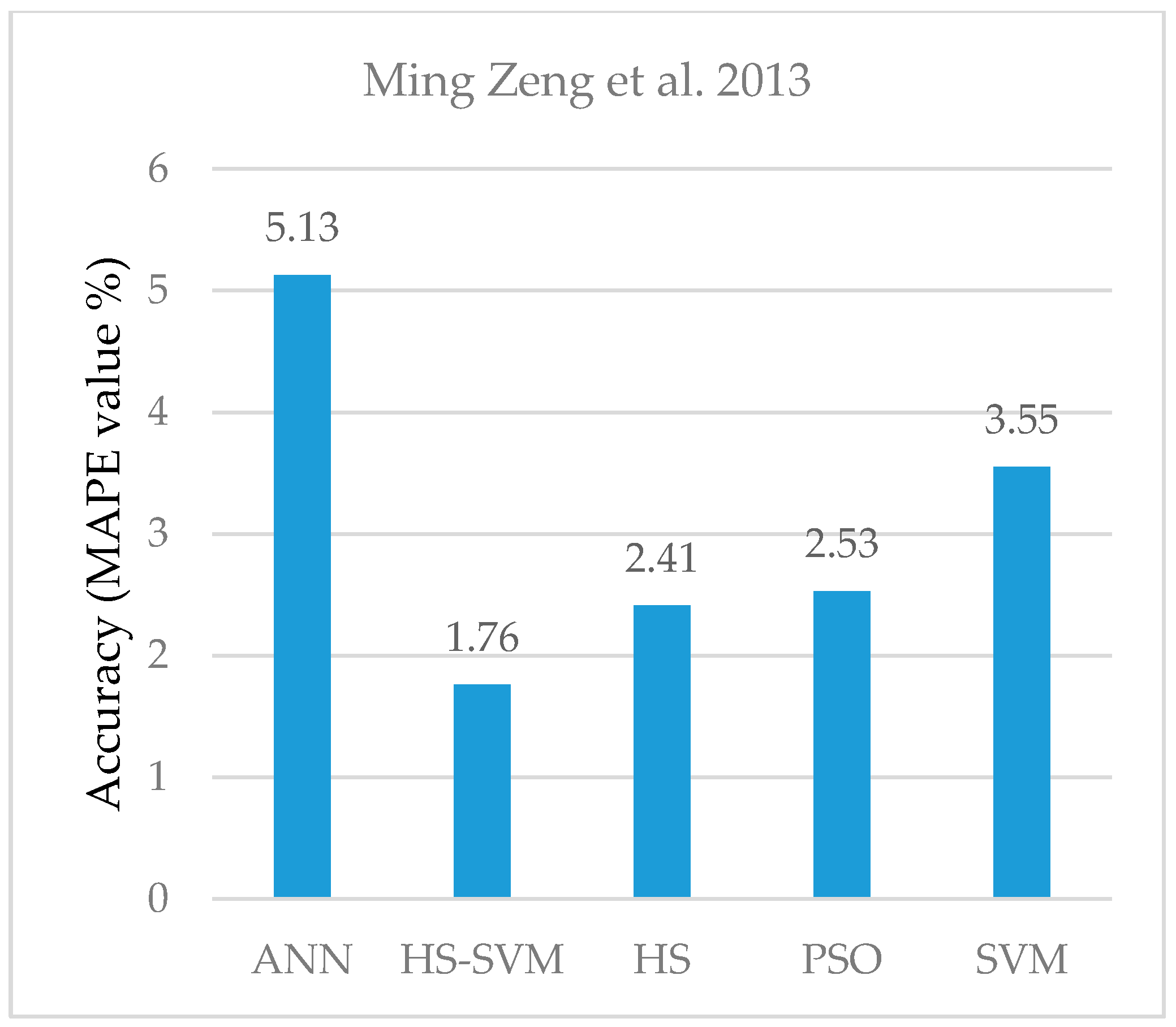
| ANN | Ming Zeng et al., 2013 [58] | 5.13% |
| SVM | Ming Zeng et al., 2013 [58] | 3.55% |
| PSO | Ming Zeng et al., 2013 [58] | 2.53% |
| HS | Ming Zeng et al., 2013 [58] | 2.41% |
| HS-SVM | Ming Zeng et al., 2013 [58] | 1.76% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fallah, S.N.; Deo, R.C.; Shojafar, M.; Conti, M.; Shamshirband, S. Computational Intelligence Approaches for Energy Load Forecasting in Smart Energy Management Grids: State of the Art, Future Challenges, and Research Directions. Energies 2018, 11, 596. https://doi.org/10.3390/en11030596
Fallah SN, Deo RC, Shojafar M, Conti M, Shamshirband S. Computational Intelligence Approaches for Energy Load Forecasting in Smart Energy Management Grids: State of the Art, Future Challenges, and Research Directions. Energies. 2018; 11(3):596. https://doi.org/10.3390/en11030596
Chicago/Turabian StyleFallah, Seyedeh Narjes, Ravinesh Chand Deo, Mohammad Shojafar, Mauro Conti, and Shahaboddin Shamshirband. 2018. "Computational Intelligence Approaches for Energy Load Forecasting in Smart Energy Management Grids: State of the Art, Future Challenges, and Research Directions" Energies 11, no. 3: 596. https://doi.org/10.3390/en11030596
APA StyleFallah, S. N., Deo, R. C., Shojafar, M., Conti, M., & Shamshirband, S. (2018). Computational Intelligence Approaches for Energy Load Forecasting in Smart Energy Management Grids: State of the Art, Future Challenges, and Research Directions. Energies, 11(3), 596. https://doi.org/10.3390/en11030596