Abstract
Energy management systems are designed to monitor, optimize, and control the smart grid energy market. Demand-side management, considered as an essential part of the energy management system, can enable utility market operators to make better management decisions for energy trading between consumers and the operator. In this system, a priori knowledge about the energy load pattern can help reshape the load and cut the energy demand curve, thus allowing a better management and distribution of the energy in smart grid energy systems. Designing a computationally intelligent load forecasting (ILF) system is often a primary goal of energy demand management. This study explores the state of the art of computationally intelligent (i.e., machine learning) methods that are applied in load forecasting in terms of their classification and evaluation for sustainable operation of the overall energy management system. More than 50 research papers related to the subject identified in existing literature are classified into two categories: namely the single and the hybrid computational intelligence (CI)-based load forecasting technique. The advantages and disadvantages of each individual techniques also discussed to encapsulate them into the perspective into the energy management research. The identified methods have been further investigated by a qualitative analysis based on the accuracy of the prediction, which confirms the dominance of hybrid forecasting methods, which are often applied as metaheurstic algorithms considering the different optimization techniques over single model approaches. Based on extensive surveys, the review paper predicts a continuous future expansion of such literature on different CI approaches and their optimizations with both heuristic and metaheuristic methods used for energy load forecasting and their potential utilization in real-time smart energy management grids to address future challenges in energy demand management.
1. Introduction
The generic idea of smart grids for energy management was created to advance a future power market that is facilitated with appropriate communication and intelligent energy control technology that is able to smartly maintain a balance between the distributed energy resources and the demand requirement in a user friendly manner. This modern electricity market is highly subjected to multiple environmental, economic, political, and social fluctuations, warranting the need for a self-adaptive and fully optimized energy management system. This is driven in part due to the underlying instabilities in the modern-day energy sector that is likely to also moderate the shape of the energy demand, leading to a difficult decision-making process by energy market operators, governments, and the consumers [1].
Demand-side management is an essential part of a smart grid that creates a decision platform for key stakeholders to trade the energy between the consumers and providers. This can enable the providers able to cut the peak load demand and reshape the energy load profile in such times when stringent measures need to be implemented, while the consumers have an option to make more informed decisions about their energy consumption schedules [2].
Effective operation of demand-side management requires an accurate prior knowledge about energy load patterns. Knowing the probable load pattern can also lead to better policy and scientific decisions being made by the energy utility operators. Even in a direct load monitoring system, a minute-based load prediction can prevent the system from misleading due to the deficiency of smart meters and other anomalies. It is therefore prudent that smart grid systems deploy the relevant knowledge-driven system to appropriately and sufficiently control and supply the correct energy load to the consumer market [3].
In order to manage their demand amicably, utilities are often tempted to create suitable databases of historical loads at a house level within a neighborhood or over a regional scale to extract the outline of energy usage [4]. There have been many studies in this regard, for instance; a survey [5] was carried out between 1999–2000 to address the domestic household energy usage patterns of major appliances in different type of houses with the average monthly electricity consumption of about 100 kWh or more. Another study performed by the TxAIRE Research and Demonstration House aimed to trace the outline of energy consumption of heat pumps in the residential sector, considering the environmental factors that were likely to moderate the demand [5]. However, by introducing smart meters as a new component of their smart grid system, an avalanche of immensely useful energy usage information became available to the energy markets [6].
Demand patterns are potentially influenced by several factors, such as climate change, time periods, and holiday or working days. Some of the other factors may contribute the social and behavioral factors of a given community, economic situations, and other social activities—including power market policies. The demand pattern, however, is more complicated in a smart market with the variation of the electricity price tariff. Therefore, these influential factors can make the load forecasting much more complex, thereby placing an increasing emphasis on smart, self-adaptive, and optimized energy management and modeling system.
Although load forecasting is a decisive process in power market design, optimization, distribution, planning, and accurate and reliable forecasting techniques can help increase power system reliability and the practical functionality of a load management system to satisfy consumers and energy utilities. Such systems can also assist National Electricity Markets (NEMs) in saving considerable operating and maintenance costs.
Early research works have been conducted to predict the load (or energy demands) by conventional regression analysis approaches [7]. However, it is difficult to capture the demand patterns only by a statistical analysis of data using historical load data that has much more complex features in the independent variables that are directly used for statistical calculations [8]. The statistically-based approaches are very significantly data-dependent, and so, they do not perform well when applied to another utility where the features in that data are discernibly different from the original data used to formulate a predictive equation. In order to obtain a greater forecasting precision, more elaborate, flexible, and non-linear forecasting methods must be developed and evaluated in a real-time energy management system.
Computational intelligence (CI), reviewed in this paper, through their self-adaptive mechanisms, can enable the demand management system to mimic the intelligent behaviors present in complicated and continuously varying environments such as the smart grid energy market [9]. CI normally denotes the ability of computer algorithms to intelligently learn a specific task from the experimental perceptions or features present in prior usage (and potentially repeating) energy data [10]. The unique feature of CI methods is related to their ability for autonomous operation without requiring any complex mathematical formulations or quantitative correlations between the inputs and the output.
Intelligent load forecasting (ILF) techniques, whose state-of-art is reviewed in this paper, are generally the CI-based smart solutions used to identify load patterns in energy demand-side management. The ILF algorithms are able to learn from historical load data and the related influential factors that have governed the use of energy based on the consumers’ needs. Common ILF techniques implemented for very short time horizons—i.e., the one minute to the next hour—are known as the very short-term load forecasting (VSTLF), while predictions for daily or weekly prediction time horizons are known as short-term load forecasting (STLF). For longer time spans—ranging from a month to a few years—the phrase medium-term load forecasting (MTLF) is used, and if the time cycle is from a year to a few decades, the phrase long-term load forecasting (LTLF) is commonly used [11]. All of these time horizon categorical predictions have been addressed in several previous studies (e.g., [8,9]). The time horizons of load predictions depend on their specific applications in power system planning. For example, the operational and maintenance scheduling is coupled with VSTLF, while the distribution and transmission planning requires daily scheduling with STLF. On the other hand, medium- and long-term forecasts are used for finance or power supply planning [12]. For a demand-side management in smart grid, most of the activities belong to daily operation with minutely and hourly cycling, such as decision making for load control and voltage reduction. However, longer-term planning is also essential in smart grid which can be accomplished through MTLF and LTLF [11].
In published literature, various CI-based machine learning algorithms have been applied to develop an ILF model, where the common algorithms include artificial neural networks (ANN), fuzzy logic (FL), support vector machines (SVM), etc. However, given that these algorithms have been applied in separate and often isolated fields of study, there has been a lack of extensive evaluation of these algorithms according to their single model or their hybridized model applications. In most of the studies, however, the hybridized version of CI models (incorporating metaheuristic optimizers) have yielded significantly better performance than their single model counterparts.
In the context of the present discussion, CI-based single technique models refer to the studies where only a heuristic, single machine learning algorithm (e.g., multi-layer perceptron (MLP) or SVM) is used as the primary forecasting method whereas the other (hybrid modeling) arrangement refers to those studies that have used a combination of each of the two or more than two metaheuristic modeling approaches, such as the firefly algorithm neural network (FANN) and the genetic support vector machine (GSVM). For example, Dudek [13] designed a CI-learning algorithm for ILF using the artificial immune system (AIS) with a local feature selection process driven by a metaheuritic algorithm. In a study by Azadeh et al. [14], the performance of an integrated genetic algorithm (GA) and an ANN algorithm (constructing a genetic neural network (GNN) model) was assessed to construct a logarithmic-linear model for energy load forecasting. In these investigations, the accuracy of the hybrid CI-method far exceeded that of a standalone, single model method.
The focus of this research review is to explore the current state-of-the-art of CI techniques used to advance ILF in energy smart grid and also to categorize the different CI techniques (i.e., both single and hybrid models) according to their chronological schemes. Furthermore, the review also performs a qualitative analysis of ILF method including the examination of the accuracy of results that were predicted by these different methods for ILF in real energy management systems.
The rest of the paper is ordered as follows. Section 2 describes the methodology applied to perform a review of the state-of-art techniques for ILF in practical scenarios. Section 3 addresses the effective information sampling provided as the load database and Section 4 provides the state-of-the-art of single and hybrid CI techniques applied in area of ILF. Section 5 outlines the criteria for model evaluation, followed by the methods for evaluation detailed in Section 6. Lastly, Section 7 draws the overall conclusions of this review paper.
2. Methodology
This current review is based on more than 50 capstone papers detailing the design, evaluation, and application of ILF systems to formulate potential solutions to the load scheduling problems in real-time smart energy grids
According to literature, the most widely employed CI approaches for load forecasting were the multilayer perceptron (MLP), self-organizing maps (SOMs), deep learning (DL), extreme learning machine (ELM), SVM, fuzzy rule base (FRB), fuzzy C-means (FCM), wavelet transform (WT), particle swarm optimization (PSO), AIS, genetic programming (GP), firefly algorithm (FA), fruit fly optimization algorithm (FOA), differential evolutionary algorithm (DE), artificial bee colony (ABC), harmony search algorithm (HS), simulated annealing algorithm (SA), and K-shape clustering. These techniques were basically designed to deduce the relevant knowledge about the different load patterns via model feature identification and learning stage process. The results indicated that the sample complexity must be analyzed to extract information relevant for the forecasting process, and that a set of concepts related to the problem at hand were required to develop efficient learning algorithms.
Learning algorithms are basically data-driven methods based on the multi-disciplinary ideas that combine the power of computer science and statistical inference, including probability and optimizations [15]. Figure 1 provides schematic flowchart of the simple learning model including the various stages that are commonly known as:
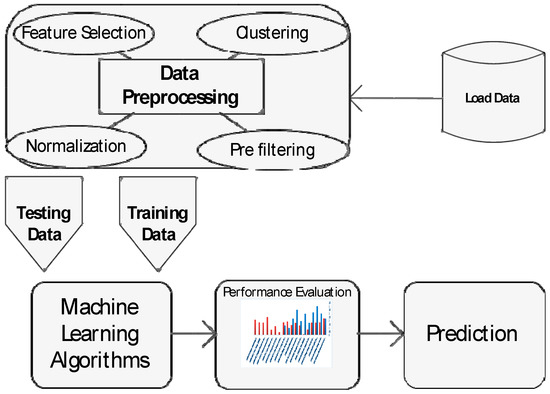
Figure 1.
Schematic of a machine learning model.
- Pre-processing stage
- Learning stage
- Performance evaluation stage
In an intelligent learning model, the algorithm is started with a given collection of the labeled data samples, which provide the input features for the model. Commonly, the load datasets consist of historical energy consumption, weather information, and the time period such as the different hours of the weekdays and holidays that are likely to affect the energy demand. However, in a smart grid environment with a higher volatility and sharper variations, more information must be provided in databases in order to enable the learning algorithm to be autonomous and self-adaptive. This additional information contributes to the demand/production dynamics of the smart grid. Therefore, different studies have discussed on collecting additional information, such as the behavioral load usage patterns, electricity price tariff, economic, and social factors to the databases. This has been discussed in greater detail in Section 3 with some examples of the smart meter databases and other related datasets.
The first phase in the learning algorithm is the pre-processing stage, as schematized in Figure 1, which consists of a set of data processing techniques such as a feature selection (or dimensionality reduction) procedure, data normalization, clustering of the data patterns, etc. The normalization is the process of removing the inappropriate and possibly disturbing effects of different variation ranges of the input features in the model’s training phase. The normalized data range in between 0 and 1 and constitute the input-target matrix values. The input matrix which is the main subject of the training phase is then incorporated with duplicated data. A proper feature selection method is used to eliminate the redundancy of data by extracting the most prominent feature in the training data.
Pre-filtering is a preliminary technique that is used to classify the data with multiple components into different clusters. This technique is basically used to reduce the possibility of the clustering failures. Pre-filtering can also be applied for the detection of the incorrect measures, for example, due to the malfunctioning of the demand meters or particular anomalous behaviors of the customers (e.g., low demand in holidays).
Pre-processing techniques are highly essential in fast and efficient CI methods, especially for the massive datasets measured by the smart grid energy meters or sensors. To deal with these massive databases, researchers have applied different methods for reducing the volume of data and to extract the most pertinent data features, as well as any anomalies in the training data that are detected due to the deficiencies found in the energy meter and the measurements. These techniques are discussed in greater detail in Section 4.
The second phase of the ILF, as illustrated in Figure 1, is the learning phase, intends to incorporate a number of learning algorithms into a precise and a carefully integrated class of forecast engines to predict future energy demand. For this purpose, the data are partitioned randomly into a training sample and a testing sample. The size of the training sample is dependent on the associated relevant features driven from input dataset, which can guide the learning algorithm in an effective fashion to forecast the future energy demand. The selected features are also required to help attain a greater accuracy in the training of the learning algorithm by determining the most suitable model parameter values. Finally, the optimal model with the smallest mean square error in the training stages is selected and validated with an independent set of test samples.
Several learning algorithms have been embraced for load forecasting by energy researchers. These algorithms can be organized into those trained via a supervised or an unsupervised learning procedure. Some studies use an isolated (or single, standalone) technique while the others combine (or integrate) different algorithms to better augment the learning procedure. In some studies, the integration of a supervised clustering stage prior to an unsupervised learning procedure might also considerably increase the performance of final prediction model. In Section 4, the state-of-the-art of the common techniques used for ILF is discussed and the potential solutions resulting from the analysis of several ILF approaches have been highlighted.
Performance evaluation of the algorithm is considered to be the last stage, where the performance of the learning algorithm is evaluated based on the test error criterion, such as the mean square error. However, various other error functions have been defined for this task considering different evaluation measures. More details about the most popular model evaluation functions utilized for load forecasting are discussed in Section 5.
Table 1 lists the investigations currently existent in published literature, including a brief overview on the commonly used single and hybrid CI methods for ILF. The table consists of two horizontal main division (i.e., single and hybrid algorithms) and four vertical columns indicating the type of the classifier, title of the paper and the paper’s primary objective.

Table 1.
Publications on CI techniques for ILF.
3. Datasets Used in CI Approaches for ILF
ILF development at a very first stage that involves the generation of a database representative of the historical load profiles in a regional power market or in a smaller residential or a commercial sector. Table 2 indicates some of the electricity load datasets provided in a number of technical papers either as private datasets or online databases.

Table 2.
Datasets classifications.
In accordance with Table 2, several datasets were used by researchers with different time interval records, such as sub-hourly, hourly, daily, weekly monthly, and annual periods. The types of loads in these datasets were acquired from residential, commercial, industrial, or more generally the regional utility sectors. For instance, the hourly load of an office building located in Guangzhou, China was used to predict the one hour ahead load [63]. Furthermore, three public loads for Spanish, Australian, and New York power market were selected for daily load prediction [65].
Thanks to the smart meters and sensors available in smart grid, the users’ information in the power market is available over minute based measurement databases. In [50] the smart meter datasets for the residential sector in the United States of America and Ireland are utilized for load forecasting. However, these databases are not informative enough to enable the learning algorithm to deduce existing load features.
Databases also include further information about the weather conditions and calendar data, which are correlated to these energy load profiles. For example, in a private dataset generated in [61] the weather and season information are provided together with the historical load in the database. Hernandez et al. [49] suggested that even in a small market of a micro grid, the local energy management system can still benefit from the influence of weather on the load profile.
Electricity price provides important information about the demand for energy. That is, in a smart grid market, the energy load profile is highly influenced by the price tariff variations. One example of such a study is the work of Ghasemi et al. [66] that has used the public New York Independent System Operator (NYISO) Electricity Market data consisting of the electricity price and demand information to design a demand-side management system in a real-time smart energy grid.
Increasing the volume and variety of model design data is likely to lead to more prominent features of the loads and therefore, make the model more accurate. The choice of the features among the data samples is left to the users and reflects the prior knowledge about the risks (or uncertainties) in the learning algorithm. Different-sized databases are shown in the table. The amount of training sample is related to the size of dataset, but normally the training samples must be large enough to provide pertinent information for future status of the energy demand. For example, if the sample size is relatively small, the train sample should better to be larger than test data, as the learning and prediction by a CI approach is directly related to the training sample size.
Finally, according to the data values and the range, the issues of non-linearity, data redundancy, and the type of the data in a modeling dataset must be addressed to develop a suitable CI technique.
4. State-Of-The-Art of Single and Hybrid CI Techniques Applied for ILF
In this section the most applied CI methods for ILF are discussed on the basis of single or a hybridization of several modeling techniques. Single methods including the FL, ANN, AIS, GP, ABC, PSO, and SVM are brought in the single classifier system used to develop a precisely modeled energy demand forecasting system. The section continues with a discussion of hybrid methods applied by several researchers for advancing or improving the accuracy of an ILF system. These methods are technically invented by combining different CI algorithms in order to develop the performance skill of the integrated forecasting techniques. However, choosing proper algorithms for a combined technique are of prime importance towards developing a successful hybrid energy management system.
Some studies have aimed at integrating feature extracting algorithms in the data pre-processing stage. These algorithms can be employed to improve the training procedure of the learning algorithm used in a smart grid system. For example, a clustering algorithm such as the k-shape clustering or a classification algorithm like the FL are used to classify the data based on their similarity in the input feature. Therefore, each cluster can be trained individually that can lead to an enhancement in the forecasting performance.
Other algorithms might be combined to find the optimal parameters in the learning stage. Some of these optimization algorithms are advanced enough to find the global optimum, while the others may suffer from being trapped in the local minima while forecasting the future value of the energy demand.
Finally, the advantages and the disadvantages of each of these forecasting techniques are argued to provide a critical overview with condensed information useful for early researchers in energy demand management.
4.1. Single (Stand-Alone Modeling) Methods
4.1.1. Fuzzy Logic Sets
Fuzzy set theory is one of the principal modeling technologies in artificial intelligence (AI) domain. This theory was primarily introduced by Zadeh in 1965 [68] as a generalized classical set theory. A FL model maps a set of input variables to a set of output variables using IF–THEN logic statements. Such a set is defined by a membership function, which determines the membership values for each object.
The primary application of fuzzy sets to the field of power system was presented in solving power systems long-range decision making problems [8]. Since the early work of Economakos (1991) [69], fuzzy set has been widely used as an aid for decision making on load data, aimed at dealing with numerical aspects and uncertainties of load demand in power markets.
An advantage of the FL approach is related to its capability to represent meaningful description out of blurred concepts. This feature of FL can be useful for load datasets with uncertainties and non-linear relations between the input and output parameters. For instance, Danladi Ali [70] developed a FL approach to map the highly non-linear relationships between the weather parameters, such as temperature and humidity and peak load profiles. The results represented the feasibility of the proposed model to forecast a year-ahead load with approximately 6.9% mean absolute percentage error (MAPE) value.
FL also has been used for smart data analytics for smart grid energy systems. Smart meters which are installed at the entry point to the consumer premise are monitored in a so-called non-intrusive load management (NILM) system to find the load activities. Welikala et al. [17] proposed a load prediction model to augment the smart meter readings in case of a deficiency and anomaly detection process. The models constructed on fuzzy system use the individual appliance usage pattern to predict data ahead of the real time. The feasibility of the proposed method has been confirmed by a real-time implementation of the system.
Although FL systems are able to decide on uncertain information and explain the related decisions, but they cannot acquire control rules and their precise parameters in the rules. To avoid such difficulties, the artificial neural network model can offer a learning mechanism to deal with the cognitive uncertainties. Hence, the incorporation of the fuzzy concept into the neural network model is likely to enable the system to reason more like a human.
4.1.2. Artificial Neural Networks (ANN)
ANN is an intelligent method in machine learning and cognitive neurosciences that is motivated by the functional aspect of the biological neural networks [71]. ANNs can be organized in different arrangements to implement a range of tasks including, data mining, classification, pattern recognition, forecasting, and process modeling. It provides solutions where linear or nonlinear mapping of the model’s input–target features are required, due to its learning ability, parallel processing, generalization, and the error tolerance. The main advantage of neural network is that no clear relationship between the input variable and the output variable is required to be specified before the prediction process. Thus, it is the most popular learning tool for non-linear regression modeling used in load forecasting.
Different architectures of the ANN model can be divided into the MLP, SOM, DL, and ELM.
MLP is a typical arrangement of the feed-forward neural networks containing multiple layers of nodes, each of which is connected to the next layer. This algorithm is designed to train the data via an unsupervised learning procedure using back propagation training technique [72].
In the early work of Park et al. [73], an MLP architecture was developed to predict the one hour ahead and 24 h ahead load. The results were consistent with the actual load by approximately 1.40% and 2.06% error for the hourly prediction and daily prediction data, respectively. However, the only weather data considered in this study was temperature. Besides this, according to the error of performance, specified days such as holidays had different patterns compared to the weekly start up days like Mondays. In that study, it was suggested that one must add sophisticated topology to the neural networks in order to capture these data features.
Alireza Khotanzad et al. [74] designed an MLP load forecasting model by dividing the relationship between load and temperature into three types of hourly, daily and weekly trend. By combining these three forecasting modules, the hourly load of the one- to k-days ahead (k ranged from two to seven) can be predicted dynamically by adaptive weight update strategy. The best results were obtained with approximately 1.67% and 2.34% MAPE values for the hourly and daily forecasts, respectively. Besides the satisfactory results obtained by this model, a significant disadvantage was that it is likely to take a large MLP structure to train the real load data. In addition to this, the fact that the input data for three modules are likely to raise the redundancy issue, were also a major drawback of the proposed method. The model was further improved by the authors to address the aforementioned issues [75]. The new generated MLP model, considered of 24 small MLPs, each designed and applied for every hour of the day, while the input data were divided in four categories of time of the day due to similar affecting variables for each category. The primary weather information (temperature and humidity) was then fed to the engine both by the actual weather values and the online forecasted values. The obtained results with forecasting accuracy below 3.0% were considered rather well for the electric utility. However, using the forecasted weather information in the model lead to 1% increase in the error values.
Recently, several studies have examined neural networks to predict the demand in a smart grid environment. For example, Javed et al. [76] determined anthropological data (i.e., general behavior of the house occupants) and structural data (i.e., physical property houses) to develop an MLP based STLF model for multiple houses. The model improved the overfitting problem for large data of multiple houses by training the variable time series instead of one. The results showed a greater level of accuracy for multiple loads and a decrease in the error considering the richer dataset.
SOM neural network is an unsupervised clustering method [77], with a special property of creating local representations of the input data. Lamedica et al. [78] developed a two stage load forecasting model where the Kohonen SOM was used as unsupervised method for clustering the historical load into various load profiles by extracting multiple features in anomalous days. The forecasting was then performed in a second stage via the supervised MLP arrangement. The proposed method led to a decrease in the error value comparing to the results of MLP method without clustering. Later on, Lopez et al. [22] developed a SOM algorithm for STLF. The map was trained using meteorological and historical load data. In addition, the effect of different input selection and data frame on training the map has been investigated. The model was also validated by applying it to the Spanish electricity market.
More recently, the study of Llanos et al. [23] determined social aspects of the community, such as the types of homes and families, to obtain the residential load profile of a micro grid environment. Individual community aspects clustered by the SOM algorithm and the load profile for each cluster was selected from the database. The results of the proposed method were favorable and consistent.
DL is a division of machine learning approach depending on ‘deep’ architectures, which are arranged by multiple processing layers in a neural network, to solve highly nonlinear relationships between the independent and response variable. Although DL has received broad attention in the forecasting community, it is thought to suffer from over-fitting issues due to a large amount of layers compared to the classical neural network model. The overfitting issue in DL has been addressed in a study by Shi et al. [24] that attempted to increase the data diversity and volume fed into a developed pooling-based deep recurrent neural networks (RNNs). The proposed method was able to increase the input volume by adding historical load data of the neighbors. The method also deduced the correlation between neighboring households by generating more learning layers before the occurrence of overfitting by the model. By providing the pooling customers’ profiles, the information related to the common sharing uncertainties is likely to be increased, which can lead to more accurate forecasting results. The method tested on 920 smart metered customers from Ireland showed that the results were satisfactory, although the author recommended further research necessary to exploit the optimal pooling strategy by pooling customers with differing features.
ELMs is a learning scheme used for single hidden layer feed forward neural networks. ELM has a remarkable generalization capability and is considered to be a faster learning algorithm than the conventional neural network models [79]. Ertugrul [26] applied the ELM approach incorporated into the RNN, named as the recurrent extreme learning machine (RELM) to achieve higher accuracy and lower estimation error frothier load prediction model. RNN was seen to lead to better results in the forecasting dynamic systems compared to the feed forward ANN model. Thus corporation of the ELM into the recurrent neural network (RELM) with the same training (much lower) time as the ELM can be an effective solution for load forecast modeling in real-time dynamical systems.
In spite of many attractive features of neural networks mentioned above, there are some drawbacks which can lead to over-parameterized model and thus, poor generalization ability. Such disadvantages include the overfitting of the data and uncertainties in the optimal arrangement and initial parameter values.
4.1.3. Support Vector Machine (SVM)
SVM is a machine learning method proposed by Vapnik et al. [80] that supersedes ANNs for solving classification and regression problems. Structural risk minimization (SRM) is a distinctive feature of the SVM model that aims to address the overfitting problem since it does not consider empirical risk minimization. Minimizing the upper bound of the generalization error instead of minimizing the training error (as with the case of the ANN model), the SVM model can be used to improve the generalization performance as an important feature of this learning model.
The work of [63] indicates the superiority of SVM method to reduce the error of load forecasting compared to back propagation neural network. It concluded that SVM method is a promising alternative approach for the prediction of the cooling load in building area.
For a study in Queensland, Australia’s largest state, Al-Musaylh and co-authors [81] used the Australian Electricity Market Operator (AEMO) historical demand to model the very short-term (0.5 h, 1.0 h and 24 h) demand using SVM, and benchmarked the performance with multivariate adapter regression spline (MARS) and auto-regressive moving average (ARIMA) model. The results showed for 0.5 h and 1.0 h short-term forecasting horizons, the MARS model outperforms SVR and ARIMA displaying the largest Willmott’s Index (0.993 and 0.990) and lowest mean absolute error (45.363 and 86.502 MW), respectively. In contrast, the SVR model was superior for daily (24 h) forecast horizon demonstrating a larger value of the Willmott’s Index (0.890) and a lower value of the error (162.363 MW).
Chen et al. [28] proposed a mid-term load forecast (daily maximum load for next 31 days) model utilizing SVM in a competition for load prediction in EUNITE Network. The model considered week days and holidays as selected parameters, as well as the historical load demand in a time series order. However, the temperature data was not considered conservatively due to imprecise information. It has been shown that by selecting the proper data segment, the performance of the forecasting model enhanced.
SVM has good generalization capability and is able to overcome the shortcomings of the ANN algorithm. The SVM model is seen to perform quite accurately for small sized datasets while the neural network performance is be highly dependent on the training sample size and information quality. Therefore, according to the sample size one must be selected.
4.1.4. Clustering Techniques
Clustering algorithms have received a significant attention over the last decade to deal with time series data. In a smart grid environment facilitated by smart meters, huge amount of load data is generated in the shape of time series sequences datasets. The popularity of clustering techniques with time series is not only due to its powerful unsupervised heuristic strategy as a stand-alone algorithm, but also its combination with other algorithms to provide preprocessing steps to the forecasting task [82].
K-shape is an iterative clustering algorithm like k-means in which the degree of similarity is recognized by measuring the distance to the centroid of each cluster. However, the k-shape designed to maintain the shape of time series sequences as comparing them. For example, Alvarez et al. [30] employed k-shape clustering algorithm in order to group and label the data. The prediction is made by averaging all the samples instantly after the founded similar sequences. Moreover, the author has claimed that the predictions performed using the labeled pattern of data do not the real data values until the last step. The results for three different time series indicate the adaptability of the proposed method.
4.1.5. Genetic Algorithm (GA)
GA is one of the most famous evolutionary algorithms providing optimization solutions for search problems. It has the ability to search through a space to find the nearly optimal solution. GP is a specialization of GA used to evaluate how well the computer has performed by the measure of the fitness function [83]. One of the specifications of GP is that it does not need a presumption of any functional relationship between dependent and independent variables, which leads to better performance compared to the regression methods. This has been proven by Lee et al. [33] who investigated the application of GP to solve the LTLF problem where the results of GP model were seen to outperform the results of the regression methods.
4.1.6. Artificial Bee Algorithm
Artificial Bee algorithms inspired by the intelligent foraging manners of a honeybee swarm.
Two popular algorithms are the honey bee mating optimization (HBMO) algorithm and the ABC algorithm [84].
Safamehr et al. [31] utilized ABC algorithm and quasi-static technique for minimizing the energy cost and reshaping the load profile by reducing the peak demand. Simulation results show that applying this method for optimal energy scheduling will lead to about 8.33% and 11.11% cost reduction and peak reduction, respectively.
4.1.7. Artificial Immune System (AIS)
AIS is a bio-inspired optimization technique [85] that stimulates the adaptive immune system of a living creature to solve the real-world problems. Some attractive features of AIS such as its ability to organize and optimize automatically, training form examples, multilayer architecture, and generalization capacity make it a proper learning and optimization tool in wide applications [86]. AIS has been used in a study by Grzegorz Dudek [13] to design a learning regression algorithm for STLF with local feature selection (AISLFS). The simulation studies have shown high accuracy of AISLFS, which is a strong competitor for other popular STLF models such as regression methods, exponential smoothing (ES), and neural network.
4.1.8. Particle Swarm Optimization (PSO)
PSO Is an optimization technique first identified by Kennedy and Eberhart [87] inspired by social behavior of bird flocks, wherein a number of individual solutions (particles) are engaged to search for the optimum answer in a hyperdimensional space. Even though PSO is similar to evolutionary algorithms such as GA, it obtains better convergence efficiency which makes it a well-known alternative for evolutionary algorithms. It also searches a larger portion of the problem space than traditional optimization techniques.
M.R. Al Rashidi et al. [32] applied a PSO method to estimate the long-term load pattern which is formulated as an optimization problem. It was found that the PSO method forecasts better than least square method (LES) and is an effective tool for parameter estimation.
4.2. Hybrid Methods
4.2.1. Neuro-Fuzzy (NF)
Neuro-fuzzy is a combined method for applying neural network learning method to fuzzy interference systems [88]. This hybrid method first introduced by J.S.R. Jang [89] to cover the fuzzy system lack capabilities of leaning and having memories, by combining the reasoning mechanism of fuzzy sets with the learning arrangement of neural network. In fact, fuzzy classification technique help neural network to find the best parameters by arranging the rule base. This can help the forecasting task with the rough datasets which is common in databases [90].
FL is an effective technique for characterizing the uncertainty in load behavior caused by different environmental or behavioral factors (consumers’ reaction to the price signal). For instance, a neuro-fuzzy model has been applied to consider the effect of human behavior on load profile in an hourly priced tariff utility market by Khotanzad et al. [91]. In this study FL was used to create price sensitive load data from the historical dataset without price information. It has been shown that the performance of NF based approach was superior to single neural network.
In addition, Yun et al. [34] also evaluated the effect of real electricity price on electricity consumption and comparing the forecasting results using neural network and neuro-fuzzy systems. It has been observed that determining the electricity price decreased the forecasting accuracy from 2.71% to 1.8%. Although the results using hybrid neuro-fuzzy was slightly better than neural network.
4.2.2. Artificial Neural Network and Wavelet Transform
WT is a powerful tool for analysis of non-stationary signals in time-frequency domains [92]. This transform is able to decompose time-series data into different level containing low frequency and high frequency components. Transformation of load inputs is a technique to improve the data stationary which has been reported to be used in integration with neural network for input selection. An example is a study by Guan et al. [37] wherein the wavelet technique was applied to decompose the load into multiple frequency components. The transformed normalized data was fed to the neural network where the features of individual components were learned. Results on a dataset form ISO New England indicated the well performance of wavelet neural method.
In a different study by Zhang et al. [93] the WT was utilized to capture the useful information on various time scales. The proposed method employed a neural network learning algorithm fed by recomposed data to predict electricity load. The method was validated with promising results on the Australian national market.
4.2.3. Optimization Algorithms Integrated with Artificial Neural Network
Artificial neural network is a very promising forecasting engine and has been widely used for demand prediction; however, the performance of the prediction depends on how well the model fit to actual data. A neural network with predefined arrangement using a backpropagation training algorithm suffers from convergence to the local minimum and sensitivity to initial values of parameters. In fact, the possibility of finding the optimal solution in a multi-layered neural network with gradient-based learning algorithm is low which results in multiple local minima in cost function. Thus, different optimization algorithms have been proposed in literature, providing various searching techniques to find the optimal solution as explained in following.
Artificial Neural Network and Genetic Algorithm
GA is one of the optimization engines providing a global search technique which has been suggested to solve non-linear optimization problem of neural network. This integration implemented in a study by S.H. Ling et al. [38] to develop a load forecasting model. The GA with arithmetic crossover and non-uniform mutation employed to aid adjusting the parameters of proposed network. Hence the number of parameters reduced by proposed technique, the performance of the prediction model improved in comparison with traditional feed forward neural network.
In another study, A. Azadeh et al. [14] assessed the performance of an integrated GA and ANN algorithm to create a logarithmic-linear model for energy forecasting. Variables such as price, number of customers, and the actual value of electricity consumption employed to the GNN. By tuning the parameters via GA, the best coefficient with minimum error has been identified. The proposed method performed more accurately compared to regression and time series.
Artificial Neural Network and Fruit Fly Optimization Algorithm (ANN-FOA)
FOA proposed by Pan [94] is a type of evolutionary computation and optimization technique. This optimization algorithm is based on swarm intelligence with the advantage of being easy to understand and code compared to other algorithms. The searching feasibility of FOA algorithm is a help for parameter selection of neural network. For example, Li et al. [39] developed a hybrid annual power load forecasting model combining FOA and generalized regression neural network (GRNN), where the FOA was used to automatically select the appropriate spread parameter value for the GRNN power load forecasting model. The outcome demonstrates that the proposed hybrid model outperforms the GRNN model with default parameter.
Artificial Neural Network and Firefly Algorithm (ANN-FA)
FA is inspired by the flashing performance of fireflies and was first introduce by Yang [95] to address the optimization problem. FA was developed as a solution to the local optimal drawback of neural network.
A new modification of FA was developed by Liye Xiao et al. [41] to optimize the weight coefficients of combined FA neural network model for load forecast. The forecasting ability evaluated using the dataset from New South Wales, the State of Victoria, and the State of Queensland in Australia. The results of the proposed algorithm using FA were compared with other combined algorithms such as GA-ANN and WT-ANN. The results of the proposed method outperformed the later techniques.
Artificial Neural Network and Artificial Immune Systems (ANN-AIS)
Both the AIS and the artificial neural network are biologically-inspired algorithms advanced to identify the complex patterns. The immune algorithm can maintain the diversity of population and overcome the flaw of premature phenomenon. This special characteristic of AIS improves the speed of searching and precision of optimization.
You Yong [42] applied AIS to design a neural network system for STLF. The proposed method (AIN) benefits from the fast searching capability of AIS algorithm to find the optimized parameters. The results prove the feasibility of AIN for STLF model.
Artificial Neural Network and Particle Swarm Optimization (ANN-PSO)
PSO algorithm adapted to neural network to find the optimal arrangement as well as network weights. Telbany [96] evaluated the forecasting feasibility of MLP recurrent network trained by PSO for daily load forecasting. PSO aided to shed some of the neuron weights by decreasing their values via global searching. The results for PSO outperform the back-propagation algorithm.
Liu et al. [44] also described a hybrid model including PSO for parameter optimization to predict the load in a micro grid with small capacity and high randomness. This hybrid method uses an extreme learning tool to train the preprocessed dataset after filtering and decomposition techniques. It was concluded that the proposed hybrid method performs well in micro grids with high load fluctuations.
4.2.4. Artificial Neural Network and Clustering Techniques
In unsupervised leaning algorithms such as neural network, classification of variable features into multiple clusters helps the training accuracy. Various clustering techniques are widely used on load data to divide the customers into sub-populations with similar demand profile [97]. Thus, a more precise model is provided for each cluster instead of developing one single model for accumulated load while the final forecasting model is a combination of individual models.
Fahiman et al. [98] improved the accuracy of DL-based forecast model by using k-shape clustering algorithm. In this method, k-shape clustering technique was an aid to determine the load consumption behavior of customers into prediction model and to increase the model accuracy. It has been pointed out that the accuracy of the prediction model depends on accuracy of the clustering method as well as the load forecasting method. The new method validated on a publicly available real-life dataset demonstrates the model accuracy improvement over existing methods.
In another example by Hernandez et al. [49] k-means clustering algorithm integrated with MLP for load prediction in a micro grid environment. The outcome confirms that the model produces low errors compared to other simple models that are not specialized by means of classification and clustering.
Improving the clustering technique may contribute to the optimal number of clusters. For example, Quilumba et al. [50] evaluated the suitable number of clusters in k-shape clustering technique to identify the similar load consumption pattern based on forecasting performance. Results indicated that by increasing the number of clusters from one to four, the forecasting accuracy was improved by 1.7% reduction in average MAPE value.
4.2.5. Optimization Algorithms Integrated with Support Vector Machine
SVM is a promising learning tool for load prediction that theoretically guarantee to obtain the unique global minimum. However, this unique solution is dependent upon providing necessary parameter for the user-selected kernel function. There are different optimization algorithms to optimize types of kernel function and all parameter values of SVM.
Genetic Algorithm and Support Vector Machine
Several studies proposed optimization methods using a GA for optimizing the SVR parameter values. Pai et al. [51] employed GA to capture the optimal parameters for annual load forecasting. The proposed method is an integration of recurrent SVM and GA, outperformed ANN and SVM in terms of accuracy. In addition, Wu et al. [52] developed a hybrid GA to search the optimal kernel type and parameter values of SVR. The model was able to identify the optimal values with lower prediction error compared to traditional SVR models without variable selection and data segmentation.
Support Vector Machine and Simulated Annealing Algorithm (SVM-SA)
Pai et al. [53] evaluated the feasibility of SVM based prediction model for electricity consumption due to its capability in nonlinear mapping. However, the lack of optimized parameter selection is covered by SA. The experimental results illustrate that the suggested method outperformed the harmonic model and hybrid model.
Support Vector Machine and Particle Swarm Optimization (SVM-PSO)
GAs and SA suffers from the lack of memory or storage function, which means by changing the population (GA) or temperature (SA), all the former information of the problem is demolished. In spite of the later algorithms, PSO has memory storage to keep the good solutions of all particles. Another unique feature of PSO is its few parameters to be adjusted which makes it an attractive optimization tool to solve the non-linear problems [99]. Hong [100] adopted PSO algorithm to select optimal parameters of a SVR model developed for load forecasting. Results illustrate that the proposed method generates better results compared to other SVR methods integrated with GA and SA. However, PSO like GA and SA could not efficiently overcome the local minimization drawback.
Support Vector Machine and Artificial Bee Colony (SVM-ABC)
ABC is a famous optimization algorithm to be combined with SVM for parameter determination. The unique feature of ABC is its ability make a good balance between global search and local search by conducting both in each iteration instead of initiating global search at the beginning and the local search at the ending stage as in PSO [101]. Hong [56] developed a hybrid ABC algorithm (chaotic ABC) for a better accuracy of an electric load forecasting model based on SVR and RNNs. The model deals with seasonal electric load vulnerability due to economic activities and climate changes. Results demonstrate that the hybrid of recurrent mechanism, seasonal adjustment, and chaotic sequence is useful to improve the forecasting accuracy.
Support Vector Machine and Harmony Search Algorithm (SVM-HS)
HS is a meta-heuristic optimization algorithm inspired by a musician effort to search for the better harmony [102]. This search algorithm is called during training phase to select the optimum parameter. In a study by Zeng et al. [58] harmony search adopted to LS-SVM in order to develop the process of determining the parameters of a short-term load prediction model. The results indicate the improvement in terms of efficiency in training speed and solution quality. Besides HS algorithm, PSO was also implemented to optimize SVM values for comparison purpose. Comparing results indicates that the MAPE of the proposed method is 0.77 percent lower than PSO while the training time and the training speed are 36.8% and 2.59% higher, respectively.
Support Vector Machine and Fruit Fly Optimization Algorithm (SVM-FOA)
The advantages of FOA algorithm is its easy understanding structure with shorter codes, and more importantly the fast searching ability to find the global solution. This algorithm has been used to find the two parameters of SVM applied for annual load prediction model in a work by Hongze Li et al. [59]. Computation results indicated lower forecasting error (within the range of 3%) for annual load, with faster searching time to find the global optimum compared to other heuristic optimization algorithm such as SA and genetic. Moreover, the superiority of FOA over PSO algorithm for SVM parameter optimization has been proved by Guohua Cao et al. [60]. This paper [60] focused on improving support vector regression feasibility to forecast the electricity load with seasonal tendency and complex non-linear characteristics. This improvement has been achieved by hybridizing SVM with FOA and seasonal index adjustment.
Support Vector Regression and Firefly Algorithm (SVR-FA)
FA is an evolutionary algorithm inspired by the behavior of firefly animals in the summer of the tropical areas introduce by Yang [102]. The stochastic characteristic of firefly is a help in solving complex non-linear multi-modal optimization problems. One of the advantages of FA is its searching ability to find the global and local optima simultaneously [103]. Another advantage is the independent work of individual fireflies which is in favor for parallel implementation. With all the benefits, FOA efficiency is still related to the initial parameters which are a drawback for the algorithm, as well as trapping in local optimal.
Application of FA for load forecasting has been evaluated by Kavousi-Fard et al. [61] through SVM model. The FA modified based on the crossover, mutation operators, and adaptive formulation to determine the SVM parameter values. The results for the proposed prediction model tested on the practical daily regional load data from Iran outperformed other searching algorithm such as GA and PSO.
Figure 2 outlined the tree plan classification of single and hybrid CI techniques applied for ILF. Figure shows great diversity along single and hybrid methods.
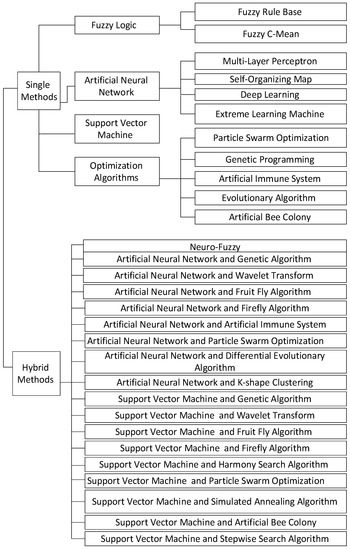
Figure 2.
Tree plan classification of CI approaches for ILF.
Table 3 listed the main advantages and disadvantages of single and hybrid methods as discussed earlier for each individual method. For example, FL algorithm is a proper tool for deciding on uncertain information, although it suffers from the drawback of cognitive uncertainties. This disadvantage of FL overcome by offering learner algorithms based on cognitive neurosciences such as neural network. However, some disadvantages—such as poor generalization ability, overfitting, and uncertainties in initial parameter values—are addressed as shown in the Table 3.

Table 3.
The advantages and disadvantages of single and hybrid methods.
Basically, hybrid algorithms benefit from the advantages of their constituent algorithms, thus higher accuracy and robustness is expected. For instance, combination of clustering algorithms into the neural network (ANN-k), provide prominent features before learning stage leading to improved forecasting performance. Although the optimal number of clusters is a critical factor in determining the features, it does not guarantee to cover optimal number of clusters. Other combinations such as SVM-FOA or SVM-HS benefit from optimal searching of the optimization algorithms in spite of more complicated architecture.
The dominance of hybrid methods over single algorithms demonstrated by qualification analysis and via evaluation metrics in Section 6.
5. Criteria Used for Evaluation
Evaluation indices of ILF techniques express how correct they are able to predict the actual load values. Several error metrics are provided to quantify the accuracy of each model based on statistical error properties.
Table 4 listed the broadly used static metrics for accuracy evaluation in load forecasting. The two commonly used metrics to evaluate the variance of forecast error are root mean square error (RMSE) and MAPE. Both these metrics indicate the spread in the errors, while over-under prediction is not differentiated [48]. To measure how likely a specific model over-under estimation the actual load value, the mean bias error (MBE) is used [64]. Another popular indicator is the coefficient of determination R2, which measures how the model predicts the trend of actual values. As it can be seen in the table, R2 is directly related to RMSE.

Table 4.
Evaluation metrics applied for ILF.
As an example, Ghasemi et al. [66] evaluated the efficiency of the proposed forecasting algorithm using MAPE and RMSE metrics. The MAPE value was reported to be within the range of 1.72–2.54% as well as RMSE value lower than 4%. In another study by Edwards et al. [64] the model was evaluated using MBE metric besides MAPE. The best forecast obtained by 1.38% MAPE value and 0.01 ± 0.11% MBE result. Furthermore, Kalogirou et al. [104] applied coefficient of determination (R2) to assess the qualification of the proposed method. The results for R2 value were equal to 0.9985.
6. Method Evaluation
In this section, single and hybrid methods are evaluated based on the reported results by several researchers. As mentioned in previous section, the model accuracy can be assessed by error metrics. Note that since the applied databases were not same for different studies, only the models within one dataset can be compared quantitatively. Therefore, here the comparing results of different studies brought together to gain better perspective.
Table 5 represents the MAPE values of the developed ILF techniques using the MLP and NF as single and hybrid classifiers, respectively. The results emerged from [34,91] and illustrated in Figure 3 to provide a better overview. As can be observed in both studies, integrating the FL along with neural network resulted in more accurate forecast with lower MAPE values.

Table 5.
Comparison of MLP and NF methods developed by [34,91] in terms of MAPE values.
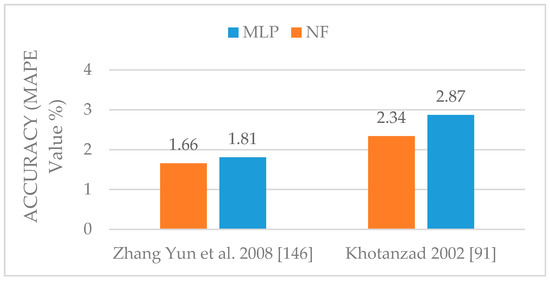
Figure 3.
Comparison of MLP and NF algorithms developed by [34,91] in terms of accuracy.
According to the values in Figure 4, combining the FOA optimization algorithm with ANN leads to more accurate performance compared to PSO, while both hybrid algorithms outperform the single ANN. Table 6 represents several advanced CI algorithms integrated with ANN. The MAPE values exhibited in Table 6 are the obtained result from forecasting model in [39,46]. These results are also represented by column diagrams individually in Figure 5 and Figure 6.
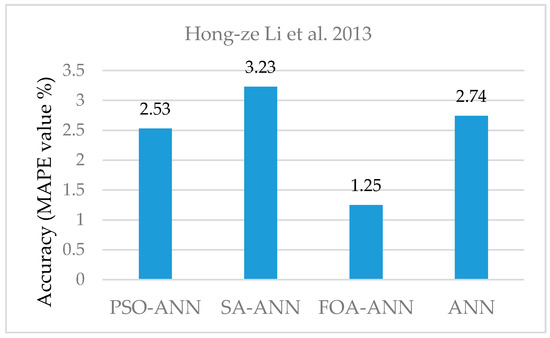
Figure 4.
Comparison of MAPE values of hybrid algorithms developed by [39].

Table 6.
Comparison of MAPE values of hybrid algorithms improved by [39,46].
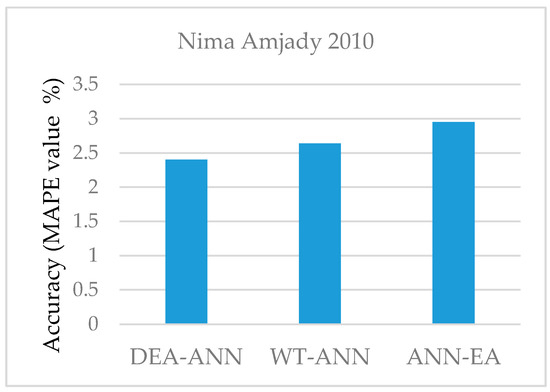
Figure 5.
Comparison of MAPE values of hybrid algorithms developed by [46].
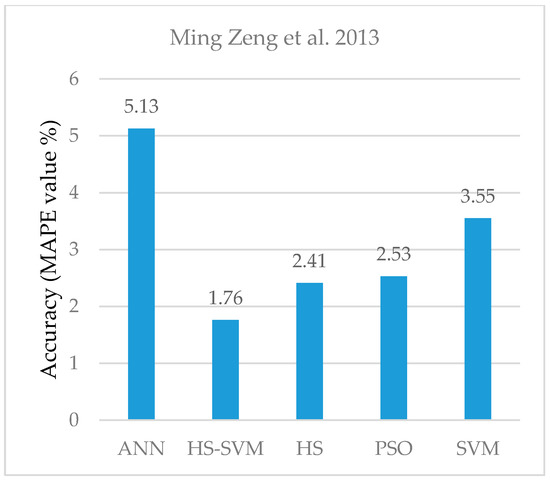
Figure 6.
MAPE values of several hybrid and single algorithms developed for ILF by [58].
MAPE values of three other hybrid algorithms improved by Amjady et al. [46] shown in Figure 5. It shows that the combined DE-ANN algorithm resulted in best with 2.4% MAPE value. By comparing this value to the MAPE value of EA-ANN, the superiority of DE over EA for optimizing the ANN parameters are proven. It also is evident that DE-ANN preceded WT-ANN by a 0.24% decrease in MAPE value.
Table 7 indicates the error values (in terms of the MAPE) of the single and hybrid methods developed for load forecasting by the study of Zeng et al. [58]. As can be seen in Figure 6, the single ANN algorithm has resulted in the highest error value. By applying an SVM algorithm, the accuracy level in terms of MAPE is seen to enhance by about 1.58% compared to the ANN model. The model performance is seen to further increase by developing the PSO and the HS algorithms for load forecasting by almost 1%. However, the best result obtained by integrating the HS algorithm with the SVM model with approximately 1.76% error value, confirming the superior performance of hybrid method over each single components.

Table 7.
MAPE values of several hybrid and single algorithms developed for ILF by [58].
Table 8 shows the accuracy level (in terms of the MAPE) for several hybrid algorithms combining the multiple optimization algorithms with the standalone SVM model. The error values for the forecasting models developed by Jiang et al. [54] have also been illustrated in Figure 7. It is shown that both of the GA-SVM and the PSO-SVM hybrid algorithms outperformed the single ANN technique. However, the PSO-based model has performed remarkably better than the GA-based model used to select the most optimal SVM parameters.

Table 8.
MAPE values of several SVM hybrid algorithms and ANN developed for ILF in [54,100].
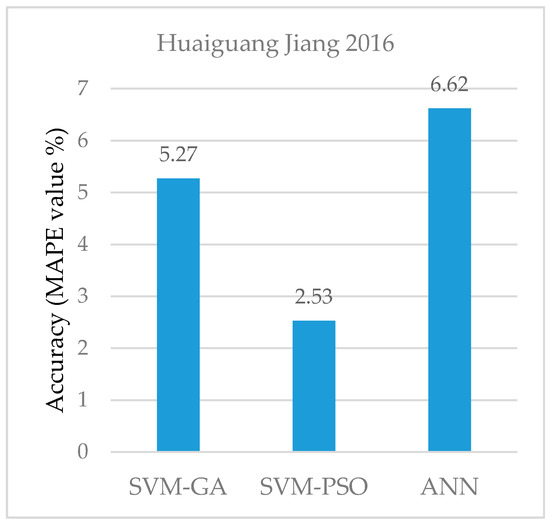
Figure 7.
MAPE values of several SVM hybrid algorithms and ANN developed for ILF in [54].
The error values shown in Table 8 has been reproduced from the forecasting model improved by the study of Hong et al. [100], as also exhibited in Figure 8. These results, which show an error value largely less than 5%, confirm the very good performance of the hybrid algorithms for load prediction. As it is shown in the table, the PSO-SVM and the SA-SVM hybrid algorithms can predict the load with highly accurate results where the MAPE values are 1.61% and 1.76%, respectively.
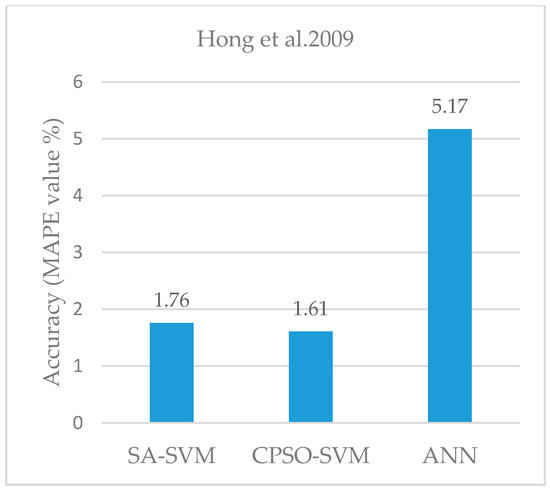
Figure 8.
MAPE values of several Hybrid SVM and single ANN algorithms developed for ILF in [100].
Figure 9 provides the chronology of the CI approaches that have focused on single and hybrid methods. The figure shows that some of the approaches originate from the other approaches used to strengthen their design efficiency and productiveness. For example, in single methods, Elatta et al. [29] used the SVM model, which originated from the Kernel method (Cortes and Vapnik) [80] whereas the study of load forecasting presented by the work of Chih et al. [52] used the hybrid approach of the SVM-GA where the SVM method originated from Cortes and Vepnik [80] and the GA method originated from Koza [105], which are elaborated in the chronological graph (Figure 9).
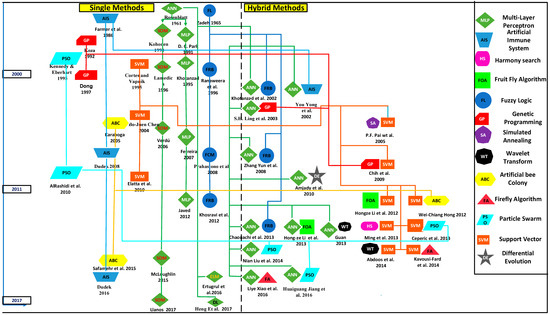
Figure 9.
Chronological order of the single and hybrid CI approaches applied to load forecasting.
Moreover, in the hybrid side in Figure 8, the chronological order of developed hybrid algorithms for ILF are illustrated which are basically combination of different isolated algorithms with ANN and SVM. For example, the PSO algorithm is used to improve the neural network in a forecasting model proposed by Liu et al. [44] in 2014. Later in 2016, Jiang et al. [54] developed the same combination (PSO-ANN) for load forecasting. PSO algorithm also integrated to SVM algorithm in a model developed by Ceperic et al. [55] in year 2013.
7. Conclusions
This investigation has reviewed research conducted for load forecasting using different CI techniques. The literature concerning the issues and challenges of load data preparation and the proper methods and real applications have been briefly discussed. The methods discussed in this review can be classified into two main categories: the single (or standalone model) and hybrid (or integrated model) based CI method. The evaluation has been conducted using the previous results of most relevant papers on different datasets in terms of the accuracy of the prediction (MAPE). Basically, the study indicates that the suitability of methods depends on the target dataset. However, the hybrid methods performed more accurate compared to the single model algorithms. Specifically, the incorporation of metaheuristic (or optimizer) algorithms such as the PSO and the HS algorithm into the standalone SVM model has resulted in a more accurate load forecasting model, while the FOA algorithm was highly effective with hybrid model employing the ANN algorithm.
Author Contributions
All authors together proposed, discussed and finalized the main idea of this work. Seyedeh Narjes Fallah and Shahaboddin Shamshirband proposed the idea, calculated and plotted the feasible regions, and compared and classified the background and taxonomy presentation and evaluated their pros and cons. Mohammad Shojafar and Ravinesh Chand Deo technically supported the content, verified the accuracy, and revised the clarity of the work as well as helping to write and organize the paper. Finally, Mauro Conti helped in the paper preparations, English corrections, and submission.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| ABC | Artificial bee colony |
| AIS | Artificial immune system |
| ANN | Artificial neural network |
| CI | Computational intelligence |
| DE | Differential evolutionary algorithm |
| DL | Deep learning |
| ELM | Extreme learning machine |
| FA | Firefly algorithm |
| FANN | Firefly neural network |
| FCM | Fuzzy C-means |
| FL | Fuzzy logic |
| FOA | Fruit fly optimization algorithm |
| FRB | Fuzzy rule base |
| GA | Genetic algorithm |
| GNN | Genetic neural network |
| GP | Genetic programming |
| GSVM | Genetic support vector machine |
| HS | Harmony search algorithm |
| ILF | Intelligent load forecasting |
| LTLF | Long-term load forecasting |
| MLP | Multilayer perceptron |
| MTLF | Medium-term load forecasting |
| NF | Neuro fuzzy |
| NILM | Non-Intrusive Load Management |
| RNNs | recurrent neural networks |
| WT | Wavelet transform |
References
- Mohsenian-Rad, A.-H.; Wong, V.W.S.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Diamantoulakis, D.P.; Kapinas, V.M.; Karagiannidis, G.K. Big data analytics for dynamic energy management in smart grids. Big Data Res. 2015, 2, 94–101. [Google Scholar] [CrossRef]
- Tso, G.K.; Yau, K.K. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Depuru, S.S.S.R.; Wang, L.; Devabhaktuni, V. Smart meters for power grid: Challenges, issues, advantages and status. Renew. Sustain. Energy Rev. 2011, 15, 2736–2742. [Google Scholar] [CrossRef]
- Charytoniuk, W.; Chen, M.; Van Olinda, P. Nonparametric regression based short-term load forecasting. IEEE Trans. Power Syst. 1998, 13, 725–730. [Google Scholar] [CrossRef]
- Momoh, J.; Ma, X.; Tomsovic, K. Overview and literature survey of fuzzy set theory in power systems. IEEE Trans. Power Syst. 1995, 10, 1676–1690. [Google Scholar] [CrossRef]
- Soheilirad, M.; Hizam, H.; Farzan, P.; Hojabri, M.; Fallah, S.N.; Soheilirad, G. Wind farm reactive power optimization by using imperialist competitive algorithm. In Proceedings of the 2013 International Conference on Power, Energy and Control (ICPEC), Sri Rangalatchum Dindigul, India, 6–8 February 2013. [Google Scholar]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Hong, T. Short Term Electric Load Forecasting; North Carolina State University: Raleigh, NC, USA, 2010. [Google Scholar]
- Hong, T.; Wilson, J.; Xie, J. Long term probabilistic load forecasting and normalization with hourly information. IEEE Trans. Smart Grid 2014, 5, 456–462. [Google Scholar] [CrossRef]
- Dudek, G. Artificial immune system with local feature selection for short-term load forecasting. IEEE Trans. Evol. Comput. 2017, 21, 116–130. [Google Scholar] [CrossRef]
- Azadeh, A.; Moghadam, R.T.; Ghaderi, S.F.; Tarverdian, S.; Saberi, M. Integration of artificial neural networks and genetic algorithm to predict electrical energy consumption. Appl. Math. Comput. 2007, 186, 1731–1741. [Google Scholar] [CrossRef]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Zhu, Y.; He, Y. Short-term load forecasting model using fuzzy c means based radial basis function network. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, ISDA’06, Jinan, China, 16–18 October 2006. [Google Scholar]
- Welikala, S.; Dinesh, C.; Ekanayake, M.P.B.; Godaliyadda, R.I.; Ekanayake, J. Incorporating Appliance Usage Patterns for Non-Intrusive Load Monitoring and Load Forecasting. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Srinivasan, D. Interval type-2 fuzzy logic systems for load forecasting: A comparative study. IEEE Trans. Power Syst. 2012, 27, 1274–1282. [Google Scholar] [CrossRef]
- Ferreira, V.H.; da Silva, A.P.A. Toward estimating autonomous neural network-based electric load forecasters. IEEE Trans. Power Syst. 2007, 22, 1554–1562. [Google Scholar] [CrossRef]
- Ding, N.; Benoit, C.; Foggia, G.; Bésanger, Y.; Wurtz, F. Neural network-based model design for short-term load forecast in distribution systems. IEEE Trans. Power Syst. 2016, 31, 72–81. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- López, M.; Valero, S.; Senabre, C.; Aparicio, J.; Gabaldonc, A. Application of SOM neural networks to short-term load forecasting: The Spanish electricity market case study. Electr. Power Syst. Res. 2012, 91, 18–27. [Google Scholar] [CrossRef]
- Llanos, J.; Morales, R.; Núñez, A.; Sáez, D.; Lacalle, M.; Marín, L.G.; Hernández, R.; Lanas, F. Load estimation for microgrid planning based on a self-organizing map methodology. Appl. Soft Comput. 2017, 53, 323–335. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep Learning for Household Load Forecasting—A Novel Pooling Deep RNN. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Hill, D.J.; Luo, F.; Xu, Y. Short-Term Residential Load Forecasting based on Resident Behaviour Learning. IEEE Trans. Power Syst. 2018, 33, 1087–1088. [Google Scholar] [CrossRef]
- Ertugrul, Ö.F. Forecasting electricity load by a novel recurrent extreme learning machines approach. Int. J. Electr. Power Energy Syst. 2016, 78, 429–435. [Google Scholar] [CrossRef]
- Ekici, S. Electric Load Forecasting using Regularized Extreme Learning Machines. Int. J. Ind. Electr. Electr. Eng. 2016, 4, 119–122. [Google Scholar]
- Chen, B.-J.; Chang, M.-W. Load forecasting using support vector machines: A study on EUNITE competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Elattar, E.E.; Goulermas, J.; Wu, Q.H. Electric load forecasting based on locally weighted support vector regression. IEEE Trans. Syst. Man Cybern. Part C 2010, 40, 438–447. [Google Scholar] [CrossRef]
- Alvarez, F.M.; Troncoso, A.; Riquelme, J.C.; Aguilar Ruiz, J.S. Energy time series forecasting based on pattern sequence similarity. IEEE Trans. Knowl. Data Eng. 2011, 23, 1230–1243. [Google Scholar] [CrossRef]
- Safamehr, H.; Rahimi-Kian, A. A cost-efficient and reliable energy management of a micro-grid using intelligent demand-response program. Energy 2015, 91, 283–293. [Google Scholar] [CrossRef]
- AlRashidi, M.; El-Naggar, K. Long term electric load forecasting based on particle swarm optimization. Appl. Energy 2010, 87, 320–326. [Google Scholar] [CrossRef]
- Lee, D.G.; Lee, B.W.; Chang, S.H. Genetic programming model for long-term forecasting of electric power demand. Electr. Power Syst. Res. 1997, 40, 17–22. [Google Scholar] [CrossRef]
- Yun, Z.; Quan, Z.; Caixin, S.; Shaolan, L.; Yuming, L.; Yang, S. RBF neural network and ANFIS-based short-term load forecasting approach in real-time price environment. IEEE Trans. Power Syst. 2008, 23, 853–858. [Google Scholar]
- Chaouachi, A.; Kamel, R.M.; Andoulsi, R.; Nagasaka, K. Multiobjective intelligent energy management for a microgrid. IEEE Trans. Ind. Electr. 2013, 60, 1688–1699. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Goel, L. Short-term load forecasting by wavelet transform and evolutionary extreme learning machine. Electr. Power Syst. Res. 2015, 122, 96–103. [Google Scholar] [CrossRef]
- Guan, C.; Luh, P.B.; Michel, L.D.; Wang, Y.; Friedland, P.B. Very short-term load forecasting: Wavelet neural networks with data pre-filtering. IEEE Trans. Power Syst. 2013, 28, 30–41. [Google Scholar] [CrossRef]
- Ling, S.-H.; Leung, F.H.F.; Lam, H.K.; Lee, Y.-S.; Tam, P.K.S. A novel genetic-algorithm-based neural network for short-term load forecasting. IEEE Trans. Ind. Electr. 2003, 50, 793–799. [Google Scholar] [CrossRef]
- Li, H.-Z.; Guo, S.; Li, C.-J.; Sun, J.-Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl.-Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Hu, R.; Wen, S.; Zeng, Z.; Huang, T. A short-term power load forecasting model based on the generalized regression neural network with decreasing step fruit fly optimization algorithm. Neurocomputing 2017, 221, 24–31. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Liang, T.; Wang, C. A combined model based on multiple seasonal patterns and modified firefly algorithm for electrical load forecasting. Appl. Energy 2016, 167, 135–153. [Google Scholar] [CrossRef]
- Yong, Y.; Sun’an, W.; Wanxing, S. Short-term load forecasting using artificial immune network. In Proceedings of the International Conference on Power System Technology, PowerCon 2002, Kunming, China, 13–17 October 2002. [Google Scholar]
- Mishra, S.; Patra, S.K. Short term load forecasting using a neural network trained by a hybrid artificial immune system. In Proceedings of the IEEE Region 10 and the Third international Conference on Industrial and Information Systems, ICIIS 2008, Kharagpur, India, 8–10 December 2008. [Google Scholar]
- Liu, N.; Tang, Q.; Zhang, J.; Fan, W.; Liu, J. A hybrid forecasting model with parameter optimization for short-term load forecasting of micro-grids. Appl. Energy 2014, 129, 336–345. [Google Scholar] [CrossRef]
- Lee, C.-M.; Ko, C.-N. Time series prediction using RBF neural networks with a nonlinear time-varying evolution PSO algorithm. Neurocomputing 2009, 73, 449–460. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. Short-term load forecast of microgrids by a new bilevel prediction strategy. IEEE Trans. Smart Grid 2010, 1, 286–294. [Google Scholar] [CrossRef]
- Ahmad, A.; Javaid, N.; Guizani, M.; Alrajeh, N.; Khan, Z.A. An accurate and fast converging short-term load forecasting model for industrial applications in a smart grid. IEEE Trans. Ind. Inform. 2017, 13, 2587–2596. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Construction of optimal prediction intervals for load forecasting problems. IEEE Trans. Power Syst. 2010, 25, 1496–1503. [Google Scholar] [CrossRef]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Pérez, F.; Fernández, Á.; Lloret, J. Artificial neural network for short-term load forecasting in distribution systems. Energies 2014, 7, 1576–1598. [Google Scholar] [CrossRef]
- Quilumba, F.L.; Lee, W.-J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using smart meter data to improve the accuracy of intraday load forecasting considering customer behavior similarities. IEEE Trans. Smart Grid 2015, 6, 911–918. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, W.-C. Forecasting regional electricity load based on recurrent support vector machines with genetic algorithms. Electr. Power Syst. Res. 2005, 74, 417–425. [Google Scholar] [CrossRef]
- Wu, C.-H.; Tzeng, G.-H.; Lin, R.-H. A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression. Expert Syst. Appl. 2009, 36, 4725–4735. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, W.-C. Support vector machines with simulated annealing algorithms in electricity load forecasting. Energy Convers. Manag. 2005, 46, 2669–2688. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Y.; Muljadi, E.; Zhang, J.; Gao, W. A short-term and high-resolution distribution system load forecasting approach using support vector regression with hybrid parameters optimization. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Ceperic, E.; Ceperic, V.; Baric, A. A strategy for short-term load forecasting by support vector regression machines. IEEE Trans. Power Syst. 2013, 28, 4356–4364. [Google Scholar] [CrossRef]
- Hong, W.-C. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm. Energy 2011, 36, 5568–5578. [Google Scholar] [CrossRef]
- Daut, M.A.M.; Hassan, M.Y.; Abdullah, H.; Abdul, R.H.; Abdullah, M.P.; Hussin, F. An Improved Building Load Forecasting Method using a combined Least Square Support Vector Machine and modified Artificial Bee Colony. ELEKTRIKA-J. Electr. Eng. 2017, 16, 1–5. [Google Scholar]
- Zeng, M.; Xue, S.; Wang, Z.; Zhu, X.; Zhang, G. Short-term load forecasting of smart grid systems by combination of general regression neural network and least squares-support vector machine algorithm optimized by harmony search algorithm method. Appl. Math. 2013, 7, 291–298. [Google Scholar] [CrossRef]
- Li, H.; Guo, S.; Zhao, H.; Su, C.; Wang, B. Annual electric load forecasting by a least squares support vector machine with a fruit fly optimization algorithm. Energies 2012, 5, 4430–4445. [Google Scholar] [CrossRef]
- Cao, G.; Wu, L. Support vector regression with fruit fly optimization algorithm for seasonal electricity consumption forecasting. Energy 2016, 115, 734–745. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid modified firefly algorithm and support vector regression model for accurate short term load forecasting. Expert Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Abdoos, A.; Hemmati, M.; Abdoos, A.A. Short term load forecasting using a hybrid intelligent method. Knowl.-Based Syst. 2015, 76, 139–147. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Applying support vector machine to predict hourly cooling load in the building. Appl. Energy 2009, 86, 2249–2256. [Google Scholar] [CrossRef]
- Edwards, R.E.; New, J.; Parker, L.E. Predicting future hourly residential electrical consumption: A machine learning case study. Energy Build. 2012, 49, 591–603. [Google Scholar] [CrossRef]
- Jin, C.H.; Pok, G.; Lee, Y.; Park, H.-W.; Kim, K.D.; Yun, U.; Ryu, K.H. A SOM clustering pattern sequence-based next symbol prediction method for day-ahead direct electricity load and price forecasting. Energy Convers. Manag. 2015, 90, 84–92. [Google Scholar] [CrossRef]
- Ghasemi, A.; Shayeghi, H.; Moradzadeh, M.; Nooshyar, M. A novel hybrid algorithm for electricity price and load forecasting in smart grids with demand-side management. Appl. Energy 2016, 177, 40–59. [Google Scholar] [CrossRef]
- Tong, C.; Li, J.; Lang, C.; Kong, F.; Niu, J.; Rodrigues, J.J.P.C. An efficient deep model for day-ahead electricity load forecasting with stacked denoising auto-encoders. J. Parallel Distrib. Comput. 2017. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Economakos, E. Application of fuzzy concepts to power demand forecasting. IEEE Trans. Syst. Man Cybern. 1979, 9, 651–657. [Google Scholar]
- Ali, D.; Yohanna, M.; Puwu, M.I.; Garkida, B.M. Long-term load forecast modelling using a fuzzy logic approach. Pac. Sci. Rev. A 2016, 18, 123–127. [Google Scholar] [CrossRef]
- Chen, C.P.; Zhang, C.-Y. Data-intensive applications, challenges, techniques and technologies: A survey on Big Data. Inf. Sci. 2014, 275, 314–347. [Google Scholar] [CrossRef]
- Rosenblatt, F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms; Cornell Aeronautical Laboratory: Buffalo, NY, USA, 1961; Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/256582.pdf (accessed on 1 March 2018).
- Park, D.C.; El-Sharkawi, M.A.; Marks, R.J.; Atlas, L.E.; Damborg, M.J. Electric load forecasting using an artificial neural network. IEEE Trans. Power Syst. 1991, 6, 442–449. [Google Scholar] [CrossRef]
- Khotanzad, A.; Hwang, R.-C.; Abaye, A.; Maratukulam, D. An adaptive modular artificial neural network hourly load forecaster and its implementation at electric utilities. IEEE Trans. Power Syst. 1995, 10, 1716–1722. [Google Scholar] [CrossRef]
- Khotanzad, A.; Afkhami-Rohani, R.; Lu, T.-L.; Abaye, A.; Davis, M.; Maratukulam, D.J. ANNSTLF-a neural-network-based electric load forecasting system. IEEE Trans. Neural Netw. 1997, 8, 835–846. [Google Scholar] [CrossRef] [PubMed]
- Javed, F.; Arshad, N.; Wallin, F.; Vassileva, I.; Dahlquist, E. Forecasting for demand response in smart grids: An analysis on use of anthropologic and structural data and short term multiple loads forecasting. Appl. Energy 2012, 96, 150–160. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Lamedica, R.; Prudenzi, A.; Sforna, M.; Caciotta, M.; Cencellli, V.O. A neural network based technique for short-term forecasting of anomalous load periods. IEEE Trans. Power Syst. 1996, 11, 1749–1756. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Adamowski, J.F.; Li, Y. Short-term electricity demand forecasting with MARS, SVR and ARIMA models using aggregated demand data in Queensland, Australia. Adv. Eng. Inf. 2018, 35, 1–16. [Google Scholar] [CrossRef]
- Paparrizos, J.; Gravano, L. k-shape: Efficient and accurate clustering of time series. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, Melbourne, VIC, Australia, 31 May–4 June 2015; ACM: New York, NY, USA, 2015. [Google Scholar]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1941, 4, 87–112. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Farmer, J.D.; Packard, N.H.; Perelson, A.S. The immune system, adaptation, and machine learning. Phys. D Nonlinear Phenom. 1986, 22, 187–204. [Google Scholar] [CrossRef]
- De Castro, L.N.; Timmis, J. Artificial Immune Systems: A New Computational Intelligence Approach; Springer Science & Business Media: Berlin, Germany, 2002. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Lin, C.-T.; Lee, C.S.G. Neural-network-based fuzzy logic control and decision system. IEEE Trans. Comput. 1991, 40, 1320–1336. [Google Scholar] [CrossRef]
- Jang, J.-S.; Sun, C.-T. Neuro-fuzzy modeling and control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Li, K.; Su, H.; Chu, J. Forecasting building energy consumption using neural networks and hybrid neuro-fuzzy system: A comparative study. Energy Build. 2011, 43, 2893–2899. [Google Scholar] [CrossRef]
- Khotanzad, A.; Zhou, E.; Elragal, H. A neuro-fuzzy approach to short-term load forecasting in a price-sensitive environment. IEEE Trans. Power Syst. 2002, 17, 1273–1282. [Google Scholar] [CrossRef]
- Jawerth, B.; Sweldens, W. An overview of wavelet based multiresolution analyses. SIAM Rev. 1994, 36, 377–412. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Dong, Z.-Y. An adaptive neural-wavelet model for short term load forecasting. Electr. Power Syst. Res. 2001, 59, 121–129. [Google Scholar] [CrossRef]
- Pan, W.-T. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- El-Telbany, M.; El-Karmi, F. Short-term forecasting of Jordanian electricity demand using particle swarm optimization. Electr. Power Syst. Res. 2008, 78, 425–433. [Google Scholar] [CrossRef]
- Koprinska, I.; Rana, M.; Troncoso, A.; Martinez-Alvarez, F. Combining pattern sequence similarity with neural networks for forecasting electricity demand time series. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013. [Google Scholar]
- Fahiman, F.; Erfani, S.M.; Rajasegarar, S.; Palaniswami, M.; Leckie, C. Improving load forecasting based on deep learning and K-shape clustering. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017. [Google Scholar]
- Shi, Y. Particle swarm optimization: developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001. [Google Scholar]
- Hong, W.-C. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Akay, B. A study on particle swarm optimization and artificial bee colony algorithms for multilevel thresholding. Appl. Soft Comput. 2013, 13, 3066–3091. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspir. Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms, 1st ed.; Elsevier: Waltham, MA, USA, 2014. [Google Scholar]
- Kalogirou, S.A.; Bojic, M. Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy 2000, 25, 479–491. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).