Abstract
Active power steady-state security regions (APSSRs), which can provide guidance for prevention and control through security checks, is of great importance for the safe operation of power systems in which more and more sustainable energy power generation is integrated. As a mature flexible AC transmission system (FACTS) device, thyristor-controlled series compensators (TCSCs) can carry out series compensation for the transmission line by controlling its equivalent reactance. With the change of the equivalent reactance parameter of a TCSC, the nodal admittance matrix and power flow distribution of the power system also changes. Inevitably, the APSSR will be different. Therefore, it is necessary and important to further incorporate the equivalent reactance parameters of TCSCs in the APSSR expression, which is generally established in the space of node active power injections. In this paper, a rapid construction method of APSSRs incorporating the equivalent reactances of TCSCs is proposed. Firstly, applicability and efficiency of the conventional APSSR construction method for power systems with TCSCs are analyzed. Further, with equivalent disconnection of TCSC branches, the effect of TCSC equivalent reactances on the distribution of active power flow through changing the structure parameters is treated as modifying node active power injections. On this basis, explicit expressions of APSSRs with a single TCSC equivalent reactance parameter and double TCSC equivalent reactance parameters are derived, respectively. Moreover, by deducing the general formula of APSSRs with multiple TCSC equivalent reactance parameters, the feasibility of the proposed method for power systems with multiple TCSCs is analyzed. Eventually, via benchmarks with different scales and a different number of TCSCs, validity and superiorities of the proposed method in computational efficiency are demonstrated.
1. Introduction
With the continuous integration of sustainable energy power generation such as wind power and photovoltaics, and the increase of load uncertainty in power markets under competitive mechanisms, the power flow of smart grids is becoming more complex with random variations of power supply output and uncertainty of load [1,2,3,4]. As an important part of security region methodology, steady-state security regions can be used for real-time on-line security analysis and monitoring as well as prevention and control of the power system [5].
The concept of a steady-state security region (SSR) was first proposed by [6] in 1975. It is the set of node power injections that can ensure the safe and stable operation of a power system under a given network structure. An active power SSR (APSSR), which is more concerned with the transmission network, mainly considers the branch active power flow constraint and output active power constraints of generators. In the DC power flow model, there exists a linear relationship between the node active power injections and the branch active power flow/phase difference. On this basis, an APSSR can be approximated as a convex superset polyhedron, which is formed by the hyperplanes in the parameter space of node active power injections [7,8,9]. Furthermore, in [10,11,12], when the APSSR is applied in analyzing unit commitment, optimal power flow, and power pricing, good results have been achieved. However, existing research focuses on the analysis of APSSRs in the parameter space of node active power injections. Research on APSSRs rarely considers the effect of structural parameters that can change continuously, for example, the equivalent reactance of TCSCs.
As one of the most important features of the modern smart grid, the flexible AC transmission system (FACTS), which can realize the fast and flexible control of the structure and parameters of the AC transmission system, is used to promote reliability, economy, and stability of the power grid. In particular, as a mature FACTS device, the thyristor-controlled series compensator (TCSC), which can carry out series compensation for the transmission line by controlling its equivalent reactance, is an effective means to adjust the power flow of the power system [13,14,15,16]. The equivalent reactance of the TCSC can be adjusted continuously by controlling the trigger angle. With the change of equivalent reactance parameters of the TCSC, the nodal admittance matrix also changes. Further, power flow distribution of the power system is varied. Inevitably, the APSSR will be different. Therefore, it is necessary to further incorporate the equivalent reactance parameter of TCSCs in the APSSR expression, which is generally established in the space of node active power injections. Relationships among SSR, APSSR, and TCSC are as shown in Figure 1.

Figure 1.
Relationships among steady-state security region (SSR), active power steady-state security region (APSSR), and thyristor-controlled series compensator (TCSC).
For the conventional construction method of APSSRs, the nodal admittance matrix is parameterized by considering the equivalent reactance parameter of the TCSC. As there is a high computational burden caused by the inversion of the parameter matrix, the efficiency of the conventional method is not ideal to construct an APSSR incorporating the equivalent reactance of the TCSC.
In this paper, a rapid construction method of APSSRs, which incorporates the equivalent reactance parameter of TCSCs, is proposed. Firstly, the applicability and efficiency of the conventional APSSR construction method for the power system with a TCSC are analyzed. It is pointed out that the efficiency of the existing method will not be ideal due to the heavy computational burden in obtaining the inversion of a high-dimensional parametric matrix caused by the parameterization of the node admittance matrix. To avoid this issue with equivalent disconnection of TCSC branches, the effect of TCSC equivalent reactances on the distribution of active power flow through changing the structure parameters is treated as modifying node active power injections. On this basis, the explicit expressions of APSSRs with a single TCSC equivalent reactance parameter and double TCSC equivalent reactance parameters are deduced, respectively. Moreover, by deducing the general formula of the APSSR with multiple TCSC equivalent reactance parameters, the applicability of the proposed method for a power system with multiple TCSCs is analyzed.
2. Applicability Analysis of the Existing APSSR Construction Method for a Power System with TCSC
2.1. Brief Illustrations of the Existing APSSR Construction Method
According to the literature [7,8], brief illustrations of the existing APSSR construction method can be summarized as follows.
For a high voltage transmission network, by ignoring the effect of reactive power, the following assumptions can be established with the DC power flow model:
- (1)
- The resistance of transmission lines is much smaller than the reactance, thus Gij ≈ 0. Gij is the element of the real part of the nodal admittance matrix.
- (2)
- Voltage phase angle difference θij of branch i-j is very small, therefore sinθij ≈ θij, cosθij ≈ 1.
Under these assumptions, the active power flow equation of the power system can be simplified as follows:
where PGi and PDi are generation output active power and load active power of node i, respectively. bij is the susceptance of branch i-j.
Further, Equation (1) can be transformed into the following Equation (2):
where P is the vector of node active power injection. θ is the vector of node voltage phase. X = B−1, B is the imaginary part of nodal admittance matrix Y.
θ = XP
Thus, the active power flow of branch i-j can be expressed as a function of node active power injections as Equation (3).
where Kl = (kd1, kd2, …, kdm, …, kdn), n is the total number of nodes without the slack node. kdm = −bij(Xim − Xjm), Xim is the element of X in row i and column m.
Therefore, the APSSR of branch i-j can be represented as:
where kdm is the hyper-plane coefficient (HPC) of Pm.
From Equations (1)–(4), it can be found that:
When the system contains a TCSC, Y will be changed with the variation of the equivalent reactance of the TCSC. Then, X = B−1 is about to change and further affect the APSSR via essentially influencing kdm.
Therefore, it is necessary to further incorporate the equivalent reactance parameter of the TCSC in the existing APSSR expression, which is established in the space of node active power injections.
2.2. Applicability Analysis for Power System with TCSC
For the grid whose structure parameters are fixed values, and Y, B and X are both constant matrices, the APSSR can be constructed conveniently with the existing method as Equations (1)–(4).
However, if there is a TCSC whose equivalent reactance is denoted as XTCSC, Y will be parameterized as Y(XTCSC). Correspondingly, B and X will be parameter matrices as B(XTCSC) and X(XTCSC) = B(XTCSC)−1 as well.
And, it can be seen that:
- (1)
- When using Equations (1)–(4) to construct an APSSR of power grid with a TCSC, inversion of the n-order parameter matrix B(XTCSC) is needed.
- (2)
- Moreover, the inversion of a parameter matrix is much more time-consuming than the inversion of a numerical matrix with the same dimension.
Therefore, the efficiency of the existing method is not ideal to construct an APSSR incorporating the equivalent reactance of a TCSC, due to the high computational burden caused by the inversion of parameter matrix B(XTCSC).
In other words, to realize rapid construction of the APSSR expression with XTCSC, the key issue that needs to be solved is to avoid or overcome the inversion of the n-order parameter matrix B(XTCSC) caused by the parameterization of Y.
3. Derivations of APSSRs with a Single TCSC and Double TCSCs
To avoid parameterization of the X = B−1 calculation, this paper proposes to equivalently disconnect the TCSC branch. The active power flowing through the original TCSC branch is equivalent to two XTCSC related node active power injections. Then:
- (1)
- Via the equivalent disconnection of the TCSC branch, the network structure parameter no longer contains the variable XTCSC, and Y and B will be constant matrices. That is, X = B−1 is also the constant matrix, which can be obtained conveniently.
- (2)
- The effect of XTCSC on the APSSR can be analyzed by influencing node active power injections rather than parameterization of X = B−1.
With the above analysis, the explicit expressions of APSSR with a single TCSC and double TCSCs are derived, respectively.
3.1. APSSR Incorporating a Single TCSC
As in the DC power flow model shown in Figure 2, assume that TCSC1 is located near node l on branch l-m. Also, the original active power injection of each node is defined as (P10, P20, …, Pm0, …, Pn0).
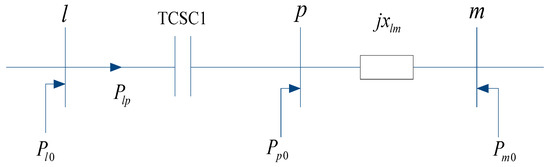
Figure 2.
DC power flow model with TCSC1.
Active power flows out from node l and injects into node p through the TCSC branch is as Equation (5).
As in the equivalent schematic diagram shown in Figure 3, by the substitution theorem, the TCSC branch can be disconnected. Also, Plp can be equivalent to two active power injection net increments ΔPT1 and ΔPT2 at node l and node p, respectively.
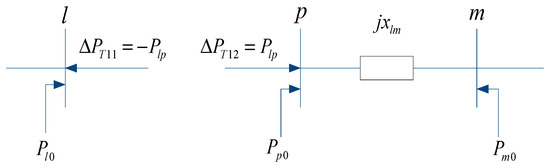
Figure 3.
Equivalent schematic diagram of TCSC1.
(1) According to Equation (6), via the above equivalent disconnection of TCSC branch l-p, active power injections of the two endpoints l and p can be modified as the following Equation (7):
(2) With the disconnection of the TCSC branch, the structure parameters of the system will no longer contain the variable XTCSC1. That is, Y, B and X are constant matrices. Therefore, according to Equations (4) and (6), the APSSR of branch i-j can be expressed as follows:
(3) In Equation (8), it can be seen that there still exists an intermediate variable θlp, which shall be eliminated and be written as an expression composed of (P10, P20, …, Pm0, …, Pn0) and XTCSC1. Referring to Equation (2), the following equation can be derived:
where em = (Xlm − Xpm), kr1 = (Xll − Xpl), kr2 = (Xlp − Xpp).
Therefore, θlp can be obtained as follows:
(4) Substituting Equation (10) into Equation (8), the APSSR of branch i-j for the system with a single TCSC can be derived as Ω1.
From Equation (11), the hyper-plane coefficient (HPC) of Pm0 for Ω1 can be obtained as λm1.
3.2. APSSR Incorporating Double TCSCs
Based on section A in this chapter, it is further assumed that branch s-t is also a TCSC branch (namely TCSC2), whose equivalent impedance is denoted as XTCSC2.
According to Equations (5)–(7), equivalent disconnection is carried out for TCSC2 as well. Thus, active power injections of node s and node t can be modified as the following equation.
(1) With the disconnections of TCSC1 and TCSC2, Y, B and X are constant matrices. Referring to Equations (4) and (8), the APSSR of branch i-j with double TCSCs can be expressed as Equation (14).
where kdt = −Bij(Xit − Xjt), kds = −Bij(Xis − Xjs).
(2) In Equation (14), it can be seen that there are two intermediate variables θst and θlp, which shall be eliminated and be written as the expressions composed of (P10, P20, …, Pm0, …, Pn0), XTCSC1, and XTCSC2. Referring to Equations (2) and (9), the following equations can be established.
where,
For Equation (15), there are two variables and two equations. Therefore, the explicit expressions of θlh and θst can be achieved as Equation (16).
(3) Substituting Equation (16) into Equation (14), the specific expression of the APSSR for the system with two TCSCs can be derived as Ω2.
From Equation (17), the hyper-plane coefficient (HPC) of Pm0 for Ω2 can be obtained as λm2.
4. Feasibility Analysis of the Proposed Method for the System with Multiple TCSCs
Moreover, the feasibility of the proposed method for the system with multiple TCSCs is analyzed from the perspective of the solvability of linear equations.
Based on the derivations in Chapter 3, the following analyses can be illustrated.
(1) If the number of TCSCs in the system is K, with equivalent disconnections of the TCSCs, the general expression of the APSSR of branch i-j can be summarized as Equation (19) according to Equations (9) and (14).
where XTCSC1, XTCSC2, …, XTCSCK are the equivalent reactance parameters of the TCSCs. ∆θ1, ∆θ2, …, ∆θK are the phase angle differences of each TCSC branch. kdm, γx are constants that can be obtained via X = B−1.
(2) For eliminating ∆θ1, ∆θ2, …, ∆θK, the following linear equations can be established referring to Equations (9) and (15).
where aKm, bKx are constants that can be obtained based on X.
(3) For Equation (20), it has K variables and K linear equations. Therefore, the explicit expressions of ∆θ1, ∆θ2, …, ∆θK, which consist of P10, P20, …, Pn0 and XTCSC1, XTCSC2, …, XTCSCK, can be derived as the following Equation (21).
(4) Substituting Equation (21) into Equation (19), the explicit general expression of the APSSR with multiple TCSCs can be eventually derived as the following equation.
(5) From Equation (22), the hyper-plane coefficient (HPC) of Pm0 for ΩK can be obtained as λmK.
where,
From Equations (19)–(23), the following conclusions can be summarized:
- (1)
- The feasibility of the proposed method is theoretically not affected by the number of TCSCs. Of course, with the increase of K, concrete expression of Equation (22) will be gradually complicated.
- (2)
- The computational burden of the proposed method mainly depends on the inversion of K-order matrix TsK×K(XTCSC1, …, XTCSCK). Also, the number of TCSCs is generally much smaller than the number of nodes of a power grid (i.e., K << n). Therefore, the proposed method has much higher computational efficiency compared with the existing method, by avoiding inversion of the n-order parameter matrix B(XTCSC).
5. Cases Studies
The effectiveness and superiorities of the proposed method are verified with different scale benchmarks. Specifically, this chapter will firstly demonstrate the effectiveness of the proposed method via the IEEE 10-generator 39-node system [17] shown in Figure 4.
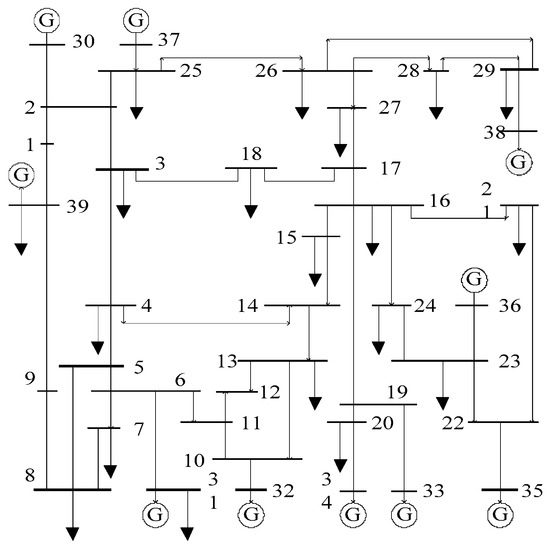
Figure 4.
IEEE 10-machine 39-node system.
Further, with the IEEE 3-generator 9-node system [18], IEEE 18-node system [19], and IEEE 10-generator 39-node system, the superiorities of the proposed method in computational efficiency are verified by changing system scale and the number of TCSCs.
All data in this chapter are obtained by a desktop computer with i7-4790@3.60GHZ CPU and 8G RAM. The software environment is Windows 10 Professional and MATLAB 2013a.
5.1. Verification of the Effectiveness of the Proposed Method
5.1.1. The Scenario with a Single TCSC
Firstly, the effectiveness of the proposed method is tested by scenario 1 as follows:
Scenario 1: Suppose a TCSC, whose equivalent reactance is defined as XTCSC1, is connected in series with branch 9-39 in Figure 4, and the APSSR of branch 3-4 incorporating XTCSC1 is to be constructed.
After equivalent disconnection of the TCSC branch, via Equations (5)–(10), kdm and em can be obtained as shown in Table 1. kr1, kr2, kdl and kdp can be derived as listed in Table 2.

Table 1.
Results of kdm and em for scenario 1.

Table 2.
kr1, kr2, kdl and kdp for scenario 1.
Then, according to Equation (11), the APSSR of branch 3-4 can be obtained as the following equation:
On one hand, set XTCSC1 = 0.003, hyper-plane coefficients (HPCs) of Equation (24) can be obtained as the results in the 2nd and 5th columns of Table 3.

Table 3.
HPCs obtained by the proposed method and the existing method under XTCSC1 = 0.0030 for scenario 1.
On the other hand, the reactance parameter of branch 9-39 is set as 0.025–0.003 (namely 0.022; 0.025 is the original reactance of branch 9-39), then the existing method is used to construct the APSSR. The obtained HPCs are as shown in the 3rd and 6th columns of Table 3.
In Table 3, it can be seen that the results in the 2nd and 5th columns are in perfect agreement with the results in the 3rd and 6th columns, respectively. That is, for XTCSC1 = 0.0030, an APSSR of Equation (24), which is constructed by the proposed method, is correct.
For other scenarios with different values of XTCSC1 at different branches, test results are in line with the above conclusion.
5.1.2. The Scenario with Multiple TCSCs
Moreover, the effectiveness of the proposed method is tested for scenario 2 with multiple TCSCs.
Scenario 2: Suppose three TCSCs, whose equivalent reactances are defined as XTCSC1, XTCSC2, and XTCSC3, are connected in series with branch 2-25, branch 3-4, and branch 4-5 in Figure 4, and the APSSR of branch 14-4 incorporating XTCSC1, XTCSC2, and XTCSC3 is to be constructed.
On one hand, via Equations (19)–(22), the APSSR of branch 14-4 can be obtained as the following Equation (25):
Set XTCSC1, XTCSC2, and XTCSC3 all equal to −0.002, the HPCs can be obtained by Equation (25) as shown in the 2nd column and 5th column of Table 4.

Table 4.
HPCs obtained by the proposed method and the existing method.
On the other hand, the reactances of branch 2-25, branch 3-4, and branch 4-5 are set as 0.0086−0.002, 0.0213−0.002, and 0.0128−0.002, respectively. (0.0086, 0.0213, and 0.0128 are the original reactances of branch 2-25, branch 3-4, and branch 4-5.) Then, the existing method is used to construct the APSSR. The obtained HPCs are as shown in the 3rd and 6th columns of Table 4.
In Table 4, it can be seen that the results in the 2nd and 5th columns are in perfect agreement with the results in the 3rd and 6th columns, respectively. That is, for XTCSC1 = −0.002, XTCSC2 = −0.002, and XTCSC3 = −0.002, the APSSR of Equation (25) constructed by the proposed method is correct.
For other scenarios with multiple TCSCs, test results are in line with the above conclusion.
Therefore, from the above comparisons and analyses, the following conclusions can be obtained:
- (1)
- The proposed method can correctly construct the explicit expression of the APSSR, which consists of the equivalent reactance parameters of TCSCs and node active power injections.
- (2)
- The effectiveness of the proposed method is not influenced by the number of TCSCs and the values of TCSC equivalent reactances.
5.2. Effects of System Scale and the Number of TCSCs on the Computational Efficiency of the Proposed Method
In the above section, the effectiveness of the proposed method is verified. Further, the effects of system scale and the number of TCSCs on the computational efficiency of the proposed method are tested.
For illustration, the following definitions are given:
- (1)
- Method 1: The existing method via inversion of parameter matrix B(XTCSC)
- (2)
- Method 2: The proposed method
Detailed tests are illustrated as follows.
5.2.1. The Effect of System Scale
On one hand, the following tests are conducted to investigate the impact of system size/number of nodes on computational efficiency. Under the premise of only one TCSC, Method 1 and Method 2 are used to construct the APPSR incorporating the TCSC equivalent reactance parameter for the three benchmarks in different scale. Eventually, the results for computing time listed in Table 5 below can be obtained.

Table 5.
Comparisons of computing time for three different benchmarks.
From Table 5, the following conclusions can be obtained:
- (1)
- When node number increases, the computing times of both Method 1 and Method 2 increase.
- (2)
- Compared with the proposed Method 2, the computing time of Method 1 increases much faster.
For quantitive comparison, an index of computing time ratio is defined as rct as follows:
where tm1 and tm2 are the computing times of Method 1 and Method 2, respectively.
From Table 5, the change of rct with the increase of the number of nodes can be obtained as shown in Figure 5.
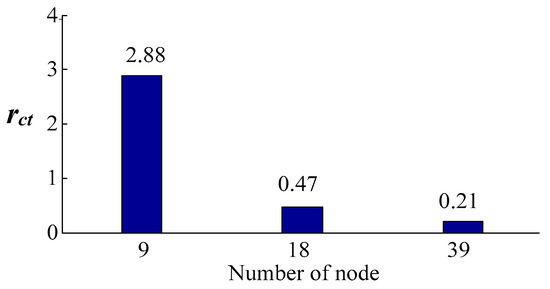
Figure 5.
Change of rct with the number of nodes.
From Figure 5, it can be seen that rct shows a trend of decrease with the increase of system scale. When the number of nodes is 9, 18, and 39, rct is 2.88%, 0.47%, and 0.21%, respectively.
To sum up, it shows that the superiority of the proposed method in computational efficiency will be more prominent with the increase of benchmark scale.
5.2.2. The Effect of the Number of TCSCs
On the one hand, the following tests are conducted to investigate the impact of the number of TCSCs on computational efficiency. For the IEEE 10-generator 39-node benchmark, Method 1 and Method 2 are used to construct the APSSR for the three scenarios with three TCSCs, four TCSCs, and five TCSCs, respectively. Eventually, the results for computing time listed in Table 6 below can be obtained.

Table 6.
Comparison of computing time with the change of TCSC number.
From Table 6, the following conclusions can be obtained:
- (1)
- When the number of TCSCs increases, the computing times of both Method 1 and Method 2 increase.
- (2)
- Compared with the proposed Method 2, the computing time of the proposed Method 1 increases much faster.
From Table 6, the change of rct with the increase of the number of TCSCs can be obtained as shown in Figure 6.
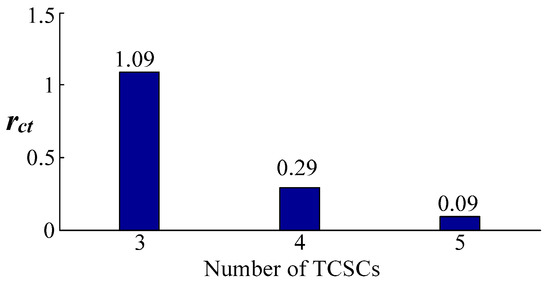
Figure 6.
Change trend of rct with the number of TCSCs.
From Figure 6, it can be seen that rct shows a trend of decrease with the increase of the number of TCSCs. When the number of TCSCs is 9, 18, and 39, rct is 1.09%, 0.29%, and 0.09%, respectively.
To sum up, it shows that the superiority of the proposed method in computational efficiency will be more prominent with the increase of the number of TCSCs.
6. Conclusions
In this paper, a fast construction method of active power steady-state security regions (APSSRs) incorporating equivalent reactance parameters of TCSCs is proposed. Concretely, with equivalent disconnection of TCSC branches, the effect of TCSC equivalent reactances on the distribution of active power flow through changing the structure parameters is treated as modifying node active power injections. On this basis, the explicit expressions of APSSRs with a single TCSC equivalent reactance parameter and double TCSC equivalent reactance parameters are deduced, respectively. Furthermore, the general formula of an APSSR with multiple TCSC equivalent reactance parameters is generalized. Eventually, via benchmarks with different scales and different numbers of TCSCs, validity and superiorities of the proposed method are demonstrated as follows:
- (1)
- It can correctly construct an explicit expression of the APSSR, which consists of the equivalent reactance parameters of TCSCs and node active power injections.
- (2)
- It is suitable for a system with a single TCSC, two TCSCs, and multiple TCSCs. That is, its feasibility is not influenced by the number of TCSCs.
- (3)
- Compared with the conventional method, it shows much higher efficiency in constructing explicit expressions of APSSRs incorporating the equivalent reactance parameters of TCSCs. Moreover, the larger the system scale or the greater the number of TCSCs, the more significant the superiority in computational efficiency the proposed method is.
In future, the construction method of APSSRs for the system with other FACTS devices, for example, a unified power flow controller (UPFC), will be further studied.
Acknowledgments
The authors would like to gratefully acknowledge the joint supports of the National Key R&D Program of China (2017YFB0902600, 2017YFB0902604); State Grid Corporation of China Project (SGJS0000DKJS1700840), Science and Technology Project of China State Grid (Research on security and stability assessment and assistant decision-making technology of power grid based on security region).
Author Contributions
Rusi Chen and Tao Lin conceived of the main idea, performed simulations, and wrote the manuscript. Baoping Chen and Ruyu Bi analyzed the data. Xialing Xu contributed the simulation environment.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Charles Smith, J.; Michael, R.M.; Edgar, A.D.; Brian, P. Utility wind integration and operating impact state of the art. IEEE Trans. Power Syst. 2007, 22, 900–908. [Google Scholar] [CrossRef]
- Miao, F.; Vijay, V.; Gerald Thomas, H.; Raja, A. Probabilistic power flow studies for transmission systems with photovoltaic generation using cumulants. IEEE Trans. Power Syst. 2012, 27, 2251–2261. [Google Scholar]
- Saber, T.; Miadreza, S.; Fei, W.; Jamshid, A.; Catalão, J.P.S. Optimal scheduling of demand response in pre-emptive markets based on stochastic bilevel programming method. IEEE Trans. Ind. Electron. 2018, PP, 1. [Google Scholar] [CrossRef]
- Juan, M.M.; Juan, P. Point Estimate Schemes to Solve the Probabilistic Power Flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar]
- Luo, J.; Shi, L.; Yao, L. A Multi-objective Optimization Model for Active Power Steady-state Security Region Analysis Incorporating Wind Power. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Hnyilicza, E.; Lee, S.T.Y.; Schweppe, F.C. Steady-state security regions: Set-theoretic approach. In Proceedings of the Power Industry Computer Applications Conference, New Orleans, LA, USA, 2–4 June 1975; pp. 347–355. [Google Scholar]
- Wu, F.F.; Kumagai, S. Steady-state security regions of Power System. IEEE Trans. Circuits Syst. 1982, 29, 703–711. [Google Scholar] [CrossRef]
- Zhu, J. Optimization of Power System Operation, 2nd ed.; Wiley-IEEE Press: Piscataway, NJ, USA, 2015. [Google Scholar]
- Yu, Y.; Feng, F. Active power steady-state security region of power system. Sci. China Ser. A-Technol. Sci. 1990, 6, 664–672. [Google Scholar]
- Yu, Y.; Qin, C. Security region based security-constrained unit commitment. Sci. China Technol. Sci. 2013, 56, 2732–2744. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, Y. Security region based real and reactive power pricing of power system. Sci. China Ser. E-Technol. Sci. 2008, 51, 2095–2111. [Google Scholar] [CrossRef]
- Alhabib, B.; Yu, Y.; Sun, G. Security region based real and reactive power optimization of power systems. Proc. CSEE 2006, 26, 1–10. [Google Scholar]
- Mohsen, H.S.; Gholamreza, A.M.; Ehsan, D.; Navid, R.A.; Abbas, K. Application of brain emotional learning-based intelligent controller to power flow control with thyristor-controlled series capacitance. IET Gener. Transm. Distrib. 2015, 9, 1964–1976. [Google Scholar]
- Duong, T.L.; Yao, J.G.; Truong, V.A. A new method for secured optimal power flow under normal and network contingencies via optimal location of TCSC. Int. J. Electr. Power Energy Syst. 2013, 52, 68–80. [Google Scholar] [CrossRef]
- Sundar, K.S.; Ravikumar, H.M. Selection of TCSC location for secured optimal power flow under normal and network contingencies. Int. J. Electr. Power Energy Syst. 2012, 34, 29–37. [Google Scholar] [CrossRef]
- Abdel-Moamen, M.A.; Padhy, N.P. Power flow control and transmission loss minimization model with TCSC for practical power networks. In Proceedings of the IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003; pp. 1–5. [Google Scholar]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability, 1st ed.; Iowa State University Press: Ames, IA, USA, 1977. [Google Scholar]
- Pai, A. Energy Function analysis For Power System Stability, 2nd ed.; Kluwer Academic Publishers: Norwell, MA, USA, 1989. [Google Scholar]
- Thorp, J.S.; Wang, H.Y. Computer Simulation of Cascading Disturbances in Electric Power Systems; University of Wisconsin: Madison, WI, USA, 2001. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).