Remote Power Control Injection of Grid-Connected Power Converters Based on Virtual Flux
Abstract
:1. Introduction
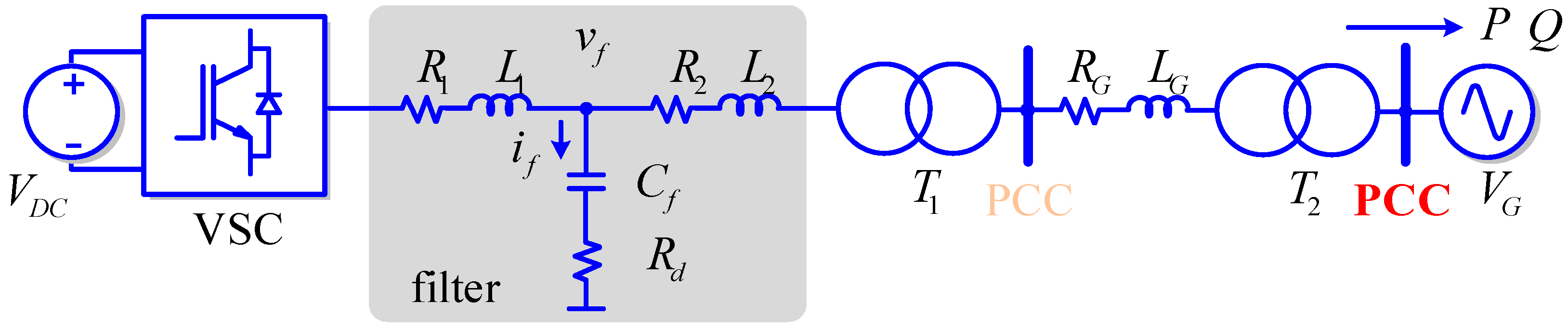
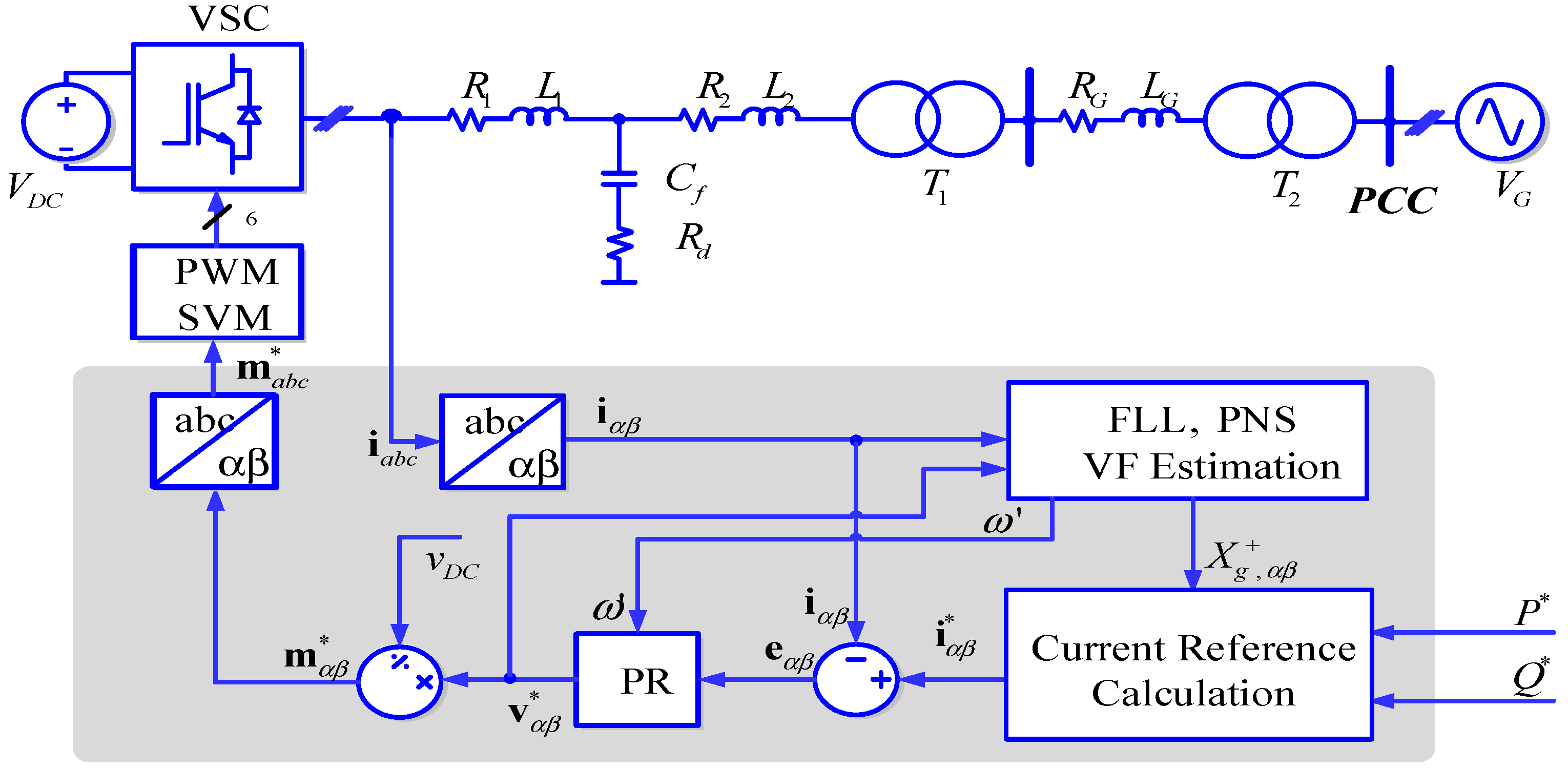
2. Proposed Control Method Based on VF for Power Converters with LCL Filters
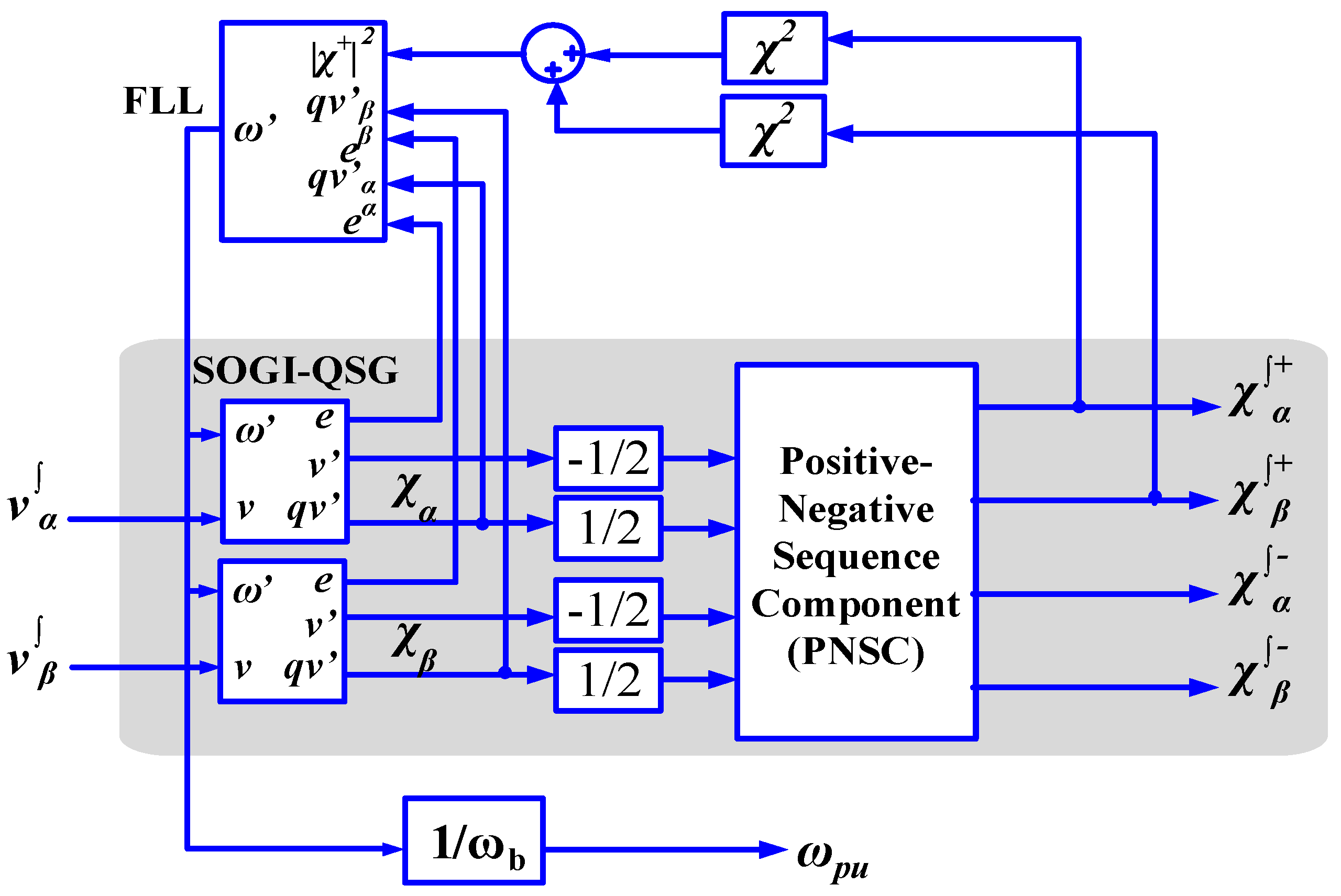
2.1. Introduction to VF Estimation
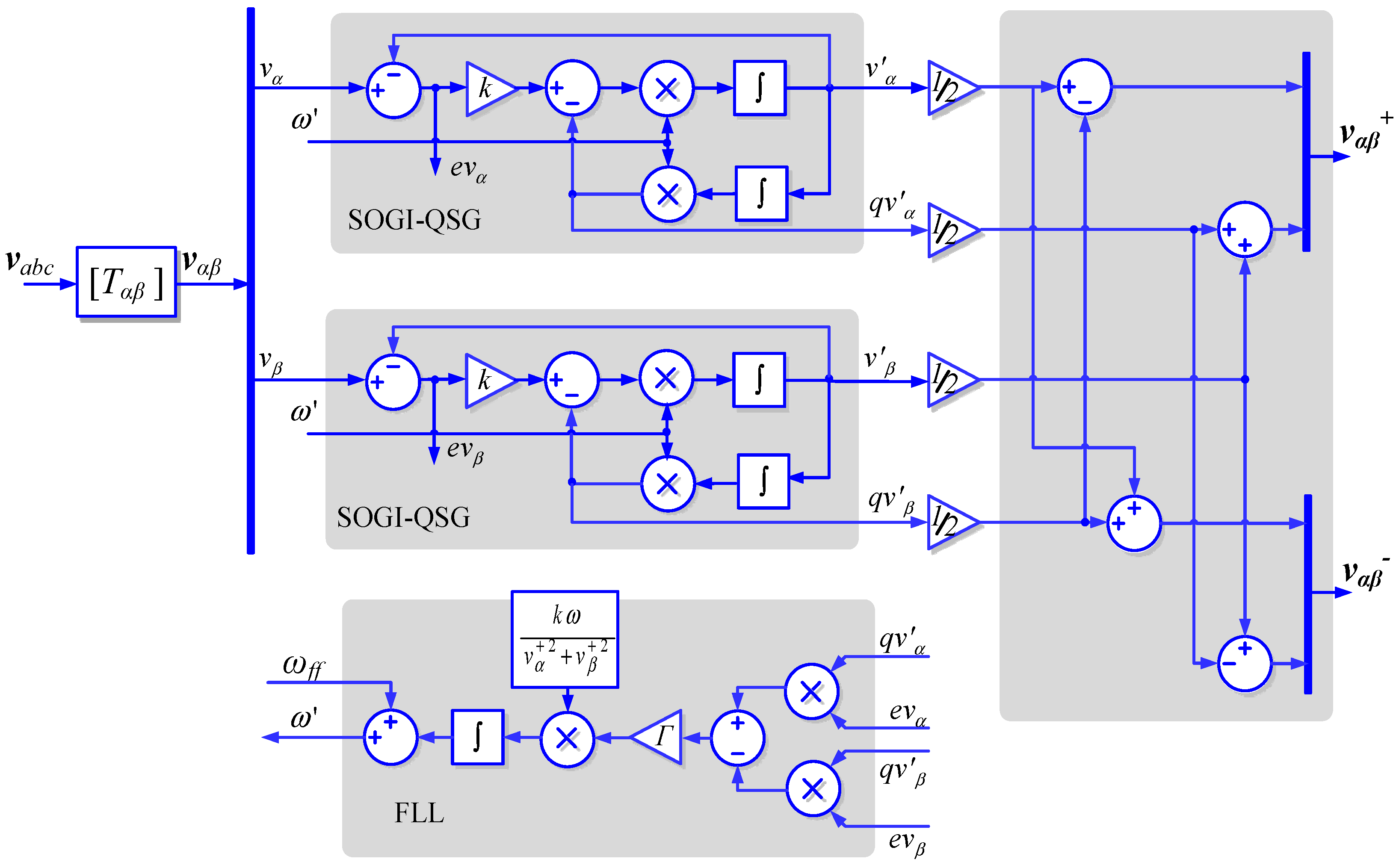
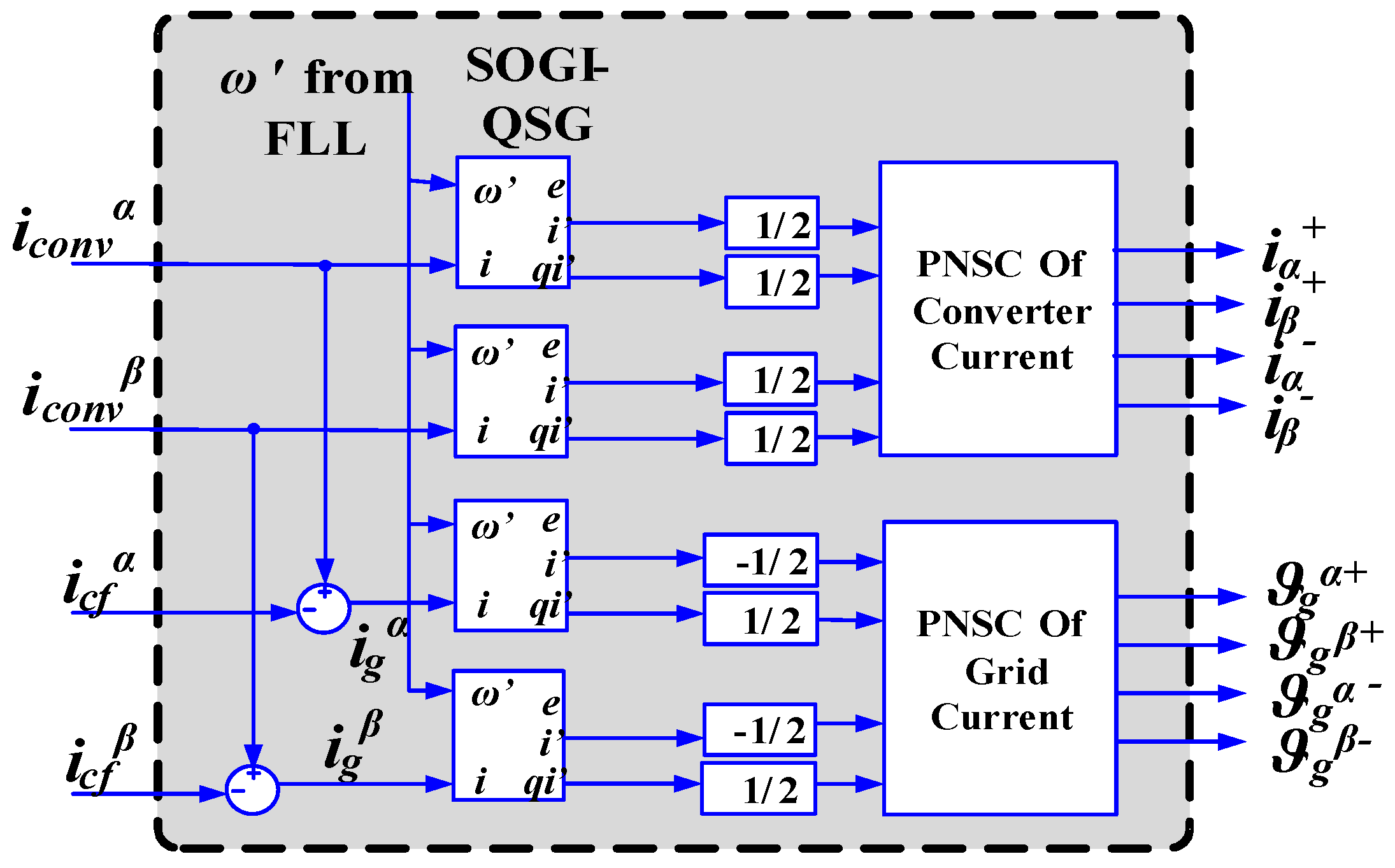
2.2. Grid Synchronization by Using DSOGI-FLL
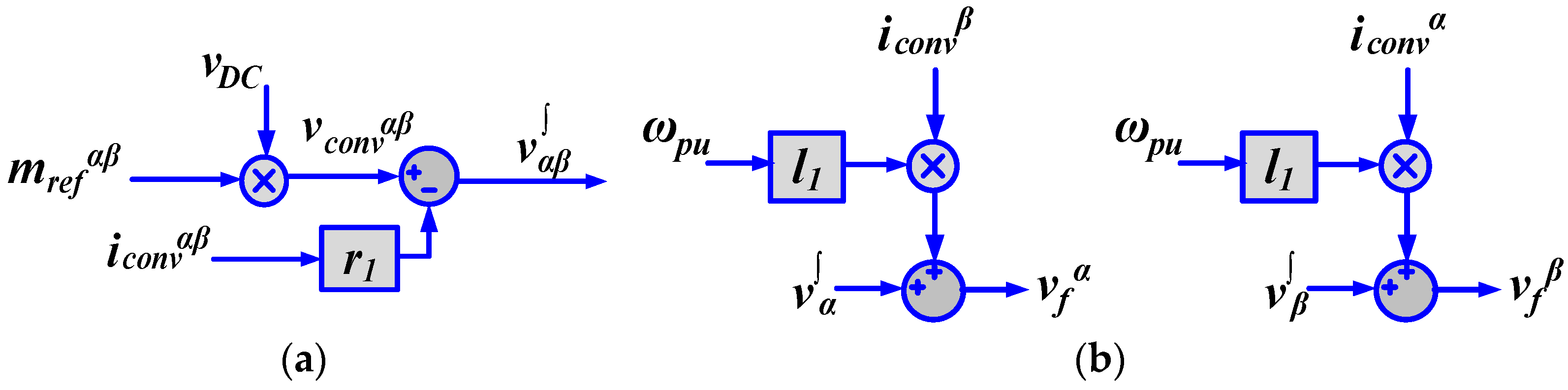
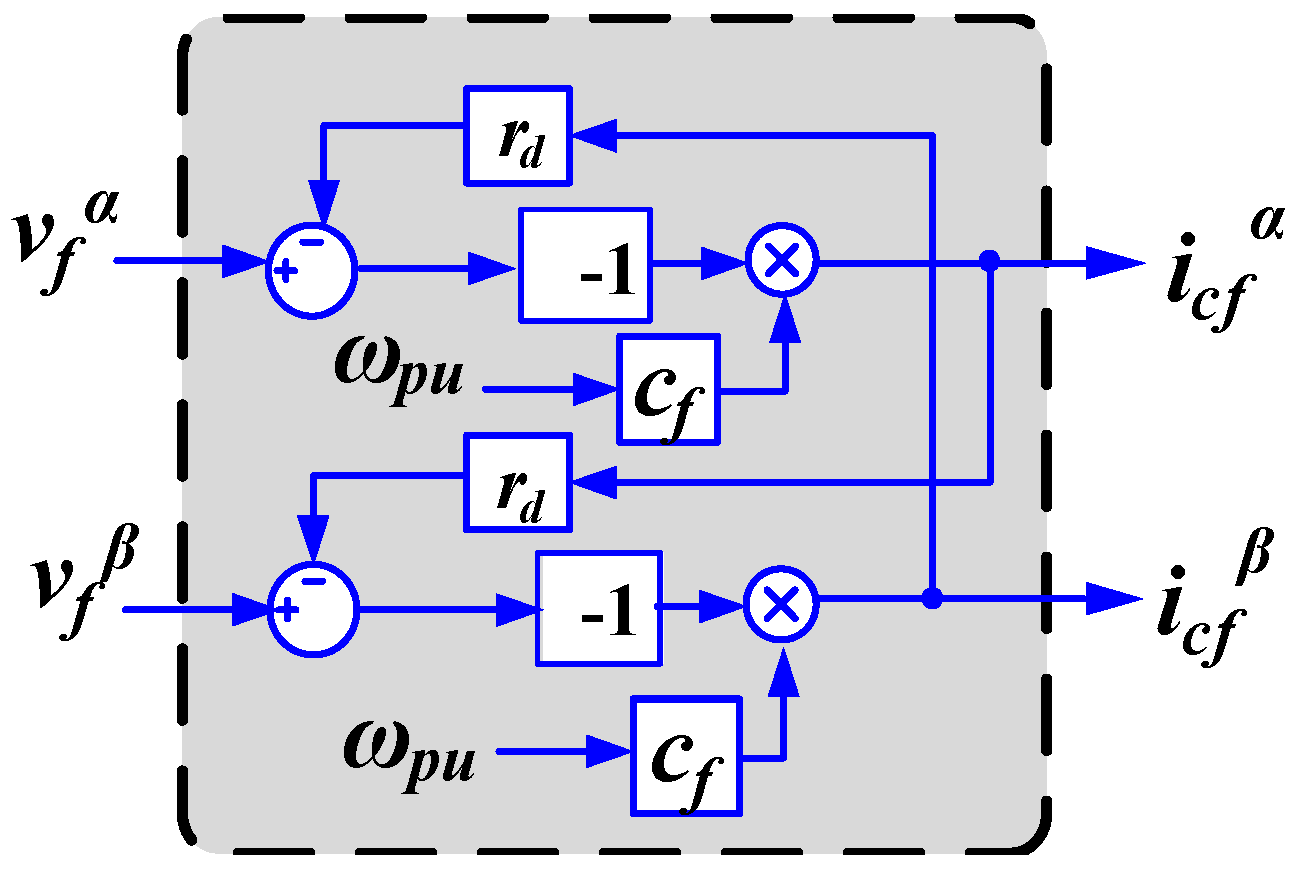
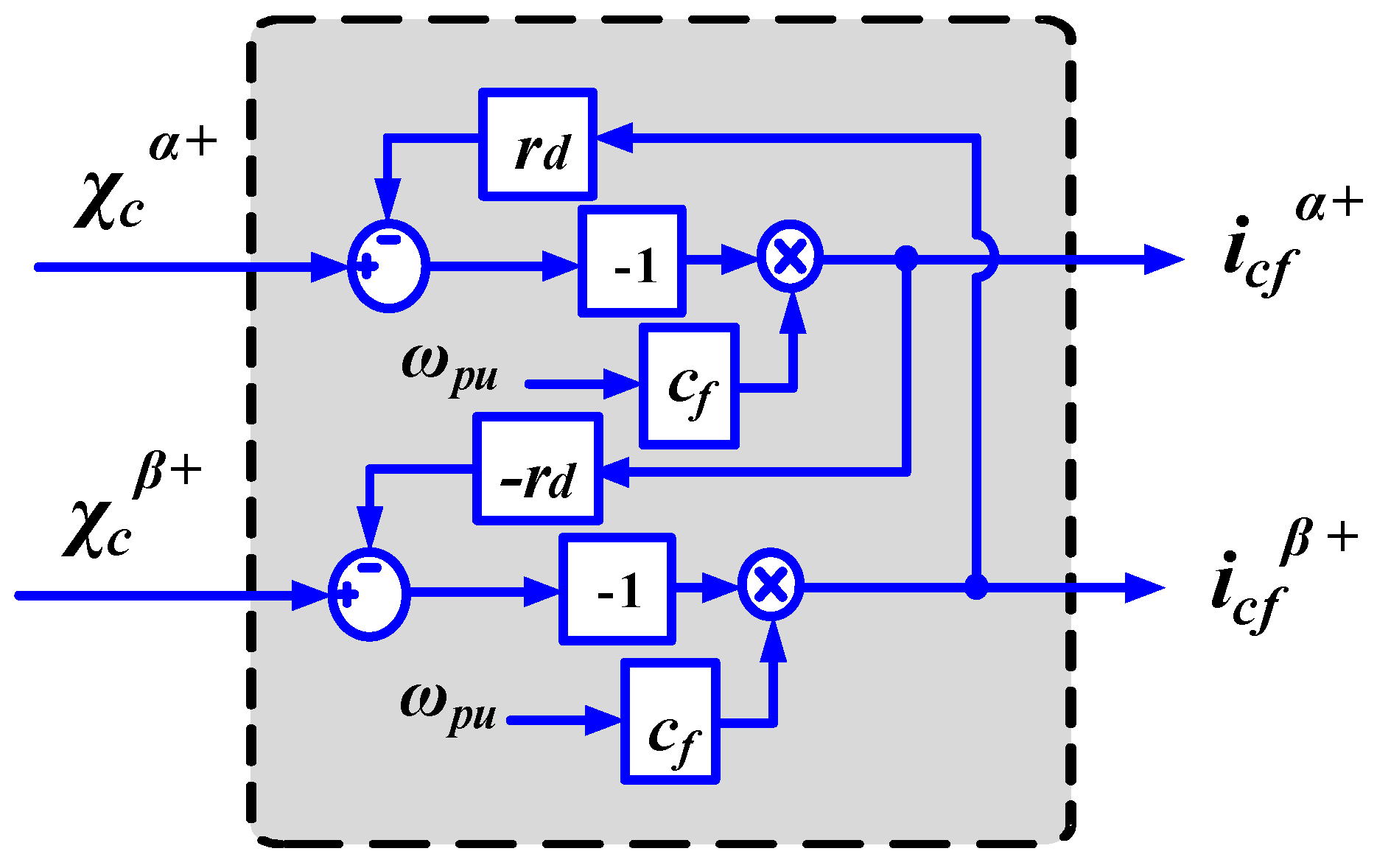
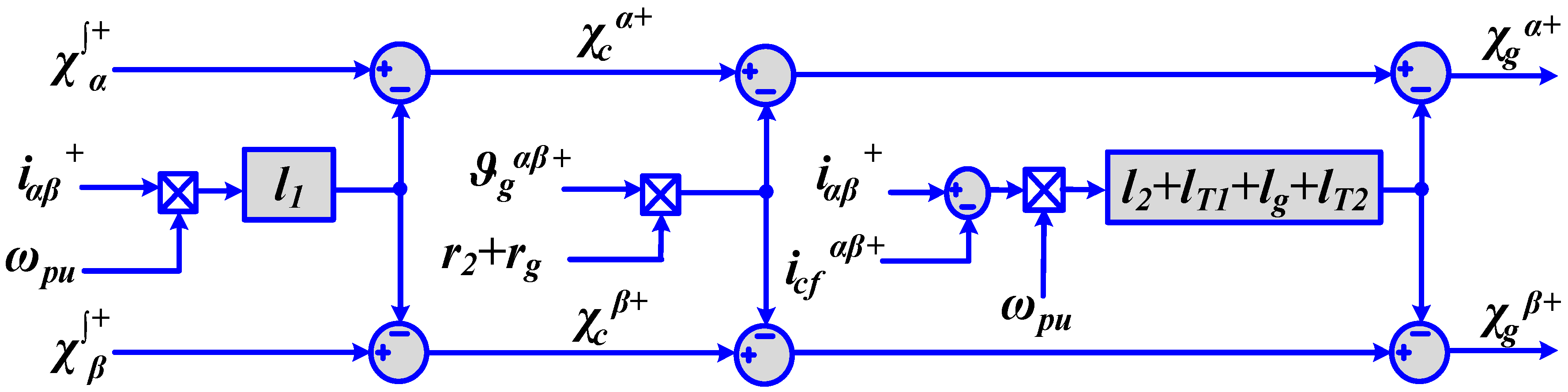
2.3. Implementation of VF Estimation with LCL Filter
2.4. Effect of Filtering Configuration in the VF Implementation
2.5. Inner Loop Control of VSC
2.6. Current Reference Generated for PR Current Controller
3. Simulation Results
3.1. Change in Active Power Delivery at the Point after T1 and PCC
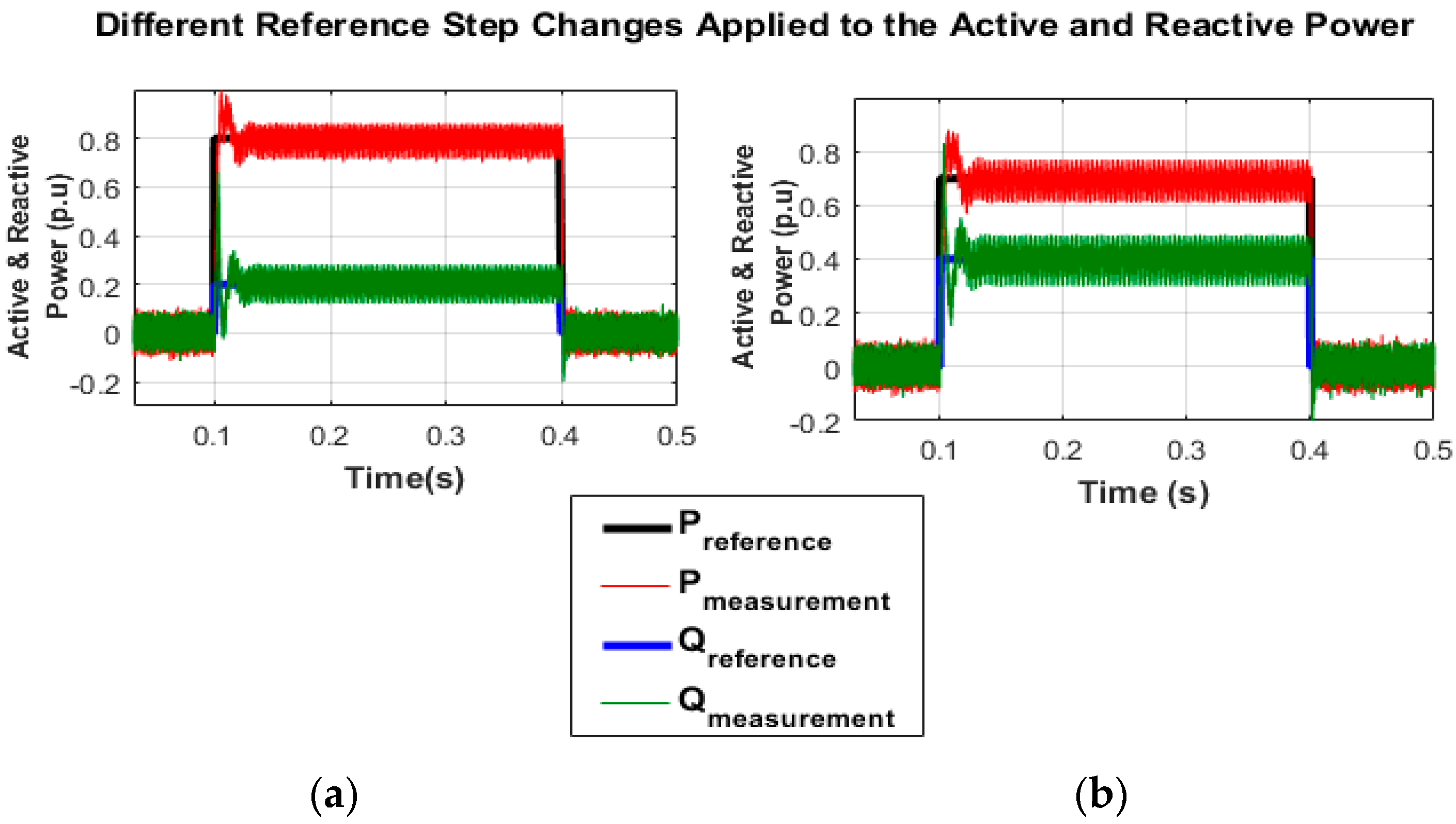
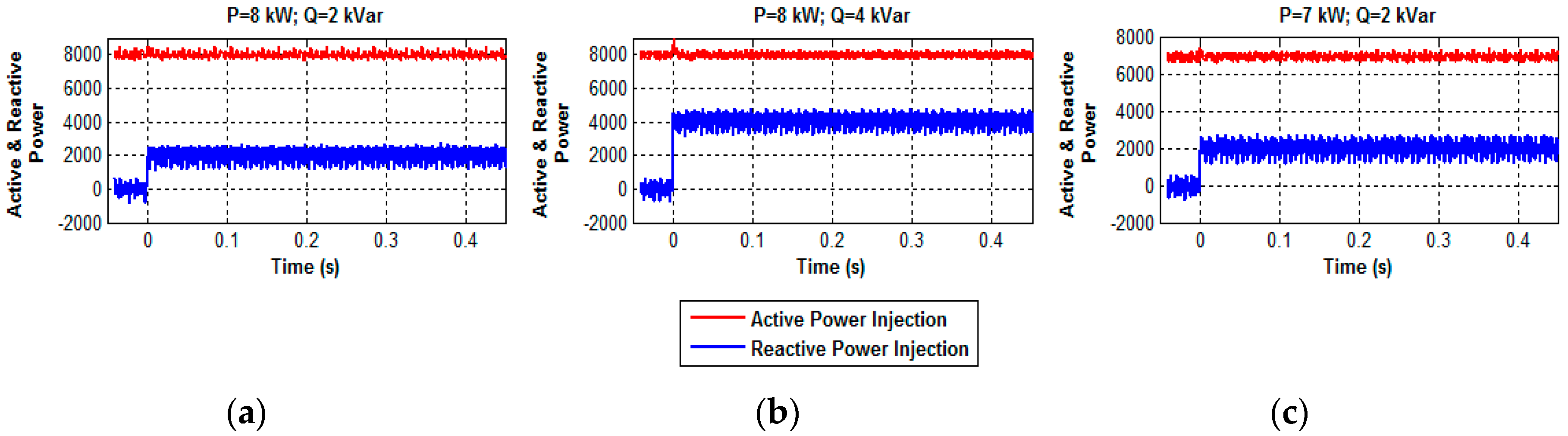
3.2. Change in Active and Reactive Power Injection
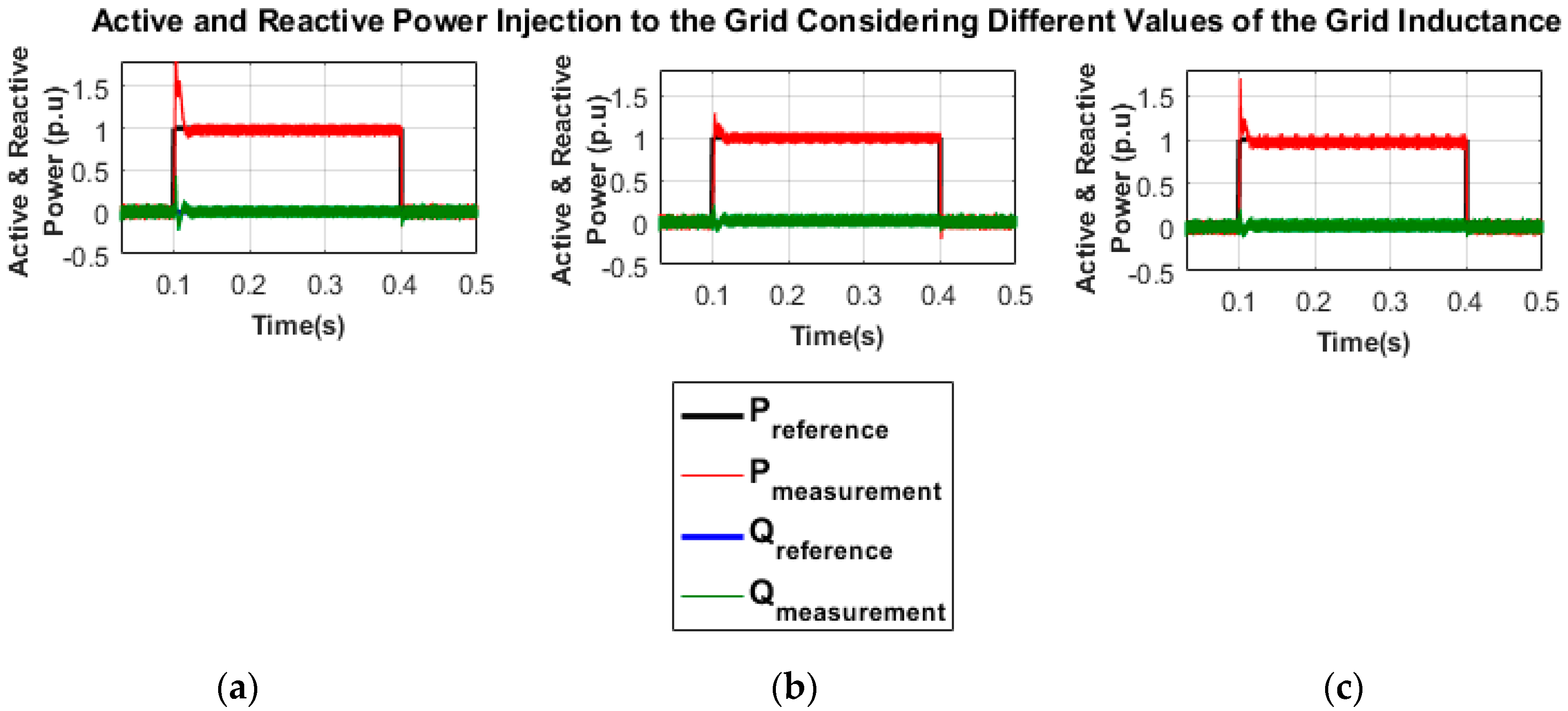
3.3. Change in Active and Reactive Power Injection Using Different Values of Grid Inductance
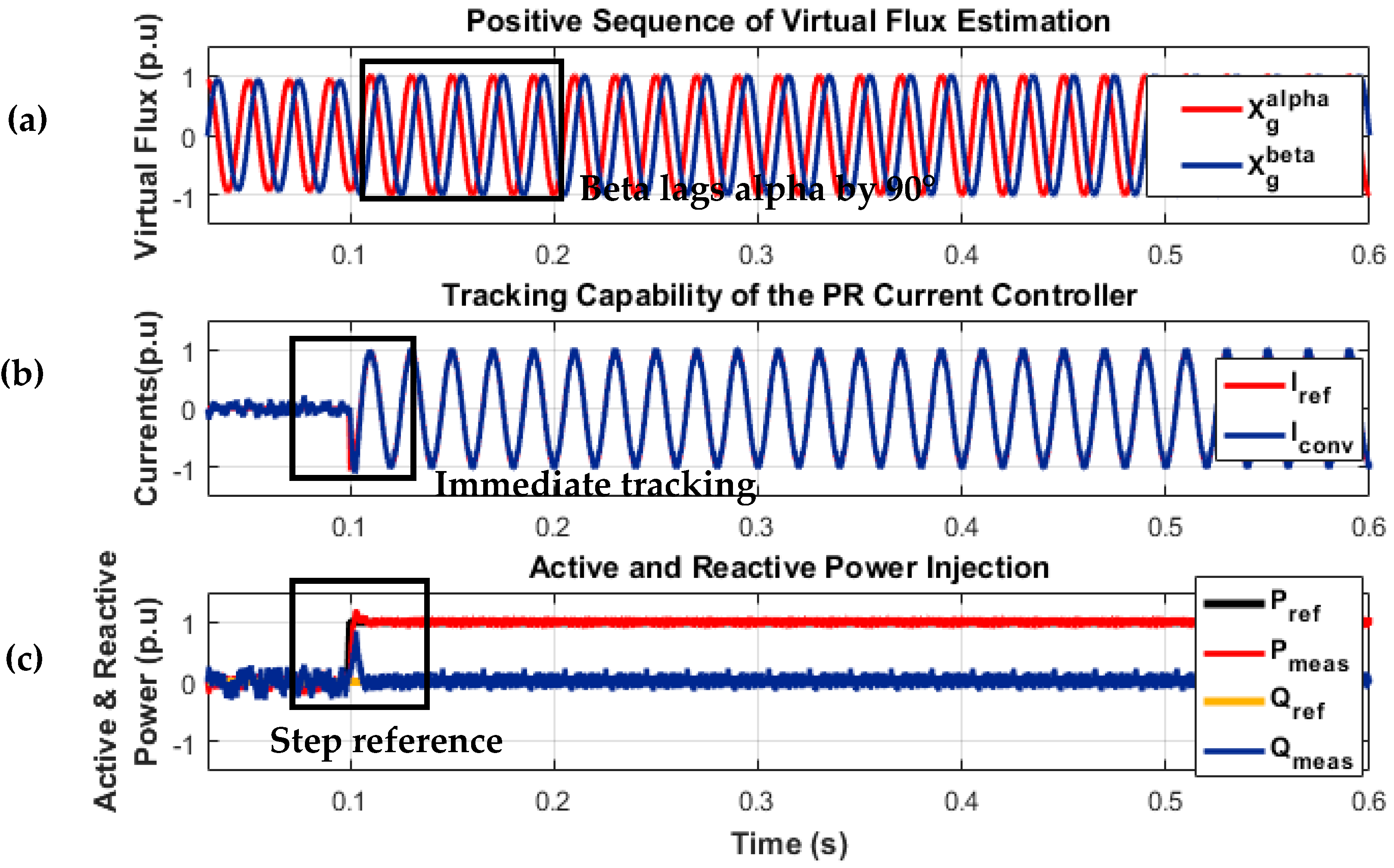
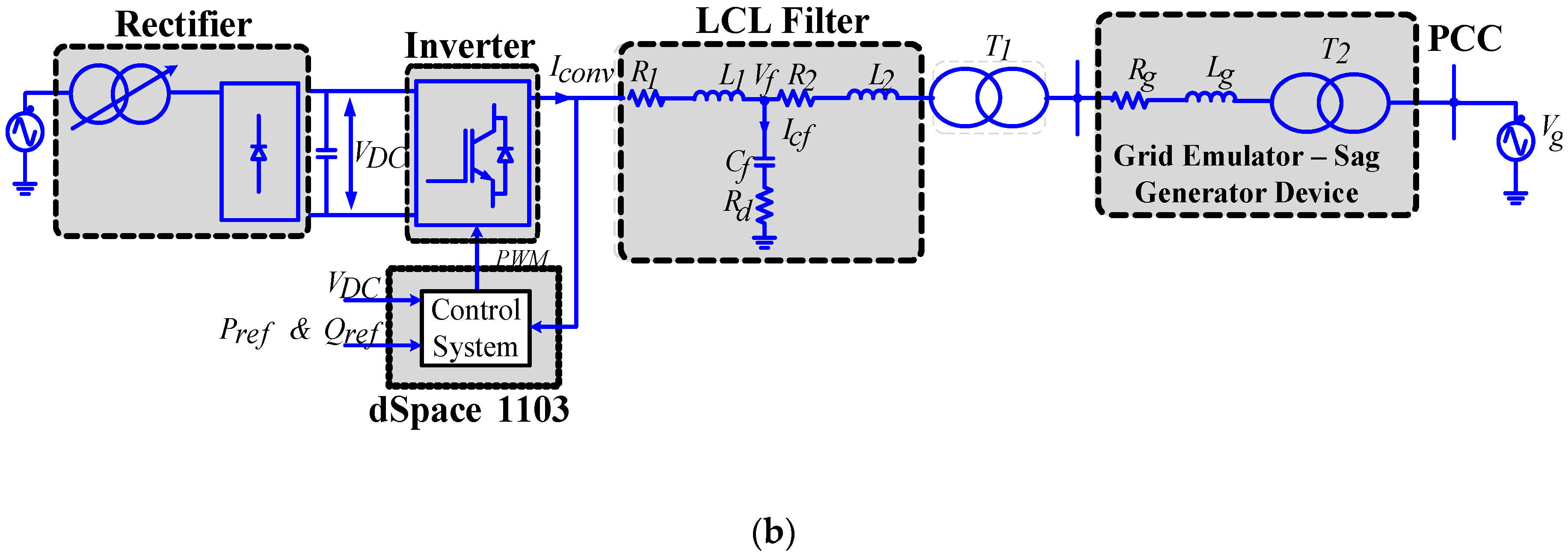
4. Experimental Results
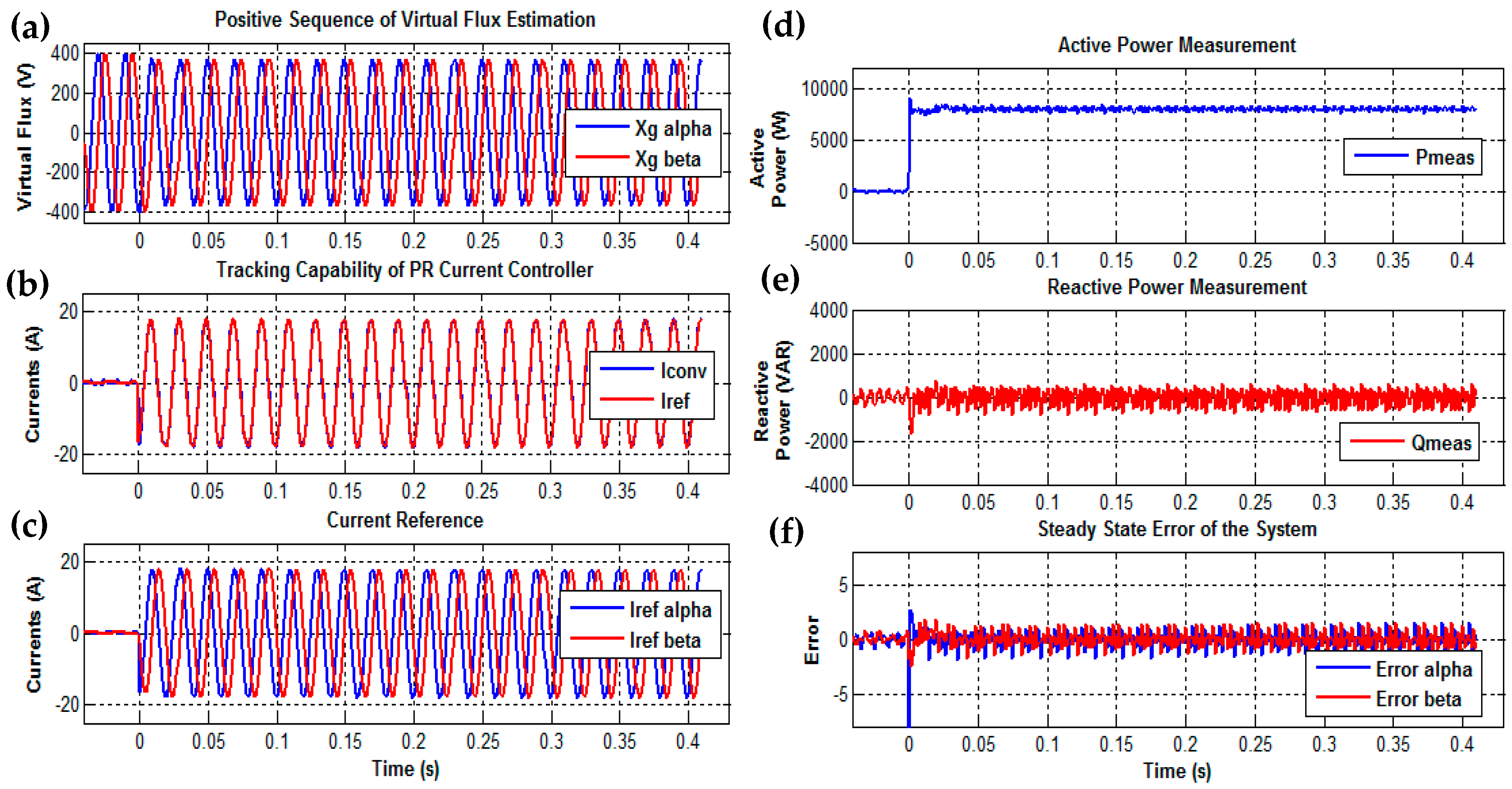
4.1. Performance of VF Based Controller
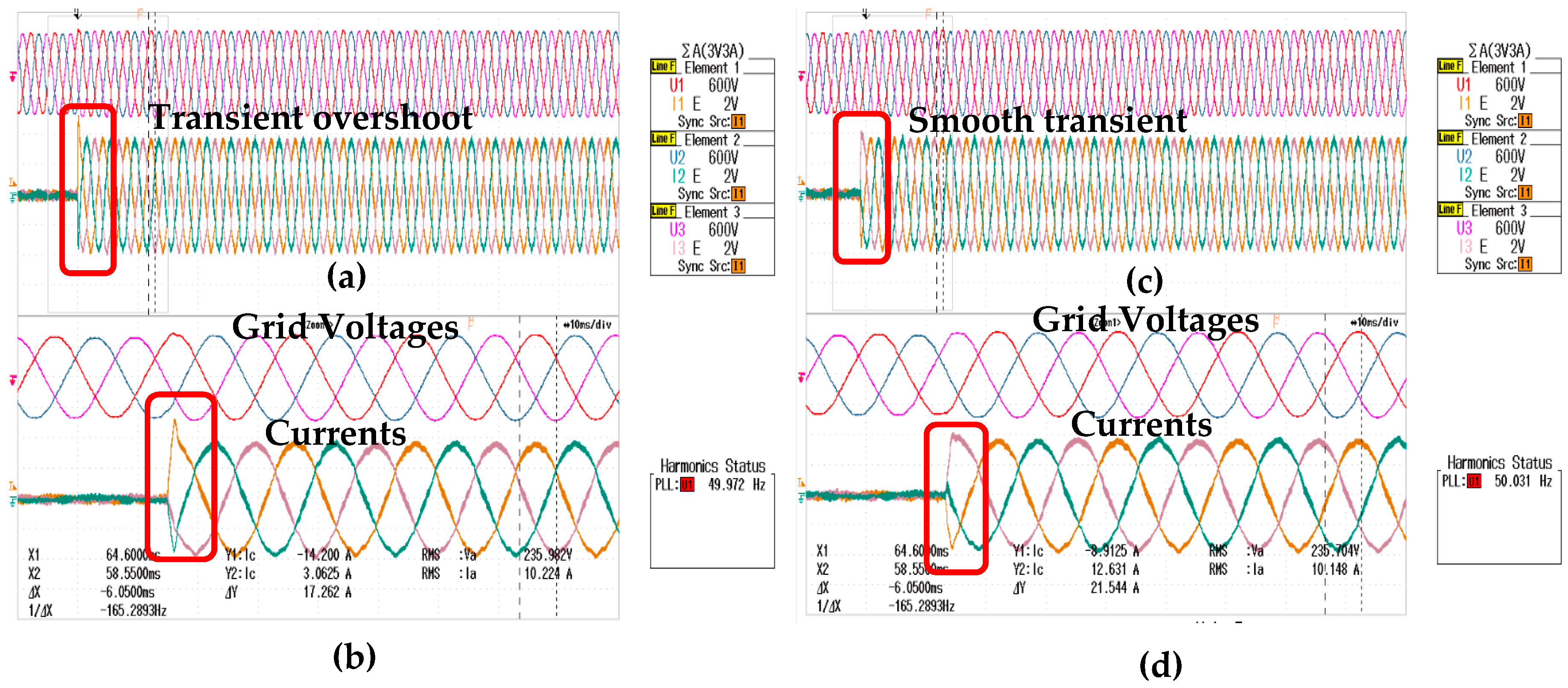
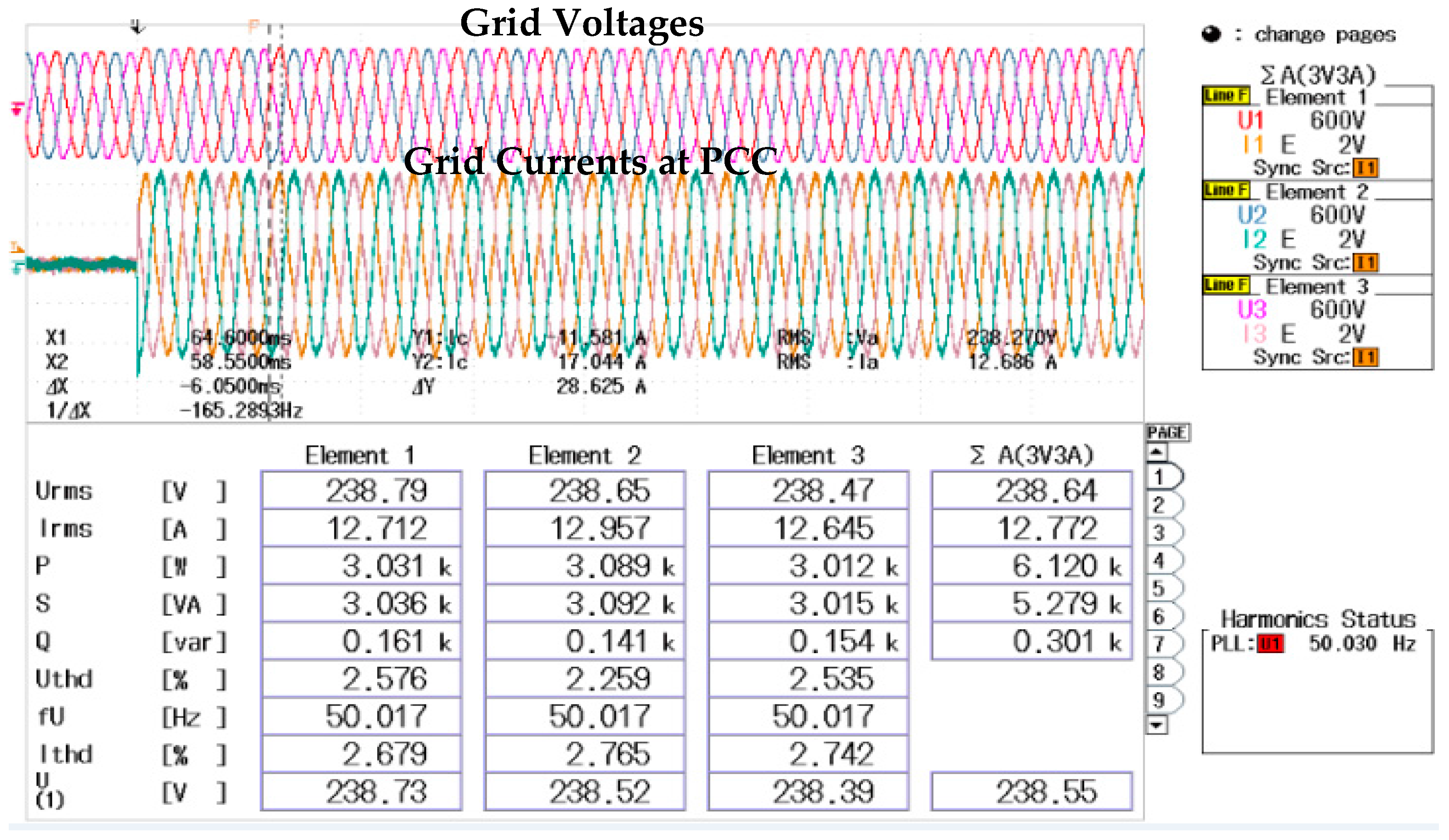
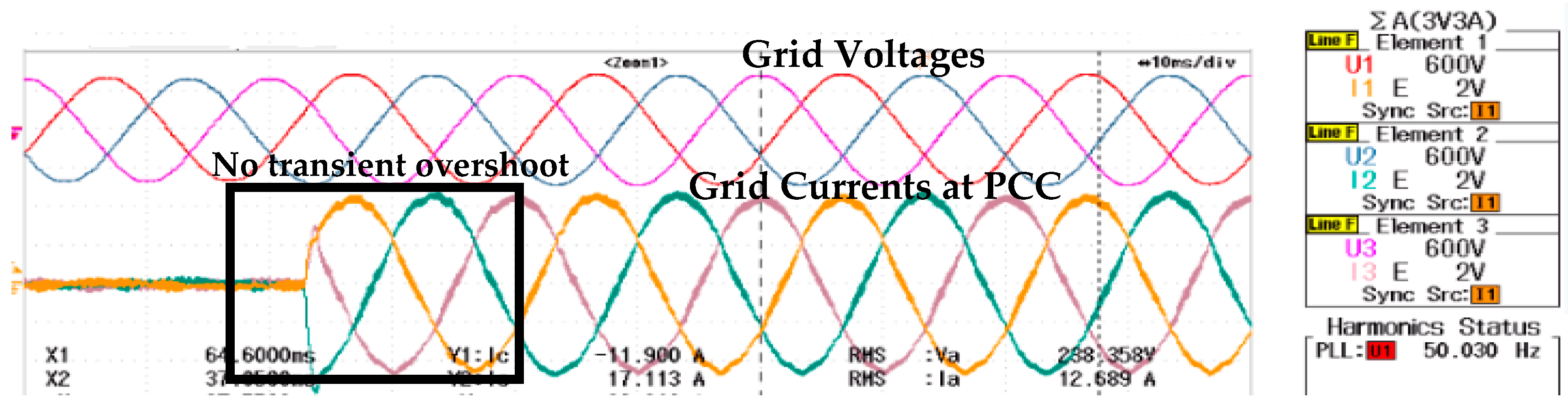
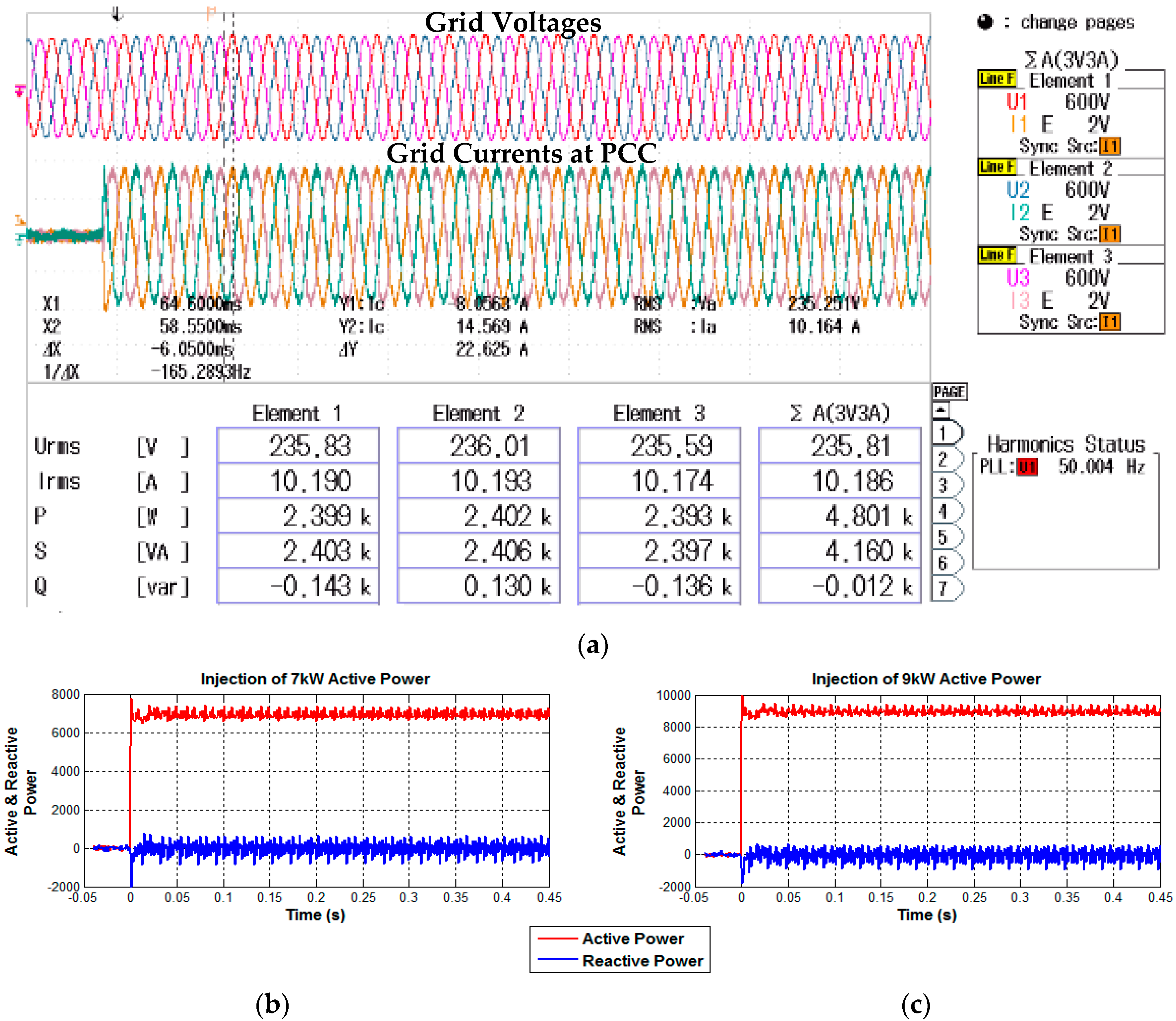
4.2. Control of Active Power Delivery
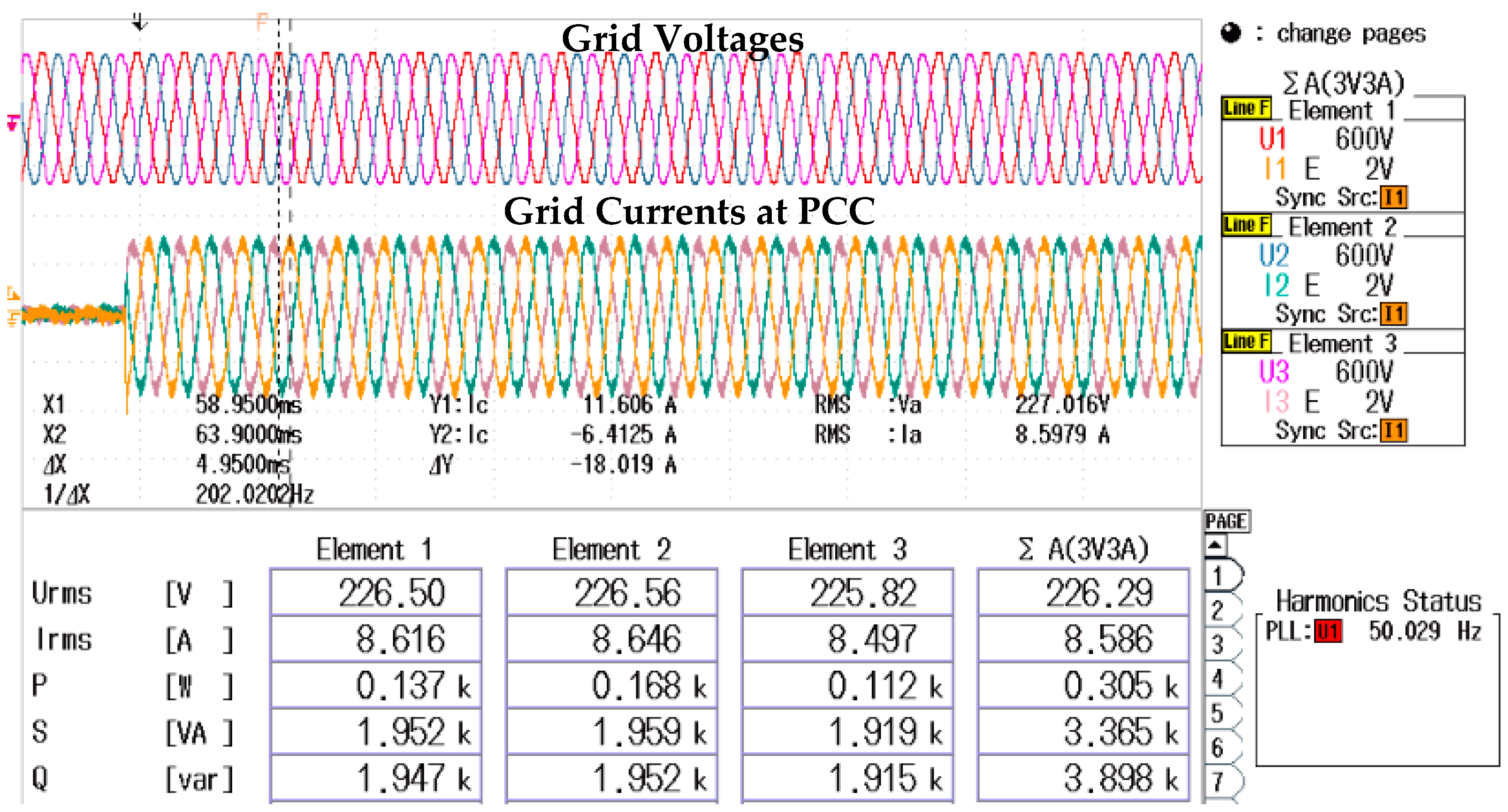
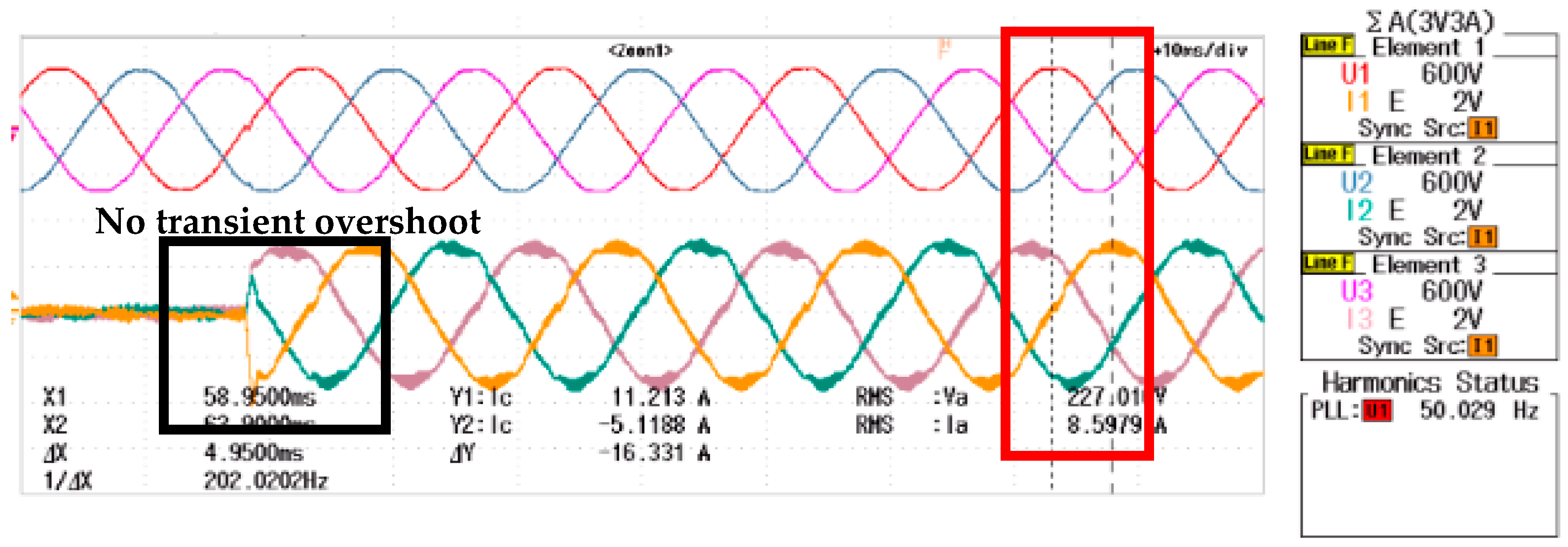
4.3. Control of Reactive Power Delivery
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| RES | Renewable Energy Source |
| PCC | Point of Common Connection |
| TSO | Transmission System Operators |
| VSC | Voltage Source Converters |
| VF | Virtual Flux |
| LCL | Inductor (L), Capacitor (C), Inductor (L) |
| DPC | Direct Power Control |
| VOC | Voltage Oriented Control |
| DSOGI-FLL | Dual Second Order Generalized Integrator with Frequency Locked Loop |
| DSOGI-QSG | Dual Second Order Generalized Integrator with Quadrature Signal Generator |
| FLL | Frequency Locked Loop |
| PNSC | Positive and Negative Sequence Components extractor |
| DSOGI-VF | Dual Second Order Generalized Integrator based Virtual Flux |
| PI | Proportional Integral |
| PR | Proportional Resonant |
| GI | Generalized Integrator |
| PWM | Pulse Width Modulation |
| SVM | Space Vector Modulation |
| PNS | Positive and Negative Sequence |
References
- IRENA. REthinking Energy 2017: Accelerating Global Energy Transformation; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2017; Available online: http://www.irena.org/Document Downloads/Publications/IRENA_REthinking_Energy_2017.pdf (accessed on 1 December 2017).
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Son: Hoboken, NJ, USA, 2011. [Google Scholar]
- Rodriguez, P.; Luna, A.; Munoz Aguilar, R.S.; Teodorescu, R.; Blaabjerg, F.; Otadui, I.E. A stationary reference frame grid synchronization converters under adverse grid conditions. IEEE Trans. Power Electron. 2012, 27, 99–112. [Google Scholar] [CrossRef]
- Hassaine, L.; Olias, E.; Quintero, J.; Salas, V. Overview of power inverter topologies and control structures for grid connected photovoltaic systems. Renew. Sustain. Energy Rev. 2014, 30, 796–807. [Google Scholar] [CrossRef]
- Luna, A.; Rocabert, J.; Ignacio Candela, J.; Hermoso, J.R.; Teodorescu, R.; Blaabjerg, F.; Rodriquez, P. Grid voltage synchronization for distributed generation systems under grid fault conditions. IEEE Trans. Ind. Appl. 2015, 51, 3414–3425. [Google Scholar] [CrossRef]
- Hansen, S.; Malinowski, M.; Blaabjerg, F.; Kazmierkowski, M.P. Sensor-less control strategies for PWM rectifier. In Proceedings of the 15th Annual IEEE Applied Power Electronics Conference and Exposition, New Orleans, Louisiana, 6–10 February 2000; pp. 832–838. [Google Scholar]
- Malinowski, M.; Kazmierkowski, M.P.; Hansen, S.; Blaabjerg, F.; Marques, G.D. Virtual-flux-based direct power control of three-phase PWM rectifiers. IEEE Trans. Ind. Appl. 2001, 37, 1019–1027. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Trzynadlowski, A.M. A comparative study of control techniques for PWM rectifiers in AC adjustable speed drives. IEEE Trans. Power Electron. 2003, 18, 1390–1396. [Google Scholar] [CrossRef]
- Norniella, J.G.; Cano, J.M.; Orcajo, G.A.; Rojas, C.H.; Pedrayes, J.F.; Cabanas, M.F.; Melero, M.G. Improving the dynamics of virtual-flux-based control of three-phase active rectifiers. IEEE Trans. Ind. Electron. 2014, 61, 177–187. [Google Scholar] [CrossRef]
- Razali, A.M.; George, G. An Analysis of Direct Power Control for Three Phase AC-DC Converter; IEEE Industry Applications Society Annual Meeting (IAS): Las Vegas, NV, USA, 2012; pp. 1–7. [Google Scholar]
- Razali, A.; Rahman, A.; George, G.; Rahim, N. Analysis and design of new switching look-up table for virtual flux direct power control of grid connected three phase PWM AC-DC converter. IEEE Trans. Ind. Appl. 2015, 51, 1189–1200. [Google Scholar] [CrossRef]
- Antoniewicz, P.; Kazmierkowski, M.P. Virtual-flux-based predictive direct power control of AC/DC converters with online inductance estimation. IEEE Trans. Ind. Electron. 2008, 55, 4381–4390. [Google Scholar] [CrossRef]
- Tao, Y.; Wu, Q.; Tang, W.; Wang, L. Voltage sensorless predictive direct power control of three-phase PWM converters. IET Power Electron. 2016, 9, 1009–1018. [Google Scholar] [CrossRef]
- Bian, C.; Shi, C.; Song, C.; Wang, A. Study of the control system of three-level PWM rectifier based on virtual flux oriented. In Proceedings of the International Conference. Intelligent Human-Machine Systems and Cybernetics, College of Computer Science & Technology of Zhejiang University, Hangzhou, China, 26–27 August 2011; pp. 53–56. [Google Scholar]
- Kulka, A. Sensor-Less Digital Control of Grid Connected Three Phase Converters For Renewable Sources. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2009. [Google Scholar]
- Suul, J.A. Control of Grid Integrated Voltage Source Converters under Unbalanced Conditions—Development of an Online Frequency Adaptive Virtual Flux Based Approach. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2012. [Google Scholar]
- Suul, J.A.; Luna, A.; Rodríguez, P.; Undeland, T. Voltage-sensor-less synchronization to unbalanced grids by frequency-adaptive virtual flux estimation. IEEE Trans. Ind. Electron. 2012, 59, 2910–2923. [Google Scholar] [CrossRef]
- Suul, J.A.; Luna, A.; Rodriguez, P.; Undeland, T. Frequency-adaptive virtual flux estimation for grid synchronization under unbalanced conditions. In Proceedings of the Industrial Electronics Conference, Glendale, AZ, USA, 7–10 November 2010; pp. 486–492. [Google Scholar]
- Zhang, J.; Wang, H.; Zhu, M.; Cai, X. Control implementation of the full-scale wind power converter without grid voltage sensors. In In Proceedings of the 2014 International Power Electronics Conference, Hiroshima, Japan, 18–21 May 2014; pp. 1753–1760. [Google Scholar]
- Wrona, G.; Malon, K. Sensorless operation of an active front end converter with LCL filter. In In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics, ISIE 2014, Istanbul, Turkey, 1–4 June 2014; pp. 2697–2702. [Google Scholar]
- Gullvik, W.; Norum, L.; Nilsen, R. Active damping of resonance oscillations in LCL-filters based on virtual flux and virtual resistor. In In Proceedings of the 12th European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–10. [Google Scholar]
- Roslan, N.F.; Suul, J.A.; Luna, A.; Candela, J.I.; Rodriguez, P. A simulation study of proportional resonant controller based on the implementation of frequency adaptive virtual flux estimation with the LCL ilter. In Proceedings of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 1934–1941. [Google Scholar]
- Peña-Alzola, R.; Liserre, M.; Blaabjerg, F.; Sebastían, R.; Dannehl, J.; Fuchs, F.W. Analysis of the passive damping losses in LCL-filter-based grid converters. IEEE Trans. Power Electron. 2013, 28, 2642–2646. [Google Scholar] [CrossRef]
- Zammit, D.; Staines, C.S.; Apap, M. Comparison between PI and PR current controllers in grid connected PV inverters. Int. J. Electr. Comput. Electron. Commun. Eng. 2014, 8, 224–229. [Google Scholar]



| Abbreviation | Nomenclature | Values |
|---|---|---|
| SN | Rated Apparent Power | 10 kVA |
| Vg(p-p) | Phase to Phase Grid Voltage | 400 V |
| Vg(p) | Phase Voltage | 230 V |
| VDC | DC-Link Voltage | 700 V |
| L1(abc) | Inductor, L1 | 3.4 mH |
| L2(abc) | Inductor, L2 | 0.588 mH |
| Lg(abc) | Grid Inductance, Lg | 10 mH |
| Cf(abc) | Filter Capacitor | 4.7 μF |
| Rd(abc) | Damping Resistor | 1.8 Ω |
| fsw & fs | Switching & Sampling Frequency | 10 kHz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roslan, N.F.; Luna, A.; Rocabert, J.; Candela, J.I.; Rodriguez, P. Remote Power Control Injection of Grid-Connected Power Converters Based on Virtual Flux. Energies 2018, 11, 488. https://doi.org/10.3390/en11030488
Roslan NF, Luna A, Rocabert J, Candela JI, Rodriguez P. Remote Power Control Injection of Grid-Connected Power Converters Based on Virtual Flux. Energies. 2018; 11(3):488. https://doi.org/10.3390/en11030488
Chicago/Turabian StyleRoslan, Nurul Fazlin, Alvaro Luna, Joan Rocabert, Jose Ignacio Candela, and Pedro Rodriguez. 2018. "Remote Power Control Injection of Grid-Connected Power Converters Based on Virtual Flux" Energies 11, no. 3: 488. https://doi.org/10.3390/en11030488
APA StyleRoslan, N. F., Luna, A., Rocabert, J., Candela, J. I., & Rodriguez, P. (2018). Remote Power Control Injection of Grid-Connected Power Converters Based on Virtual Flux. Energies, 11(3), 488. https://doi.org/10.3390/en11030488







