Ensemble-Based Data Assimilation in Reservoir Characterization: A Review
Abstract
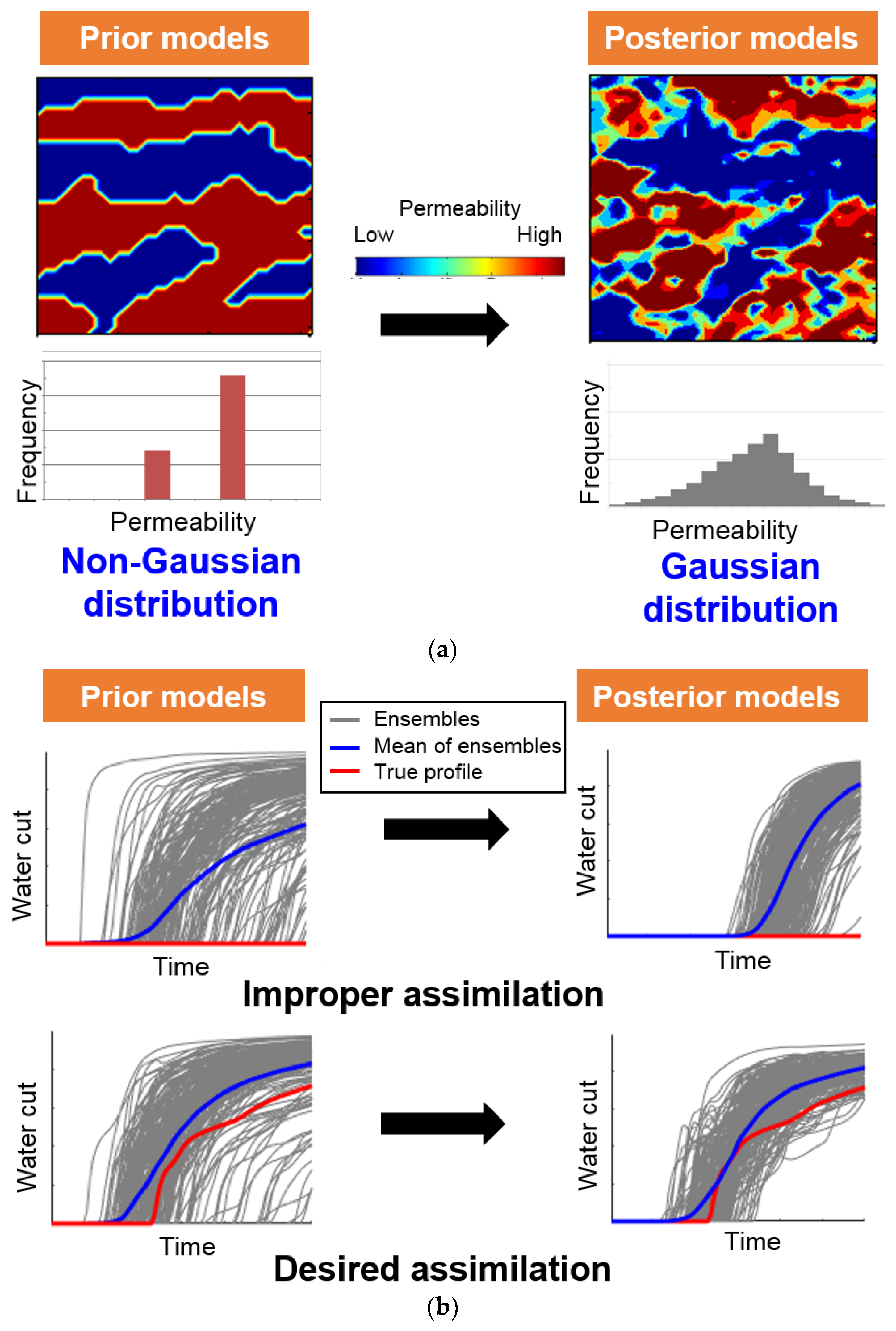
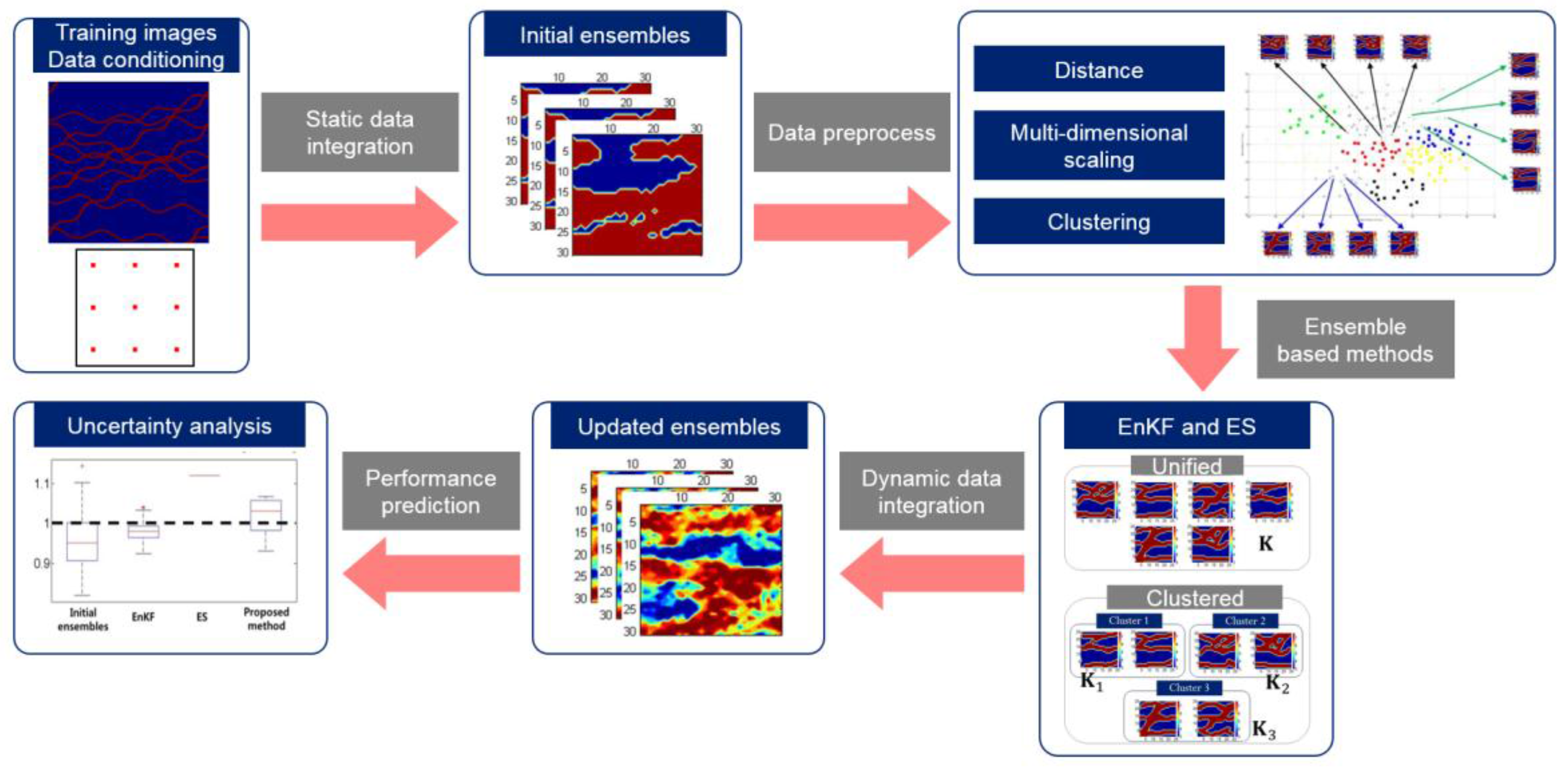
:1. Introduction
2. Theoretical Framework of Ensemble–Based Data Assimilation
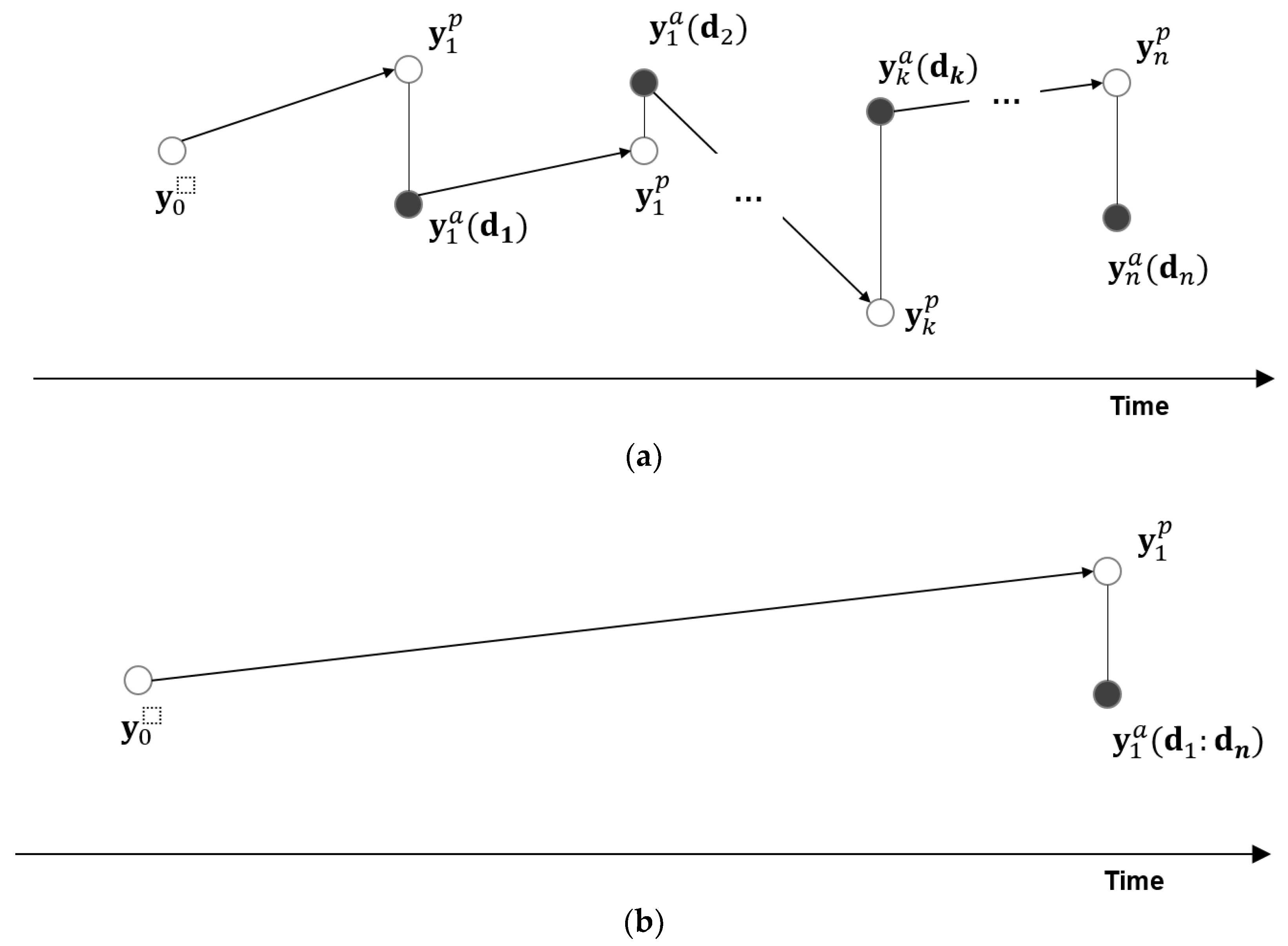
2.1. Mathematical Formulation
2.2. Characteristics of EnKF and ES
- If tn < t: Smoothing (interpolation)
- If tn = t: Filtering
- If tn > t: Predicting
- Easy-coupling with forward models
- Various applications for model parameters
- Uncertainty analysis
- Well-established in mathematics
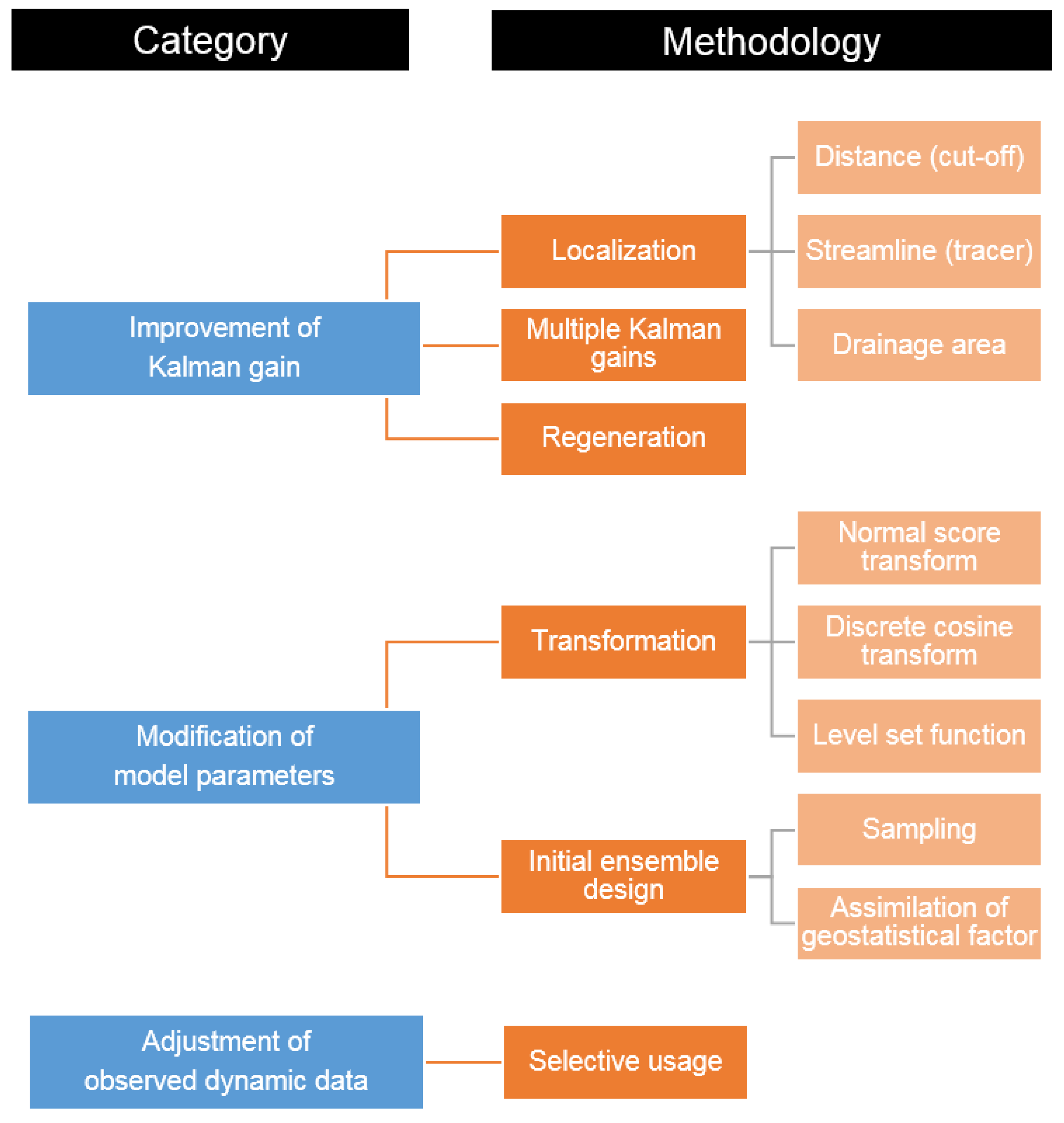
3. Methods to Overcome the Limitations of Ensemble–Based History Matching
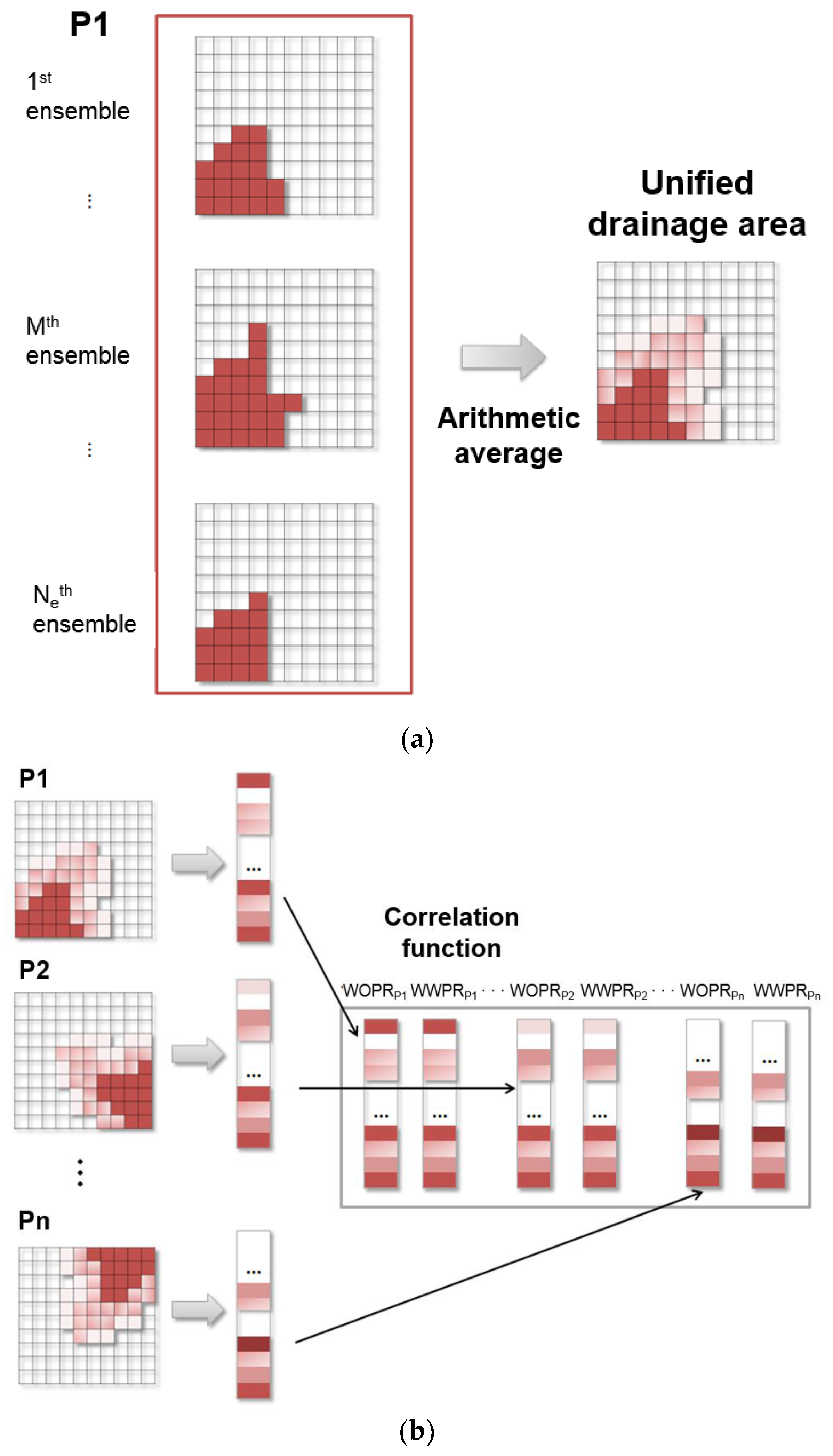
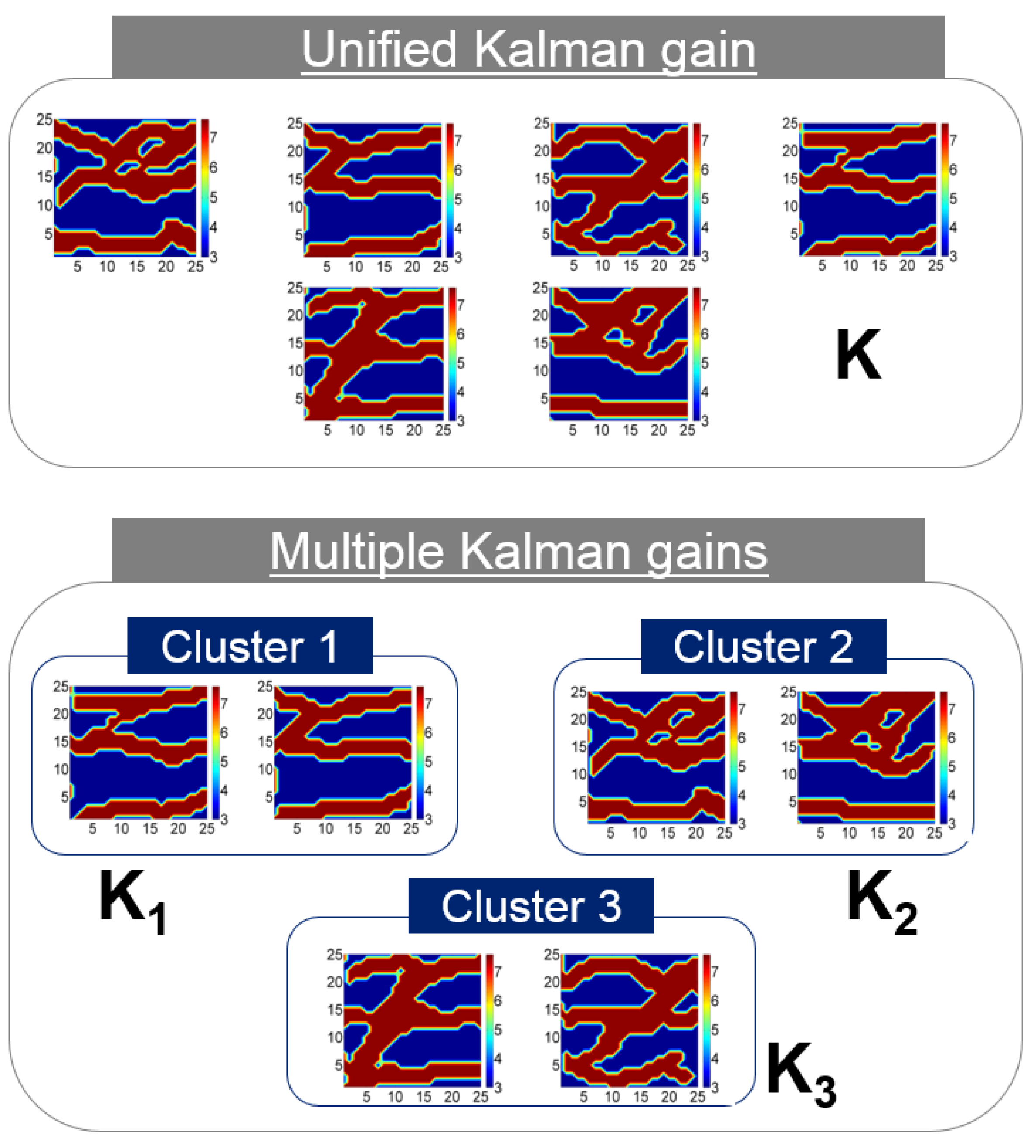
3.1. Importance of the Kalman Gain
- Distance (cut-off)
- Streamline or tracer simulation
3.2. Modification of Model Parameters
- Normal score transform (NST)
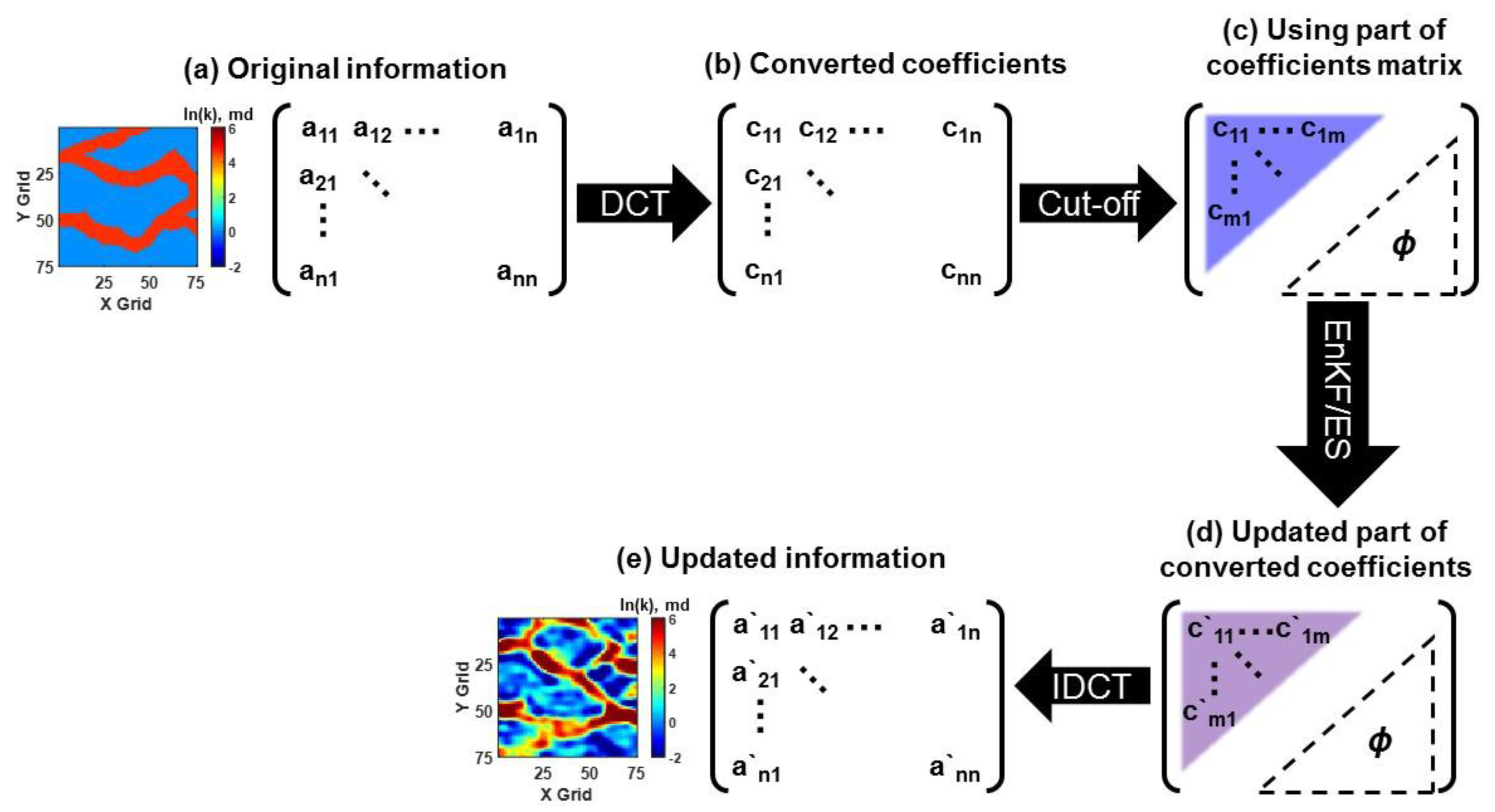
- Discrete cosine transform (DCT)
- Level set function (LSF)
- Sampling
- Assimilation of uncertain geological factors
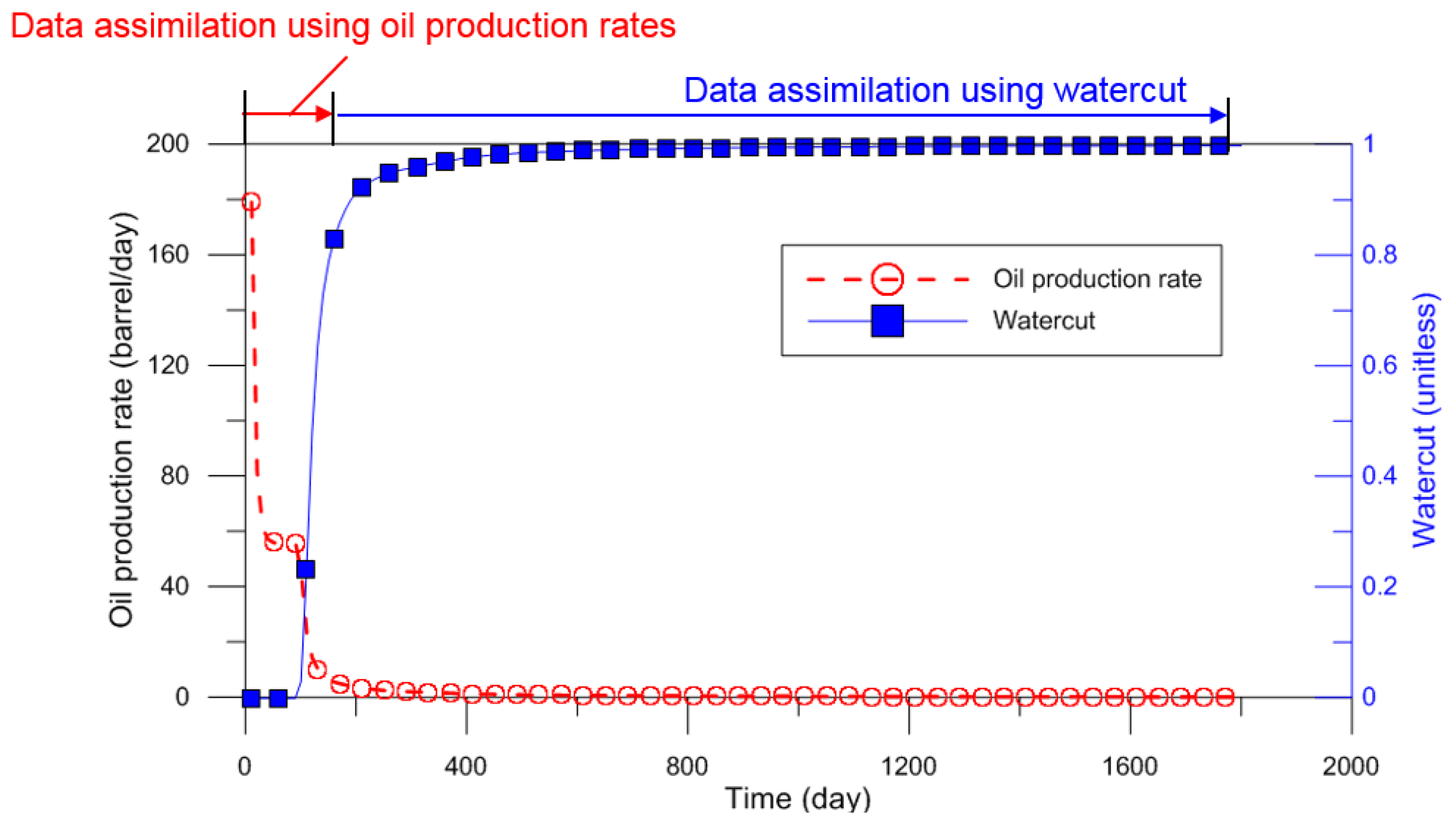
3.3. Adjustment of Observed Dynamic Data
4. Applications of Ensemble-Based History Matching in Reservoir Simulation
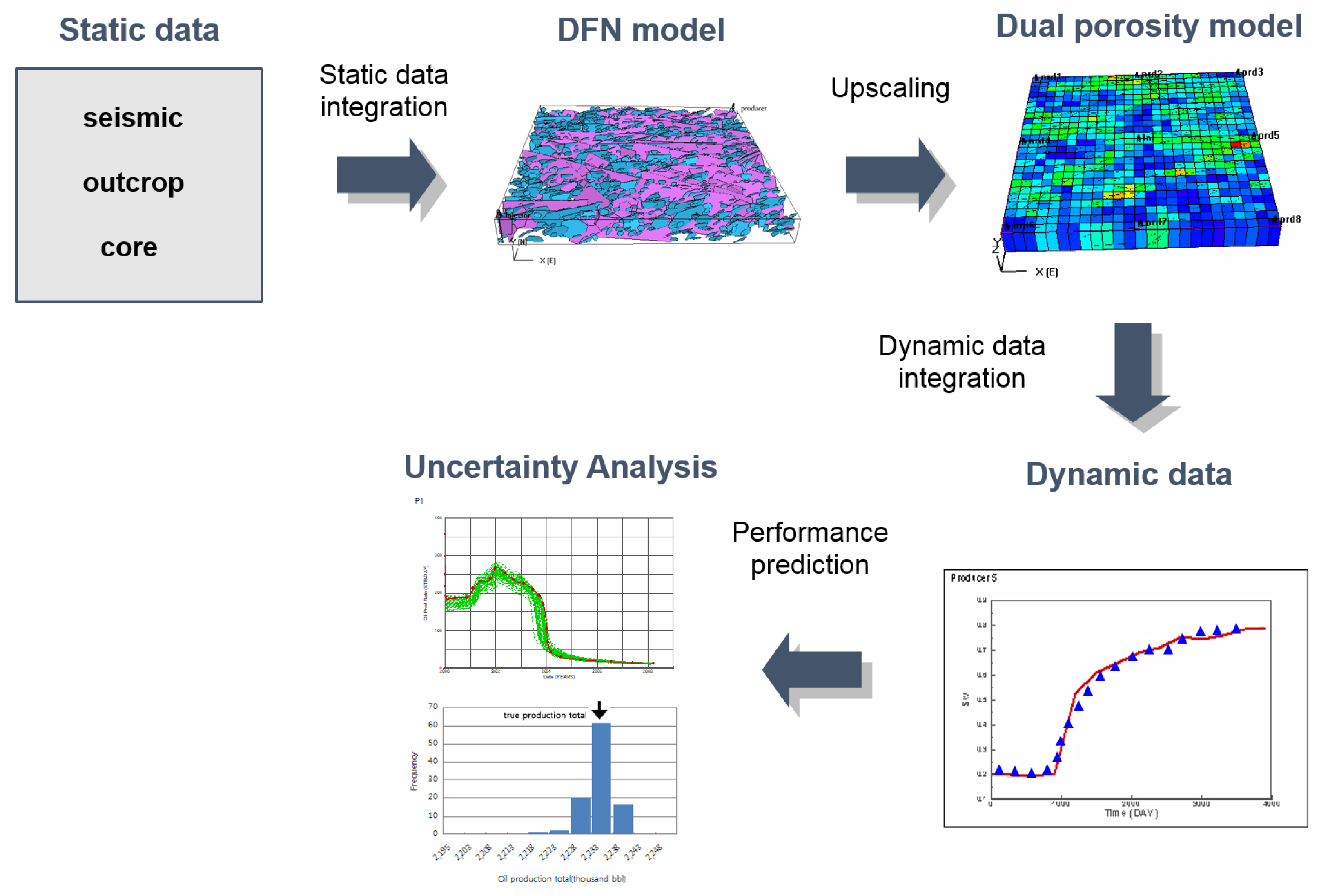
4.1. Naturally Fractured Reservoirs
4.2. Channelized Reservoir
4.3. Tight Reservoir with Hydraulic Fracturing
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blayo, E.; Bocquet, M.; Cosme, E.; Cugliandolo, L.F. Advanced Data Assimilation for Geosciences: Lecture Notes of the Les Houches School of Physics, 1st ed.; Oxford University Press: Oxford, UK, 2014; ISBN 978-0-19-872384-4. [Google Scholar]
- Evensen, G. Data Assimilation: The Ensemble Kalman Filter; Springer: New York, NY, USA, 2006; pp. 119–138. [Google Scholar]
- Asch, M.; Bocquet, M.; Nodet, M. Data Assimilation: Methods, Algorithms, and Applications, 1st ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016; ISBN 978-1-61-197454-6. [Google Scholar]
- Fletcher, S.J. Data Assimilation for the Geosciences: From Theory to Application; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 978-0-12-804484-1. [Google Scholar]
- Griffith, A.K.; Nichols, N.K. Data Assimilation Using Optimal Control Theory; Numerical Analysis Report; The University of Reading: Reading, UK, 1994. [Google Scholar]
- Ide, K.; Courtier, P.; Ghil, M.; Lorenc, A. Unified notation for data assimilation: Operational, sequential and variational. J. Met. Soc. Japan 1997, 75, 181–189. [Google Scholar] [CrossRef]
- Zou, X.; Navon, I.M.; Ledimet, F.X. An optimal nudging data assimilation scheme using parameter estimation. Q. J. R. Meteorol. Soc. 1992, 118, 1163–1186. [Google Scholar] [CrossRef]
- Liu, C.; Xiao, Q.; Wang, B. An ensemble-based four-dimensional variational data assimilation scheme. Part I: Technical formulation and preliminary test. Mon. Weather Rev. 2008, 136, 3363–3373. [Google Scholar] [CrossRef]
- Bocquet, M.; Sakov, P. An iterative Kalman smoother. Q. J. R. Meteorol. Soc. 2013, 140, 1521–1535. [Google Scholar] [CrossRef]
- Oliver, D.S.; Reynolds, A.C.; Liu, N. Inverse Theory for Petroleum Reservoir Characterization and History Matching; Cambridge University Press: Cambridge, UK, 2008; pp. 347–366. [Google Scholar]
- Houtekamer, P.L.; Mitchell, H.L. Data assimilation using an ensemble Kalman filter technique. Mon. Weather Rev. 1998, 126, 796–811. [Google Scholar] [CrossRef]
- Arroyo-Negrete, E.; Devegowda, D.; Datta-Gupta, A.; Choe, J. Streamline-assisted ensemble Kalman filter for rapid and continuous reservoir model updating. SPE Reserv. Eval. Eng. 2008, 11, 1046–1060. [Google Scholar] [CrossRef]
- Watanabe, S.; Datta-Gupta, A. Use of phase streamlines for covariance localization in ensemble Kalman filter for three-phase history matching. SPE Reserv. Eval. Eng. 2012, 15, 273–289. [Google Scholar] [CrossRef]
- Jafarpour, B.; McLaughlin, D.B. Estimating channelized-reservoir permeabilities with the ensemble Kalman filter: The importance of ensemble design. SPE J. 2009, 14, 374–388. [Google Scholar] [CrossRef]
- Skjervheim, J.A.; Evensen, G. An ensemble smoother for assisted history matching. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 21–23 February 2011. [Google Scholar] [CrossRef]
- Chen, Y.; Oliver, D.S. Ensemble randomized maximum likelihood method as an iterative ensemble smoother. Math. Geosci. 2012, 44, 1–26. [Google Scholar] [CrossRef]
- Emerick, A.; Reynolds, A.C. Combining sensitivities and prior information for covariance localization in the ensemble Kalman filter for petroleum reservoir applications. Comput. Geosci. 2011, 15, 251–269. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. A sequential ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 2001, 129, 123–137. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.; Lee, K.; Choe, J. Aquifer characterization of gas reservoirs using ensemble Kalman filter and covariance localization. J. Pet. Sci. Eng. 2016, 146, 446–456. [Google Scholar] [CrossRef]
- Jung, S.; Choe, J. Reservoir characterization using a streamline-assisted ensemble Kalman filter with covariance localization. Energy Explor. Exploit. 2012, 30, 645–660. [Google Scholar] [CrossRef]
- Chen, Y.; Oliver, D.S. Cross-covariances and localization for EnKF in multiphase flow data assimilation. Comput. Geosci. 2010, 14, 579–601. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Damiani, M.C. Determinacao de Padroes de Fluxo em Simulacoes de Reservatorio de Petroleo Utilizando Tracadores (In Portuguese). Master’s Thesis, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil, May 2007. [Google Scholar] [CrossRef]
- Emerick, A.A.; Reynolds, A.C. History matching a field case using the ensemble Kalman filter with covariance localization. SPE Reserv. Eval. Eng. 2011, 14, 443–452. [Google Scholar] [CrossRef]
- Yeo, M.J.; Jung, S.P.; Choe, J. Covariance matrix localization using drainage area in an ensemble Kalman filter. Energy Sources Part A Recovery Util. Environ. Eff. 2014, 36, 2154–2165. [Google Scholar] [CrossRef]
- Gu, Y.; Oliver, D.S. The ensemble Kalman filter for continuous updating of reservoir simulation models. ASME J. Energy Resour. Technol. 2005, 128, 79–87. [Google Scholar] [CrossRef]
- Zafari, M.; Reynolds, A.C. Assessing the uncertainty in reservoir description and performance predictions with the ensemble Kalman filter. SPE J. 2007, 12, 382–391. [Google Scholar] [CrossRef]
- Lee, K.; Jeong, H.; Jung, S.; Choe, J. Characterization of channelized reservoir using ensemble Kalman filter with clustered covariance. Energy Explor. Exploit. 2013, 31, 17–29. [Google Scholar] [CrossRef]
- Lee, K.; Jeong, H.; Jung, S.; Choe, J. Improvement of ensemble smoother with clustering covariance for channelized reservoirs. Energy Explor. Exploit. 2013, 31, 713–726. [Google Scholar] [CrossRef]
- Lee, K.; Jung, S.; Lee, T.; Choe, J. Use of clustered covariance and selective measurement data in ensemble smoother for three-dimensional reservoir characterization. J. Energy Resour. Technol. Trans. ASME 2017, 139, 022905. [Google Scholar] [CrossRef]
- Park, K.; Choe, J. Use of ensemble Kalman filter to 3-dimensional reservoir characterization during waterflooding. In Proceedings of the SPE Europe/EAGE Annual Conference and Exhibition, Vienna, Austria, 12–15 June 2006. [Google Scholar] [CrossRef]
- Nejadi, S.; Leung, J.; Trevedi, J. Characterization of non-Gaussian geologic facies distribution using ensemble Kalman filter with probability weighted re-sampling. Math. Geosci. 2015, 47, 193–225. [Google Scholar] [CrossRef]
- Jo, H.; Jung, H.; Ahn, J.; Lee, K.; Choe, J. History matching of channel reservoirs using ensemble Kalman filter with continuous update of channel information. Energy Explor. Exploit. 2017, 35, 3–23. [Google Scholar] [CrossRef]
- Jung, H.; Jo, H.; Kim, S.; Lee, K.; Choe, J. Recursive update of channel information for reliable history matching of channel reservoirs using EnKF with DCT. J. Pet. Sci. Eng. 2017, 154, 19–37. [Google Scholar] [CrossRef]
- Jafarpour, B.; McLaughlin, D.B. History matching with an ensemble Kalman filter and discrete cosine parameterization. Comput. Geosci. 2008, 12, 227–244. [Google Scholar] [CrossRef]
- Jafarpour, B.; McLaughlin, D.B. Reservoir characterization with the discrete cosine transform. SPE J. 2009, 14, 182–201. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.; Lee, K.; Choe, J. Characterization of channelized gas reservoirs using ensemble Kalman filter with application of discrete cosine transformation. Energy Explor. Exploit. 2016, 34, 319–336. [Google Scholar] [CrossRef]
- Panwar, W.; Trivedi, J.J.; Nejadi, S. Importance of distributed temperature sensor data for steam assisted gravity drainage reservoir characterization and history matching within ensemble Kalman filter framework. ASME J. Energy Resour. Technol. 2015, 137, 042902. [Google Scholar] [CrossRef]
- Moreno, D.L.; Aanonsen, S.I. Continuous facies updating using the ensemble Kalman filter and the level set method. Math. Geosci. 2011, 43, 951–970. [Google Scholar] [CrossRef]
- Lorentzen, R.J.; Flornes, K.M.; Nævdal, G. History matching channelized reservoirs using the ensemble Kalman filter. SPE J. 2012, 17, 137–151. [Google Scholar] [CrossRef]
- Lorentzen, R.J.; Nævdal, G.; Shafieirad, A. Estimating facies fields by use of the ensemble Kalman Filter and distance functions—Applied to shallow-marine environments. SPE J. 2012, 3, 146–158. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.; Lee, K.; Choe, J. Characterization of channel oil reservoirs with an aquifer using EnKF, DCT, and PFR. Energy Explor. Exploit. 2016, 34, 828–843. [Google Scholar] [CrossRef]
- Aanonsen, S.I.; Nævdal, G.; Oliver, D.S.; Reynolds, A.C.; Vallès, B. The ensemble Kalman filter in reservoir engineering—A review. SPE J. 2009, 14, 393–412. [Google Scholar] [CrossRef]
- Jafarpour, B.; Tarrahi, M. Assessing the performance of the ensemble Kalman filter for subsurface flow data integration under variogram uncertainty. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Oliver, D.S.; Chen, Y. Recent progress on reservoir history matching: A review. Comput. Geosci. 2011, 15, 185–221. [Google Scholar] [CrossRef]
- Lee, K.; Jo, G.; Choe, J. Improvement of ensemble Kalman filter for improper initial ensembles. Geosyst. Eng. 2011, 14, 79–84. [Google Scholar] [CrossRef]
- Scheidt, C.; Caers, J. Representing spatial uncertainty using distances and kernels. Math. Geosci. 2009, 41, 397–419. [Google Scholar] [CrossRef]
- Suzuki, S.; Caers, J. A distance-based prior model parameterization for constraining solutions of spatial inverse problems. Math. Geosci. 2008, 40, 445–469. [Google Scholar] [CrossRef]
- Kang, B.; Lee, K.; Choe, J. Improvement of ensemble smoother with SVD-assisted sampling scheme. J. Pet. Sci. Eng. 2016, 141, 114–124. [Google Scholar] [CrossRef]
- Kim, S.; Lee, C.; Lee, K.; Choe, J. Initial ensemble design scheme for effective characterization of 3D channel gas reservoirs with an aquifer. J. Energy Resour. Technol. Trans. ASME 2017, 139, 022911. [Google Scholar] [CrossRef]
- Kang, B.; Yang, H.; Lee, K.; Choe, J. Ensemble Kalman filter with PCA-assisted sampling for channelized reservoir characterization. J. Energy Resour. Technol. Trans. ASME 2017, 139, 032907. [Google Scholar] [CrossRef]
- Gao, G.; Zafari, M.; Reynolds, A.C. Quantifying uncertainty for the PUNQ-S3 problem in a Bayesian setting with RML and EnKF. SPE J. 2006, 11, 506–515. [Google Scholar] [CrossRef]
- Li, H.; Yang, D. Estimation of multiple petrophysical parameters for the PUNQ-S3 model using ensemble-based history matching. In Proceedings of the SPE EUROPEC/EAGE Annual Conference and Exhibition, Vienna, Austria, 23–26 May 2011. [Google Scholar] [CrossRef]
- Le, D.H.; Emerick, A.A.; Reynolds, A.C. An adaptive ensemble smoother with multiple data assimilation for assisted history matching. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 23–25 February 2015. [Google Scholar] [CrossRef]
- Nævdal, G.; Mannseth, T.; Vefring, E.H. Near-well reservoir monitoring through ensemble Kalman filter. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 13–17 April 2002. [Google Scholar] [CrossRef]
- Emerick, A.A.; Reynolds, A.C. Ensemble smoother with multiple data assimilation. Comput. Geosci. 2013, 55, 3–15. [Google Scholar] [CrossRef]
- Peters, E.; Chen, Y.; Leeuwenburgh, O. Extended Brugge benchmark case for history matching and water flooding optimization. Comput. Geosci. 2013, 50, 16–24. [Google Scholar] [CrossRef]
- Chen, Y.; Oliver, D.S. Ensemble-based closed-loop optimization applied to Brugge field. SPE Reserv. Eval. Eng. 2010, 13, 56–71. [Google Scholar] [CrossRef]
- Wen, X.H.; Chen, W.H. Real-time reservoir model updating using ensemble Kalman filter. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 31 January–2 February 2005. [Google Scholar] [CrossRef]
- Jung, S. Stochastic Characterization for Fractured Reservoirs with Ensemble Kalman Filter. Ph.D. Dissertation, Seoul National University, Seoul, Korea, 2008. [Google Scholar]
- Jung, S. Integration of the production logging tool and production data for post-fracturing evaluation by the ensemble smoother. Energies 2017, 19, 859. [Google Scholar] [CrossRef]
- Ghods, P.; Zhang, D. Ensemble based characterization and history matching of naturally fractured tight/shale gas reservoirs. In Proceedings of the SPE Western Regional Meeting, Anaheim, CA, USA, 27–29 May 2010. [Google Scholar] [CrossRef]
- Tanaka, M.; Tanaka, S.; Arihara, N.; Okabe, H. Estimation of fracture effective permeability by upscaling using ensemble Kalman filter. In Proceedings of the Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 18–20 October 2010. [Google Scholar] [CrossRef]
- Sebacher, B.; Stordal, A.S.; Hanea, R. Bridging multipoint statistics and truncated Gaussian fields for improved estimation of channelized reservoirs with ensemble methods. Comput. Geosci. 2015, 19, 341–369. [Google Scholar] [CrossRef]
- Lee, K.; Jung, S.; Choe, J. Ensemble smoother with clustered covariance for 3D channelized reservoirs with geological uncertainty. J. Pet. Sci. Eng. 2016, 145, 423–435. [Google Scholar] [CrossRef]
- Tarrahi, M.; Gildin, E.; Moreno, J.; Gonzales, S. Dynamic integration of DTS data for hydraulically fractured reservoir characterization with the ensemble Kalman filter. In Proceedings of the SPE Biennial Energy Resources Conference, Port of Spain, Trinidad, 9–11 June 2014. [Google Scholar] [CrossRef]
- Elahi, S.H.; Jafarpour, B. Characterization of fracture length and conductivity from tracer test and production data with ensemble Kalman filter. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 20–22 July 2015. [Google Scholar] [CrossRef]
- Reiso, E.; Haver, M.C.; Aga, M. Integrated workflow for quantitative use of time-lapse seismic data in history matching: A North sea field case. In Proceedings of the SPE Europe/EAGE Annual Conference, Madrid, Spain, 13–16 June 2005. [Google Scholar] [CrossRef]
- Skjervheim, J.A.; Evensen, G.; Aanonsen, S.I.; Ruud, B.O.; Jonasen, T.A. Incorporating 4D seismic data in reservoir simulation models using ensemble Kalman filter. SPE J. 2007, 12, 282–292. [Google Scholar] [CrossRef]
- Emerick, A.A. Analysis of the performance of ensemble-based assimilation of production and seismic data. J. Pet. Sci. Eng. 2016, 139, 219–239. [Google Scholar] [CrossRef]
- Lin, B.; Crumpton, P.I.; Dogru, A.H. Field scale assisted history matching using a systematic, massively parallel ensemble Kalman smoother procedure. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. SPE J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Oda, M. Permeability tensor for discontinuous rock masses. Geotechnique 1985, 35, 483–495. [Google Scholar] [CrossRef]
| EnKF | ES | |
|---|---|---|
| Strength |
|
|
| Drawback |
|
|
| Jung [60] | Ghods and Zhang [62] | Tanaka et al. [63] | |
|---|---|---|---|
| No. of ensemble | 40 | 60 | 40 |
| state vectors | |||
| ∙ Model static | x-permeability y-permeability Fracture porosity | Fracture permeability Fracture porosity Matrix porosity Sigma factor | x-permeability y-permeability |
| ∙ Model dynamic | Water saturation Reservoir pressure | - | Water saturation Reservoir pressure |
| ∙ Observation | Bottom hole pressure Oil rate Water-cut | Gas rate Water rate | Bottom hole pressure Oil rate |
| Number of producer | 8 | 4 | 4 |
| Number of injector | 1 | - | 1 |
| Forward simulator | ECLIPSE 100 | ECLIPSE 100 | Streamline-based |
| Ensemble generation | DFN | Random | SGS and DFN |
| Assimilation method | EnKF | EnKF | EnKF |
| Supplemental Technique | Localization | - | Refinement with velocity |
| Jafarpour and McLaughlin [14] | Nejadi et al. [32] | Lee et al. [65] | |
|---|---|---|---|
| No. of ensemble | 100, 200, 300, 400 | 100 | 200 |
| State vector | |||
| ∙ Model static | Permeability | Permeability | Permeability |
| ∙ Model dynamic | - | - | - |
| ∙ Observation | Bottom hole pressure Oil rate Water rate | Water injection rate Oil rate Water cut | Oil production rate Water-cut |
| Number of producer | 1 (45 ports) | 1 (6 ports) | 8 |
| Number of injector | 1 (45 ports) | 1 (7 ports) | 1 |
| Forward simulator | ECLIPSE 100 | Not Specified | ECLIPSE 100 |
| Ensemble generation | SNESim | SNESim | SNESim |
| Assimilation method | EnKF | EnKF | ES |
| Technical supplementary | - | Re-sampling | Clustered covariance Selective update |
| Tarrahi et al. [66] | Elahi and Jafarpour [67] | Jung [61] | |
|---|---|---|---|
| No. of ensemble | 100 | Not specified | 100 |
| State vector | |||
| ∙ Model static | Fracture half-length Fracture permeability | Fracture half-length Fracture permeability | Permeability |
| ∙ Model dynamic | - | - | - |
| ∙ Observation | Temperature | Tracer concentration Cumulative oil | Oil rate Water-cut |
| Number of producer | 1 (8 stages) | 1 (4 stages) | 1 (7 stages) |
| Number of injector | - | - | - |
| Forward simulator | ECLIPSE 300 | ECLIPSE 100 | ECLIPSE 100 |
| Ensemble generation | Random | Random | Random |
| Assimilation method | EnKF | EnKF | ES |
| Technical supplementary | - | Ensemble inflation Localization | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S.; Lee, K.; Park, C.; Choe, J. Ensemble-Based Data Assimilation in Reservoir Characterization: A Review. Energies 2018, 11, 445. https://doi.org/10.3390/en11020445
Jung S, Lee K, Park C, Choe J. Ensemble-Based Data Assimilation in Reservoir Characterization: A Review. Energies. 2018; 11(2):445. https://doi.org/10.3390/en11020445
Chicago/Turabian StyleJung, Seungpil, Kyungbook Lee, Changhyup Park, and Jonggeun Choe. 2018. "Ensemble-Based Data Assimilation in Reservoir Characterization: A Review" Energies 11, no. 2: 445. https://doi.org/10.3390/en11020445
APA StyleJung, S., Lee, K., Park, C., & Choe, J. (2018). Ensemble-Based Data Assimilation in Reservoir Characterization: A Review. Energies, 11(2), 445. https://doi.org/10.3390/en11020445






