A Fully Three Dimensional Semianalytical Model for Shale Gas Reservoirs with Hydraulic Fractures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Development
2.2. 3D Semianalytical Methods
2.3. Slanted Rectangles Fracture with Strike Angle
2.4. Slanted Rectangles Fracture with Dip Angle
2.5. Pressure Solutions for Rectangle, Ellipse, and Disk Fractures
2.6. Semianalytical Model for 3D Fractures in Shale Gas Reservoir
- (1)
- The reservoir is bounded;
- (2)
- The reservoir is isotropic and homogeneous;
- (3)
- It only allows gas flow from fractures to wellbore;
- (4)
- There is no gravity effect.
- (1)
- gas flux at fracture segments, .
- (2)
- gas flow rates at all nodes .
- (3)
- pressure at all nodes , but the pressure at the well node is known, so that there are pressure unknowns at nodes.
- (1)
- mass balance equations at all nodes:
- (2)
- non-Darcy flow equations at all fracture segments, which are described by Equation (9).
- (3)
- pressure continuity equations of all fracture segments by equating Equations (9) and (25).
3. Results
3.1. Model Validation
3.2. Model Applications
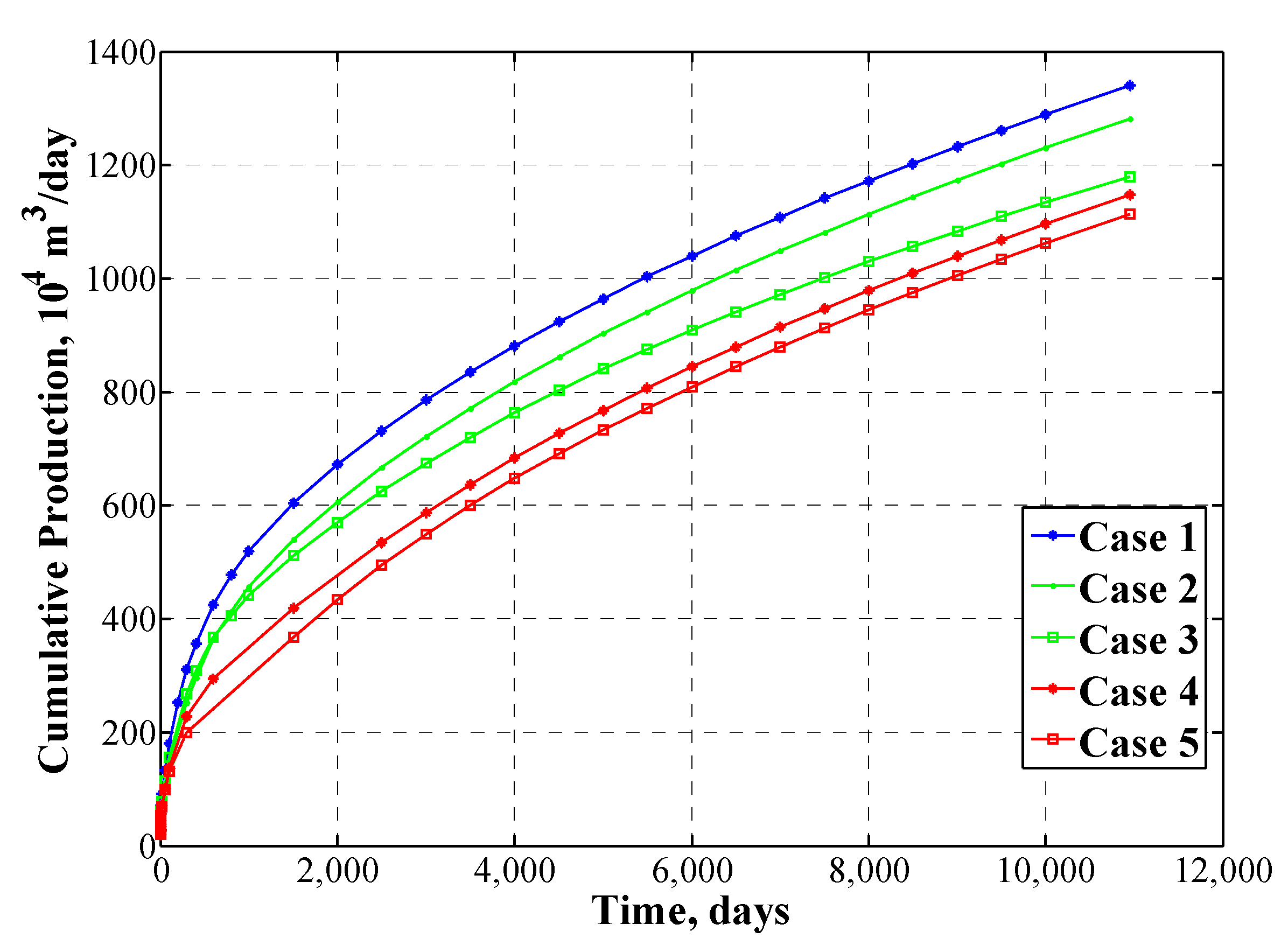
- Case 1: Three fully penetrated fractures, with fracture heights 50 m, 50 m and 50 m, and strike angles 0°, 0°and 0°.
- Case 2: Three partially penetrated fractures, with fracture heights are 45 m, 40 m, and 45 m, and strike angles 0°, 0°and 0°.
- Case 3: Three partially penetrated fractures, with fracture heights are 45 m, 40 m, and 45 m, and strike angles −10°, 0°and 10°.
- Case 4: Three partially penetrated fractures, with fracture heights are 40 m, 35 m, and 40 m, and strike angles 0°, 0°and 0°.
- Case 5: Three partially penetrated fractures, with fracture heights are 40 m, 35 m, and 40 m, and strike angles −10°, 0°and 10°.
4. Discussion
5. Conclusions
- The pressure for partially penetrated fractures with different strike angles, dip angles and shapes could be derived by integrating the instantaneous point source solution on the fracture plane;
- Based on comprehensive shale gas transport equations considering complex gas transport mechanisms and complex fracture patterns, a novel semianalytical model to simulate the gas transport and production is developed by discretizing each fracture to multiple segments;
- This semianalytical mode has been verified with a commercial simulator and an analytical model for a shale gas reservoir with three fully penetrated fractures, and the relative error is within 3%;
- Five shale gas reservoir cases with different fracture heights and strike angles have been investigated by using this semianalytical model. It is found that the decreasing of fracture height will lead to decreasing production rate and cumulative shale gas production, by a ratio close to the fracture areas ratio; and strike angles could cause well interference and decrease the daily production rate and cumulative shale gas production.
- The technique proposed in this study and the partial results shed a light on the importance of fracture shapes and heights. In most of the shale gas models, the hydraulic fractures are always assumed to be rectangle and fully penetrated in the pay zone. But from the results of this study, the fracture shapes and heights play essential roles in influencing the shale gas production. On the other hand, these explicit pressure results derived in this study for fracture planes with different shapes and angles could also be used in well testing to investigate the fracture and reservoir properties. Thirdly, although the cases studied here are all synthetic and simple, the methods could still be used for complex fracture patterns with the help of more accurate geophysical measurement. In conclusion, the method proposed in this work will be widely used by petroleum engineers dealing with unconventional reservoirs with complex fractures.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Reservoir temperature, K | |
| Initial reservoir pressure, MPa | |
| Pressure, MPa | |
| Initial reservoir permeability, nD | |
| Reservoir permeability, nD | |
| dimensionless tortuosity factor | |
| Initial gas saturation | |
| Molar mass of methane, kg/mol | |
| Diameter of methane molecule, nm | |
| Universal gas constant, J/mol/K | |
| Critical pressure of methane, MPa | |
| Langmuir pressure, MPa | |
| Langmuir volume, m3/ton | |
| Coordinates of the target point, m | |
| Coordinates of the reference source point, m | |
| Layers of the mirrored zones | |
| Minimum of z, m | |
| x, y, z coordinate of the target point | |
| x, y, z coordinate of the center of the fracture plane | |
| Reservoir thickness, m | |
| Fracture half length, m | |
| Fracture height, m | |
| Fracture half-length, m | |
| Flow rate of each fracture segment, m3/s | |
| Fluid density, kg/m3 | |
| Bulk density of shale, kg/m3 | |
| Gas density, kg/m3 | |
| Porosity | |
| Total compressibility | |
| Isothermal gas compressibility factor | |
| Gas viscosity, Pa∙s | |
| Pore volume fraction of adsorbed gas | |
| Knudsen number | |
| Fracture conductivity, m2∙m | |
| A gas diffusion constant and close to 1 | |
| Fickian diffusivity of gas component through the pore | |
| A dimensionless constrictivity factor (≤1) | |
| Gas molecule diameter, m | |
| Pore diameter, m | |
| A dimensionless tortuosity factor (≥1) | |
| Differential equilibrium partitioning coefficient of gas at a constant temperature | |
| Adsorbed gas mass per unit shale volume | |
| Saturation pressure of the gas, MPa | |
| Maximum adsorption gas volume when the entire adsorbent surface is being covered with a complete monomolecular layer, m3 | |
| A constant related to the net heat of adsorption | |
| Number of the adsorption layers | |
| Velocity, m/s | |
| Non-Darcy Forchheimer coefficient, ft−1 | |
| Fracture permeability, mD | |
| Hydraulic conductivity | |
| Pressure target point | |
| Pressure source point | |
| Total number of fractures | |
| Total number of fracture nodes | |
| Total length of the reservoir, x-direction | |
| Total length of the reservoir, y-direction | |
| Total length of the reservoir, z-direction |
References
- Energy Information Administration (EIA). Shale Gas Production Drives World Natural Gas Production Growth. 2016. Available online: http://www.eia.gov/todayinenergy/detail.cfm?id527512 (accessed on 20 December 2017).
- Energy Information Administration (EIA). Annual Energy Outlook. 2017. Available online: https://www.eia.gov/outlooks/aeo/pdf/0383(2017).pdf (accessed on 10 December 2017).
- Wu, K.; Li, X.; Wang, C.; Yu, W.; Chen, Z. Model for surface diffusion of adsorbed gas in nanopores of shale gas reservoirs. Ind. Eng. Chem. Res. 2015, 54, 3225–3236. [Google Scholar] [CrossRef]
- Wang, K.; Liu, H.; Luo, J.; Wu, K.; Chen, Z. A comprehensive model coupling embedded discrete fractures, multiple interacting continua, and geomechanics in shale gas reservoirs with multiscale fractures. Energy Fuel 2017, 31, 7758–7776. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability effect on nanoconfined water flow. Proc. Natl. Acad. Sci. USA 2017, 114, 3358–3363. [Google Scholar] [CrossRef] [PubMed]
- Warren, J.E.; Root, P.J. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Kazemi, H.; Gilman, J.R.; Eisharkawy, A.M. Analytical and numerical solution of oil recovery from fractured reservoirs with empirical transfer functions. SPE Reserv. Eng. 1992, 7, 219–227. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, B.; Li, J.; Li, H. Discrete Fracture Modeling of 3D Heterogeneous Enhanced Coalbed Methane Recovery with Prismatic Meshing. Energies 2015, 8, 6153–6176. [Google Scholar] [CrossRef]
- Noorishad, J.; Mehran, M. An upstream finite element method for solution of transient transport equation in fractured porous media. Water Resour. Res. 1982, 18, 588–596. [Google Scholar] [CrossRef]
- Matthäi, S.K.; Mezentsev, A.; Belayneh, M. Control-Volume Finite-Element Two-Phase Flow Experiments with Fractured Rock Represented by Unstructured 3D Hybrid Meshes. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 31 January–2 February 2005; Society of Petroleum Engineers: Richardson, TX, USA, 2005. [Google Scholar]
- Sandve, T.H.; Berre, I.; Nordbotten, J.M. An efficient multi-point flux approximation method for Discrete Fracture–Matrix simulations. J. Comput. Phys. 2012, 231, 3784–3800. [Google Scholar] [CrossRef]
- Olorode, O.; Freeman, C.M.; Moridis, G.; Blasingame, T.A. High-Resolution Numerical Modeling of Complex and Irregular Fracture Patterns in Shale-Gas Reservoirs and Tight Gas Reservoirs. SPE Reserv. Eval. Eng. 2013, 16, 443–455. [Google Scholar] [CrossRef]
- Lee, S.H.; Lough, M.F.; Jensen, C.L. Hierarchical modeling of flow in naturally fractured formations with multiple length scales. Water Resour. Res. 2001, 37, 443–455. [Google Scholar] [CrossRef]
- Li, L.Y.; Lee, S.H. Efficient Field-Scale Simulation of Black Oil in a Naturally Fractured Reservoir through Discrete Fracture Networks and Homogenized Media. SPE Reserv. Eval. Eng. 2008, 11, 750–758. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of a Coupled Dual Continuum and Discrete Fracture Model for the Simulation of Unconventional Reservoirs. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 18–20 February 2013; Society of Petroleum Engineers: Richardson, TX, USA, 2013. [Google Scholar]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of an Efficient Embedded Discrete Fracture Model for 3D Compositional Reservoir Simulation in Fractured Reservoirs. SPE J. 2014, 19, 289–303. [Google Scholar] [CrossRef]
- Hajibeygi, H.; Karvounis, D.; Jenny, P. A hierarchical fracture model for the iterative multiscale finite volume method. J. Comput. Phys. 2011, 230, 8729–8743. [Google Scholar] [CrossRef]
- De Araujo Cavalcante Filho, J.S.; Shakiba, M.; Moinfar, A.; Sepehrnoori, K. Implementation of a preprocessor for embedded discrete fracture modeling in an IMPEC compositional reservoir simulator. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 23–25 February 2005; pp. 219–227. [Google Scholar]
- Shakiba, M.; Sepehrnoori, K. Using Embedded Discrete Fracture Model (EDFM) and Microseismic Monitoring Data to Characterize the Complex Hydraulic Fracture Networks. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015; Society of Petroleum Engineers: Richardson, TX, USA, 2015. [Google Scholar]
- Xu, Y.; Yu, W.; Sepehrnoori, K. Discrete-Fracture Modeling of Complex Hydraulic-Fracture Geometries in Reservoir Simulators. SPE Reserv. Eval. Eng. 2016, 20, 403–422. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J., Jr. The Use of Source and Green’s Functions in Solving Unsteady-flow Problems in Reservoirs. Soc. Pet. Eng. J. 1973, 13, 285–296. [Google Scholar] [CrossRef]
- Cinco-Ley, H. Transient Pressure Analysis for Fractured Wells. J. Pet. Technol. 1981, 33, 1749–1766. [Google Scholar] [CrossRef]
- Wan, J.; Aziz, K. Semi-Analytical Well Model of Horizontal Wells with Multiple Hydraulic Fractures. SPE J. 2002, 7, 437–445. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, D. Modeling well performance for fractured horizontal gas wells. J. Nat. Gas Sci. Eng. 2014, 18, 180–193. [Google Scholar] [CrossRef]
- Zhou, W.; Banerjee, R.; Poe, B.D.; Spath, J.; Thambynayagam, M. Semianalytical Production Simulation of Complex Hydraulic-Fracture Networks. SPE J. 2014, 19, 6–18. [Google Scholar] [CrossRef]
- Yu, W.; Wu, K.; Sepehrnoori, K. A Semianalytical Model for Production Simulation from Nonplanar Hydraulic-Fracture Geometry in Tight Oil Reservoirs. SPE J. 2016, 21, 1028–1040. [Google Scholar] [CrossRef]
- Yang, R.; Huang, Z.; Yu, W.; Li, G.; Ren, W.; Zuo, L.; Tan, X.; Sepehrnoori, K.; Tian, S.; Sheng, M. A Comprehensive Model for Real Gas Transport in Shale Formations with Complex Non-planar Fracture Networks. Sci. Rep. 2016, 6, 36673. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Cheng, S.; Li, S.; Huang, Y.; Qin, J.; Hu, L.; Yu, H. A Semianalytical Methodology to Diagnose the Locations of Underperforming Hydraulic Fractures through Pressure-Transient Analysis in Tight Gas Reservoir. SPE J. 2017, 22, 924–939. [Google Scholar] [CrossRef]
- Wang, W.; Yu, W.; Hu, X.; Liu, H.; Chen, Y.; Wu, K.; Wu, B. A semianalytical model for simulating real gas transport in nanopores and complex fractures of shale gas reservoirs. AIChE J. 2017, 64, 326–337. [Google Scholar] [CrossRef]
- Castonguay, S.T.; Mear, M.E.; Dean, R.H.; Schmidt, J.H. Predictions of the Growth of Multiple Interacting Hydraulic Fractures in Three Dimensions. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013; Society of Petroleum Engineers: Richardson, TX, USA, 2013. [Google Scholar]
- Lee, S.; Wheeler, M.F.; Wick, T. Pressure and fluid-driven fracture propagation in porous media using an adaptive finite element phase field model. Comput. Methods Appl. Mech. Eng. 2016, 305, 111–132. [Google Scholar] [CrossRef]
- Weng, X. Modeling of complex hydraulic fractures in naturally fractured formation. J. Unconv. Oil Gas Resour. 2015, 9, 114–135. [Google Scholar] [CrossRef]
- Xu, W. Modeling Gas Transport in Shale Reservoir—Conservation Laws Revisited. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014. [Google Scholar]
- Satterfield, C.N.; Colton, C.K.; Pitcher, W.H., Jr. Restricted diffusion in liquids within fine pores. AIChE J. 1973, 19, 628–635. [Google Scholar] [CrossRef]
- Smith, D.M.; Williams, F.L. Diffusional Effects in the Recovery of Methane from Coalbeds. Soc. Pet. Eng. J. 1982, 24, 529–535. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Porous Media; Fluid Transport and Pore Structure; Academic Press: New York, NY, USA; London, UK, 1979. [Google Scholar]
- Patzek, T.W.; Male, F.; Marder, M. Gas production in the Barnett Shale obeys a simple scaling theory. Proc. Natl. Acad. Sci. USA 2013, 110, 19731–19736. [Google Scholar] [CrossRef] [PubMed]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Chem. Phys. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Forchheimer, P.H. Wasserbewegung durch boden [Movement of water through soil]. Z. Acker Pflanzenbau 1901, 49, 1736–1749. [Google Scholar]
- Evans, R.D.; Civan, F. Characterization of Non-Darcy Multiphase Flow in Petroleum Bearing Formations. Final Report; U.S. DOE Contract No. DE-AC22-90BC14659; School of Petroleum and Geological Engineering, University of Oklahoma: Norman, OK, USA, 1994. [Google Scholar]
- Thambynayagam, R.K.M. The Diffusion Handbook: Applied Solutions for Engineers; Mcgraw Hill Book Co.: New York, NY, USA, 2000. [Google Scholar]
- Yu, W.; Wu, K.; Zuo, L.H.; Tan, X.S.; Weijermars, R. Physical Models for Inter-Well Interference in Shale Reservoirs: Relative Impacts of Fracture Hits and Matrix Permeability. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016. [Google Scholar]
- Yu, W.; Xu, Y.; Weijermars, R.; Wu, K.; Sepehrnoori, K. A Numerical Model for Simulating Pressure Response of Well Interference and Well Performance in Tight Oil Reservoirs With Complex-Fracture Geometries Using the Fast Embedded-Discrete-Fracture-Model Method. SPE Reserv. Eval. Eng. 2017. [Google Scholar] [CrossRef]
- He, K.; Xu, L.; Lord, P.; Lozano, M.; Kenzhekhanov, S.; Yin, X.; Neeves, K.; Huang, T. Rock-On-A-Chip approach provides new insight for well interference in Liquids-rich shale plays. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Yang, R.; Huang, Z.; Li, G.; Yu, W.; Sepehrnoori, K.; Lashgari, H.R.; Tian, S.; Song, X.; Sheng, M. A Semianalytical Approach to Model Two-Phase Flowback of Shale-Gas Wells with Complex-Fracture-Network Geometries. SPE J. 2017, 22. [Google Scholar] [CrossRef]
- Weijermars, R.; van Harmelen, A.; Zuo, L.; Alves, I.N.; Yu, W. High-Resolution Visualization of Flow Interference Between Frac Clusters (Part 1): Model Verification and Basic Cases. In Proceedings of the Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017; pp. 963–988. [Google Scholar] [CrossRef]
- Weijermars, R.; van Harmelen, A.; Zuo, L. Flow Interference Between Frac Clusters (Part 2): Field Example From the Midland Basin (Wolfcamp Formation, Spraberry Trend Field) with Implications for Hydraulic Fracture Design. In Proceedings of the Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017; pp. 989–1004. [Google Scholar] [CrossRef]
- Luchko, Y.; Zuo, L.H. Theta-function method for a time-fractional reaction-diffusion equation. J. Algerian Math. Soc. 2014, 1, 1–15. [Google Scholar]
- Luchko, Y.; Rundell, W.; Yamamoto, M.; Zuo, L.H. Uniqueness and reconstruction of an unknown semilinear term in a time-fractional reaction-diffusion equation. Inverse Probl. 2013, 29. [Google Scholar] [CrossRef]
- Rundell, W.; Xu, X.; Zuo, L.H. Determination of an unknown boundary condition in a fractional diffusion equation. Appl. Anal. 2013, 92, 1511–1526. [Google Scholar] [CrossRef]
- Yu, W.; Tan, X.; Zuo, L.H.; Liang, J.T.; Liang, H.C.; Wang, S. A New Probabilistic Approach for Uncertainty Quantification in Well Performance of Shale Gas Reservoirs. SPE J. 2016, 21, 2038–2048. [Google Scholar] [CrossRef]
- Zuo, L.H.; Yu, W.; Wu, K. A fractional decline curve analysis model for shale gas reservoirs. Int. J. Coal Geol. 2016, 163, 140–148. [Google Scholar] [CrossRef]


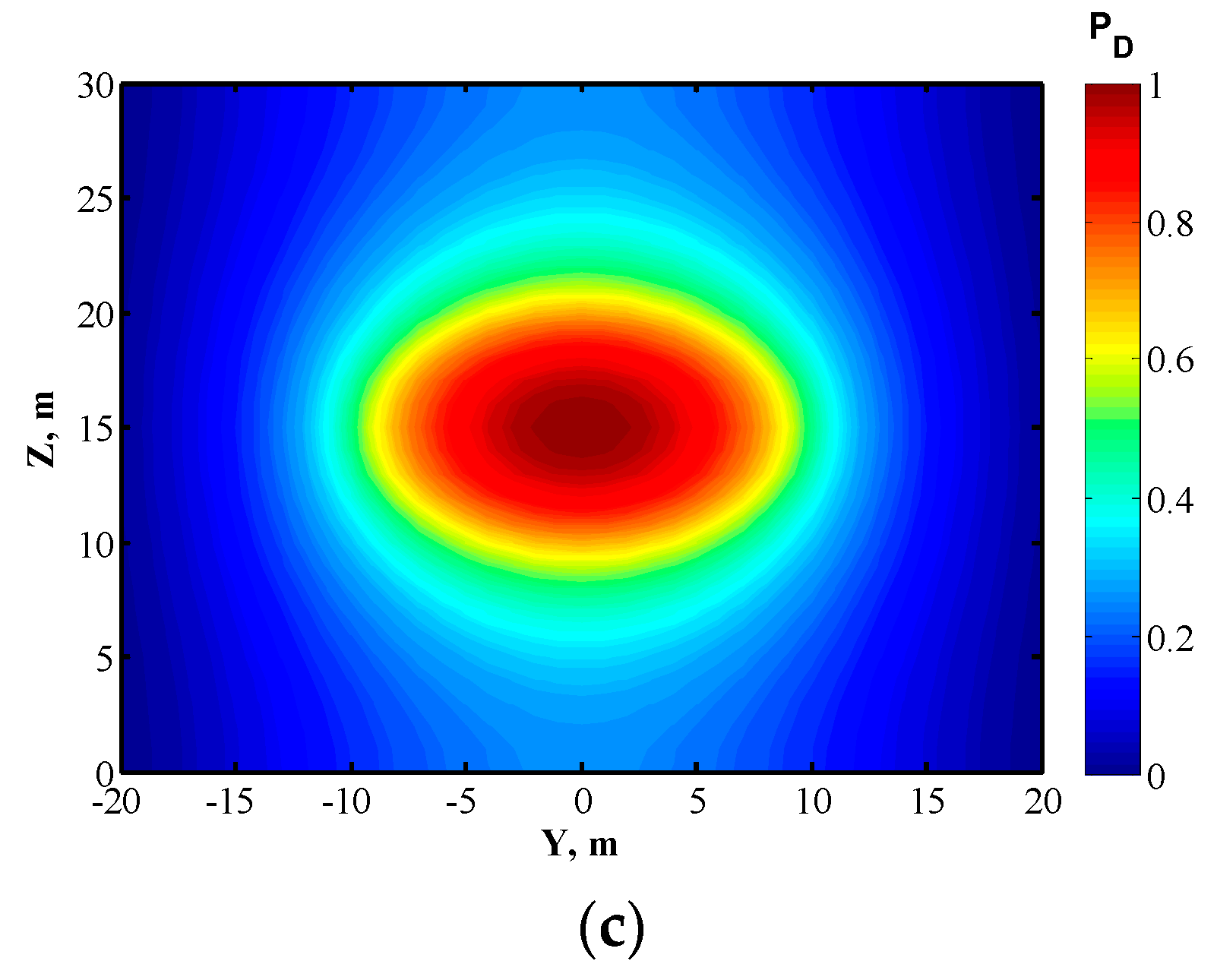
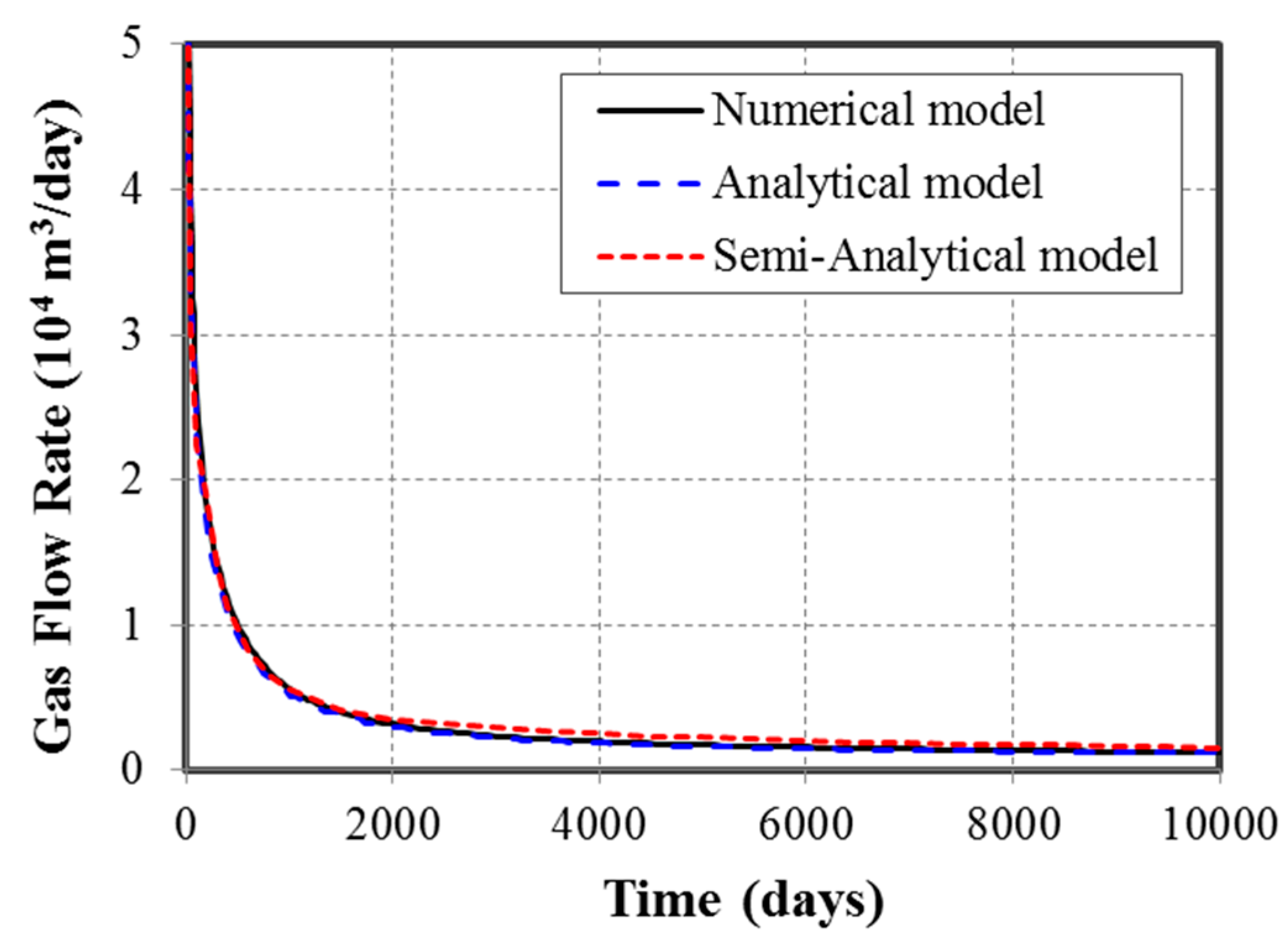
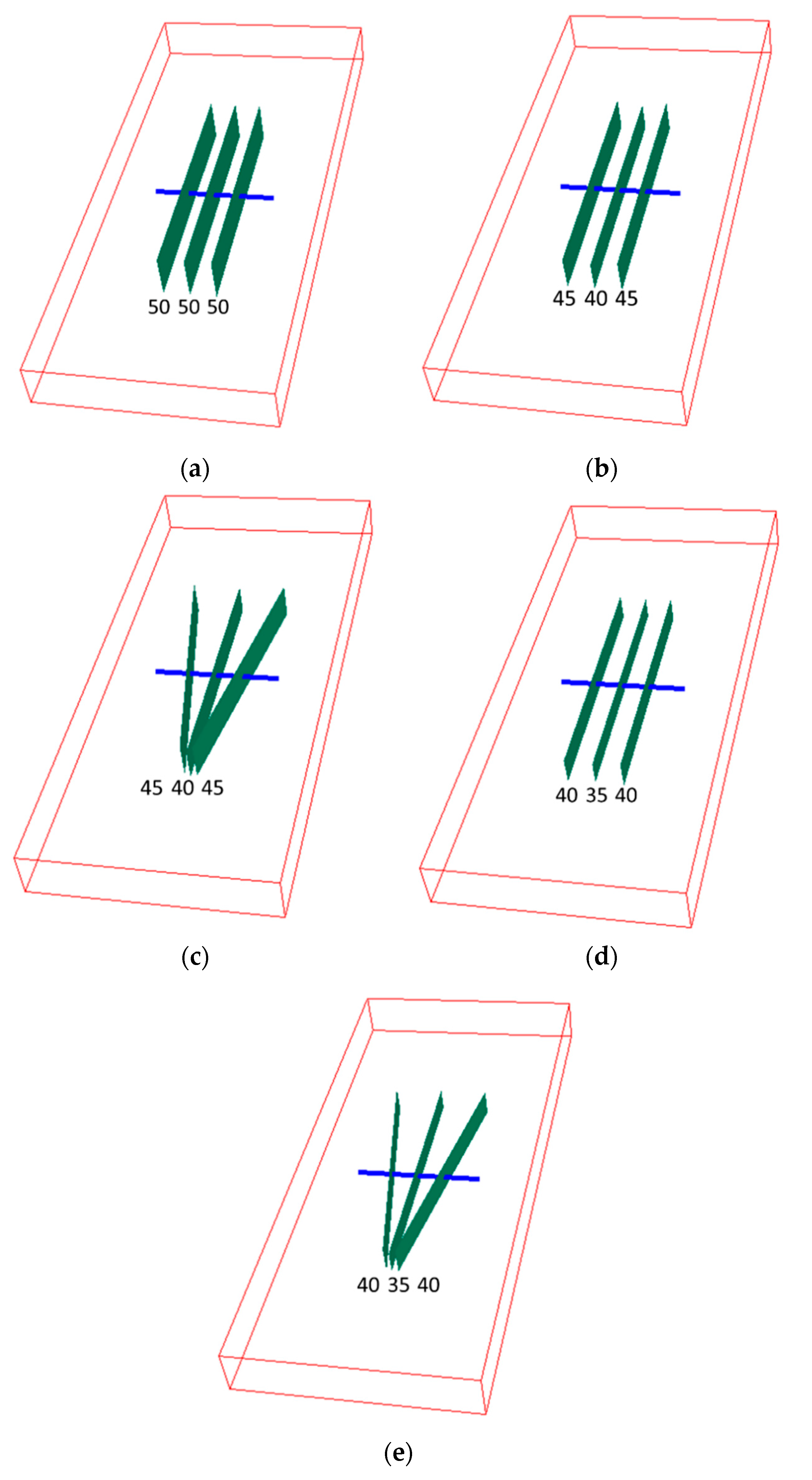
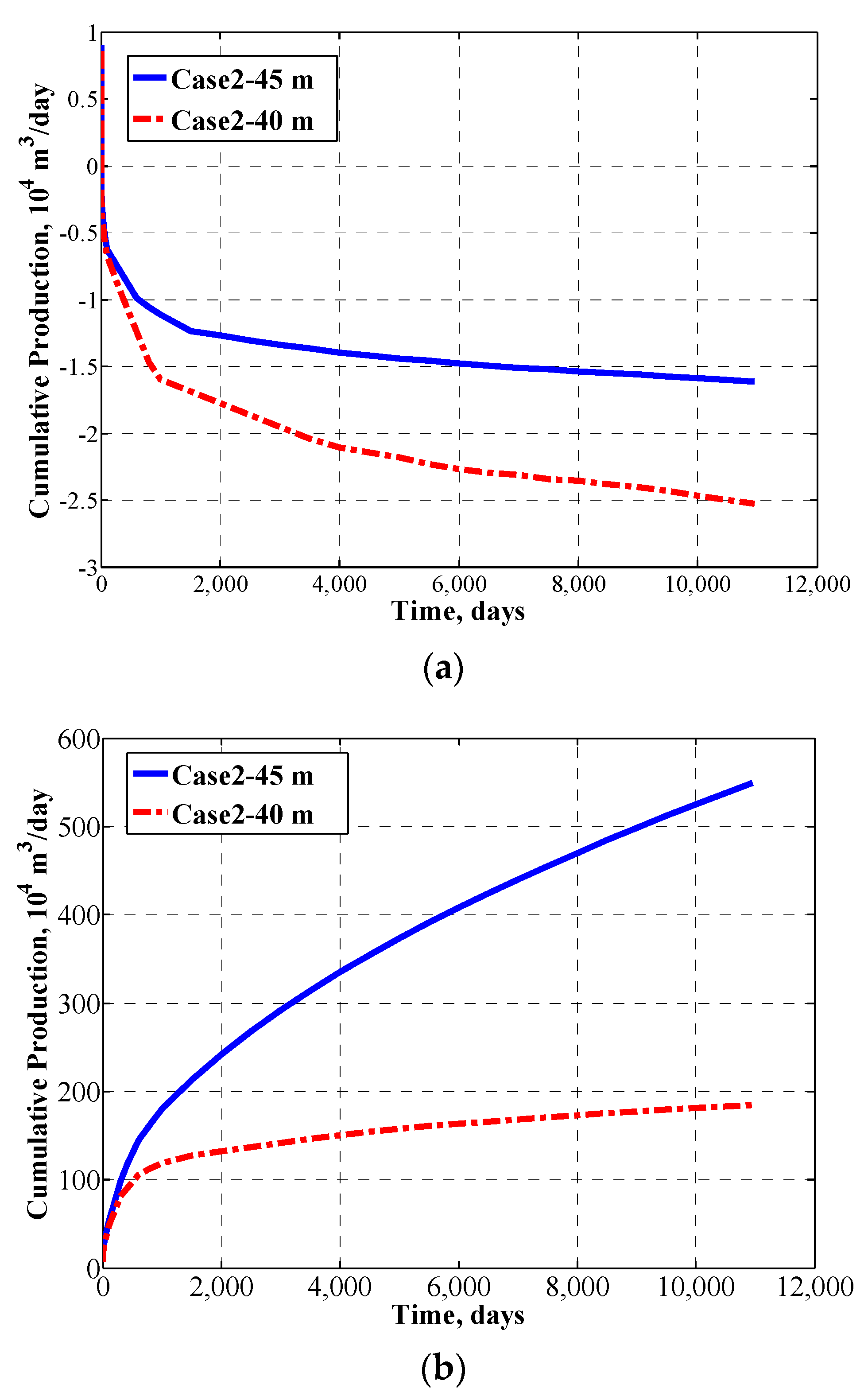
| Parameter | Symbol | SI Unit | Value |
|---|---|---|---|
| Reservoir temperature | K | 353.15 | |
| Initial reservoir pressure | MPa | 38 | |
| Initial reservoir permeability | nD | 100 | |
| Reservoir thickness | m | 50 | |
| Reservoir porosity | - | 4% | |
| Initial gas saturation | - | 100% | |
| Specific gas gravity | - | - | 0.5432 |
| Molar mass of methane | kg/mol | 0.016 | |
| Diameter of methane molecule | nm | 0.41 | |
| Universal gas constant | J/mol/K | 8.3145 | |
| Critical pressure of methane | MPa | 4.64 | |
| Langmuir pressure | MPa | 6 | |
| Langmuir volume | m3/ton | 2.5 | |
| Bulk density of shale | kg/m3 | 2.6 × 103 | |
| Fracture half-length | m | 150 | |
| Fracture height | m | 50 | |
| Fracture spacing | - | m | 30 |
| Fracture conductivity | FC | m2∙m | 3.048 × 10−14 |
| Fracture width | m | 0.003 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zuo, L.; Yu, W.; Chen, Y. A Fully Three Dimensional Semianalytical Model for Shale Gas Reservoirs with Hydraulic Fractures. Energies 2018, 11, 436. https://doi.org/10.3390/en11020436
Li Y, Zuo L, Yu W, Chen Y. A Fully Three Dimensional Semianalytical Model for Shale Gas Reservoirs with Hydraulic Fractures. Energies. 2018; 11(2):436. https://doi.org/10.3390/en11020436
Chicago/Turabian StyleLi, Yuwei, Lihua Zuo, Wei Yu, and Youguang Chen. 2018. "A Fully Three Dimensional Semianalytical Model for Shale Gas Reservoirs with Hydraulic Fractures" Energies 11, no. 2: 436. https://doi.org/10.3390/en11020436
APA StyleLi, Y., Zuo, L., Yu, W., & Chen, Y. (2018). A Fully Three Dimensional Semianalytical Model for Shale Gas Reservoirs with Hydraulic Fractures. Energies, 11(2), 436. https://doi.org/10.3390/en11020436





