Analysis and Design of Fuel Cell Systems for Aviation
Abstract
:1. Introduction
2. Model
3. Results and Discussion
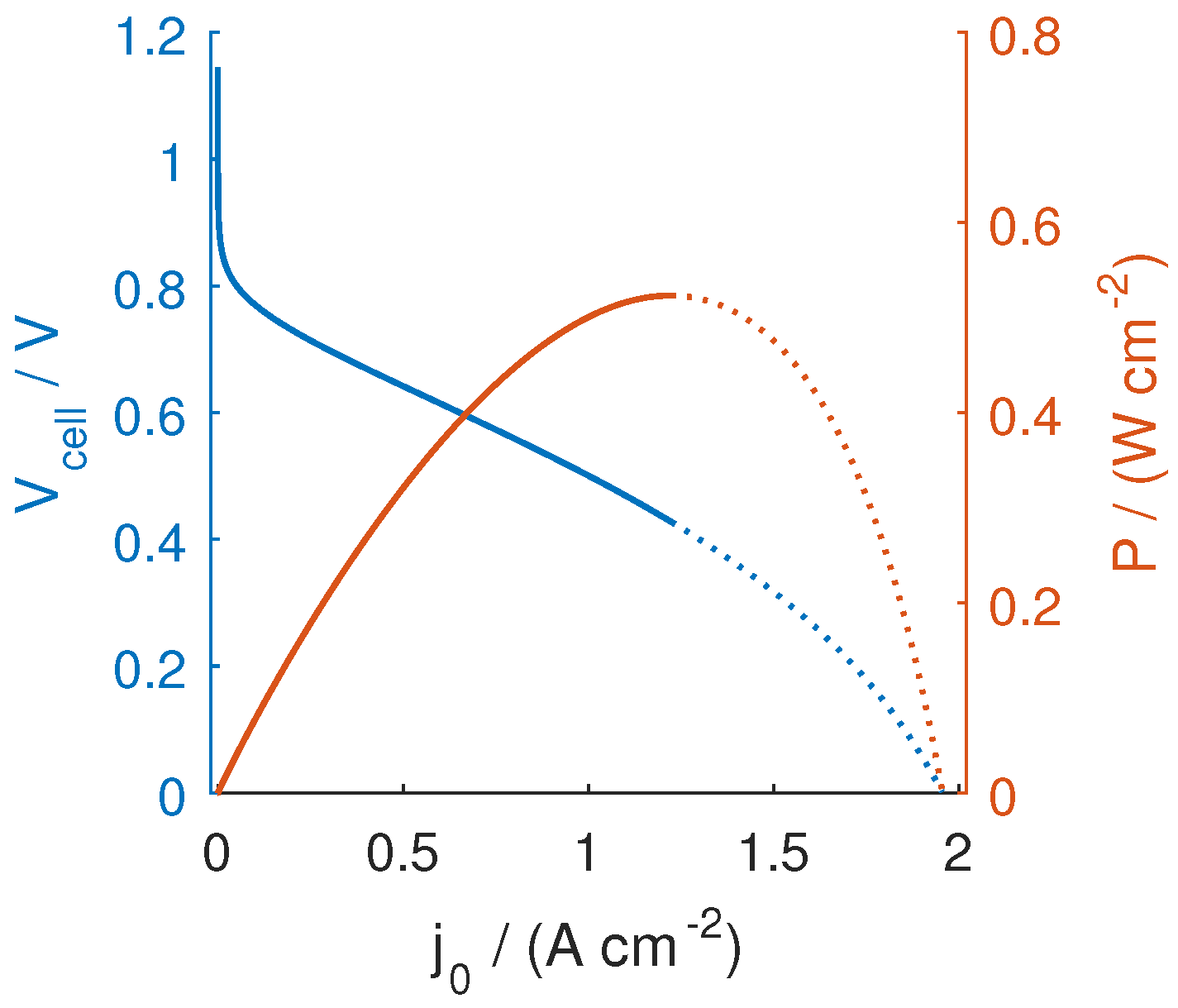
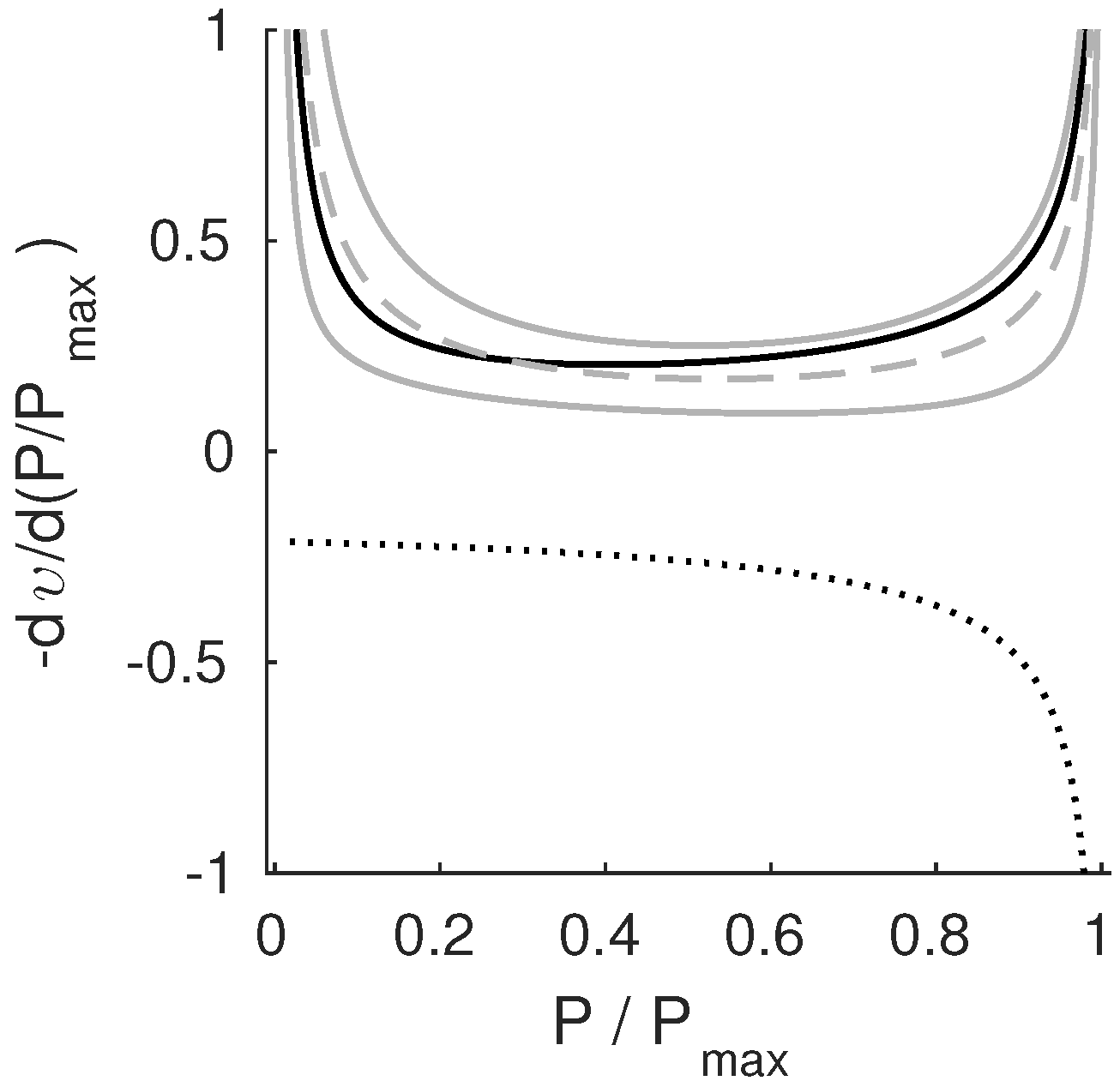
3.1. General Design Considerations
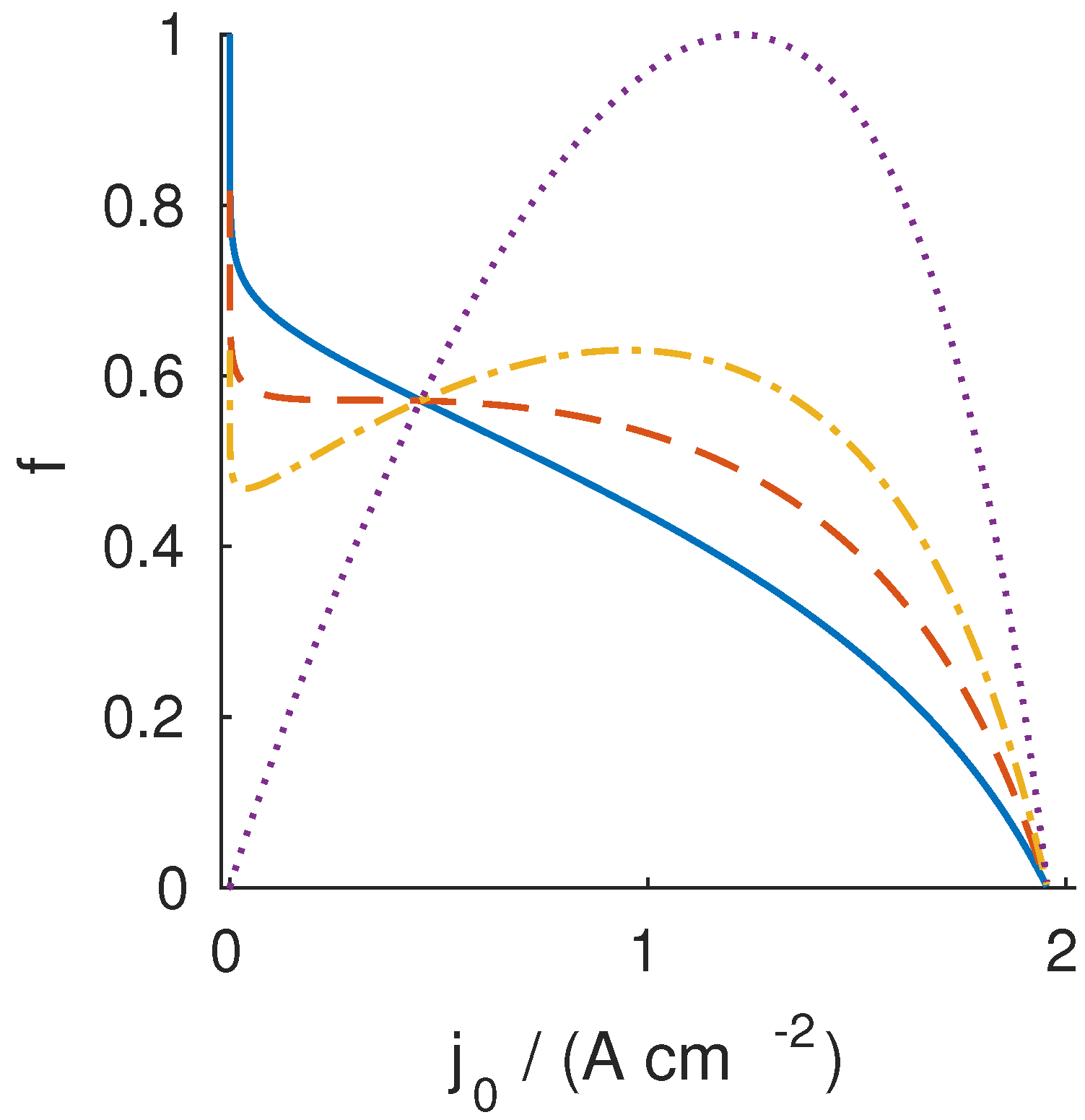
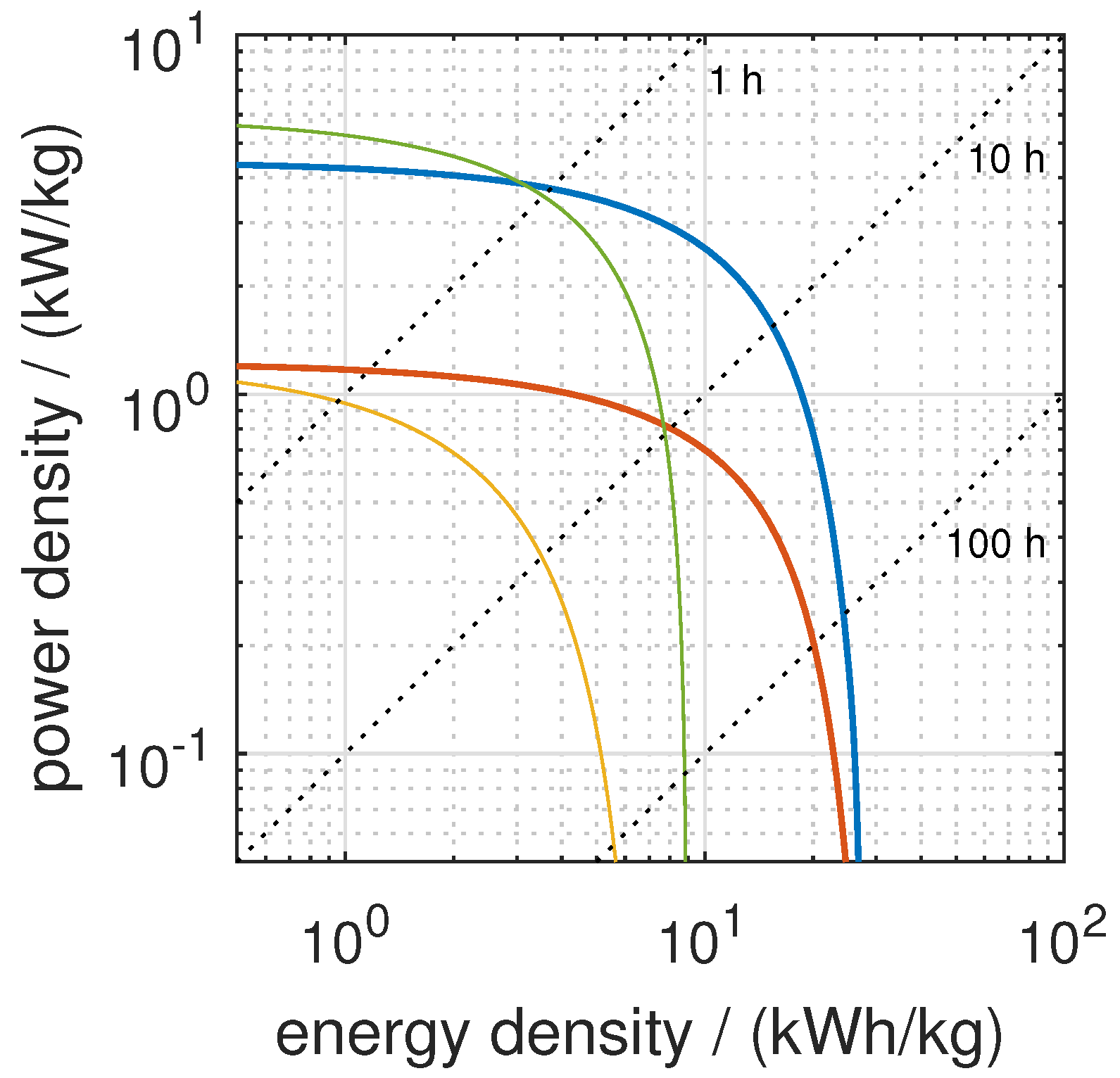
3.2. Design for Passenger Aircraft
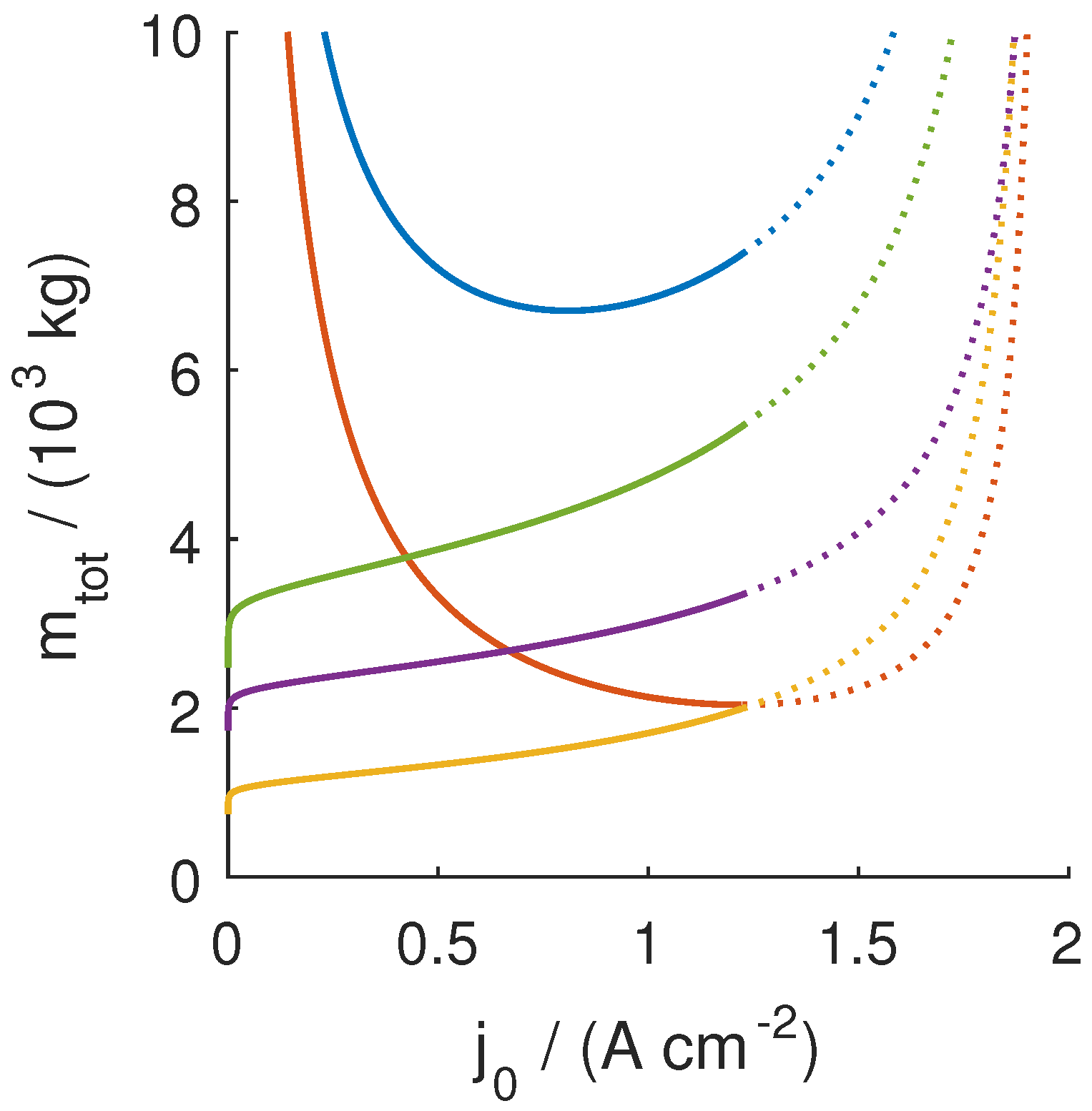
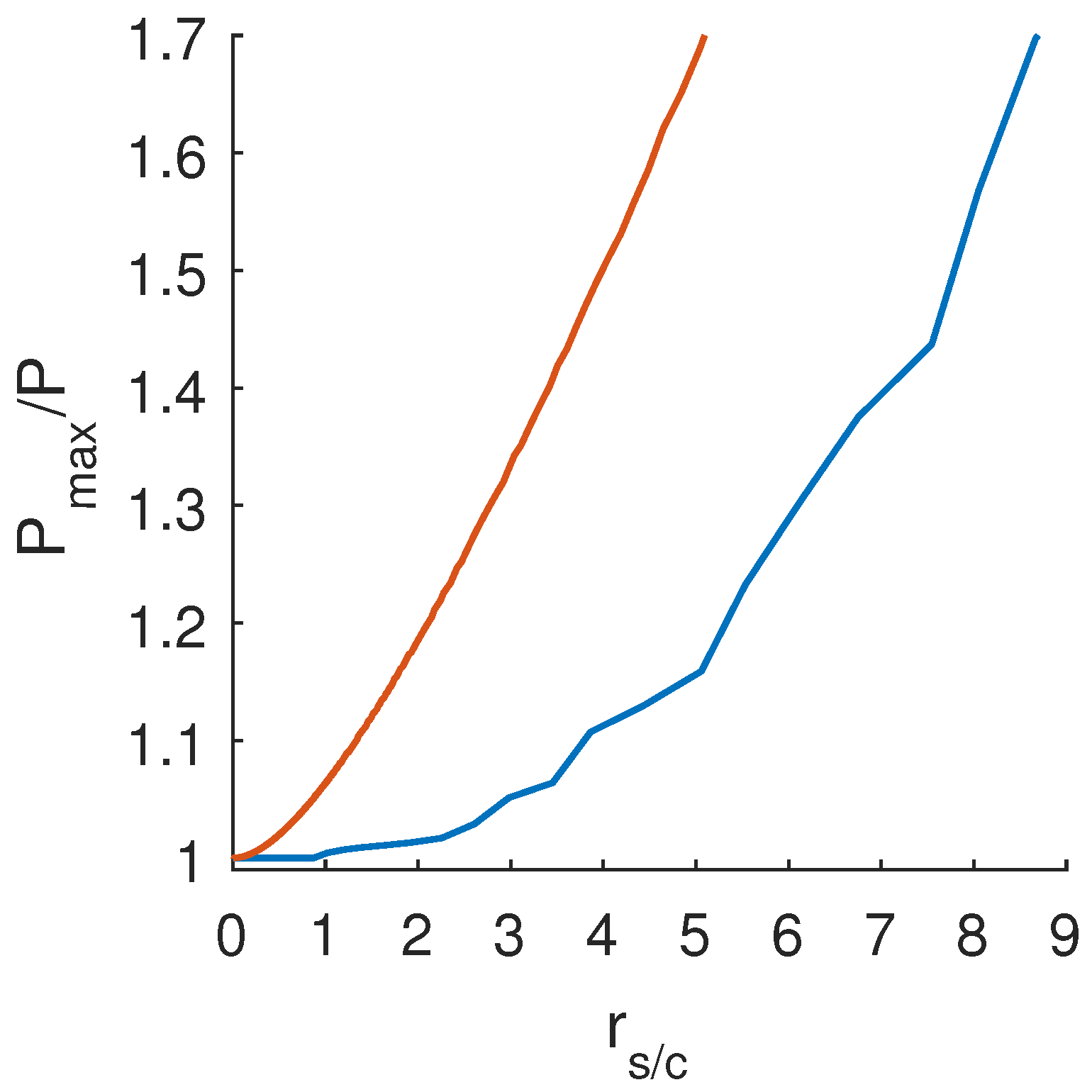
3.3. Sensitivity Analysis for Future Aircraft
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CCL | Cathode catalyst layer |
| EM | Electric motor |
| FCS | Fuel cell system |
| GDL | Gas diffusion layer |
| MEA | Membrane electrode assembly |
| PEMFC | Polymer electrolyte membrane fuel cell |
List of Symbols
| b | Tafel slope, V |
| oxygen concentration in the channel, mol cm | |
| D | effective diffusion coefficient, cm s |
| required energy | |
| f | objective function |
| Gibbs free energy | |
| reaction enthalpy | |
| volumetric exchange current density, A cm | |
| j | local current density, A cm |
| cell current density, A cm | |
| l | thickness, m |
| m | mass, kg |
| required power | |
| r | ratio, dimensionless |
| ohmic resistance, | |
| weight parameter w.r.t power |
Greek
| local overpotential, V | |
| cell overpotential, V | |
| specific power of the fuel cell, kW kg | |
| area-specific tank mass, kg m | |
| proton conductivity in the catalyst, S m | |
| efficiency | |
| specific energy of hydrogen, 33.3 kWh kg |
Subscripts and Superscripts
| backing or gas diffusion layer | |
| converter | |
| fuel cell | |
| membrane | |
| maximum | |
| open circuit | |
| oversize | |
| required | |
| storage | |
| cathode catalyst layer | |
| tank |
Appendix A. Mass of a Spherical Tank
References
- International Energy Agency. CO2 Emissions From Fuel Combustion: Highlights 2017; Technical Report; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Air Transport Action Group. Aviation Benefits Beyond Borders; Technical Report; Air Transport Action Group: Geneva, Switzerland, 2016. [Google Scholar]
- Darecki, M.; Edelstenne, C.; Enders, T.; Fernandez, E.; Hartman, P.; Herteman, J.P.; Kerkloh, M.; King, I.; Ky, P.; Mathieu, M.; et al. Flightpath 2050; Technical Report; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Müller, C.; Kieckhäfer, K.; Spengler, T.S. The influence of emission thresholds and retrofit options on airline fleet planning: An optimization approach. Energy Policy 2018, 112, 242–257. [Google Scholar] [CrossRef]
- Bockris, J.; Justi, E.W. Wasserstoff—Energie für alle Zeiten; Pfriemer Verlag: München, Germany, 1980. [Google Scholar]
- Brewer, G.; Morris, R. Study of LH2 Fueled Subsonic Passenger Transport Aircraft; Technical Report, NASA CR-144935; NASA: Washington, DC, USA, 1976.
- Khandelwal, B.; Karakurt, A.; Sekaran, P.R.; Sethi, V.; Singh, R. Hydrogen powered aircraft: The future of air transport. Prog. Aerosp. Sci. 2013, 60, 45–59. [Google Scholar] [CrossRef]
- Verstraete, D. Long range transport aircraft using hydrogen fuel. Int. J. Hydrogen Energy 2013, 38, 14824–14831. [Google Scholar] [CrossRef]
- Friedrich, K.A.; Kallo, J.; Schirmer, J.; Schmitthals, G. Fuel Cell Systems for Aircraft Application. ECS Trans. 2009, 25, 193–202. [Google Scholar]
- Jenssen, D.; Berger, O.; Krewer, U. Improved PEM fuel cell system operation with cascaded stack and ejector-based recirculation. Appl. Energy 2017, 195, 324–333. [Google Scholar] [CrossRef]
- Zenith, F.; Weinzierl, C.; Krewer, U. Model-based analysis of the feasibility envelope for autonomous operation of a portable direct methanol fuel-cell system. Chem. Eng. Sci. 2010, 65, 4411–4419. [Google Scholar] [CrossRef]
- Na, Y.; Zenith, F.; Krewer, U. Highly integrated direct methanol fuel cell systems minimizing fuel loss with dynamic concentration control for portable applications. J. Process Control 2017, 57, 140–147. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. A Physically-Based Analytical Polarization Curve of a PEM Fuel Cell. J. Electrochem. Soc. 2014, 161, F263–F270. [Google Scholar] [CrossRef]
- Perry, M.L.; Newman, J.; Cairns, E.J. Mass Transport in Gas-Diffusion Electrodes: A Diagnostic Tool for Fuel-Cell Cathodes. J. Electrochem. Soc. 1998, 145, 5–15. [Google Scholar] [CrossRef]
- Eikerling, M.; Kornyshev, A. Modelling the performance of the cathode catalyst layer of polymer electrolyte fuel cells. J. Electroanal. Chem. 1998, 453, 89–106. [Google Scholar] [CrossRef]
- Winnefeld, C.; Kadyk, T.; Krewer, U.; Hanke-Rauschenbach, R. Modelling and Designing Cryogenic Hydrogen Tanks in Terms of Aircraft Applications. Energies 2018, 11, 105. [Google Scholar] [CrossRef]
- Leachman, J.W.; Jacobsen, R.T.; Penoncello, S.G.; Lemmon, E.W. Fundamental equations of state for parahydrogen, normal hydrogen, and orthohydrogen. J. Phys. Chem. Ref. Data 2009, 38, 721–748. [Google Scholar] [CrossRef]
- Dobson, P.; Lei, C.; Navessin, T.; Secanell, M. Characterization of the PEM Fuel Cell Catalyst Layer Microstructure by Nonlinear Least-Squares Parameter Estimation. J. Electrochem. Soc. 2012, 159, B514–B523. [Google Scholar] [CrossRef]
- Liu, Y.; Elham, A.; Horst, P.; Hepperle, M. Exploring vehicle level benefits of revolutionary technology progress via aircraft design and optimization. Energies 2018, 11, 166. [Google Scholar] [CrossRef]
- Linde, A.G. Cryogenic Standard Tanks; Technical Report; Linde AG: Tacherting, Germany, 2016. [Google Scholar]
- Intelligent Energy Ltd. Ultra Lightweight Fuel Cell Systems—UAV Application Guide; Technical Report; Intelligent Energy Ltd.: Loughborough, UK, 2016. [Google Scholar]
- Siemens, A.G. Factsheet Rekord-Motor SP260D und Extra 330LE; Technical Report; Siemens AG: München, Germany, 2017. [Google Scholar]
- Muzaffar, T.; Kadyk, T.; Eikerling, M. Tipping Water Balance in Polymer Electrolyte Fuel Cells with Ultra-Low Pt Loading. Energy Environ. Sci. 2017. submitted. [Google Scholar]
- United States Department of Energy. Fuel Cell Technologies Office Multi-Year Research, Development, and Demonstration Plan, 2016 Fuel Cells Section; Technical Report; United States Department of Energy: Washington, DC, USA, 2016.
- Eslamibidgoli, M.J.; Huang, J.; Kadyk, T.; Malek, A.; Eikerling, M. How theory and simulation can drive fuel cell electrocatalysis. Nano Energy 2016, 29, 334–361. [Google Scholar] [CrossRef]
- Klingele, M.; Breitwieser, M.; Zengerle, R.; Thiele, S. Direct deposition of proton exchange membranes enabling high performance hydrogen fuel cells. J. Mater. Chem. A 2015, 3, 11239–11245. [Google Scholar] [CrossRef]
- Yoshida, T.; Kojima, K. Toyota MIRAI Fuel Cell Vehicle and Progress Toward a Future Hydrogen Society. Interface Mag. 2015, 24, 45–49. [Google Scholar] [CrossRef]
- Tsuchiya, H.; Kobayashi, O. Mass production cost of PEM fuel cell by learning curve. Int. J. Hydrogen Energy 2004, 29, 985–990. [Google Scholar] [CrossRef]
- Hermann, A.; Chaudhuri, T.; Spagnol, P. Bipolar plates for PEM fuel cells: A review. Int. J. Hydrogen Energy 2005, 30, 1297–1302. [Google Scholar] [CrossRef]
- Yuan, X.Z.; Wang, H.J.; Zhang, J.J.; Wilkinson, D.P. Bipolar plates for PEM fuel cells—From materials to processing. J. New Mater. Electrochem. Syst. 2005, 8, 257–267. [Google Scholar]
- Tawfik, H.; Hung, Y.; Mahajan, D. Metal bipolar plates for PEM fuel cell-A review. J. Power Sources 2007, 163, 755–767. [Google Scholar] [CrossRef]
- Antunes, R.A.; Oliveira, M.C.L.; Ett, G.; Ett, V. Corrosion of metal bipolar plates for PEM fuel cells: A review. Int. J. Hydrogen Energy 2010, 35, 3632–3647. [Google Scholar] [CrossRef]
- Wang, H.; Turner, J.A. Reviewing metallic PEMFC bipolar plates. Fuel Cells 2010, 10, 510–519. [Google Scholar] [CrossRef]
- Karimi, S.; Fraser, N.; Roberts, B.; Foulkes, F.R. A review of metallic bipolar plates for proton exchange membrane fuel cells: Materials and fabrication methods. Adv. Mater. Sci. Eng. 2012, 2012, 828070. [Google Scholar] [CrossRef]

| Parameter | Value | Reference |
|---|---|---|
| GDL thickness | 250 m | [13,18] |
| CCL thickness | 10 m | [13,18] |
| Membrane thickness | 25 m | [13,18] |
| oxygen concentration (p = 1 bar) | 7.36 × 10 mol cm | [13] |
| Cell open-circuit potential | 1.145 V | [13,18] |
| CCL proton conductivity | 0.03 S m | [13] |
| Tafel slope b | 0.03 V | [13] |
| exchange current density | 0.817 × 10 A cm | [13] |
| effective diffusion coefficient of GDL | 0.0259 cm s | [13] |
| effective diffusion coefficient of CCL D | 1.36 × 10 cm s | [13] |
| required energy for flight mission, | 63.7 MWh | [16] |
| required power of current aircraft, | 27.6 MW | [19] |
| required power of future aircraft, | 16.3 MW | [19] |
| area-specific tank mass, | 75 kg m | [20] |
| specific power of fuel cell+periphery (currently), | 1.6 kW kg | [21] |
| specific power of fuel cell+periphery (future), | 8 kW kg | estimate |
| specific power of electric motor (currently), | 5.2 kW kg | [22] |
| specific power of electric motor (future), | 10 kW kg | estimate |
| Aircraft Tech., P | Current FCS | Future FCS |
|---|---|---|
| 1.6 kW/kg FC | 8 kW/kg FC | |
| 5.8 kW/kg EM | 10 kW/kg EM | |
| current, 27.6 MW | 25,028 kg | 10,900 kg |
| future, 16.3 MW | 16,758 kg | 8197 kg |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadyk, T.; Winnefeld, C.; Hanke-Rauschenbach, R.; Krewer, U. Analysis and Design of Fuel Cell Systems for Aviation. Energies 2018, 11, 375. https://doi.org/10.3390/en11020375
Kadyk T, Winnefeld C, Hanke-Rauschenbach R, Krewer U. Analysis and Design of Fuel Cell Systems for Aviation. Energies. 2018; 11(2):375. https://doi.org/10.3390/en11020375
Chicago/Turabian StyleKadyk, Thomas, Christopher Winnefeld, Richard Hanke-Rauschenbach, and Ulrike Krewer. 2018. "Analysis and Design of Fuel Cell Systems for Aviation" Energies 11, no. 2: 375. https://doi.org/10.3390/en11020375
APA StyleKadyk, T., Winnefeld, C., Hanke-Rauschenbach, R., & Krewer, U. (2018). Analysis and Design of Fuel Cell Systems for Aviation. Energies, 11(2), 375. https://doi.org/10.3390/en11020375





