Generalized Dynamical Modeling of Multiple Photovoltaic Units in a Grid-Connected System for Analyzing Dynamic Interactions
Abstract
1. Introduction
2. Dynamical Modeling of a Grid-Connected System with Multiple PV Units
2.1. Dynamical Modeling of a Single PV Unit Connected to the Grid
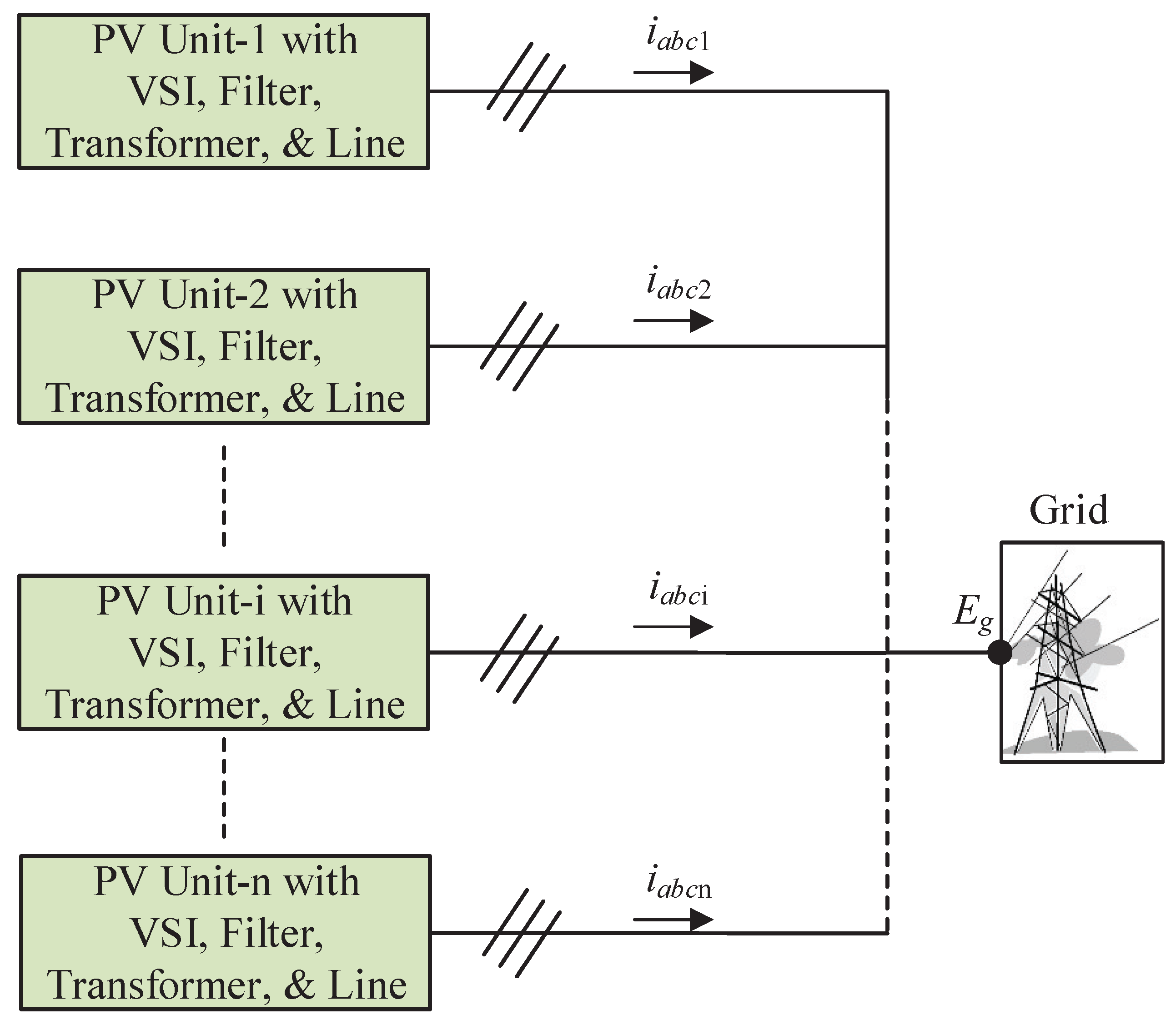
2.2. Dynamical Modeling of a Grid-Connected System with Directly Connected Multiple PV Units
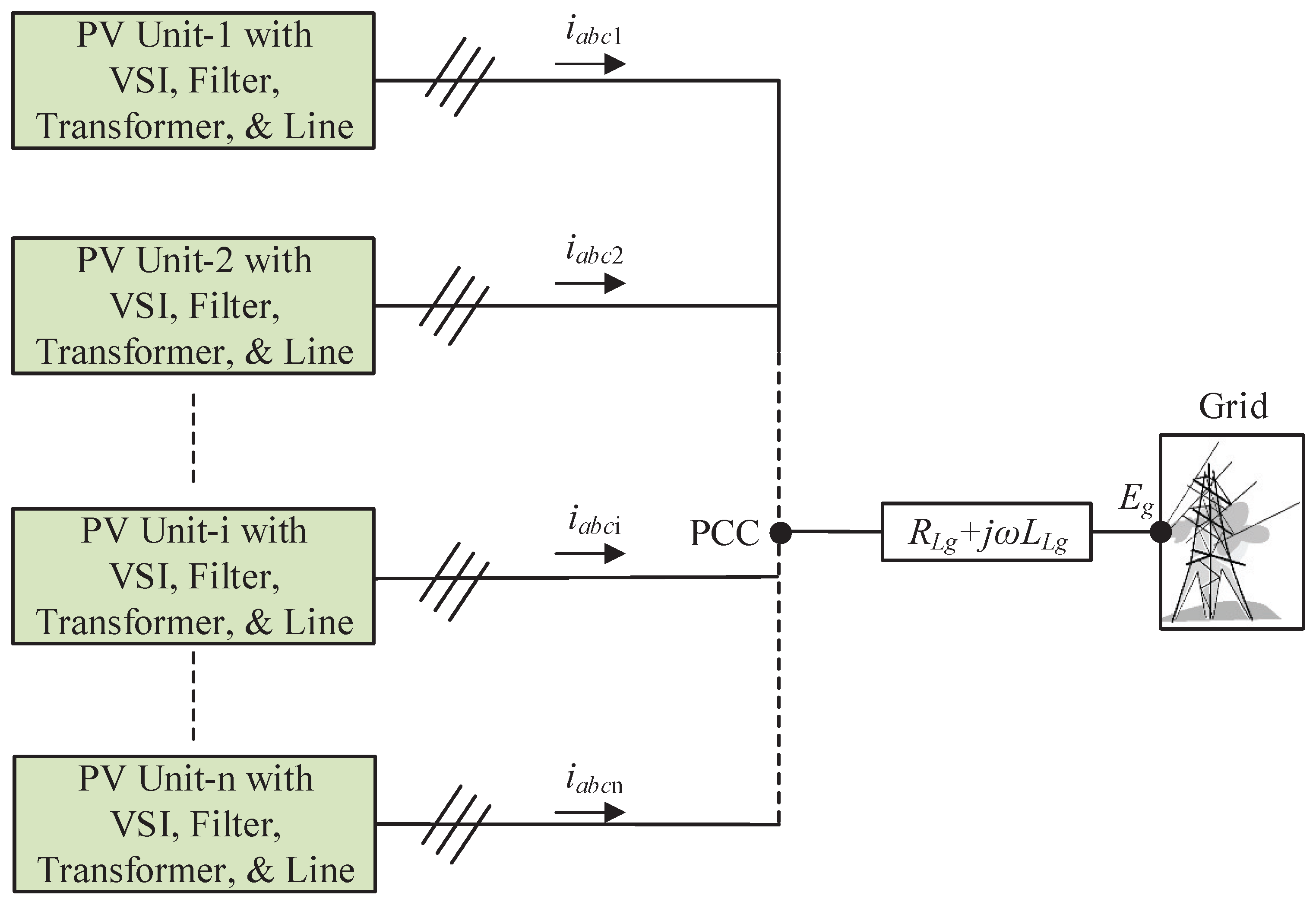
2.3. Dynamical Modeling of a Grid-Connected System with Multiple PV Units Connected through a PCC
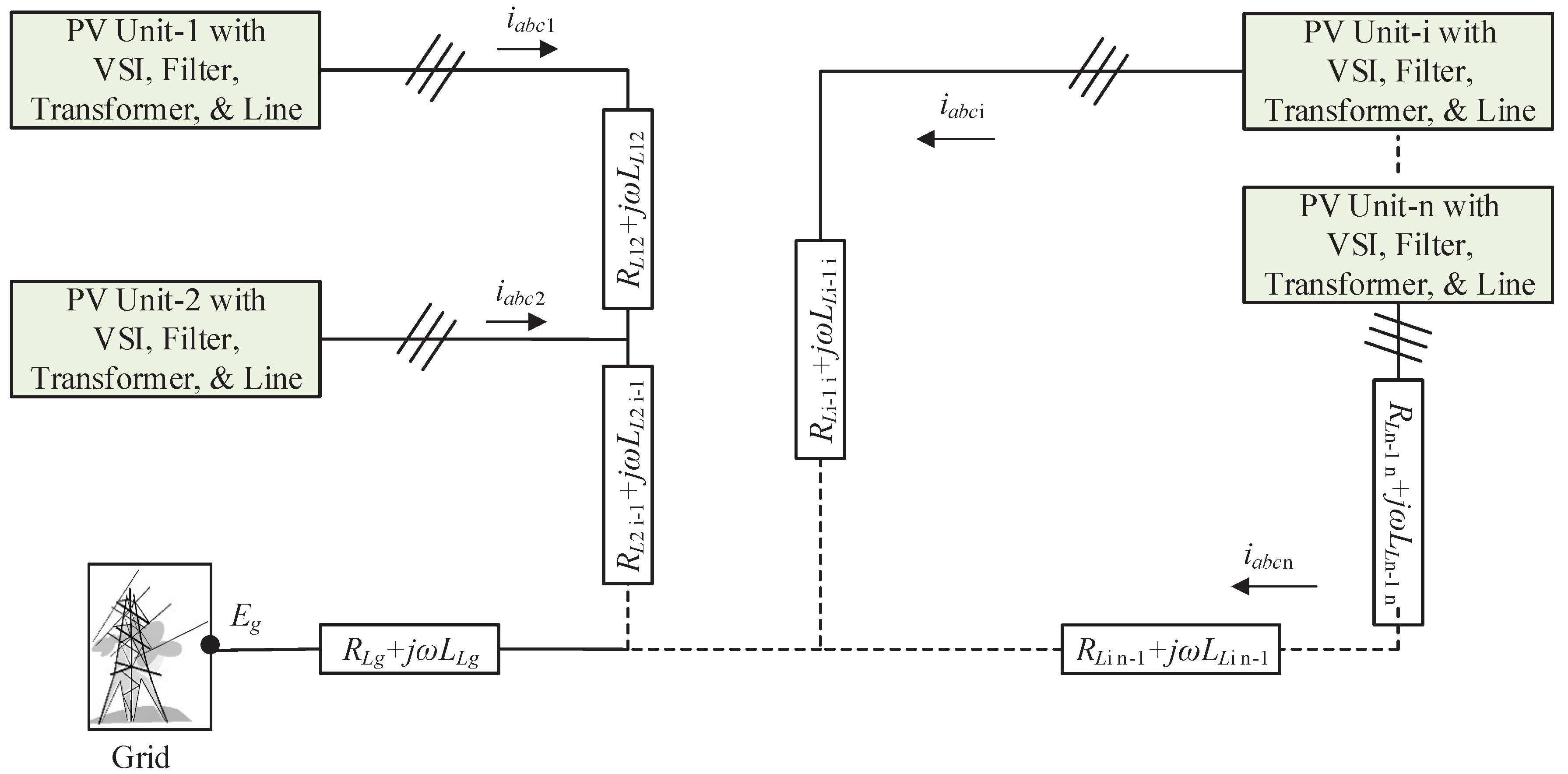
2.4. Dynamical Modeling of a Grid-Connected System with Multiple PV Units Interconnected through Lines
3. Analysis of Dynamic Interactions
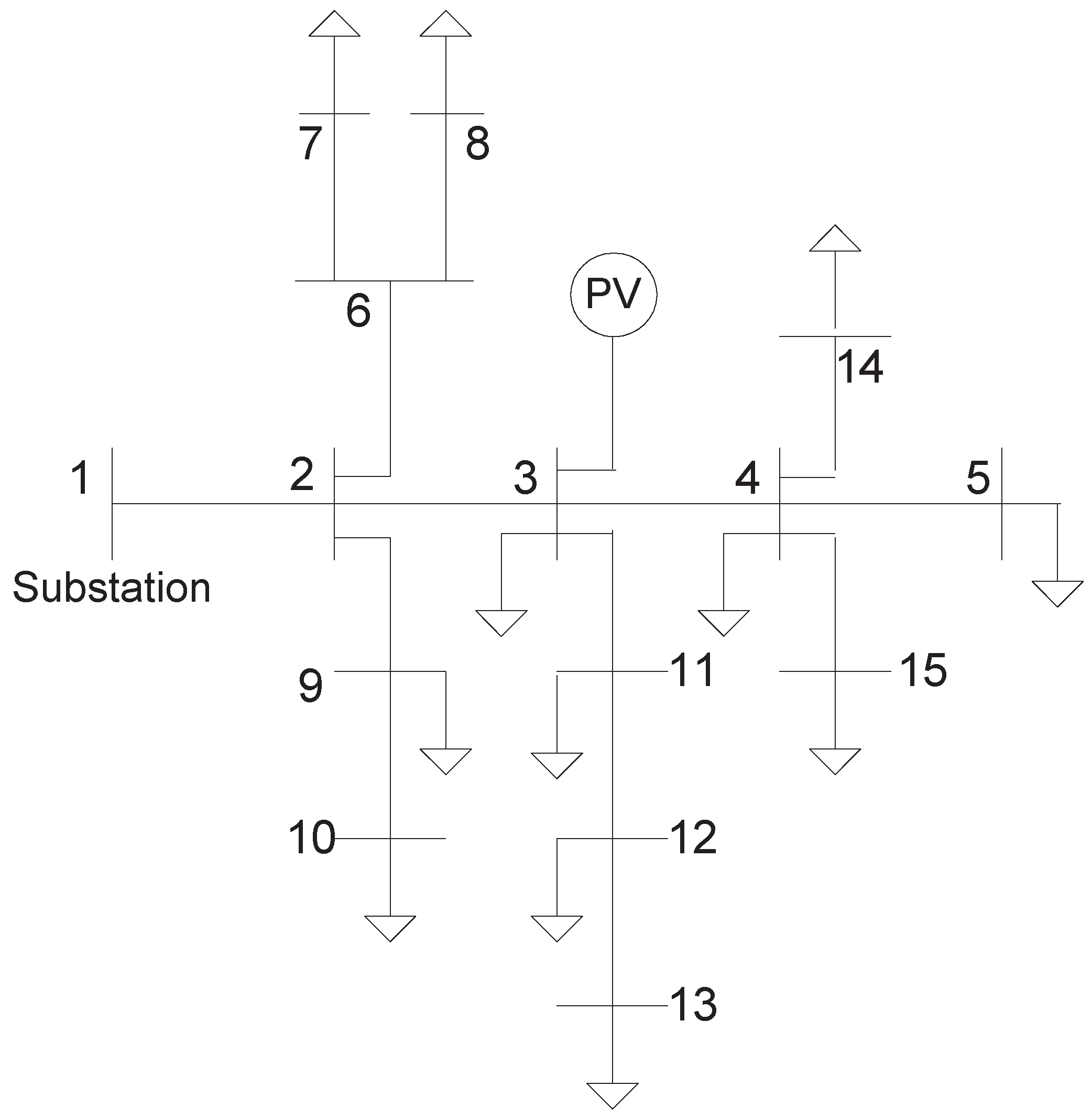
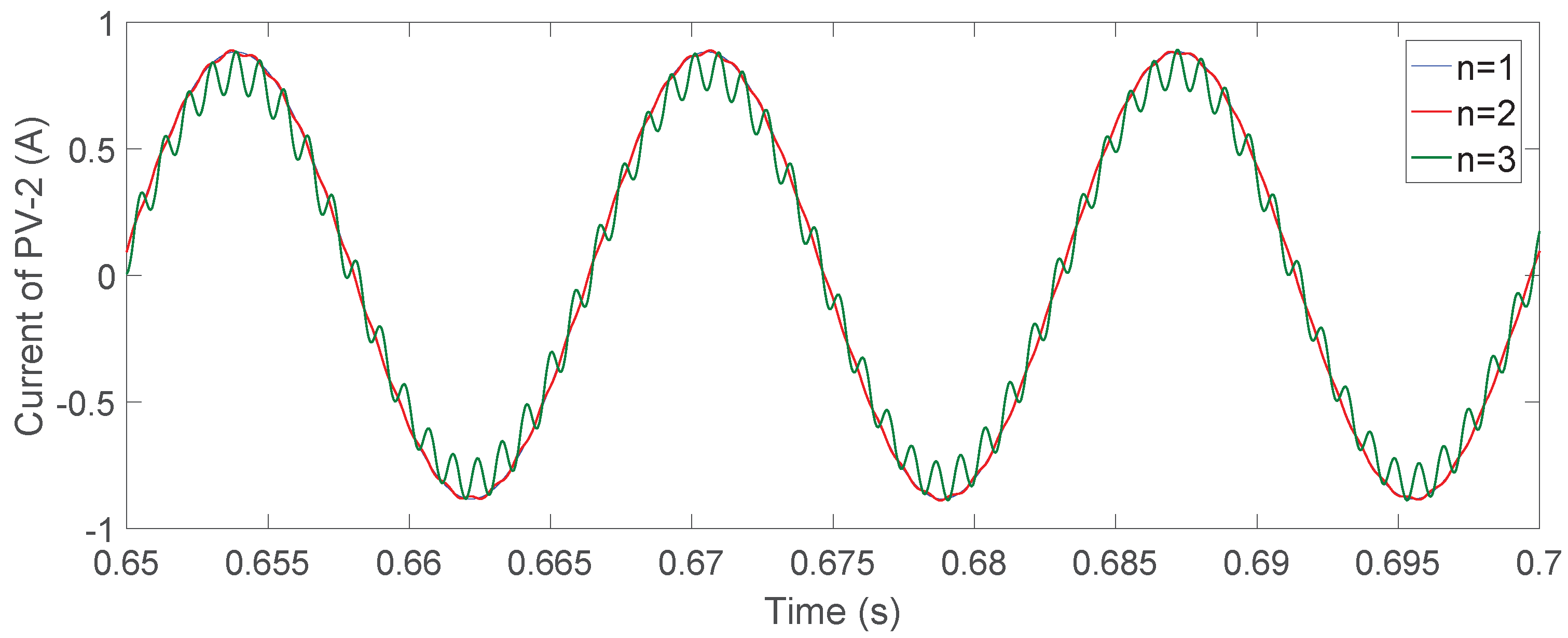
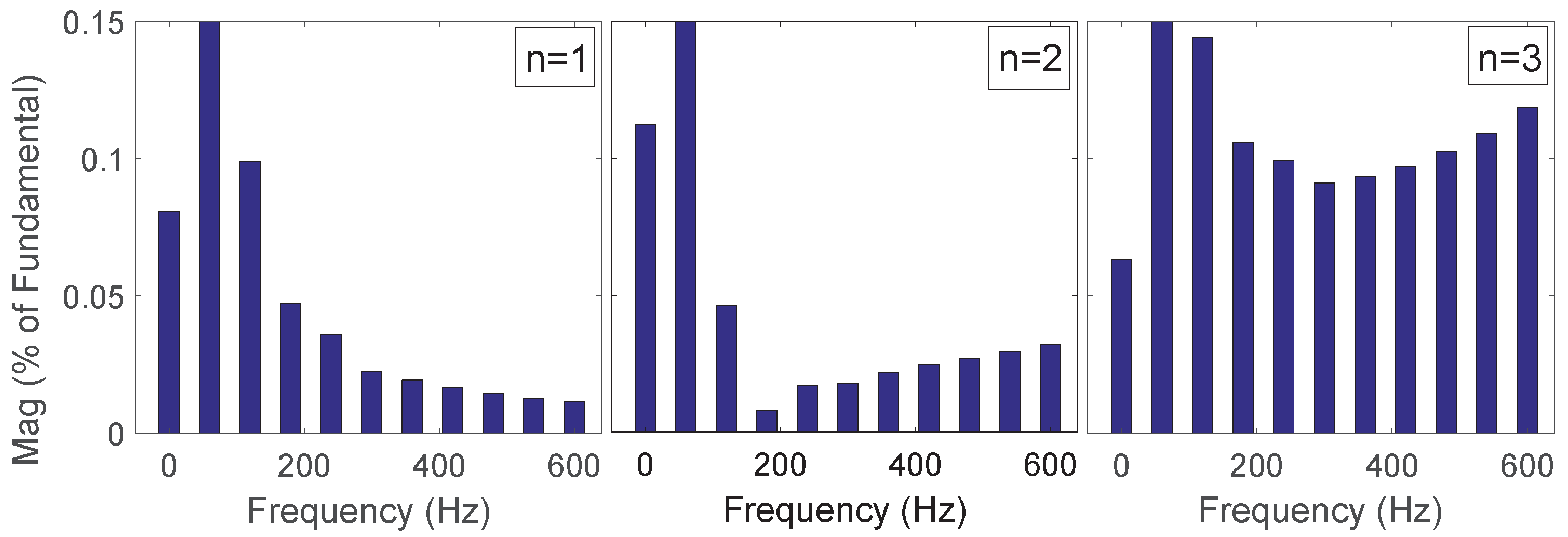
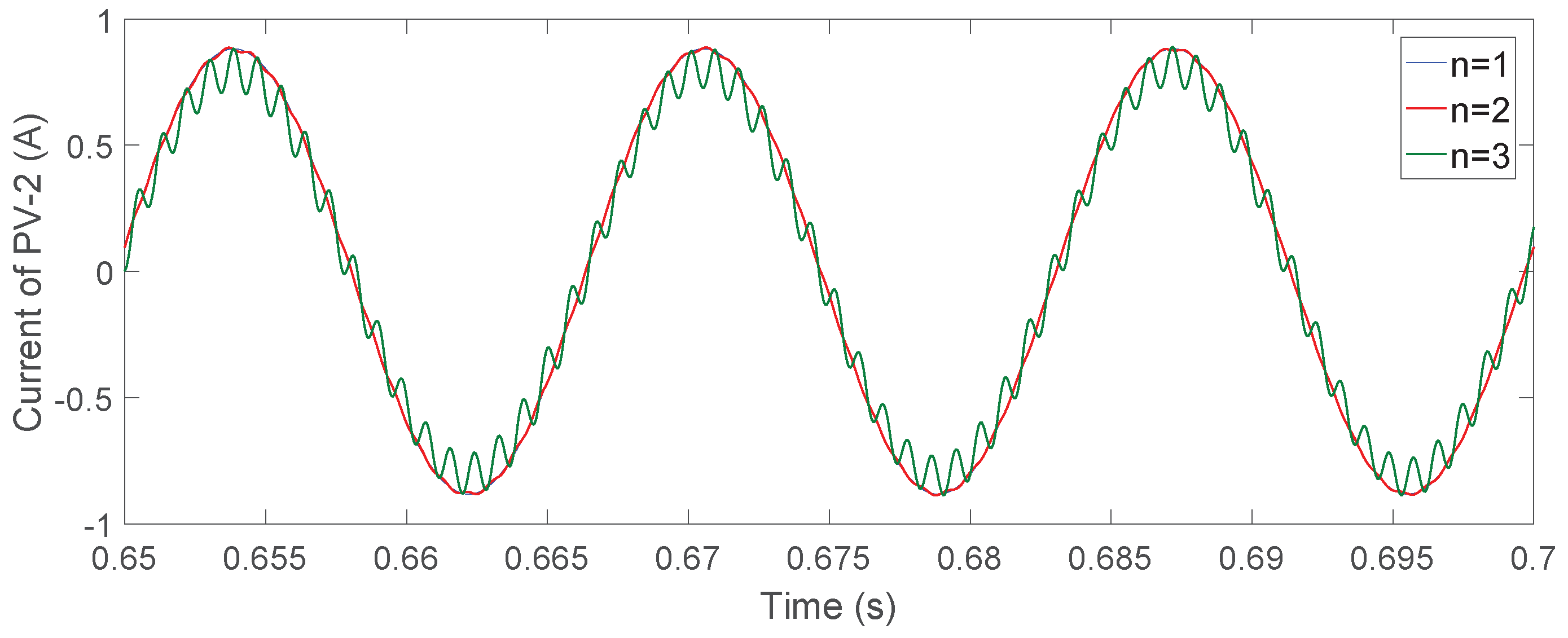
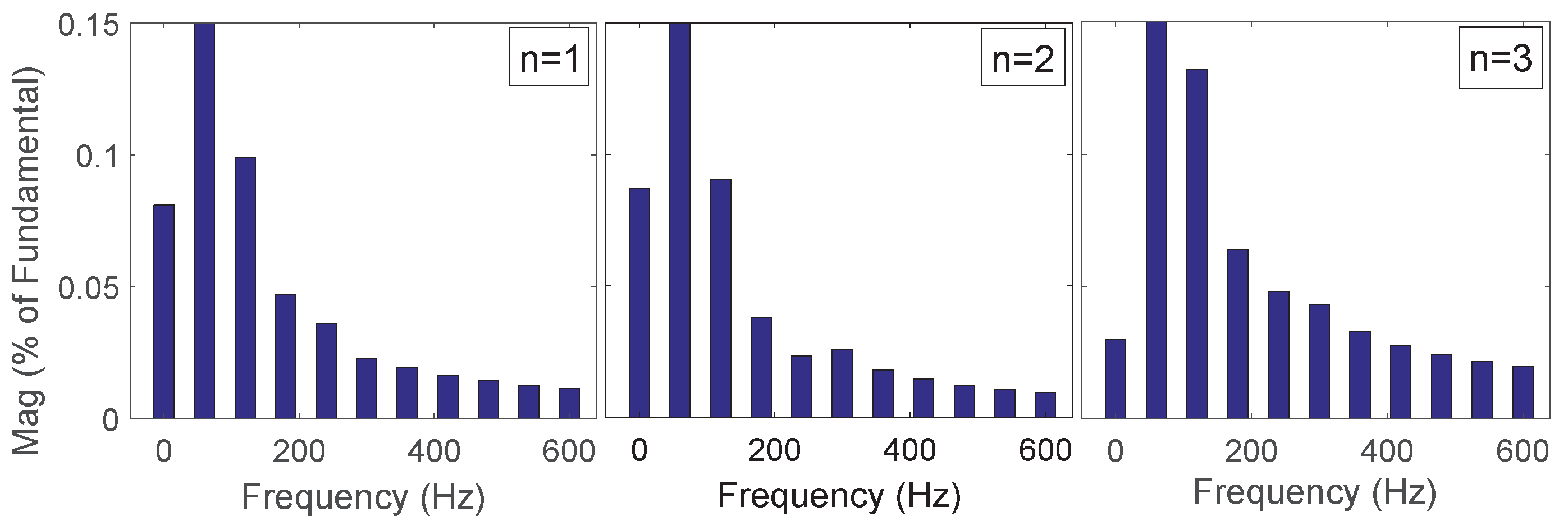
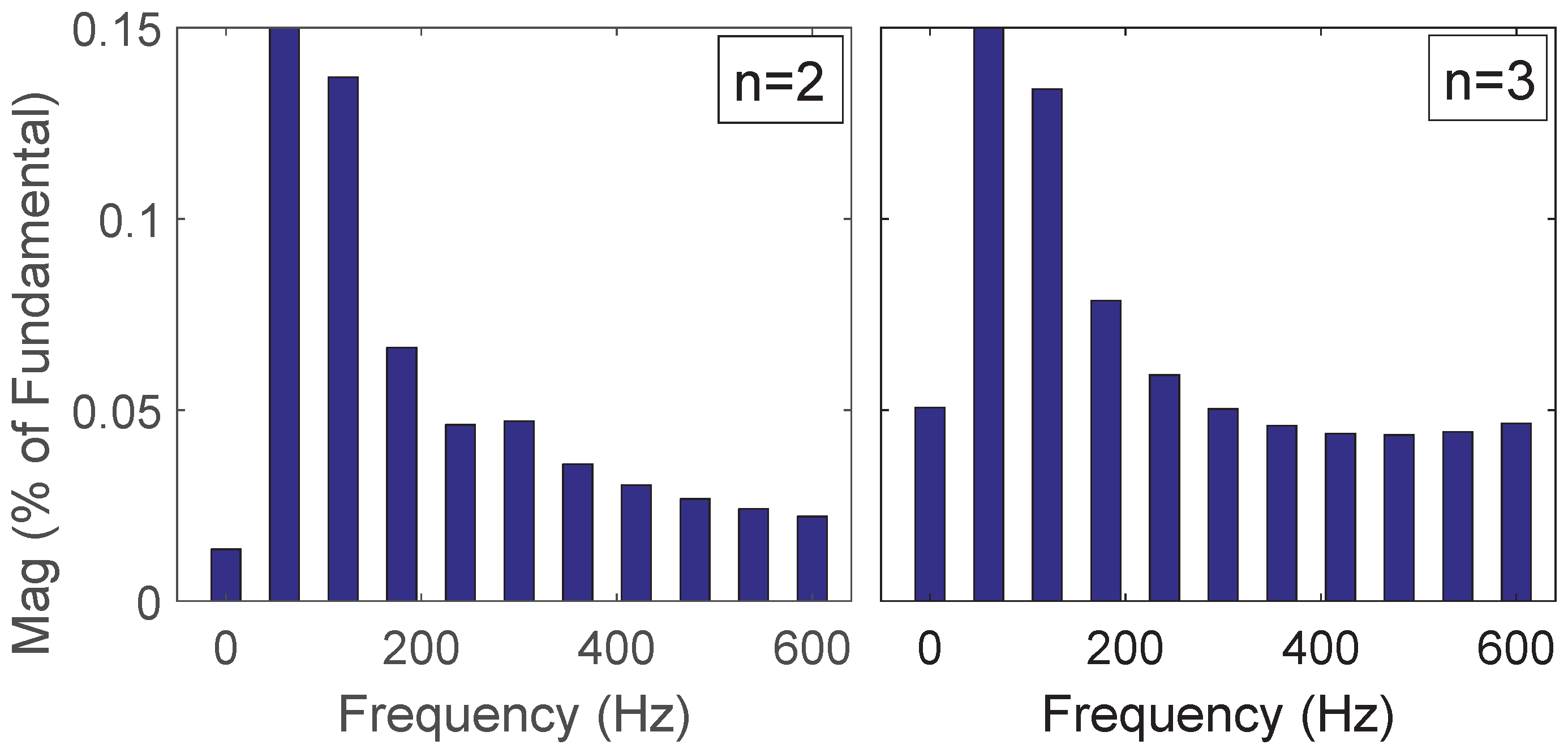
4. Simulation Results
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Korkas, C.D.; Baldi, S.; Michailidis, I.; Kosmatopoulos, E.B. Occupancy-based demand response and thermal comfort optimization in microgrids with renewable energy sources and energy storage. Appl. Energy 2016, 163, 93–104. [Google Scholar] [CrossRef]
- Baldi, S.; Karagevrekis, A.; Michailidis, I.T.; Kosmatopoulos, E.B. Joint energy demand and thermal comfort optimization in photovoltaic-equipped interconnected microgrids. Energy Convers. Manag. 2015, 101, 352–363. [Google Scholar] [CrossRef]
- Navarro, A.A.; Ramírez, L.; Domínguez, P.; Blanco, M.; Polo, J.; Zarza, E. Review and validation of Solar Thermal Electricity potential methodologies. Energy Convers. Manag. 2016, 126, 42–50. [Google Scholar] [CrossRef]
- Marzband, M.; Yousefnejad, E.; Sumper, A.; Dominguez-Garcia, J.L. Real time experimental implementation of optimum energy management system in standalone Microgrid by using multi-layer ant colony optimization. Int. J. Electr. Power Energy Syst. 2016, 75, 265–274. [Google Scholar] [CrossRef]
- Marzband, M.; Ghadimi, M.; Sumper, A.; Dominguez-Garcia, J.L. Experimental validation of a real-time energy management system using multi-period gravitational search algorithm for microgrids in islanded mode. Appl. Energy 2014, 128, 164–174. [Google Scholar] [CrossRef]
- Australian Energy Market Operator. National Electricity Forecasting Report for the National Electricity Market; Technical Report; Australian Energy Market Operator (AEMO): Melbourne, Australia, 2016. [Google Scholar]
- Hossain, E.; Kabalci, E.; Bayindir, R.; Perez, R. Microgrid testbeds around the world: State of art. Energy Convers. Manag. 2014, 86, 132–153. [Google Scholar] [CrossRef]
- Hossain, M.J.; Saha, T.K.; Mithulananthan, N.; Pota, H.R.; Lu, J. Dynamic interactions among multiple DER controllers in distribution systems. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012; pp. 1–6. [Google Scholar]
- Enslin, J.H.R.; Heskes, P.J.M. Harmonic interaction between a large number of distributed power inverters and the distribution network. IEEE Trans. Power Electron. 2004, 19, 1586–1593. [Google Scholar] [CrossRef]
- Infield, D.G.; Onions, P.; Simmons, A.D.; Smith, G.A. Power quality from multiple grid-connected single-phase inverters. IEEE Trans. Power Deliv. 2004, 19, 1983–1989. [Google Scholar] [CrossRef]
- Tan, Y.T.; Kirschen, D.S.; Jenkins, N. A model of PV generation suitable for stability analysis. IEEE Trans. Energy Convers. 2004, 19, 748–755. [Google Scholar] [CrossRef]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-Connected Photovoltaic Systems: An Overview of Recent Research and Emerging PV Converter Technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Tan, Y.T.; Kirschen, D.S. Impact on the Power System of a Large Penetration of Photovoltaic Generation. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Perera, B.K.; Pulikanti, S.R.; Ciufo, P.; Perera, S. Simulation model of a grid-connected single-phase photovoltaic system in PSCAD/EMTDC. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012; pp. 1–6. [Google Scholar]
- Refaat, S.S.; Abu-Rub, H.; Sanfilippo, A.P.; Mohamed, A. Impact of grid-tied large-scale photovoltaic system on dynamic voltage stability of electric power grids. IET Renew. Power Gener. 2017. [Google Scholar] [CrossRef]
- Kim, S.K.; Jeon, J.H.; Cho, C.H.; Kim, E.S.; Ahn, J.B. Modeling and simulation of a grid-connected PV generation system for electromagnetic transient analysis. Solar Energy 2009, 83, 664–678. [Google Scholar] [CrossRef]
- Xiao, W.; Edwin, F.F.; Spagnuolo, G.; Jatskevich, J. Efficient Approaches for Modeling and Simulating Photovoltaic Power Systems. IEEE J. Photovolt. 2013, 3, 500–508. [Google Scholar] [CrossRef]
- Yazdani, A.; Fazio, A.R.D.; Ghoddami, H.; Russo, M.; Kazerani, M.; Jatskevich, J.; Strunz, K.; Leva, S.; Martinez, J.A. Modeling Guidelines and a Benchmark for Power System Simulation Studies of Three-Phase Single-Stage Photovoltaic Systems. IEEE Trans. Power Deliv. 2011, 26, 1247–1264. [Google Scholar] [CrossRef]
- Baimel, D.; Belikov, J.; Guerrero, J.M.; Levron, Y. Dynamic Modeling of Networks, Microgrids, and Renewable Sources in the dq0 Reference Frame: A Survey. IEEE Access 2017, 5, 21323–21335. [Google Scholar] [CrossRef]
- Shah, R.; Mithulananthan, N.; Bansal, R.C. Oscillatory stability analysis with high penetrations of large-scale photovoltaic generation. Energy Convers. Manag. 2013, 65, 420–429. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, L.; Li, B.; Zheng, C.; Xie, B. Modeling and Analysis of a Digitally Controlled Grid-Connected Large-Scale Centralized PV System. IEEE Trans. Power Electron. 2017, PP, 1. [Google Scholar] [CrossRef]
- Nduka, O.S.; Pal, B.C. Harmonic Domain Modeling of PV System for the Assessment of Grid Integration Impact. IEEE Trans. Sustain. Energy 2017, 8, 1154–1165. [Google Scholar] [CrossRef]
- Tamimi, B.; Cañizares, C.; Bhattacharya, K. System Stability Impact of Large-Scale and Distributed Solar Photovoltaic Generation: The Case of Ontario, Canada. IEEE Trans. Sustain. Energy 2013, 4, 680–688. [Google Scholar] [CrossRef]
- Yazdani, A.; Dash, P.P. A Control Methodology and Characterization of Dynamics for a Photovoltaic (PV) System Interfaced with a Distribution Network. IEEE Trans. Power Deliv. 2009, 24, 1538–1551. [Google Scholar] [CrossRef]
- Agorreta, J.L.; Borrega, M.; López, J.; Marroyo, L. Modeling and Control of N -Paralleled Grid-Connected Inverters with LCL Filter Coupled Due to Grid Impedance in PV Plants. IEEE Trans. Power Electron. 2011, 26, 770–785. [Google Scholar] [CrossRef]
- Akhavan, A.; Mohammadi, H.R.; Guerrero, J.M. Modeling and design of a multivariable control system for multi-paralleled grid-connected inverters with LCL filter. Int. J. Electr. Power Energy Syst. 2018, 94, 354–362. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, P.; Wang, Y.; Xu, Z.; Guerrero, J.M. Dynamic Characteristics Analysis and Stabilization of PV-Based Multiple Microgrid Clusters. IEEE Trans. Smart Grid 2017, PP. [Google Scholar] [CrossRef]
- Lalili, D.; Mellit, A.; Lourci, N.; Medjahed, B.; Berkouk, E.M. Input output feedback linearization control and variable step size MPPT algorithm of a grid-connected photovoltaic inverter. Renew. Enegry 2011, 36, 3282–3291. [Google Scholar] [CrossRef]
- Marouani, R.; Mami, A. Robust maximum power point tracker using sliding mode controller for the three-phase grid-connected photovoltaic system. Am. J. Appl. Energy 2010, 7, 1168–1173. [Google Scholar]
- Mahmud, M.A.; Pota, H.R.; Hossain, M.J. Dynamic Stability of Three-Phase Grid-Connected Photovoltaic System Using Zero Dynamic Design Approach. IEEE J. Photovolt. 2012, 2, 564–571. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| m | |
| H | |
| m | |
| H | |
| m | |
| 34 H | |
| 3 mH | |
| mH | |
| mH | |
| mH |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orchi, T.F.; Mahmud, M.A.; Oo, A.M.T. Generalized Dynamical Modeling of Multiple Photovoltaic Units in a Grid-Connected System for Analyzing Dynamic Interactions. Energies 2018, 11, 296. https://doi.org/10.3390/en11020296
Orchi TF, Mahmud MA, Oo AMT. Generalized Dynamical Modeling of Multiple Photovoltaic Units in a Grid-Connected System for Analyzing Dynamic Interactions. Energies. 2018; 11(2):296. https://doi.org/10.3390/en11020296
Chicago/Turabian StyleOrchi, Tahsin Fahima, Md Apel Mahmud, and Amanullah Maung Than Oo. 2018. "Generalized Dynamical Modeling of Multiple Photovoltaic Units in a Grid-Connected System for Analyzing Dynamic Interactions" Energies 11, no. 2: 296. https://doi.org/10.3390/en11020296
APA StyleOrchi, T. F., Mahmud, M. A., & Oo, A. M. T. (2018). Generalized Dynamical Modeling of Multiple Photovoltaic Units in a Grid-Connected System for Analyzing Dynamic Interactions. Energies, 11(2), 296. https://doi.org/10.3390/en11020296







