1. Introduction
Compound Parabolic Solar Concentrators (CPCs) were described as a collector for cosmic light from Cherenkov counters by Hinterberger in Winston’s book [
1]. CPCs are considered to be ideal concentrators, identified in the family of non-image concentrators. According to Kalogirou, CPC is classified as a medium temperature application (100–250 °C) [
2,
3]. The application, design, and geometrical parameters for solar concentrators with cylindrical receivers are described by Winston [
1]. Rabl conducted a study to determine the optical and thermal properties of a CPC [
4]. From this work, it was determined that the CPC is very close to be the ideal solar concentrator, because it reaches the highest concentration possible for any angle of acceptance [
5,
6]. This study also provides the formulae for calculating average reflections in a CPC. For an ideal CPC, only two parameters are required, acceptance angle and receiver diameter; in this way, these parameters define the concentrator’s width and height [
7]. A CPC usually requires few or no adjustments to its angular position, for example, throughout a typical seasonal year [
7,
8,
9,
10,
11]. A CPC system usually has construction imperfections that impact its efficiency; therefore, a common task is to minimize losses by taking into account the restrictions imposed by the design, material properties, and cost considerations [
8,
12,
13]. In this manner, the quality of the optical properties and the shape of the reflecting surface of a concentrator determine the level of concentration that the receiver can reach. The deviations from the ideal performance are due to optical errors of the concentrator [
14,
15]. These can be classified into two types: First, the shape of the surface of the concentrator, the closer it is to the ideal, the smaller the error will be; this error is commonly called contour error. The second is the error produced by the specular reflection of the material; this error is mainly due to surface roughness, i.e., surface imperfections at microscale [
16].
In this type of collector, the lack of solar radiation on the lower part of the receiver can be resolved by matching the acceptance angle of the concentrator with the solar vector, thereby obtaining a more homogeneous impinging of the sun’s rays on the concentrator. It is important to consider that a uniform solar illumination of the receiver area is desired, due to the intense radiation generated by the concentration effect. If there are deformations or manufacturing defects on the concentrator surface (or misalignment), radiation hot spots will be promoted, giving an uneven distribution of heat on the receiver. These types of errors can be ignored for a high conductivity receiver, but practical systems require the minimization of this issue if proper heat transfer is desired [
16,
17,
18].
A solar concentrator depends greatly on its focal alignment, thus, in static systems, a significant loss in energy availability can occur [
1]. Ray tracing software is a very useful tool, since it allows the user to estimate the amount and distribution of concentrated solar energy that the receiver is capable of transmitting at any moment, defining geometry and construction materials. For example, in 2010, Colina-Marquez et al. used a solar tracing software tool to determine energy distribution on a receiver, testing three reflective surfaces [
19]. In 2014, Chia-Wei et al. [
20] proposed a modification in the positioning of the receiver, varying the focal point from the relationship between height and diameter, and found that the optimal ratio between them was 0.46; the angle of incidence from 1.5 to 6 degrees was also evaluated using a ray tracing analysis to estimate the amount of concentrated energy in the receiver. In the same year, Waghmare et al. presented a ray tracing-based analysis, which analyzed the effect of limiting the diameter of the receiver in order to reduce optical losses [
21]. Yurchenko et al. established a ray tracing analysis for the optical and thermal optimization of a CPC, resulting in the use of a configuration of V vents with which an optimal value was obtained for the positioning of these in the receiver for a typical CPC [
8]. In 2015, Lin et al. analyzed a two-dimensional CPC with a tubular receiver, varying the collector’s profile and truncating the reflector to a lower height; the CPC was seasonal tilted and was oriented to east–west. Using the ray tracing method, a numerical model was developed to study the performance of the modified collector [
22]. In 2016, Bellos et al. applied the use of a ray tracing tool combined with finite element analysis to optimize a CPC design from optical and thermal performance [
23].
This work proposes to study the use of a CPC in a lower temperature range (40–60 °C) as a residential solar heater, taking advantage of the greater efficiency provided by the system for a given temperature. In this collector type, the opening area of the CPC is more reduced than other systems, such as flat plate heater (FPH), combined with the use of high reflective surface and the geometry of the concentrator, allowing concentrating more energy in the receiver. In this sense, the dimensions of the CPC system can be more reduced (and lighter), decreasing the material used. In addition to this, it has been quantified that the parts used for a FPH are more than those used in a CPC; therefore, the use of less material and less assembly time opens an opportunity window to evaluate the potential use of CPCs for residential applications.
To achieve this, the study proposes the dimensioning of a CPC system that operates in a low temperature range (40 to 60 °C), using a ray tracing software to determine the energy availability in two scenarios, static and multi-position setups [
23,
24]. The analysis for this particular work was carried out in the geographic location of Merida, Mexico; however, it could be used in any region of interest. In addition to the optical study, the construction and instrumentation of an experimental prototype was carried out in order to evaluate the proposed system in real conditions.
2. Materials and Methods
2.1. Concentrator Ratio
The concentration ratio,
CR, together with the receiver diameter, represent the basic parameters for a CPC design. For the
CR, the relative movement of the sun in the celestial vault throughout the year (Analemma) is taken into account, and the calculation is carried out with reference to the solar noon
θz using the equations proposed by Duffie et al. [
5]. For the coordinates of this study (21.02° N, −89.63° W), the summer solstice, the maximum angle of the sun is −4.27°, taking as a reference the vertical (Y axis), whereas in the winter solstice, the maximum angle reached is 42.16°.
It is well known that a high concentration factor gathers more energy; however, this entails the need for more periodical adjustments during the day to capture solar rays. Based on this, and taking into consideration the solar trajectory in the celestial vault, in order to reduce the loss of solar incidence throughout the year, a concentrator acceptance angle of 45° was selected.
Before calculating the available energy at the receiver and in order to facilitate a better understanding of the results of solar ray trace campaign, the concentrator acceptance angle aligned with
β (inclination angle of CPC) was evaluated.
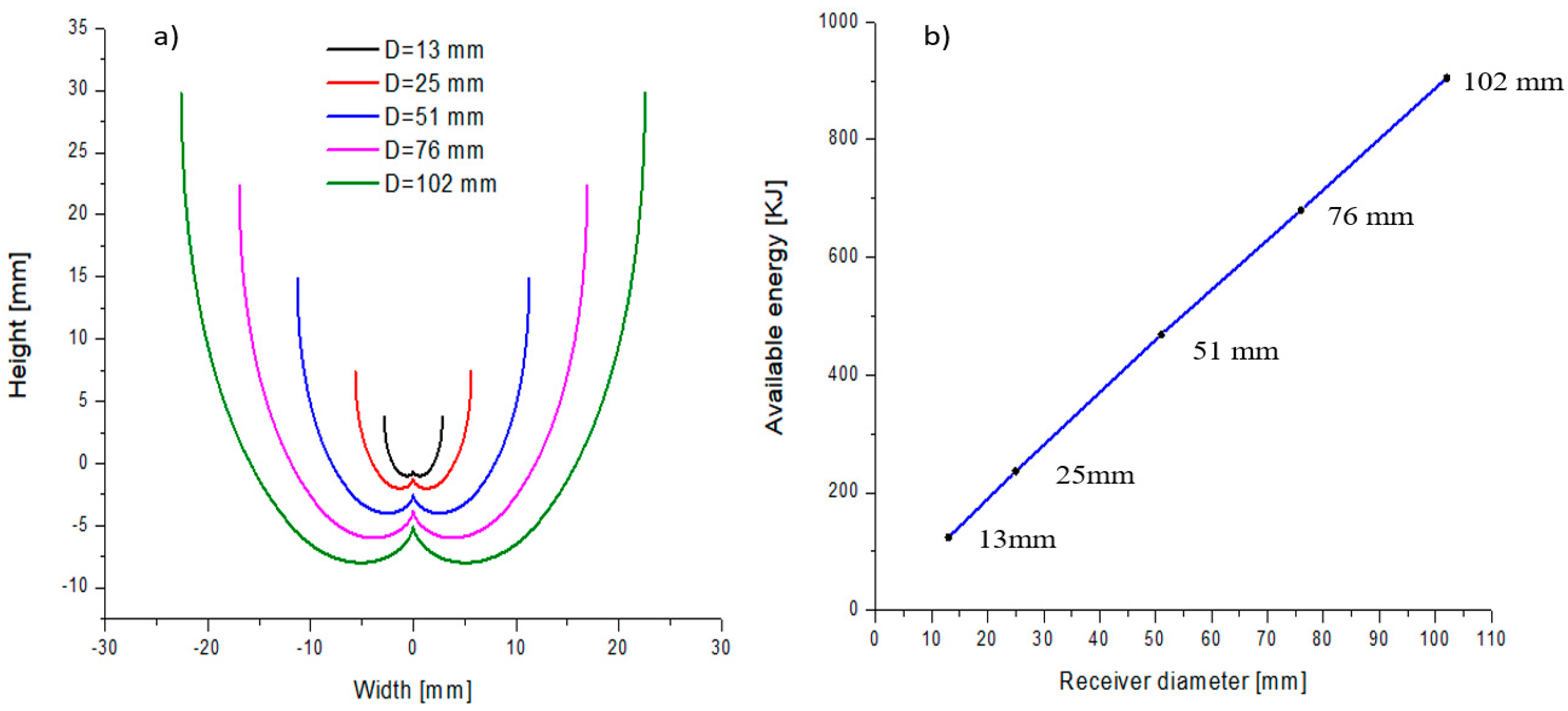
Figure 1a presents an evaluation of the CPC profiles calculated for nominal commercial copper tubing of 13, 25, 51, and 102 mm and their dimensions to aid in the selection of the best concentrator. From these profiles, and taking one meter as the tube length for this study, virtual models were created with Tonatiuh software (open source software 2.2.2, University of Texas, Brownsville, TX, USA) to obtain the available energy in each receiver; the results are shown in
Figure 1b. Here, a 13 mm tube was selected as reference, as this is the nominal size of common residential installations. The graph shows that for the 25 mm tube, there would be twice the available energy compared to the 13 mm diameter, which is congruent since the area exposed to the sun’s energy increases in the same proportion, applying the same correspondence for other diameters.
In order to select the receiver diameter, and for comparison purposes, the volume of a commercial flat plate solar heater of 1 m2 was taken as a reference, which has 10 copper tubes of 13 mm in diameter and a volume capacity of 2.17 L. In order to have similar volume capacity in a length of 1 m, a tube with an internal diameter of 51 mm was chosen. This allows simplifying the hydraulic system, which generates a reduction of time and effort in the manufacturing stage.
2.2. Concentrator Design
The concentrator is composed of two identical curved reflecting surfaces placed in such a way that both surfaces are oppositely reflecting a focal point [
1,
5,
23,
25,
26,
27]; in 2004, Chaves provided the appropriate description for the design which uses a cylindrical receiver, contemplating the total illumination of the receiver [
26].
Equations for the CPC profile in the Cartesian plane were described by different authors [
1,
5,
23]; however, the equations applicable to this study were described by González et al. [
28], projecting the profile of the concentrator from the external diameter of the tubular receiver. The profile is composed of two parts with their respective governing equations. The first part is the bottom profile denominated the involute; the second part at the top is the cup. These equations are evaluated at the lower and upper limits which allow the identification of the points of intersection between the involute and the lower part of the cup. The upper limit sets the maximum width of the cup, which consequently determines the concentrator height. The idea is based on taking advantage of the geometric principle of focusing two curves that shape the cup, which match with the receiver at a certain angle at opposite ends, as well as at the bottom (involute), receiving the solar rays and redirecting them to the receiver. The equations used and their limits for the profile design are as follows.
Evaluated between the limits of
Evaluated between the limits of
where:
For the present study, Equations (1)–(4) with their respective evaluation limits, and the receiver diameter, were used to determine the width and height of the concentrator.
2.3. Virtual Model
A virtual model was generated using Tonatiuh software, taking into consideration characteristic materials available in the market for its construction. The model was positioned in the coordinates (21.02° N, −89.63° W) of the city of Merida, Mexico and it was oriented in the direction of the solar path, i.e., along the east–west direction, tilted to the south at angle
β. The present system intends to occupy as little space as possible with low weight, considering its utilization in low- to medium-income residential areas. One alternative optimization is to explore a few adjustments of the concentrator with the inclination angle
β, according to the season of the year, the aim being to increase energy availability; therefore, it was necessary to determine the relationship (Sn-
θz) of solar angle.
Table 1 shows the values of the Sn-
θz as a function of the months of the year for Merida, and the corresponding recommended value of the inclination angle (
β) of the collector, which applies to any angle of acceptance between −4.27° and 42.16°, thus valid for the proposed coordinates.
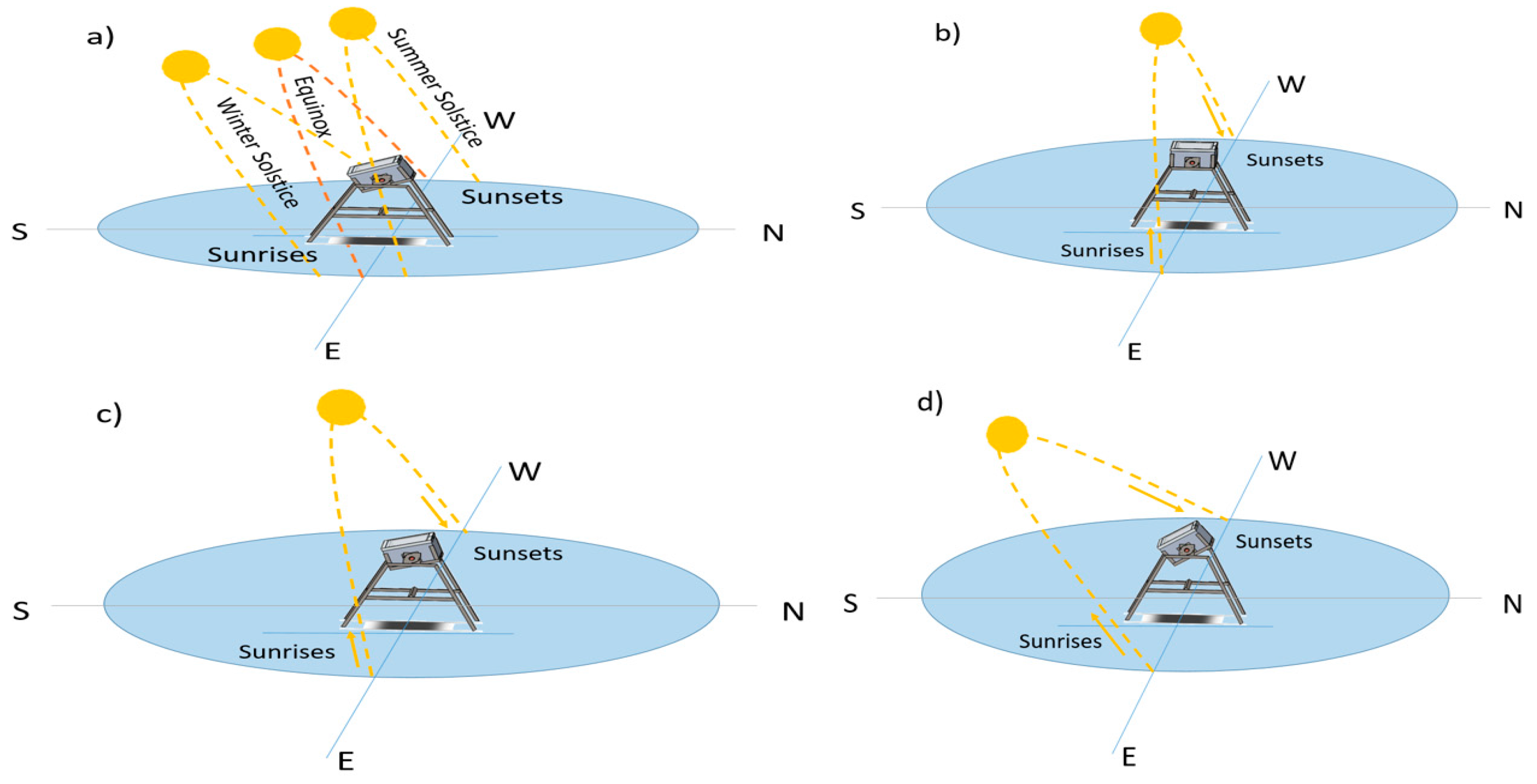
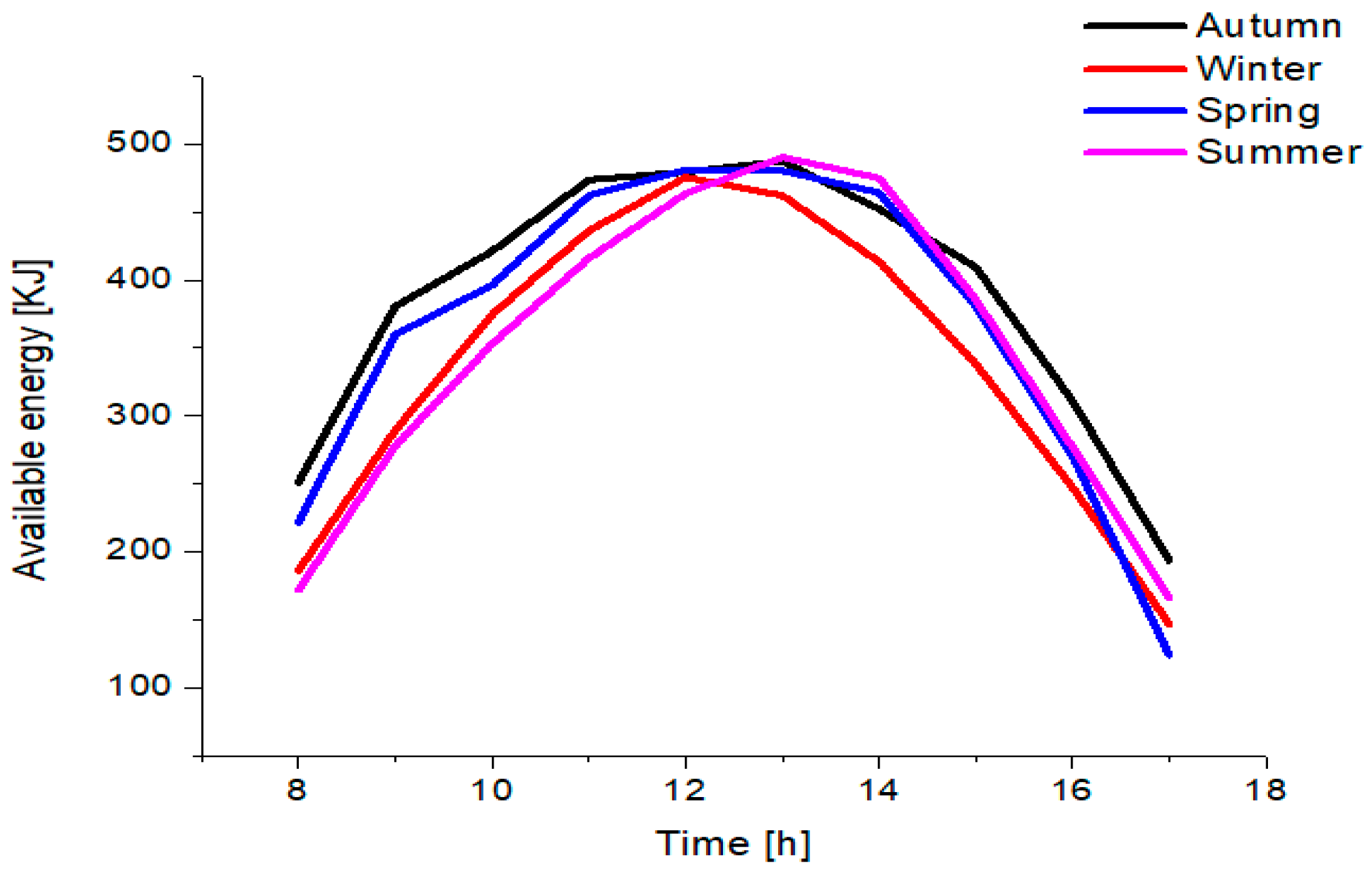
Two cases were analyzed here; static and multi-position setups. For the first case, the inclination angle
β throughout the year of the CPC is equal to the present latitude of Merida city, 21° (with respect to the horizontal), as represented in
Figure 2a. With the information provided in
Table 1, three angles of inclination were selected for the multi-position setup: 0° for summer, 16° for autumn/spring, and 32° for winter, as represented in
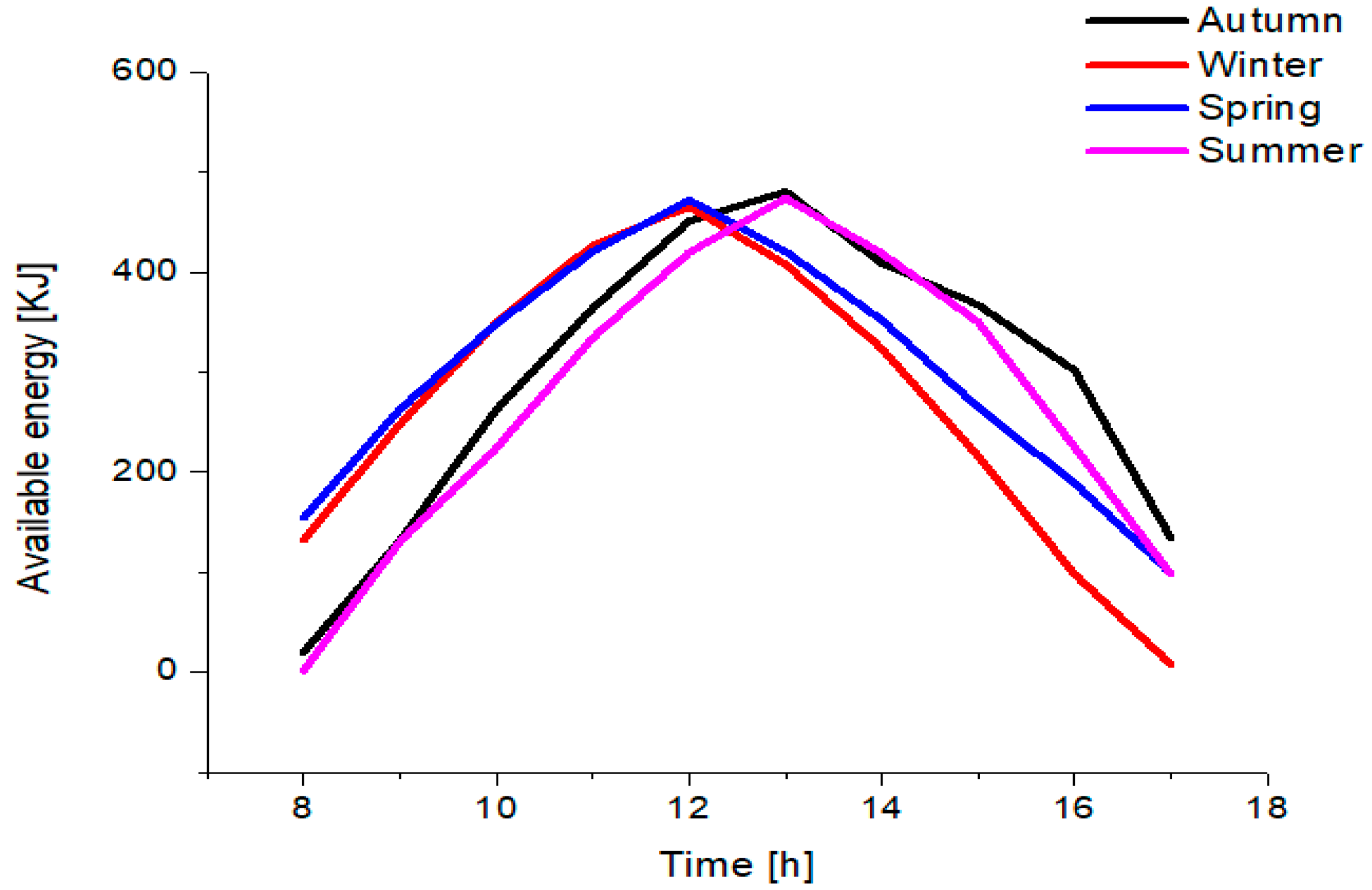
Figure 2b–d, all tilted anticlockwise with respect to east view. This involves four adjustments a year in three different angular positions. With these data, an analysis campaign was carried out, with the respective seasonal tilted adjustment.
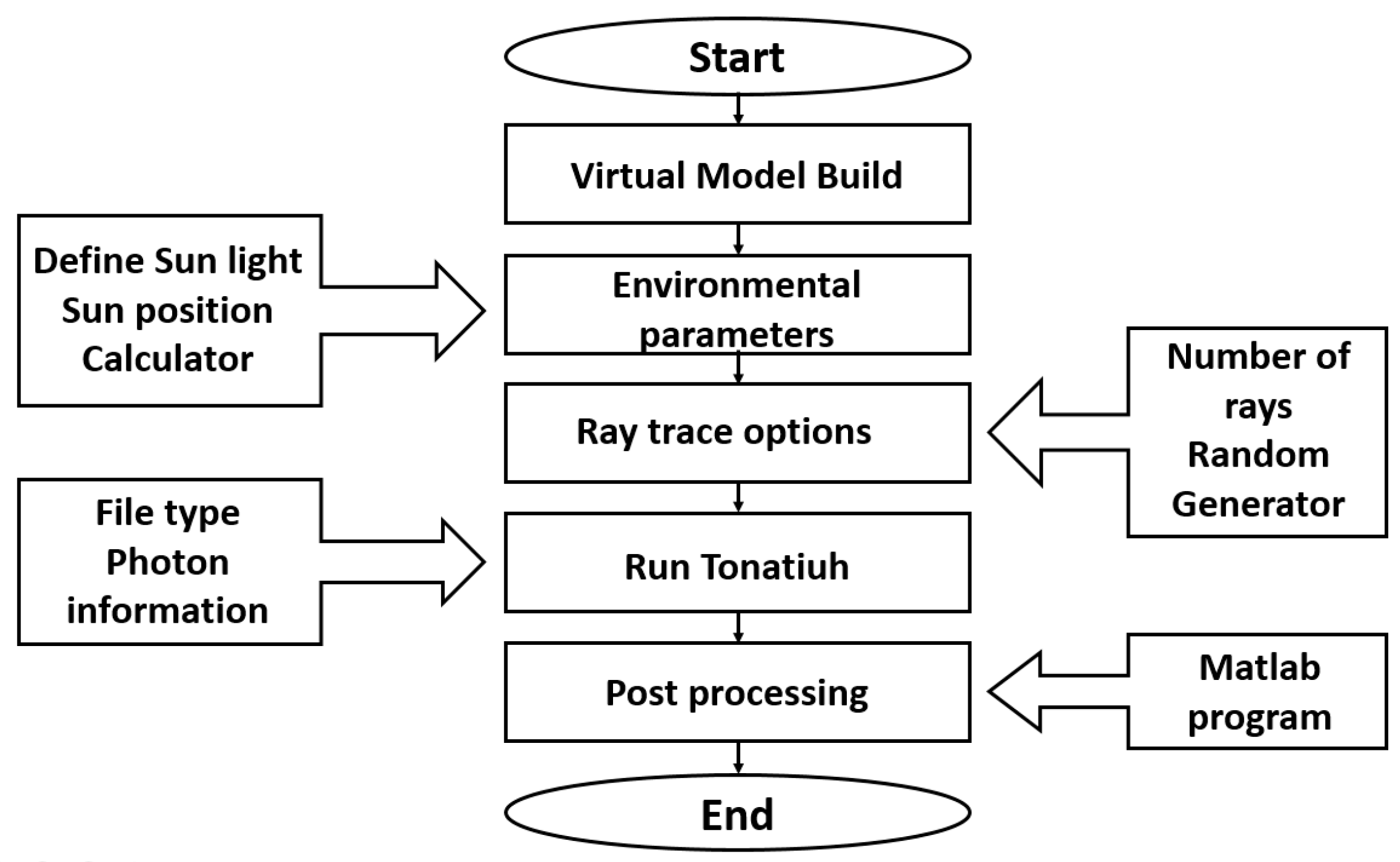
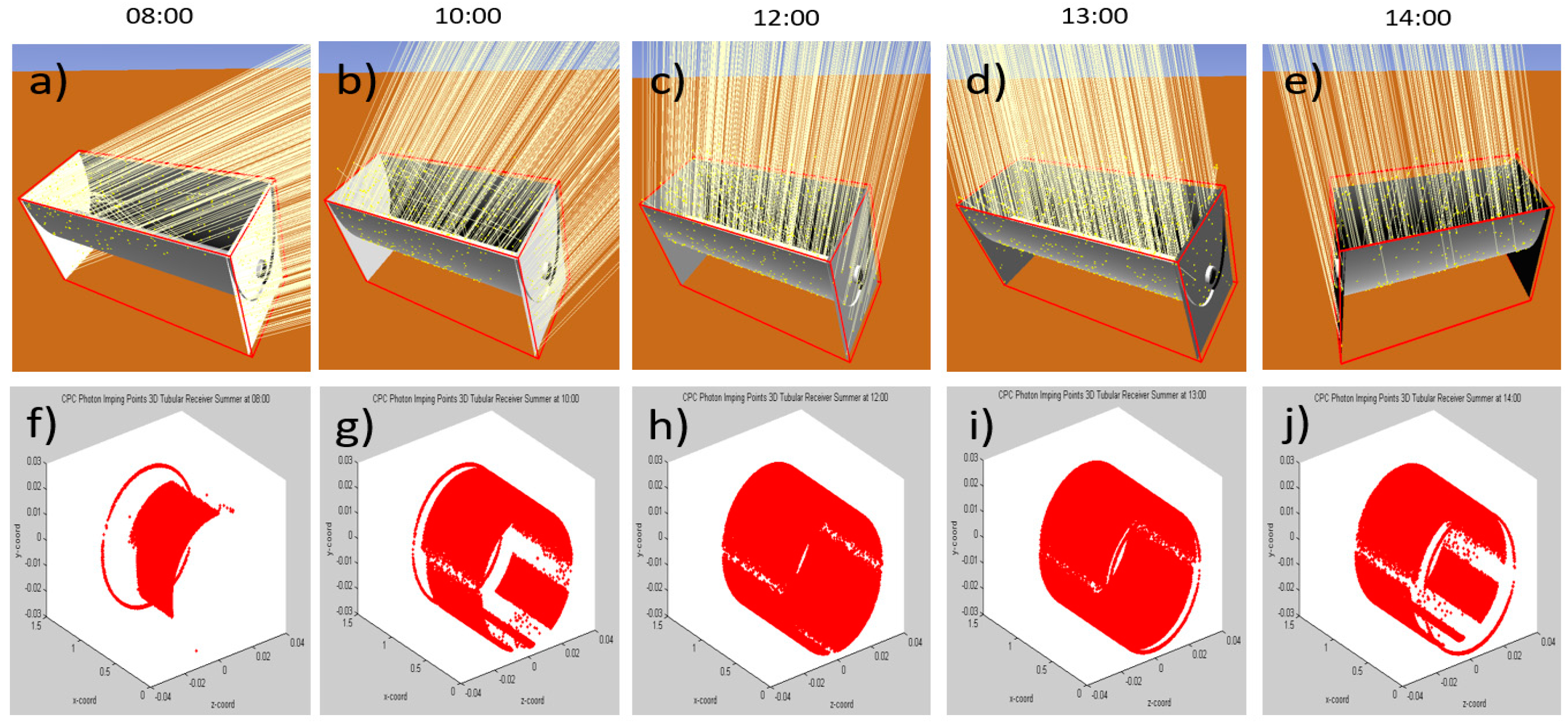
The ray tracing evaluation period was carried out from 8 to 17 h local time. A flowchart of the analysis is shown in
Figure 3. From the determination of the concentration ratio (
CR) and external diameter of the selected tube, the virtual model is generated, assigning the concentrator and receiver optical properties; subsequently, the environmental parameters are adjusted, which indicate the sun shape, time, and date, for the following random generator and the number of rays. Then we set the receiver type as the target, and the data is stored for further processing with mathematical algorithm software.
Tonatiuh ray tracing software has a fixed sunshape, with the shape of the sun being understood as the variation in the radial energy distribution of the sun derived from its consideration as a non-point light source. There are two techniques to evaluate this: Pillbox and Buie, both were evaluated using the same weather conditions (season, radiation, and time value). The results obtained are shown in
Table 2, where values in Pillbox are slightly higher than in Buie, with the highest difference corresponding to spring with 9.36 kJ (0.31%) and the lowest difference corresponding to autumn with 3.39 kJ (0.11%), indicating that no significant differences were found. Further analysis was conducted with the multi-position setup in order to prove the similarity response, finding an agreement in all cases.
Since both techniques gave similar results, for this study the Pillbox sunshape was chosen due to the simplicity of its process. Although Tonatiuh software used here has the capability to carry out a complete analysis with irradiation variations, in this work we are using a fixed irradiation value of 1000 W/m
2 as a constant, to simplify the analysis and concentrate on the comparative evaluation of the optical design and the variables such as the influence of the orientation angle throughout the year, in order to evaluate the feasibility for the system to be fixed in a static position or if this requires angle adjustments throughout the year. The importance of this comparative study is to determine whether the CPC could perform satisfactorily in a fixed position throughout the year (or need periodical adjustments), which could make it more attractive for its implementation (in static position). In all cases, the equinoxes of spring and autumn are taken into account, as well as the summer and winter solstices. Since the highest and lowest apparent positions of the sun in the sky are reached in the solstice, the maximum is in summer with the angle of −4.27° and the lowest in winter with the angle of 42.16°, both with respect to the vertical; subsequently, the location coordinates were considered. This allows us to calculate the angular parameters, azimuth, and elevation angle in the study. In order to obtain a confidence level of 97%, according to Blanco [
29], a ray tracing of 1,000,000 rays was chosen for the analysis.
Data generated from the ray trace software requires the designing of a post-processing algorithm for data analysis. A MATLAB (R2016a, MathWorks, Natick, MA, USA) algorithm was designed to identify data from sun photons and to classify them as primary, secondary (by rebound), tertiary, etc., in order to provide numerical values (ID, coordinates, power per photon, etc.) and the location of photon impact on the receiver.
2.4. Optical Modeling
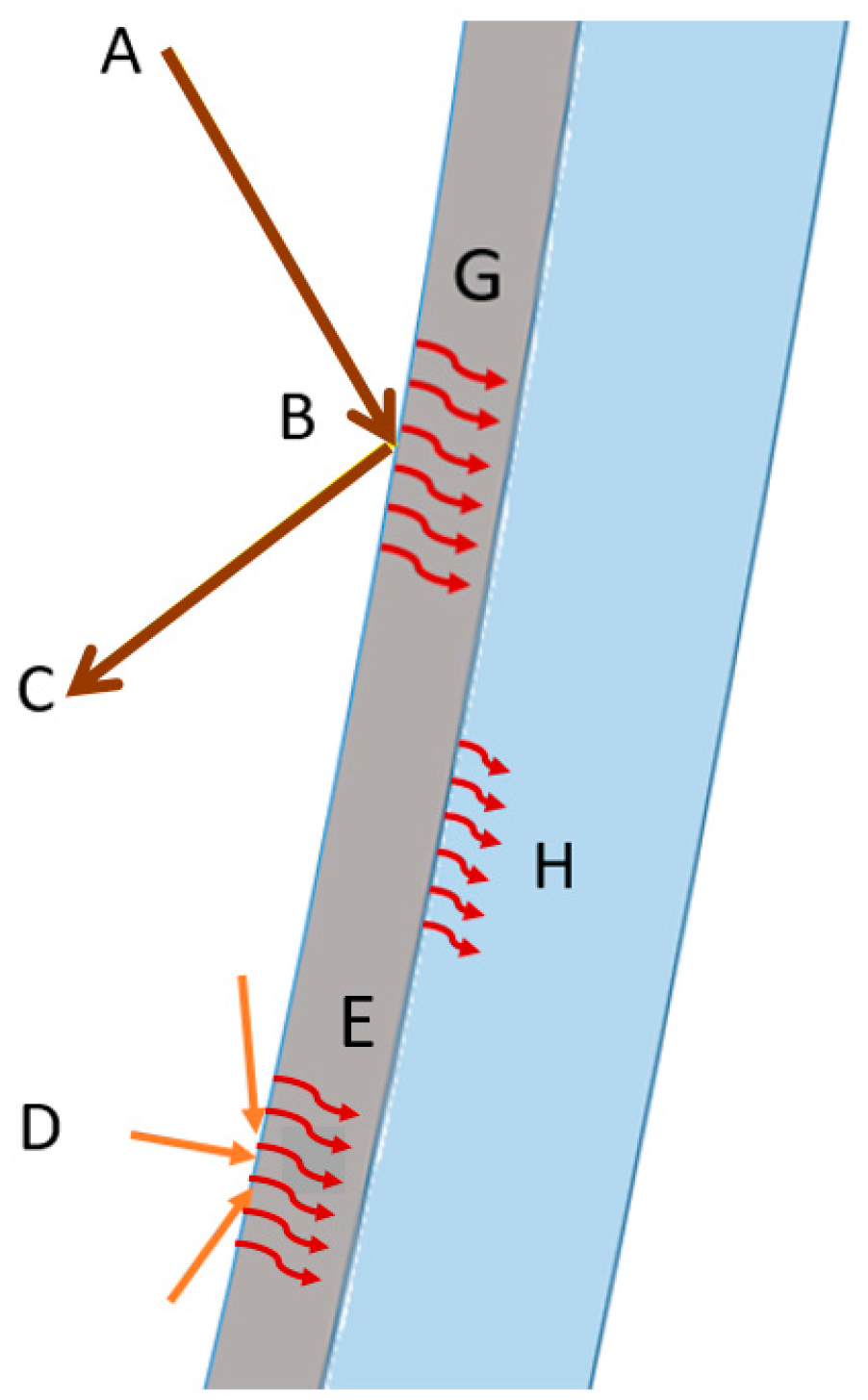
The importance of the optical analysis lies in the fact that it provides information regarding the available energy at the receiver. The input energy was determined using the ray tracing tool and evaluating the energy distribution by incident beam radiation on the collector surface, as represented in
Figure 4. The beam radiation follows the path A, B, C, where A and C comply with Fresnel’s law, and B is the energy absorbed by the concentrator. If the angle and energy value of the photon coming from the sun are known (in addition to specular properties of the concentrator), we can determine the path that it follows, impinging the receiver or leaving it out, thereby determining the energy that the receiver reaches.
If the diffuse radiation is taken into account, it is important to consider that the energy and impact angle of a photon is difficult to estimate, since the path depends on the particles present in the atmosphere with which it may impact (dust, water steam, and aerosol), therefore the trajectory and the energy can be affected by the constantly changing environmental composition, making it difficult for the program to predict the amount of diffuse energy aligned to the receivers direction. It is important to consider that diffuse radiation can contribute up to 50% of the energy available in a CPC with a concentration ratio of one (CR = 1), particularly on cloudy days. This study is based on clear skies, where diffuse radiation is low compared to beam radiation and a value of CR equal to 1.41, which minimizes its contribution. Also, given that the objective of this system is to heat water for residential use, beam radiation is way more effective.
In the same
Figure 4, D represents the diffuse trajectory, with different energy path and angle of incidence in comparison with A. In the same way, E is the diffuse energy absorbed by the concentrator, G represents the beam energy absorbed by the concentrator, and H is the energy transferred from the concentrator to the insulation material [
30].
To determine the available energy at the receiver, a virtual model is proposed which takes into account the properties of the materials (concentrator, receiver, covers) as well as dimensions, system configuration, position of the sun, and the amount of available solar irradiation.
For this study, the following assumptions were made:
- (1)
The CPC geometric concentration ratio (
CR) is expressed using the formula used by Hsieh [
31]:
- (2)
The system is considered to be free of manufacturing errors.
- (3)
The physical and optical properties of the materials are assumed to be temperature independent.
- (4)
The geographical coordinates correspond to the city of Merida, Mexico (21.0291° N, 89.6381° W).
Once the virtual model is implemented, with the characteristics of sun and materials introduced, the energy availability at receiver can be obtained.
2.5. Ray Tracing Analysis
The ray tracing software is based on the Monte Carlo method. It uses the principles of geometric optics, as well as a statistical method that simulates the behavior of a solar concentration system, by generating rays from a simulated source and observing the interactions between the rays and the surfaces of the system. It is conceived as a useful tool in the design and analysis of solar concentration systems [
32].
For the analysis, it is assumed that the ray trajectory equals the angle of incidence and the reflected radiation (
R); that is, they comply with the Fresnel law. In this sense, the spectral reflectance depends on the reflective material with its refractive index. Before proceeding, it was necessary to determine the incidence angle of the rays (
I); this angle is formed between the normal surface (
N) and the incident radiation. In order to establish the ray tracing model, the following equation of reflected radiation is used [
33]:
To facilitate the analysis, this is decomposed into Cartesian coordinates, applying the following equations:
where:
The incident angle for reflected radiation can be determined by:
In practice, real surfaces are far from ideal; they are related to solar wavelength λ and incidence angle
θi (specular reflection). The specular reflection is subjected in the same way to Fresnel’s law; which can be determined by the following equation [
33]:
where
and
, refers to the perpendicular and parallel reflectivity, determined by the following equations:
2.6. Experimental Evaluation
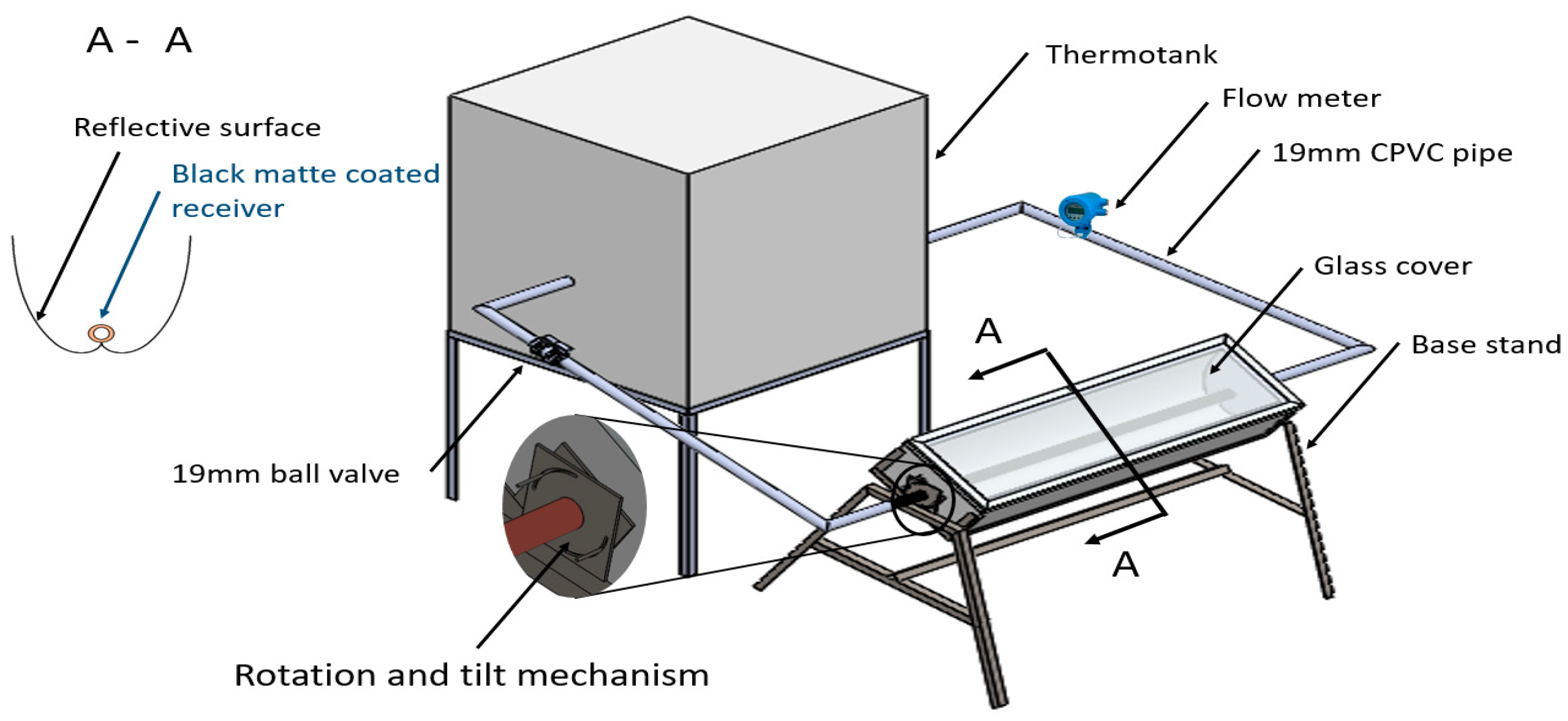
The proposed prototype was constructed to evaluate its feasibility, which is represented in
Figure 5. The system uses a heat isolated metallic box (with polyurethane) to support and hold the receiver tube; the walls of the box also help to avoid heat exchange between the receiver and the ambient. In addition, a commercial 4 mm thick, flat glass cover was placed on top to reduce convective heat losses to the environment, and mainly due to the influence of constant air currents.
The concentrator was designed with 95% high reflectance aluminum (specular reflectivity), according to the American Standard Test Methods; ASTM STP478 (Specular and Diffuse Reflectance Measurements of Aluminum Surfaces), where the incident ray on this surface is reflected at the same angle of incidence with respect to the normal surface. The values of the optical properties of the materials are shown in
Table 3.
Thermal efficiency for the experimental evaluation was obtained using the following equation:
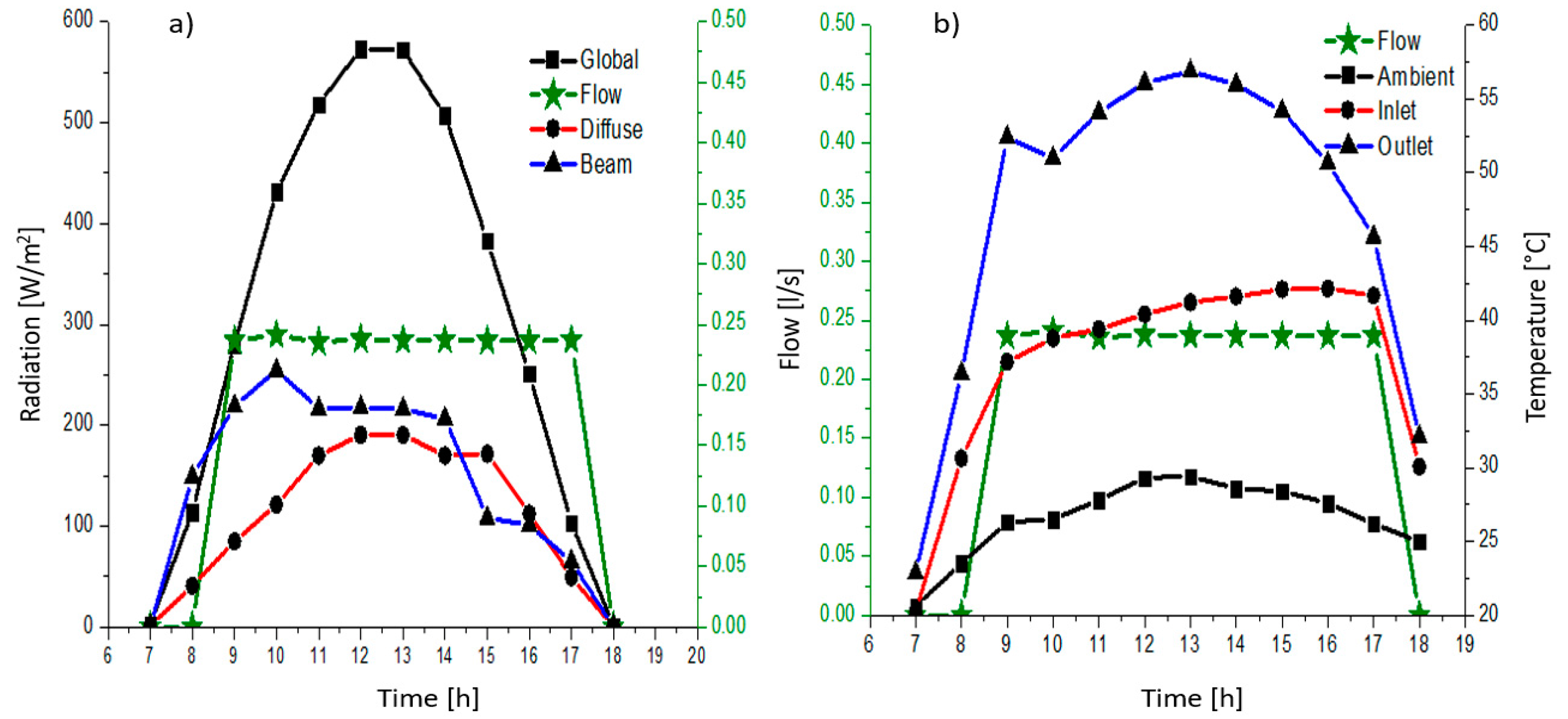
In order to speed up the thermosiphon effect and reduce the scale accumulation in the receiver wall (at higher temperatures), which interferes with the heat transfer process and, in consequence, reduces the efficiency; a 3 W submersible solar pump was installed in the system, which provides a maximum flow of 0.05 L/s, reporting this way, a ∆T of 7 °C between inlet and outlet of receiver. For these conditions, if the internal diameter is reduced, the flow velocity of the fluid used, increases, which directly results in a reduction in the temperature difference between inlet and outlet. On the other hand, if the diameter increases, the material and therefore the cost, also increases. Consequently, it was decided to evaluate a CPC using a copper receiver with 54 mm external diameter (51 mm internal diameter), coated with matte, non-selective, high-temperature black paint.
A complete CPC was constructed using the following dimensional parameters: 0.24 m aperture width, 0.19 m height and 1 m length, with an acceptance angle of 45°, which correspond to a concentration ratio of 1.41 [
31]. The theoretical temperature of the thermodynamic limit for this concentration ratio is 156.5 °C [
34]. However, this presents some challenges to take into account; the manufacture of a complex involute and cup profile, with a high reflective material (thin sheet of aluminum) high cost of materials and greater energy demand for heating the fluid due to volume increase.
4. Conclusions
This paper presents a prediction tool to analyze the energy performance of a CPC system under different working conditions over a seasonal year. Here, setups in two modalities were evaluated: stationary and multi-position. The analysis was performed using a ray tracing software and a mathematical algorithm software for data processing. The tool proved to be useful to estimate the maximum theoretical energy present in the solar collector, to study the relevant optical–structural response and to determine the strength and weakness of a prototype before its construction. Adverse conditions such as winter can be predicted, and adjustments can be made to adequate the CPC design prior to its construction. The annual energy distribution in the receiver was analyzed, and it proved to be useful for predicting the energy availability, allowing the implementation and use of strategies to reduce heat losses, based on the ideal conditions.
From this study, with the data provided theoretically, it was possible to determine that, with the use of the multi-position setup of the CPC throughout the year, the energy availability was 22% more than the static setup, resulting in a more attractive alternative. Therefore, the multi-position setup can be taken into consideration as part of a further study for an improved system construction and its validation.
Complementary to the theoretical analysis, an implementation and evaluation of a CPC was carried out. With the experimental test conducted, it was proven that it is possible to obtain temperatures corresponding to residential use with a CPC of reduced dimensions, thus providing feasibility, when compared to other collectors such as FPH—an option with reduced materials and possible reduced manufacturing time and costs, too. Further works are needed for technical improvements.