2. Proposed Converter
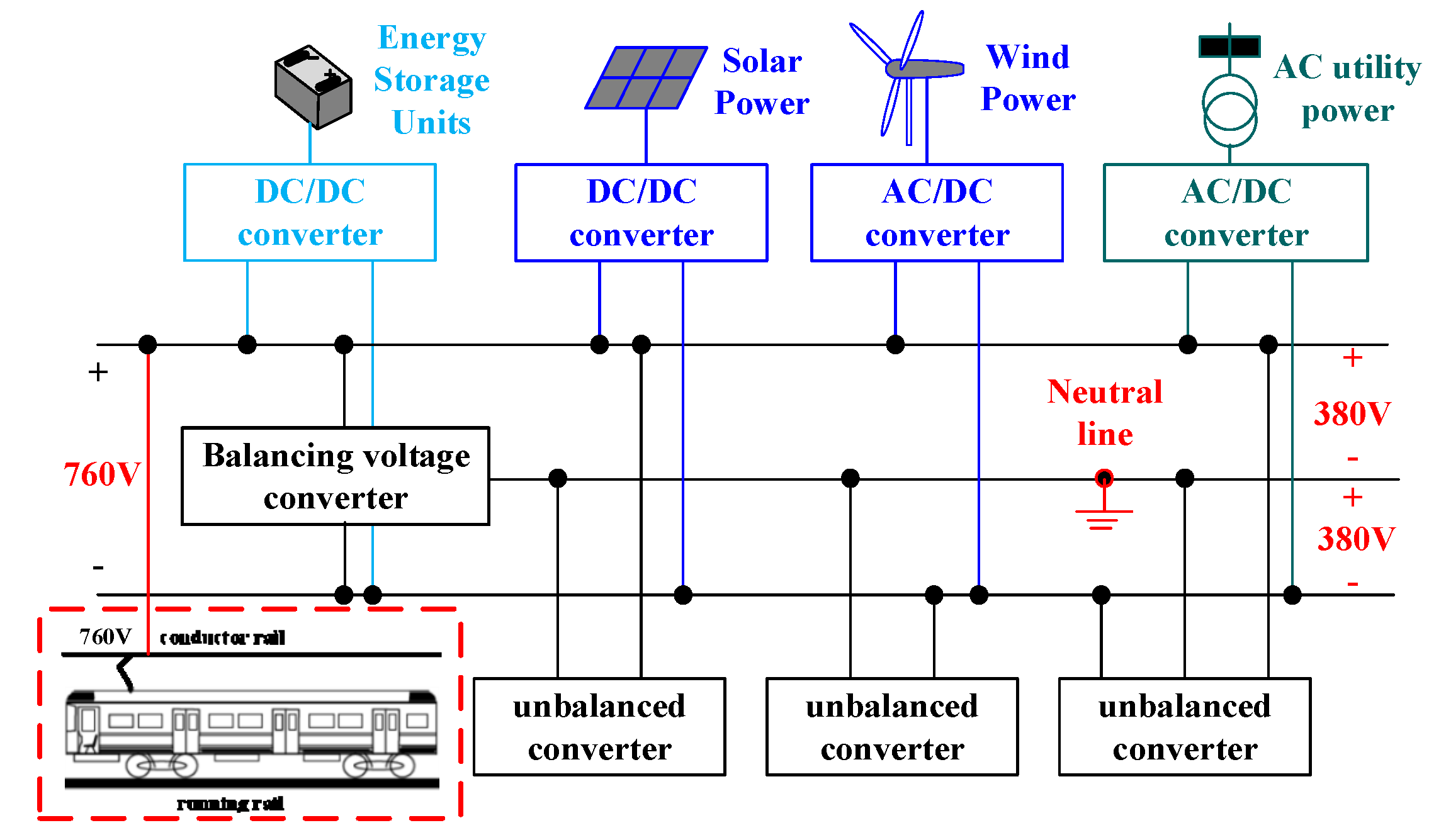
The basic circuit structure of a DC microgrid is given in
Figure 1. The bidirectional AC/DC converters are used between the AC utility system and the DC microgrid to stabilize the DC bus voltage. Renewable energy sources from solar cell panels and wind power generators provide clear energy to the DC microgrid system through the unidirectional DC/DC converters and the AC/DC converters. Energy storage units are used to store/release energy from/to the DC microgrid through the bidirectional DC/DC converters in order to stabilize the DC bus voltage. In order to increase the voltage reliability, the bipolar voltage system (+
Vdc, −
Vdc and neutral line) can be adopted on the DC microgrid. When a fault condition in one of the DC poles occurs, the DC power is still suppled to the local load by the other two wires and an auxiliary converter. It is clear that the reliability of the DC mircogrid system is increased during fault condition. Therefore, three voltage levels (2
Vdc, +
Vdc and −
Vdc) can be used to provide industry and transportation with the 2
Vdc voltage level and future residential and commercial buildings with the +
Vdc or −
Vdc voltage level. To keep two voltage levels (+
Vdc and −
Vdc) balanced during unbalanced loads, a voltage balancing circuit is normally needed to realize this goal. The DC/DC converter can be used to convert a high input voltage to a low output voltage and it does not relate to the bipolar voltage system. For a DC light rail vehicle, the input voltage is normally around 760 V. Power devices such as the 1500 V IGBT can be adopted in two-level power converters to supply auxiliary low voltage power for control units, telecommunication units and lighting systems in the light rail vehicle. The MOSFETs with a 600 V rating can be adopted in the three-level power converter to achieve the same goal but with a much higher switching frequency to reduce converter size. The studied converter is concentrated on power conversion for light rail vehicle applications.
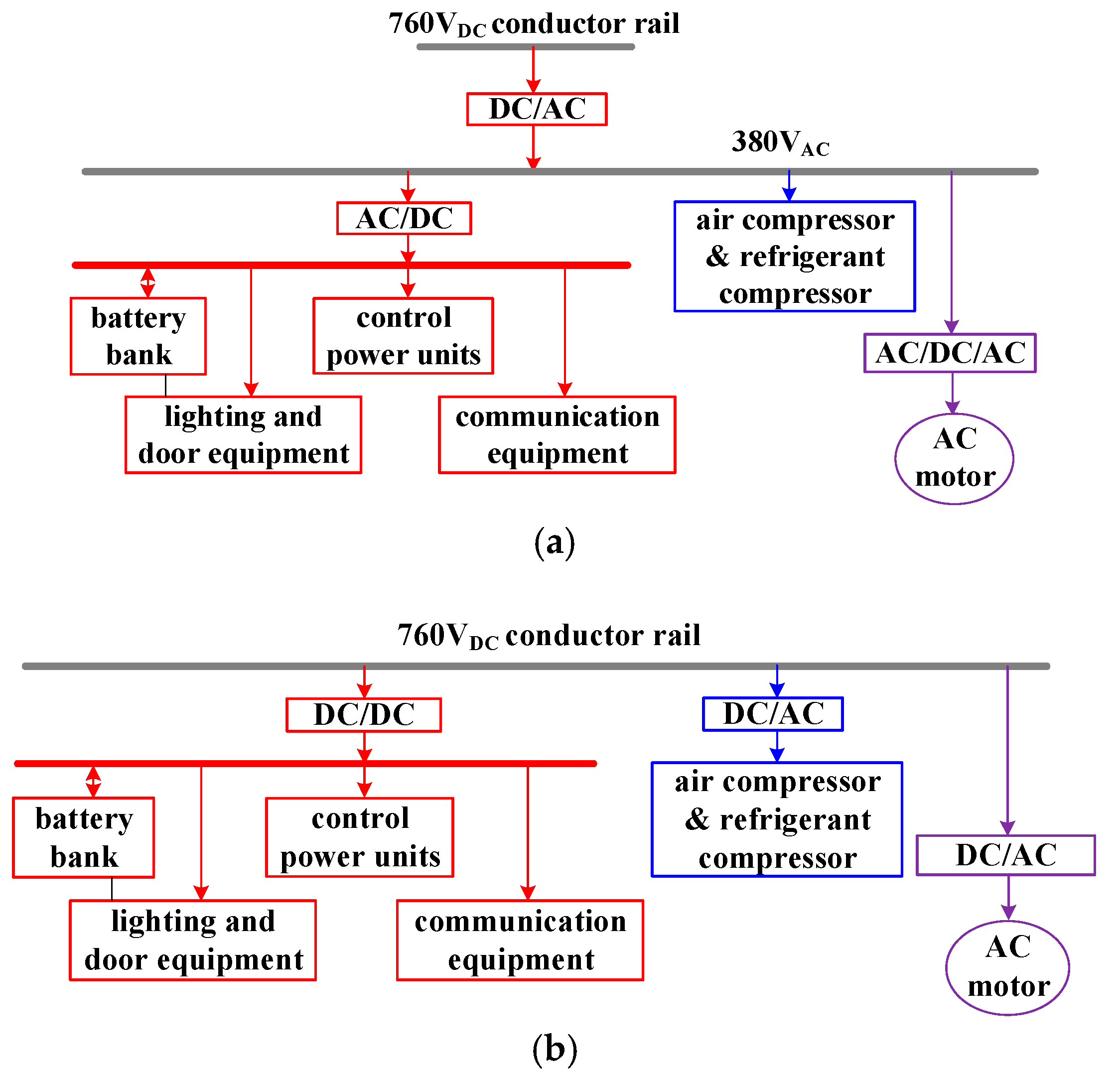
Figure 2a shows the basic block diagrams of power distribution in a conventional light rail vehicle. First, 750
Vdc is converted to the three-phase AC voltage 380
Vac by the DC/AC inverter. Second, the AC/DC converter is adopted to convert 380
Vac to a low DC voltage in an auxiliary power distribution system to supply a necessary amount of DC voltage for the battery bank, lighting equipment, door equipment, control power units and communication equipment in a light rail vehicle system. The AC/DC/AC converter is also adopted to convert 380
Vac to a variable AC voltage output for the AC motor drive. If the power of the DC light rail vehicle is supplied directly from the DC microgrid, then some power conversion stages can be saved to reduce costs and increase circuit efficiency. The basic power distribution diagrams in the proposed light rail vehicle are illustrated in
Figure 2b. The auxiliary power in a light rail vehicle is directly converted from 760 V through a DC/DC converter. The AC motor drive and the air compressor are controlled by the DC/AC converters. Therefore, the AC/DC conversion can be saved to reduce costs and increase circuit efficiency and reliability.
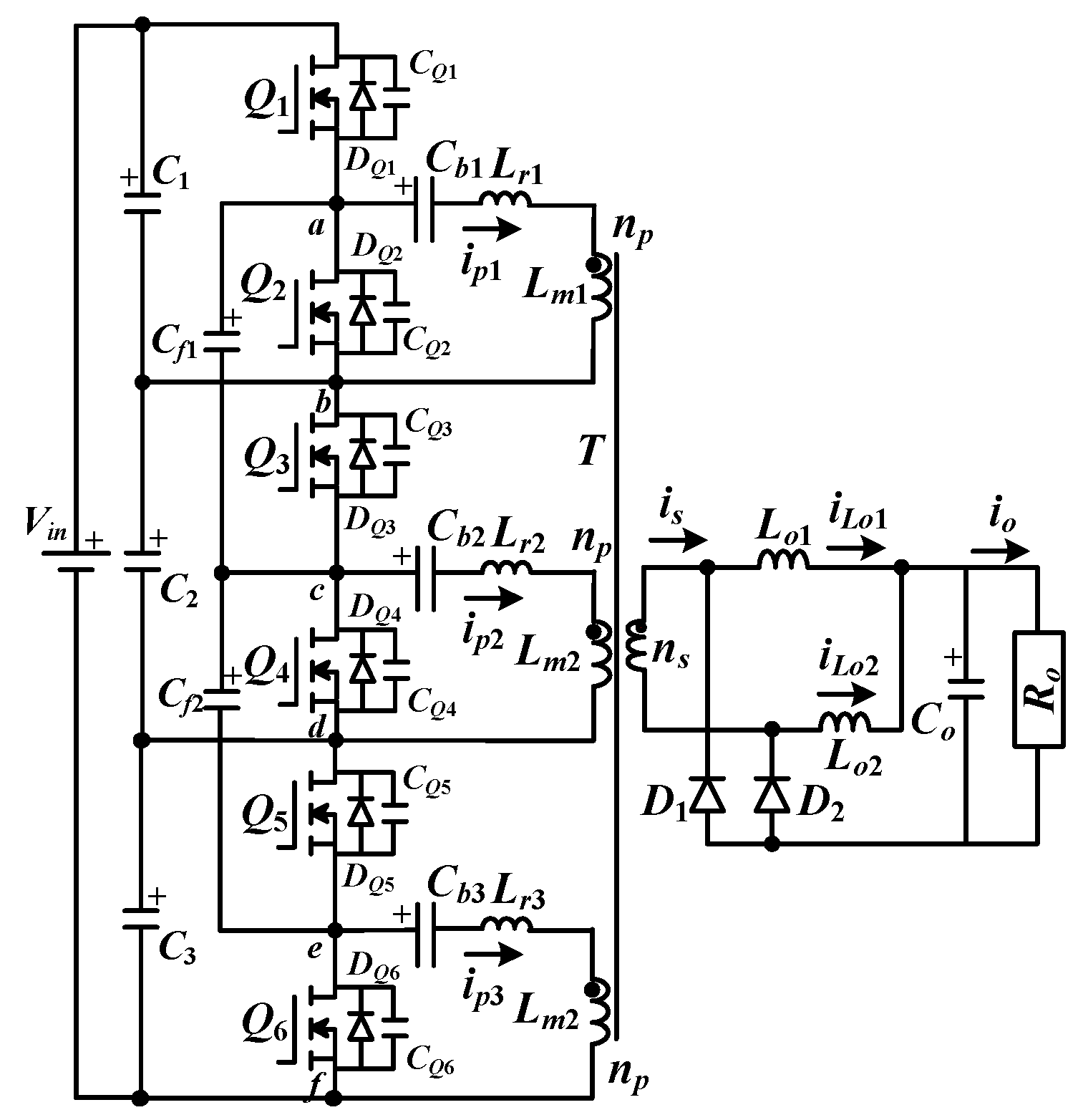
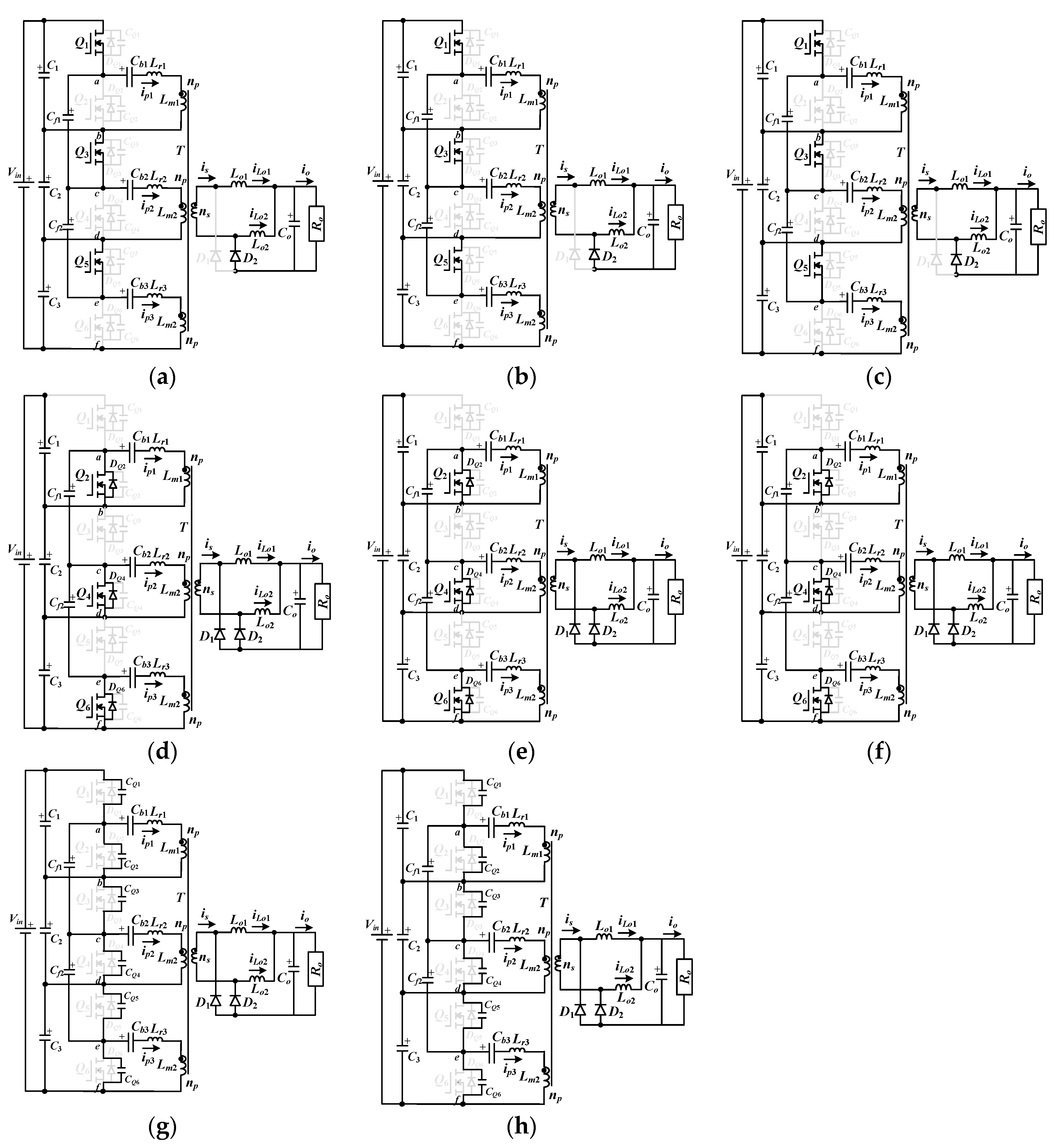
The studied DC/DC converter is given in
Figure 3. It directly converts a 760 V voltage input from the DC microgrid to a low voltage output by using low voltage rating power MOSFETs to provide auxiliary power in a light rail vehicle. The studied converter includes three HB circuits connected in a primary-series secondary-parallel with a single transformer. The primary sides of the HB circuits are connected in a series so that the voltage stress of the power switches
Q1~
Q6 is reduced to
Vin/3 and the low turn-on resistance of power MOSFETs is adopted to reduce conduction losses and increase circuit efficiency. Each HB circuit provides
Po/3 to the output load. Flying capacitors are widely used in a multilevel inverter to reduce voltage stress and balance input split voltages. Thus, two flying capacitors
Cf1 and
Cf2 are used on the high voltage side to achieve an input voltage balance of
VC1~
VC3. The current doubler rectifier is used on the low voltage side to reduce the output ripple current. The driving signals of each HB circuit use asymmetric pulse-width modulation. Due to the resonant behavior between the output capacitor of the power MOSFETs and the primary leakage inductor at switch on/off instant, the power MOSFETs can be turned on at zero-voltage switching to reduce the switching loss.
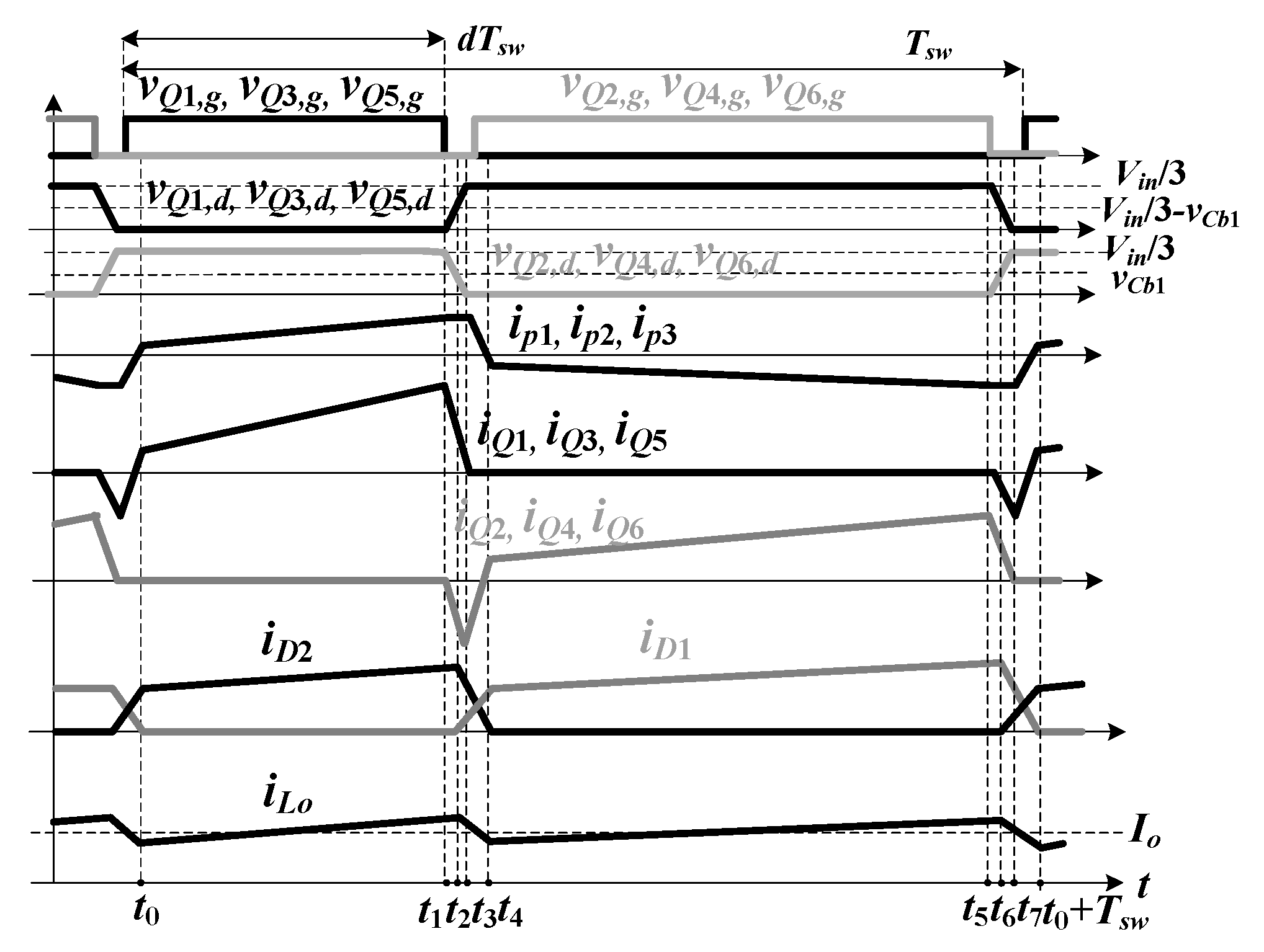
Figure 4 shows the timing sequence of switches
Q1~
Q6 and the main PWM waveforms in the proposed converter. The operation principle and circuit analysis of the studied circuit are assumed under the following conditions: (1) the output capacitor
Co is large enough to be treated as a constant voltage
Vo, (2) power devices
Q1~
Q6,
D1 and
D2 are ideal, (3)
Cf1 =
Cf2 =
Cf,
Cb1 =
Cb2 =
Cb3 =
Cb,
Lr1 =
Lr2 =
Lr3 =
Lr, and
Lm1 =
Lm2 =
Lm3 =
Lm, (4)
n1 =
n2 =
n3 =
np/
ns, and (5)
VCb1 =
VCb2 =
VCb3 =
VCb and
VC1 =
VC2 =
VC3 =
VCf1 =
VCf2 =
Vin/3. The duty cycles of
Q1,
Q3 and
Q5 are
d. Conversely, the duty cycles of
Q2,
Q4 and
Q6 are 1 −
d. The equivalent circuits of the operating steps in the proposed circuit are shown in
Figure 5. There are eight operating stages for every switching period.
Step 1 [t0~t1]: Before step 1, power switches Q1, Q3 and Q5 are conducting and the output current freewheels through D1 and D2. After time t0, iD1 is decreased to zero and D1 becomes reverse biased. io flows through D2. Power is transferred from Vin to Ro in this step. In step 1, VCf1 = VC1, VCf2 = VC2, vQ2,ds = VC1, vQ4,ds = VC2, vQ6,ds = VC3, vLm1 ≈ VC1 − vCb1, vLm2 ≈ VC2 − vCb2, vLm3 ≈ VC3 − vCb3, and . Thus, ip1~ip3 and iLo1 increase and iLo2 decreases. Since all circuit components in three HB circuits are identical and n1 = n2 = n3 = np/ns, it can obtain vLm1 = vLm2 = vLm3 = nvns and ip1 = ip2 = ip3 ≈ is/(3n1). Since iLo1 increases and iLo2 decreases in this step, the ripple current of iLo1 + iLo2 is reduced.
Step 2 [t1~t2]: When Q1, Q3 and Q5 are turned off at time t1; the positive primary currents ip1~ip3 rapidly discharge CQ2, CQ4 and CQ6, respectively. On the other hand, CQ1, CQ3 and CQ5 are charged by ip1~ip3 respectively. The secondary winding voltage vns is decreased in this step.
Step 3 [t2~t3]: When CQ2, CQ4 and CQ6 are discharged to vCb1, vCb2 and vCb3 respectively, then the secondary winding voltage vns = 0. Then the output current io freewheels through D1 and D2. In this operation step, vLo1 = vLo2 = −Vo and iLo1 and iLo2 decrease.
Step 4 [t3~t4]: At time
t3,
CQ2,
CQ4 and
CQ6 are discharged to zero voltage. Since
ip1(
t3)~
ip3(
t3) are all positive, the body diodes
DQ2,
DQ4 and
DQ6 are forward biased. Therefore,
Q2,
Q4 and
Q6 can be turned on at this moment to realize a zero-voltage turn-on. Because
io is still freewheeling through
D1 and
D2, it can obtain
vns = 0,
vLo1 =
vLo2 = −
Vo,
vLr1 = −
vCb1,
vLr2 = −
vCb2 and
vLr3 = −
vCb3.
ip1~
ip3,
iLo1 and all
iLo2 decrease. This step is ended when
iD2 = 0. During this freewheeling interval, the currents
iLr1~
iLr3 are decreased from
iLo1/(3
n1) to −
iLo2/(3
n1) and the current variation on
Lr1~
Lr3 is about
Io/(3
n1). The duty loss in step 4 is obtained as (1) shows:
Step 5 [t4~t5]: After t4, iD2 is decreased to zero so that D2 is reverse biased. io flows through D1, Lo1 and Lo2. In step 5, power is transferred from Vin to Ro, VCf1 = VC2, VCf2 = VC3, vQ1,ds = VC1, vQ3,ds = VC2, vQ5,ds = VC3, vLm1 ≈ −vCb1, vLm2 ≈ −vCb2, vLm3 ≈ −vCb3, and . Thus, ip1~ip3 and iLo1 decrease and iLo2 increases.
Step 6 [t5~t6]: When Q2, Q4 and Q6 turn off at time t5, the negative primary currents ip1~ip3 rapidly charge CQ2, CQ4 and CQ6, respectively. On the other hand, CQ1, CQ3 and CQ5 are discharged by ip1~ip3 respectively. The secondary winding voltage vns is increased in this step.
Step 7 [t6~t7]: When CQ2, CQ4 and CQ6 are charged to vCb1, vCb2 and vCb3 respectively at t6, it can obtain vns = 0. Thus, io freewheels through D1 and D2 in this step and vLo1 = vLo2 = −Vo.
Step 8 [t7~t0 + Tsw]: When
CQ1,
CQ3 and
CQ5 are discharged to zero voltage at
t7, the body diodes
DQ1,
DQ3 and
DQ5 are forward biased. Power switches
Q1,
Q3 and
Q5 can be turned on at this moment to realize zero-voltage turn-on. Since
io still freewheels through
D1 and
D2, it can obtain
vns = 0,
vLo1 =
vLo2 = −
Vo and
vLr1 =
vLr2 =
vLr3 =
Vin/3 −
vCb1. Thus,
ip1~
ip3 increase and
iLo1 and
iLo2 decrease. This step is ended when
iD1 = 0. During this freewheeling interval,
iLr1~
iLr3 increase from −
iLo2/(3
n1) to
iLo1/(3
n1). The duty loss in step 8 is obtained as (2) shows.
At time t0 + Tsw, iD1 is decreased to zero and this switching period is completed. Since the duty cycle of all switches equals 0.5, the voltage balance of C1, C2 and C3 is well achieved with two balance capacitors Cf1 and Cf2. If Q1, Q3 and Q5 are in the on-state and Q2, Q4 and Q6 are in the off-state, it obtains vCf1 = VC1 and vCf2 = VC2. If VC1 > VC2 or VC1 < VC2, then C1 charges or discharges Cf1 through Q1 and Q3. When Q1, Q3 and Q5 are in the off-state and Q2, Q4 and Q6 are in the on-state, it obtains vCf1 = VC2 and vCf2 = VC3. If VC1 > VC2 or VC1 < VC2, Cf1 charges or discharges C2 through Q2 and Q4. In a similar way, Cf2 can be used to balance VC2 and VC3. Therefore, VC1~VC3 are all controlled at Vin/3.
3. Circuit Characteristics
The asymmetric PWM scheme is adopted to drive
Q1~
Q6. Based on the flux balance of primary inductors such as (
Lr1 and
Lm1), (
Lr2 and
Lm2) and (
Lr3 and
Lm3), the DC capacitor voltages
VC1~
VC3 in a steady state can be obtained as
, where
d is the duty cycle of
Q1,
Q3 and
Q5. In the same way, the output voltage can be derived from the flux balance of output inductors
Lo1 and
Lo2 in a steady state.
where
Vf is the voltage drop on
D1 and
D2.
Since the average winding currents
ip1~
ip3 equal zero and
ILo1 +
ILo2 =
Io, the average inductor currents
ILo1 and
ILo2 are derived as
ILo1 = (1 −
d)
Io and
ILo2 =
dIo. The ripple currents on
Lo1 and
Lo2 are given in (4) and (5).
The asymmetric PWM is adopted to regulate load voltage. From
Figure 4, the turn-on time of
D1 is related to the duty cycle of
Q2 and the turn-on time of
D2 is related to the duty cycle of
Q1. Therefore, the average diode currents
ID1 and
ID2 are expressed as
ID1 = (1 −
d)
Io and
ILo2 =
dIo. The voltage stress of diodes
D1 and
D2 is related to the secondary winding voltage. The secondary winding voltage
vns is dependent on the input voltage
Vin and clamped voltage
VCb1. Thus, the voltage stress of
D1 and
D2 can be given in (6) and (7).
The conduction losses on rectifier diodes
D1 and
D2 are approximately equal to
IoVf. If the transformer is constructed, then the magnetizing inductances
Lm1~
Lm3 are given. Thus, the ripple currents
iLm1~
iLm3 are obtained in (8).
Three HB circuits are connected in a series on the high voltage side to reduce the voltage stress of active switches. Therefore, it is able to obtain the voltage stress of each active switch clamped at
Vin/3. If the ripple currents on magnetizing inductors and output inductors are neglected, the root-mean-square (
rms) currents
iQ1,rms~
iQ1,rms can be derived as (9) and (10) show.
The conduction losses on
Q1~
Q6 are approximately equal to
, where
Ron is turn-on resistance of
Q1~
Q6. The positive peak currents of
ip1~
ip3 at time
t1 are given in (11).
Likewise, the negative peak currents of
ip1~
ip3 at time
t5 are given in (12).
The minimum primary current to realize zero-voltage turn-on switching of
Q1,
Q3 and
Q5 is given in (13).
Similarly, the minimum primary current to realize zero-voltage turn-on switching of
Q2,
Q4 and
Q6 is given in (14).
where
CQ =
CQ1 =
CQ2 =
CQ3 =
CQ4 =
CQ5 =
CQ6.
4. Experimental Results
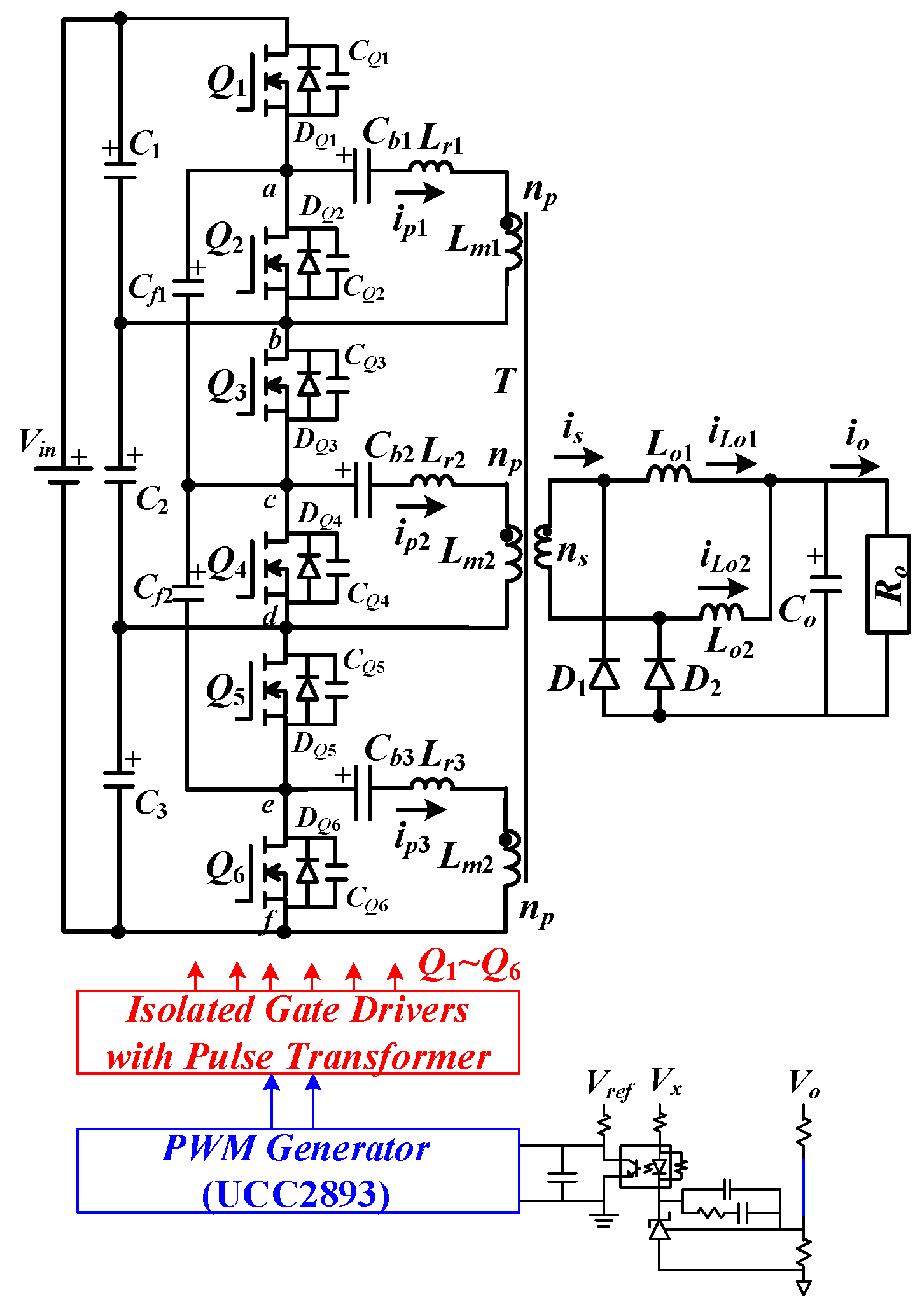
A laboratory prototype with 1.44 kW rated power was constructed and tested in order to verify the feasibility of the studied converter to supply the auxiliary power in a light rail vehicle from the DC microgrid system. The experimental circuit diagram of the developed converter is provided in
Figure 6. The TL431 voltage regulator and photocoupler PC817 are used to regulate load voltage. The PWM UCC2893 is used to achieve asymmetric pulse-width modulation (APWM) generation. Pulse transformers are adopted to achieve electrical isolation and gate drive. The specifications of the experimental prototype are given in
Table 1. The power rating of the magnetic transformer is the same as the transformer in the three-level converter and the two-level full-bridge converter. The turns-ratio of the transformer in the developed converter is one-third of the turns-ratio in the two-level full-bridge converter. The magnetizing voltage and primary turns of the transformer in the studied converter are only one-third of the magnetizing voltage and primary turns in the two-level full-bridge converter. The PC40 EER-42 magnetic core is used with 15 primary turns and 8 secondary turns to build the isolated transformer. The experimental results of the proposed converter while it supplies 1.44 kW to the output load under a 760 V input are shown in
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11 and
Figure 12. Based on the test results, the measured waveforms agree well with the theoretical waveforms as given in
Figure 4.
Figure 7 shows the gate voltages of
Q1~
Q6 at 20% and 100% loads. It is clear that
Q1,
Q3 and
Q5 have the same PWM waveforms. In the same manner,
Q2,
Q4 and
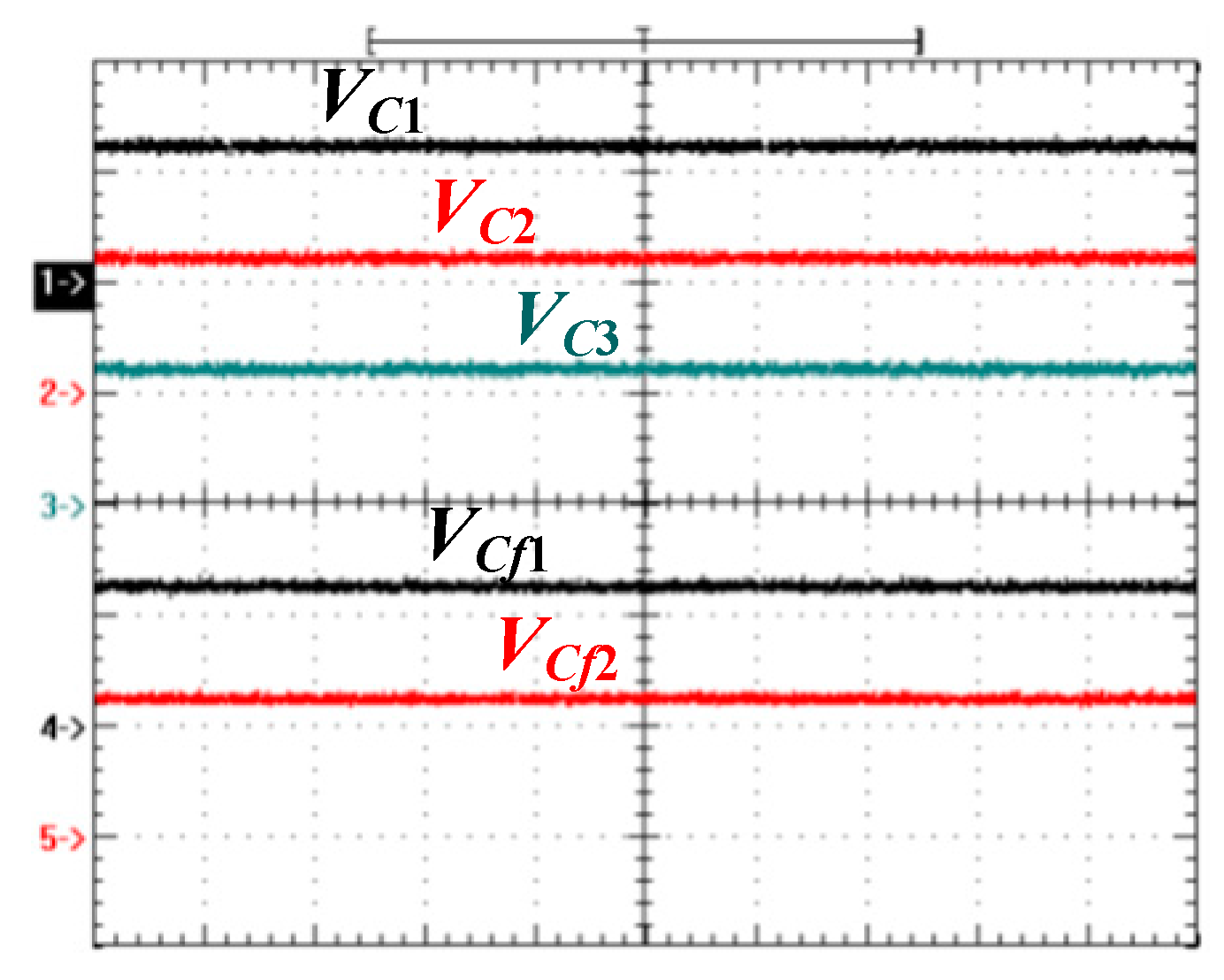
Q6 have the same PWM waveforms. The input split voltages and balance capacitor voltages at a full load are shown in
Figure 8. From the experimental results, the input split voltages and two flying voltages are balanced well. The primary side currents of three HB circuits are illustrated in
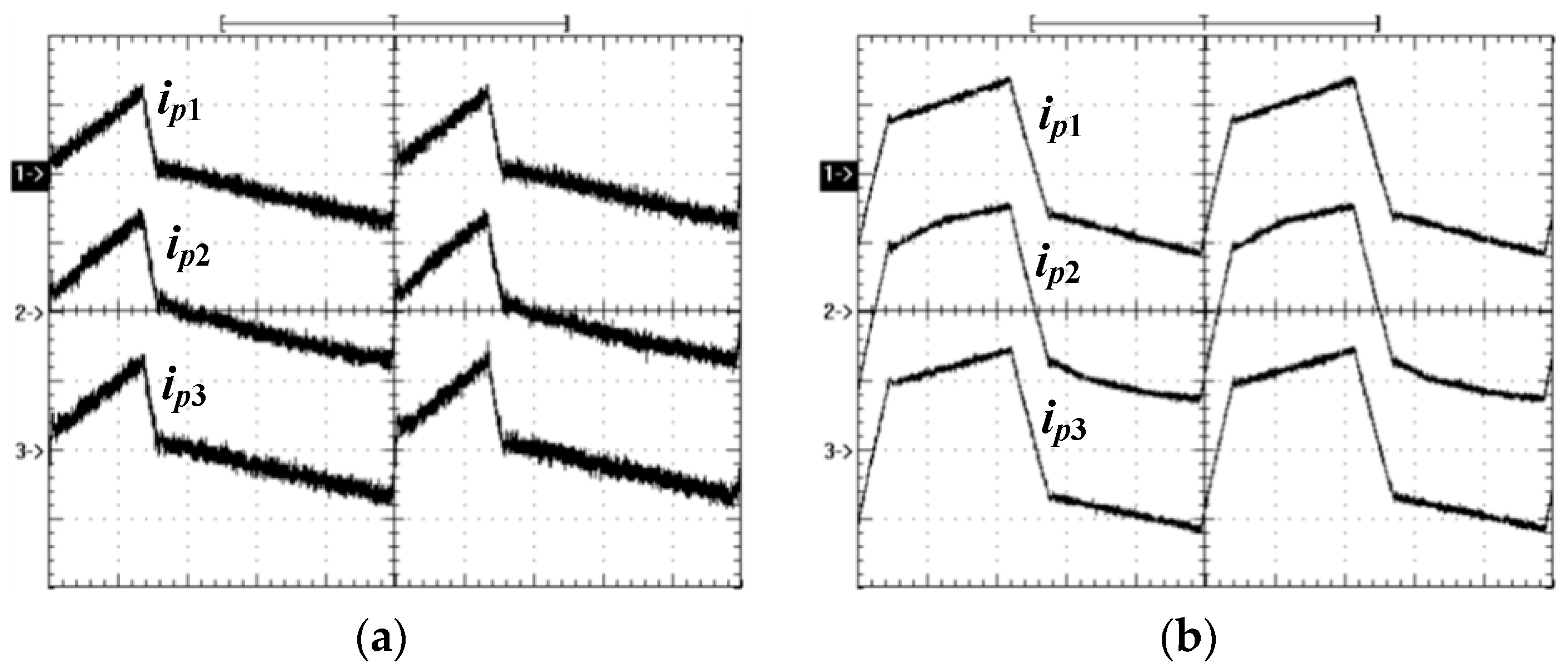
Figure 9. It is observed that the three primary currents are balanced well.
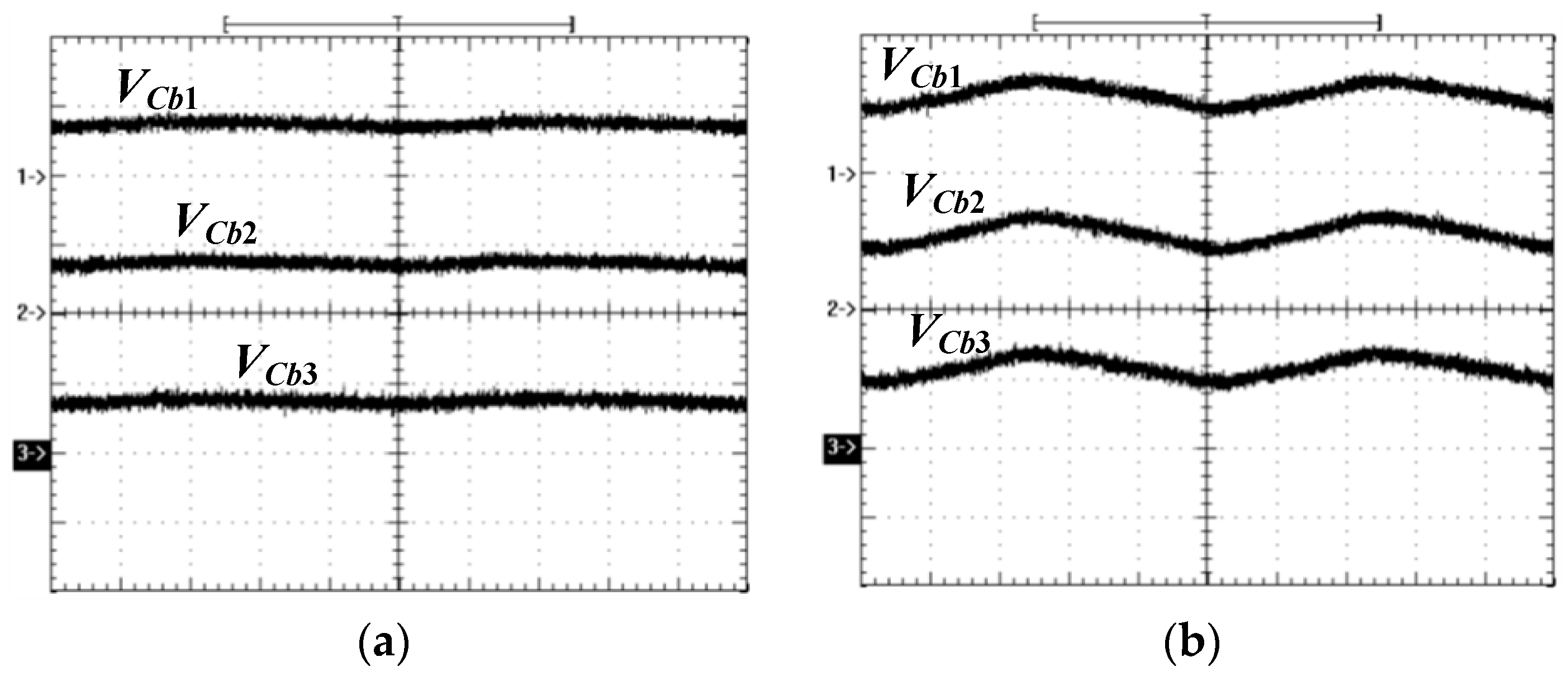
Figure 10 gives the measured waveforms of three DC block capacitor voltages. It can be observed that the three voltages are balanced and the capacitor voltages are related to the duty cycle of
Q1,
Q3 and
Q5.
Figure 11 shows the experimental waveforms of the secondary side currents. The ripple currents on
Lo1 and
Lo2 partially cancel each other so that the resultant ripple current on the load side is reduced.
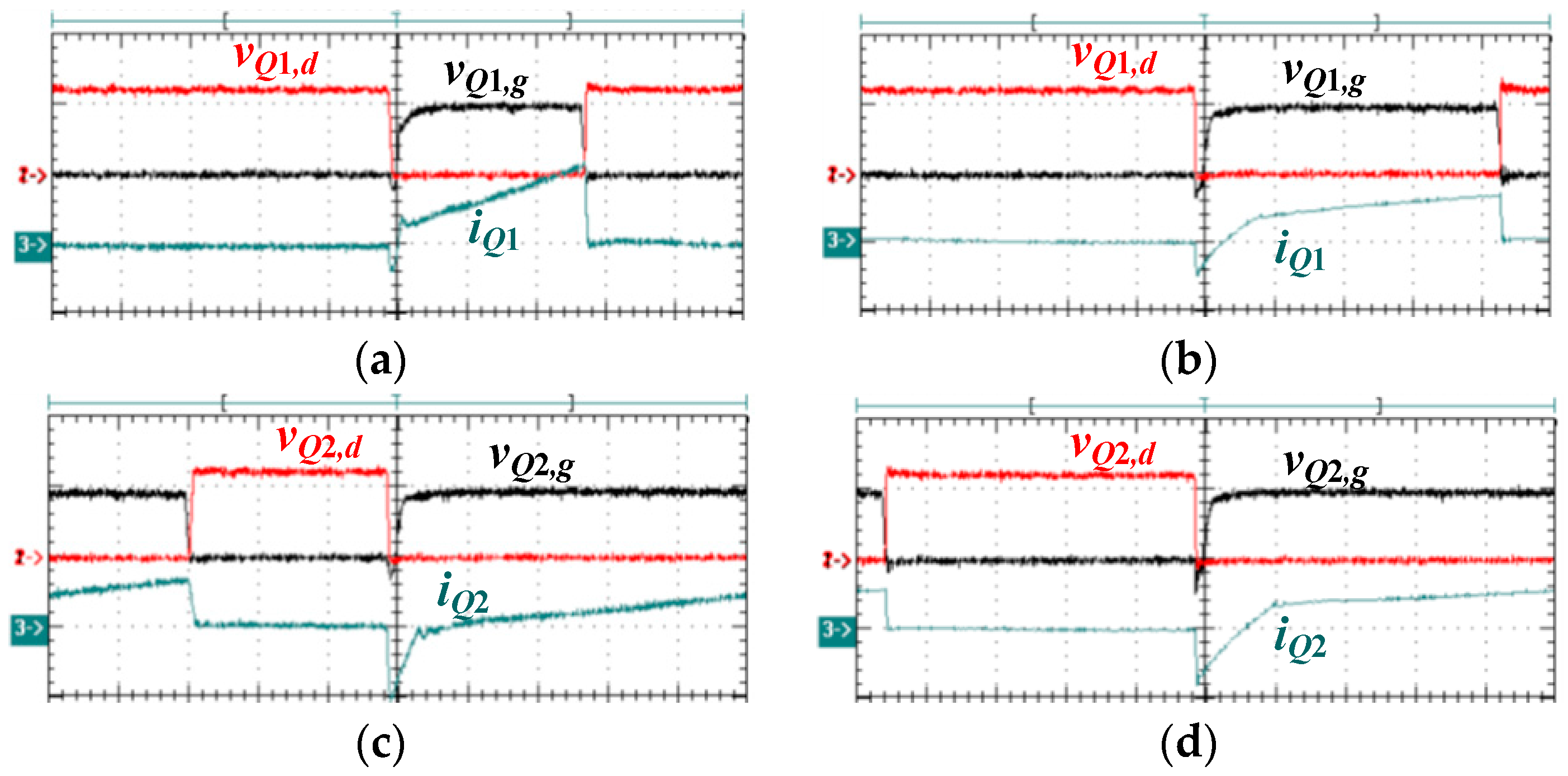
Figure 12 shows the test results of
Q1 and
Q2 at 20% and 100% loads. Before the switch is turned on, the switch current is negative to discharge the output capacitor
CQ to zero voltage. Thus, the mechanism of the zero-voltage turn-on switching is clearly achieved for both
Q1 and
Q2 from a 20% load. It can also be observed that all drain voltages of
Q1 and
Q2 are clamped at
Vin/3. Since the PWM signals of the three HB circuits are identical and the input split voltages are also balanced,
Q3~
Q6 can also be turned on at zero-voltage from a 20% load.
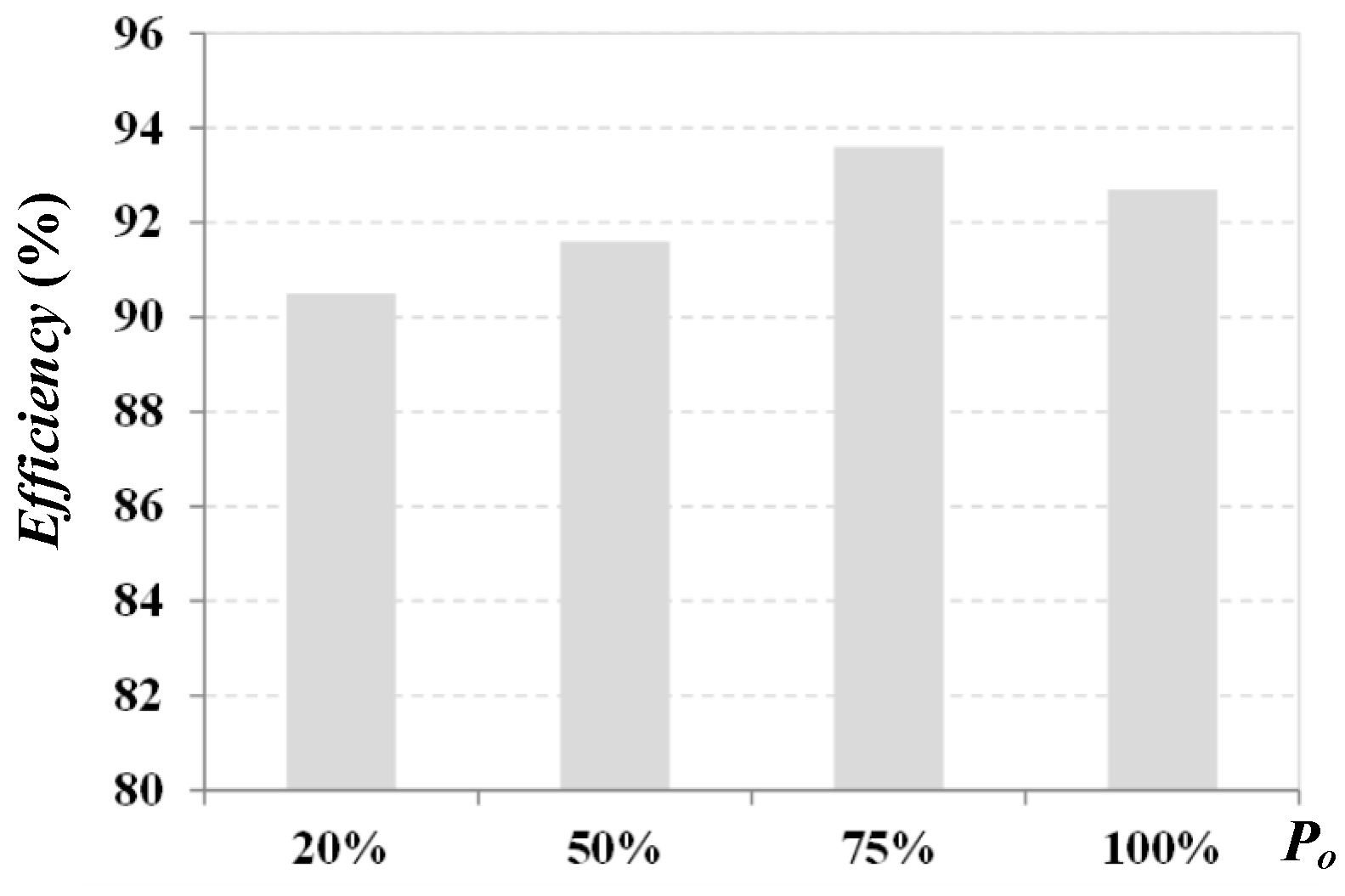
Figure 13 shows the circuit efficiency of the studied converter under different load cases. The measured maximum efficiency is about 93.6%. The main advantage of the studied converter is the lower voltage rating of power switches compared to the conventional three-level converter with eight MOSFETs and the two-level full-bridge converter with four IGBTs. Considering the turns-ratio of the transformer, the root-mean-square current of the studied converter is the same as the three-level and two-level converters. However, the lower conduction resistance of MOSFETs with lower voltage rating is used in the developed converter. Therefore, the total conduction losses (six MOSFETs) in the studied converter can be reduced compared to the three-level converter with eight MOSFETs and the full-bridge converter with four IGBTs.