Simplified Analytic Approach of Pole-to-Pole Faults in MMC-HVDC for AC System Backup Protection Setting Calculation
Abstract
:1. Introduction
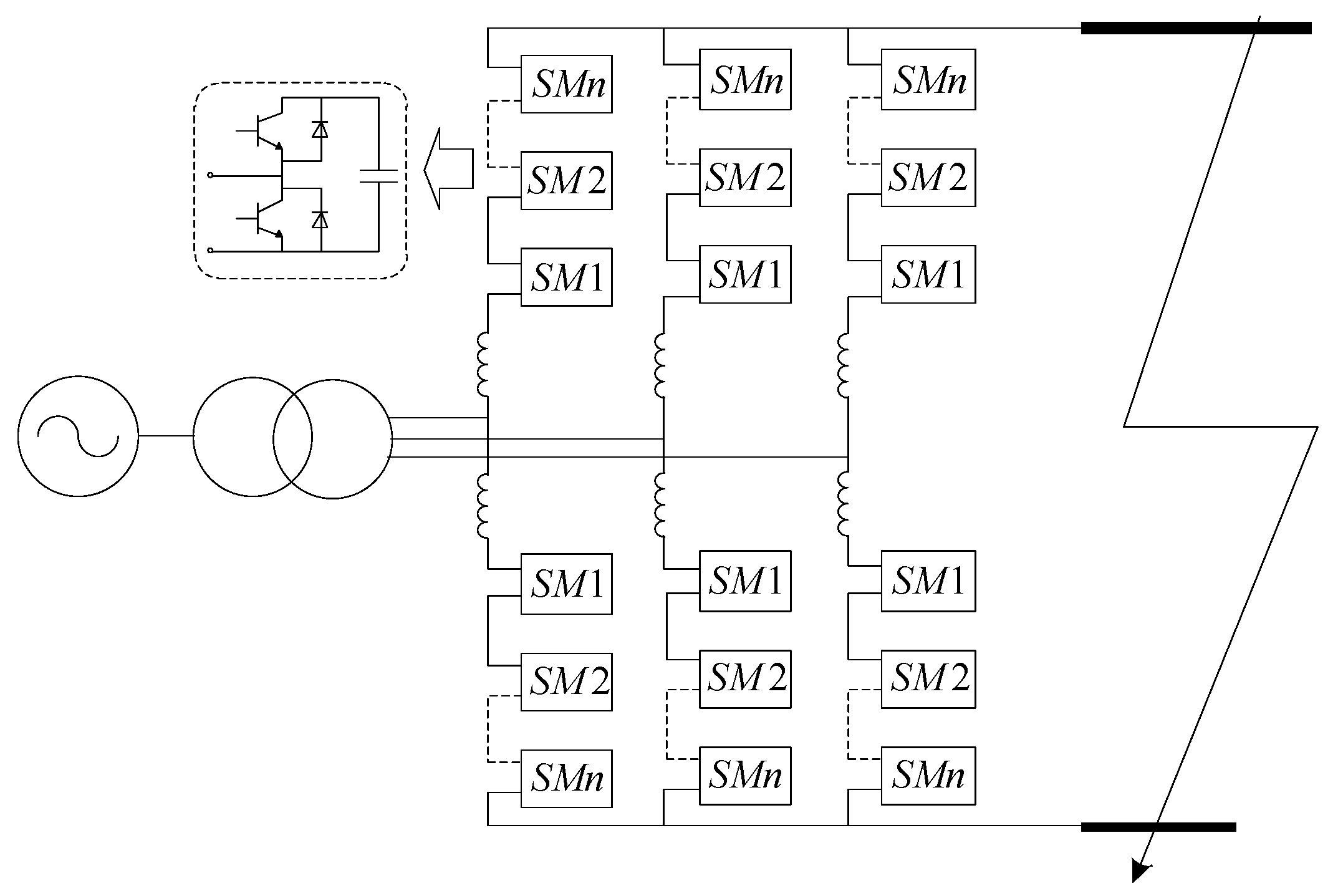
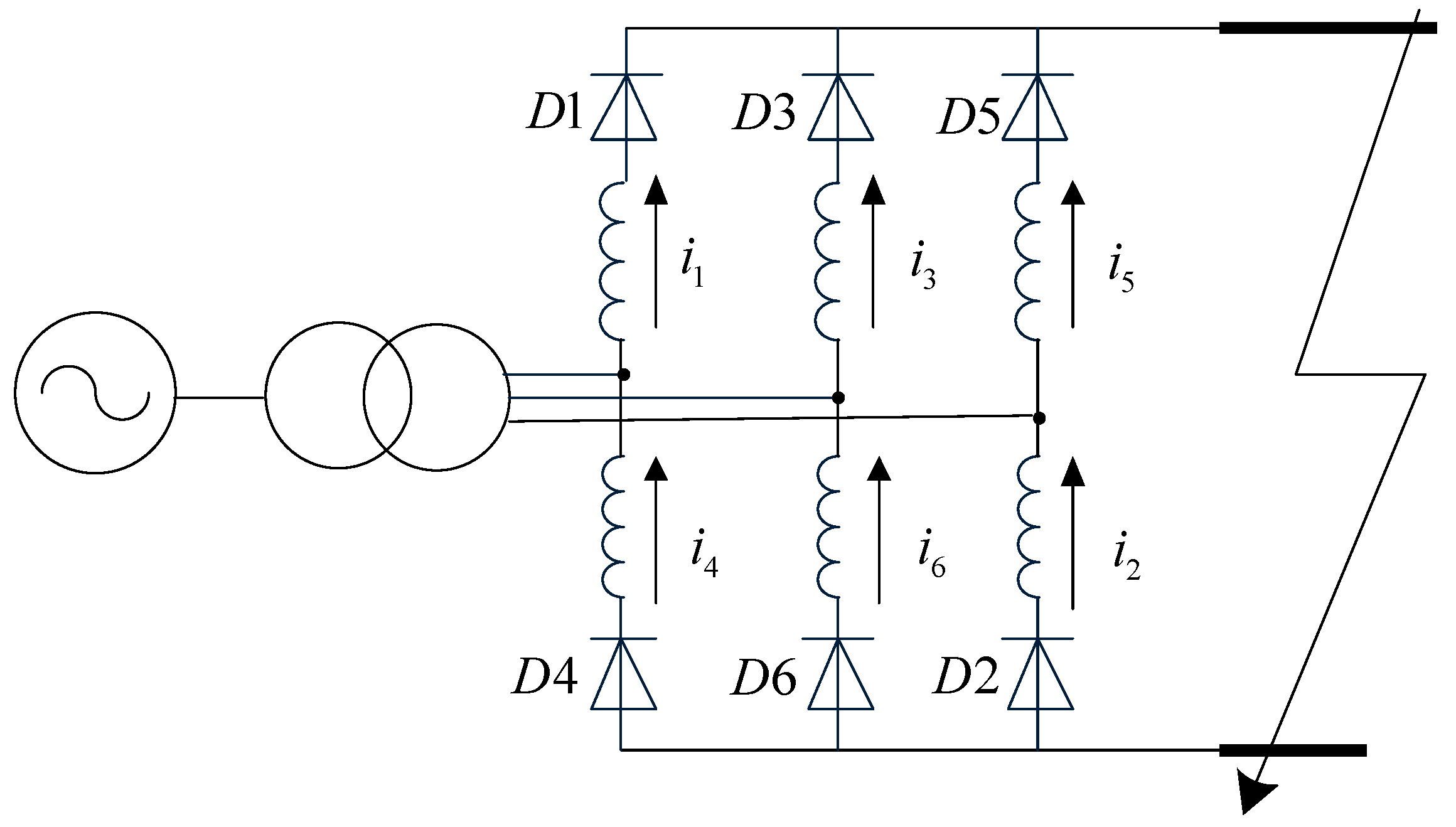
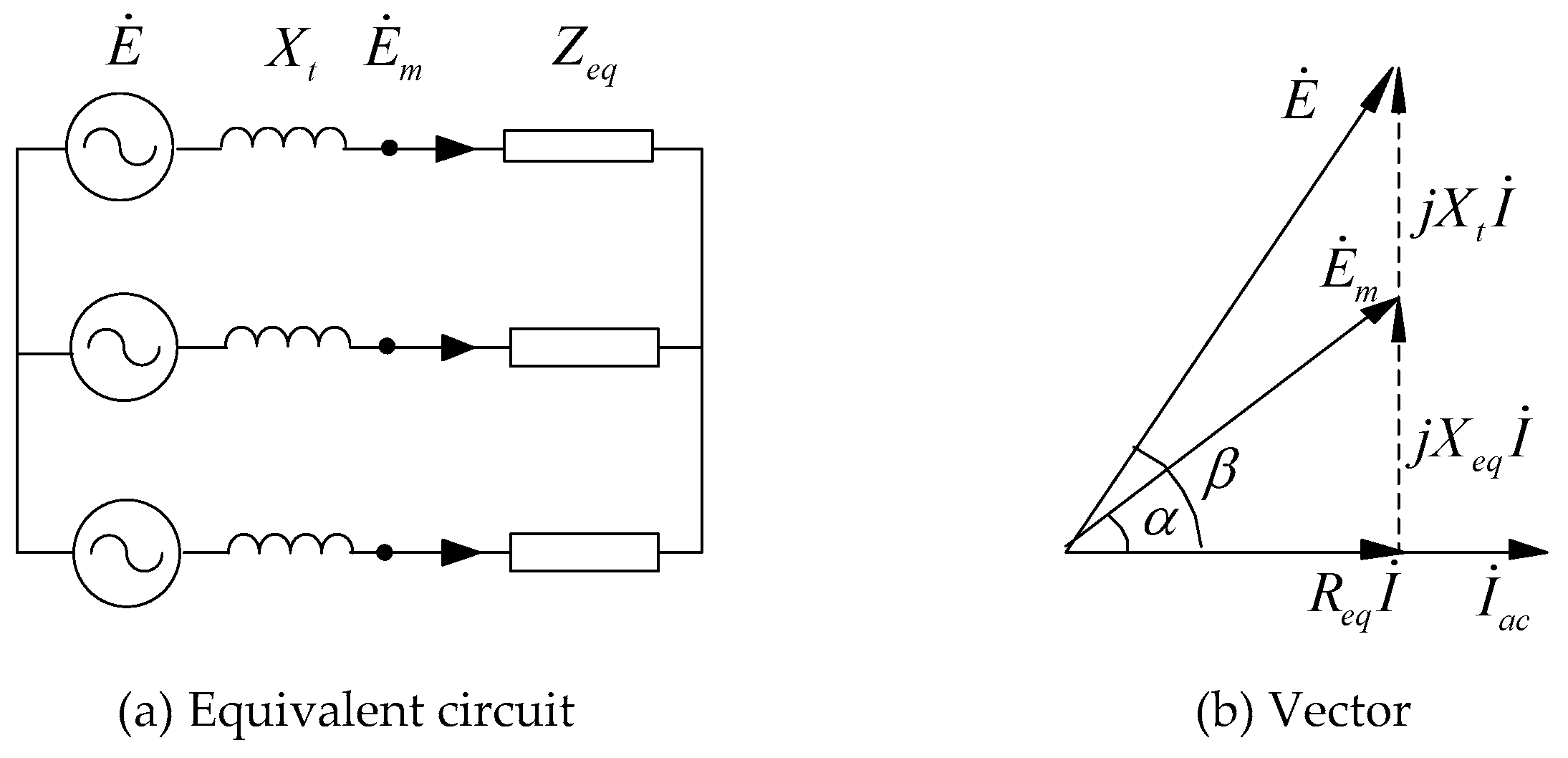
2. Principles of Pole-to-Pole Fault Analysis
- Only the steady state is considered.
- Only the fundamental frequency current is considered.
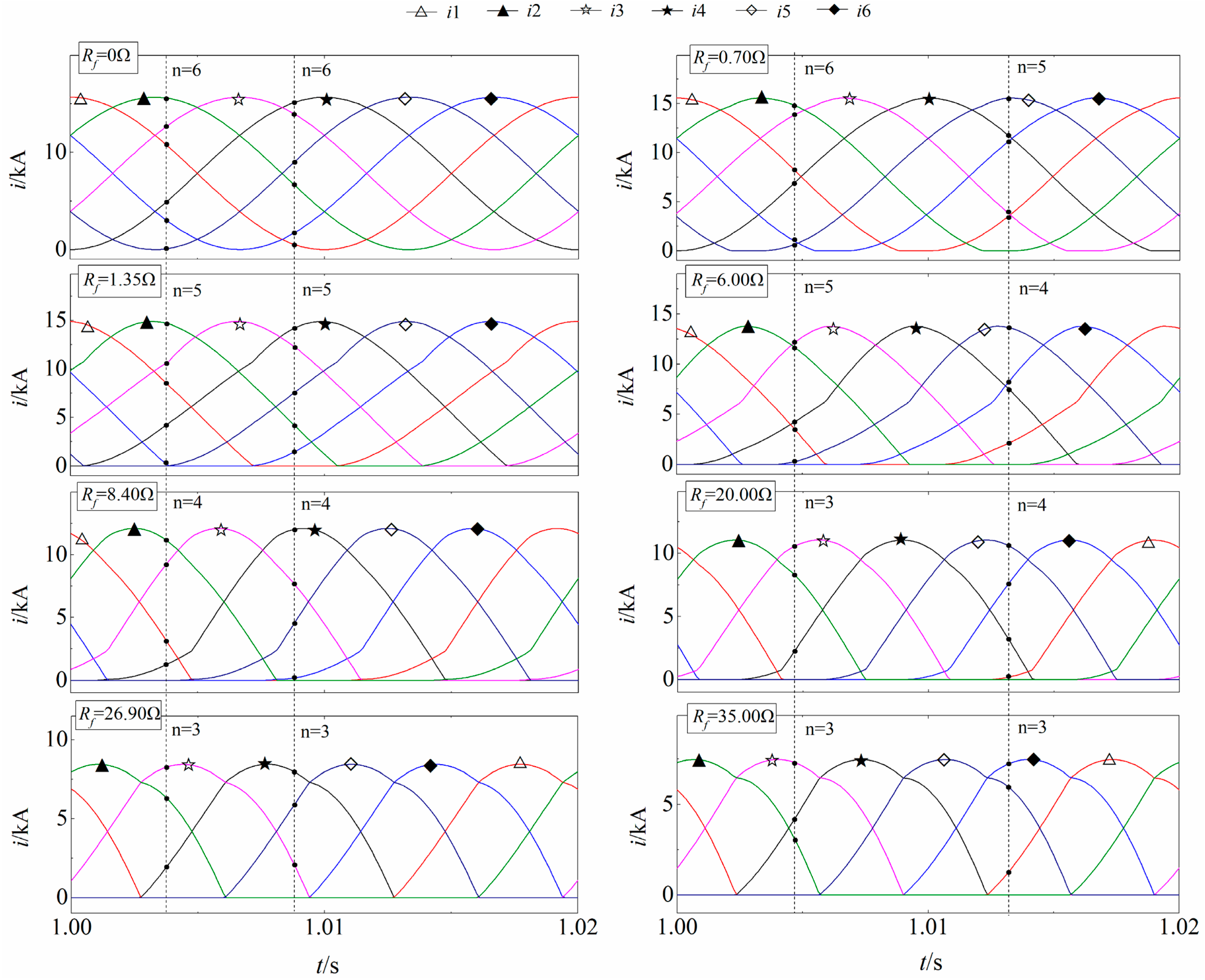
3. Influence of Fault Resistance on Pole-to-Pole Faults
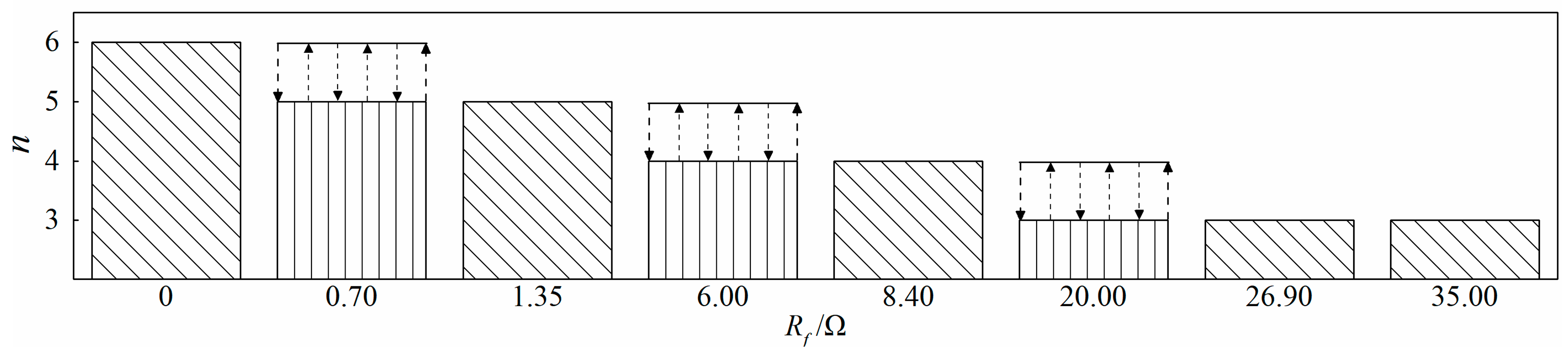
- The NOCD decreases as the fault resistance rises.
- The NOCD remains constant when fault resistance is equal to certain values. Specific values of Rf are adopted here as 0/1.35/8.40/26.90 Ω for example. This could vary with different systems and will be discussed in Section 4.
- The NOCD alternately changes when the fault resistance is between the above certain values.
4. Simplified Analytic Approach of Pole-to-Pole Faults
4.1. Definition of Critical Resistance and Critical State
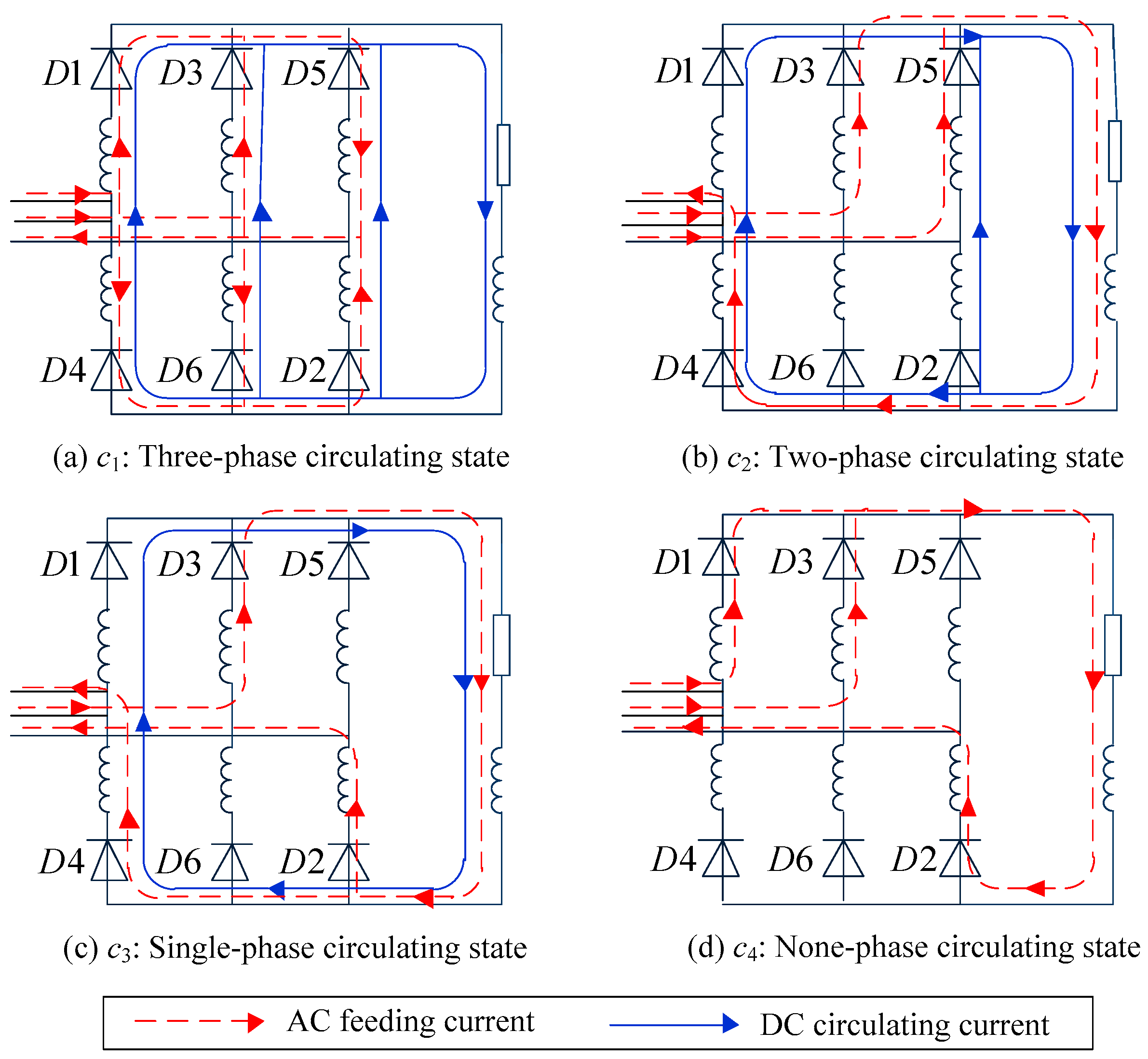
- Critical resistance: When the NOCD remains constant, the fault resistance is defined as critical resistance. Obviously, there are multiple critical resistances, and they are symbolized as Rc1, Rc2, Rc3, and Rc4, where the corresponding NOCD are 6, 5, 4, and 3, respectively.
- Critical state: The fault process under critical resistance is defined as the critical state, and the critical states are symbolized as c1, c2, c3, and c4, where the corresponding fault resistances are Rc1, Rc2, Rc3, and Rc4, respectively.
4.2. Analysis of Critical States
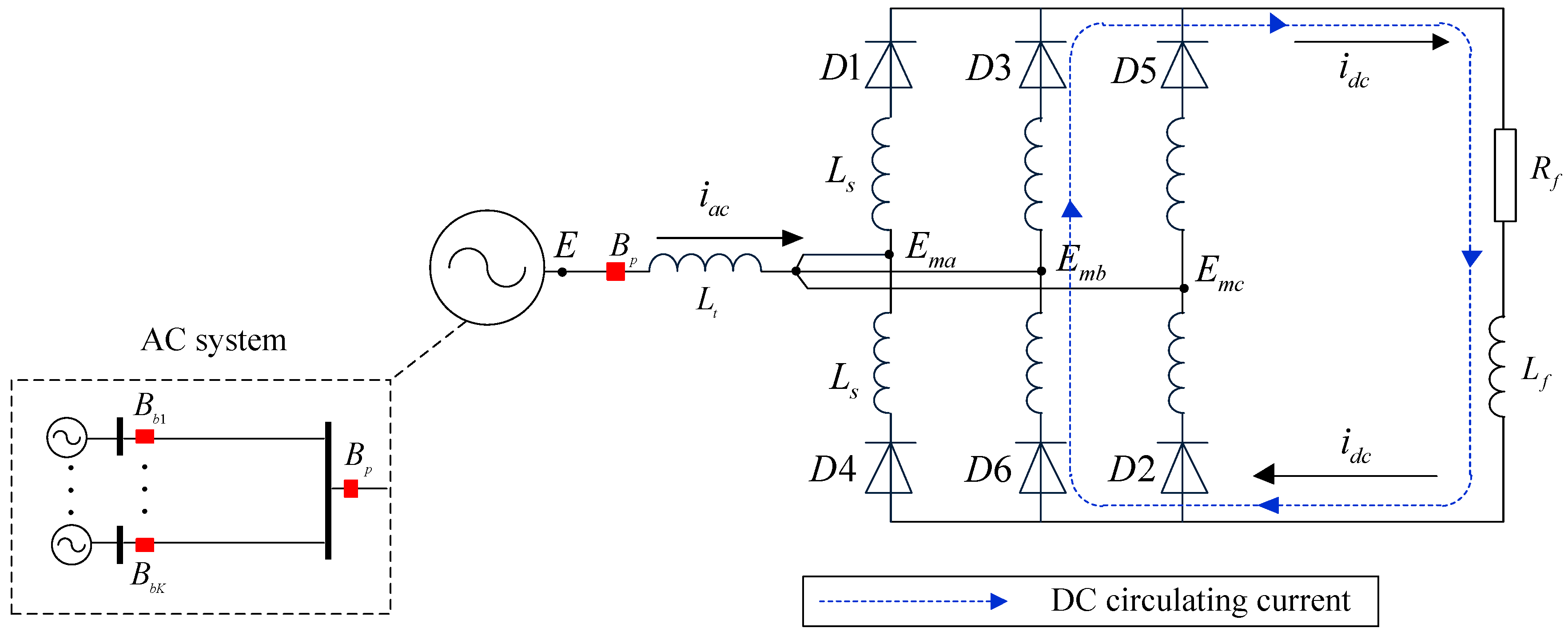
4.2.1. Determination of Current Loops
4.2.2. Determination of Boundary Conditions
4.2.3. Derivation of Fault Current and Critical Resistance
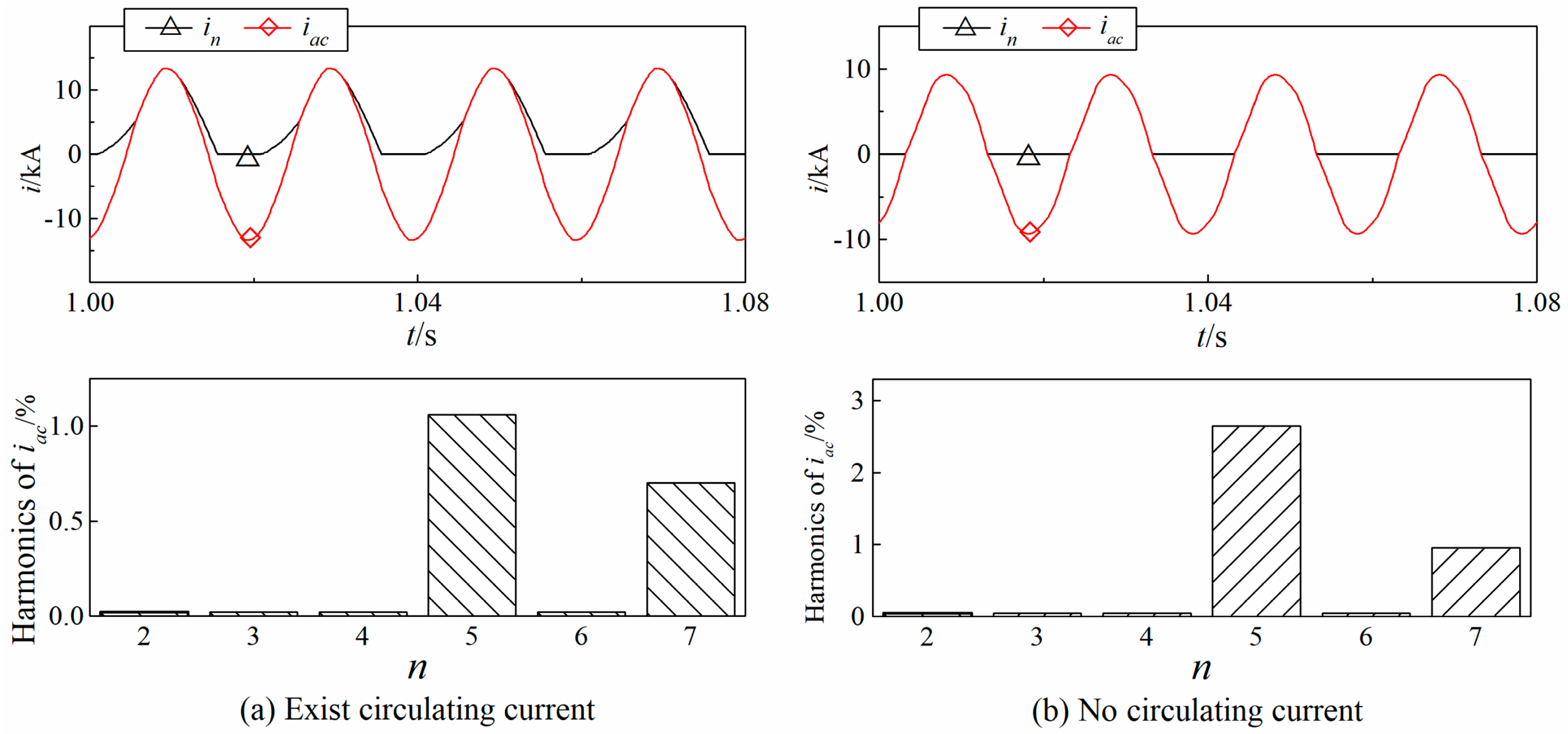
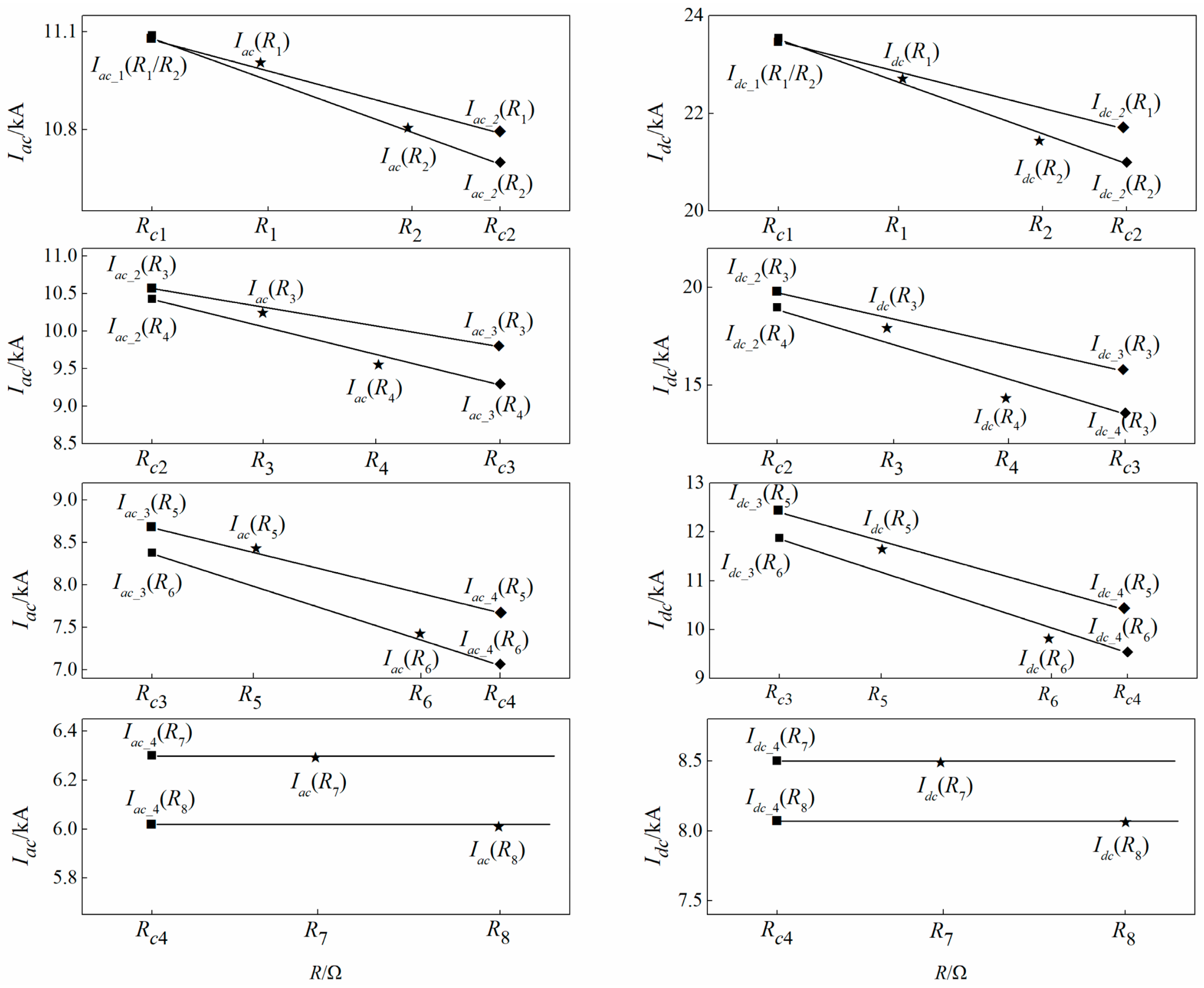
4.3. Analysis of Fault Process under Arbitrary Fault Resistance
- Rf = [Rci,Rc(i+1)) (i = 1, 2, 3)
- Rf ≥ Rc4
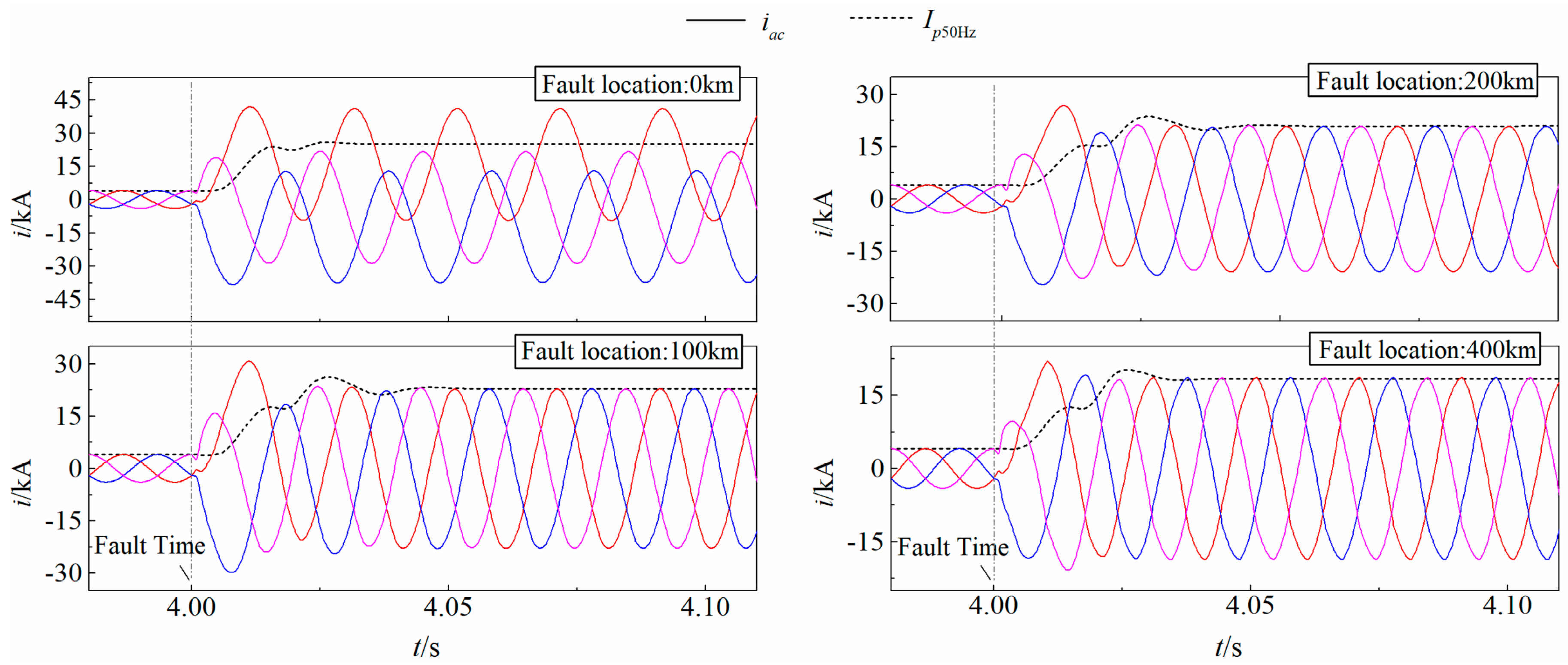
5. Validations
5.1. MMC-HVDC System
5.2. Validations of the Proposed Approach
6. Conclusions
- The calculation errors of the fault current by the proposed approach were within 10%, which is acceptable for the AC system backup protection setting calculation. In addition, the proposed approach could provide a fast, preliminary calculation for the reference of planning MMC-HVDC projects.
- The arm reactor plays a significant role in the formation of the DC circulating current, and the fault process is influenced by the fault resistance. The concept of critical resistance and critical state were defined, and the fault process can be regarded as a combination of critical states.
- The expressions of fault current for critical states, and the approximated expressions of fault current for fault processes under arbitrary fault resistance were derived. When the fault resistance is between two adjacent critical resistances, the results calculated by the expressions for corresponding critical states are the upper and lower limits of the simulation results.
- For the faults with arbitrary fault resistance, the expressions of fault currents for the adjacent critical states could be applied in the AC system backup protection settings calculation, depending on requirements of selectivity or sensitivity. If a more precise result is needed, the approximated expressions, a linear combination of the expressions for the critical states, could be applied in the setting calculation.
- The simplified analytic approach of pole-to-pole faults in two-level and three-level VSC-HVDCs for AC system backup protection will be investigated in our future work, since the two-level and three-level VSCs are also not capable of clearing the pole-to-pole fault by blocking the converter.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| AC System Line-to-Line Voltage/kV | 370 | DC Bus Voltage/kV | ±320 |
| Transformer Inductance/mH | 25.4 | Active Power/MW | 1000 |
| Arm Reactor/mH | 30 | Reactive Power/MVar | 0 |
| DC Line Resistance Ω/km | 0.0139 | Numbers of Sub-module | 152 |
| DC Line Inductance mH/km | 0.159 | Sub-module Capacitor/μF | 2800 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| AC System Line-to-Line Voltage/kV | 370 | DC Bus Voltage/kV | ±320 |
| Transformer Inductance/mH | 36.3 | Active Power/MW | 1000 |
| Arm Reactor/mH | 50 | Reactive Power/MVar | 0 |
| DC Line Resistance Ω/km | 0.0139 | Numbers of Sub-module | 152 |
| DC Line Inductance mH/km | 0.159 | Sub-module Capacitor/μF | 2800 |
Appendix B
References
- Li, S.H.; Naoto, Y.; Ding, M.; Zoka, Y. Sensitivity analysis to operation margin of zone 3 impedance relays with bus power and shunt susceptance. IEEE Trans. Power Deliv. 2008, 23, 102–108. [Google Scholar] [CrossRef]
- Garlapati, S.; Lin, H.; Heiber, A.; Shukla, S.K.; Thorp, J. A hierarchically distributed non-intrusive agent aided distance relaying protection scheme to supervise zone 3. Electr. Power Energy Syst. 2013, 42–49. [Google Scholar] [CrossRef]
- Zhong, Y.; Kang, X.N.; Jiao, Z.B.; Wang, Z.C.; Suonan, J.L. A novel distance protection algorithm for the phase-ground fault. IEEE Trans. Power. Deliv. 2014, 29, 1718–1725. [Google Scholar] [CrossRef]
- Saumendra, S.; Ashok, K.P. Synchronised data-based adaptive backup protection for series compensated line. IET Gener. Transm. Distrib. 2014, 8, 1979–1986. [Google Scholar]
- Ma, J.; Xiang, X.Q.; Kang, W.B.; Thorp, J.S. A novel algorithm of regional backup protection using adaptive current protection suiting factor. Int. Trans. Electr. Energy Syst. 2017, 27, 2399. [Google Scholar] [CrossRef]
- Denholm, P.; Margolis, R.; Mai, T.; Brinkman, G.; Drury, E.; Hand, M.; Mowers, M. Bright future: Solar power as a major contributor to the U.S. grid. IEEE Power Energy Mag. 2013, 11, 22–32. [Google Scholar] [CrossRef]
- Máslo, K.; Pestana, R.; Strunz, K.; Moroni, S.; Centeno, P. Innovative grid and generation technologies for future European power system. In Proceedings of the 12th International Conference on the European Energy Market (EEM), Lisbon, Portugal, 19–22 May 2015; pp. 1–5. [Google Scholar]
- Xu, Z.; Dong, H.F.; Huang, H.Y. Debates on ultra-high-voltages synchronous power grids: The future super grid in China? IET Gener. Transm. Distrib. 2015, 9, 740–747. [Google Scholar] [CrossRef]
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the IEEE Bologna Powertech Conference, Bologna, Italy, 23–26 June 2003; pp. 1–6. [Google Scholar]
- Marquardt, R. Modular Multilevel Converter: An universal concept for HVDC-Networks and extended DC-Bus Applications. In Proceedings of the IEEE ECCE-Asia IPEC 2010, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- Suman, D.; Qin, J.C.; Behrooz, B.; Maryam, S.; Peter, B. Operation, control, and applications of the modular multilevel converter: A review. IEEE Trans. Power Deliv. 2015, 30, 37–53. [Google Scholar]
- Ding, H.; Wu, Y.K.; Zhang, Y.; Ma, Y.L.; Kuffel, R. System stability analysis of Xiamen bipolar MMC-HVDC project. In Proceedings of the 12th IET International Conference on AC and DC Power Transmission, Beijing, China, 28–29 May 2016; pp. 1–6. [Google Scholar]
- Buigues, G.; Valverde, V.; Etxegarai, A.; Eguía, P.; Torres, E. Present and future multi-terminal HVDC systems: Current status and forthcoming developments. In Proceedings of the International Conference on Renewable Energies and Power Quality, Malaga, Spain, 4–6 April 2017; pp. 83–88. [Google Scholar]
- Tang, L.X.; Ooi, B.-T. Locating and isolating DC faults in multi-terminal DC systems. IEEE Trans. Power Deliv. 2007, 22, 1877–1884. [Google Scholar] [CrossRef]
- Zhang, J.P.; Zhao, C.Y. The research of SM topology with DC fault tolerance in MMC-HVDC. IEEE Trans. Power Deliv. 2015, 30, 1561–1568. [Google Scholar] [CrossRef]
- Yang, J.; Fletcher, J.E.; O’Reilly, J. Multiterminal DC wind farm collection grid internal fault analysis and protection design. IEEE Trans. Power. Deliv. 2010, 25, 2308–2318. [Google Scholar] [CrossRef]
- Flourentzou, N.; Agelidis, V.G.; Demetrades, G.D. VSC-Based HVDC power transmission systems: An overview. IEEE Trans. Power Electron. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Xu, J.Z.; Zhao, C.Y.; Liu, W.J.; Guo, C.Y. Accelerated model of modular multilevel converters in PSCAD/EMTDC. IEEE Trans. Power Deliv. 2013, 28, 129–136. [Google Scholar] [CrossRef]
- Xu, J.Z.; Fan, S.T.; Zhao, C.Y.; Gole, A.M. High-speed EMT modeling of MMCs with arbitrary multi-port sub-module structures using generalized Norton equivalents. IEEE Trans. Power Deliv. 2017. [Google Scholar] [CrossRef]
- Khan, S.S.; Tedeschi, E. Modeling of MMC for fast and accurate simulation of electromagnetic transients: A review. Energies 2017, 10, 1161. [Google Scholar] [CrossRef]
- Bucher, M.K.; Frank, C.M. Analytic approximation of fault current contribution from AC networks to MTDC networks during pole-to-ground faults. IEEE Trans. Power Deliv. 2016, 31, 20–27. [Google Scholar] [CrossRef]
- Li, B.; He, J.W.; Tian, J.; Feng, Y.D.; Dong, Y.L. DC faults analysis for modular multilevel converter-based system. J. Mod. Power Syst. Clean Energy 2017, 5, 275–282. [Google Scholar] [CrossRef]
- Li, C.Y.; Zhao, C.Y.; Xu, J.Z.; Ji, Y.K.; Zhang, F.; An, T. A pole-to-pole short-circuit fault current calculation method for DC grids. IEEE Trans. Power Syst. 2017. [CrossRef]
- He, L.N.; Liu, C.C.; Pitto, A.; Cirio, D. Distance protection of AC grid with HVDC-connected offshore wind generators. IEEE Trans. Power Deliv. 2014, 29, 493–501. [Google Scholar] [CrossRef]
- Liu, Y.C.; Li, G.Q.; Wang, Z.H.; Yu, W.X. Research on AC line distance relay in the presence of modular multilevel converter based HVDC. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Conference, Xi’an, China, 25–28 October 2016. [Google Scholar]
- Setting Guide for 220 kV~750 kV Power System Protection Equipment. Available online: http://www.gbstandards.org/index/GB_standard.asp?id=64137 (accessed on 18 October 2017).
- Bhalja, B.; Maheshwari, R.P.; Chothani, N. Protection and Switchgear, 1st ed.; Oxford University Press: New Delhi, India, 2011; pp. 169–201. ISBN 0198075502. [Google Scholar]
| Critical Resistance | Ls = 30 mH | Ls = 50 mH | ||||
|---|---|---|---|---|---|---|
| Calculation | Simulation | Error | Calculation | Simulation | Error | |
| Rc1/Ω | 0 | 0 | 0 | 0 | 0 | 0 |
| Rc2/Ω | 0.77 | 0.80 | −3.8% | 1.29 | 1.35 | −4.4% |
| Rc3/Ω | 4.96 | 5.05 | −1.8% | 8.27 | 8.40 | −1.5% |
| Rc4/Ω | 16.32 | 16.15 | 1.1% | 27.20 | 26.90 | 1.1% |
| Inductance/mH | Fault Resistance/Ω | Iac/kA | Idc/kA | |||||
|---|---|---|---|---|---|---|---|---|
| Lt | Ls | Calculation | Simulation | Error | Calculation | Simulation | Error | |
| 25.4 | 30 | 0.00 | 16.84 | 16.83 | 0.1% | 35.72 | 35.69 | 0.1% |
| 0.50 | 16.29 | 16.48 | −1.2% | 33.14 | 31.91 | 3.9% | ||
| 0.77 | 16.03 | 16.25 | −1.4% | 31.38 | 30.46 | 3.0% | ||
| 3.00 | 15.24 | 14.45 | 5.5% | 24.44 | 22.82 | 7.1% | ||
| 4.96 | 13.76 | 13.28 | 3.6% | 20.57 | 19.16 | 7.4% | ||
| 10.00 | 11.51 | 11.66 | −1.3% | 16.27 | 15.95 | 2.0% | ||
| 16.32 | 10.41 | 10.17 | 2.4% | 14.03 | 13.70 | 2.4% | ||
| 25.00 | 8.87 | 8.59 | 3.3% | 11.95 | 11.50 | 3.9% | ||
| 36.3 | 50 | 0.00 | 11.09 | 11.08 | 0.1% | 23.54 | 23.53 | 0.1% |
| 0.70 | 10.76 | 10.89 | −1.2% | 22.00 | 21.31 | 3.2% | ||
| 1.29 | 10.51 | 10.67 | −1.5% | 20.59 | 19.99 | 3.0% | ||
| 6.00 | 9.67 | 9.10 | 6.3% | 15.24 | 13.95 | 9.2% | ||
| 8.27 | 8.89 | 8.55 | 4.0% | 13.29 | 12.34 | 7.7% | ||
| 20.00 | 6.99 | 7.07 | −1.1% | 9.81 | 9.61 | 2.1% | ||
| 27.20 | 6.55 | 6.40 | 2.3% | 8.84 | 8.62 | 2.6% | ||
| 35.00 | 5.97 | 5.79 | 3.1% | 8.06 | 7.76 | 3.9% | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, T.; Li, Y.; Duan, X.; Zhu, J. Simplified Analytic Approach of Pole-to-Pole Faults in MMC-HVDC for AC System Backup Protection Setting Calculation. Energies 2018, 11, 264. https://doi.org/10.3390/en11020264
Lan T, Li Y, Duan X, Zhu J. Simplified Analytic Approach of Pole-to-Pole Faults in MMC-HVDC for AC System Backup Protection Setting Calculation. Energies. 2018; 11(2):264. https://doi.org/10.3390/en11020264
Chicago/Turabian StyleLan, Tongkun, Yinhong Li, Xianzhong Duan, and Jia Zhu. 2018. "Simplified Analytic Approach of Pole-to-Pole Faults in MMC-HVDC for AC System Backup Protection Setting Calculation" Energies 11, no. 2: 264. https://doi.org/10.3390/en11020264
APA StyleLan, T., Li, Y., Duan, X., & Zhu, J. (2018). Simplified Analytic Approach of Pole-to-Pole Faults in MMC-HVDC for AC System Backup Protection Setting Calculation. Energies, 11(2), 264. https://doi.org/10.3390/en11020264





