Numerical Analysis of Longitudinal Residual Stresses and Deflections in a T-joint Welded Structure Using a Local Preheating Technique
Abstract
:1. Introduction
2. T-joint Fillet Weld Geometry and Welding Conditions
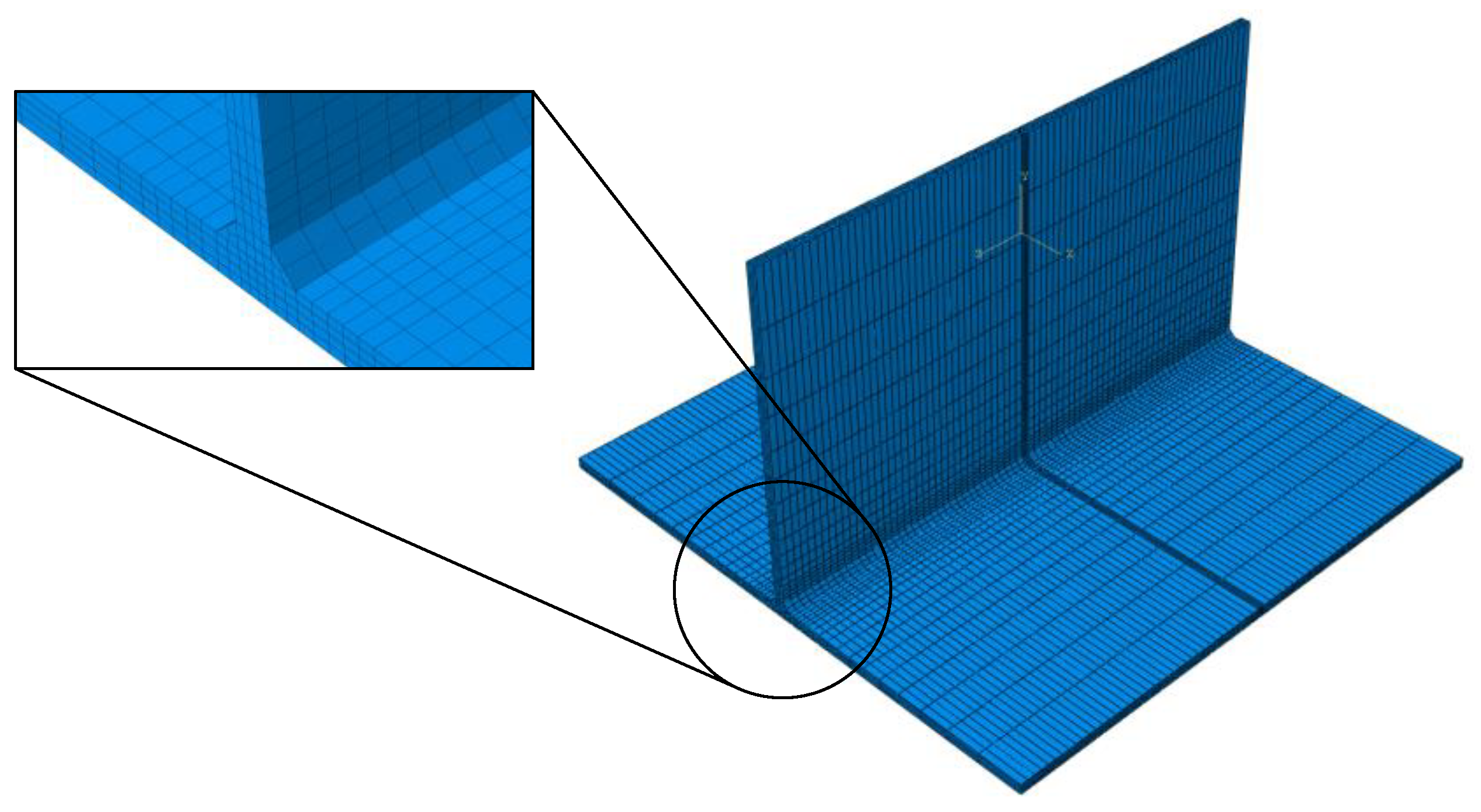
3. Numerical Model
4. Application of Preheat Temperature and Interpass Time in the Numerical Models
5. Results and Discussion
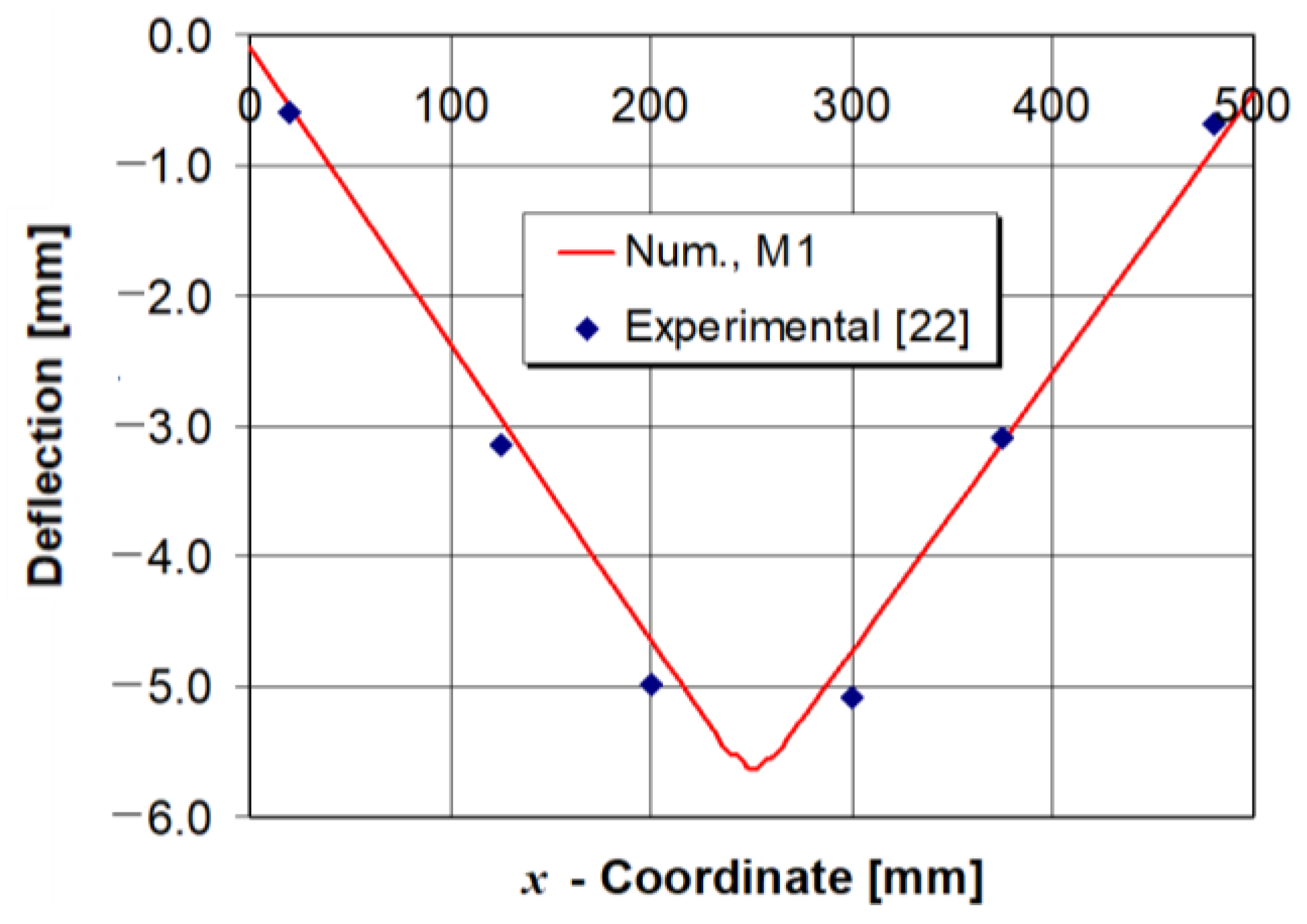
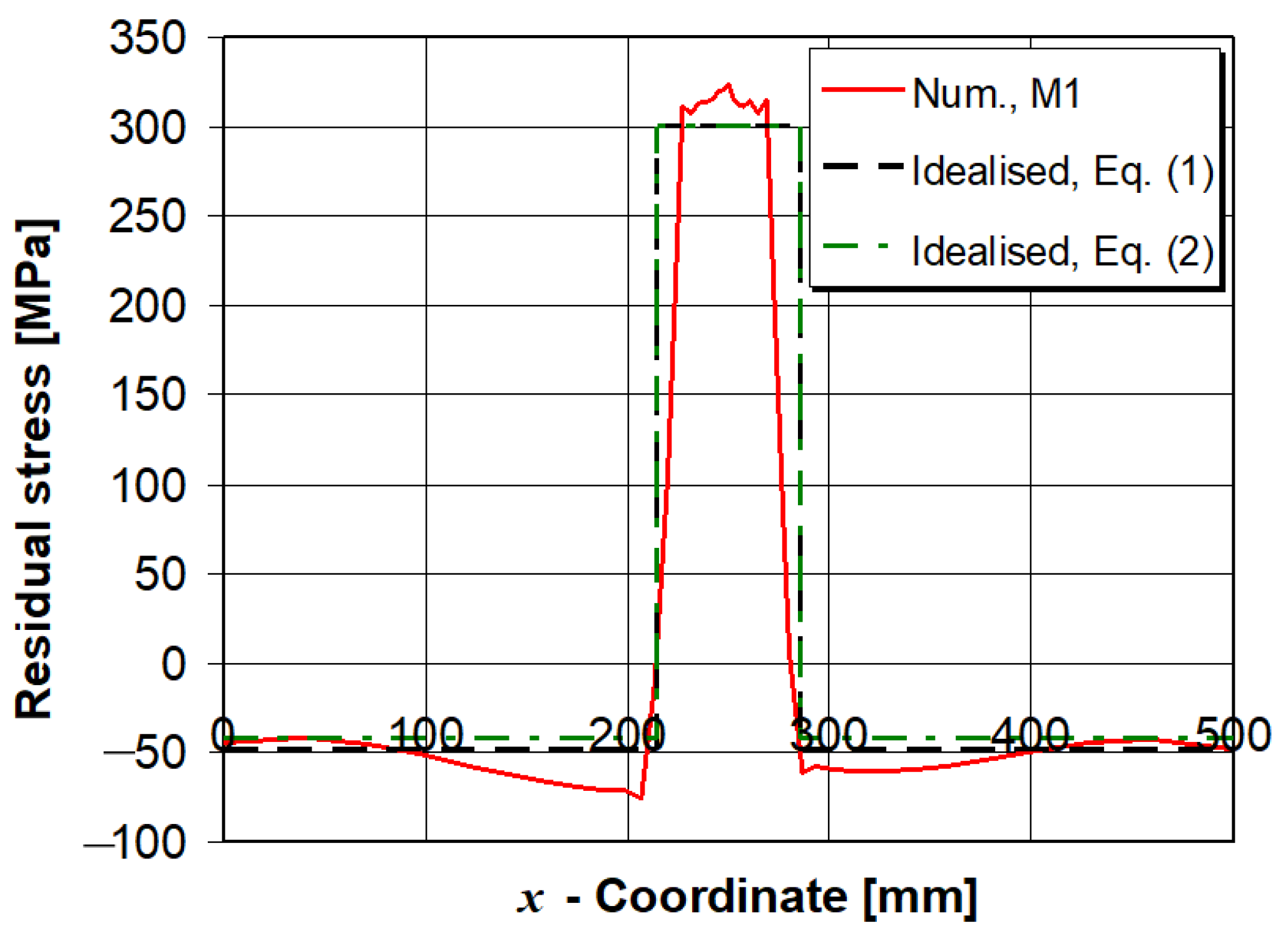
5.1. Residual Stress and Deflection Distributions—Reference Model
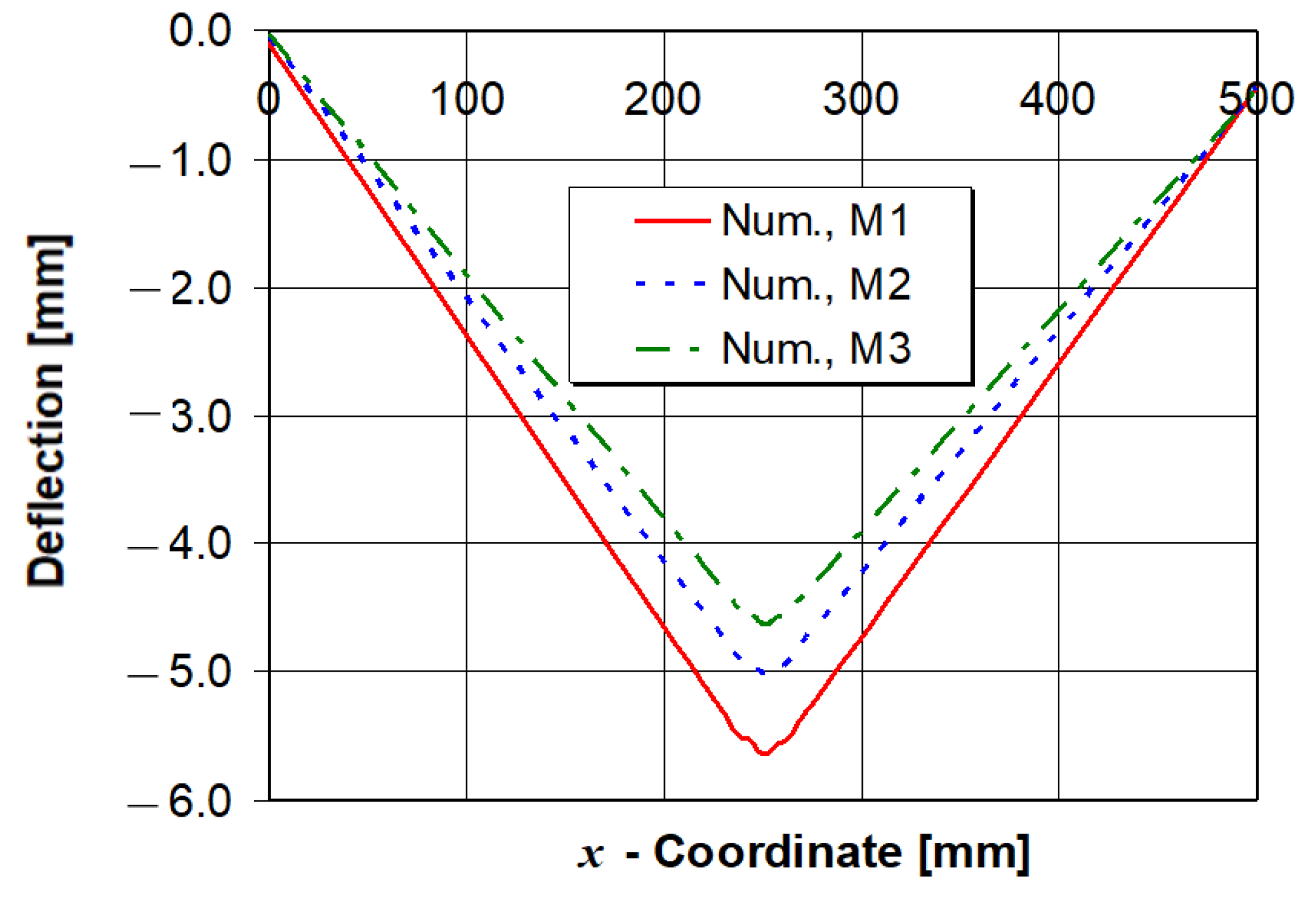
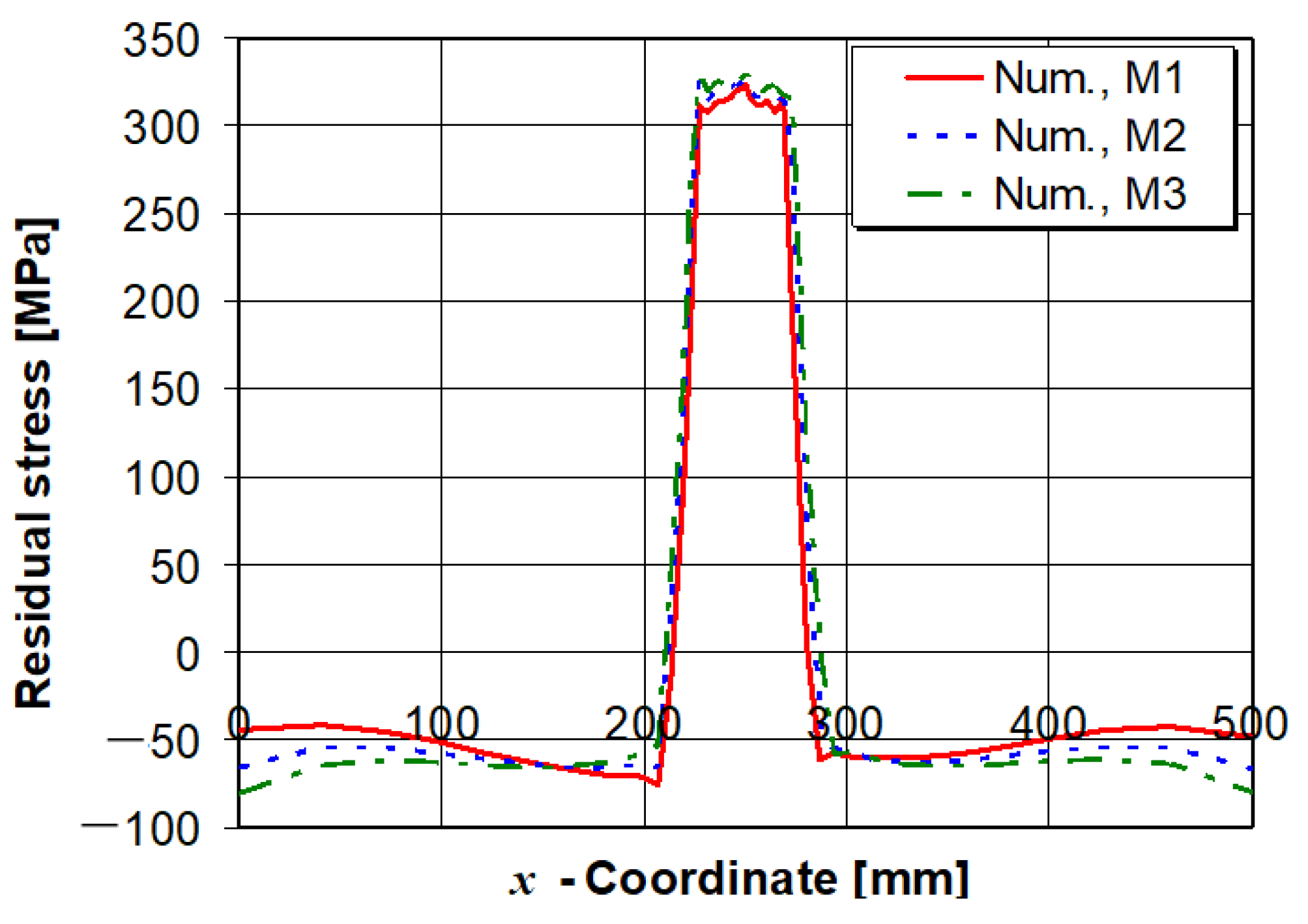
5.2. Influence of Preheat Temperature on the Longitudinal Residual Stress and Horizontal Plate Deflection
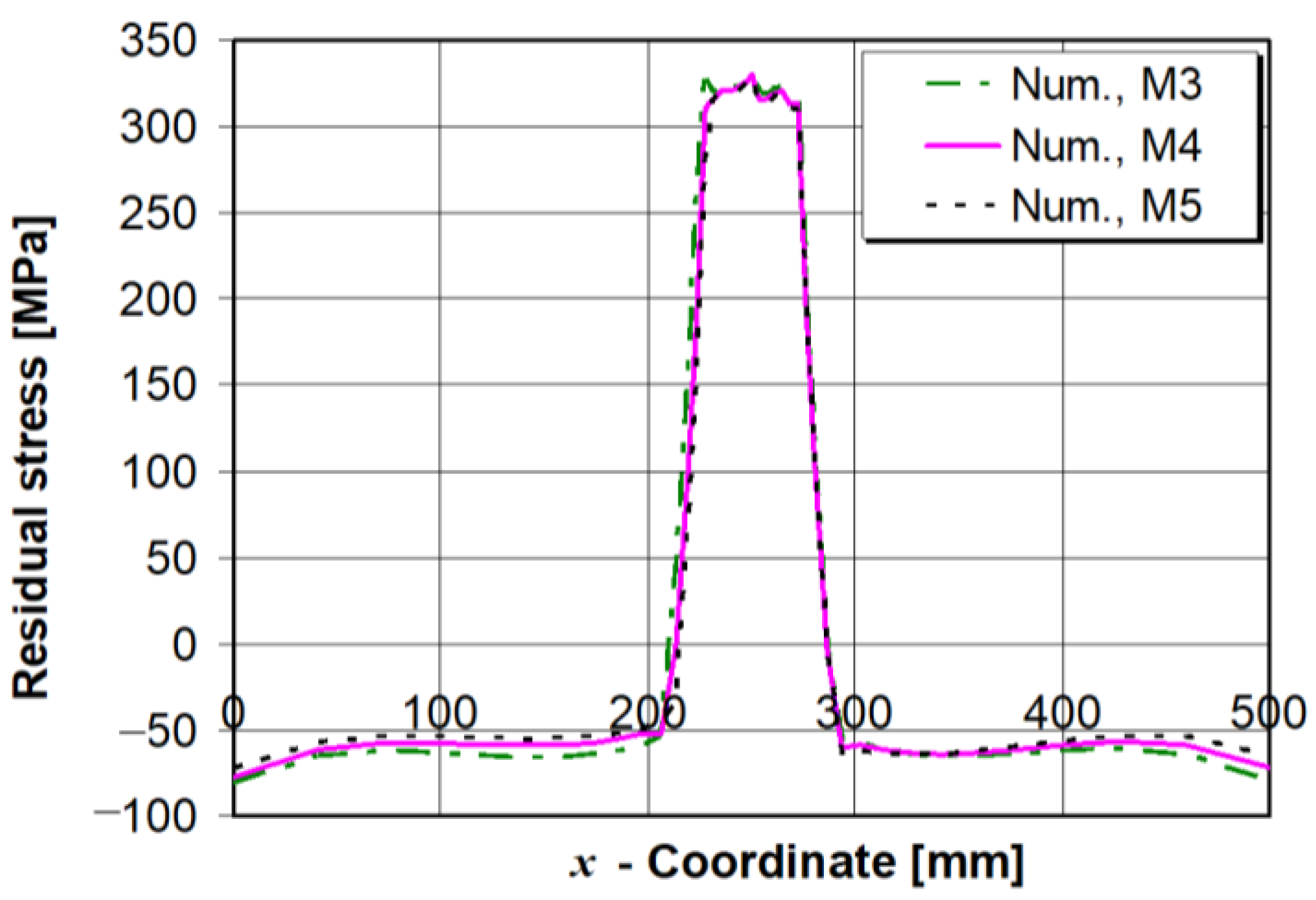
5.3. Influence of Interpass Time on the Longitudinal Residual Stress and Horizontal Plate Deflection
6. Conclusions
- The increase of the preheat temperature decreases the horizontal plate deflection of a T-joint very quickly.
- The influence of preheat temperature on the longitudinal tensile residual stress and the tensile stress zone width is negligible.
- The application of local preheating increases the compressive longitudinal stresses due to the increased temperature gradients between the preheated and non-preheated parts of the model. This occurrence is much more pronounced than in the models where the entire volume is preheated before the start of welding.
- The increase of interpass time increases the plate deflections. In cases when interpass time is prolonged, the positive effects of preheating vanish.
- The increase of interpass time minimally affects the longitudinal tensile residual stress and its tensile zone width.
- The effect of interpass time increase on compressive longitudinal stresses in preheated models can be neglected.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boljanović, S.; Maksimović, S. Computational mixed mode failure analysis under fatigue loadings with constant amplitude and overload. Eng. Fract. Mech. 2017, 174, 168–179. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, Y.; Qiu, H.; Lin, G.; Li, Z. Stress intensity factor-based prediction of solidification crack growth during welding of high strength steel. J. Mater. Process. Technol. 2018, 252, 270–278. [Google Scholar] [CrossRef]
- Oh, S.H.; Ryu, T.Y.; Park, S.H.; Won, M.G.; Kang, S.J.; Lee, K.S.; Lee, S.H.; Kim, M.K.; Choi, J.B. Evaluation of J-groove weld residual stress and crack growth rate of PWSCC in reactor pressure vessel closure head. J. Mech. Sci. Technol. 2015, 29, 1225–1230. [Google Scholar] [CrossRef]
- Božić, Ž.; Schmauder, S.; Wolf, H. The effect of residual stresses on fatigue crack propagation in welded stiffened panels. Eng. Fail. Anal. 2018, 84, 346–357. [Google Scholar] [CrossRef]
- Gannon, L.; Liu, Y.; Pegg, M.; Smith, M. Effect of welding sequence on residual stress and distortion in flat-bar stiffened plates. Mar. Struct. 2010, 23, 385–404. [Google Scholar] [CrossRef]
- Fu, G.M.; Lourenço, I.L.; Duan, M.; Estefen, S.E. Influence of the welding sequence on residual stress and distortion of fillet welded structures. Mar. Struct. 2016, 46, 30–55. [Google Scholar] [CrossRef]
- Jiang, W.; Yahiaoui, K. Effect of welding sequence on residual stress distribution in a multipass welded piping branch junction. Int. J. Press. Vessels Pip. 2012, 95, 39–47. [Google Scholar] [CrossRef]
- Li, Y.; Yoshiyuki, K.; Igarashi, K. Effects of thermal load and cooling condition on weld residual stress in a core shroud with numerical simulation. Nucl. Eng. Des. 2012, 242, 100–107. [Google Scholar] [CrossRef]
- Moat, R.J.; Stone, H.J.; Shirzadi, A.A.; Francis, J.A.; Kundu, S.; Mark, A.F.; Bhadesia, H.K.D.H.; Karlsson, L.; Withers, P.J. Design of weld fillers for mitigation of residual stresses in ferritic and austenitic steel welds. Sci. Technol. Weld. Join. 2011, 16, 279–284. [Google Scholar] [CrossRef]
- Cozzolino, L.D.; Coules, E.; Colegrove, A.P.; Wen, S. Investigation of post-weld rolling methods to reduce residual stress and distortion. J. Mater. Process. Technol. 2017, 247, 243–256. [Google Scholar] [CrossRef]
- Schenk, T.; Richardson, I.M.; Kraska, M.; Ohnimus, S. Influence of clamping on distortion of welded S355 T-joints. Sci. Technol. Weld. Join. 2009, 14, 369–375. [Google Scholar] [CrossRef]
- Chuvas, T.C.; Castello, D.A.; Fonseca, M.P.C. Residual stress relief of welded joints by mechanical vibrations. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 2449–2457. [Google Scholar] [CrossRef]
- Yang, Y.P. Understanding of vibration stress relief with computation modeling. J. Mater. Eng. Perform. 2009, 18, 856–862. [Google Scholar] [CrossRef]
- Samardžić, I.; Vuherer, T.; Marić, D.; Konjatić, P. Influence of vibrations on residual stresses distribution in welded joints. Metalurgija 2015, 54, 527–530. [Google Scholar]
- Dong, P.; Song, S.; Zhang, J. Analysis of residual stress relief mechanisms in post-weld heat treatment. Int. J. Press. Vessels Pip. 2014, 122, 6–14. [Google Scholar] [CrossRef]
- Fu, G.M.; Lourenço, I.L.; Duan, M.; Estefen, S.E. Effects of preheat and interpass temperature on the residual stress and distortion on the T-joint weld. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering OMAE2014, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Kala, S.R.; Prasad, N.S.; Phanikumar, G. Numerical studies on effect of interpass time on distortion and residual stresses in multipass welding. Adv. Mater. Res. 2013, 601, 31–36. [Google Scholar] [CrossRef]
- Ilman, M.N.; Kusmono; Muslih, M.R.; Subeki, N.; Wibovo, H. Mitigating distortion and residual stress by static thermal tensioning to improve fatigue crack growth performance of MIG AA5083 welds. Mater. Des. 2016, 99, 273–283. [Google Scholar] [CrossRef]
- Zhang, W.; Fu, H.; Fan, J.; Li, R.; Xu, H.; Liu, F.; Qi, B. Influence of multi-beam preheating temperature and stress on the buckling distortion in electron beam welding. Mater. Des. 2018, 139, 439–446. [Google Scholar] [CrossRef]
- Okano, S.; Mochizuki, M. Experimental and numerical investigation of trailing heat sink effect on weld residual stress and distortion of austenitic stainless steel. ISIJ Int. 2016, 56, 647–653. [Google Scholar] [CrossRef]
- Zubairuddin, M.; Albert, S.K.; Vasudevan, M.; Mahadevan, S.; Chaudri, V.; Suri, V.K. Thermo-mechanical analysis of preheat effect on grade P91 steel during GTA welding. Mater. Manuf. Process. 2016, 31, 366–371. [Google Scholar] [CrossRef]
- Deng, D.; Liang, W.; Murakawa, H. Determination of welding deformation in fillet-welded joint by means of numerical simulation and comparison with experimental measurements. J. Mater. Process. Technol. 2007, 183, 219–225. [Google Scholar] [CrossRef]
- Yao, T.; Astrup, O.C.; Caridis, P.; Chen, Y.N.; Cho, S.R.; Dow, R.S.; Niho, O.; Rigo, P. Ultimate hull girder strength. In Proceedings of the 14th International Ship and Offshore Structure Congress, Nagasaki, Japan, 2–6 October 2000; Volume 2, pp. 323–333. [Google Scholar]
- Chen, B.K.; Soares, G.C. Effects of plate configurations on the weld induced deformations and strength of fillet-welded plates. Mar. Struct. 2016, 50, 243–259. [Google Scholar] [CrossRef]
- Gannon, L.; Liu, Y.; Peg, N.; Smith, M.J. Effect of welding-induced residual stress and distortion on ship hull girder ultimate strength. Mar. Struct. 2012, 25, 25–49. [Google Scholar] [CrossRef]
- Perić, M.; Tonković, Z.; Rodić, A.; Surjak, M.; Garašić, I.; Boras, I.; Švaić, S. Numerical analysis and experimental investigation in a T-joint fillet weld. Mater. Des. 2014, 53, 1052–1063. [Google Scholar] [CrossRef]
- Perić, M.; Stamenković, D.; Milković, V. Comparison of residual stresses in butt-welded plates using software packages Abaqus and Ansys. Sci. Tech. Rev. 2010, 60, 22–26. [Google Scholar]
- Chen, Z.; Gongrong, L. A study on the spring-back deflections and constraint forces of a bottom grillage cling welding. Ships Offshore Struct. 2017, 12, 1077–1085. [Google Scholar] [CrossRef]
- Lostado, R.L.; Garcia, R.E.; Martinez, R.F.; Martinez Calvo, M.A. Using genetic algorithms with multi-objective optimization to adjust finite element models of welded joints. Metals 2018, 8, 230. [Google Scholar] [CrossRef]
- EN 1011-1. Welding—Recomendations for welding of metallic materials—Part 1. General guidance for arc welding. Change 2009, 30, 9. [Google Scholar]
- Seleš, K.; Perić, M.; Tonković, Z. Numerical simulation of a welding process using a prescribed temperature approach. J. Constr. Steel Res. 2018, 145, 49–57. [Google Scholar] [CrossRef]
- Perić, M.; Tonković, Z.; Garašić, I.; Vuherer, T. An engineering approach for a T-joint fillet welding simulation using simplified material properties. Ocean Eng. 2016, 128, 13–21. [Google Scholar] [CrossRef]
- Menéndez, M.C.; Rodríguez, E.; Ottolini, M.; Caixas, J.; Guirao, J. Analysis of the effect of the electron-beam welding sequence for a fixed manufacturing route using finite element simulations applied to ITER vacuum vessel manufacture. Fusion Eng. Des. 2016, 104, 84–92. [Google Scholar] [CrossRef]
- Perić, M.; Tonković, Z.; Karšaj, I.; Stamenković, D. A simplified engineering method for a T-joint welding simulation. Therm. Sci. 2018, 22, S867–S873. [Google Scholar] [CrossRef]
- Deng, D. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects. Mater. Des. 2009, 30, 359–366. [Google Scholar] [CrossRef]
- Marenić, E.; Skozrit, I.; Tonković, Z. On the calculation of stress intensity factors and J-integrals using the submodeling technique. J. Press. Vessel Technol. 2010, 132, 041203–041212. [Google Scholar] [CrossRef]
- ISO (International Organization for Standardization). Welding—Measurement of Preheating Temperature, Interpass Temperature and Preheat Maintenance Temperature; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- EN 1011-2. Welding—Recommentations for welding of metallic materials—Part 2: Arc welding of ferritic steels. Change 2001, 30, 15–23. [Google Scholar]
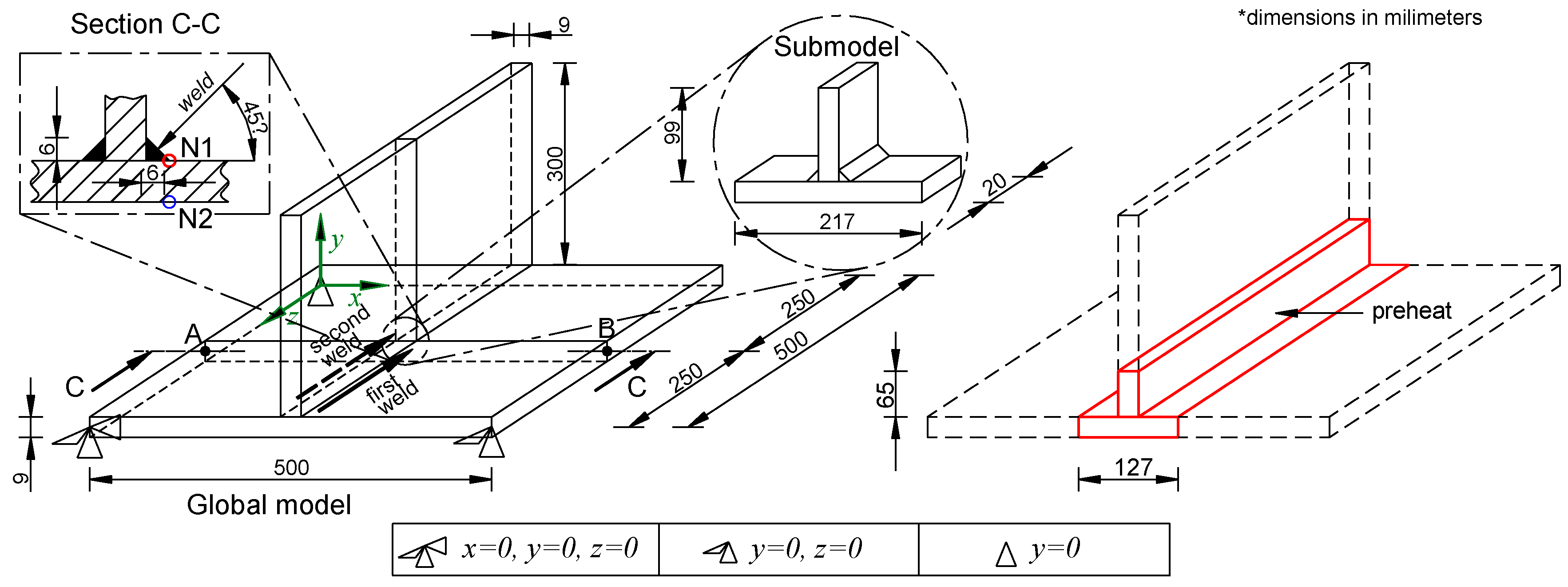
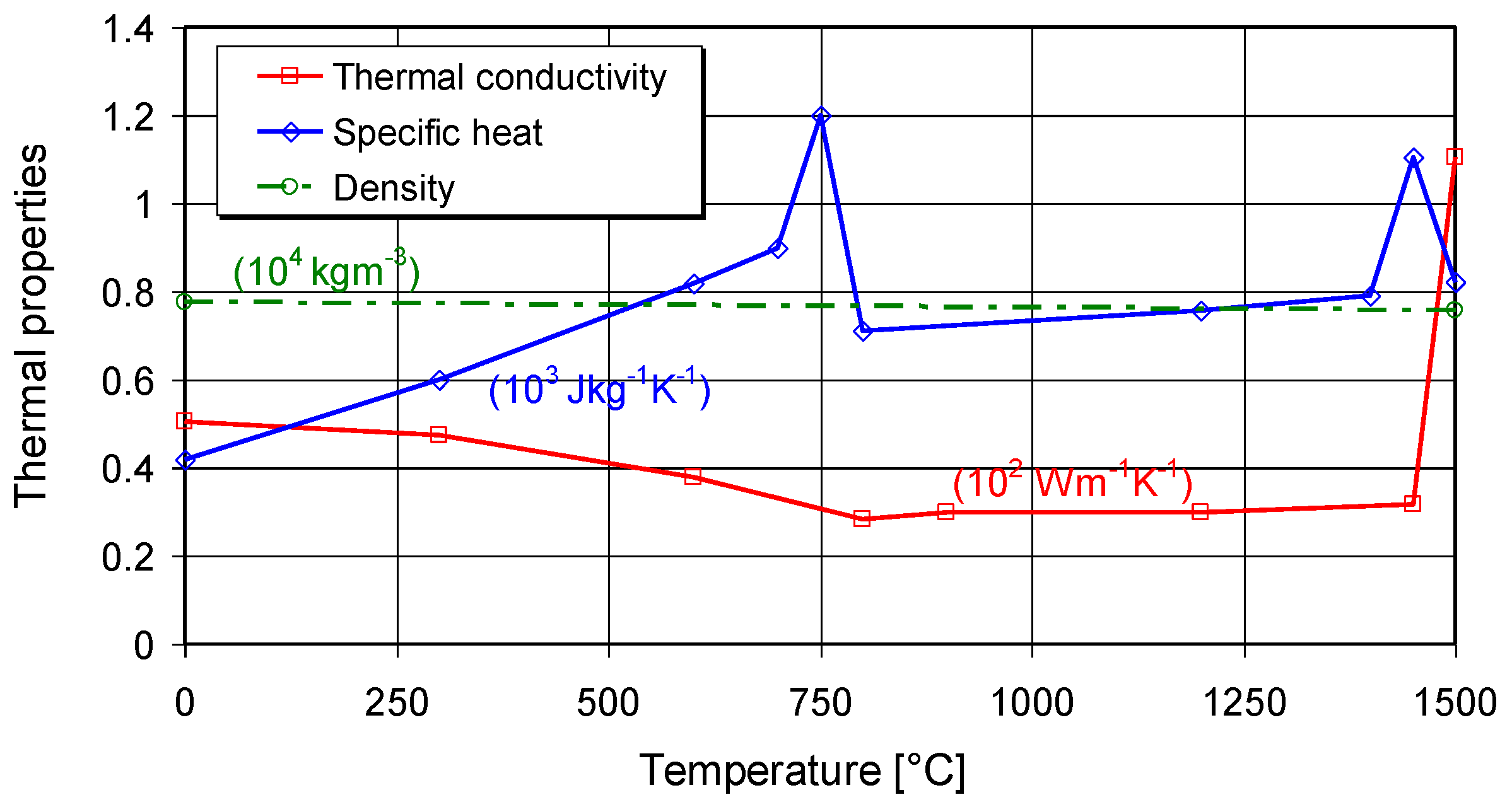
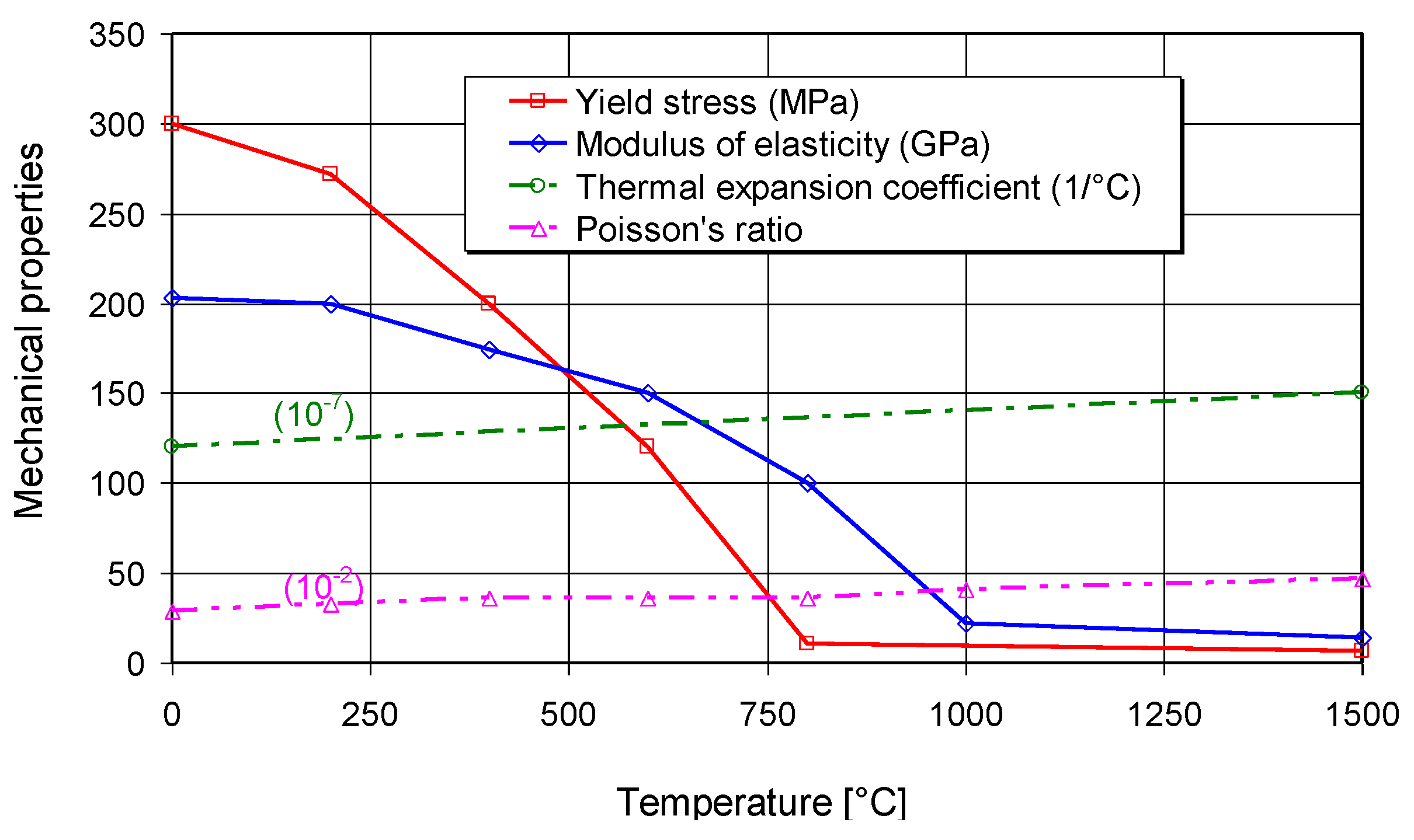
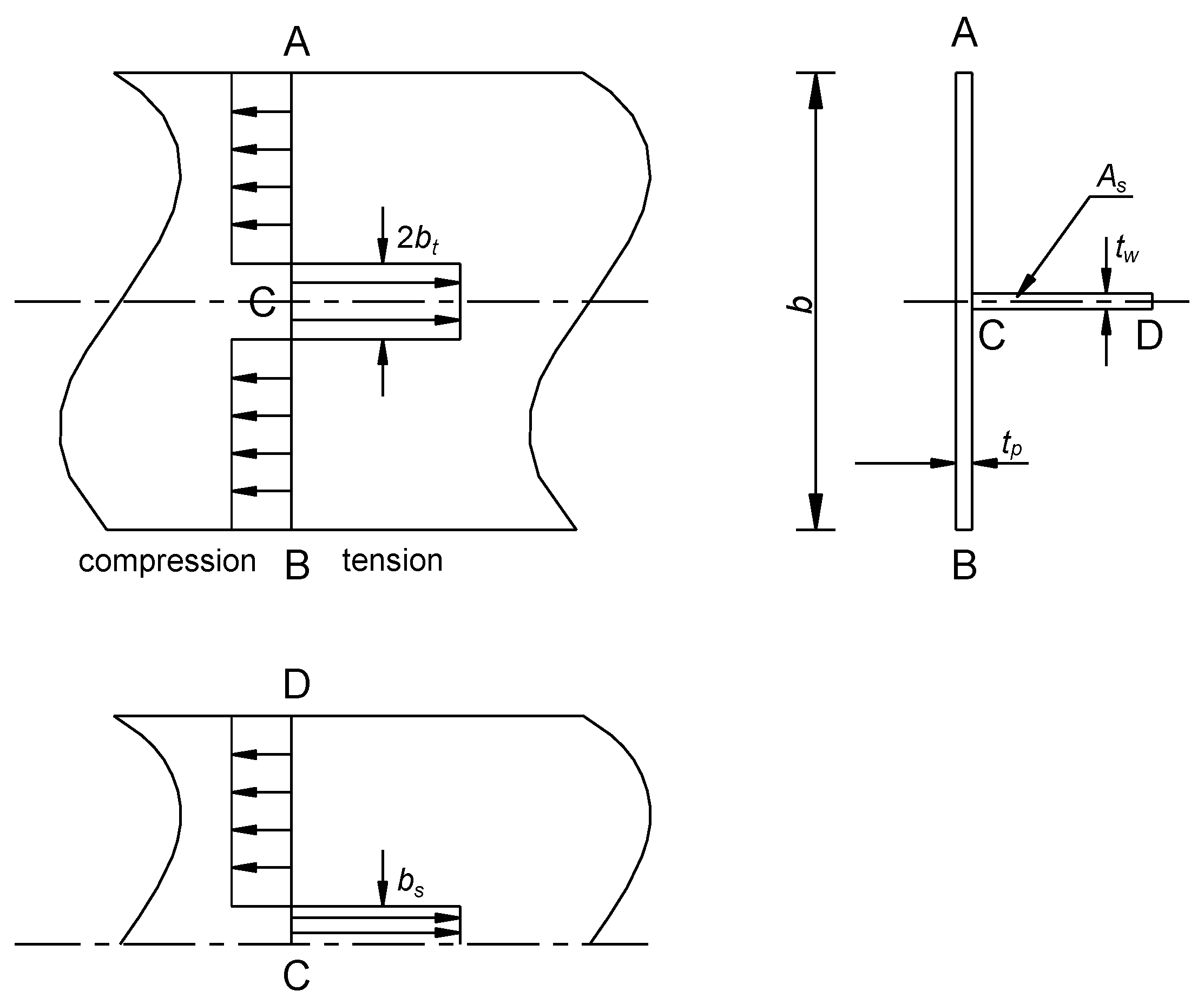

| Welding Current (A) | Welding Voltage (V) | Welding Speed (mm/min) | Angle of Torch (°) |
|---|---|---|---|
| 270 | 29 | 400 | 45 |
| C | Si | Mn | P | S |
|---|---|---|---|---|
| 0.23 | - | 0.56 | <0.035 | <0.035 |
| Model Name | Preheating Application | Interpass Time |
|---|---|---|
| M1 | No | t = 0 s |
| M2 | Yes, T = 100 °C | t = 0 s |
| M3 | Yes, T = 150 °C | t = 0 s |
| M4 | Yes, T = 150 °C | t = 60 s |
| M5 | Yes, T = 150 °C | t = 120 s |
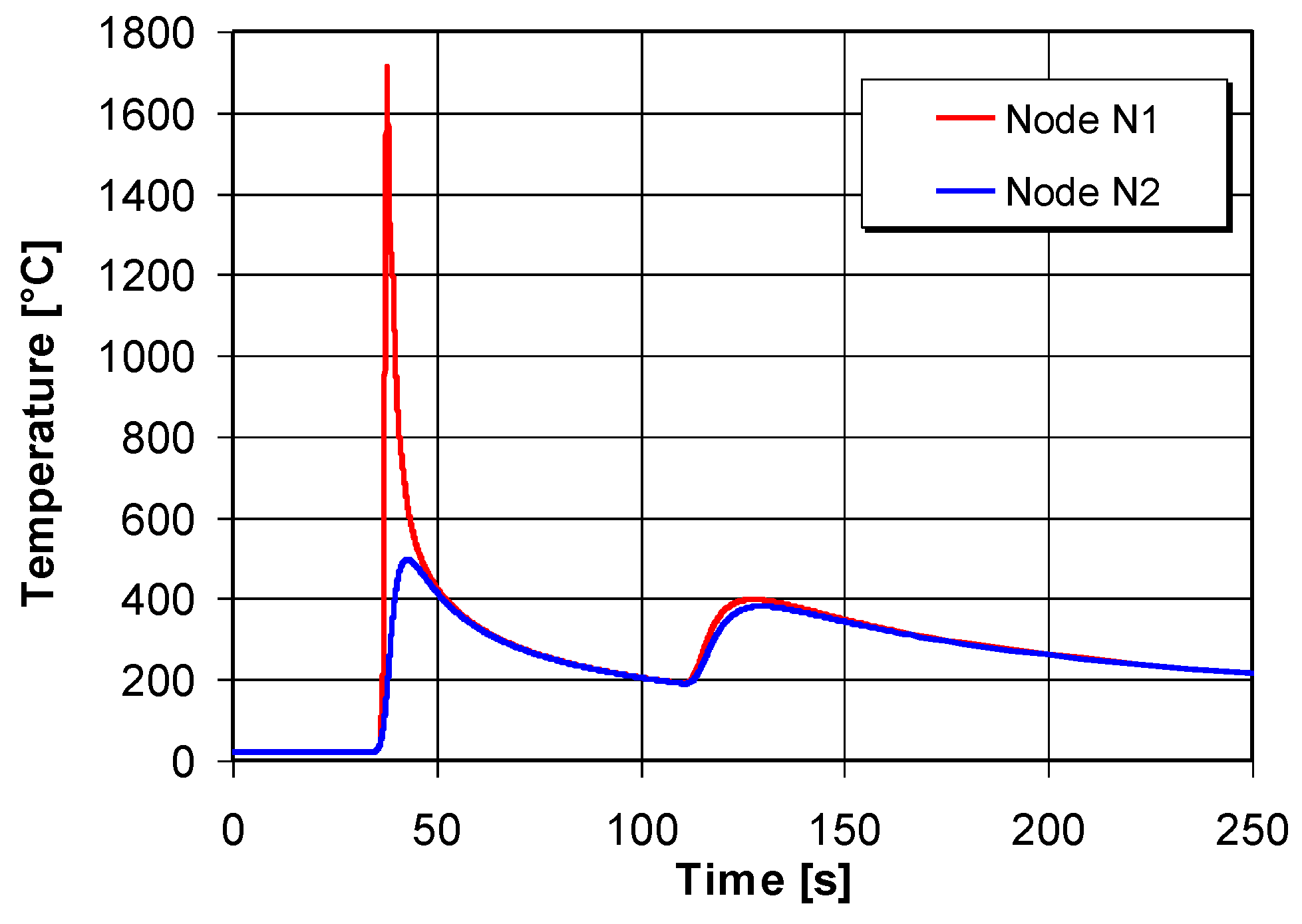
| Peak Temperatures (°C) | Node N1 (1st Pass) | Node N2 (1st Pass) | Node N1 (2nd Pass) | Node N1 (2nd Pass) |
|---|---|---|---|---|
| Current study | 1712 | 496 | 398 | 381 |
| Gannon et. al. [5] | 1730 | 500 | 374 | 356 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perić, M.; Garašić, I.; Nižetić, S.; Dedić-Jandrek, H. Numerical Analysis of Longitudinal Residual Stresses and Deflections in a T-joint Welded Structure Using a Local Preheating Technique. Energies 2018, 11, 3487. https://doi.org/10.3390/en11123487
Perić M, Garašić I, Nižetić S, Dedić-Jandrek H. Numerical Analysis of Longitudinal Residual Stresses and Deflections in a T-joint Welded Structure Using a Local Preheating Technique. Energies. 2018; 11(12):3487. https://doi.org/10.3390/en11123487
Chicago/Turabian StylePerić, Mato, Ivica Garašić, Sandro Nižetić, and Hrvoje Dedić-Jandrek. 2018. "Numerical Analysis of Longitudinal Residual Stresses and Deflections in a T-joint Welded Structure Using a Local Preheating Technique" Energies 11, no. 12: 3487. https://doi.org/10.3390/en11123487
APA StylePerić, M., Garašić, I., Nižetić, S., & Dedić-Jandrek, H. (2018). Numerical Analysis of Longitudinal Residual Stresses and Deflections in a T-joint Welded Structure Using a Local Preheating Technique. Energies, 11(12), 3487. https://doi.org/10.3390/en11123487






