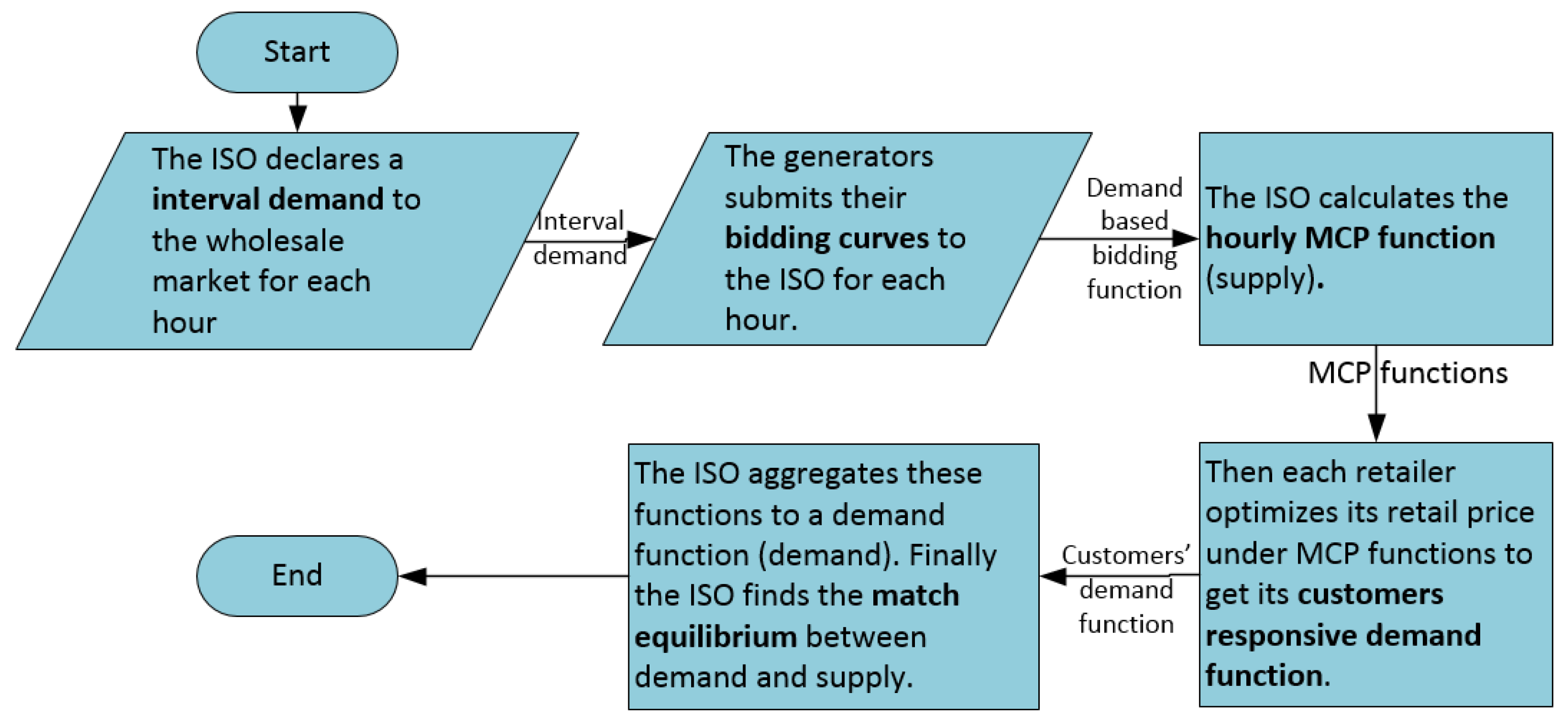
In this section, we introduce our new analytical optimization method to solve the mismatch integration problem. This method can accurately find the match equilibrium in order to best balance the supply and demand. In the first sub-section, the definition of match equilibrium will be introduced. Then we will illustrate the detail of the new analytical optimization method in the second sub-section.
5.1. Match Equilibrium
The methods involving how to obtain the MCP function on the supply side and how to find the optimal prices in order to maximize the profit for the retailer on the demand side have been discussed and solved in the previous sections. However, in the existing wholesale pricing mechanism, the supply and the demand under the demand response program cannot always be matched as aforementioned. In order to overcome this problem, we will illustrate our new analytical optimization method which can efficiently find the match equilibrium between supply and demand in this subsection.
Recall that in the fifth step of our mechanism as shown in
Figure 2, the ISO wants to find the match equilibriums between demand and supply for each hour of the next day. Here we firstly define the match equilibriums.
Definition 1. Denote the MCP vector obtained by the ISO from allfunctions (Equation (1)) as . If MCP satisfies the following condition (6), it is said that the demand and supply reach the match equilibrium under this MCP vector proposed by ISO. In Equation (6),
is the demand of all retailers in hour
h under
, where
is equal to the demand of retailer
j’s customers:
which can be calculated by solving optimization problem (5);
and
are the lower and upper bounds of
corresponding supply segment in
Table 1 respectively.
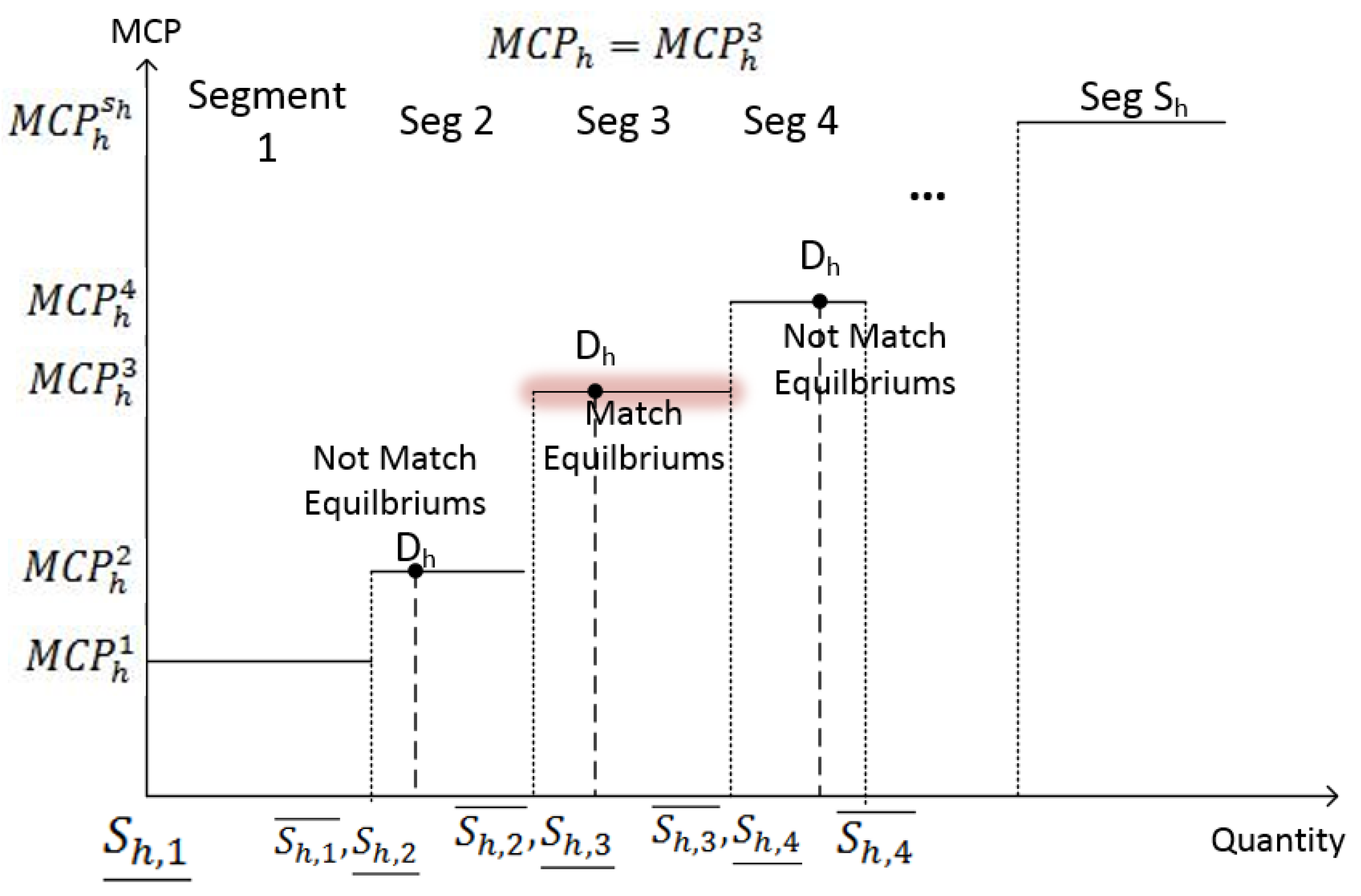
Under the match equilibrium, the total customers’ demand of hour
h:
is located within the supply segment: (
,
] in
Table 1 when the market clearing price is
. Therefore, the balance of supply and demand is matched and then avoids the shortage and surplus of electricity.
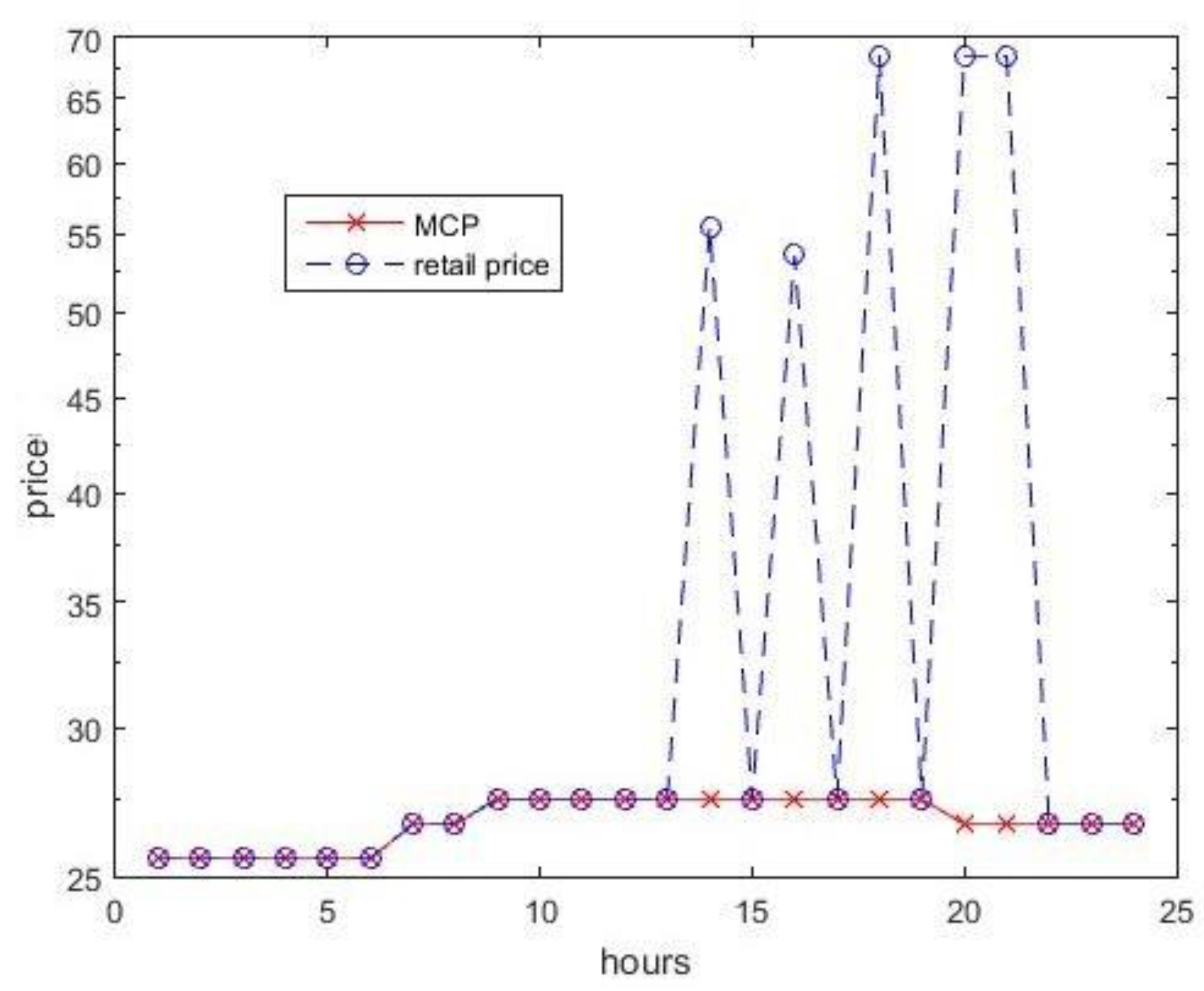
Figure 4 shows an example of match equilibrium in hour
h.
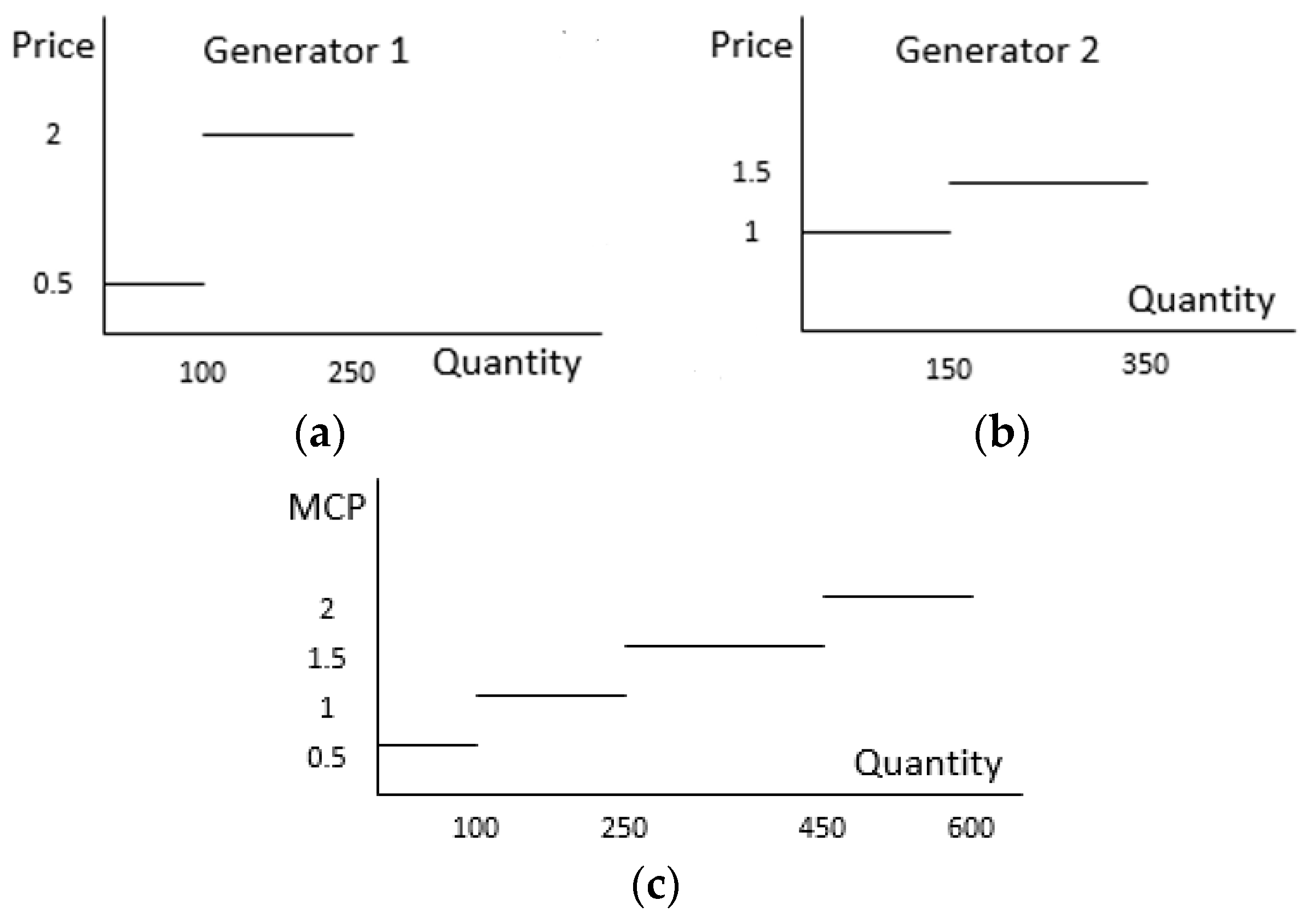
Although the MCP functions are already known, finding the match equilibrium between the demand and supply for each hour of the next day remains a complicated problem for the ISO. This is because the combination of MCP vectors for the next day amounts to a really large number. For each hour h, we use to present the maximize number of segments in the MCP function (Equation (1)) at hour h. The domain of in the MCP function is . Then the combination of all possible MCP vectors in the next day is equal to . For example, when both of are equal to 3 and H is equal to 24, the numbers of combination of all MCP vectors for the next day is 2.8243 ×1011. It is unrealistic, or impossible, for each retailer to solve the problem in Equation (5) so many times.
To the best of our knowledge, it is impossible to find an exact mathematical optimization method for such a problem. Since the number of all possible combinations of
MCP vectors is extremely large, it is also intractable to solve the problem through enumeration. Even if retailers were able to solve problem in Equation (5) for all those combinations, it would cost the ISO a lot of time to connect these results with the
MCP functions and find the match equilibriums. To overcome the problem, we have designed a Genetic Algorithm-based approach to solve this problem to an approximated solution [
26]. Although the genetic algorithm could provide a tractable solution compared to the enumeration, it still needs to calculate the pricing optimization problem for many times and is only able to get an approximate solution [
27]. Therefore, we want to propose a new algorithm to solve the integration problem more accurately and efficiently.
Based on the Equation (6), we proposed the Equations (7) and (8) to analyze whether an
MCP vector is good or not. That is, only when the ISO finds a
MCP vector:
which makes
equals to 0, we could say that the match equilibrium can be reached in the electricity market:
In Equations (7) and (8),
;
is equal to zero if the demand of all retailers in hour
h satisfies the Equation (6). When this occurs, it means that the ISO finds the match equilibrium at hour
h. Otherwise,
presents the difference between the retailers’ demand at hour
h and the supply under
, where the minimum (maximum) supply is the lower (upper) bound of
’s corresponding supply segment in
Table 1. For
possible
MCP vectors, we want to propose an algorithm to find an
MCP vector which makes
given in (8) equal to 0. In other words, the optimization objective function of the problem is given by Equation (8) and the aim of the optimization is to minimize the objective. Since the objective function takes the form of absolution values, the minimum objective of the optimization problem is zero, which means that the match equilibrium is obtained for the considered integration problem. Finally, according to this final/optimal
MCP vector, the ISO can schedule a generation scheme and retailers can price the electricity for each hour of the next day, then the match equilibrium can be reached in the electricity market.
5.2. Proposed Algorithm
In this part, our proposed new algorithm will be illustrated. From the Equation (2), we know that customers’ demand for hour
h can be affected by the price of this hour and other hours. As demonstrated in [
14], self-elasticity
is usually greater than
, we consider the self-elasticity to be the main factor affecting the demand of all customers in this paper. For hour
h, if
is less (greater) than 0 that means the retail market expects less (greater) electricity demand from the supply side (see second (third) condition in Equation (7)) due to the lower (higher)
MCP. In order to reach the match equilibrium in that hour,
should be decreased (increased) in order to increase (reduce) the demand.
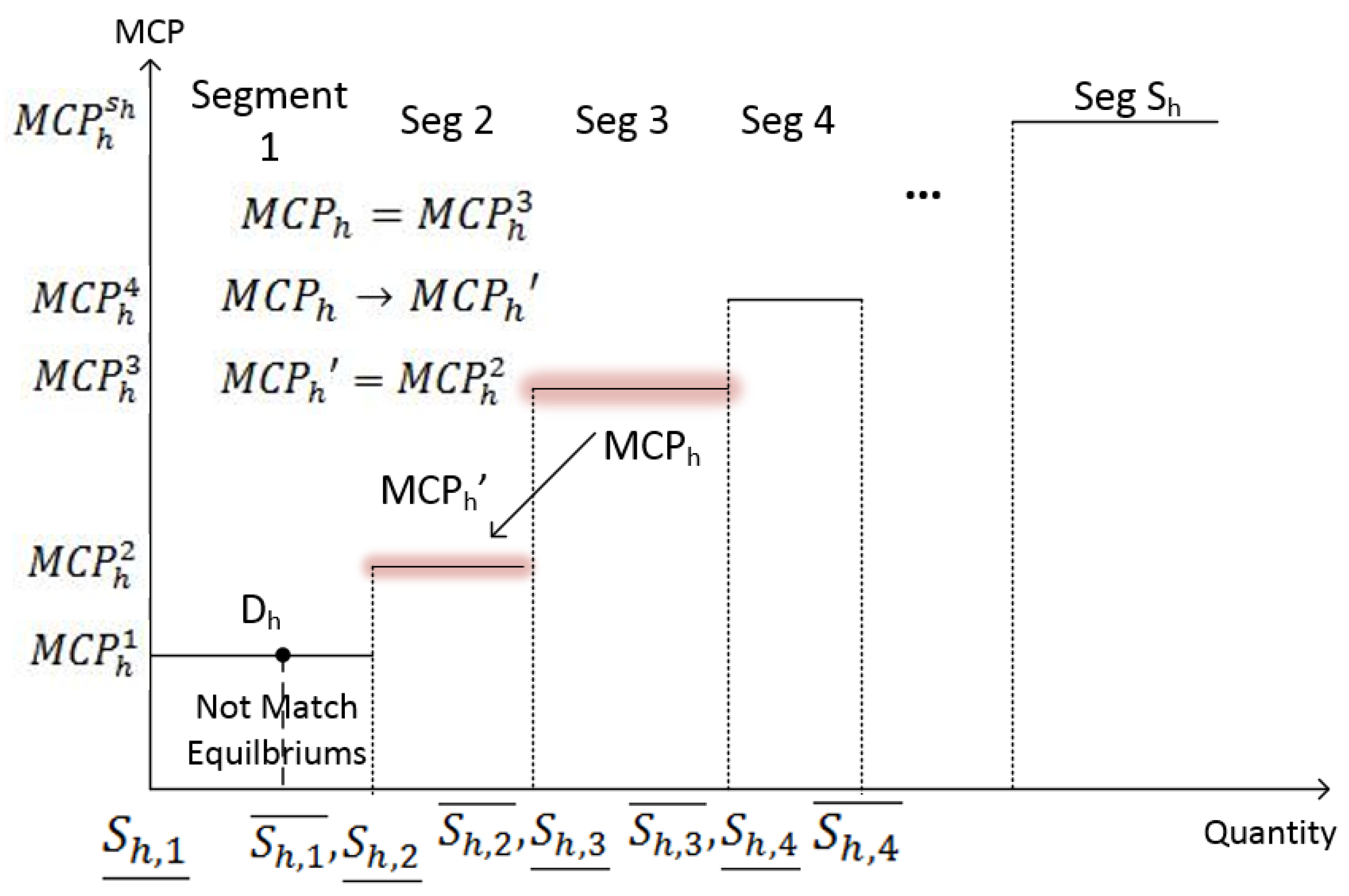
Figure 5 illustrates this scenario: under an
MCP vector:
, where
equals to
, i.e.,
equals to the value of third segment in hour
h’s
MCP function (as can be seen in Equation (1)), the total customers’ demand
is not located within the same segment as
with a less amount, which means that the match equilibrium in hour
is not reached. As a result,
should be decreased to
where
equals to
to increase the demand in order to decrease the value of
and to reach the match equilibrium in that hour. We can use the same idea to find the match equilibria for the remaining hours. Based on the above example, we propose a formal Algorithm 2 to attain the match equilibriums for
H hours of next day. Note that Algorithm 2 is the ultimate solution algorithm for the whole integration problem.
| Algorithm 2 Analytical optimization method |
| | Input:MCP function of each hour (Table 1); A random MCP vector generating from Table 1. |
| | Output: A MCP vector (which reaches the match equilibriums); |
| 1: | Retailers calculate problem (5) by using the input MCP vector; |
| 2: | The ISO calculates for each hour and gets a vector: Er = ; |
| 3: | While exists ; |
| 4: | Find hour h in the set of , where ; |
| 5: | If & ; |
| 6: | Decreases to the value of previous segment in Table 1; |
| 7: | If ; |
| 8: | Increases to the value of next segment in Table 1; |
| 9: | Retailers calculate problem (5) under the modified new MCP vector and get new for each hour; |
| 10: | End while; |
| 11: | Output the final MCP vector and each retailer’s estimated demand. |
In order to ensure the correctness and feasibility of this new algorithm in our mechanism, it is necessary to prove the monotonicity in step 3. If we can prove that the property of monotonicity is held in step 3, this means that will be decreased after each loop. Then we can say that our algorithm becomes closer to the final result (find a MCP vector which makes ) after each loop. Besides, we should also prove the convergence of Algorithm 2. If we can prove that property, which means Algorithm 2 can converge (i.e., find a MCP vector which makes ) after limited numbers of iterations, we can say that our algorithm is feasible to the proposed mechanism.
Firstly, we define the monotonicity of our algorithm:
Definition 2. For hour h, we have(or) andwhere) (or)), then change the value offromto(or), we useto present the changed . If Equation (9) holds, we can say that each iteration in step 3 is monotone. In Equation (9), mean all hours in H except for hour h, . For the scenario of and (or and ), cannot be increased (or decreased), which is the reason that we set ) (or )). It means that the preferred customers’ demand in that hour violates the given demand interval from the ISO. When this happens, the match equilibrium may not be reached. Such situations should be avoided by the ISO. A simple solution is to make sure the declared hourly demand interval be wide enough to consider all possible demand from the retail market.
To facilitate the understanding and for the purpose of illustration, we set
H equal to 2 and
j equal to 1 (that is only two time periods and one retailer are considered) in our proof process. However, the proof is also applicable to cases where there are more than one retailer and more time periods. For the case of the number of retailers, this is mainly because the cross effects of customers among different retailers can be ignored in the context of day-ahead dynamic pricing in the retail market. For the case of time periods, since in each loop of Algorithm 2 we only change a single hour’s
MCP (
changes to
) and in the proof process we split
into two parts:
and
(i.e., all other hours except
h as a whole) considering how the change in
affects these two parts separately, there is no difference when
H is set to be 2 or other values, e.g., 24. Based on the above analysis, the setting of these two parameters (i.e., number of retailers and time periods) does not affect the correctness of our proof process. As a result, in the following proof process, we consider
H = 2 (i.e., the peak hour and off-peak hour) and
j = 1 (one retailer) without loss of generality. Given the demand functions of the retailer in both time periods represented in Equations (10)–(12):
the optimization problem in Equation (5) can be written to Equations (13)–(15):
In our proof process, we will use two theorems. In the following we will prove these two theorems firstly before we present the proof of monotonicity and convergence of Algorithm 2.
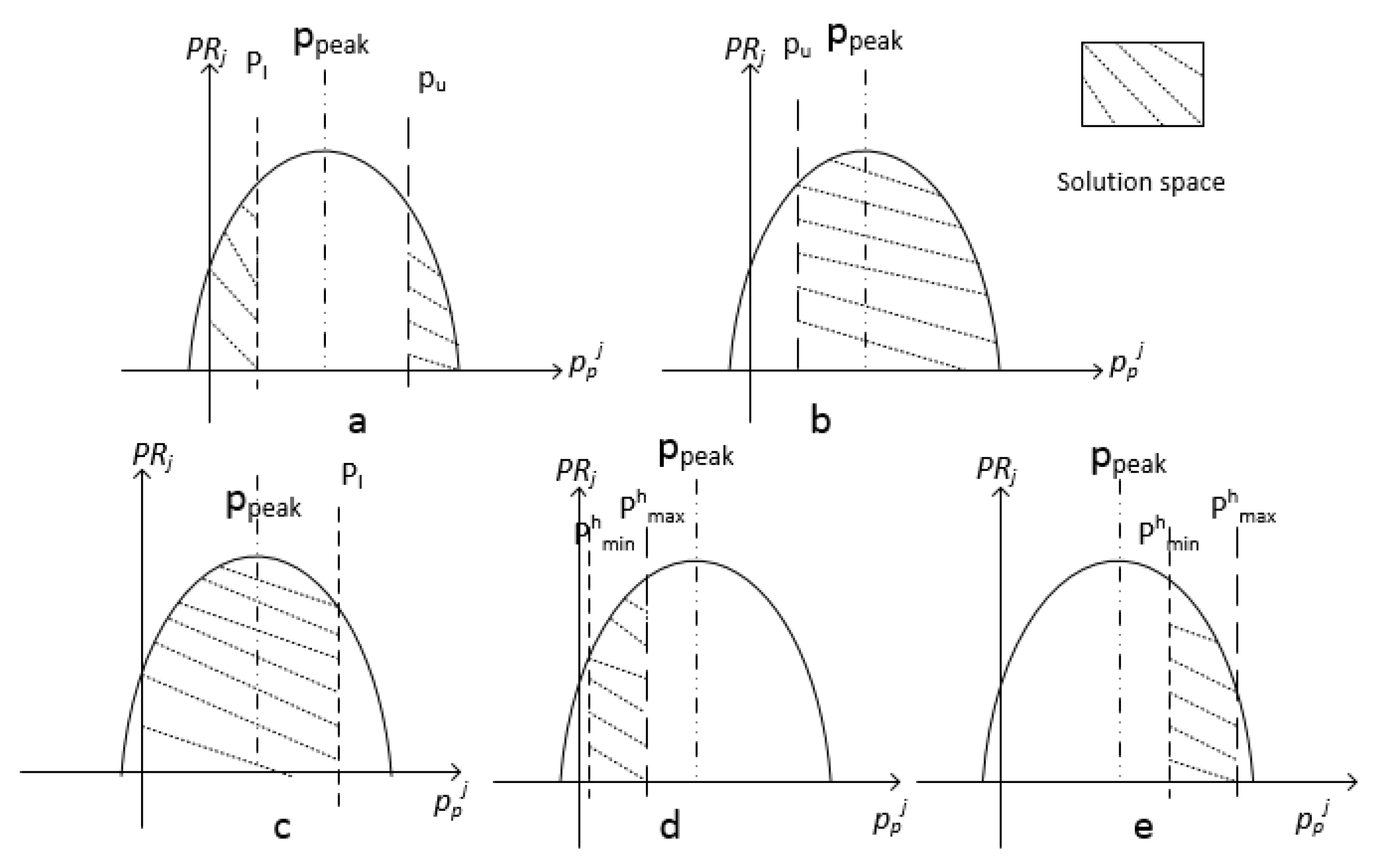
Theorem 1. In problem (13), we assume that the retailer’s optimal retail price in the peak hour will stay the same or decrease (increase) when is decreased (increased).
Proof. The optimal point of
has three different scenarios when
is unchanged. Since the Equation (13) is a quadratic equation and the decision variables are
and
, we can plot it as a parabola in the coordinate system. The
x axis represents the value of
and y axis represents the value of
. The first scenario is that the optimal solution
is in the peak point of Equation (13)’s parabola when the peak point is satisfied the constraints in Equations (14) and (15). On the contrary, the optimal solution is not the peak point in the parabola in both the second and third scenario: the optimal
is in the boundary of constraint in Equations (14) and (15) respectively. The Equation (13) can be transferred to:
☐
According to the peak-point equation in the quadratic equation, we know for equation
, the peak point is
. Based on the differential of Equation (16) of
, the value of peak point in
x axis
is:
From Equation (17), we know is decreased when is decreased. As a result, in the first scenario, we can deduce that will be decreased when is decreased.
In the second scenario, the optimal result of Equation (13) is located at the boundary of sales price constraint Equation (15), which means is equal to (when ) or (when ). We know is decreased when is decreased, which means the parabola of Equation (16) is moved to the left in the coordinate system. Therefore will stay the same when is decreased.
Now we consider the third scenario, the optimal result of (13) is in the boundary of the revenue constraint (14). Then the optimal solution
must satisfy the Equation (18):
This equation is also a quadratic equation for
. We know for equation
, the solution is
. Therefore, we can obtain the solution of Equation (18):
and
, where
. In that scenario, the following inequality must be held; otherwise the optimal result of Equation (13) is not located in the boundary of revenue constraint.
The solution space of in that scenario is: and . The optimal is either or . As a result, when Equation (16)’s parabola is moved to the left in the coordinate system, the optimal is either decreased from to or kept the same as before.
Therefore, we complete the proof of Theorem 1.
Figure 6 illustrates the solution space of these three scenarios of problem Equation (13): part (b) and (c) represents scenario 1; part (a) represents scenario 3 and part d and e represent scenario 2.
The second theorem that we used in our proof process is illustrated as follows:
Theorem 2. The necessary and sufficient condition that the electricity is a demand consistent product in the considered retail market is that, for each , the following inequality holds: The proof of the above theorem is given in [
14]. In the following, we give the proof of the monotonicity and convergence properties in Algorithm 2 (Theorem 3).
Theorem 3. The monotonicity and convergence properties are held in Algorithm 2. In other words, Algorithm 2 can arrive at the final result (find a MCP vector: , which makes ) after a limited number of iterations.
Proof. Monotonicity: for peak hour, if
is smaller than 0, the retailer’s demand is smaller than the lower bound of
corresponding segment in
Table 1. According to our new algorithm, the ISO decreases
to the value of the previous segment in the
MCP table (
Table 1) (for example, if
,
is the second value of column
h in
Table 1, then decreases
from
to
), we use
to represent the changed
. According to Theorem 1, the retailer decreases or keeps unit sales price in the peak hour from
to
when the unit cost (
MCP) in the peak hour from the supply side is decreased. According to
Table 1, we can get the Equation (21) when
is decreased to
:
☐
According to Equations (7) and (8), we calculate the change of
after
is deceased to:
According to the property of self-elasticity, the demand will increase or keep the same when the retail price in the peak hour is decreased from
to
, then we can get:
There could be two different situations for , either be bigger than 0 or smaller than 0.
If
then:
If
:
From (12) and Theorem 2 we know
and
, so we can conduct that in both of these two situations.
Therefore, we proved the monotonicity in this scenario. Similarly, we can use the same method to prove the monotonicity when is greater than 0. In addition to proving the monotonicity of Algorithm 2, we should also prove the convergence in Algorithm 2 to ensure that the program will finally stop at the point that Er is equal to 0.
Convergence: We set
equal to the value of minimum segment in the
Table 1. From Equations (24)–(26), we know that:
Assuming
is the result of Step 2 in Algorithm 2 and
,
t is the looping times of step 3 in the algorithm. From Equation (27) we know that:
If Algorithm 2 will never stop, which means
. According to Equation (28) we can deduce that:
From the Equation (8) we know . But Equation (29) is contradictory with the condition . Therefore, we can deduce that our algorithm can stop in finite steps, which completes the proof of convergence in the Algorithm 2.
After proofing the convergence and monotonicity, we can say that the using Algorithm 2 in our proposed mechanism can converge to a result that all hours in
H can be matched. Then Theorem 3 is proved. The running time
T of Algorithm 2 can be given as:
where the above equation indicates that the ISO only calculates optimization problem in Equation (5) for no more than
times in proposed mechanism. In the above,
is the greatest number in the vector (
) and
t is the running time used for solving the problem in Equation (5) once. It is worth highlighting that the derivation of the upper bound of the running time of Algorithm 2 in Equation (30) is important since it provides meaningful metrics and benchmarks in practical applications and implementation.