Operational Planning and Bidding for District Heating Systems with Uncertain Renewable Energy Production
Abstract
1. Introduction
1.1. Description of Electricity Markets
1.2. Related Work
- The above-mentioned gap is addressed by extending the VPP bidding method of [8], which only considers power production, to a DH setting. Furthermore, we add a second model to optimize the trading on the balancing market after the day-ahead market is cleared. The underlying stochastic programs for modeling the operation of the DH system are formulated in a general manner to be applicable to arbitrary sets of production units in DH systems.
- In contrast to previous work, the method explicitly accounts for the uncertainty coming from RES production in both heat and power and enables us to perform an analysis of the impact of the different uncertainty sources.
- The method is analyzed using a real case study based on the Hvide Sande DH system in Denmark that allows us to draw conclusions on: (a) the behavior of the system under uncertain RES production; (b) the impact of including balancing market trading in the planning method; (c) the benefits of including renewable power production in the portfolio; and (d) the annual system costs compared to traditional bidding methods based on forecasts.
- An additional contribution is a new approach to generate scenarios for balancing market price scenarios needed for the stochastic programming, addressing the balancing market-related operation.
2. Operational Planning Model
2.1. Optimization for the Day-Ahead Market
2.2. Optimization for the Balancing Market
3. Modeling Uncertainty
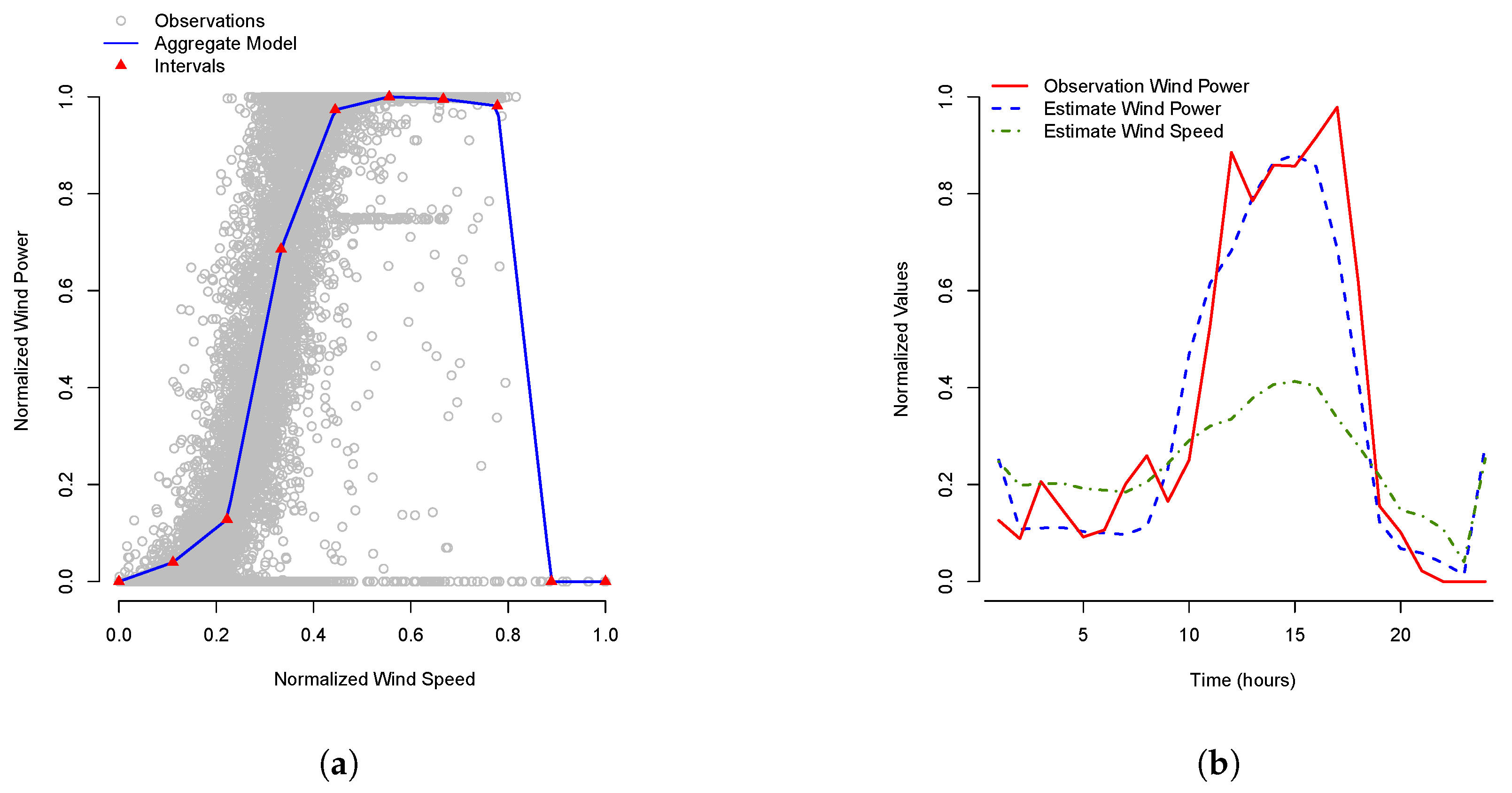
3.1. Wind Power Production Forecast
3.2. Solar Thermal Forecast
3.3. Day-Ahead Electricity Price Forecast
3.4. Scenario Generation for RES Production and Day-Ahead Market Prices
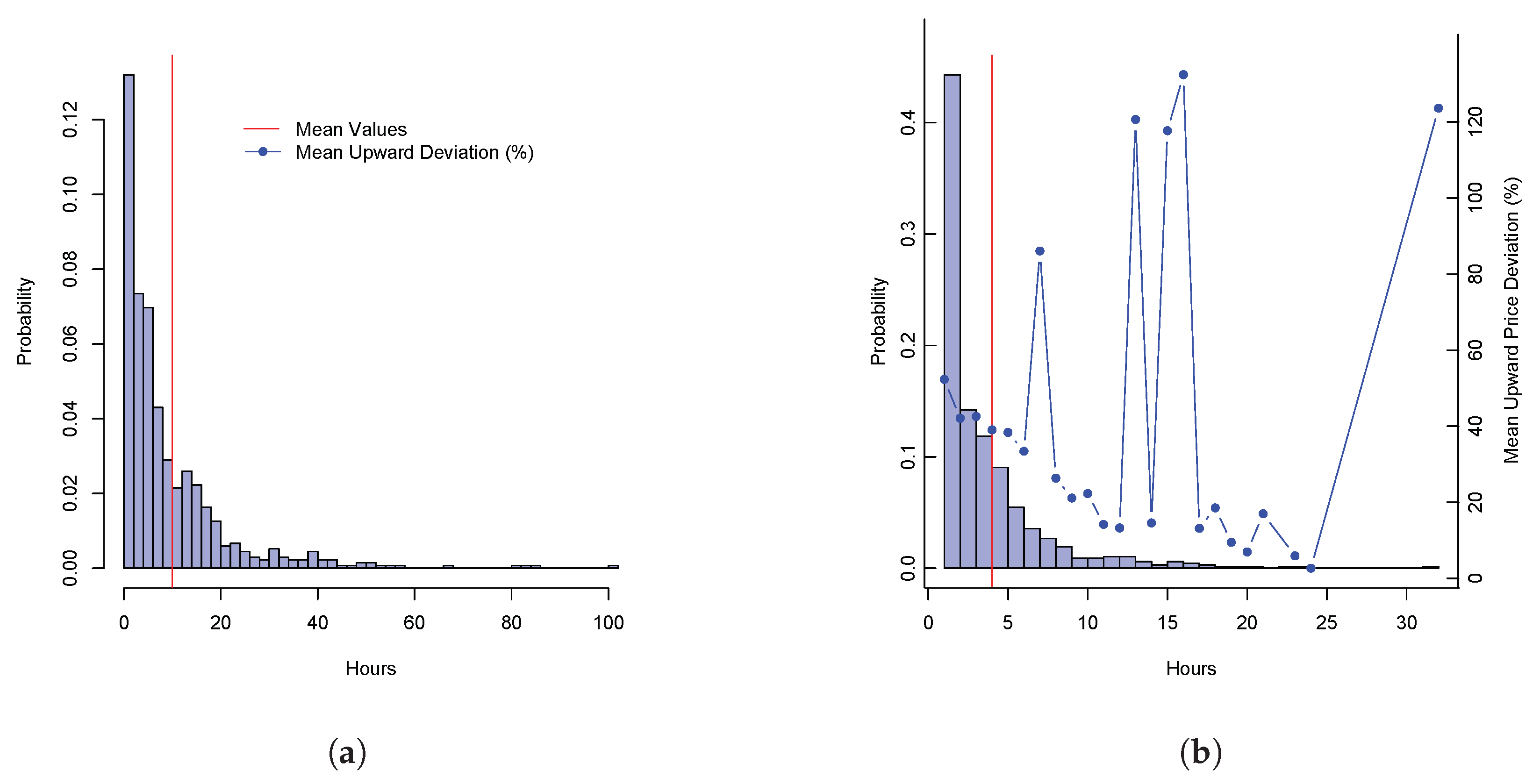
3.5. Scenario Generation for Balancing Prices
| Algorithm 1 Generate balancing price scenarios. |
| 1: for each do |
| 2: |
| 3: while do |
| 4: where is random |
| 5: where is random |
| 6: |
| 7: |
| 8: for to do |
| 9: = 0 |
| 10: end for |
| 11: for to do |
| 12: = where is random |
| 13: end for |
| 14: |
| 15: end while |
| 16: end for |
| 17: Return |
4. Operational Scheduling and Bidding Method
5. Case Study
6. Analysis of the Experimental Results
- After day-ahead market closure for day d (day ): Evaluate the day-ahead market bids with the now known electricity prices and save production amounts of won bids.
- Each hour on day d:
- (a)
- (b)
- Evaluate the balancing-market bids with the now known balancing electricity prices; fix the committed production amounts; and resolve the model to get actual costs and thermal storage levels.
- Move to the next day
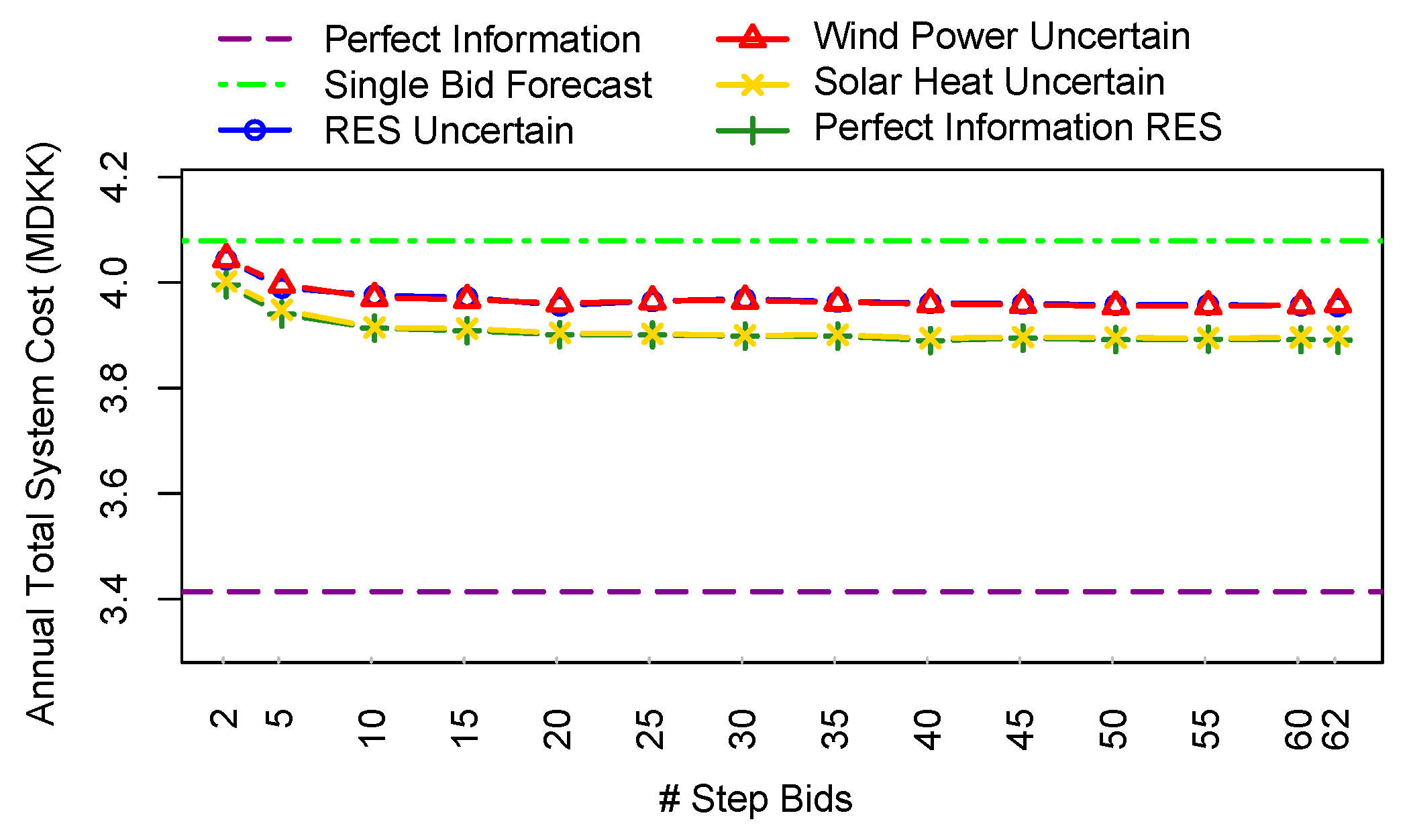
6.1. Influence of Uncertainty and Number of Bidding Curve Steps on the Day-Ahead Market Results
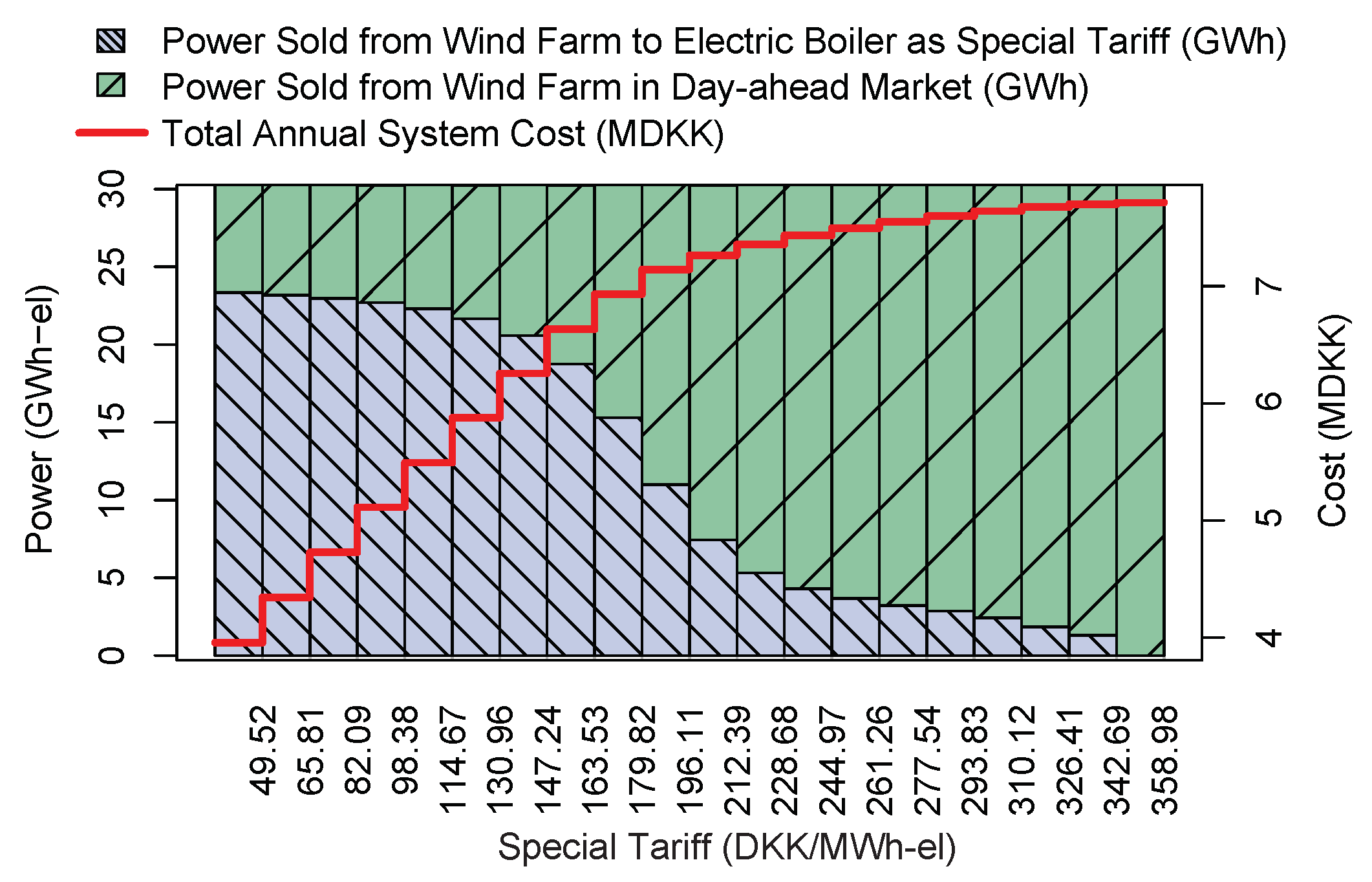
6.2. Impact of Special Tariff for the Electric Boiler
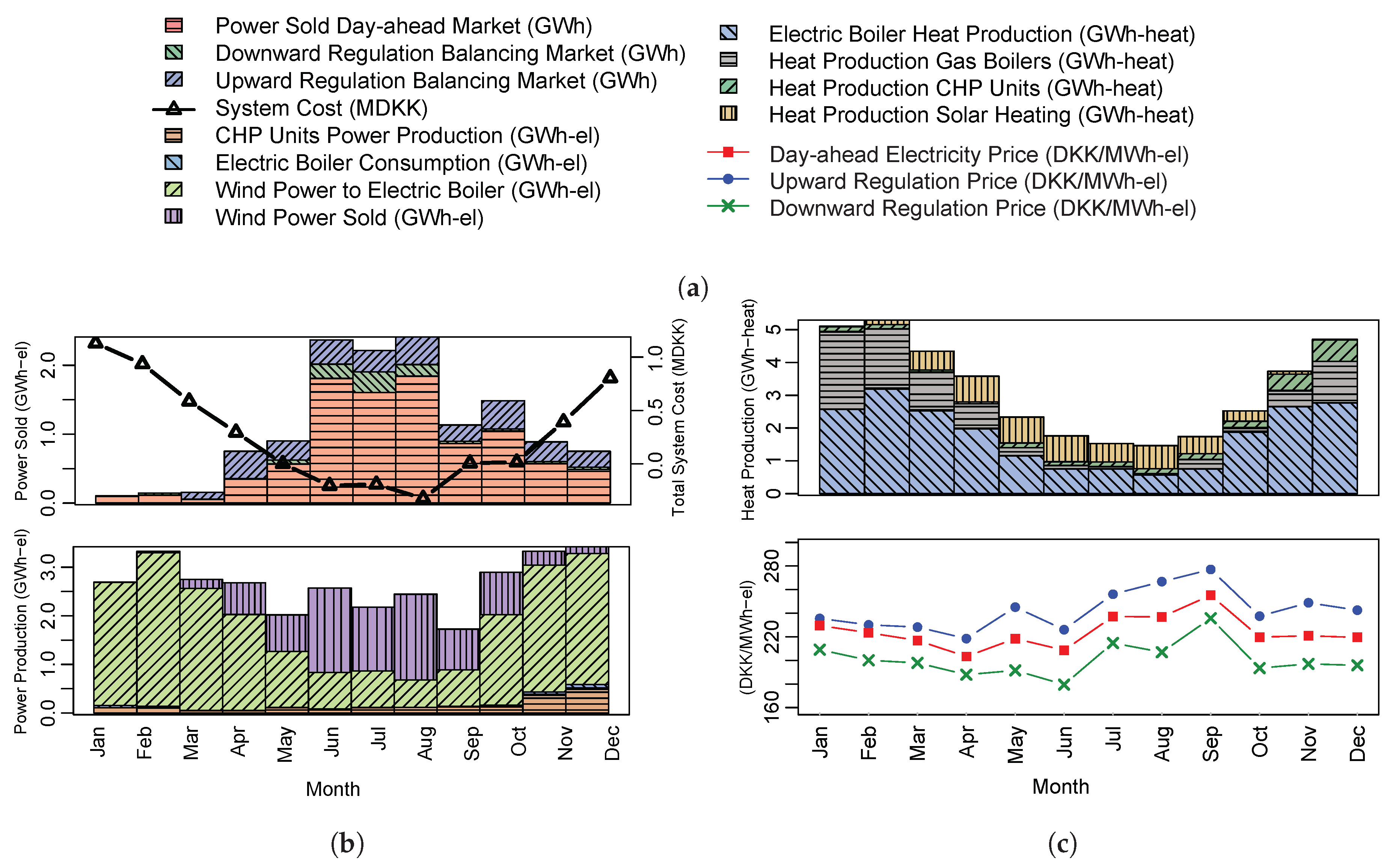
6.3. Analysis of Yearly Production
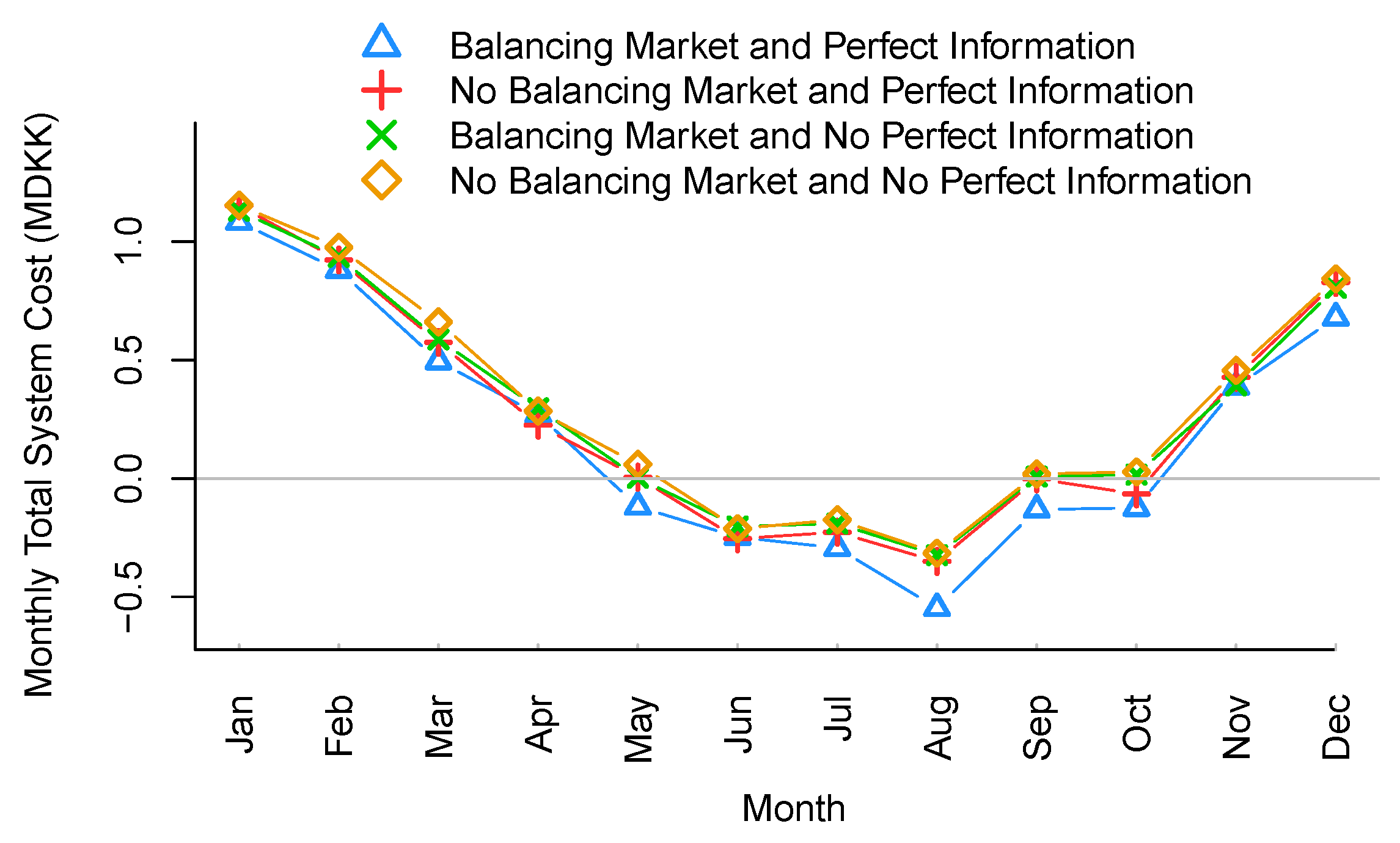
6.4. Value of Including Balancing Market Trading
6.5. Behavior of the System in the Case of Upward and Downward Regulation
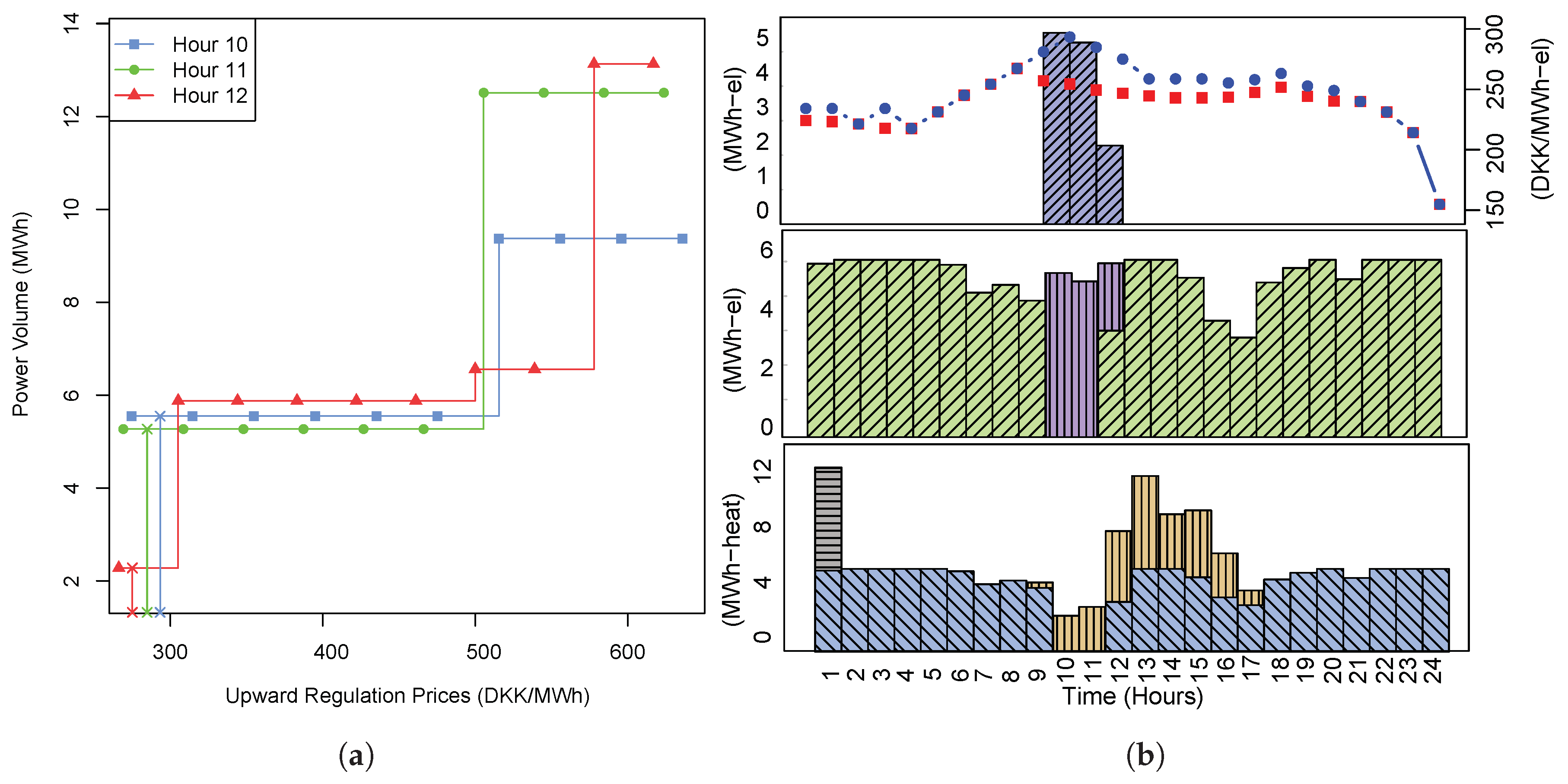
6.5.1. Upward Regulation
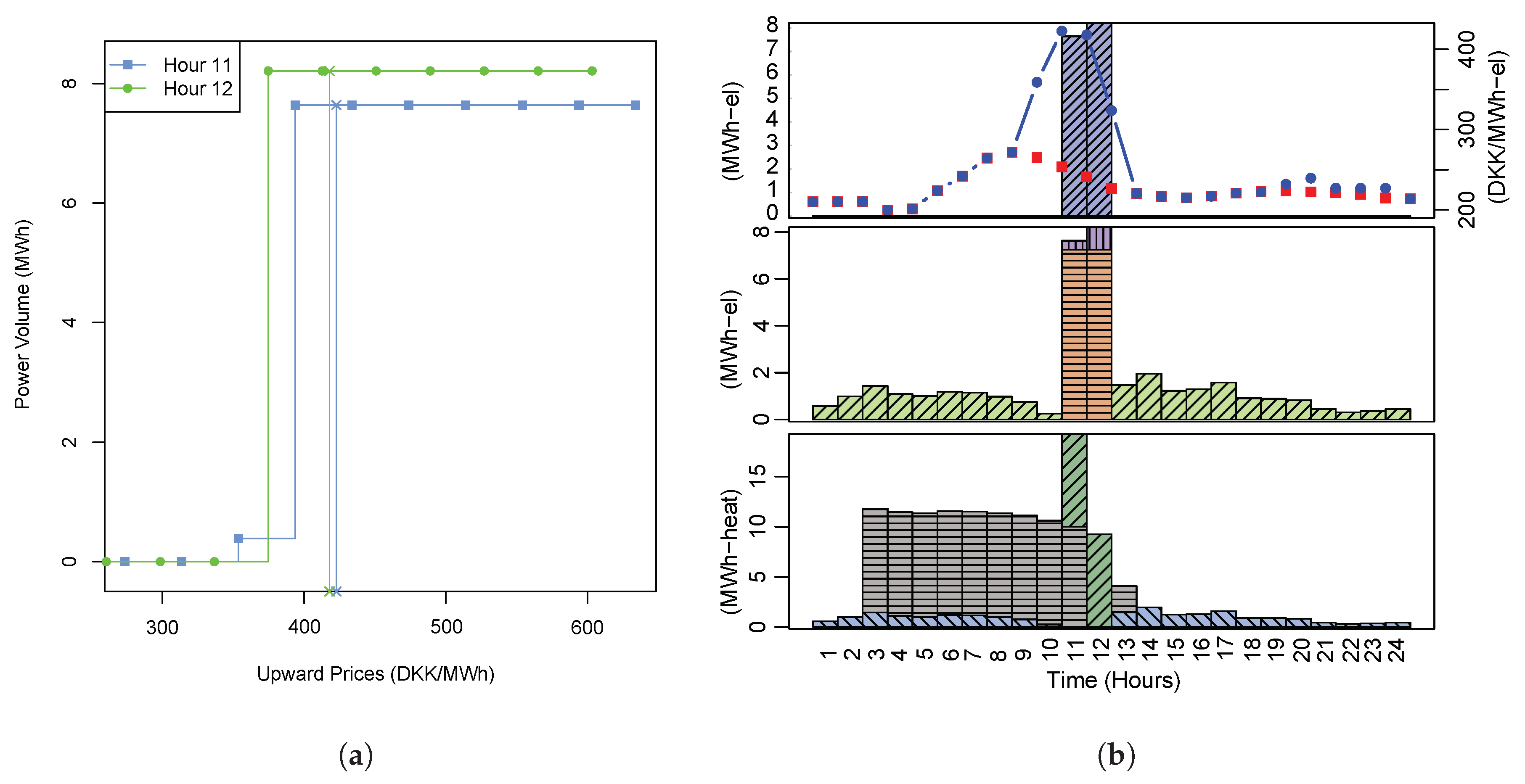
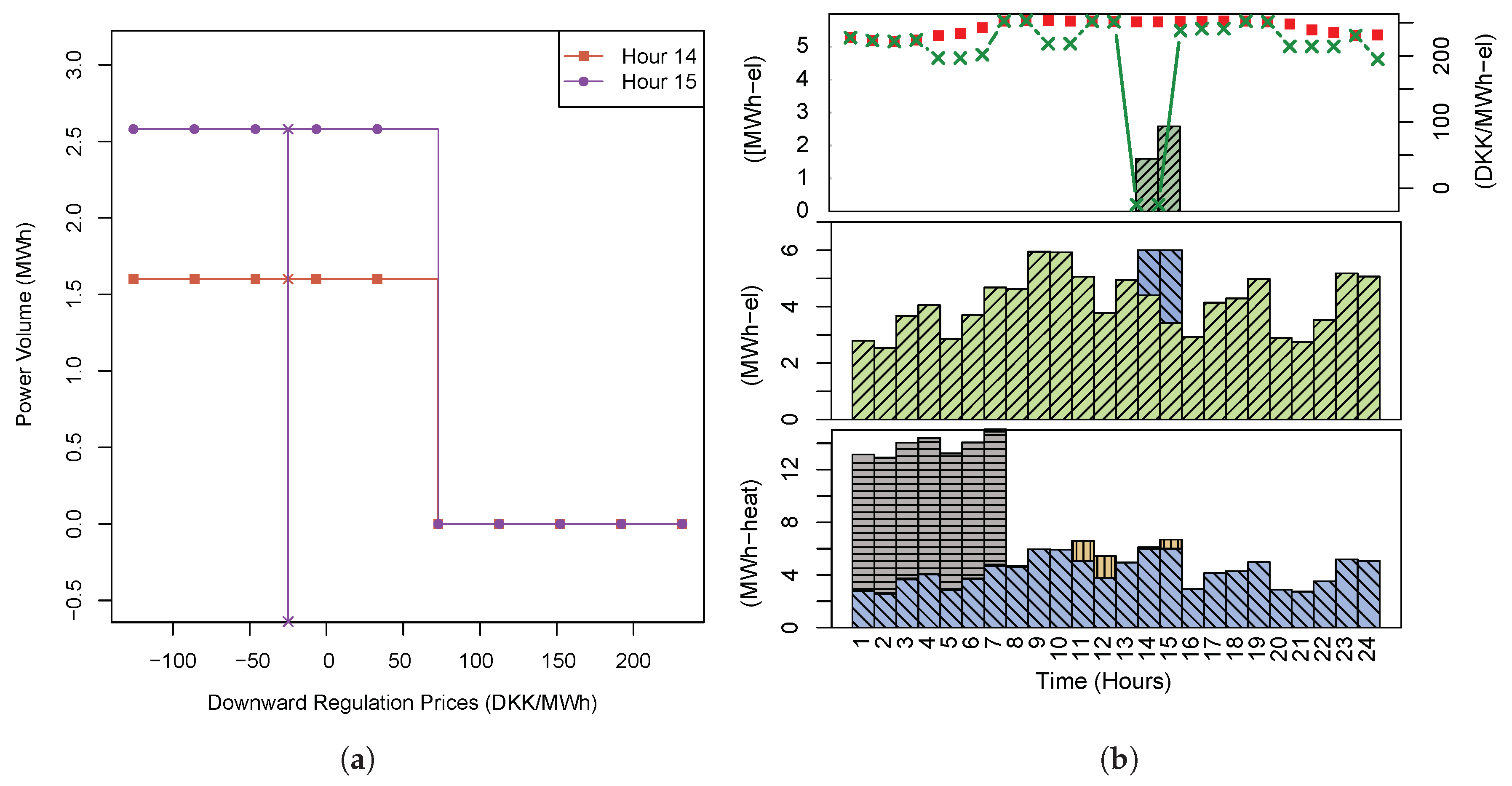
6.5.2. Downward Regulation
7. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Commission. Efficient District Heating and Cooling Systems in the EU. 2016. Available online: https://www.euroheat.org/wp-content/uploads/2017/01/study-on-efficient-dhc-systems-in-the-eu-dec2016_final-public-report6.pdf (accessed on 2 February 2018).
- Connolly, D.; Lund, H.; Mathiesen, B.; Werner, S.; Möller, B.; Persson, U.; Boermans, T.; Trier, D.; Østergaard, P.; Nielsen, S. Heat Roadmap Europe: Combining district heating with heat savings to decarbonise the EU energy system. Energy Policy 2014, 65, 475–489. [Google Scholar] [CrossRef]
- Euroheat & Power. District Energy in Denmark. 2017. Available online: https://www.euroheat.org/knowledge-centre/district-energy-denmark/ (accessed on 15 March 2018).
- Danish Energy Agency. Regulation and Planning of District Heating in Denmark. Available online: https://ens.dk/sites/ens.dk/files/Globalcooperation/regulation_and_planning_of_district_heating_in_denmark.pdf (accessed on 10 September 2018).
- Madsen, H.; Parvizi, J.; Sempreviva, A.M.; Bindner, H.W.; Dent, C.; Mackensen, R. Integrated energy systems; aggregation, forecasting, and control. In DTU International Energy Report 2015; Technical University of Denmark (DTU): Kgs. Lyngby, Denmark, 2015; pp. 34–40. [Google Scholar]
- Pezzutto, S.; Grilli, G.; Zambotti, S.; Dunjic, S. Forecasting Electricity Market Price for End Users in EU28 until 2020—Main Factors of Influence. Energies 2018, 11, 1460. [Google Scholar] [CrossRef]
- Kavvadias, K. Energy price spread as a driving force for combined generation investments: A view on Europe. Energy 2016, 115, 1632–1639. [Google Scholar] [CrossRef]
- Pandžić, H.; Morales, J.M.; Conejo, A.J.; Kuzle, I. Offering model for a virtual power plant based on stochastic programming. Appl. Energy 2013, 105, 282–292. [Google Scholar] [CrossRef]
- Carpaneto, E.; Lazzeroni, P.; Repetto, M. Optimal integration of solar energy in a district heating network. Renew. Energy 2015, 75, 714–721. [Google Scholar] [CrossRef]
- Wang, H.; Yin, W.; Abdollahi, E.; Lahdelma, R.; Jiao, W. Modelling and optimization of CHP based district heating system with renewable energy production and energy storage. Appl. Energy 2015, 159, 401–421. [Google Scholar] [CrossRef]
- Li, J.; Fang, J.; Zeng, Q.; Chen, Z. Optimal operation of the integrated electrical and heating systems to accommodate the intermittent renewable sources. Appl. Energy 2016, 167, 244–254. [Google Scholar] [CrossRef]
- Paraschiv, F.; Erni, D.; Pietsch, R. The impact of renewable energies on EEX day-ahead electricity prices. Energy Policy 2014, 73, 196–210. [Google Scholar] [CrossRef]
- Kwon, R.H.; Frances, D. Optimization-Based Bidding in Day-Ahead Electricity Auction Markets: A Review of Models for Power Producers. In Handbook of Networks in Power Systems I; Sorokin, A., Rebennack, S., Pardalos, P.M., Iliadis, N.A., Pereira, M.V.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 41–59. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Schulz, K.; Hechenrieder, B.; Werners, B. Optimal Operation of a CHP Plant for the Energy Balancing Market. In Operations Research Proceedings 2014; Springer International Publishing: Basel, Switzerland, 2016; pp. 531–537. [Google Scholar]
- Ravn, H.V.; Riisom, J.; Schaumburg-Müller, C.; Straarup, S.N. Modelling Danish local CHP on market conditions. In Proceedings of the 6th IAEE European Conference: Modelling in Energy Economics and Policy, Zürick, Switzerland, 2–3 September 2004. [Google Scholar]
- Dimoulkas, I.; Amelin, M. Constructing bidding curves for a CHP producer in day-ahead electricity markets. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Dubrovnic, Croatia, 13–16 May 2014; pp. 487–494. [Google Scholar]
- Ayón, X.; Moreno, M.Á.; Usaola, J. Aggregators’ Optimal Bidding Strategy in Sequential Day-Ahead and Intraday Electricity Spot Markets. Energies 2017, 10, 450. [Google Scholar] [CrossRef]
- Plazas, M.A.; Conejo, A.J.; Prieto, F.J. Multimarket optimal bidding for a power producer. IEEE Trans. Power Syst. 2005, 20, 2041–2050. [Google Scholar] [CrossRef]
- Pei, W.; Du, Y.; Deng, W.; Sheng, K.; Xiao, H.; Qu, H. Optimal bidding strategy and intramarket mechanism of microgrid aggregator in real-time balancing market. IEEE Trans. Ind. Inf. 2016, 12, 587–596. [Google Scholar] [CrossRef]
- Hosseini-Firouz, M. Optimal offering strategy considering the risk management for wind power producers in electricity market. Int. J. Electr. Power Energy Syst. 2013, 49, 359–368. [Google Scholar] [CrossRef]
- Vardanyan, Y.; Hesamzadeh, M.R. The coordinated bidding of a hydropower producer in three-settlement markets with time-dependent risk measure. Electr. Power Syst. Res. 2017, 151, 40–58. [Google Scholar] [CrossRef]
- Kumbartzky, N.; Schacht, M.; Schulz, K.; Werners, B. Optimal operation of a CHP plant participating in the German electricity balancing and day-ahead spot market. Eur. J. Oper. Res. 2017, 261, 390–404. [Google Scholar] [CrossRef]
- Petrichenko, R.; Baltputnis, K.; Sauhats, A.; Sobolevsky, D. District heating demand short-term forecasting. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–5. [Google Scholar]
- Pinson, P.; Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Local linear regression with adaptive orthogonal fitting for the wind power application. Stat. Comput. 2008, 18, 59–71. [Google Scholar] [CrossRef]
- EMD International A/S. Solar Collectors and Photovoltaics in Energy PRO. Available online: https://www.emd.dk/files/energypro/HowToGuides/Solar%20collectors%20and%20photovoltaics%20in%20energyPRO.pdf (accessed on 5 September 2018).
- Gonzalez, V.; Contreras, J.; Bunn, D.W. Forecasting power prices using a hybrid fundamental-econometric model. IEEE Trans. Power Syst. 2012, 27, 363–372. [Google Scholar] [CrossRef]
- Ringwood, J.; Austin, P.C.; Monteith, W. Forecasting weekly electricity consumption: A case study. Energy Econ. 1993, 15, 285–296. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrión, M.; Morales, J.M. Decision Making under Uncertainty in Electricity Markets; Springer Science & Business Media: New York, NY, USA, 2010; Volume 1. [Google Scholar]
- Reynolds, A.P.; Richards, G.; de la Iglesia, B.; Rayward-Smith, V.J. Clustering rules: A comparison of partitioning and hierarchical clustering algorithms. J. Math. Model. Algorithms 2006, 5, 475–504. [Google Scholar] [CrossRef]
- Olsson, M.; Soder, L. Modeling real-time balancing power market prices using combined SARIMA and Markov processes. IEEE Trans. Power Syst. 2008, 23, 443–450. [Google Scholar] [CrossRef]
- Energinet—Energy Data Service. Available online: https://www.energidataservice.dk/en/ (accessed on 3 October 2018).
- Nord Pool Spot Glossary. Available online: https://www.energiforetagen.se/globalassets/energiforetagen/det-erbjuder-vi/kurser-och-konferenser/krisutbildningar/nord-pool-spot-glossary.pdf (accessed on 3 October 2018).



| Sets | |
| Set of time periods t | |
| Set of heat production units u | |
| Subset of CHP production units | |
| Subset of heat-only production units | |
| Subset of power to heat production units | |
| Subset of stochastic heat production units | |
| Set of intermittent renewable power-only producers g | |
| Set of heat storage tanks s | |
| Set of scenarios | |
| Parameters | |
| Cost for producing heat with unit (DKK/MWh-heat) | |
| Tariff cost for producing power with unit and using it to produce heat in unit (DKK/MWh-el) | |
| Maximum/minimum heat production for unit (MWh-heat) | |
| Binary parameter: 1, if unit is connected to the DH system, 0 otherwise | |
| Binary parameter: 1, if unit is connected to the thermal storage s, 0 otherwise | |
| Heat-to-power ratio for unit () | |
| Initial level in storage s (MWh-heat) | |
| Maximum/minimum heat level in storage s (MWh-heat) | |
| Electricity price for time period (DKK/MWh-el) | |
| / | Penalty for positive/negative imbalance in time period (DKK/MWh-el) |
| / | Upward/downward regulating price for time period (DKK/MWh-el) |
| Heat demand for time period (MWh-heat) | |
| Stochastic power production of power-only unit | |
| Stochastic heat production from heat production unit | |
| Probability of scenario | |
| Parameter that determines the deviation of the penalty for the positive and negative imbalance | |
| Variables | |
| Power bid to the day-ahead market unit in period (MWh-el) | |
| Heat production of heat unit in period (MWh-heat) | |
| Heat production of unit inserted into the grid in period (MWh-heat) | |
| Heat production of unit inserted into storage s in period (MWh-heat) | |
| Power production of unit in period (MWh-el) | |
| Power obtained from the grid to produce heat with unit in period (MWh-el) | |
| Power production of unit that serves the heat production of unit in period (MWh-el) | |
| Power generation from unit in period (MWh-el) | |
| Positive/negative power imbalance purchased/sold in period and scenario (MWh-el) | |
| Upward/downward regulating power purchased/sold in period and scenario (MWh-el) | |
| Level in storage s at time period (MWh-heat) | |
| Heat flowing from the storage s to the DH in period (MWh-heat) | |
| Mean time to activate upward regulation (hours) | |
| Mean time to activate downward regulation (hours) | |
| Mean duration for upward regulation (hours) | |
| Mean duration for downward regulation (hours) | |
| Function for the upward regulation value given an upward time duration length | |
| Function for the downward regulation value given a downward time duration length | |
| Matrix of values for the upward regulation (%) | |
| Matrix of values for the downward regulation (%) | |
| Number of considered scenarios | |
| Forecast horizon | |
| Random variables uniformly distributed between 0 and 1 | |
| Normally-distributed random noise added to the function / |
| Unit | Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ST1 | ST2 | ||||||||
| CHP1 | 689.01 | - | 4.63 | 3.62 | 1.28 | 0 | 1 | 0 | |
| CHP2 | 689.01 | - | 4.63 | 3.62 | 1.28 | 0 | 1 | 0 | |
| GB1 | 401.30 | - | 10.37 | 0.00 | - | 0 | 1 | 0 | |
| GB2 | 416.29 | - | 3.77 | 0.00 | - | 0 | 1 | 0 | |
| EB | 359.98 | 49.52 | 6.00 | 0.00 | 1.00 | 0 | 1 | 0 | |
| SC | 0.00 | - | 100.00 | 0.00 | - | 0 | 0 | 1 | |
| WF | 0.00 | - | 0.00 | 0.00 | - | - | - | - | |
| ST1 | 115.88 | 0.00 | 57.94 | ||||||
| ST2 | 48.67 | 0.00 | 24.34 | ||||||
| Setting | Total System Cost (DKK) | |
|---|---|---|
| Perfect information incl.balancing market | 2,499,205 | - |
| Perfect information excl.balancing market | 3,414,310 | +37% |
| Stochastic incl. balancing market | 3,655,798 | +7% |
| Stochastic excl. balancing market | 3,956,530 | +8% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanco, I.; Guericke, D.; Andersen, A.N.; Madsen, H. Operational Planning and Bidding for District Heating Systems with Uncertain Renewable Energy Production. Energies 2018, 11, 3310. https://doi.org/10.3390/en11123310
Blanco I, Guericke D, Andersen AN, Madsen H. Operational Planning and Bidding for District Heating Systems with Uncertain Renewable Energy Production. Energies. 2018; 11(12):3310. https://doi.org/10.3390/en11123310
Chicago/Turabian StyleBlanco, Ignacio, Daniela Guericke, Anders N. Andersen, and Henrik Madsen. 2018. "Operational Planning and Bidding for District Heating Systems with Uncertain Renewable Energy Production" Energies 11, no. 12: 3310. https://doi.org/10.3390/en11123310
APA StyleBlanco, I., Guericke, D., Andersen, A. N., & Madsen, H. (2018). Operational Planning and Bidding for District Heating Systems with Uncertain Renewable Energy Production. Energies, 11(12), 3310. https://doi.org/10.3390/en11123310





