Energy Uncertainty Analysis of Electric Buses
Abstract
1. Introduction
2. State-of-the-Art
3. Methods
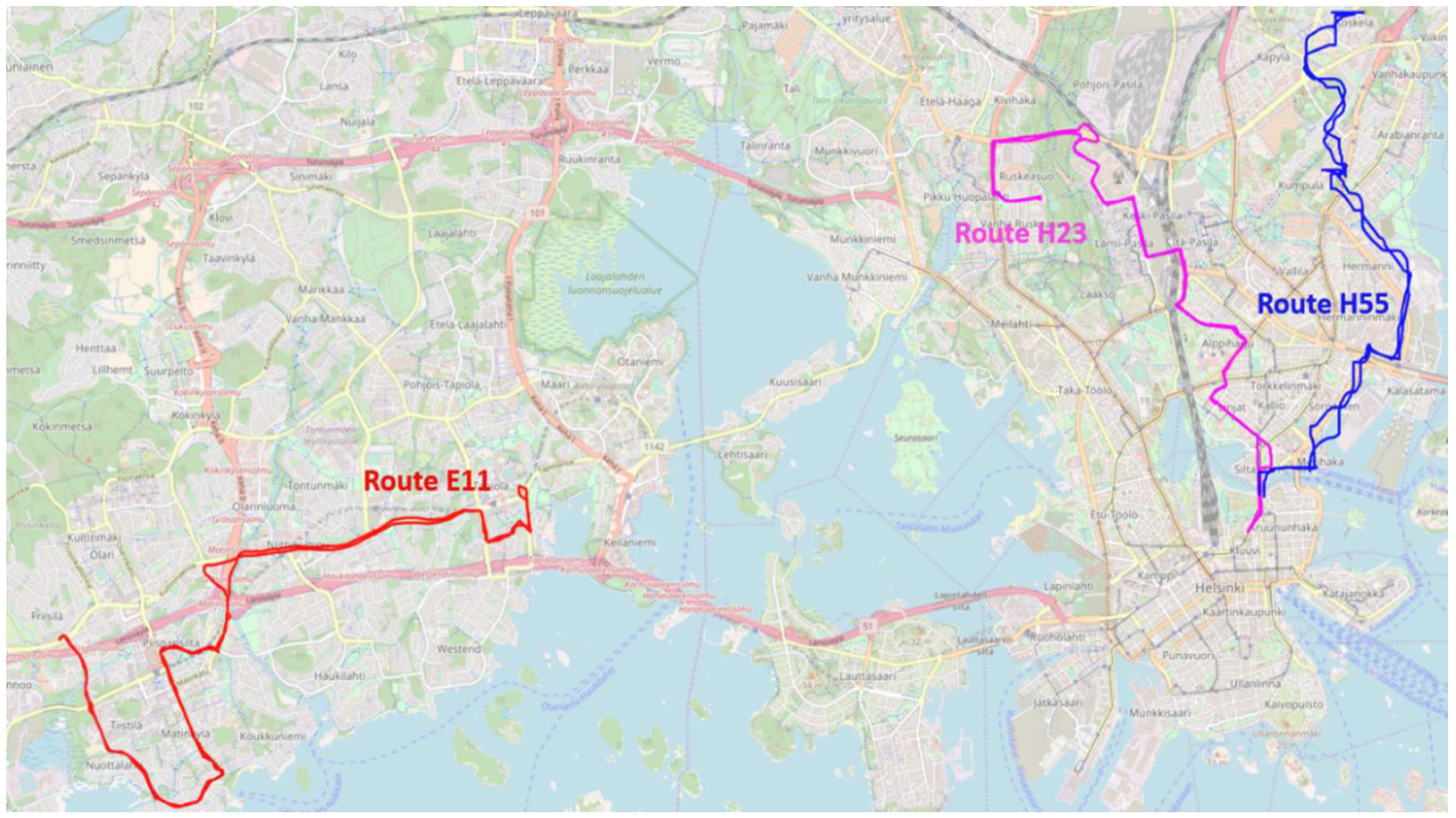
3.1. Buses and Routes
3.2. Measurements
3.2.1. Data Collection
3.2.2. Discharge Cycles
3.2.3. Charge Cycles
3.3. Sensitivity Analysis with Multiple Linear Regression
3.3.1. Background
3.3.2. MLR with Correlated Inputs
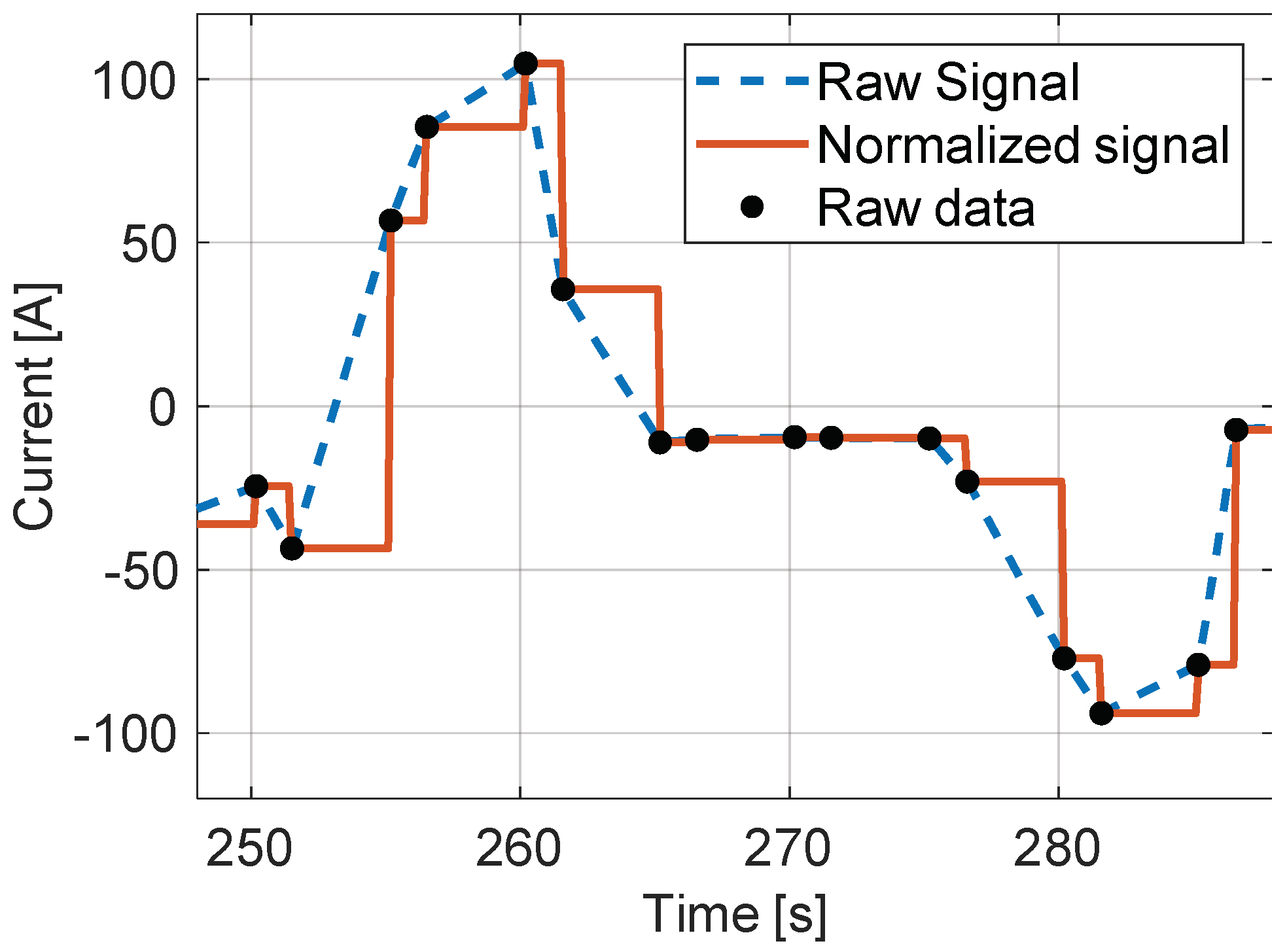
3.3.3. Normalization of Second-Order Effects
3.4. Statistical Analysis
4. Results
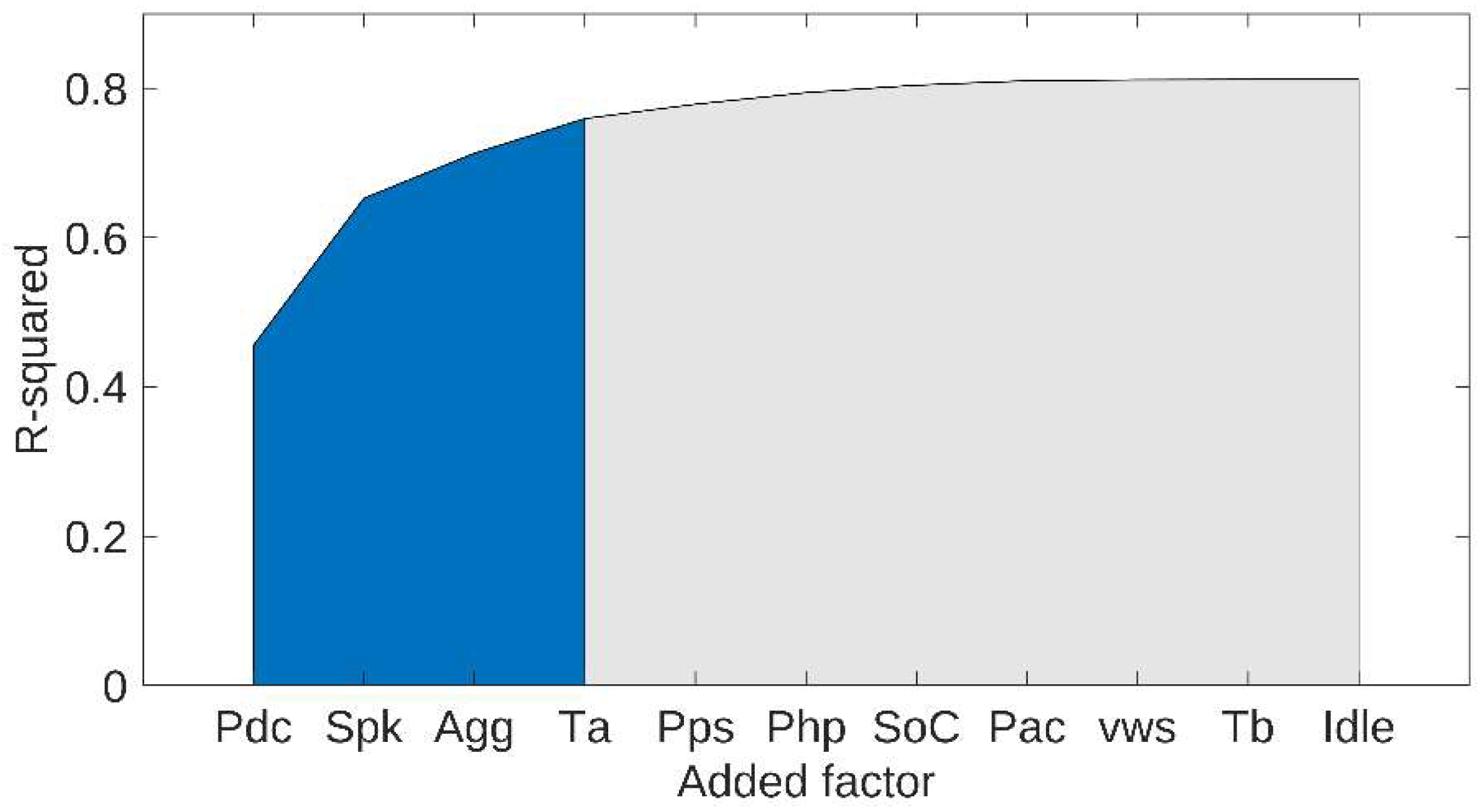
4.1. Operation Factors
4.1.1. Temperature Factors
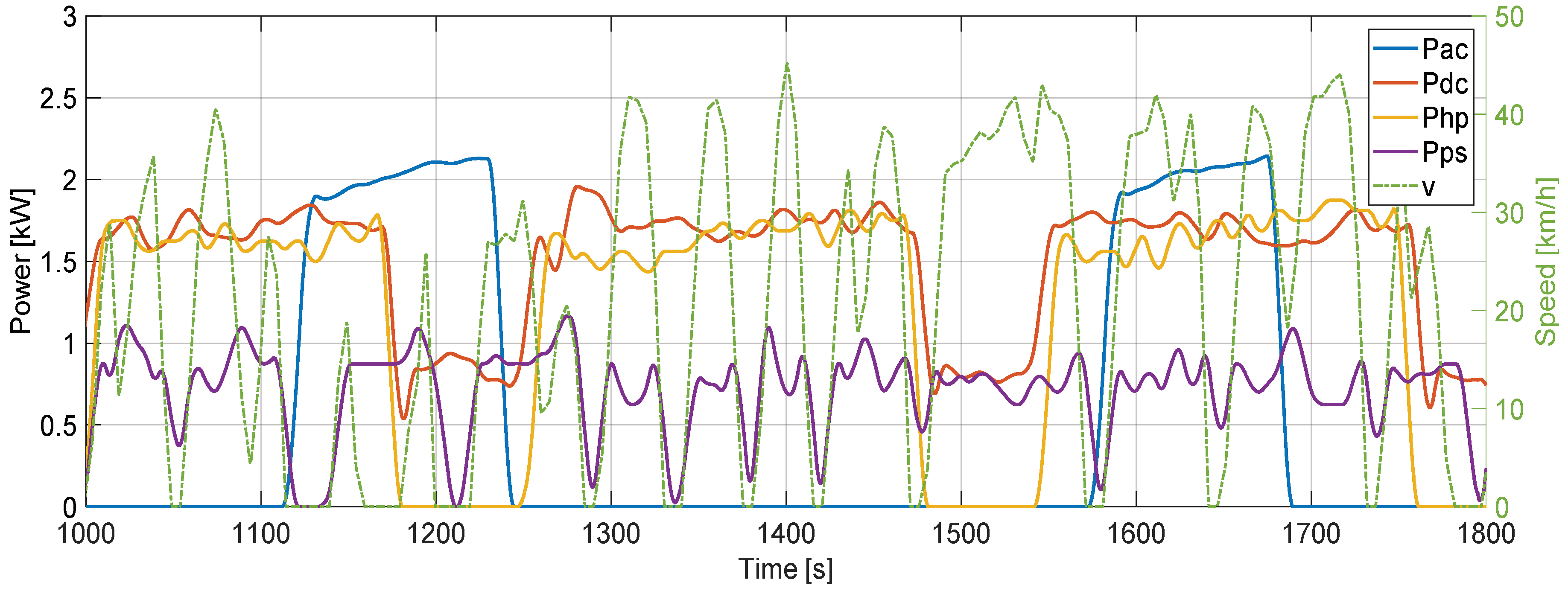
4.1.2. Auxiliary Devices
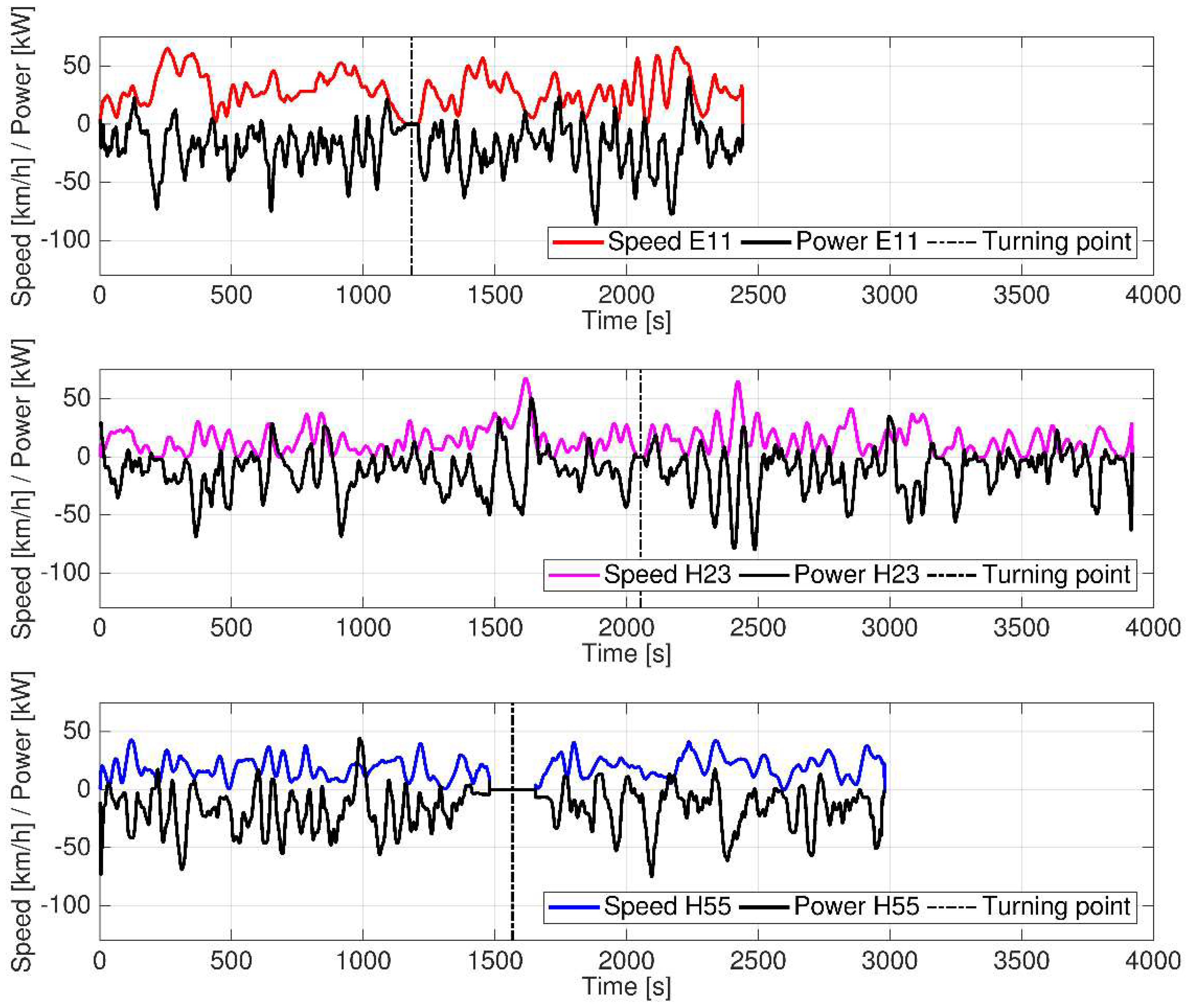
4.1.3. Route and Behavior Factors
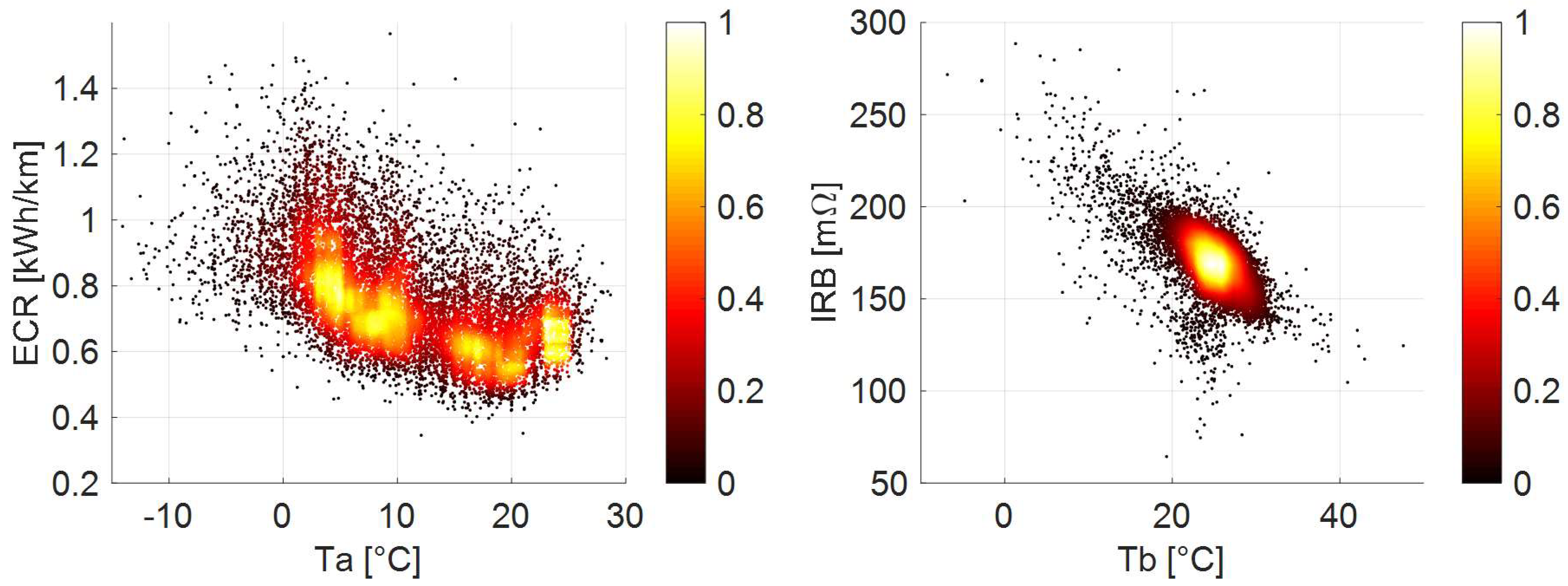
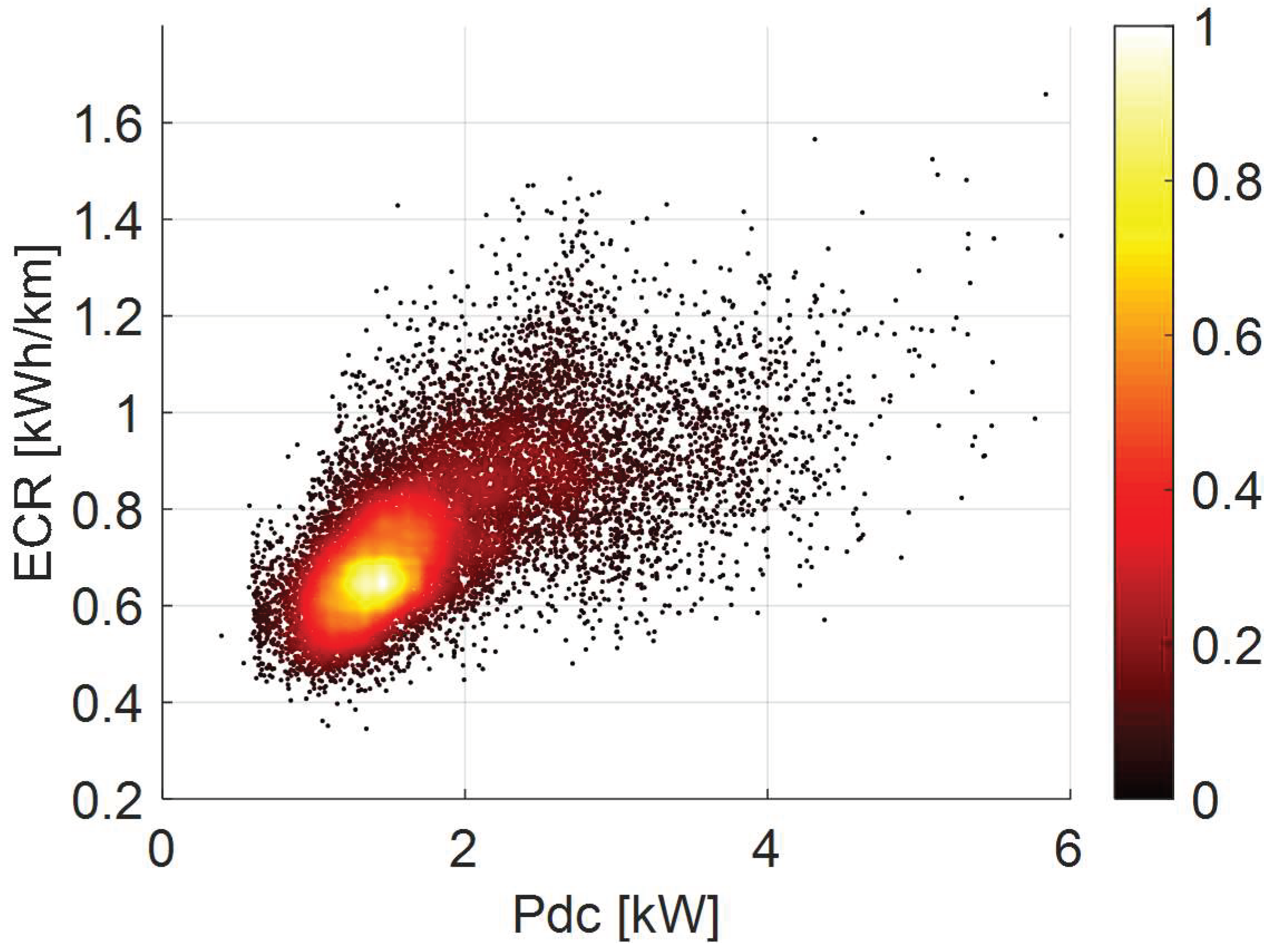
4.2. Energy Consumption Rate (ECR) on Discharges
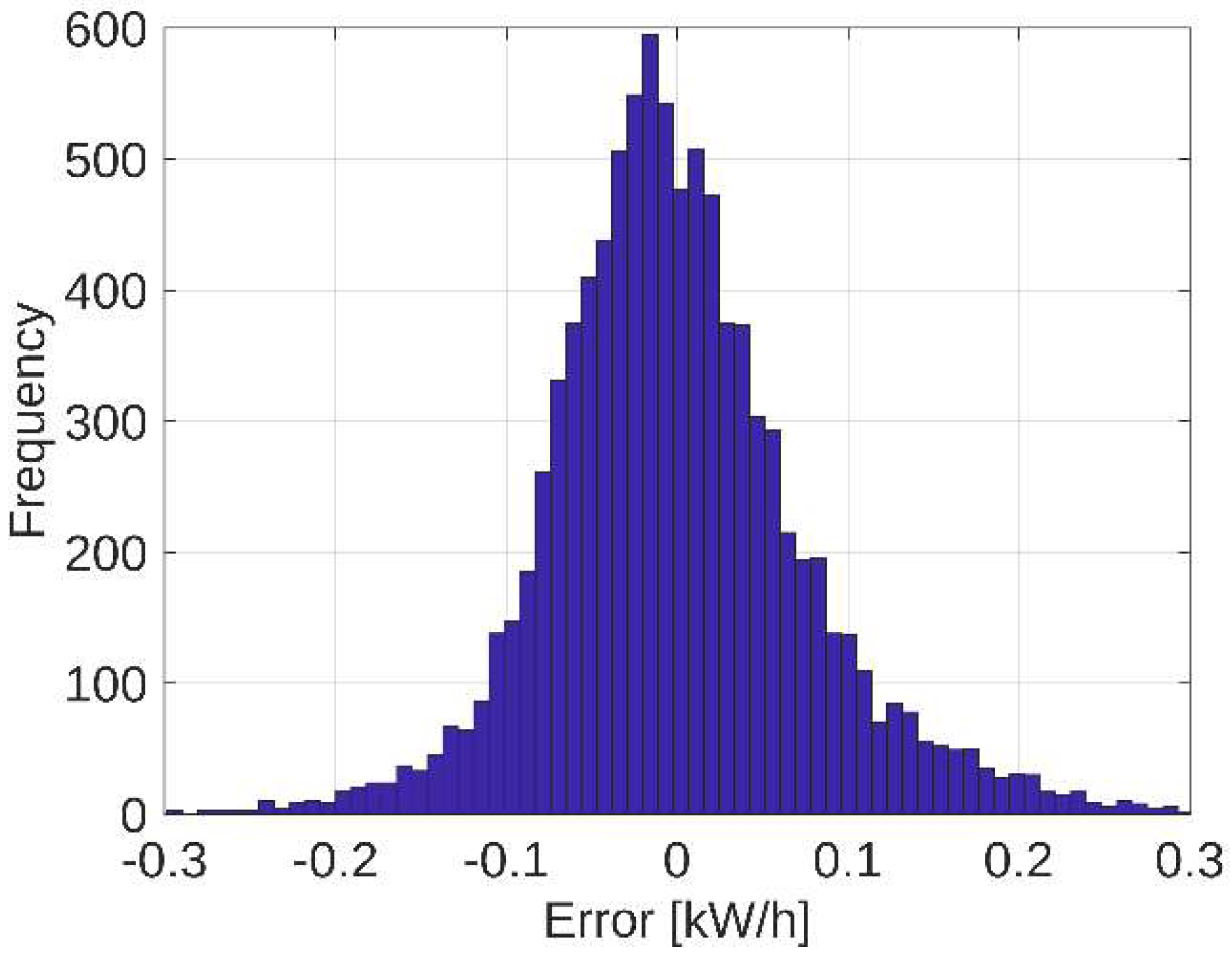
42.1. Output Analysis
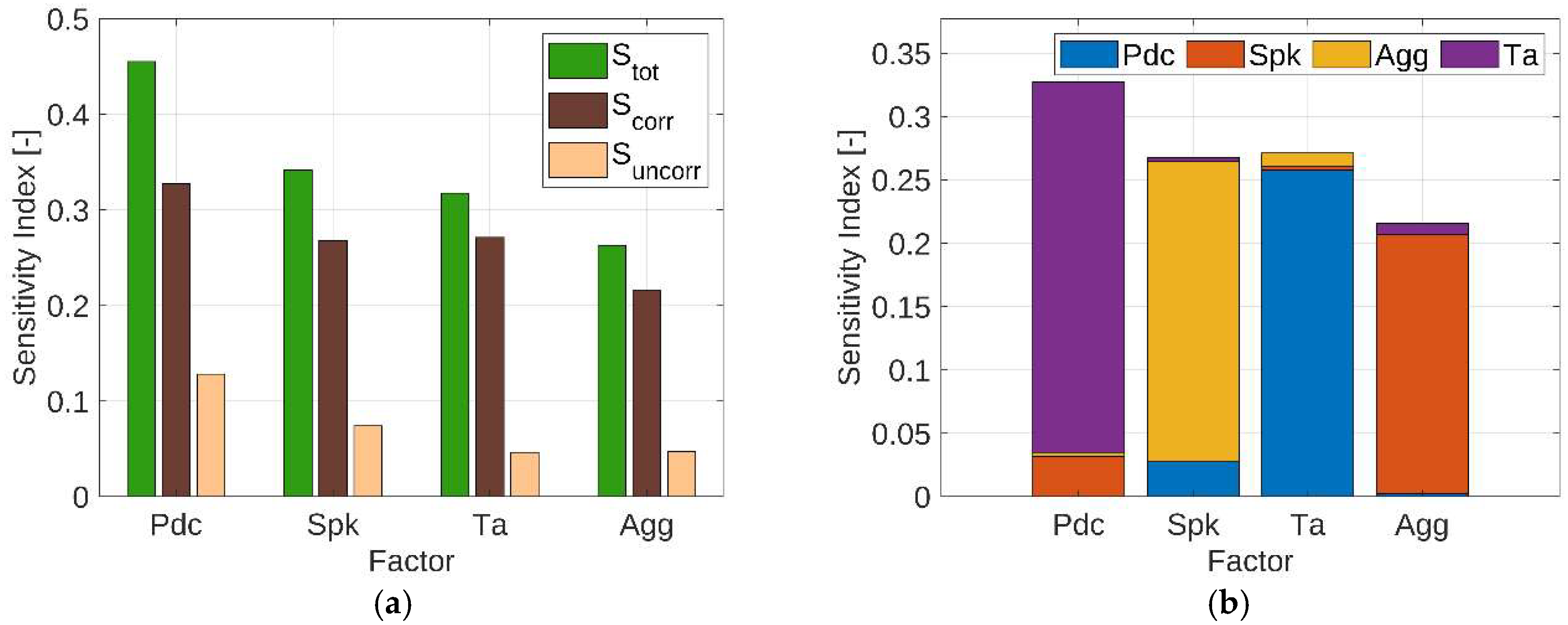
4.2.2. Input Analysis
4.3. Internal Resistance of the Battery (IRB) on Charges
4.3.1. Output Analysis
4.3.2. Input Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pihlatie, M.; Kukkonen, S.; Halmeaho, T.; Karvonen, V.; Nylund, N.O. Fully electric city buses—The viable option. In Proceedings of the IEEE International Electric Vehicle Conference, Florence, Italy, 17–19 December 2014; Volume 1. [Google Scholar] [CrossRef]
- Lajunen, A. Lifecycle costs and charging requirements of electric buses with different charging methods. J. Clean. Prod. 2018, 172, 56–67. [Google Scholar] [CrossRef]
- Vepsäläinen, J.; Kivekäs, K.; Otto, K.; Tammi, K. Development and validation of energy demand uncertainty model for electric city buses. Transp. Res. Part D Transp. Environ. 2018, 36, 347–361. [Google Scholar] [CrossRef]
- Asamer, J.; Graser, A.; Heilmann, B.; Ruthmair, M. Sensitivity analysis for energy demand estimation of electric vehicles. Transp. Res. Part D Transp. Environ. 2016, 46, 182–199. [Google Scholar] [CrossRef]
- Alvarez, A.; Serradilla Garcia, F.; Naranjo, J.E.; Anaya, J.J.; Jimenez, F. Modeling the driving behavior of electric vehicles using smartphones and neural networks. IEEE Intell. Transp. Syst. Mag. 2014, 6, 44–53. [Google Scholar] [CrossRef]
- Travesset-Baro, O.; Rosas-Casals, M.; Jover, E. Transport energy consumption in mountainous roads. A comparative case study for internal combustion engines and electric vehicles in Andorra. Transp. Res. Part D Transp. Environ. 2015, 34, 16–26. [Google Scholar] [CrossRef]
- Neubauer, J.; Wood, E. Thru-life impacts of driver aggression, climate, cabin thermal management, and battery thermal management on battery electric vehicle utility. J. Power Sources 2014, 259, 262–275. [Google Scholar] [CrossRef]
- Younes, Z.; Boudet, L.; Suard, F.; Gerard, M.; Rioux, R. Analysis of the main factors influencing the energy consumption of electric vehicles. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 247–253. [Google Scholar] [CrossRef]
- Wu, X.; Freese, D.; Cabrera, A.; Kitch, W.A. Electric vehicles’ energy consumption measurement and estimation. Transp. Res. Part D Transp. Environ. 2015, 34, 52–67. [Google Scholar] [CrossRef]
- Lorf, C.; Martínez-Botas, R.F.; Howey, D.A.; Lytton, L.; Cussons, B. Comparative analysis of the energy consumption and CO2 emissions of 40 electric, plug-in hybrid electric, hybrid electric and internal combustion engine vehicles. Transp. Res. Part D Transp. Environ. 2013, 23, 12–19. [Google Scholar] [CrossRef]
- Lajunen, A.; Kalttonen, A. Investigation of Thermal Energy Losses in the Powertrain of an Electric City Bus. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015. [Google Scholar]
- Lajunen, A. Energy-optimal velocity profiles for electric city buses. IEEE Int. Conf. Autom. Sci. Eng. 2013, 886–891. [Google Scholar] [CrossRef]
- Halmeaho, T.; Rahkola, P.; Tammi, K.; Pippuri, J.; Pellikka, A.-P.; Manninen, A.; Ruotsalainen, S. Experimental validation of electric bus powertrain model under city driving cycles. IET Electr. Syst. Transp. 2016, 7, 74–83. [Google Scholar] [CrossRef]
- Lajunen, A.; Tammi, K. Energy consumption and carbon dioxide emission analysis for electric city buses. In Proceedings of the EVS29 Symposium, Montreal, QC, Canada, 19–22 June 2016; pp. 1–12. [Google Scholar]
- Gao, Z.; Lin, Z.; LaClair, T.J.; Liu, C.; Li, J.M.; Birky, A.K.; Ward, J. Battery capacity and recharging needs for electric buses in city transit service. Energy 2017, 122, 588–600. [Google Scholar] [CrossRef]
- Kontou, A.; Miles, J. Electric Buses: Lessons to be Learnt from the Milton Keynes Demonstration Project. Procedia Eng. 2015, 118, 1137–1144. [Google Scholar] [CrossRef]
- Prohaska, R.; Kelly, K.; Eudy, L. In-Use Fleet Evaluation of Fast-Charge Battery Electric Transit Buses. In Proceedings of the IEEE Transportation Electrification Conference, Dearborn, MI, USA, 26–29 June 2016. [Google Scholar]
- Rogge, M.; Wollny, S.; Sauer, D.U. Fast charging battery buses for the electrification of urban public transport-A feasibility study focusing on charging infrastructure and energy storage requirements. Energies 2015, 8, 4587–4606. [Google Scholar] [CrossRef]
- Rothgang, S.; Rogge, M.; Becker, J.; Sauer, D.U. Battery design for successful electrification in public transport. Energies 2015, 8, 6715–6737. [Google Scholar] [CrossRef]
- Sinhuber, P.; Rohlfs, W.; Sauer, D.U. Study on power and energy demand for sizing the energy storage systems for electrified local public transport buses. In Proceedings of the 2012 IEEE Vehicle Power Propulsion Conference, Seoul, Korea, 9–12 October 2012; pp. 315–320. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Xu, J.; Barclay, N. Optimal recharging scheduling for urban electric buses: A case study in Davis. Transp. Res. Part E Logist. Transp. Rev. 2017, 100, 115–132. [Google Scholar] [CrossRef]
- Neaimeh, M.; Hill, G.A.; Blythe, P.T.; Hübner, Y. Routing systems to extend the driving range of electric vehicles. IET Intell. Transp. Syst. 2013, 7, 327–336. [Google Scholar] [CrossRef]
- Badin, F.; Berr, F.L.; Briki, H.; Petit, M.; Magand, S.; Condemine, E. Evaluation of EVs energy consumption influencing factors, driving conditions, auxiliaries use, driver’s aggressiveness. In Proceedings of the EVS27 International Batter. Hybrid Fuel Cell Electric Vehicle Symposium, Barcelona, Spain, 17–20 November 2013; Volume 6, pp. 1–12. [Google Scholar] [CrossRef]
- Shankar, R.; Marco, J. Method for estimating the energy consumption of electric vehicles and plug-in hybrid electric vehicles under real-world driving conditions. IET Intell. Transp. Syst. 2013, 7, 138–150. [Google Scholar] [CrossRef]
- De Cauwer, C.; Van Mierlo, J.; Coosemans, T. Energy consumption prediction for electric vehicles based on real-world data. Energies 2015, 8, 8573–8593. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Yamamoto, T. Improving electricity consumption estimation for electric vehicles based on sparse GPS observations. Energies 2017, 10, 129. [Google Scholar] [CrossRef]
- Spector, J. BYD’s Electric Bus Woes Threaten to Tarnish the Broader Industry. Available online: https://www.greentechmedia.com/articles/read/byds-electric-bus-woes-threaten-to-tarnish-the-broader-industry#gs.4Str9HA (accessed on 25 February 2018).
- Suh, I.S.; Lee, M.; Kim, J.; Oh, S.T.; Won, J.P. Design and experimental analysis of an efficient HVAC (heating, ventilation, air-conditioning) system on an electric bus with dynamic on-road wireless charging. Energy 2015, 81, 262–273. [Google Scholar] [CrossRef]
- GPSVisualizer. Available online: http://www.gpsvisualizer.com (accessed on 10 February 2018).
- Hentunen, A. Electrical Modeling of Large Lithium-Ion Batteries for Use in Dynamic Simulations of Electric Vehicles. Ph.D. Thesis, Aalto University, Espoo, Finland, 2012. [Google Scholar]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Gao, L.; Liu, S.; Dougal, R.A. Dynamic lithium-ion battery model for system simulation. IEEE Trans. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar] [CrossRef]
- Wu, J.; Li, K.; Jiang, Y.; Lv, Q.; Shang, L.; Sun, Y. Large-scale battery system development and user-specific driving behavior analysis for emerging electric-drive vehicles. Energies 2011, 4, 758–779. [Google Scholar] [CrossRef]
- Remmlinger, J.; Buchholz, M.; Meiler, M.; Bernreuter, P.; Dietmayer, K. State-of-health monitoring of lithium-ion batteries in electric vehicles by on-board internal resistance estimation. J. Power Sources 2011, 196, 5357–5363. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2015, 248, 869–887. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Xiao, S.; Lu, Z.; Xu, L. Multivariate sensitivity analysis based on the direction of eigen space through principal component analysis. Reliab. Eng. Syst. Saf. 2017, 165, 1–10. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; Wiley: Hoboken, NJ, USA, 2008; ISBN 9780470059975. [Google Scholar]
- Xu, C.; Gertner, G.Z. Uncertainty and sensitivity analysis for models with correlated parameters. Reliab. Eng. Syst. Saf. 2008, 93, 1563–1573. [Google Scholar] [CrossRef]
- Li, L.; Lu, Z.; Zhou, C. Importance analysis for models with correlated input variables by the state dependent parameters method. Comput. Math. Appl. 2011, 62, 4547–4556. [Google Scholar] [CrossRef]
- Mara, T.A.; Tarantola, S. Variance-based sensitivity indices for models with dependent inputs. Reliab. Eng. Syst. Saf. 2012, 107, 115–121. [Google Scholar] [CrossRef]
- Chastaing, G.; Gamboa, F.; Prieur, C. Generalized Hoeffding-Sobol decomposition for dependent variables—Application to sensitivity analysis. Electron. J. Stat. 2012, 6, 2420–2448. [Google Scholar] [CrossRef]
- Devore, J.; Berk, K. The Analysis of Variance. In Modern Mathematical Statistics with Applications; Springer: New York, NY, USA, 2012; pp. 552–612. [Google Scholar]
- Sobol’, I.M. Sensitivity Estimates for Nonlinear Mathematic Models; Mat. Model. 2; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993; pp. 112–118. [Google Scholar]
- Li, G.; Rabitz, H. General formulation of HDMR component functions with independent and correlated variables. J. Math. Chem. 2012, 50, 99–130. [Google Scholar] [CrossRef]
- Graham, M.H. Statistical confronting multicollinearity in ecological multiple regression. Ecology 2003, 84, 2809–2815. [Google Scholar] [CrossRef]
- Belsley, D.; Kuh, E.; Welsch, E. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; ISBN 978-0-471-69117-4. [Google Scholar]
- Bendel, R.B.; Afifi, A.A. Comparison of Stopping Rules in Forward “Stepwise” Regression. J. Am. Stat. Assoc. 1977, 72, 46–53. [Google Scholar] [CrossRef]
- Yuksel, T.; Michalek, J.J. Effects of regional temperature on electric vehicle efficiency, range, and emissions in the united states. Environ. Sci. Technol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Ritari, A. Tilastollinen Malli Sähköbussin Energiankulutukselle. Master Thesis, Aalto University, Espoo, Finland, 2017. [Google Scholar]
- Vepsäläinen, J. Driving Style Comparison of City Buses: Electric vs. Diesel. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Belfort, France, 11–14 December 2017. [Google Scholar]
- Pelletier, S.; Jabali, O.; Laporte, G.; Veneroni, M. Battery degradation and behaviour for electric vehicles: Review and numerical analyses of several models. Transp. Res. Part B Methodol. 2017, 103, 158–187. [Google Scholar] [CrossRef]
- Schoch, J.; Gaerttner, J.; Schuller, A.; Setzer, T. Enhancing electric vehicle sustainability through battery life optimal charging. Transp. Res. Part B Methodol. 2018, 112, 1–18. [Google Scholar] [CrossRef]
- Zhang, K.; Lu, Z.; Cheng, L.; Xu, F. A new framework of variance based global sensitivity analysis for models with correlated inputs. Struct. Saf. 2015, 55, 1–9. [Google Scholar] [CrossRef]
- Kivekas, K.; Vepsalainen, J.; Tammi, K. Stochastic driving cycle synthesis for analyzing the energy consumption of a battery electric bus. IEEE Access 2018, 6. [Google Scholar] [CrossRef]
- Kivekäs, K.; Lajunen, A.; Vepsäläinen, J.; Tammi, K. City Bus Powertrain Comparison: Driving Cycle Variation and Passenger Load Sensitivity Analysis. Energies 2018, 11, 1755. [Google Scholar] [CrossRef]
- Lajunen, A. Evaluation of Diesel and Fuel Cell Plug-In Hybrid City Buses. In Proceedings of the 2015 IEEE Vehicle Power Propulsions Conference VPPC 2015, Montreal, QC, Canada, 19–22 October 2015. [Google Scholar] [CrossRef]
- Mallon, K.R.; Assadian, F.; Fu, B. Analysis of on-board photovoltaics for a battery electric bus and their impact on battery lifespan. Energies 2017, 10, 943. [Google Scholar] [CrossRef]











| Frame | Aluminum |
|---|---|
| Curb weight | 10,500 kg |
| Gear-ratio | 4.88 |
| Manufacturing year | 2015 |
| Length | 12 m |
| Dynamic radius of tire | 43 cm |
| Battery manufacturer | Toshiba |
| Battery chemistry | Lithium Titanate Oxide |
| Battery capacity | 55 kWh, 80 Ah × 690 V |
| Motor manufacturer | Visedo |
| Motor | Max power 180 kW |
| Charging system | 350 kW roof connected pantograph |
| Diesel heater | 24 kW |
| Heat pump | 5 kW |
| Symbol | Factor | Range | Mean | Unit | Data |
|---|---|---|---|---|---|
| Discharges | |||||
| t | Time | [13.0, 49.3] | 26.3 | min | total, measured |
| Tb | Battery temperature | [−17.4, 48.5] | 24.1 | °C | mean, measured |
| Ta | Ambient temperature | [−17.4, 28.7] | 10.8 | °C | mean, measured |
| Pac | Air compressor power | [0.0, 2.0] | 0.44 | kW | mean, measured |
| Pdc | DCDC converter power | [0.4, 5.9] | 1.9 | kW | mean, measured |
| Php | Heat pump | [0.0, 3.46] | 0.81 | kW | mean, measured |
| Pps | Power steering power | [0.1, 1.0] | 0.54 | kW | mean, measured |
| SOC | Battery state-of-charge | [17.1, 99.5] | 70.4 | % | start, measured |
| Bh | Battery age | [1, 4099] | 1739 | h | start, measured |
| v | Average speed | [9.9, 44.9] | 21.2 | km/h | mean, measured |
| Agg | Driving aggressiveness | [0.06, 0.31] | 0.17 | m/s2 | single, computed |
| Dist | Distance | [6.7, 10.4] | 9.1 | km | total, computed |
| Spk | Stops per kilometer | [0.1, 5.6] | 2.1 | 1/km | total, computed |
| Idle | Idle time | [0.3, 58.0] | 22.0 | % | total, computed |
| dir | Direction | [0, 1] | 0.5 | - | single, computed |
| Charges | |||||
| t | Time | [0.5, 9.1] | 3.8 | min | total, measured |
| Tb | Battery temperature | [1.3, 47.6] | 24.9 | °C | mean, measured |
| Ta | Ambient temperature | [−12.0, 28.0] | 11.1 | °C | mean, measured |
| Ib | Battery Current | [218.8, 449.4] | 357.7 | A | mean, measured |
| Vb | Battery Voltage | [402.4, 920.0] | 758.6 | V | mean, measured |
| SOC | Battery State-of-Charge | [0.3, 77] | 50.1 | % | start, measured |
| Helsinki vs. Espoo | |||||
|---|---|---|---|---|---|
| Metric | Ta | Pac | Pdc | Spk | Agg |
| Mean | −25.6% | 36.4% | 42.0% | 29.6% | 5.7% |
| St. dev. | −20.6% | 1.5% | 60.2% | 31.0% | −11.5% |
| Metric | Pdc | Pps | Idle | Spk | Ta | v | Pac | Agg | Php | Tb | SOC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| VIF | 2.31 | 2.71 | 5.37 | 6.87 | 2.05 | 9.88 | 1.7 | 2.47 | 1.54 | 1.53 | 1.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vepsäläinen, J.; Ritari, A.; Lajunen, A.; Kivekäs, K.; Tammi, K. Energy Uncertainty Analysis of Electric Buses. Energies 2018, 11, 3267. https://doi.org/10.3390/en11123267
Vepsäläinen J, Ritari A, Lajunen A, Kivekäs K, Tammi K. Energy Uncertainty Analysis of Electric Buses. Energies. 2018; 11(12):3267. https://doi.org/10.3390/en11123267
Chicago/Turabian StyleVepsäläinen, Jari, Antti Ritari, Antti Lajunen, Klaus Kivekäs, and Kari Tammi. 2018. "Energy Uncertainty Analysis of Electric Buses" Energies 11, no. 12: 3267. https://doi.org/10.3390/en11123267
APA StyleVepsäläinen, J., Ritari, A., Lajunen, A., Kivekäs, K., & Tammi, K. (2018). Energy Uncertainty Analysis of Electric Buses. Energies, 11(12), 3267. https://doi.org/10.3390/en11123267







