Multi-Agent System with Plug and Play Feature for Distributed Secondary Control in Microgrid—Controller and Power Hardware-in-the-Loop Implementation
Abstract
1. Introduction
- Firstly, in MGs, infrastructure may be supplied by different vendors and may be compliant to different protocols. Agents are required to be able to transfer data with local controllers and measurement system through various standardized or commercialized industrial protocols, while on the other hand, has to comply with the inter-agent communication protocols.
- Secondly, in distribution network of MG, the structure of grid and the total capacity of ESSs may change/be upgraded progressively along with the increase of loads and renewable energy sources. Furthermore, ESS is an element which requires regular maintenance and replacement. The corresponding agent has to be activated or deactivated accordingly to the state of the ESS. The local control algorithm (intra-agent) needs to be flexible enough to adapt to this frequent alteration of structure and capacity without major re-configuration.
- Not only at local level, the alteration of topology is also a critical obstacle that needs to be solved to achieve "Plug and Play" capacity at system level. The micro-grid operation is based on the consensus processes of the agents which tries to find a global solution based on limited information acquired from the neighbourhood. Consensus algorithms are introduced mathematically and often adapted to a certain network topology. Therefore, the integration or removal of an agent in the network (or alteration of topology) requires a throughout re-configuration or adaptation of the entire network.
- Last but not least, the asynchronous interaction (inter-agent) under influence of various type of uncertainties in a real communications network is much more complex and is not yet covered in the mathematical model. The performance of the real system may be derived from the theoretical one if this aspect is not considered during the design and validation process. However, in aforementioned research, the communication network is typically ignored. In ref. [25], the data transfer latency is considered, as deterministic time delays which does not accurately reflect realistic communications networks. Furthermore, the design of agents and the interactions among the agents as well as with controllers and devices were ambiguous and unspecific.
- We develop a multi-agent system with “plug and play” capacity for distributed secondary control of frequency in islanded MGs. Firstly, a multi-layer structure is proposed to describe thoroughly the MG system operating with agents. The structure consists of three layers: Device layer, Control layer and Agent layer. The agent, which is an autonomous program with server/client structure, is designed to process an average consensus algorithm and send proper signal to inverter controller in a distributed scheme. The agent is also equipped with the ability of collecting and broadcasting messages via the industrial protocol IEC 61850. The “Plug and Play” capacity is realized at the agent layer, as the system will automatically adapt to the alteration of topology (integration of new agent or removal of an agent) and react accordingly to maintain seamless operation.
- The proposed distributed secondary control is implemented in a laboratory platform based on the propose in [18] with controller and power-hardware-in-the-loop (C/PHIL) setup, incorporating realistic communications network with the impact of uncertainties considered. The performance of system under realistic condition shows that the agents are able to resist to disturbances and to self-configure under alteration of grid topology.
2. MAS Based Multi-Layer Architecture for Distributed Secondary Control in MG
3. Design of Agent with the Plug and Play Feature
| Algorithm 1 The average consensus process in Agent i. |
|
- Initialization phase: Each agent receives initial state which is its local frequency deviation. Data are transferred from Device layer to Agent layer.
- Updating state phase: States of next iterations in each agent are updated using the agent current state and neighbors’ states following Metropolis rule. An agent will move from Iteration t to Iteration if and only if it collects information from all neighbors at Iteration t. Data are then transferred internally within the Agent layer.
- Returning value phase: At a specific iteration, all agents finish consensus process loop and send the same average value of frequency deviation to controllers. Data are transferred from Agent layer to Control layer.
4. Validation
4.1. Platform Design for Validation of Distributed Control in MG
4.1.1. PHIL with Power Inverter
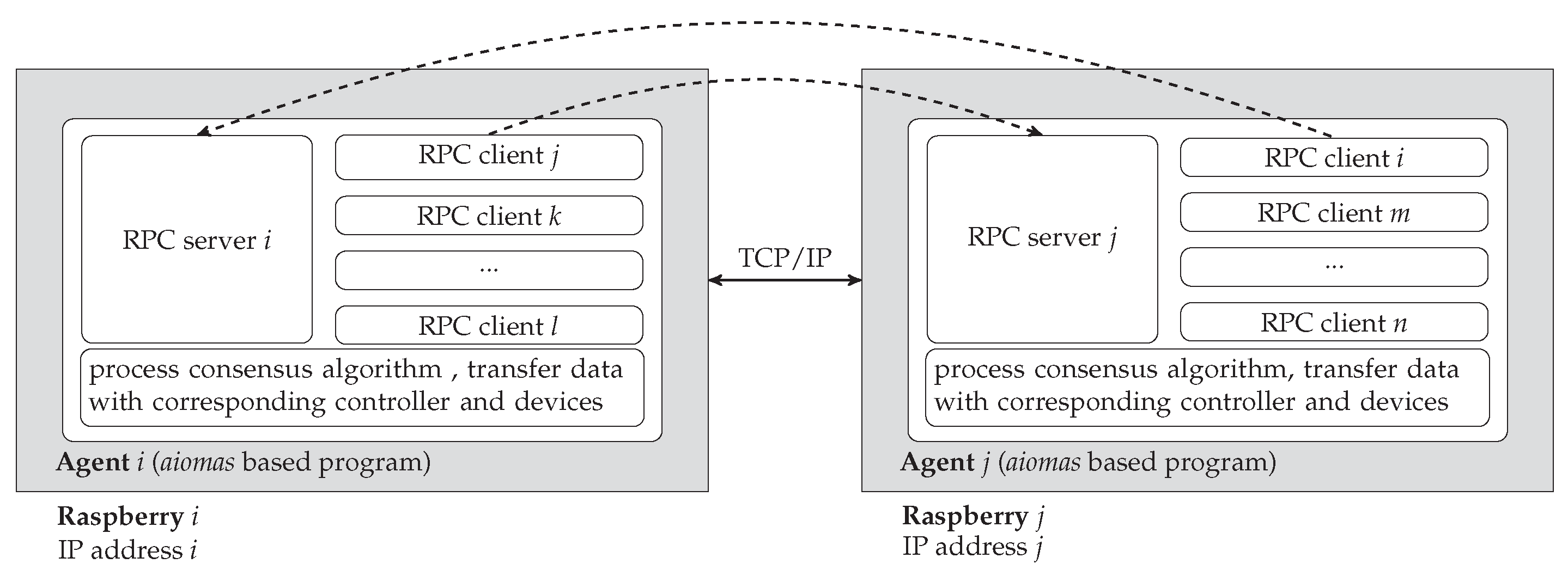
4.1.2. CHIL with MAS and Realistic Communications Network
4.1.3. Interfaces between Agents and RTDS
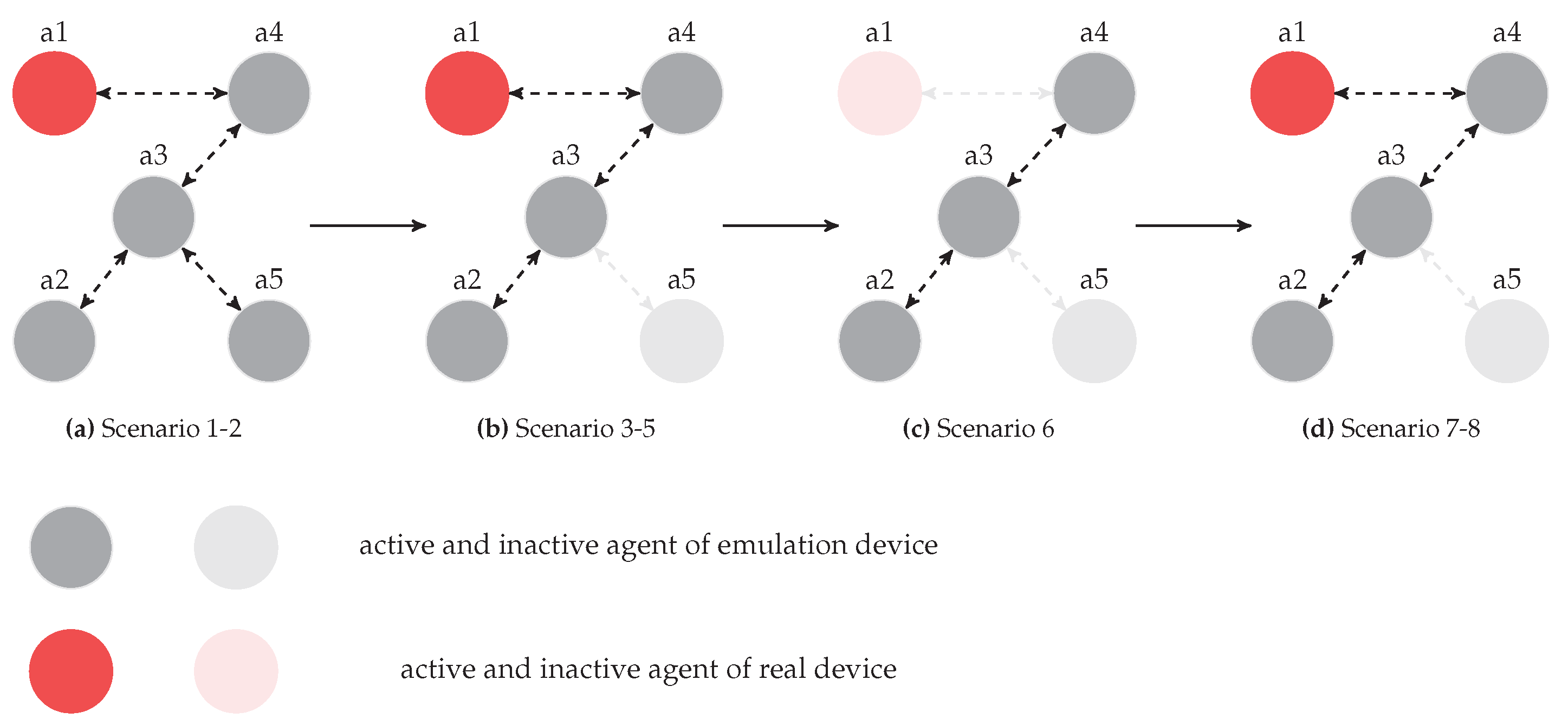
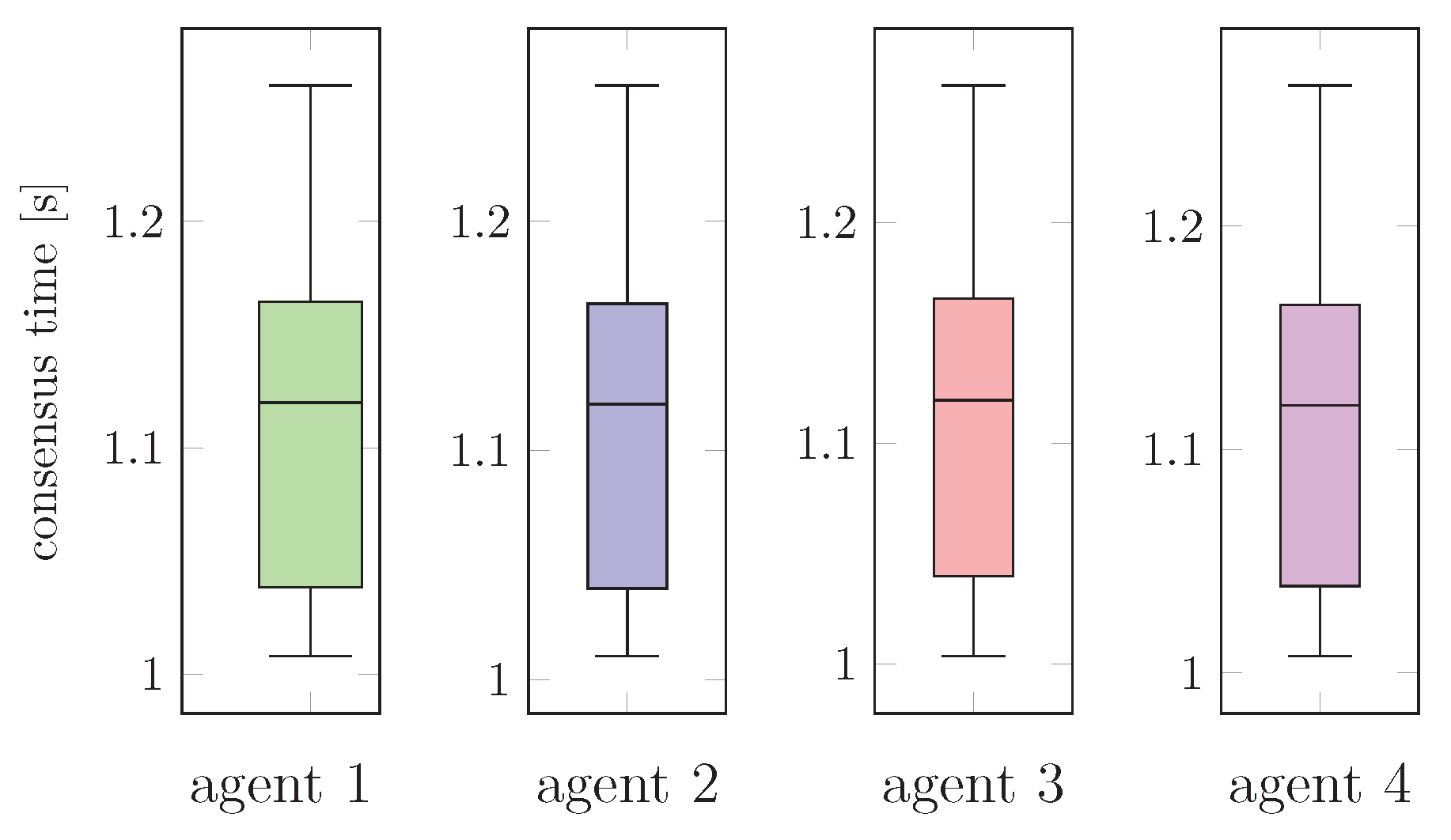
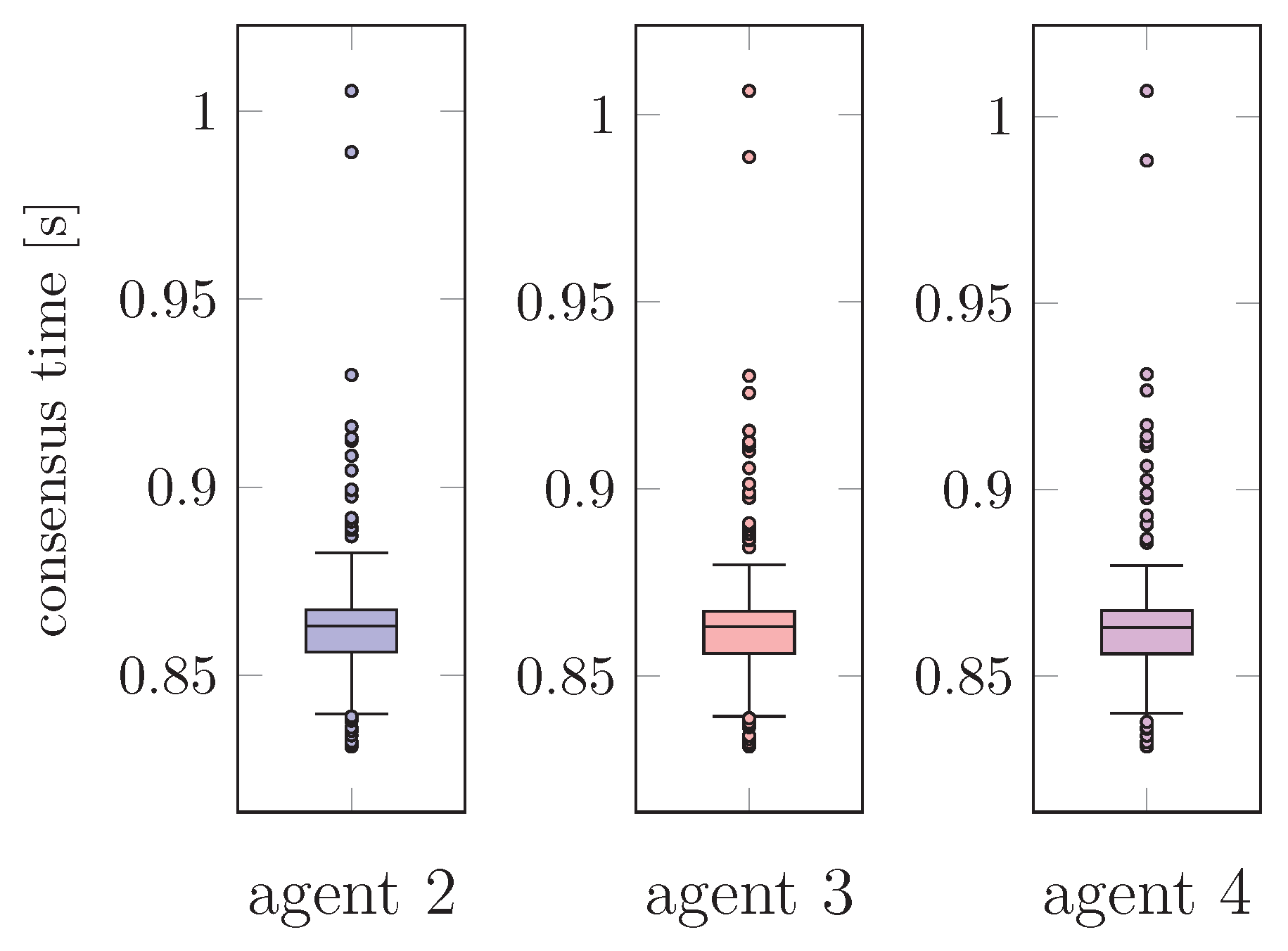
4.2. Testing Procedure
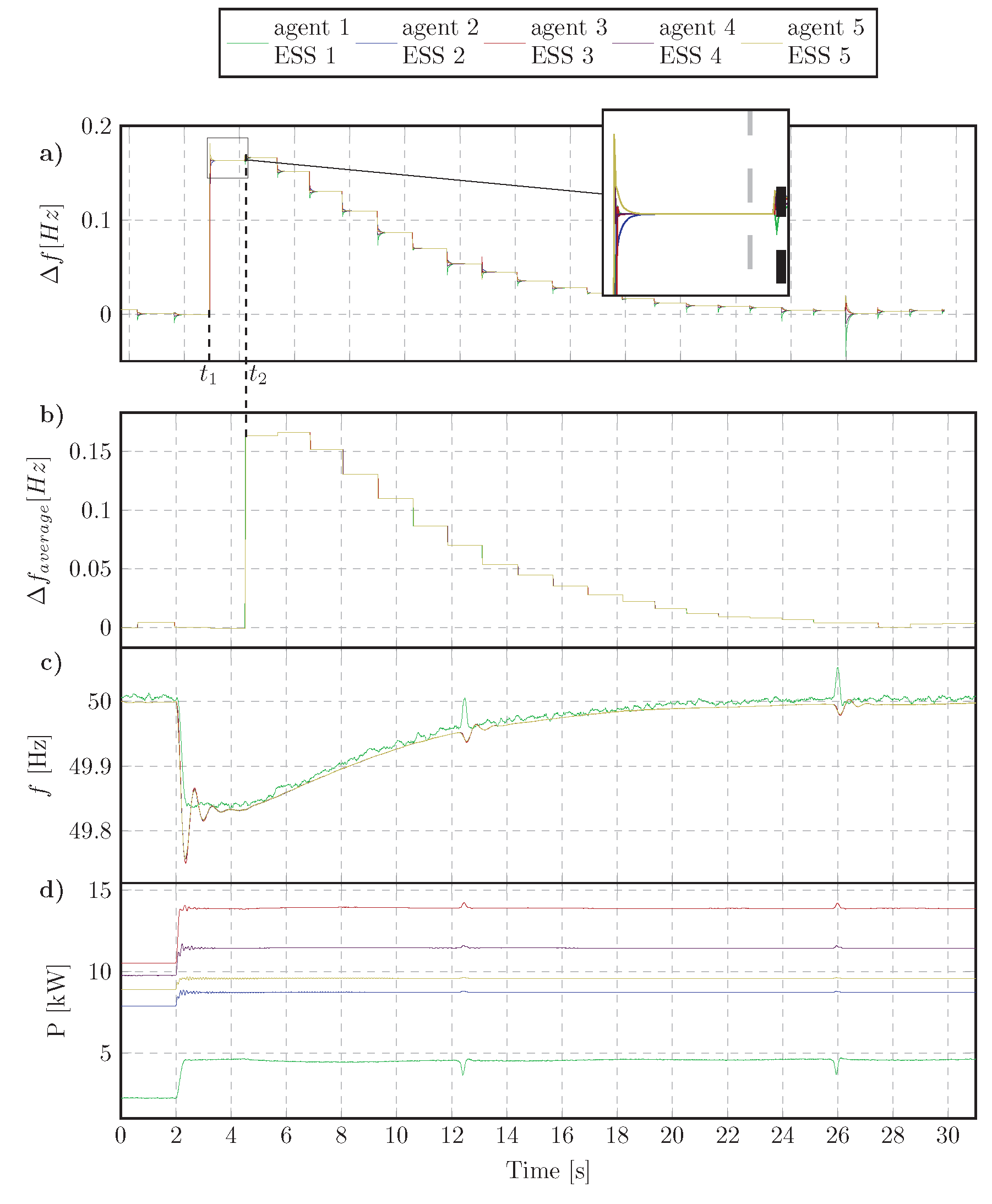
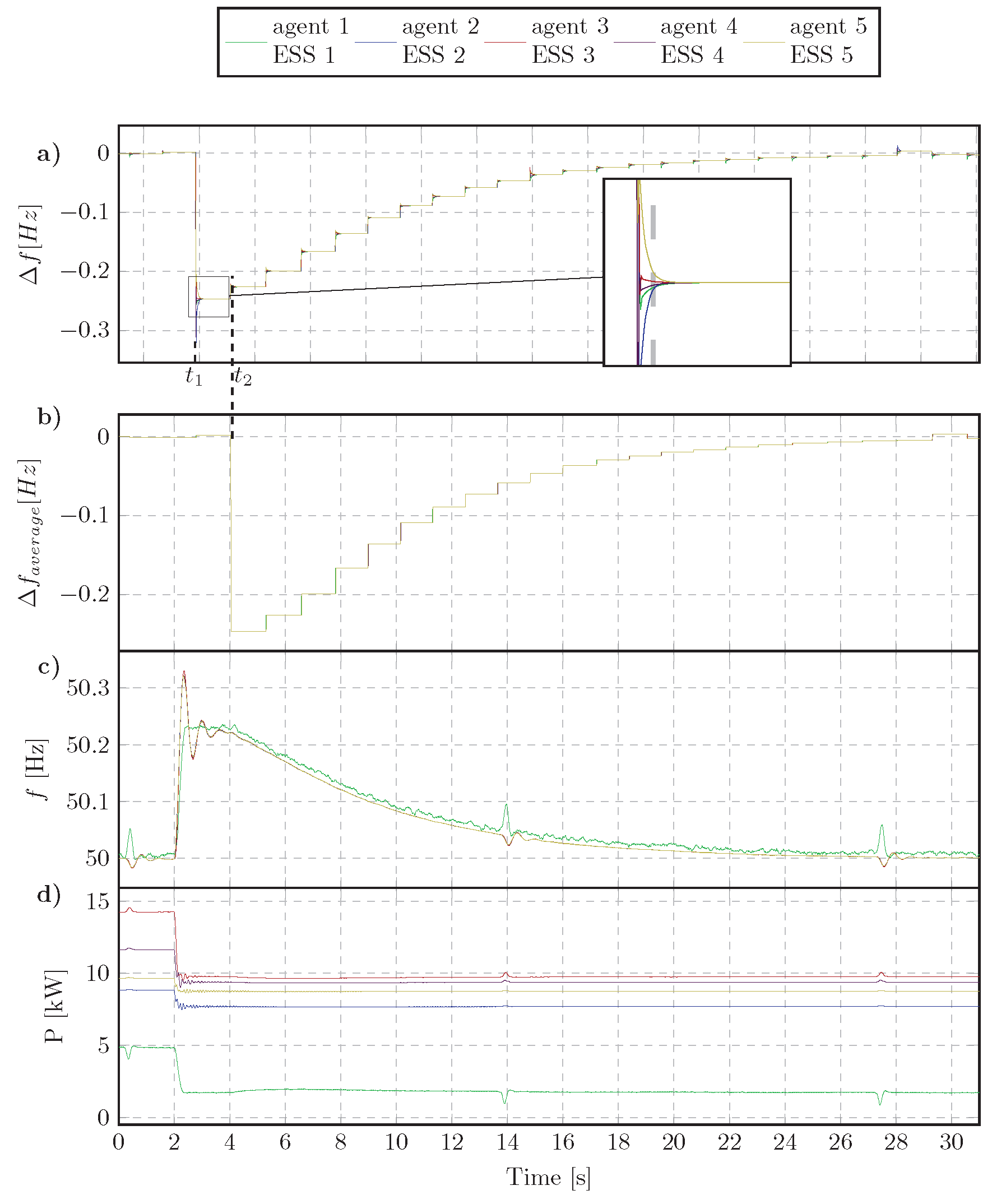
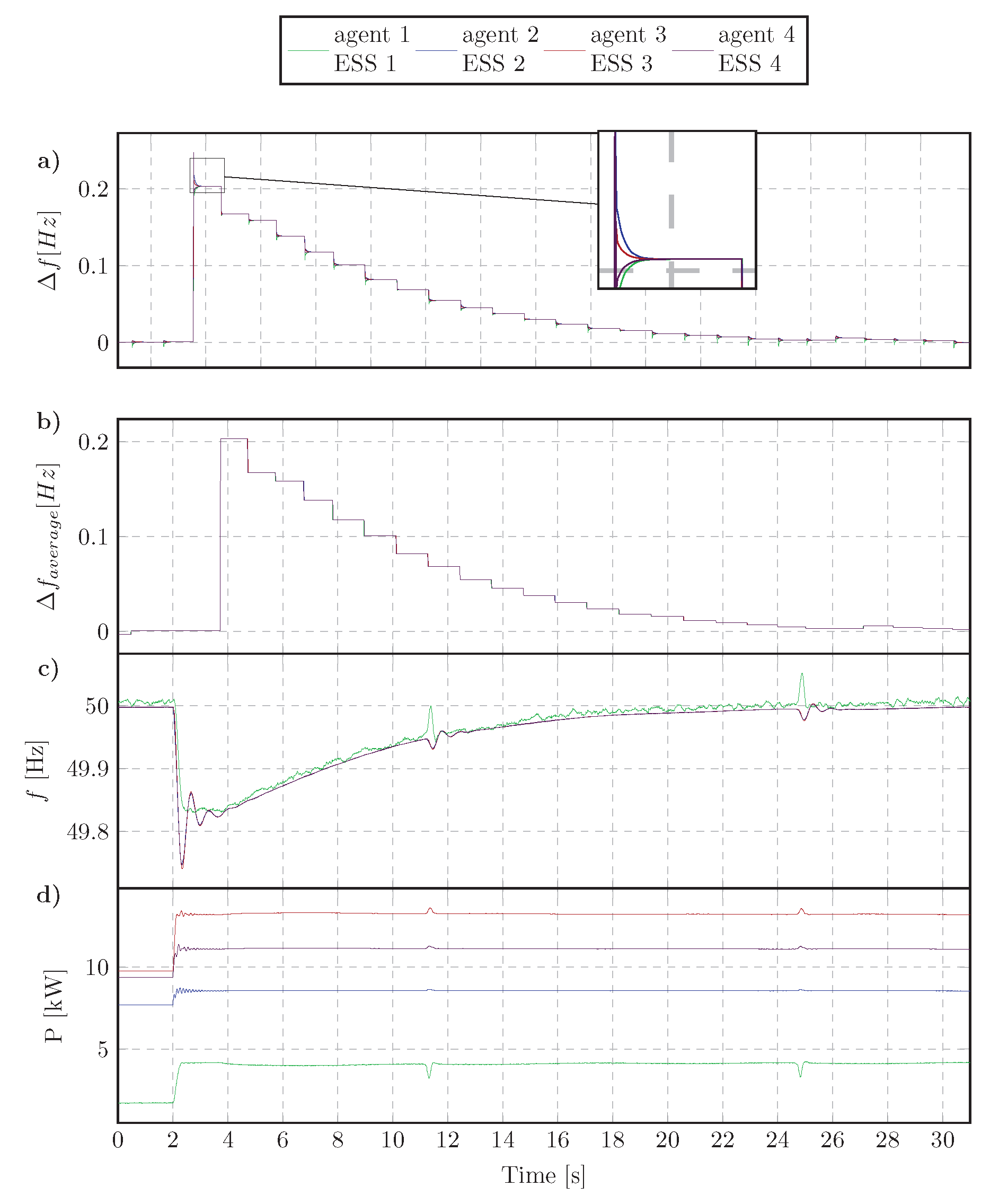
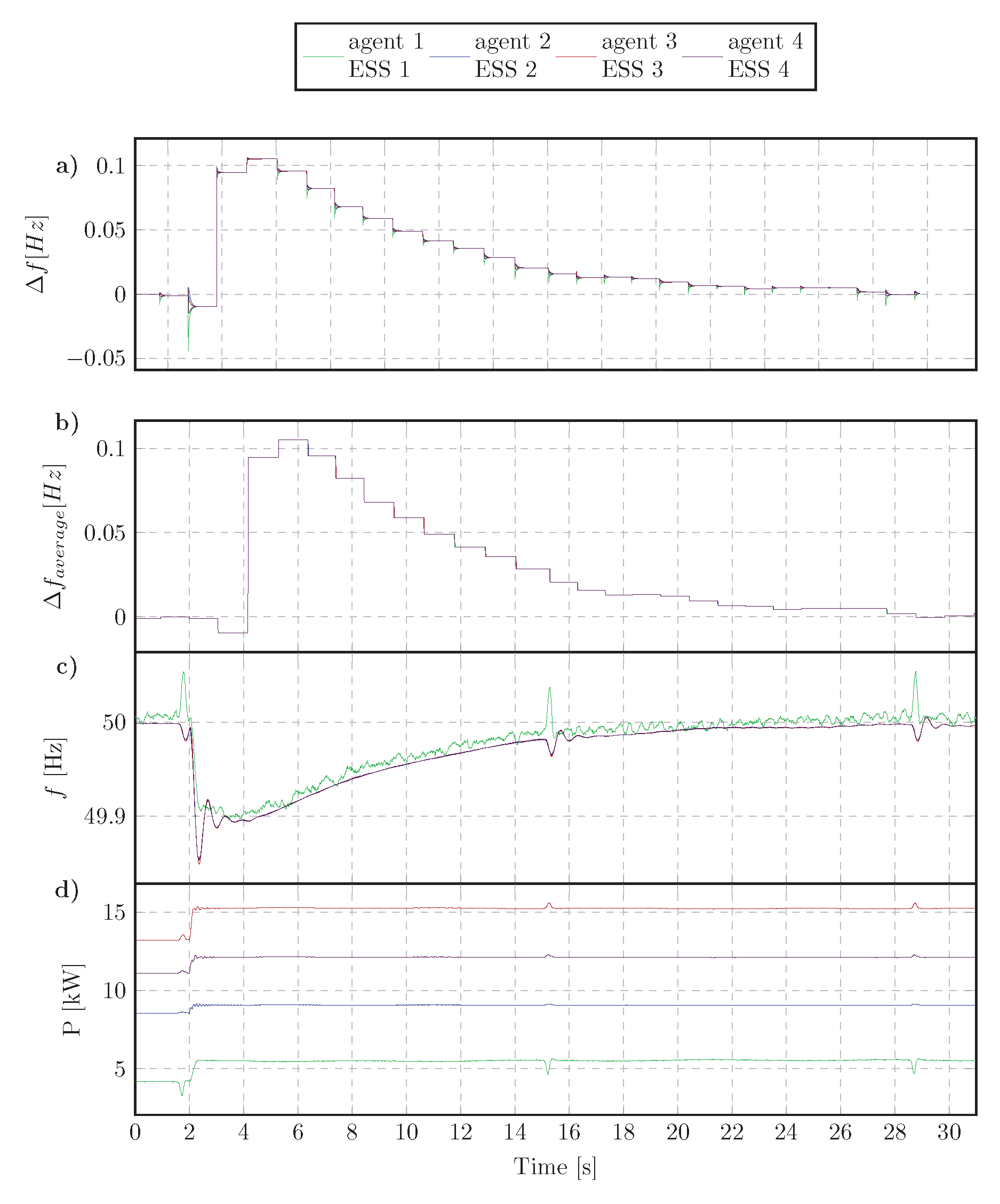
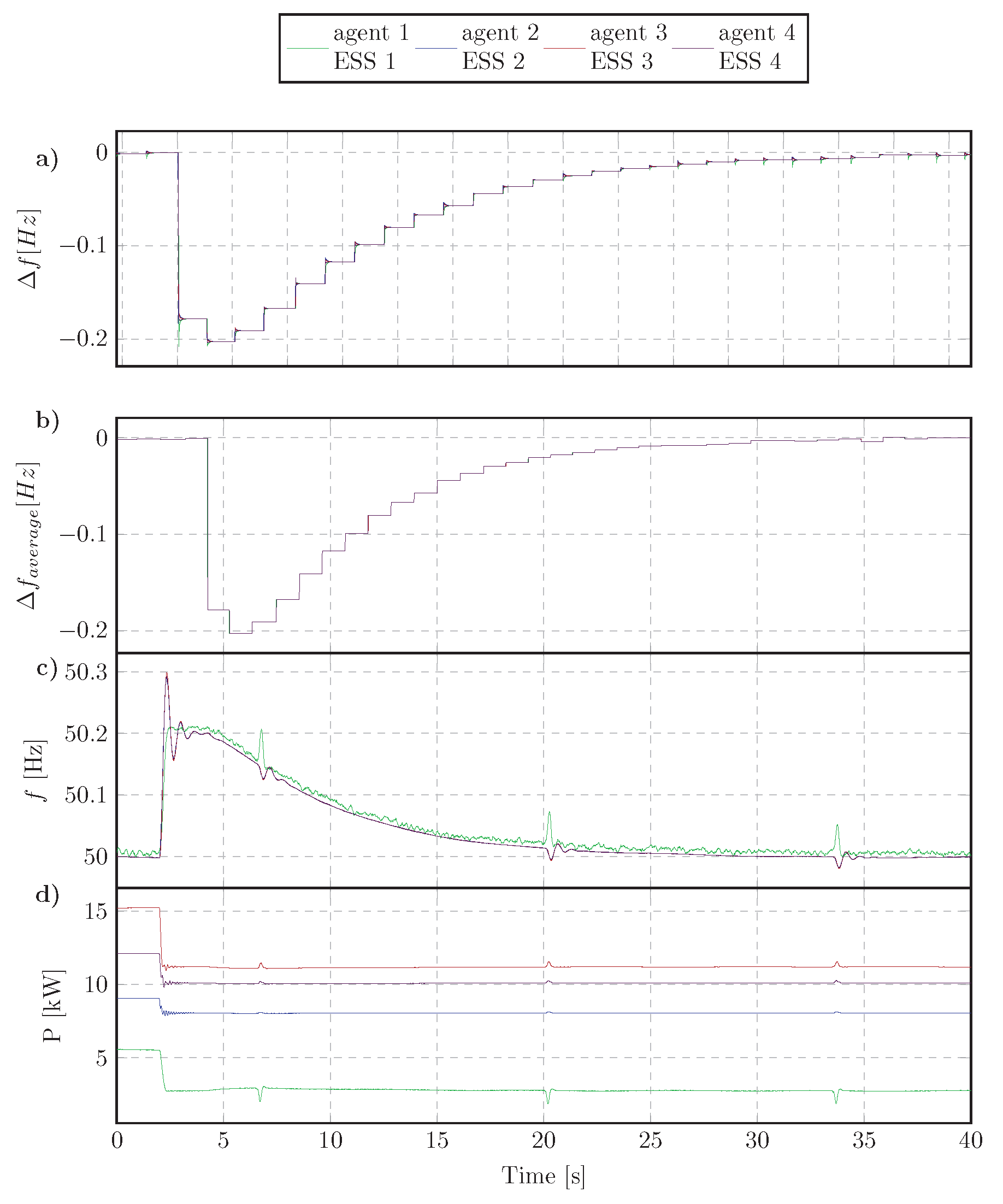
4.3. Experimental Results
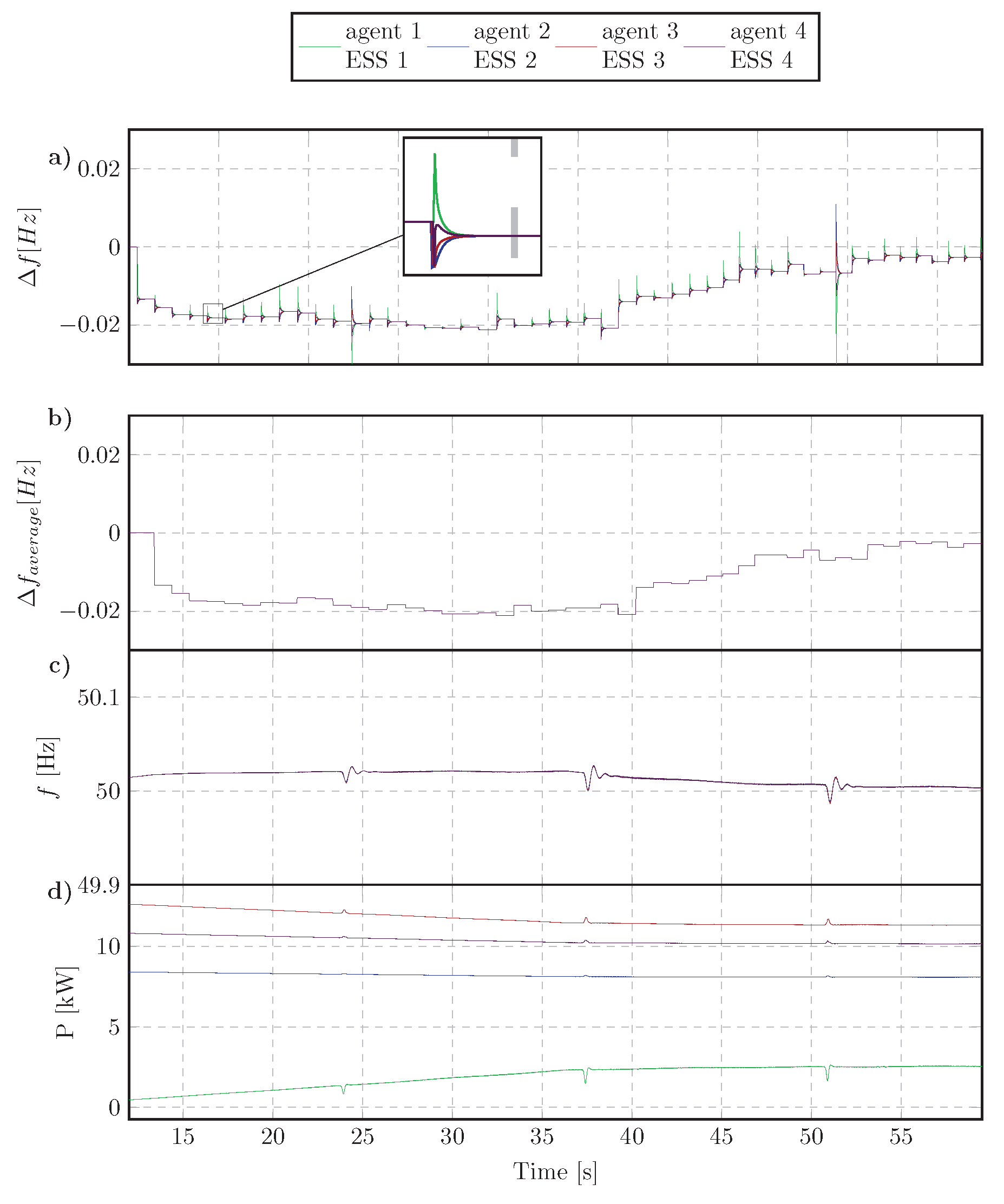
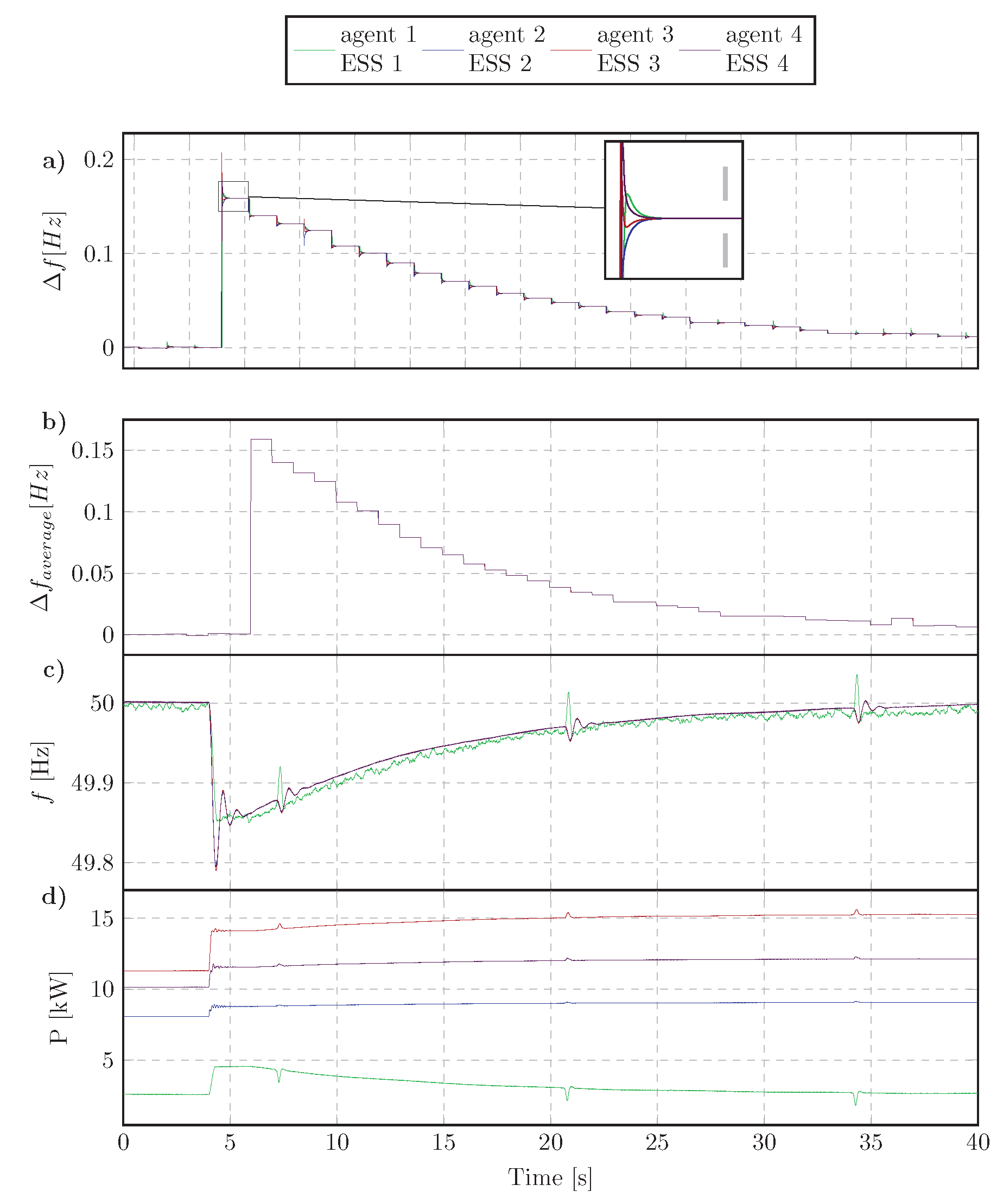
4.3.1. Step Change of Load Active Power
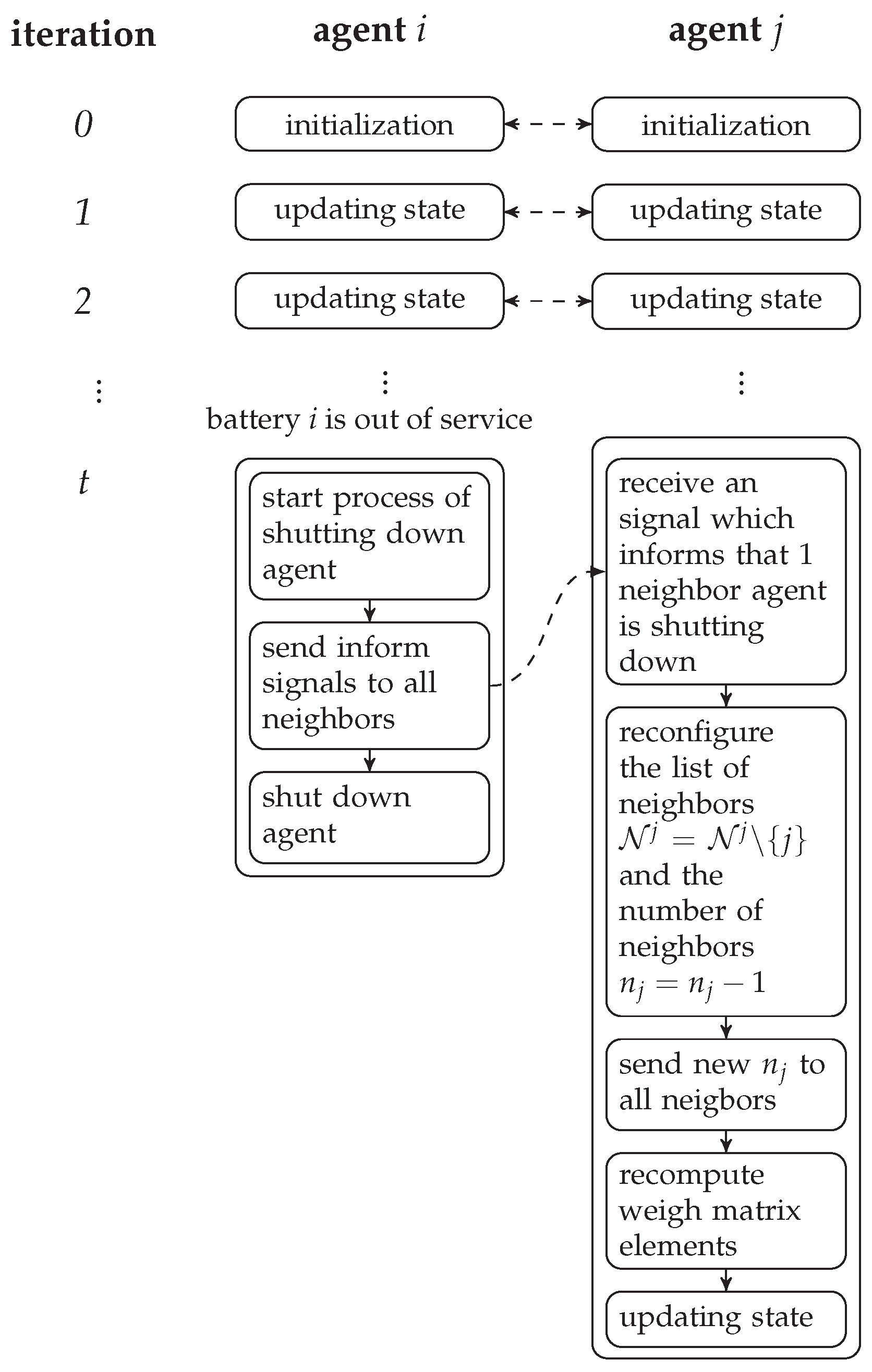
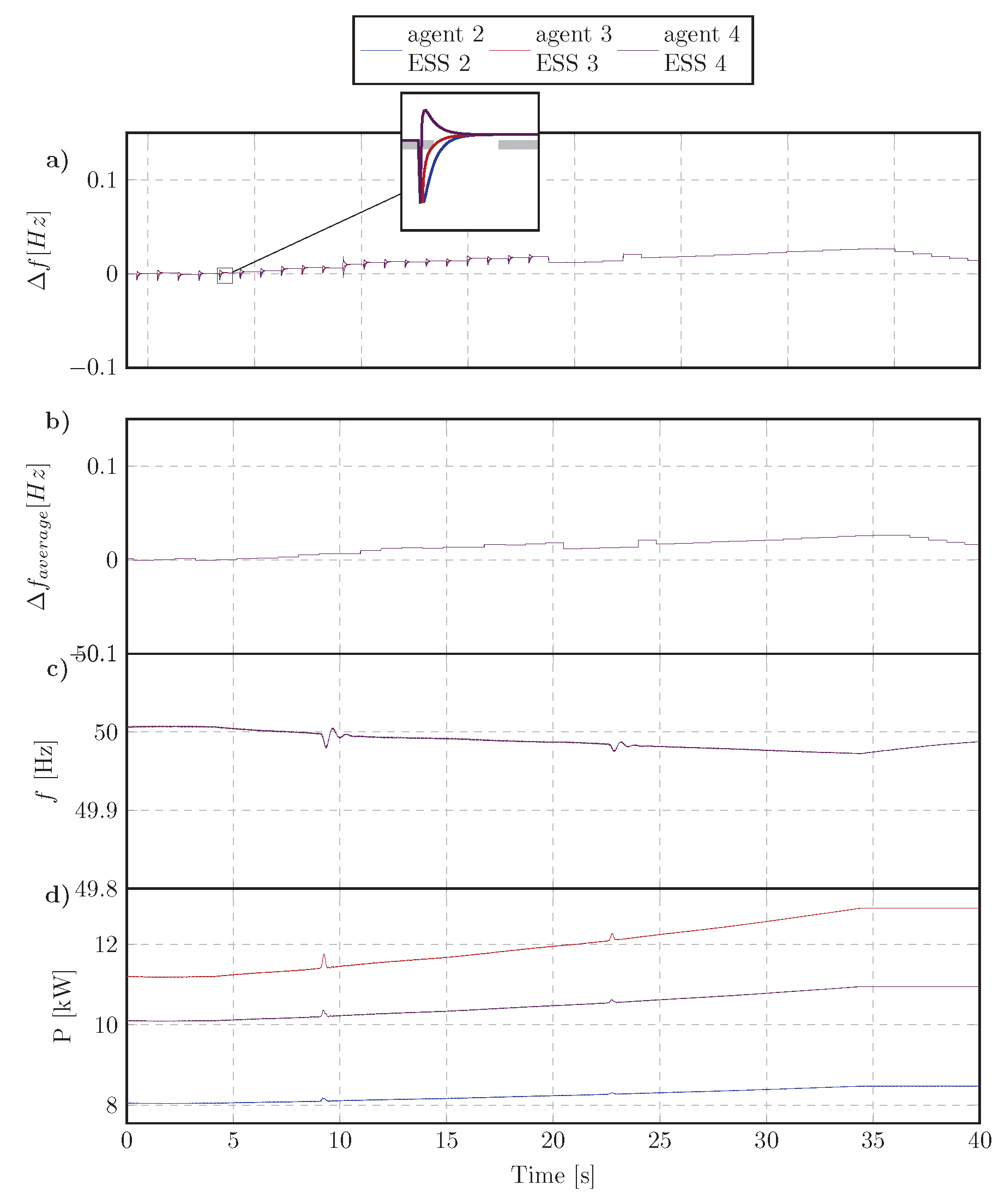
4.3.2. Disconnecting an ESS
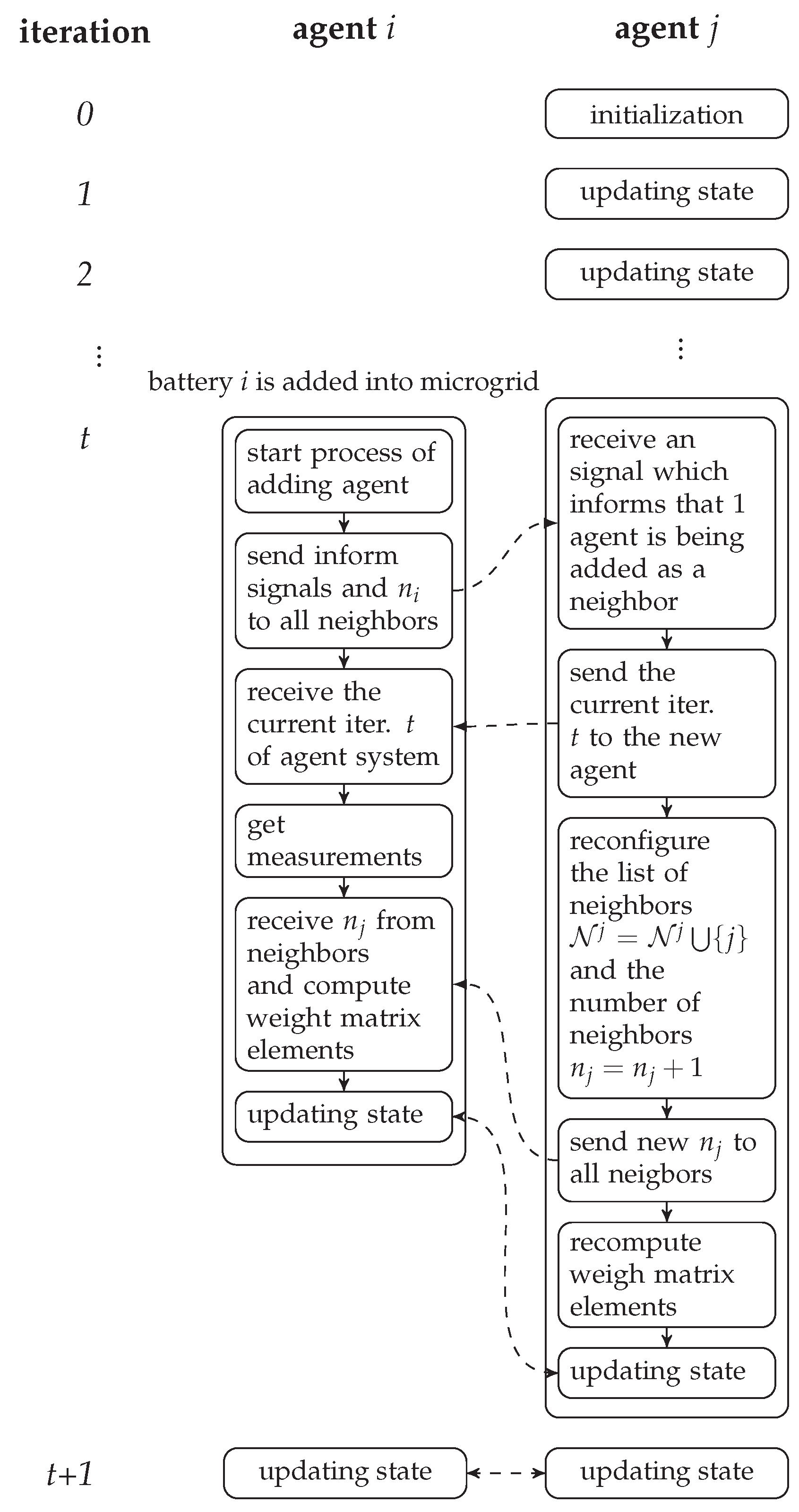
4.3.3. Connecting an ESS to MG
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hatziargyriou, N. Microgrids: Architectures and Control; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 1–344. [Google Scholar] [CrossRef]
- Yazdanian, M.; Mehrizi-Sani, A. Distributed control techniques in microgrids. IEEE Trans. Smart Grid 2014, 5, 2901–2909. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.; Loh, P.C. Advanced Control Architectures for Intelligent Microgrids; Part I: Decentralized and Hierarchical Control. IEEE Trans. Ind. Electron. 2013, 60, 1254–1262. [Google Scholar] [CrossRef]
- Gomez-Sanz, J.J.; Garcia-Rodriguez, S.; Cuartero-Soler, N.; Hernandez-Callejo, L. Reviewing microgrids from a multi-agent systems perspective. Energies 2014, 7, 3355–3382. [Google Scholar] [CrossRef]
- Colson, C.M.; Nehrir, M.H. Comprehensive real-time microgrid power management and control with distributed agents. IEEE Trans. Smart Grid 2013, 4, 617–627. [Google Scholar] [CrossRef]
- Kantamneni, A.; Brown, L.E.; Parker, G.; Weaver, W.W. Survey of multi-agent systems for microgrid control. Eng. Appl. Artif. Intell. 2015. [Google Scholar] [CrossRef]
- Dragicevic, T.; Wu, D.; Shafiee, Q.; Meng, L. Distributed and Decentralized Control Architectures for Converter-Interfaced Microgrids. Chin. J. Electr. Eng. 2017, 3, 41–52. [Google Scholar]
- Shafiee, Q.; Stefanovic, C.; Dragicevic, T.; Popovski, P.; Vasquez, J.C.; Guerrero, J.M. Robust Networked Control Scheme for Distributed Secondary Control of Islanded Microgrids. IEEE Trans. Ind. Electron. 2014, 61, 5363–5374. [Google Scholar] [CrossRef]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. Fully Distributed Cooperative Secondary Frequency and Voltage Control of Islanded Microgrids. IEEE Trans. Energy Convers. 2017, 32, 675–685. [Google Scholar] [CrossRef]
- Zhang, G.; Li, C.; Qi, D.; Xin, H. Distributed Estimation and Secondary Control of Autonomous Microgrid. IEEE Trans. Power Syst. 2017, 32, 989–998. [Google Scholar] [CrossRef]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. Distributed Robust Finite-Time Secondary Voltage and Frequency Control of Islanded Microgrids. IEEE Trans. Power Syst. 2017, 32, 3648–3659. [Google Scholar] [CrossRef]
- Raju, L.; Milton, R.S.; Mahadevan, S. Multi agent systems based distributed control and automation of micro-grid using MACSimJX. In Proceedings of the 2016 10th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 7–8 January 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Harmouch, F.Z.; Krami, N.; Benhaddou, D.; Hmina, N.; Zayer, E.; Margoum, E.H. Survey of multiagents systems application in Microgrids. In Proceedings of the 2016 International Conference on Electrical and Information Technologies (ICEIT), Tangiers, Morocco, 4–7 May 2016; pp. 270–275. [Google Scholar] [CrossRef]
- Nelson, A.; Chakraborty, S.; Wang, D.; Singh, P.; Cui, Q.; Yang, L.; Suryanarayanan, S. Cyber-physical test platform for microgrids: Combining hardware, hardware-in-the-loop, and network-simulator-in-the-loop. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016. [Google Scholar] [CrossRef]
- Kotsampopoulos, P.C.; Lehfuss, F.; Lauss, G.F.; Bletterie, B.; Hatziargyriou, N.D. The limitations of digital simulation and the advantages of PHIL testing in studying distributed generation provision of ancillary services. IEEE Trans. Ind. Electron. 2015. [Google Scholar] [CrossRef]
- Guillo-Sansano, E.; Syed, M.H.; Roscoe, A.J.; Burt, G.M. Initialization and Synchronization of Power Hardware-In-The-Loop Simulations: A Great Britain Network Case Study. Energies 2018, 11. [Google Scholar] [CrossRef]
- Nguyen, T.; Guillo-Sansano, E.; Syed, M.H.; Blair, S.M.; Reguera, L.; Tran, Q.; Caire, R.; Burt, G.M.; Gavriluta, C.; Nguyen, V. Systems Level Validation of a Distributed Frequency Control Algorithm. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Shafiee, Q.; Guerrero, J.M.; Vasquez, J.C. Distributed secondary control for islanded microgrids-a novel approach. IEEE Trans. Power Electron. 2014. [Google Scholar] [CrossRef]
- Chen, M.; Syed, M.H.; Sansano, E.G.; McArthur, S.D.; Burt, G.M.; Kockar, I. Distributed negotiation in future power networks: Rapid prototyping using multi-agent system. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe, Ljubljana, Slovenia, 9–12 October 2017. [Google Scholar] [CrossRef]
- Guo, J.; Hug, G.; Tonguz, O.K. On the Role of Communications Plane in Distributed Optimization of Power Systems. IEEE Trans. Ind. Inform. 2017. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Tran, Q.T.; Besanger, Y. SCADA as a service approach for interoperability of micro-grid platforms. Sustain. Energy Grids Netw. 2016, 8, 26–36. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Besanger, Y.; Tran, Q.T.; Nguyen, T.L. On Conceptual Structuration and Coupling Methods of Co-Simulation Frameworks in Cyber-Physical Energy System Validation. Energies 2017, 10, 1977. [Google Scholar] [CrossRef]
- Tolk, A.; Muguira, J. The levels of conceptual interoperability model. In Proceedings of the 2003 Fall Simulation Interoperability Workshop, Orlando, FL, USA, 14–19 September 2003. [Google Scholar]
- Lu, X.; Yu, X.; Lai, J.; Wang, Y.; Guerrero, J.M. A Novel Distributed Secondary Coordination Control Approach for Islanded Microgrids. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Han, Y.; Li, H.; Shen, P.; Coelho, E.; Guerrero, J. Review of Active and Reactive Power Sharing Strategies in Hierarchical Controlled Microgrids. IEEE Trans. Power Electron. 2016, 8993. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical structure of microgrids control system. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuna, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Sayed, A.H. Adaptive Networks. Proc. IEEE 2014, 102, 460–497. [Google Scholar] [CrossRef]
- Blair, S.M.; Coffele, F.; Booth, C.D.; Burt, G.M. An Open Platform for Rapid-Prototyping Protection and Control Schemes With IEC 61850. IEEE Trans. Power Deliv. 2013, 28, 1103–1110. [Google Scholar] [CrossRef]





| Parameter | Value | Unit | |
|---|---|---|---|
| Inverter 1 | 3 | kW | |
| 100 | Hz/kW | ||
| Inverter 2 | 8 | kW | |
| 200 | Hz/kW | ||
| Inverter 3 | 11 | kW | |
| 50 | Hz/kW | ||
| Inverter 4 | 10 | kW | |
| 100 | Hz/kW | ||
| Inverter 5 | 9 | kW | |
| 250 | Hz/kW | ||
| Secondary controllers | 0.01 | ||
| 0.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-L.; Guillo-Sansano, E.; Syed, M.H.; Nguyen, V.-H.; Blair, S.M.; Reguera, L.; Tran, Q.-T.; Caire, R.; Burt, G.M.; Gavriluta, C.; et al. Multi-Agent System with Plug and Play Feature for Distributed Secondary Control in Microgrid—Controller and Power Hardware-in-the-Loop Implementation. Energies 2018, 11, 3253. https://doi.org/10.3390/en11123253
Nguyen T-L, Guillo-Sansano E, Syed MH, Nguyen V-H, Blair SM, Reguera L, Tran Q-T, Caire R, Burt GM, Gavriluta C, et al. Multi-Agent System with Plug and Play Feature for Distributed Secondary Control in Microgrid—Controller and Power Hardware-in-the-Loop Implementation. Energies. 2018; 11(12):3253. https://doi.org/10.3390/en11123253
Chicago/Turabian StyleNguyen, Tung-Lam, Efren Guillo-Sansano, Mazheruddin H. Syed, Van-Hoa Nguyen, Steven M. Blair, Luis Reguera, Quoc-Tuan Tran, Raphael Caire, Graeme M. Burt, Catalin Gavriluta, and et al. 2018. "Multi-Agent System with Plug and Play Feature for Distributed Secondary Control in Microgrid—Controller and Power Hardware-in-the-Loop Implementation" Energies 11, no. 12: 3253. https://doi.org/10.3390/en11123253
APA StyleNguyen, T.-L., Guillo-Sansano, E., Syed, M. H., Nguyen, V.-H., Blair, S. M., Reguera, L., Tran, Q.-T., Caire, R., Burt, G. M., Gavriluta, C., & Luu, N.-A. (2018). Multi-Agent System with Plug and Play Feature for Distributed Secondary Control in Microgrid—Controller and Power Hardware-in-the-Loop Implementation. Energies, 11(12), 3253. https://doi.org/10.3390/en11123253






