Springback Coefficient Research of API X60 Pipe with Dent Defect
Abstract
:1. Introduction
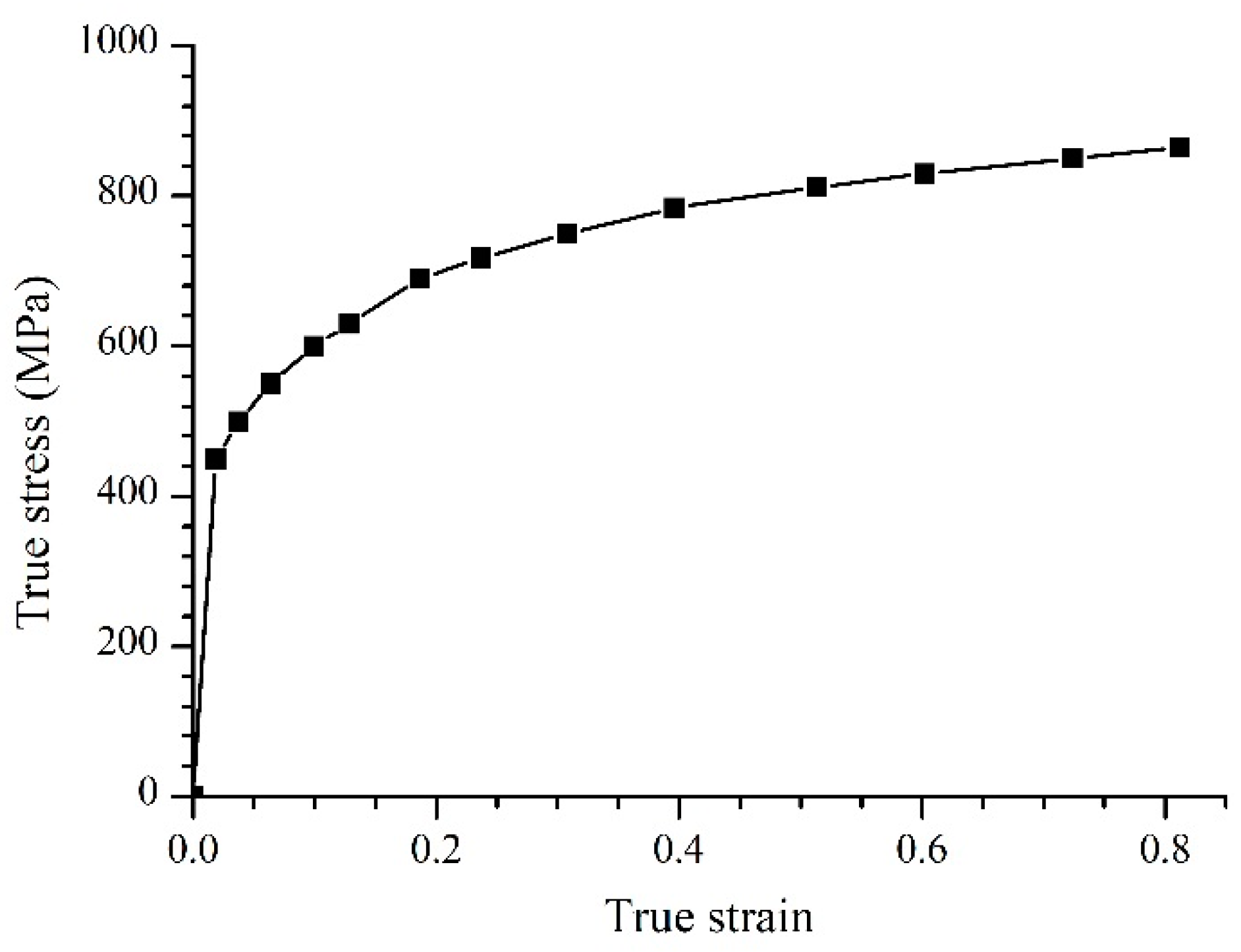
2. Material
3. Parametric Finite Element Analysis
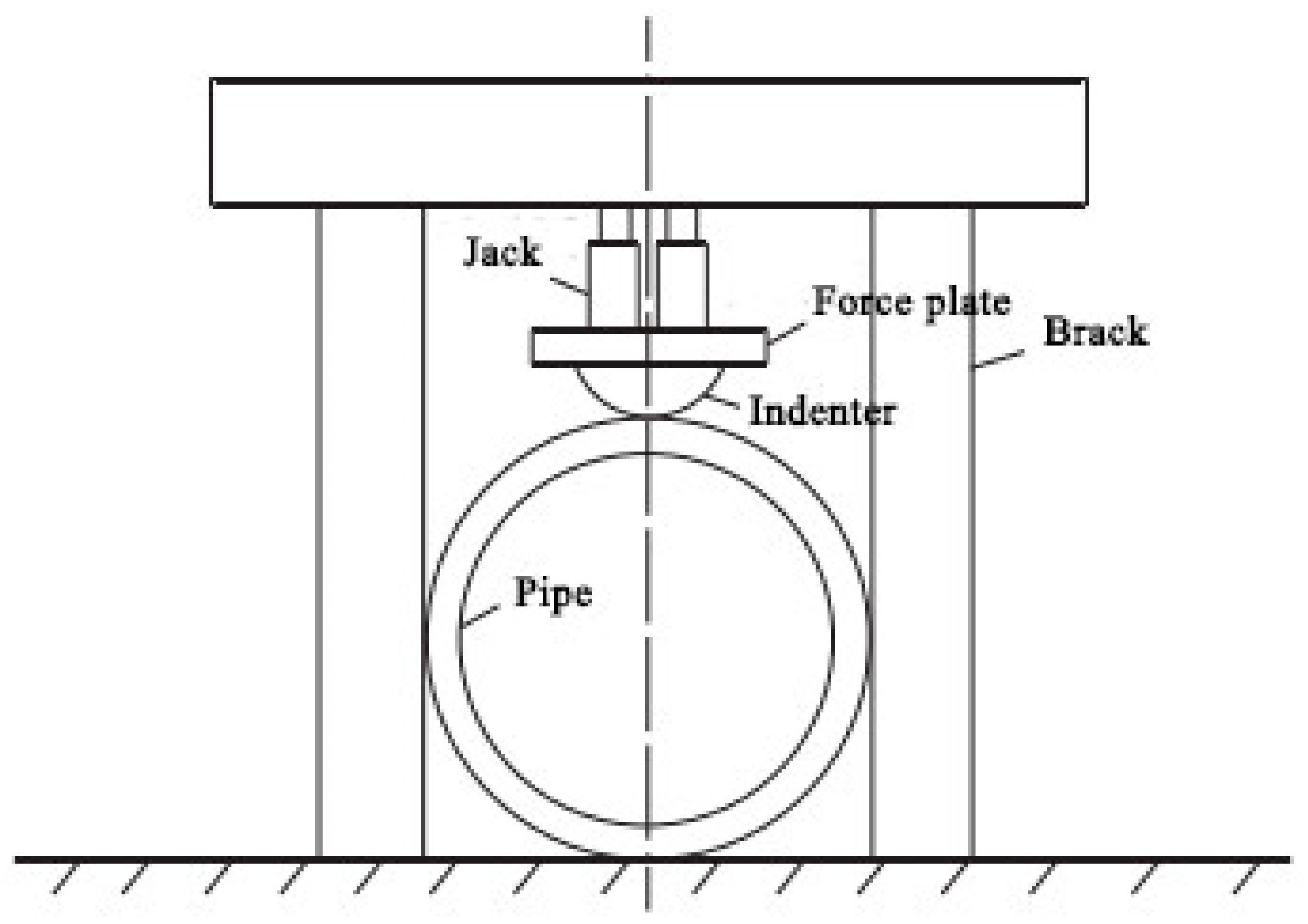
3.1. Finite Element Model
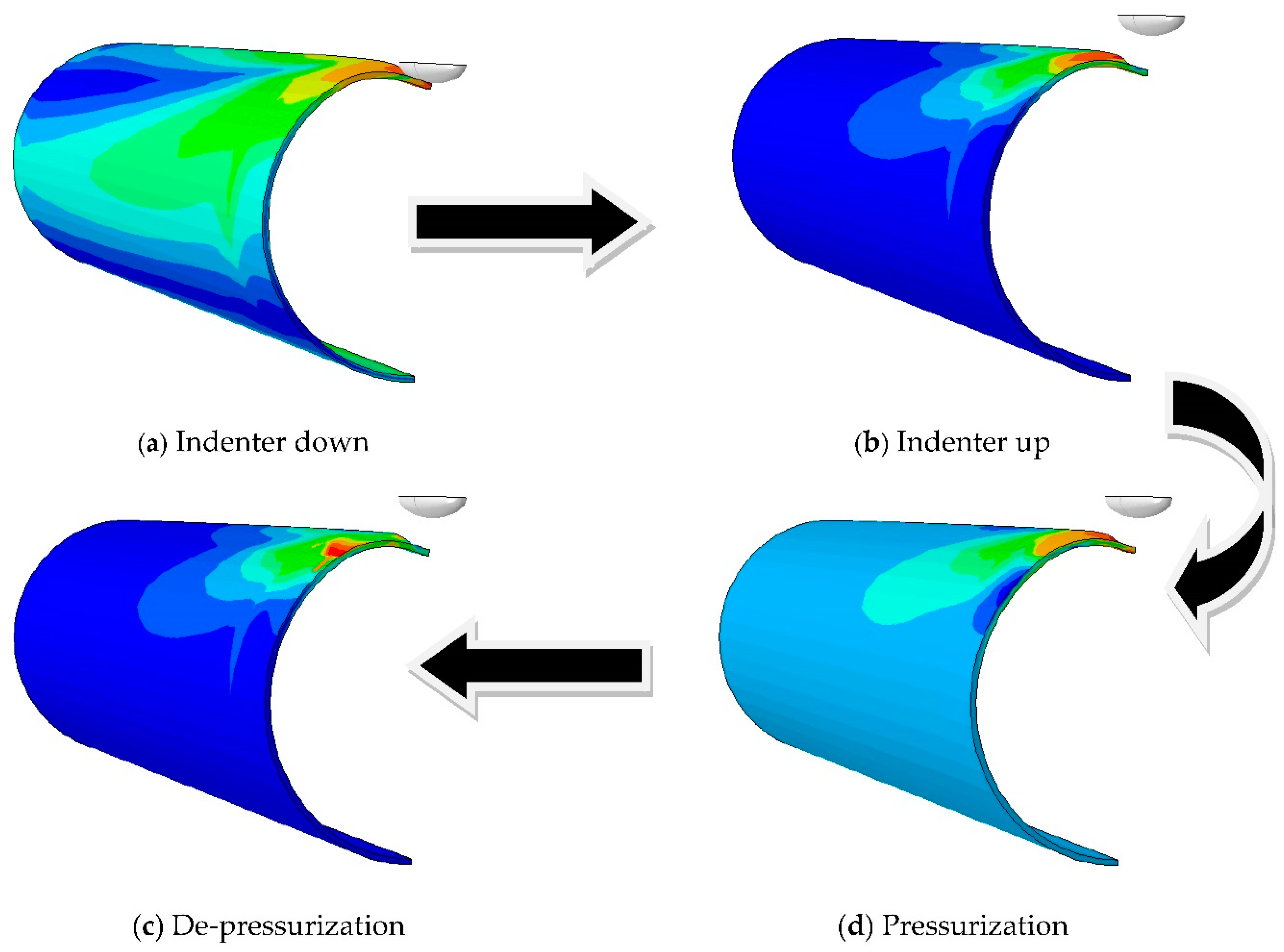
3.2. Load Model and Boundary Condition
- (1)
- The indenter was applied with a displacement load to simulate the extrusion of the pipe by an external object.
- (2)
- The indenter was applied with a reverse displacement load to simulate the process of removing the external object after the pipe was dented.
- (3)
- An internal pressure was assigned to the inner surface of the pipe to simulate the dented pipe under normal operation.
- (4)
- The internal pressure was released to evaluate the residual dent depth and observe the springback phenomenon.
3.3. Plug-In Program
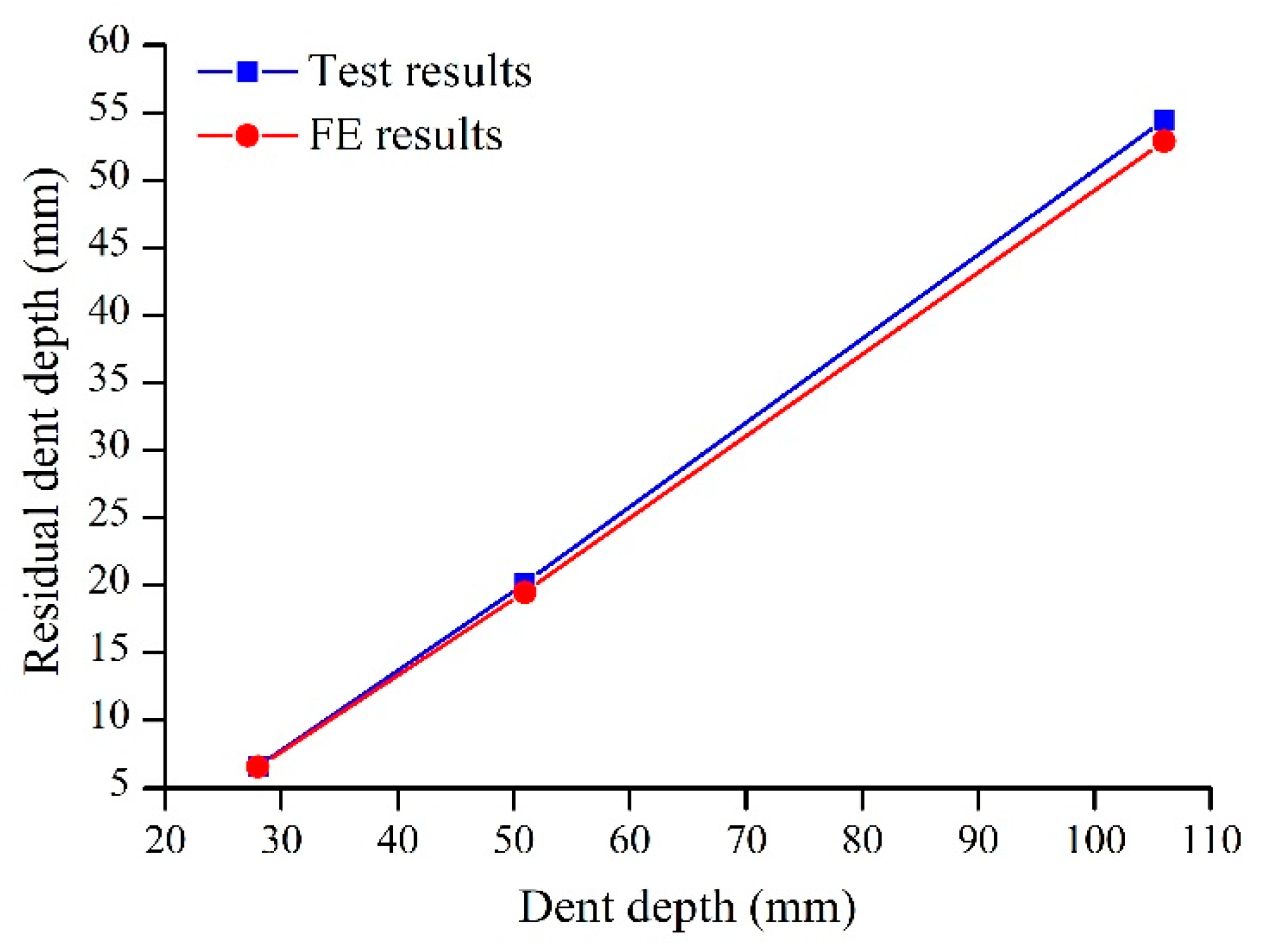
3.4. FE Model Verification
4. Results and Discussion
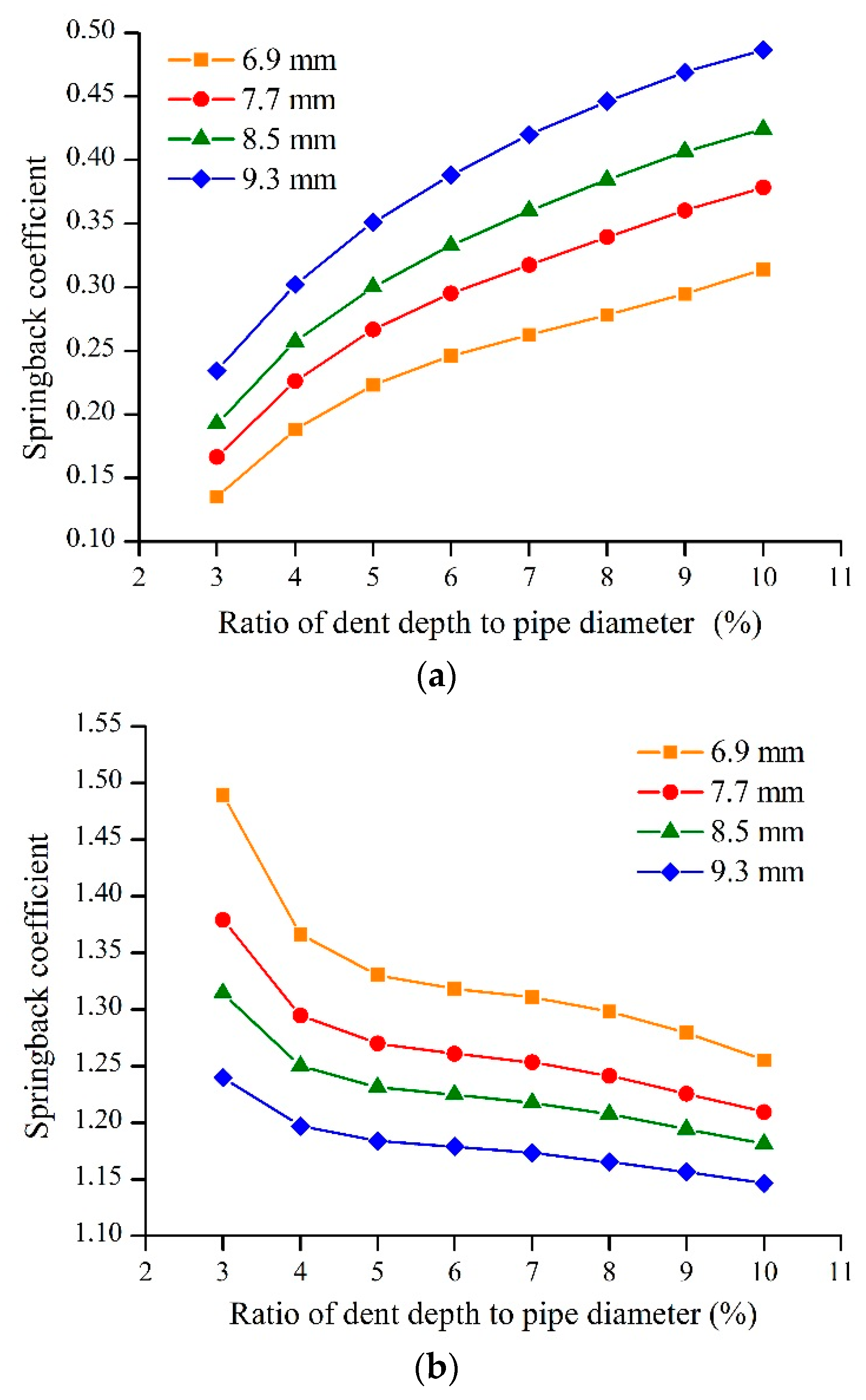
4.1. Pipe Wall Thickness
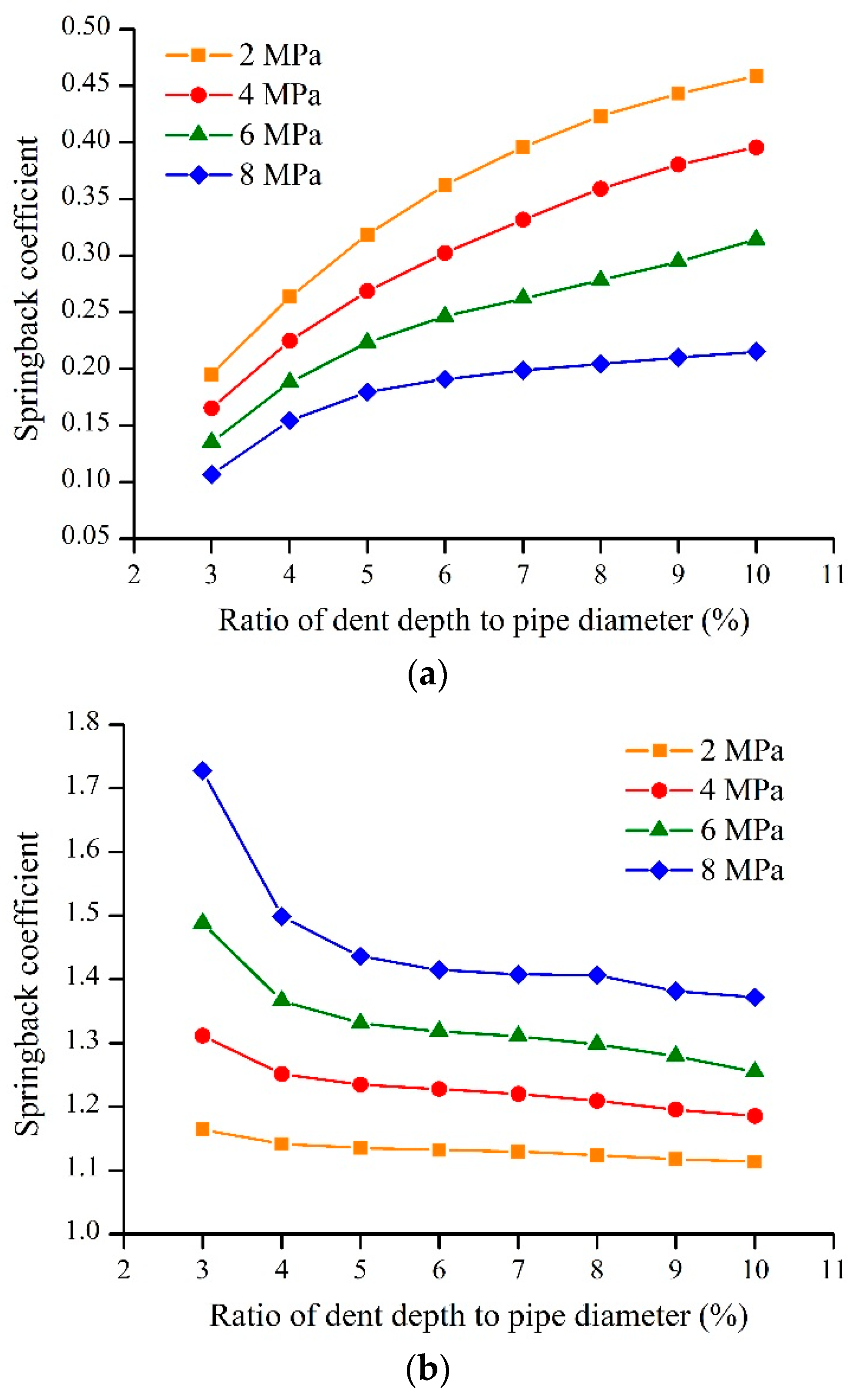
4.2. Internal Pressure
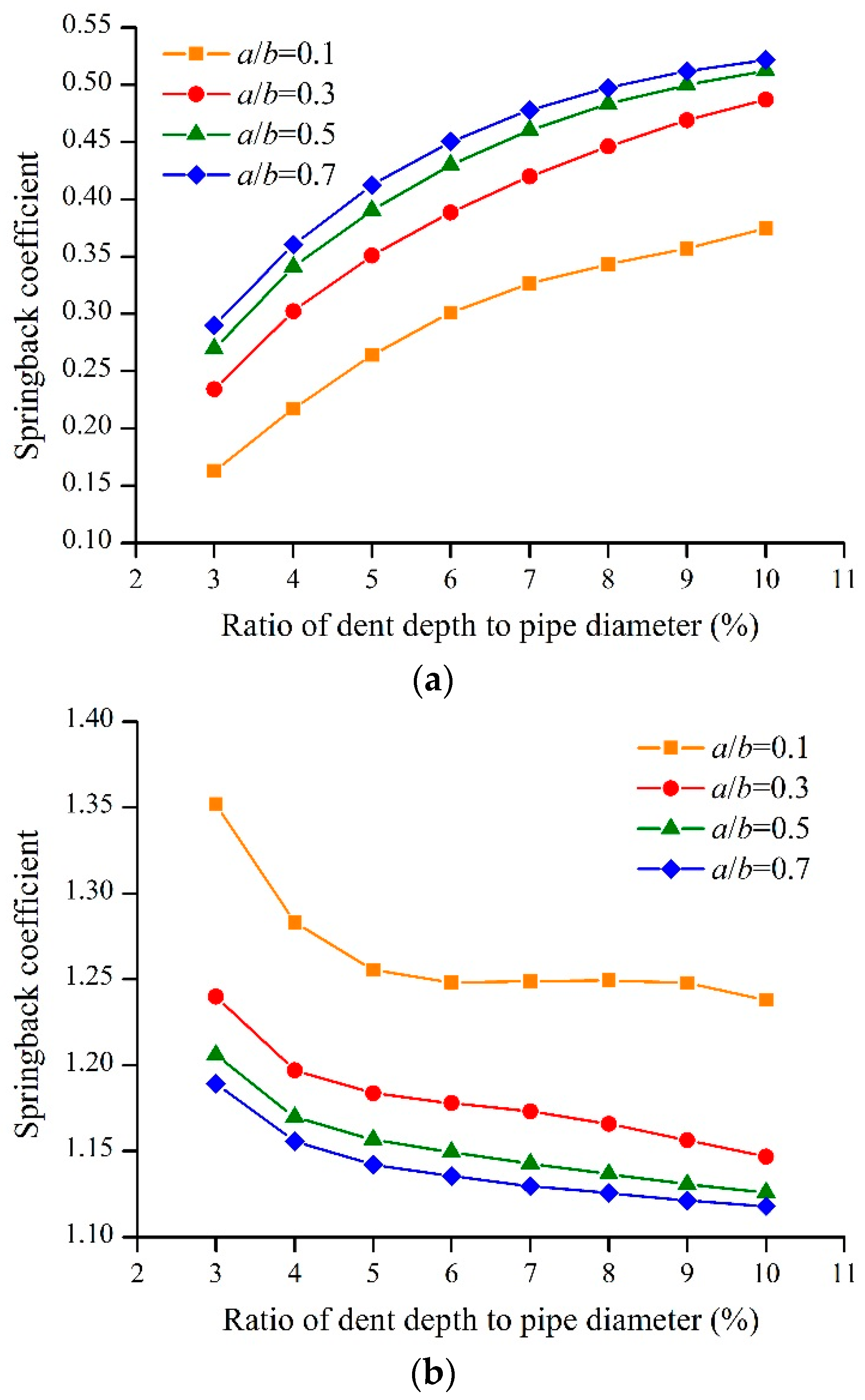
4.3. Indenter Size
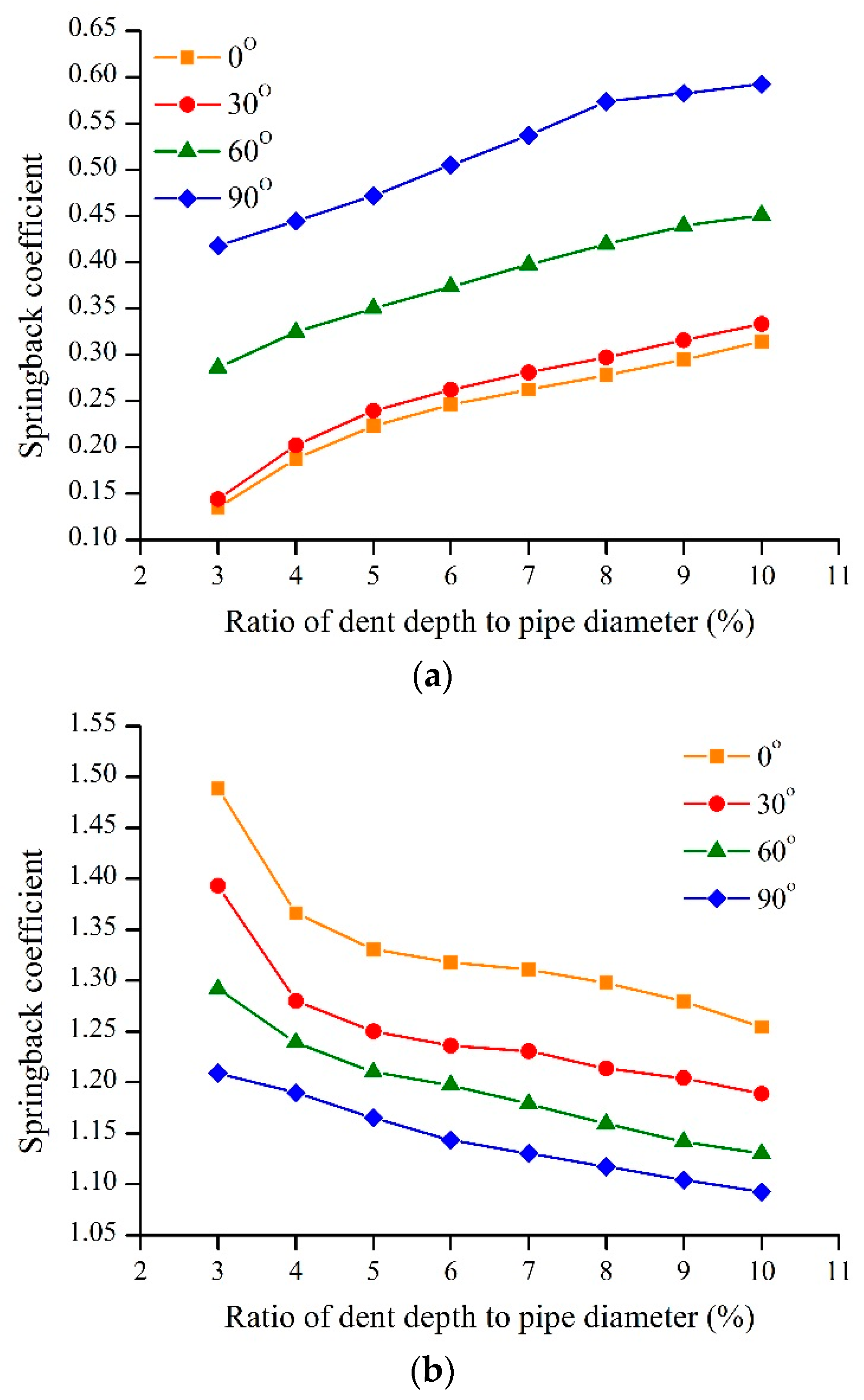
4.4. Dent Location
5. Significance Analysis of Influential Factors
5.1. Orthogonal Design
5.2. Grey Correlation Degree Calculation
5.3. Significance Analysis
6. Nonlinear Regression Analysis
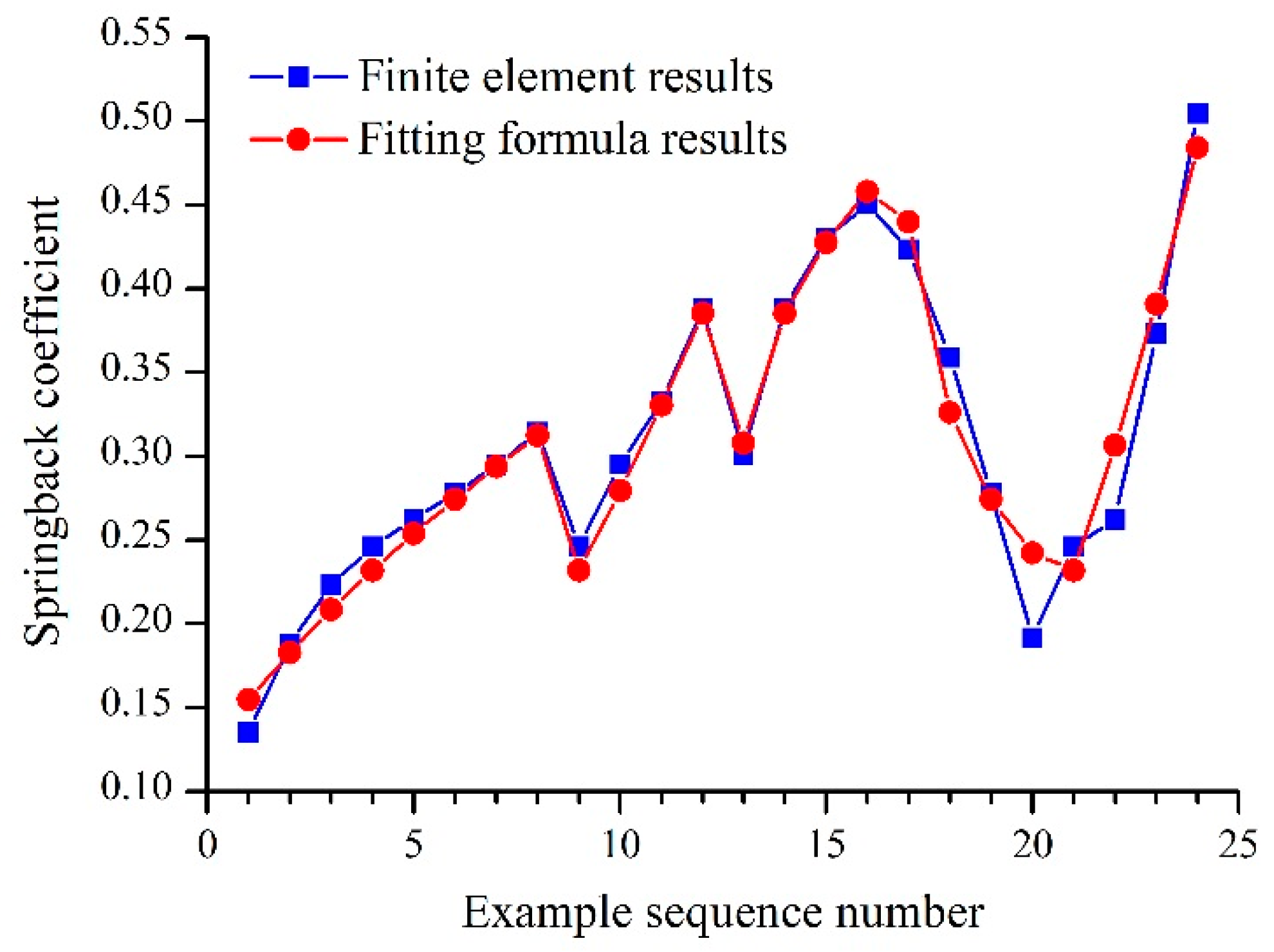
6.1. Formula of Springback Coefficient after Pressurization
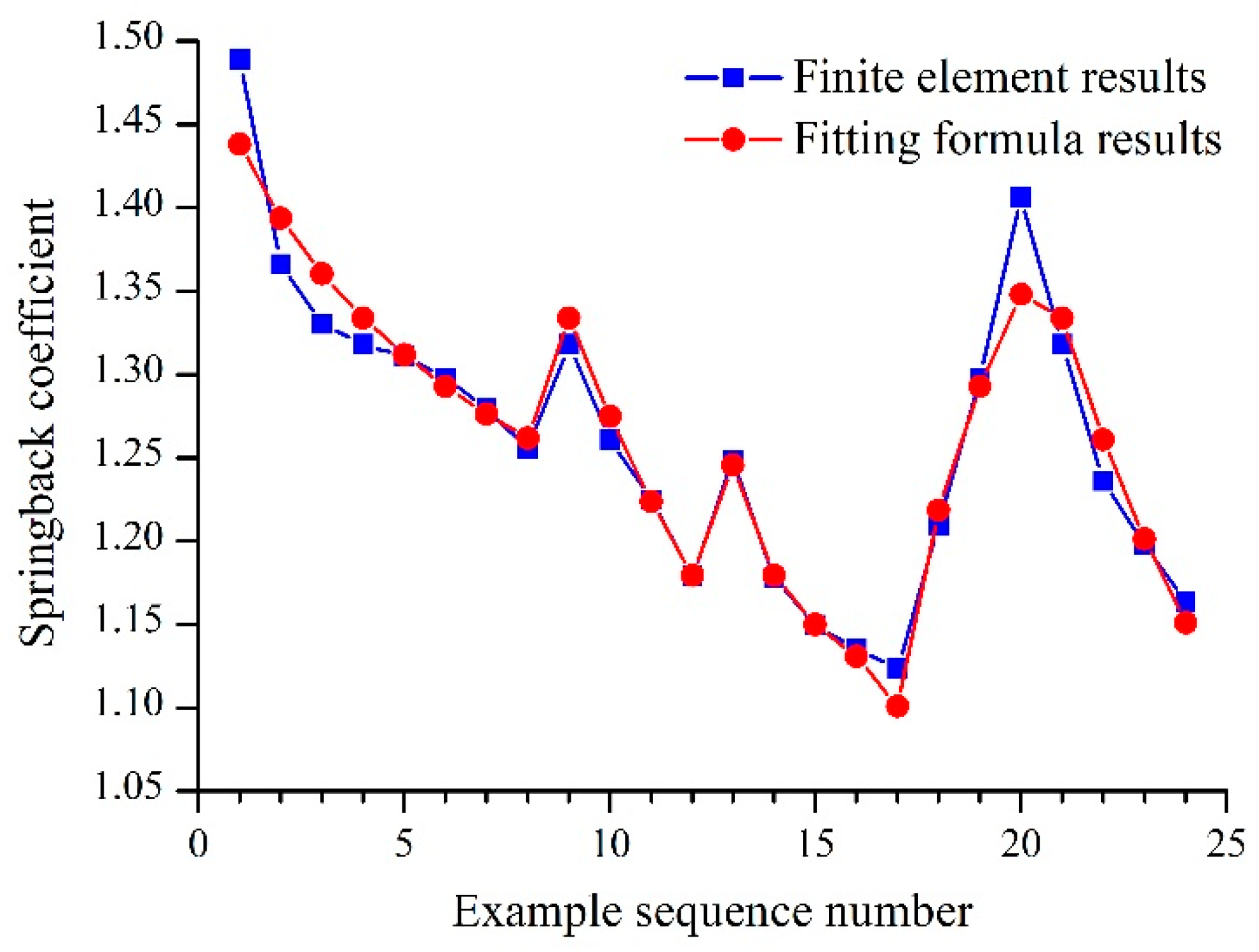
6.2. Formula of Springback Coefficient after De-Pressurization
7. Conclusions
- (1)
- To quickly and accurately establish an FE model of a dented pipe and to automate the simulation and analysis, ABAQUS secondary development technology was introduced. The plug-in interface for the parametric modeling and analysis of a dented pipe was programmed using RSG of ABAQUS, whose corresponding kernel script was compiled to cascade with it. This method avoids repeated modeling, saves time and energy, and effectively improves the automation of the simulation analysis process.
- (2)
- After pressurization, a thicker wall thickness led to larger springback coefficient. A larger internal pressure led to greater springback. The springback coefficient increased with increasing indenter size and dent depth. The closer the dent was to the bottom of the pipeline, the smaller the springback coefficient. Therefore, a dent at the top of the pipe should be of most concern in the evaluation of a dent, where the dent springs back most fully.
- (3)
- After de-pressurization, the springback coefficient decreased with increasing dent depth, wall thickness, indenter size, and dent location. However, the springback coefficient increased with increasing internal pressure. The springback coefficients were concentrated between 1.1 and 1.5. Therefore, the literature [9,11] values of the springback coefficient without internal pressure of 1.43 are not very accurate.
- (4)
- The effects of the influential factors on the springback coefficient were obtained by a combination of an orthogonal experimental design and the Grey correlation. For the springback coefficient after pressurization, the order of importance of the influential factors from largest to smallest was the dent location, dent depth, internal pressure, wall thickness, and indenter size. For the springback coefficient after de-pressurization, the order of importance of the influential factors from largest to smallest was the internal pressure, dent depth, wall thickness, indenter size, and dent location.
- (5)
- Quantitative expressions of the springback coefficient and influence factors were fit using a nonlinear regression method, which provides a reference for the calculation of springback of dented pipes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| D | outside diameter of pipe (mm) |
| t | wall thickness of pipe (mm) |
| P | internal pressure of pipe (MPa) |
| a | short axis of ellipsoidal indenter (mm) |
| b | long axis of the ellipsoidal indenter (mm) |
| β | dent location (°) |
| d | dent depth before pressurizing (mm) |
| dp | dent depth after pressurizing (mm) |
| dr | dent depth after releasing pressure (mm) |
| Hp | springback coefficient after pressurizing |
| Hr | springback coefficient after releasing pressure |
| E | Young’s modulus (MPa) |
| α | undetermined coefficient |
| δ | undetermined coefficient |
| γ | undetermined coefficient |
| ς | undetermined coefficient |
| τ | undetermined coefficient |
| υ | undetermined coefficient |
References
- Toyoshima, Y.; Hamori, S. Measuring the Time-Frequency Dynamics of Return and Volatility Connectedness in Global Crude Oil Markets. Energies 2018, 11, 2893. [Google Scholar] [CrossRef]
- Chala, G.T.; Abd Aziz, A.R.; Hagos, F.Y. Natural Gas Engine Technologies: Challenges and Energy Sustainability Issue. Energies 2018, 11, 2934. [Google Scholar] [CrossRef]
- Allouti, M.; Schmitt, C.; Pluvinage, G.; Gilgert, J.; Hariri, S. Study of the influence of dent depth on the critical pressure of pipeline. Eng. Fail. Anal. 2012, 21, 40–51. [Google Scholar] [CrossRef]
- Ghazijahani, T.G.; Jiao, H.; Holloway, D. Plastic buckling of dented steel circular tubes under axial compression: An experimental study. Thin Walled Struct. 2015, 92, 48–54. [Google Scholar] [CrossRef]
- Dawson, S.J. Emerging techniques for enhanced assessment and analysis of dents. In Proceedings of the IPC 2006 6th International Pipeline Conference, Calgary, AB, Canada, 25–29 September 2006. [Google Scholar]
- Alashti, R.A.; Jafari, S.; Hosseinipour, S.J. Experimental and numerical investigation of ductile damage effect on load bearing capacity of a dented API XB pipe subjected to internal pressure. Eng. Fail. Anal. 2015, 47, 208–228. [Google Scholar] [CrossRef]
- Adib, H.; Jallouf, S.; Schmitt, C.; Carmasol, A.; Pluvinage, G. Evaluation of the effect of corrosion defects on the structural integrity of X52 gas pipelines using the SINTAP procedure and notch theory. Int. J. Press. Vessel. Pip. 2007, 84, 123–131. [Google Scholar] [CrossRef]
- ASME B31.8-2014. Gas Transmission and Distribution Piping Systems; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- API 1156-1997. Effects of Smooth and Rock Dents on Liquid Petroleum Pipelines; American Petroleum Institute: Washington, DC, USA, 1997. [Google Scholar]
- Maxey, W.A. Outside Force Defect Behavior. In Proceedings of the 7th Symposium on Line Pipe Research, Houston, TX, USA, 14–16 October 1986. [Google Scholar]
- Corder, I.; Corbin, P. EPRG recommendations for the assessment of the resistance of pipelines to external damage. In Proceedings of the EPRG/PRC 10th Biennial Joint Technical Meeting on Line Pipe Research, Cambridge, UK, 18–21 April 1995. [Google Scholar]
- Cosham, A.; Hopkins, P. The effect of dents in pipelines-guidance in the pipeline defect assessment manual. Int. J. Press. Vessel. Pip. 2004, 81, 127–139. [Google Scholar] [CrossRef]
- Sha, S.Y.; Yan, B.C.; Jia, G.M.; Zhao, L.Y.; Tian, S.J.; Liu, Y.Q.; Yu, Z.B. Full-scale dent rebound test of X65 steel oil pipeline. Oil Gas Storage Transp. 2016, 35, 475–477. [Google Scholar]
- Yang, Q.; Shuai, J.; Zuo, S.Z. Research status of dented pipeline. Oil Gas Storage Transp. 2009, 28, 10–15. [Google Scholar]
- Hanif, W.; Kenny, S. Mechanical damage and fatigue assessment of dented pipelines using FEA. In Proceedings of the IPC 2014 10th International Pipeline Conference, Calgary, AB, Canada, 29 September–3 October 2014. [Google Scholar]
- Bastard, A.L. Influence of internal pressure for depth measurement on a dent. In Proceedings of the IPC 2006 6th International Pipeline Conference, Calgary, AB, Canada, 25–29 September 2006. [Google Scholar]
- Baek, J.H.; Kim, Y.P.; Kim, W.S.; Koo, J.M.; Seok, C.S. Load bearing capacity of API X65 pipe with dent defect under internal pressure and in-plane bending. Mater. Sci. Eng. A 2012, 540, 70–82. [Google Scholar] [CrossRef]
- Hyde, T.H.; Luo, R.; Becker, A.A. Prediction of three-dimensional residual stresses at localised indentations in pipes. Int. J. Press. Vessel. Pip. 2012, 93–94, 1–11. [Google Scholar] [CrossRef]
- Xiong, W.; Gan, Z.; Xiong, S.P.; Yuan, S.; Li, G.J. Secondary development for ABAQUS based on MATLAB, part 1: Solution and key technologies. J. Plast. Eng. 2012, 19, 21–26. [Google Scholar]
- Kormi, K.; Webb, D.C.; Johnson, W. The application of the FEM to determine the response of a pretorsioned pipe cluster to static or dynamic axial impact loading. Comput. Struct. 1997, 62, 353–368. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Ezzati, M.; Fakheri, J. Uniaxial strain ratcheting behavior of dented steel tubular: An experimental study. Eng. Fail. Anal. 2014, 44, 202–216. [Google Scholar] [CrossRef]
- Azadeh, M.; Taheri, F. On the response of dented stainless-steel pipes subject to cyclic bending moments and its prediction. Thin Walled Struct. 2016, 99, 12–20. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Ezzati, M.; Parke, G.A.R. Plastic buckling, wrinkling and collapse behaviour of dented X80 steel line pipes under axial compression. J. Loss Prev. Process Ind. 2015, 38, 67–78. [Google Scholar] [CrossRef]
- Baek, J.H.; Kim, Y.P.; Kim, C.M.; Kim, W.S.; Seok, C.S. Effects of pre-strain on the mechanical properties of API 5L X65 pipe. Mater. Sci. Eng. A 2010, 527, 1473–1479. [Google Scholar] [CrossRef]
- Hyde, T.H.; Luo, R.; Becker, A.A. Predictions of three-dimensional stress variations in indented pipes due to internal pressure fluctuations. J. Strain Anal. Eng. Des. 2011, 46, 510–522. [Google Scholar] [CrossRef]
- Li, C.B.; Dang, S.H. Plastic damage analysis of oil and gas pipelines with unconstrained and constrained dents. Eng. Fail. Anal. 2017, 77, 39–49. [Google Scholar] [CrossRef]
- Iflefel, I.B.; Moffat, D.G.; Mistry, J. The interaction of pressure and bending on a dented pipe. Int. J. Press. Vessel. Pip. 2005, 82, 761–769. [Google Scholar] [CrossRef]
- Seberry, J.; Finlayson, K.; Adams, S.S.; Wysocki, T.T. The Theory of quaternion orthogonal designs. IEEE Trans. Signal Process. 2008, 56, 256–265. [Google Scholar] [CrossRef]
- Chen, Y.M.; Zhang, M. Cubic spline based grey absolute relational grade model. Syst. Eng. Theory Pract. 2015, 35, 1304–1310. [Google Scholar]
- Lv, Y.F.; Ma, T.X.; Zou, H.X.; Liu, W.Y. Study on springback coefficient of long distance dented pipeline based on FEM. Forg. Stamp. Technol. 2017, 42, 194–200. [Google Scholar]

| Yield Stress | True Ultimate Tensile Stress | Young’s Modulus | Poisson’s Ratio |
|---|---|---|---|
| 451 MPa | 660 MPa | 2 × 105 MPa | 0.3 |
| Factors | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Levels | Wall Thickness (mm) | Internal Pressure (MPa) | Indenter Size a/b | Dent Location (°) | Ratio of Dent Depth to Pipe Diameter | |
| 1 | 6.9 | 2 | 0.1 | 0 | 0.04 | |
| 2 | 7.7 | 4 | 0.3 | 30 | 0.06 | |
| 3 | 8.5 | 6 | 0.5 | 60 | 0.08 | |
| 4 | 9.3 | 8 | 0.7 | 90 | 0.1 | |
| Number | Influence Factors | Springback Coefficient | ||||
|---|---|---|---|---|---|---|
| Wall Thickness (mm) | Internal Pressure (MPa) | Indenter Size a/b | Dent Location (°) | Ratio of Dent Depth to Pipe Diameter | ||
| 1 | 6.9 | 2 | 0.1 | 0 | 0.04 | 0.185 |
| 2 | 6.9 | 4 | 0.3 | 30 | 0.06 | 0.315 |
| 3 | 6.9 | 6 | 0.5 | 60 | 0.08 | 0.457 |
| 4 | 6.9 | 8 | 0.7 | 90 | 0.1 | 0.475 |
| 5 | 7.7 | 2 | 0.3 | 60 | 0.1 | 0.620 |
| 6 | 7.7 | 4 | 0.1 | 90 | 0.08 | 0.648 |
| 7 | 7.7 | 6 | 0.7 | 0 | 0.06 | 0.368 |
| 8 | 7.7 | 8 | 0.5 | 30 | 0.04 | 0.258 |
| 9 | 8.5 | 2 | 0.5 | 90 | 0.06 | 0.725 |
| 10 | 8.5 | 4 | 0.7 | 60 | 0.04 | 0.508 |
| 11 | 8.5 | 6 | 0.1 | 30 | 0.1 | 0.368 |
| 12 | 8.5 | 8 | 0.3 | 0 | 0.08 | 0.328 |
| 13 | 9.3 | 2 | 0.7 | 30 | 0.08 | 0.568 |
| 14 | 9.3 | 4 | 0.5 | 0 | 0.1 | 0.553 |
| 15 | 9.3 | 6 | 0.3 | 90 | 0.04 | 0.567 |
| 16 | 9.3 | 8 | 0.1 | 60 | 0.06 | 0.358 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Huang, Y.; Wu, Y. Springback Coefficient Research of API X60 Pipe with Dent Defect. Energies 2018, 11, 3213. https://doi.org/10.3390/en11113213
Zhang P, Huang Y, Wu Y. Springback Coefficient Research of API X60 Pipe with Dent Defect. Energies. 2018; 11(11):3213. https://doi.org/10.3390/en11113213
Chicago/Turabian StyleZhang, Peng, Yunfei Huang, and Ying Wu. 2018. "Springback Coefficient Research of API X60 Pipe with Dent Defect" Energies 11, no. 11: 3213. https://doi.org/10.3390/en11113213




