Energy-Efficient Multicast Precoding for Massive MIMO Transmission with Statistical CSI

Abstract

In this paper, we investigate energy-efficient multicast precoding for massive multiple-input multiple-output (MIMO) transmission. In contrast with most previous work, where instantaneous channel state information (CSI) is exploited to facilitate energy-efficient wireless transmission design, we assume that the base station can only exploit statistical CSI of the user terminals for downlink multicast precoding. First, in terms of maximizing the system energy efficiency, the eigenvectors of the optimal energy-efficient multicast transmit covariance matrix are identified in closed form, which indicates that optimal energy-efficient multicast precoding should be performed in the beam domain in massive MIMO. Then, the large-dimensional matrix-valued precoding design is simplified into an energy-efficient power allocation problem in the beam domain with significantly reduced optimization variables. Using Dinkelbach’s transform, we further propose a sequential beam domain power allocation algorithm which is guaranteed to converge to the global optimum. In addition, we use the large-dimensional random matrix theory to derive the deterministic equivalent of the objective to reduce the computational complexity involved in sample averaging. We present numerical results to illustrate the near-optimal performance of our proposed energy-efficient multicast precoding for massive MIMO.

1. Introduction

The wireless traffic demand of group-oriented services and applications such as mobile TV, satellite communications, etc., is predicted to increase significantly in future wireless networks, and physical-layer wireless multicast transmission is a promising approach for such rapidly increasing demand. Recently, physical-layer multicasting has been incorporated in the 3GPP release known as eMBMS [1] and has received extensive research interest [2,3,4]. In massive multiple-input multiple-output (MIMO) systems [5,6,7], large numbers of antennas are equipped at the base station (BS) so that a smaller number (compared with the number of BS antennas) of user terminals (UTs) can be simultaneously served in the same time and frequency resources. Compared with conventional small-scale MIMO systems [8], massive MIMO systems can significantly improve the spectral efficiency and transmission reliability. Due to the ability of massive MIMO in shaping the multicast transmission signals, physical-layer multicasting combined with massive MIMO promises to improve the multicast transmission quality of service in the evolution of future wireless networks [9,10].

Energy efficiency (EE) is an important performance metric in wireless transmission design and has received growing attention from both academia and industry [11,12]. Energy-efficient transmission design for MIMO unicasting was investigated in some existing works, e.g., [13,14,15]. Meanwhile, energy-efficient multicasting transmission was also studied in several previous works. For example, energy-efficient coordinated multicast transmission design for multi-cell scenarios was studied in e.g., [16,17]. In addition, energy-efficient joint unicast and multicast transmission design for multi-cell MIMO systems was investigated in [18]. Please note that in most of the existing works on energy-efficient physical-layer multicast transmission, e.g., [16,17,18], instantaneous channel state information (CSI) is assumed to be known at the BS and exploited for transmission design.

For physical-layer massive MIMO multicast transmission, the transmission performance will be highly dependant on the quality of the available CSI at the BS. CSI acquisition at the BS is a challenging task in massive MIMO for both frequency-division duplex (FDD) and time-division duplex (TDD) protocols. For FDD massive MIMO systems, acquisition of instantaneous CSI at the BS will lead to a huge pilot and feedback overhead. Meanwhile, the hardware limitations might destroy the reciprocity between the uplink and the downlink channels for TDD massive MIMO systems, and thus instantaneous CSI acquisition is still not an easy task [19,20,21,22]. Compared with the instantaneous CSI, the statistical CSI varies over much larger time scales and thus can be efficiently and accurately obtained. In addition, massive MIMO channels exhibit new statistical properties with a large number of antennas [23], which, then, can be exploited in energy-efficient massive MIMO multicast transmission design.

In this paper, we investigate physical-layer multicast precoding for energy-efficient massive MIMO transmission. Our work differs from previous works in that only statistical downlink CSI of the UTs is available at the BS. Our major contributions are summarized as follows:

• We identify the eigenvectors of the optimal multicast transmit covariance matrix in terms of maximizing the system EE in closed form, which reveals that optimal energy-efficient multicast transmission should be performed in the beam domain in massive MIMO and simplifies the large-dimensional matrix-valued energy-efficient massive MIMO multicast transmission design into a power allocation problem in the beam domain with significantly reduced optimization variables.
• We propose a sequential beam domain power allocation approach with guaranteed convergence to the global optimum via exploiting Dinkelbach’s transform.
• We used the large-dimensional random matrix theory to deduce the deterministic equivalent (DE) of the optimization objective function to further reduce the computational complexity involved in sample averaging.

The rest of this paper is organized as follows. We present the massive MIMO beam domain channel model in Section 2. In Section 3, energy-efficient multicast precoding for single-cell massive MIMO transmission is investigated. The eigenvectors of the optimal energy-efficient multicast transmit covariance matrix is identified in closed-form and a sequential beam domain power allocation algorithm is proposed. Numerical results are presented in Section 4. Finally, we conclude the paper in Section 5.

The notations adopted throughout the paper are listed as follows: We denote by ${\mathbb{R}}^{M\times N}$ the $M\times N$ dimensional real-valued vector space and ${\mathbb{C}}^{M\times N}$ the $M\times N$ dimensional complex-valued vector space, respectively. We adopt upper-case boldface letters to denote matrices and lower-case boldface letters to denote column vectors, respectively. We adopt $\mathbf{X}\succcurlyeq \mathbf{0}$ to denote that $\mathbf{X}$ is a positive semidefinite matrix. We use $\mathrm{tr}\left\{·\right\}$ to denote the matrix trace operation and $\det \left\{·\right\}$ to denote the matrix determinant operation, respectively. We use $\mathsf{E}\left\{·\right\}$ to denote the expectation operation. We adopt $\mathcal{CN}\left(\mathbf{a},\mathbf{B}\right)$ to denote the circular symmetric complex-valued Gaussian distribution with mean $\mathbf{a}$ and covariance $\mathbf{B}$. We adopt ${\left(·\right)}^H$, ${\left(·\right)}^T$, and ${\left(·\right)}^{*}$ to denote the conjugate-transpose, transpose, and conjugate operations, respectively. We adopt ⊙ to denote the Hadamard product. We adopt ${\left[\mathbf{A}\right]}_{m,n}$ to denote the $(m,n)$th element of matrix $\mathbf{A}$. We adopt ≜ and ∼ to denote “be defined as” and “be distributed as”, respectively.

2. Massive MIMO Beam Domain Channel Model

We consider a single-cell massive MIMO system consisting of one BS which is equipped with M antennas, and K UTs, where UT k is equipped with $N_k$ antennas. In this paper, we focus on the single group multicast transmission case where the BS sends one common message to all the UTs in the multicast group.

We denote by $\mathbf{x}\in {\mathbb{C}}^{M\times 1}$ the multicast signal intended for the UTs in the multicast group, then the signal received at UT k at a time instant can be written as

$${\mathbf{y}}_k={\mathbf{H}}_k\mathbf{x}+{\mathbf{n}}_k\in {\mathbb{C}}^{N_k\times 1},$$

(1)

where ${\mathbf{H}}_k$ represents the downlink channel matrix from the BS to UT k at the given time instant, and ${\mathbf{n}}_k\sim \mathcal{CN}\left(\mathbf{0},{\sigma }^2{\mathbf{I}}_{N_k}\right)$ denotes the additive Gaussian noise with ${\sigma }^2$ being the noise power. We assume that the multicast signal $\mathbf{x}$ satisfies $\mathsf{E}\left\{\mathbf{x}\right\}=\mathbf{0}$ and $\mathsf{E}\left\{\mathbf{x}{\mathbf{x}}^{\mathrm{H}}\right\}=\mathbf{Q}\in {\mathbb{C}}^{M\times M}$ where $\mathbf{Q}$ is the multicast signal transmit covariance matrix.

Before investigating the energy-efficient massive MIMO multicast transmission design, we first introduce the channel model adopted in our work which has a great impact on the considered multicast design. Specifically, Weichselberger’s channel model [24,25] is adopted in our work. Please note that in the adopted Weichselberger’s channel model, the channel correlation properties between the transmitter (BS) and the receiver (UT) are jointly taken into account, which is different from the Kronecker channel model where only the correlations at both ends are considered. With Weichselberger’s jointly correlated channel model, the channel matrix ${\mathbf{H}}_k$ in (1) can be written as follows

$${\mathbf{H}}_k={\mathbf{U}}_k{\mathbf{G}}_k{\mathbf{V}}_k^H\in {\mathbb{C}}^{N_k\times M},$$

(2)

where ${\mathbf{U}}_k\in {\mathbb{C}}^{N_k\times N_k}$ and ${\mathbf{V}}_k\in {\mathbb{C}}^{M\times M}$ are both deterministic unitary matrices, and ${\mathbf{G}}_k\in {\mathbb{C}}^{N_k\times M}$ is a random matrix where the elements are all zero-mean independently distributed. Please note that in massive MIMO related literature, ${\mathbf{G}}_k$ is usually referred to as the beam domain channel matrix [19,21,23]. The second-order channel statistics of ${\mathbf{G}}_k$ can be fully characterized by the following matrix

$${\mathsf{\Omega }}_k=\mathsf{E}\left\{{\mathbf{G}}_k\odot {\mathbf{G}}_k^{*}\right\}\in {\mathbb{R}}^{N_k\times M}.$$

(3)

As the $\left(i,j\right)$th element of ${\mathsf{\Omega }}_k$ corresponds to the average power of the $\left(i,j\right)$th element of the beam domain channel matrix, ${\mathsf{\Omega }}_k$ is usually referred to the beam domain channel power matrix. Please note that ${\mathsf{\Omega }}_k$ varies in a larger time scale than instantaneous CSI. In addition, the channel statistics are approximately constant for a wide range of frequencies [23,26]. Therefore, statistical CSI can be obtained via averaging the samples over time and frequency in a realistic wideband wireless transmission system with guaranteed accuracy. In this paper, we assume that the statistical CSI of the multicast UTs can be perfectly known at the BS.

In massive MIMO systems with a sufficiently large number of BS antennas, the channels usually exhibit new properties. One particular property of the massive MIMO channels is that the eigenvector matrices of the correlation matrices at the BS of different transmission links (UTs) tend to be the same and can be uniquely determined by the array topology equipped at the BS asymptotically [19,21,23]. Specifically, we denote by $\mathbf{V}$ this unique matrix, then the massive MIMO channel adopted in this paper can be modeled as

$${\mathbf{H}}_k\stackrel{M\to \infty }{=}{\mathbf{U}}_k{\mathbf{G}}_k{\mathbf{V}}^H.$$

(4)

It is worth noting that the above channel model has been verified in typical scenarios [19,21,23] and has been extensively adopted in previous works. The massive MIMO channel model in (4) will be adopted throughout this paper.

3. Energy-Efficient Multicast Precoding for Massive MIMO

In this section, we investigate energy-efficient multicast precoding for massive MIMO where the BS only has knowledge of the statistical CSI of all multicast UTs and all the UTs know their own instantaneous CSI perfectly. In particular, with multicast transmit covariance matrix $\mathbf{Q}$, the achievable ergodic multicast can be written as follows

$$R_{\mathrm{mc}}=\underset{k}{\min }{R}_k,$$

(5)

where $R_k$ is UT k’s achievable ergodic rate which can be written as

$$\begin{array}{ll}{R}_k& =\mathsf{E}\left\{\log \det \left\{{\mathbf{I}}_{N_k}+\frac{1}{{\sigma }^2}{\mathbf{H}}_k\mathbf{Q}{\mathbf{H}}_k^H\right\}\right\}\\ & \stackrel{\left(\mathrm{a}\right)}{=}\mathsf{E}\left\{\log \det \left\{{\mathbf{I}}_{N_k}+\frac{1}{{\sigma }^2}{\mathbf{G}}_k{\mathbf{V}}^H\mathbf{Q}\mathbf{V}{\mathbf{G}}_k^H\right\}\right\},\end{array}$$

(6)

where (a) follows from the massive MIMO beam domain channel model in (4), and the determinant identity $\det \left\{\mathbf{I}+\mathbf{A}\mathbf{B}\right\}=\det \left\{\mathbf{I}+\mathbf{B}\mathbf{A}\right\}$.

Before proceeding, we present the power consumption model. In massive MIMO systems, the BS consumes most of the power and we focus on the power consumption at the BS. Specifically, we adopt the power consumption model as follows [11,13]

$$P=\zeta \mathrm{tr}\left\{\mathbf{Q}\right\}+M{P}_{\mathrm{c}}+P_{\mathrm{s}},$$

(7)

where $\mathrm{tr}\left\{\mathbf{Q}\right\}$ is the multicast transmit power, which is scaled by a coefficient $\zeta \ge 1$ modeling the reciprocal of the transmit amplifier drain efficiency, $P_{\mathrm{c}}$ denotes the circuit power consumption of each BS antenna, and $P_{\mathrm{s}}$ denotes the static power consumption at the BS. Then, the system EE of multicast transmission with bandwidth W is given by

$${\mathrm{EE}}_{\mathrm{mc}}\triangleq \frac{W{R}_{\mathrm{mc}}}{P}.$$

(8)

In the following, we investigate energy-efficient multicast precoding with statistical CSI. We aim to design the optimal transmit covariance $\mathbf{Q}$ that can maximize the multicast EE in (8). The problem to be dealt with can be formulated as follows

$$\begin{array}{cc}\hfill \underset{\mathbf{Q}}{\arg \max }& {\mathrm{EE}}_{\mathrm{mc}},\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathrm{tr}\left\{\mathbf{Q}\right\}\le P_{\max },\mathbf{Q}⪰\mathbf{0},\hfill \end{array}$$

(9)

where $P_{\max }$ denotes the multicast power budget at the BS.

We denote by $\mathbf{Q}=\mathsf{\Phi }\mathsf{\Lambda }{\mathsf{\Phi }}^H$ the eigenvalue decomposition of the transmit covariance matrix $\mathbf{Q}$. Please note that the columns of $\mathsf{\Phi }$ denote the eigenvectors of $\mathbf{Q}$ and can represent the multicast signaling directions. Meanwhile, diagonal elements of $\mathsf{\Lambda }$ denote the eigenvalues of $\mathbf{Q}$ and the powers allocated to each beam can be reflected in $\mathsf{\Lambda }$. We first investigate the eigenvectors of the optimal multicast transmit covariance matrix in the following theorem.

Theorem 1.

The eigenvectors of the optimal transmit covariance matrix ${\mathbf{Q}}^{\mathrm{opt}}$ in terms of maximizing the systems EE are constituted by the columns of the matrix $\mathbf{V}$ in (4), i.e.,

$${\mathbf{Q}}^{\mathrm{opt}}=\mathbf{V}\mathsf{\Lambda }{\mathbf{V}}^H.$$

(10)

Proof. 

Please refer to Appendix A.    □

The result presented in Theorem 1 shows that the optimal energy-efficient multicast signaling directions should align with the eigenvectors of the transmit correlation matrices at the BS. Thus, the optimal multicast precoding in terms of maximizing the systems EE should be performed in the beam domain. With Theorem 1, the matrix-valued energy-efficient transmit covariance matrix design can be simplified into a vector-valued beam domain power allocation problem with significantly reduced optimization variables. In particular, without loss of optimality, the energy-efficient multicast transmit precoding optimization problem in (9) can be simplified to the following problem

$$\begin{array}{cc}\hfill \underset{\mathsf{\Lambda }}{\arg \max }& \frac{W{R}_{\mathrm{mc}}\left(\mathsf{\Lambda }\right)}{P\left(\mathsf{\Lambda }\right)},\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathrm{tr}\left\{\mathsf{\Lambda }\right\}\le P_{\max },\mathsf{\Lambda }⪰\mathbf{0},\mathsf{\Lambda }\mathrm{diagonal},\hfill \end{array}$$

(11)

in which

$$R_{\mathrm{mc}}\left(\mathsf{\Lambda }\right)\triangleq \underset{k}{\min }{R}_k\left(\mathsf{\Lambda }\right),$$

(12)

$$R_k\left(\mathsf{\Lambda }\right)\triangleq \mathsf{E}\left\{\log \det \left\{{\mathbf{I}}_{N_k}+\frac{1}{{\sigma }^2}{\mathbf{G}}_k\mathsf{\Lambda }{\mathbf{G}}_k^H\right\}\right\},$$

(13)

$$P\left(\mathsf{\Lambda }\right)\triangleq \zeta \mathrm{tr}\left\{\mathsf{\Lambda }\right\}+M{P}_{\mathrm{c}}+P_{\mathrm{s}}.$$

(14)

In the objective function of the beam domain power allocation problem (11), $R_{\mathrm{mc}}\left(\mathsf{\Lambda }\right)$ and $P\left(\mathsf{\Lambda }\right)$ are concave and linear functions with respect to $\mathsf{\Lambda }$, respectively. Thus, the optimization problem in (11) is a concave-linear fractional program. Dinkelbach’s transform and Charnes-Cooper transform are two classic approaches to solve the concave-linear fractional program [11]. In this work, we adopt Dinkelbach’s transform to solve this optimization problem. Compared to Charnes-Cooper transform, Dinkelbach’s transform has an advantage that no extra constraints must be included. Via invoking Dinkelbach’s transform, the energy-efficient precoding optimization problem in (11) can be solved via iteratively solving the following sequence of convex optimization problems

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}^{\left(\ell +1\right)}=\underset{\mathsf{\Lambda }}{\arg \max }& W{R}_{\mathrm{mc}}\left(\mathsf{\Lambda }\right)-{\eta }^{\left(\ell \right)}P\left(\mathsf{\Lambda }\right),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathrm{tr}\left\{\mathsf{\Lambda }\right\}\le P_{\max },\mathsf{\Lambda }⪰\mathbf{0},\mathsf{\Lambda }\mathrm{diagonal},\hfill \end{array}$$

(15)

where ${\eta }^{\left(\ell \right)}$ is an introduced auxiliary variable in Dinkelbach’s transform, which is iteratively updated as follows

$${\eta }^{\left(\ell \right)}=\frac{W{R}_{\mathrm{mc}}\left({\mathsf{\Lambda }}^{\left(\ell \right)}\right)}{P\left({\mathsf{\Lambda }}^{\left(\ell \right)}\right)},$$

(16)

with ℓ denoting the iteration index. It can be shown that the above Dinkelbach’s transform-based iteration approach is guaranteed to converge to the global optimum of the original optimization problem in (11) with a super-linear convergence rate [11].

Although each transformed sub-problem in (15) is a convex program, the optimization complexity might still be high in practice due to the sample average in calculating the expectation operation. To reduce the implementation complexity in Monte-Carlo averaging over channel realizations, we further employ the large-dimensional random matrix theory [27,28] to calculate the DE of the ergodic rate. By replacing the multicast rate with its DE, the sequence of the convex optimization problems in (15) can be rewritten as follows

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}^{\left(\ell +1\right)}=\underset{\mathsf{\Lambda }}{\arg \max }& \underset{k}{\min }W{\overline{R}}_k\left(\mathsf{\Lambda }\right)-{\eta }^{\left(\ell \right)}P\left(\mathsf{\Lambda }\right),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathrm{tr}\left\{\mathsf{\Lambda }\right\}\le P_{\max },\mathsf{\Lambda }⪰\mathbf{0},\mathsf{\Lambda }\mathrm{diagonal}.\hfill \end{array}$$

(17)

In (17), ${\overline{R}}_k\left(\mathsf{\Lambda }\right)$ is the DE of $R_k\left(\mathsf{\Lambda }\right)$ given by

$${\overline{R}}_k\left(\mathsf{\Lambda }\right)=\sum _{i=0}^{M-1}\log \left\{1+{\left[{\mathsf{\Gamma }}_k\right]}_{i,i}{\left[\mathsf{\Lambda }\right]}_{i,i}\right\}+\sum _{j=0}^{N_k-1}\log \left\{{\left[{\tilde{\mathsf{\Phi }}}_k\right]}_{j,j}\right\}-\sum _{m=0}^{N_k-1}{\left[{\tilde{\mathsf{\Gamma }}}_k\right]}_{m,m}{\left[{\left({\tilde{\mathsf{\Phi }}}_k\right)}^{-1}\right]}_{m,m},$$

(18)

where ${\mathsf{\Gamma }}_k\in {\mathbb{C}}^{M\times M}$, ${\tilde{\mathsf{\Gamma }}}_k\in {\mathbb{C}}^{N_k\times N_k}$, and ${\tilde{\mathsf{\Phi }}}_k\in {\mathbb{C}}^{N_k\times N_k}$ can be efficiently calculated via solving the following fixed-point equations

$${\mathsf{\Gamma }}_k={\mathbf{B}}_k\left({\left({\tilde{\mathsf{\Phi }}}_k\right)}^{-1}\right),$$

(19a)

$${\tilde{\mathsf{\Gamma }}}_k={\mathbf{C}}_k\left(\mathsf{\Lambda }{\left({\mathbf{I}}_M+\mathsf{\Lambda }{\mathsf{\Gamma }}_k\right)}^{-1}\right),$$

(19b)

$${\tilde{\mathsf{\Phi }}}_k={\mathbf{I}}_{N_k}+{\tilde{\mathsf{\Gamma }}}_k.$$

(19c)

It is worth noting that ${\mathbf{B}}_k\left(\mathbf{X}\right)\triangleq \frac{1}{{\sigma }^2}\mathsf{E}\left\{{\mathbf{G}}_k^H\mathbf{X}{\mathbf{G}}_k\right\}\in {\mathbb{C}}^{M\times M}$ and ${\mathbf{C}}_k\left(\mathbf{X}\right)\triangleq \frac{1}{{\sigma }^2}\mathsf{E}\left\{{\mathbf{G}}_k\mathbf{X}{\mathbf{G}}_k^H\right\}\in {\mathbb{C}}^{N_k\times N_k}$ appeared in (19) are both matrix-valued functions which both output diagonal matrices with the corresponding ith output diagonal elements given by

$${\left[{\mathbf{B}}_k\left(\mathbf{X}\right)\right]}_{i,i}=\frac{1}{{\sigma }^2}\mathrm{tr}\left\{\mathrm{diag}\left\{{\left[{\mathsf{\Omega }}_k\right]}_{:,i}\right\}\mathbf{X}\right\},$$

(20)

$${\left[{\mathbf{C}}_k\left(\mathbf{X}\right)\right]}_{i,i}=\frac{1}{{\sigma }^2}\mathrm{tr}\left\{\mathrm{diag}\left\{{\left({\left[{\mathsf{\Omega }}_k\right]}_{i,:}\right)}^T\right\}\mathbf{X}\right\},$$

(21)

respectively. The DE ${\overline{R}}_k\left(\mathsf{\Lambda }\right)$ can be efficiently calculated using the channel statistics ${\mathsf{\Omega }}_k$ in a few iterations without exhaustive averaging involved in the Monte-Carlo approach, and then the computational complexity of the optimization problem in (15) can be further reduced.

Please note that the DE ${\overline{R}}_k\left(\mathsf{\Lambda }\right)$ is a quite tight approximation of $R_k\left(\mathsf{\Lambda }\right)$ for massive MIMO channels in typical settings [27,28]. In addition, as ${\overline{R}}_k\left(\mathsf{\Lambda }\right)$ in (18) is a concave function with respect to the power allocation matrix $\mathsf{\Lambda }$, each sub-problem in (17) is a convex program and can be efficiently solved using standard techniques. Formally, we present the description of our proposed energy-efficient multicast beam domain power allocation algorithm for massive MIMO transmission using Dinkelbach’s transform and large-dimensional random matrix theory in Algorithm 1. The computational complexity of Algorithm 1 is presented as follows. From [11], we can obtain that the convergence rate of Dinkelbach’s transform-based iteration will exhibit a super-linear trend in the sub-problem sequence (15). In addition, each sub-problem in (15) is a convex program and thus the computational complexity of each sub-problem is polynomial in the numbers of variables and constraints [29]. Moreover, the complexity of calculating DE involved in the objective of each sub-problem is relatively low due to the quick convergence [28] in solving (19).

Algorithm 1 Beam Domain Energy-Efficient Multicast Power Allocation Algorithm

Require: Initialization power allocation ${\mathsf{\Lambda }}^{\left(0\right)}$, beam domain statistical CSI ${\mathsf{\Omega }}_k$, threshold $ϵ$ Ensure: Beam domain energy-efficient multicast power allocation pattern $\mathsf{\Lambda }$   1: Initialization: $\ell =0$, calculate ${\eta }^{\left(\ell \right)}$ using (16)   2: while$|\underset{k}{\min }W{\overline{R}}_k\left({\mathsf{\Lambda }}^{\left(\ell \right)}\right)-{\eta }^{\left(\ell \right)}P\left({\mathsf{\Lambda }}^{\left(\ell \right)}\right)|\ge ϵ$ do   3:       Update $\ell \leftarrow \ell +1$   4:       Calculate ${\mathsf{\Lambda }}^{\left(\ell \right)}$ via solving (17) with ${\eta }^{\left(\ell -1\right)}$   5:       Calculate ${\eta }^{\left(\ell \right)}$ using (16)   6: end while   7: Return $\mathsf{\Lambda }={\mathsf{\Lambda }}^{\left(\ell \right)}$

4. Numerical Results

Extensive numerical results are provided in this section to corroborate the performance of the proposed energy-efficient multicast precoding for massive MIMO transmission with only statistical CSI available at the BS. In the simulation, we adopt the 3GPP SCM channel model and the suburban macro-cell propagation scenario [30]. In addition, both the BS and the UTs are equipped with the uniform linear arrays (ULAs) where the antennas are spaced with half wavelength. We list the major simulation parameters in

Table 1. Simulation Setup Parameters.

Parameter	Value
Channel model	3GPP SCM
Propagation scenario	Suburban macro-cell
Pathloss	$-120$ dB $\left(\forall k\right)$
Array topology	ULA with half wavelength antenna spacing
Number of antennas at the BS	$M=128$
Number of UTs	$K=8$
Number of antennas at the UTs	$N_k=4(\forall k)$
Bandwidth	$W=10$ MHz
Amplifier inefficiency factor	$\zeta =5$
Hardware dissipated power per antenna	$P_{\mathrm{c}}=30$ dBm
Static power consumption	$P_{\mathrm{s}}=40$ dBm
Noise variance	${\sigma }^2=-131$ dBm

.

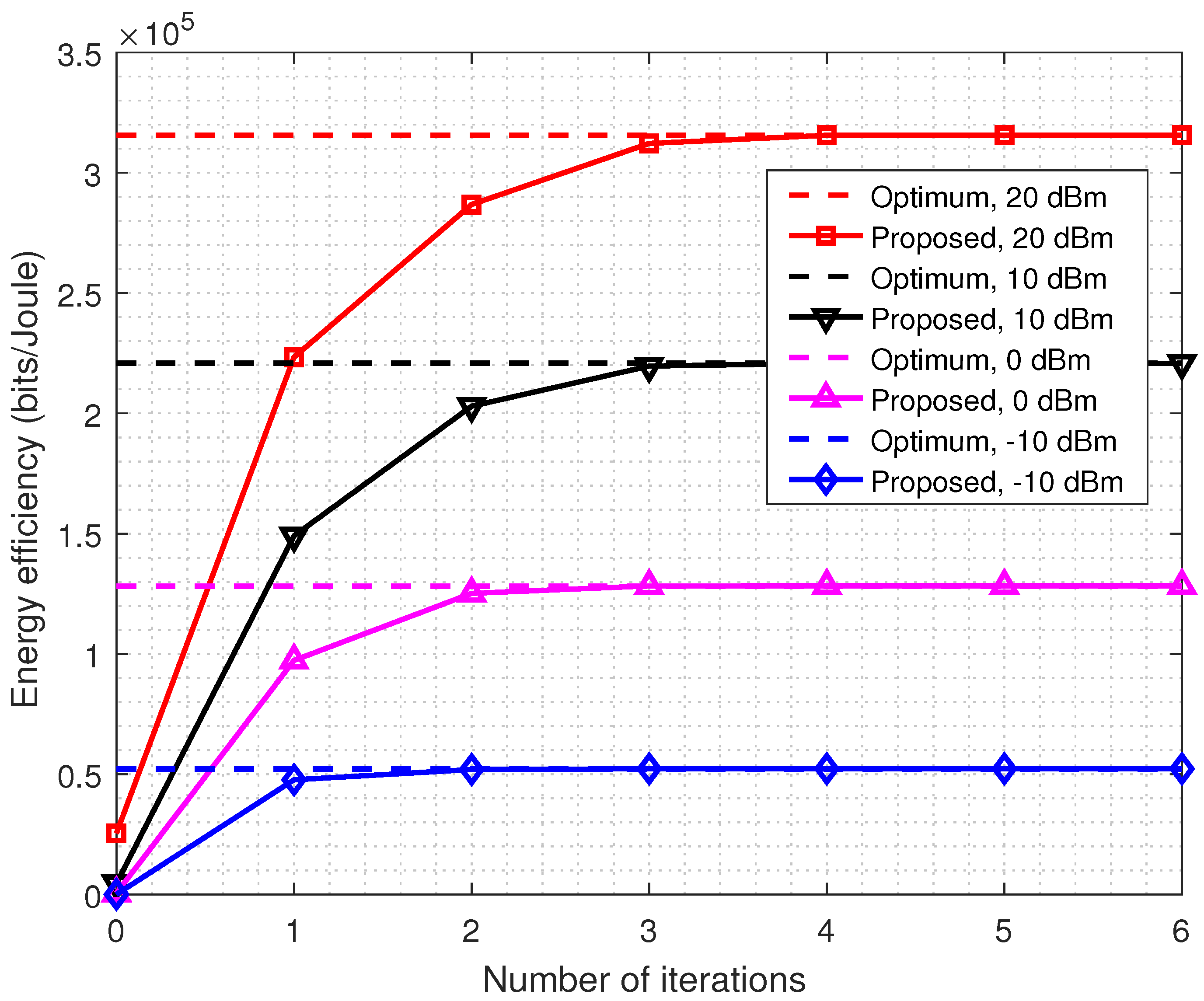
Firstly, the convergence performance of the proposed energy-efficient multicast power allocation algorithm is evaluated in Figure 1. We can observe from Figure 1 that the proposed energy-efficient multicast power allocation algorithm converges very rapidly for different values of multicast power budget $P_{\max }$. Usually, the proposed algorithm converges after very few iterations. In addition, we can observe that the proposed multicast power allocation algorithm achieves near-optimal EE performance.

We then compare the EE performance of the proposed EE maximization approach with that of the rate maximization approach which aims to maximize the achievable ergodic multicast rate in Figure 2. We can observe from Figure 2 that the proposed EE maximization approach and the conventional rate maximization approach achieve similar EE performance in the low transmit power regime, which indicates that using the maximum power budget is almost EE optimal. Meanwhile, in the high transmit power regime, our proposed EE maximization approach significantly outperforms the conventional rate maximization approach. In addition, we can also observe that the proposed DE result is quite accurate compared with the Monte-Carlo results in a wide range of power budget values.

Finally, the EE performance of our proposed approach versus the number of BS antennas is evaluated in Figure 3. We can observe from Figure 3 that the EE performance of our proposed approach will reduce as the number of BS antennas M increases, which indicates that power consumption dominates the EE performance in the case with large numbers of antennas.

5. Conclusions

In this paper, we have investigated energy-efficient physical-layer multicast precoding for massive MIMO transmission where the BS only has access to the statistical CSI of all UTs. We first introduced a massive MIMO beam domain channel model. Via exploiting the statistical properties of the massive MIMO beam domain channels, we then showed the optimal energy-efficient multicast signaling directions, which reduces the matrix-valued precoding design into a beam domain energy-efficient power allocation problem. We further proposed a sequential power allocation algorithm with guaranteed convergence to the global optimal solution via exploiting Dinkelbach’s transform. In addition, we derived the DE of the design objective via exploiting the large-dimensional random matrix theory. Simulation results showed the near-optimal EE performance of our proposed approach for energy-efficient massive MIMO multicast precoding. The EE performance gain of the proposed approach over the conventional rate optimization approach was also demonstrated in the numerical results.