Wave Velocity and Power Spectral Density of Hole-Containing Specimens with Different Moisture Content under Uniaxial Compression
Abstract
:1. Introduction
2. Method and Theory
2.1. Calculation of Velocity
2.2. Power Spectral Density Estimation Method
3. Experiments Details
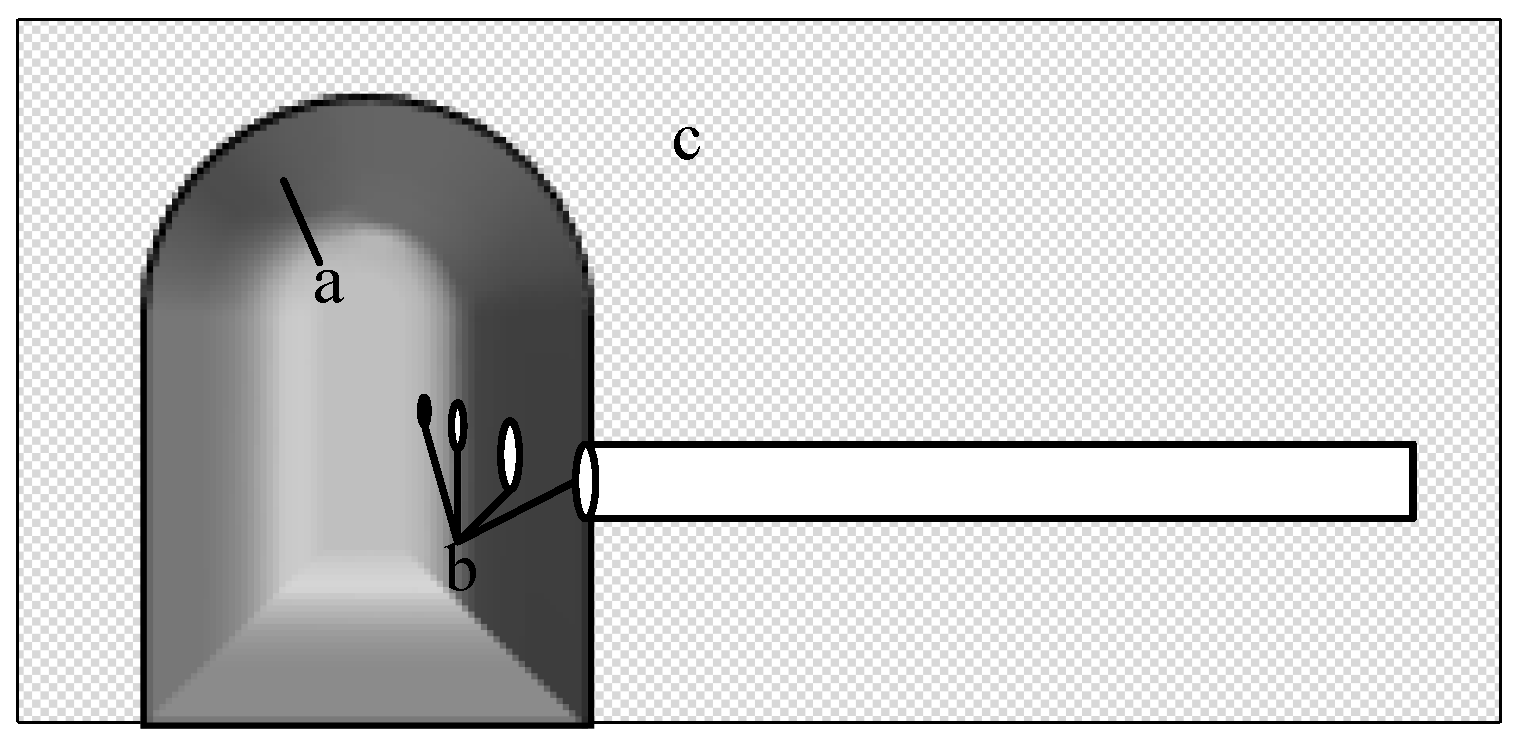
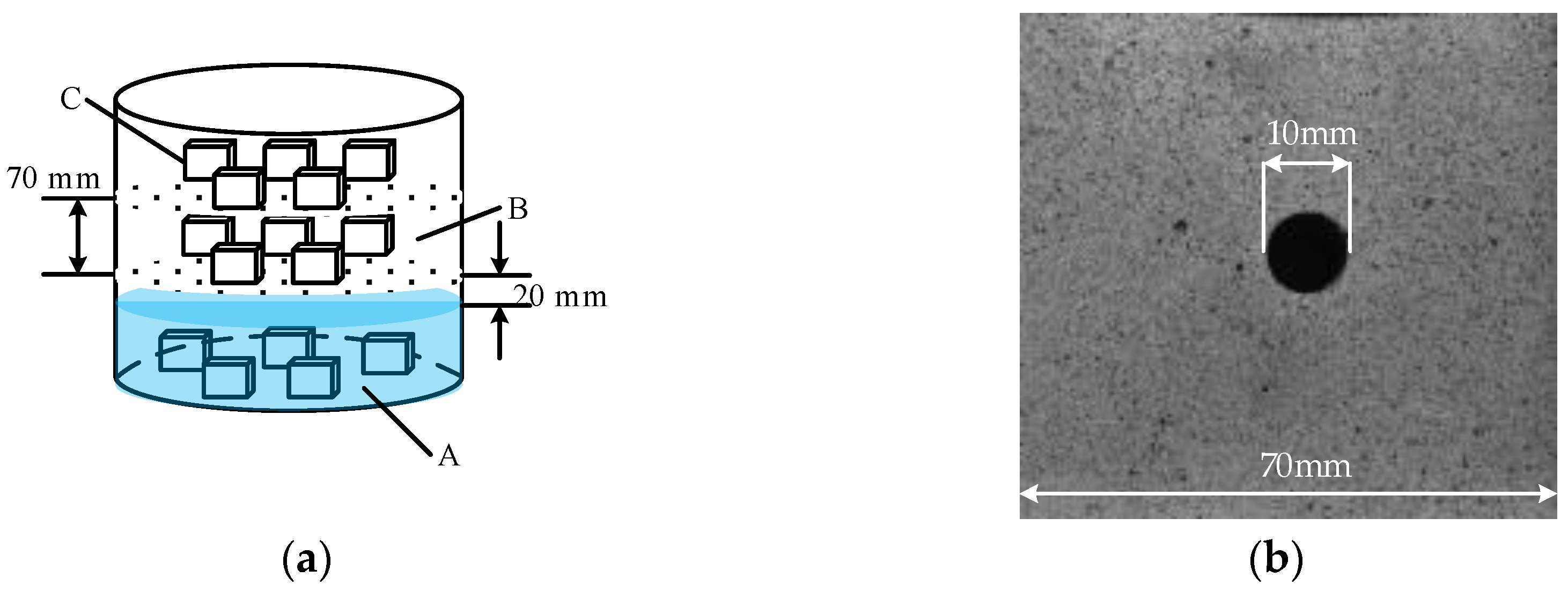
3.1. Preparation of Hole-Containing Specimens with Different Moisture Contents
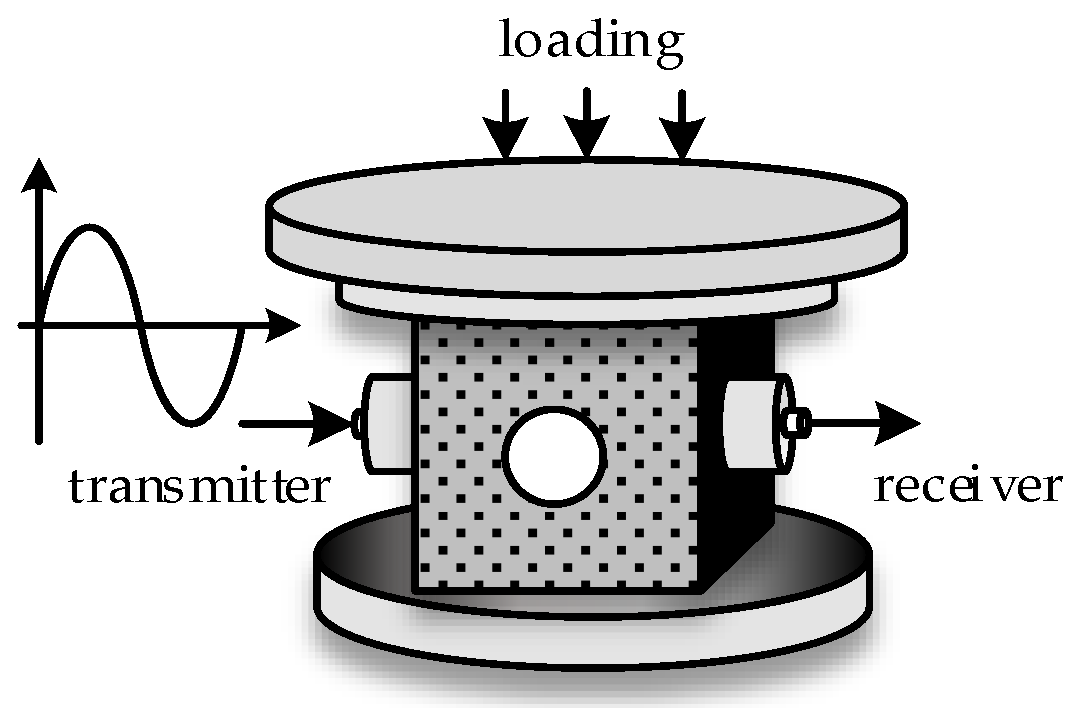
3.2. Wave Velocity Measurement Test Process
4. Results and Discussion
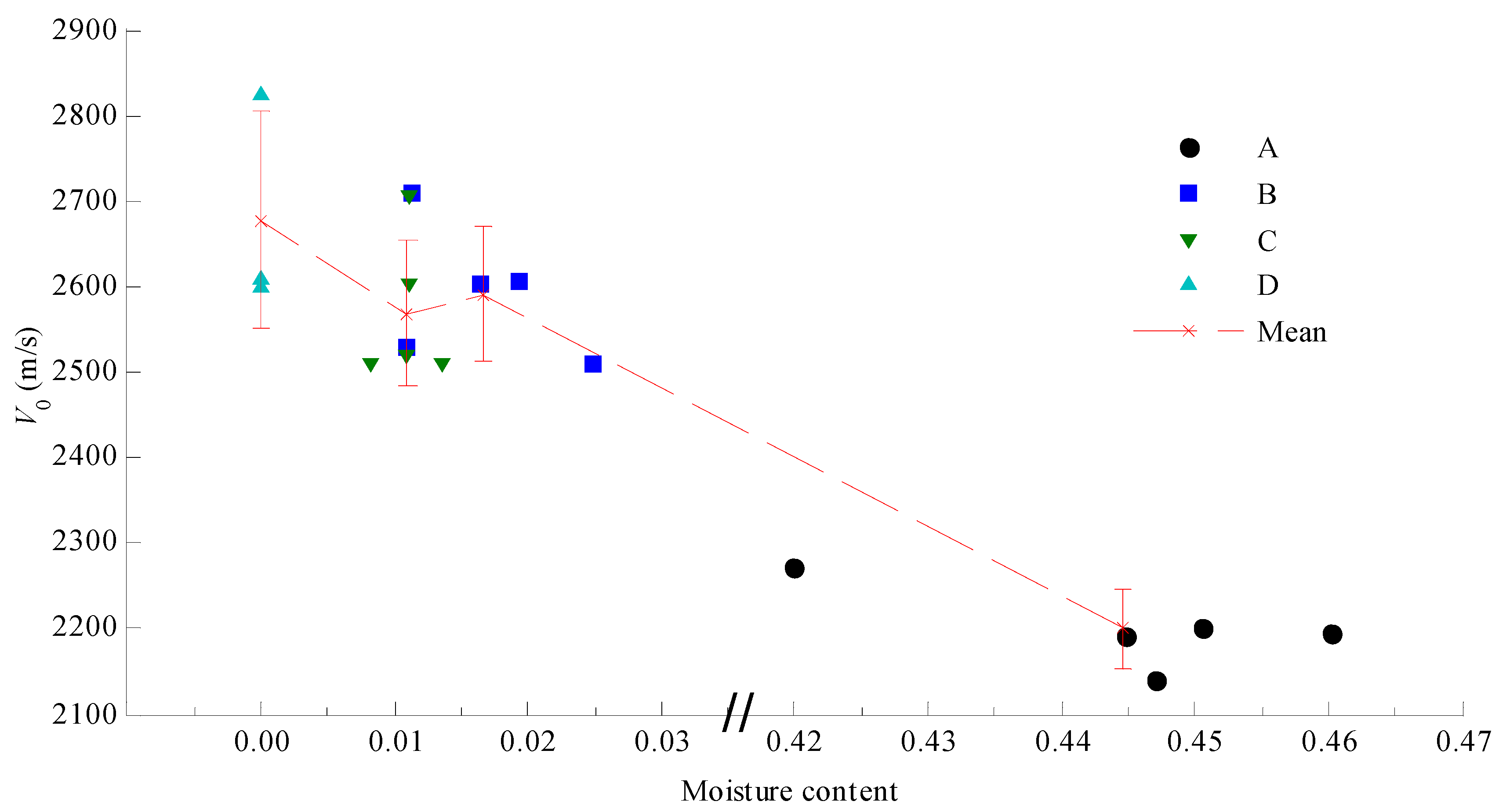
4.1. Initial Wave Velocity of Specimens
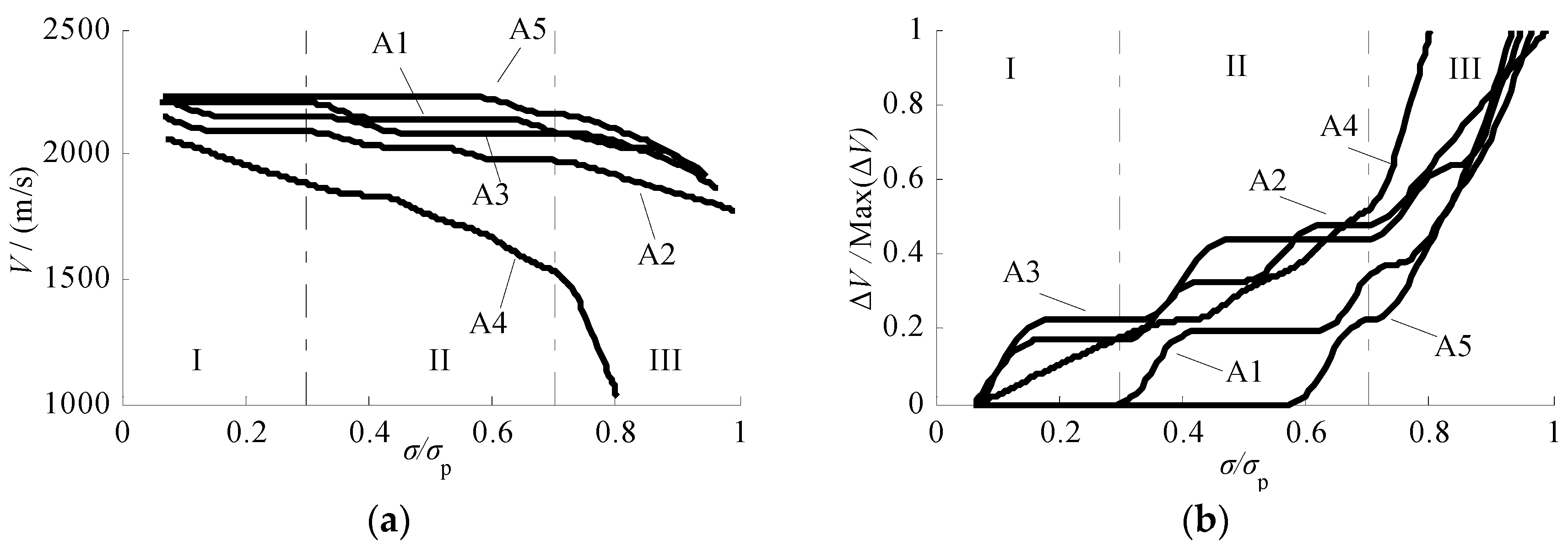
4.2. Wave Velocity During Specimens Failure
4.3. Wave Velocity of Specimens With Different Moisture Content
4.4. Initial Power Spectral Density of Specimens
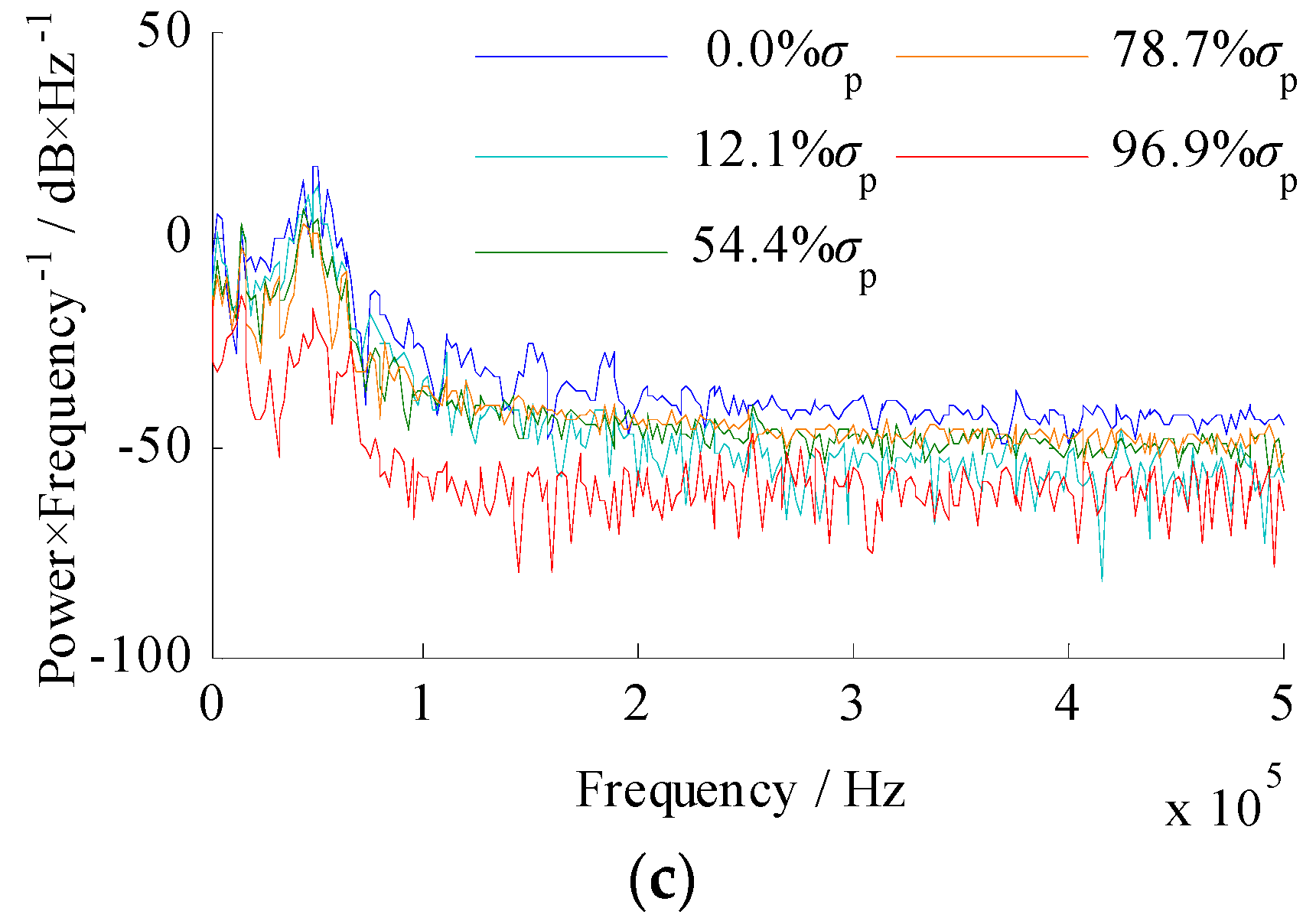
4.5. Power Spectral Density During Destruction
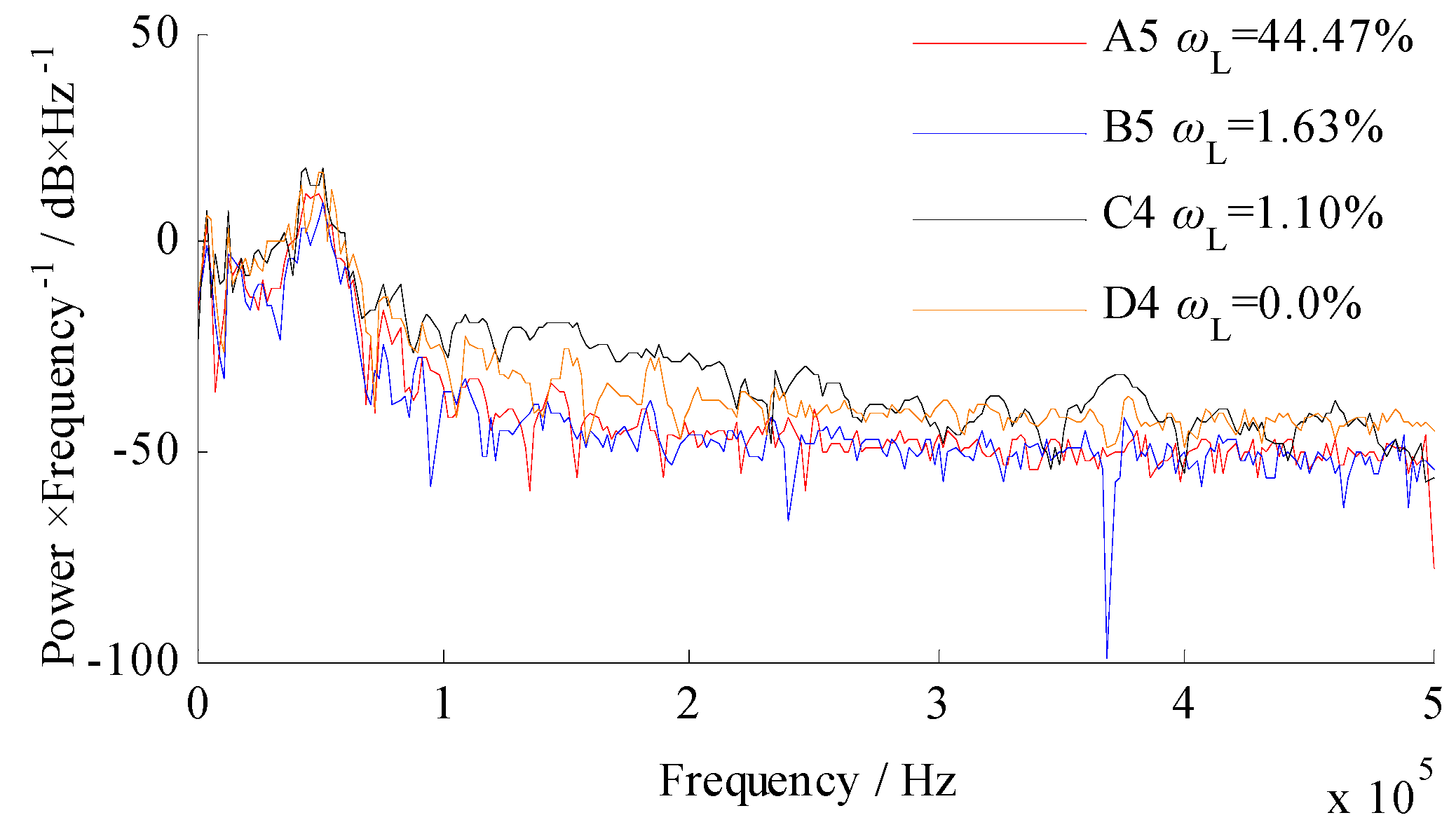
4.6. Power Spectral Density of Specimens with Different Moisture Content
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, T.; Zhang, L.; Li, S.; Liu, J.; Pan, H.; Song, S. Stress inversion of coal with a gas drilling borehole and the law of crack propagation. Energies 2017, 10, 1743. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, X.J.; Liang, L.X.; Wang, S. Numerical simulation of the fractured model acoustic attenuation coefficient. Chin. J. Geophys. 2012, 55, 2044–2052. [Google Scholar]
- Wang, Z.Z.; Wang, R.H.; Tian-Yang, L.I.; Shan, X.; Qiu, H. Numerical-modeling of pore structure effects on acoustic attenuation in dry rocks. Prog. Geophys. 2014, 29, 2766–2773. [Google Scholar]
- Thill, R.E.; Bur, T.R.; Steckley, R.C. Velocity anisotropy in dry and saturated rock spheres and its relation to rock fabric. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1973, 10, 535–557. [Google Scholar] [CrossRef]
- Oda, M.; Yamabe, T.; Kamemura, K. A crack tensor and its relation to wave velocity anisotropy in jointed rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1986, 23, 387–397. [Google Scholar] [CrossRef]
- Kano, S.; Tsuchiya, N. Parallelepiped cooling joint and anisotropy of p-wave velocity in the takidani granitoid, japan alps. J. Volcanol. Geotherm. Res. 2002, 114, 465–477. [Google Scholar] [CrossRef]
- Takemura, T. Changes in crack density and wave velocity in association with crack growth in triaxial tests of inada granite. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Best, A.I.; McCann, C.; Sothcott, J. The relationships between the velocities, attenuations and petrophysical properties of reservoir sedimentary rocks. Geophys. Prospect. 1994, 42, 151–178. [Google Scholar] [CrossRef]
- Tary, J.B.; van der Baan, M.; Herrera, R.H. Applications of high-resolution time-frequency transforms to attenuation estimation. Geophysics 2017, 82, 7–20. [Google Scholar] [CrossRef]
- Liao, Q.; McMechan, G.A. Tomographic imaging of velocity and q, with application to crosswell seismic data from the gypsy pilot site, oklahoma. Geophysics 1997, 62, 1804–1811. [Google Scholar] [CrossRef]
- Pham, N.H.; Carcione, J.M.; Helle, H.B.; Ursin, B. Wave velocities and attenuation of shaley sandstones as a function of pore pressure and partial saturation. Geophys. Prospect. 2002, 50, 615–627. [Google Scholar] [CrossRef]
- Benson, P.; Schubnel, A.; Vinciguerra, S.; Trovato, C.; Meredith, P.G.; Young, P.R. Physical and transport properties of isotropic and anisotropic cracked rocks under hydrostatic pressure. J. Geophys. Res. 2006, 111, B04202. [Google Scholar]
- Lokajicek, T.; Svitek, T. Laboratory measurement of elastic anisotropy on spherical rock samples by longitudinal and transverse sounding under confining pressure. Ultrasonics 2015, 56, 294–302. [Google Scholar] [CrossRef] [PubMed]
- Vajdová, V.; Přikryl, R.; Pros, Z.; Klíma, K. The effect of rock fabric on p-wave velocity distribution in amphibolites. Phys. Earth Planet. Inter. 1999, 114, 39–47. [Google Scholar] [CrossRef]
- Han, D.; Nur, A.; Morgan, D. Effects of porosity and clay content on wave velocities in sandstones. Geophysics 1986, 51, 2093. [Google Scholar] [CrossRef]
- Ayres, A.; Theilen, F. Relationship between p- and s-wave velocities and geological properties of near-surface sediments of the continental slope of the barents sea. Geophys. Prospect. 1999, 47, 431–441. [Google Scholar] [CrossRef]
- Shatilo, A.P.; Sondergeld, C.; Rai, C.S. Ultrasonic attenuation in glenn pool rocks, northeastern oklahoma. Geophysics 1998, 63, 465–478. [Google Scholar] [CrossRef]
- King, M.S.; Marsden, J.R.; Dennis, J.W. Biot dispersion for p- and s-wave velocities in partially and fully saturated sandstones. Geophys. Prospect. 2000, 48, 1075–1089. [Google Scholar] [CrossRef]
- Elghadamsi, F.E.; Mohraz, B.; Lee, C.T.; Moayyad, P. Time-dependent power spectral density of earthquake ground motion. Soil Dyn. Earthq. Eng. 1988, 7, 15–21. [Google Scholar] [CrossRef]
- Elson, J.M.; Bennett, J.M. Calculation of the power spectral density from surface profile data. Appl. Opt. 1995, 34, 201. [Google Scholar] [CrossRef] [PubMed]
- Cusidócusido, J.; Romeral, L.; Ortega, J.A.; Rosero, J.A.; Espinosa, A.G. Fault detection in induction machines using power spectral density in wavelet decomposition. IEEE Trans. Ind. Electron. 2008, 55, 633–643. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Z. The ultrasonic p-wave velocity-stress relationship of rocks and its application. Bull. Eng. Geol. Environ. 2016, 76, 661–669. [Google Scholar] [CrossRef]
- Fathollahy, M.; UroMeiehy, A.; Riahi, M.A. Evaluation of p-wave velocity in different joint spacing. Boll. Geofis. Teor. Appl. 2017, 58, 157–168. [Google Scholar]
- Lee, I.-M.; Han, S.-I.; Kim, H.-J.; Yu, J.-D.; Min, B.-K.; Lee, J.-S. Evaluation of rock bolt integrity using fourier and wavelet transforms. Tunn. Undergr. Space Technol. 2012, 28, 304–314. [Google Scholar] [CrossRef]
- Kilic, O. Application of ultrasonic velocity measurement and thermal analysis for determination of limestone quality. Physicochem. Probl. Miner. Process. 2014, 50, 525–534. [Google Scholar]
- Madhubabu, N.; Singh, P.K.; Kainthola, A.; Mahanta, B.; Tripathy, A.; Singh, T.N. Prediction of compressive strength and elastic modulus of carbonate rocks. Measurement 2016, 88, 202–213. [Google Scholar] [CrossRef]
- Lajtai, E.Z.; Lajtai, V.N. The collapse of cavities. Int. J. Rock Mech. Min. Sci. Geo. Abs. 1975, 12, 81–86. [Google Scholar] [CrossRef]
- Carter, B.J.; Lajtai, E.Z.; Petukhov, A. Primary and remote fracture around underground cavities. Int. J. Numer. Anal. Methods Geomechan. 1991, 15, 21–40. [Google Scholar] [CrossRef]
- Zhu, W.C.; Bruhns, O.T. Simulating excavation damaged zone around a circular opening under hydromechanical conditions. Int. J. Rock Mech. Min. Sci. 2008, 45, 815–830. [Google Scholar] [CrossRef]
- Wang, S.Y.; Sloan, S.W.; Sheng, D.C.; Tang, C.A. Numerical analysis of the failure process around a circular opening in rock. Comput. Geotech. 2012, 39, 8–16. [Google Scholar] [CrossRef]
- Yang, H.Q.; Zeng, Y.Y.; Lan, Y.F.; Zhou, X.P. Analysis of the excavation damaged zone around a tunnel accounting for geostress and unloading. Int. J. Rock Mech. Min. Sci. 2014, 69, 59–66. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Zhou, Z.; Li, X.; Ranjith, P.G. Fracture analysis of marble specimens with a hole under uniaxial compression by digital image correlation. Eng. Fract. Mech. 2017, 183, 109–124. [Google Scholar] [CrossRef]
- Yang, X.-X.; Jing, H.-W.; Chen, K.-F.; Yang, S.-Q. Failure behavior around a circular opening in a rock mass with non-persistent joints: A parallel-bond stress corrosion approach. J. Cent. South Univ. 2017, 24, 2406–2420. [Google Scholar] [CrossRef]
- Cohen, L. Generalization of the wiener-khinchin theorem. IEEE Signal Process. Lett. 1998, 5, 292–294. [Google Scholar] [CrossRef]
- Strube, H.W. A generalization of correlation functions and the wiener-khinchin theorem. Signal Process. 1985, 8, 63–74. [Google Scholar] [CrossRef]
- Ricker, D.W. Echo Signal Processing; Kluwer Academic Publishers: New York, NY, USA, 2003; pp. 1–484. [Google Scholar]
- Zbilut, J.P.; Marwan, N. The wiener–khinchin theorem and recurrence quantification. Phys. Lett. A 2008, 372, 6622–6626. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, L.; Li, S.; Zhang, C.; Song, S.; Bao, R. Characteristics of the surface deformation of specimens with a hole during the progressive failure. Meitan Xuebao/J. China Coal Soc. 2017, 42, 2623–2630. [Google Scholar]
- Amalokwu, K.; Chapman, M.; Best, A.I.; Minshull, T.A.; Li, X.-Y. Water saturation effects onp-wave anisotropy in synthetic sandstone with aligned fractures. Geophys. J. Int. 2015, 202, 1088–1095. [Google Scholar] [CrossRef]
- Chen, X.; Yu, J.; Li, H.; Cai, Y.-Y.; Zhang, Y.-Z.; Mu, K. Experimental study of propagation characteristics of acoustic wave in rocks with different lithologies and water contents. Rock Soil Mech. 2013, 9, 2527–2533. [Google Scholar]
- Song, S.; Zhang, J.G.; Ji-Ye, M.A.; Hao, A.G.; Wang, H.W. Theoretical research of acoustic wave propagation in reservoir. Oil Field Equip. 2009, 38, 1–7. [Google Scholar]
- Liu, X.; Hong, L.; Xiaolei, X.U.; Lin, H.; Liang, L. Experimental reasearch on acoustic wave propagation characteristic of low porosity and permeability sandstone under loading conditions. Chin. J. Rock Mech. Eng. 2009, 28, 560–567. [Google Scholar]




| Index | Initial Mass/g | Size/(mm × mm × mm) | Mass After Absorption/(g) | ||||
|---|---|---|---|---|---|---|---|
| 24 h | 48 h | 72 h | 96 h | 120 h | |||
| A1 | 364 | 70.45 × 70.64 × 70.46 | 525 | 527 | 528 | 528 | - |
| A2 | 369 | 70.64 × 71.04 × 70.48 | 531 | 533 | 534 | 534 | - |
| A3 | 365 | 70.27 × 70.87 × 70.52 | 530 | 532 | 533 | 533 | - |
| A4 | 350 | 70.45 × 66.05 × 70.45 | 495 | 497 | 497 | 497 | - |
| A5 | 371 | 70.09 × 71.26 × 71.19 | 533 | 535 | 536 | 536 | - |
| B1 | 365 | 70.80 × 70.23 × 70.23 | 366 | 368 | 369 | 369 | 370 |
| B2 | 361 | 70.36 × 69.15 × 70.31 | 362 | 367 | 366 | 368 | 369 |
| B3 | 356 | 70.42 × 69.42 × 70.24 | 357 | 359 | 360 | 360 | 361 |
| B4 | 361 | 70.27 × 69.53 × 70.60 | 363 | 368 | 370 | 370 | 369 |
| B5 | 367 | 70.29 × 70.46 × 70.67 | 369 | 371 | 372 | 373 | 373 |
| C1 | 363 | 70.27 × 69.49 × 70.55 | 364 | 366 | 366 | 366 | 367 |
| C2 | 359 | 70.33 × 66.45 × 70.01 | 362 | 363 | 363 | 363 | 364 |
| C3 | 369 | 70.26 × 70.89 × 70.31 | 371 | 372 | 374 | 374 | 374 |
| C4 | 363 | 70.24 × 69.65 × 70.37 | 364 | 366 | 367 | 367 | 367 |
| C5 | 367 | 70.53 × 69.89 × 70.37 | 368 | 369 | 371 | 371 | 371 |
| D1 | 346 | 70.41 × 66.89 × 70.13 | - | - | - | - | - |
| D2 | 360 | 70.44 × 68.63 × 70.34 | - | - | - | - | - |
| D3 | 346 | 70.62 × 63.32 × 70.05 | - | - | - | - | - |
| D4 | 374 | 70.18 × 71.48 × 70.36 | - | - | - | - | - |
| D5 | 349 | 70.00 × 69.25 × 70.35 | - | - | - | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.-j.; Zhang, L.; Li, S.-g.; Liu, J.-l.; Pan, H.-y.; Ji, X. Wave Velocity and Power Spectral Density of Hole-Containing Specimens with Different Moisture Content under Uniaxial Compression. Energies 2018, 11, 3166. https://doi.org/10.3390/en11113166
Zhang T-j, Zhang L, Li S-g, Liu J-l, Pan H-y, Ji X. Wave Velocity and Power Spectral Density of Hole-Containing Specimens with Different Moisture Content under Uniaxial Compression. Energies. 2018; 11(11):3166. https://doi.org/10.3390/en11113166
Chicago/Turabian StyleZhang, Tian-jun, Lei Zhang, Shu-gang Li, Jia-lei Liu, Hong-yu Pan, and Xiang Ji. 2018. "Wave Velocity and Power Spectral Density of Hole-Containing Specimens with Different Moisture Content under Uniaxial Compression" Energies 11, no. 11: 3166. https://doi.org/10.3390/en11113166
APA StyleZhang, T.-j., Zhang, L., Li, S.-g., Liu, J.-l., Pan, H.-y., & Ji, X. (2018). Wave Velocity and Power Spectral Density of Hole-Containing Specimens with Different Moisture Content under Uniaxial Compression. Energies, 11(11), 3166. https://doi.org/10.3390/en11113166





