Numerical Investigation of an OxyfuelNon-Premixed CombustionUsing a Hybrid Eulerian Stochastic Field/Flamelet Progress Variable Approach: Effects of H2/CO2 Enrichment and Reynolds Number
Abstract
1. Introduction
2. Modelling Approach
2.1. Reynolds Averaged Transport Equations
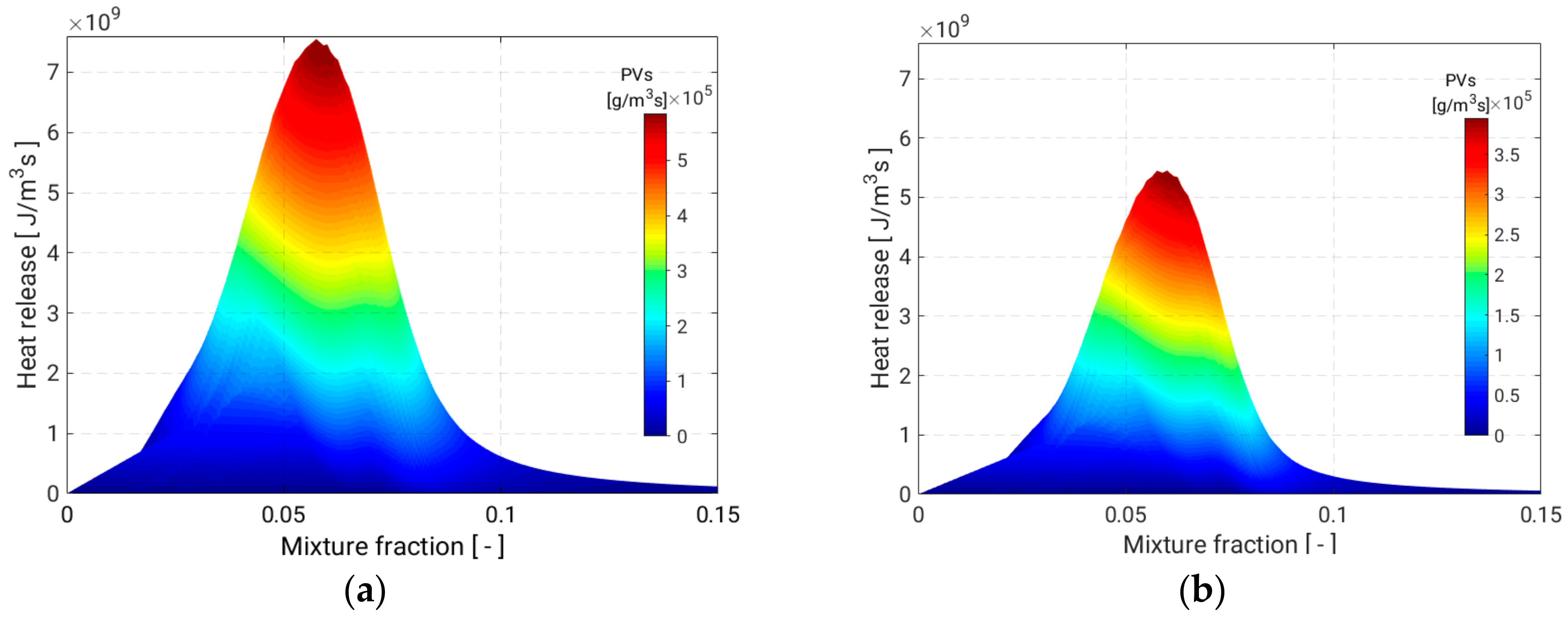
2.2. Chemistry Modelling Using Flamelet/Progress Variable FPV Approach
2.3. Modelling of Turbulence-Chemistry Interaction
2.3.1. Joint Probability Density Function and Eulerian Stochastic Field Method
2.3.2. Presumed Probability Density Function Approach
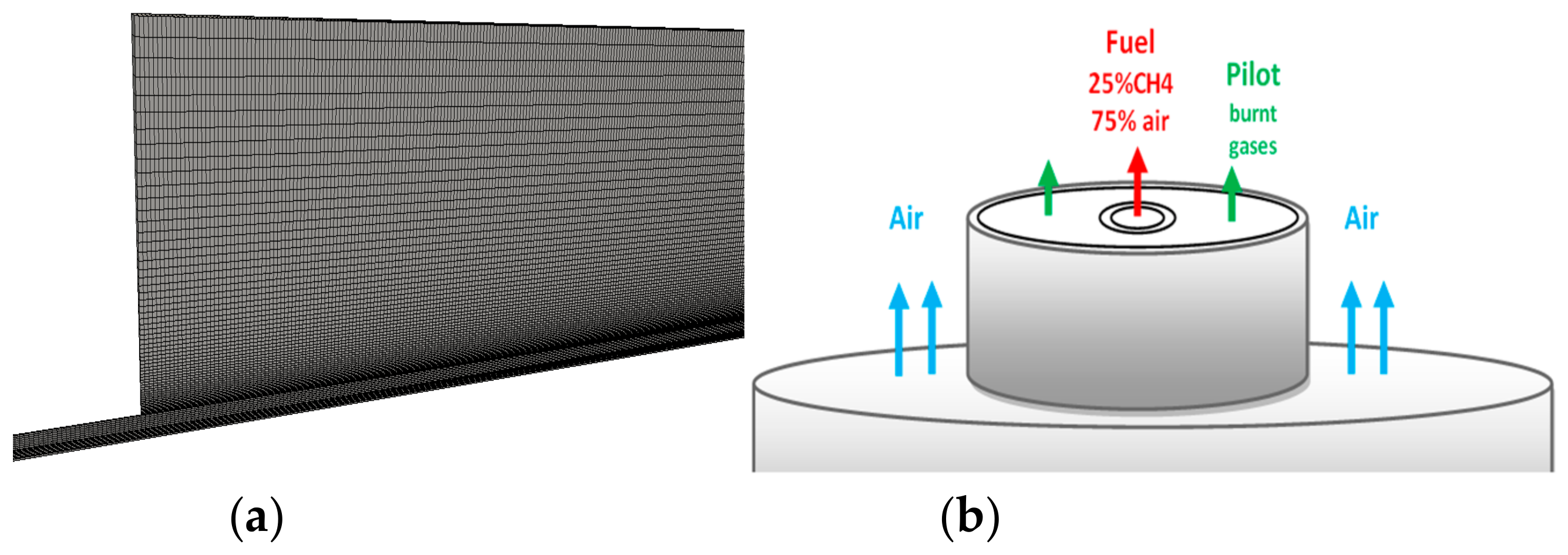
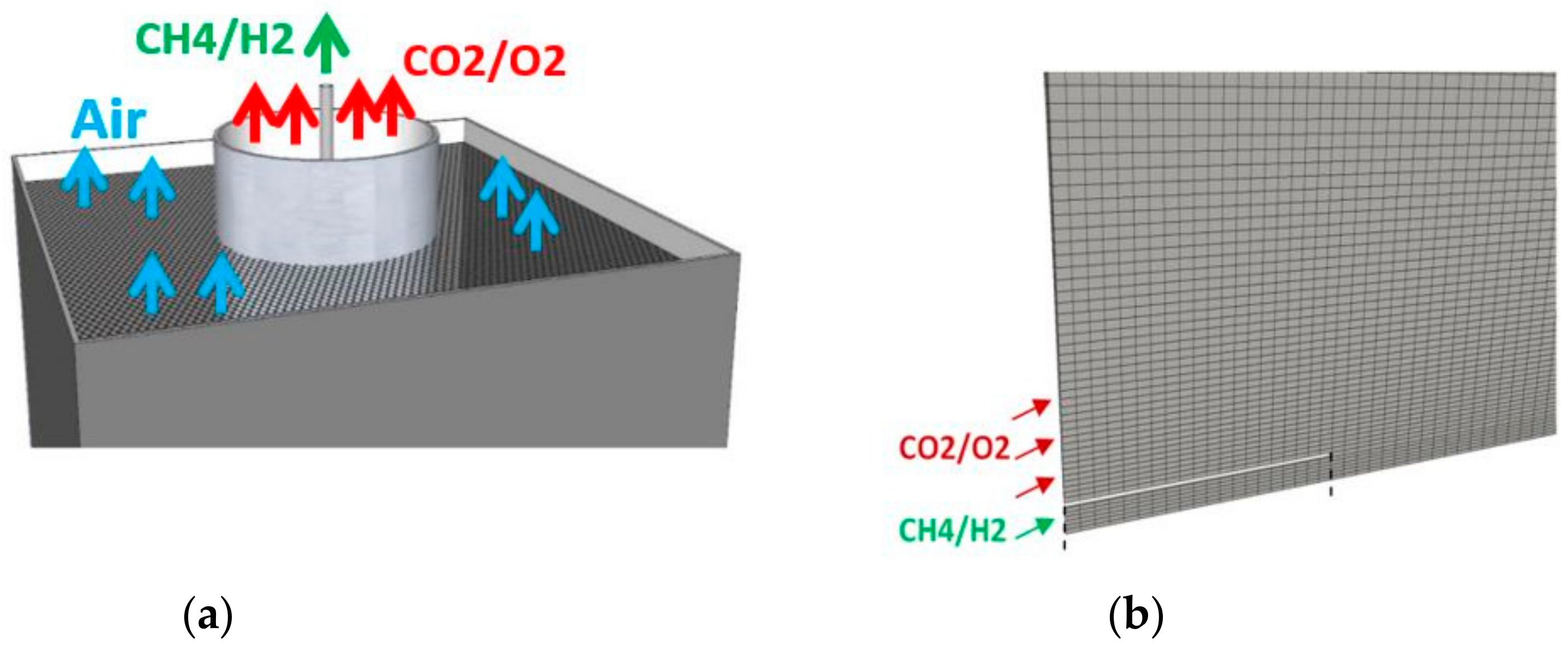
2.4. Numerical Set Ups
2.4.1. Presumed PDF/FPV
2.4.2. Eulerian Stochastic Field/FPV
3. Experimental Configurations and Case Setups
3.1. Validation case: Sandia Flame D
3.2. Oxy-Fuel Jet Flame Series
4. Results and Discussion
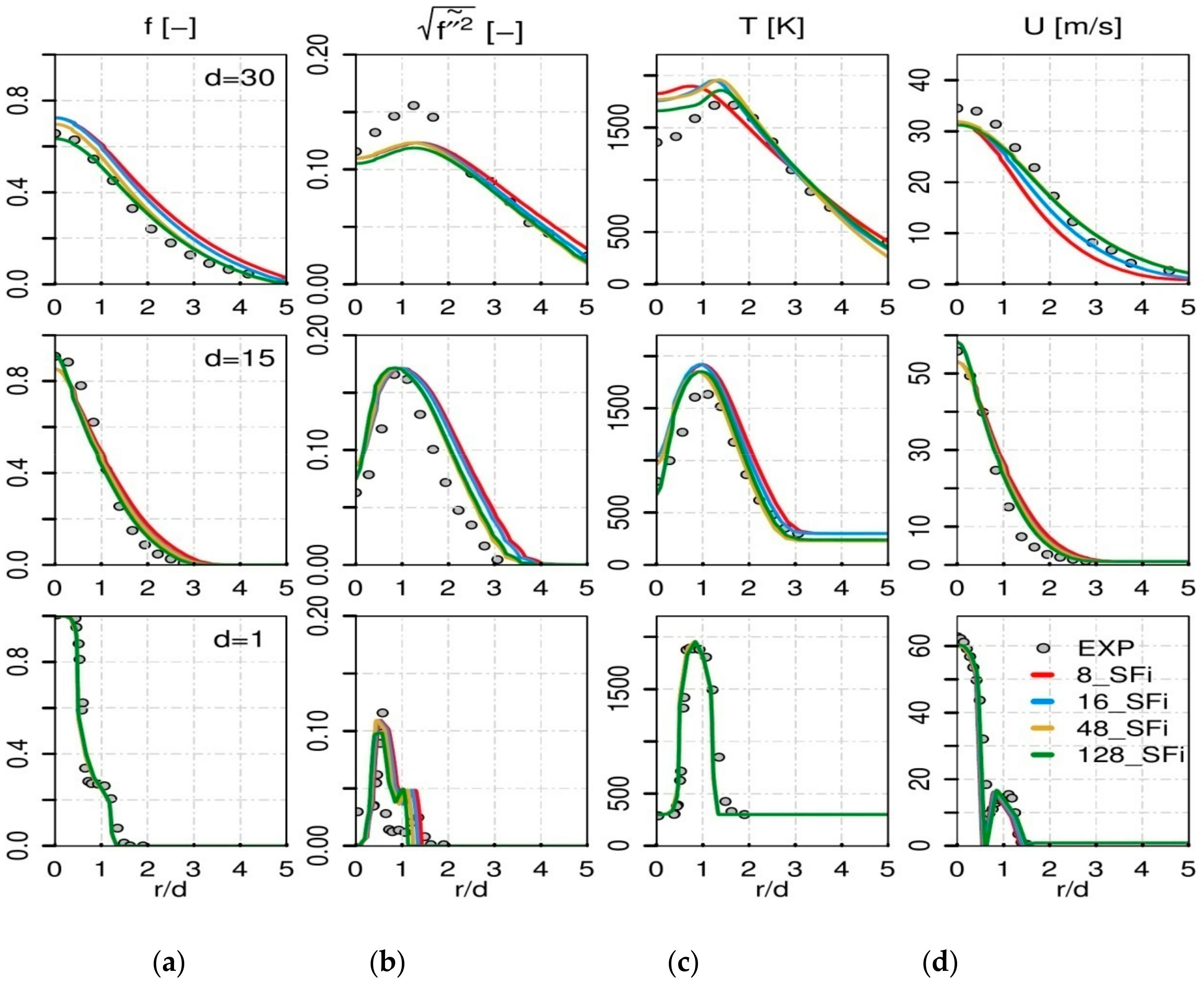
4.1. Validation Case: Sandia Flame D
4.2. Application to a Turbulent OxyfuelJet Flame
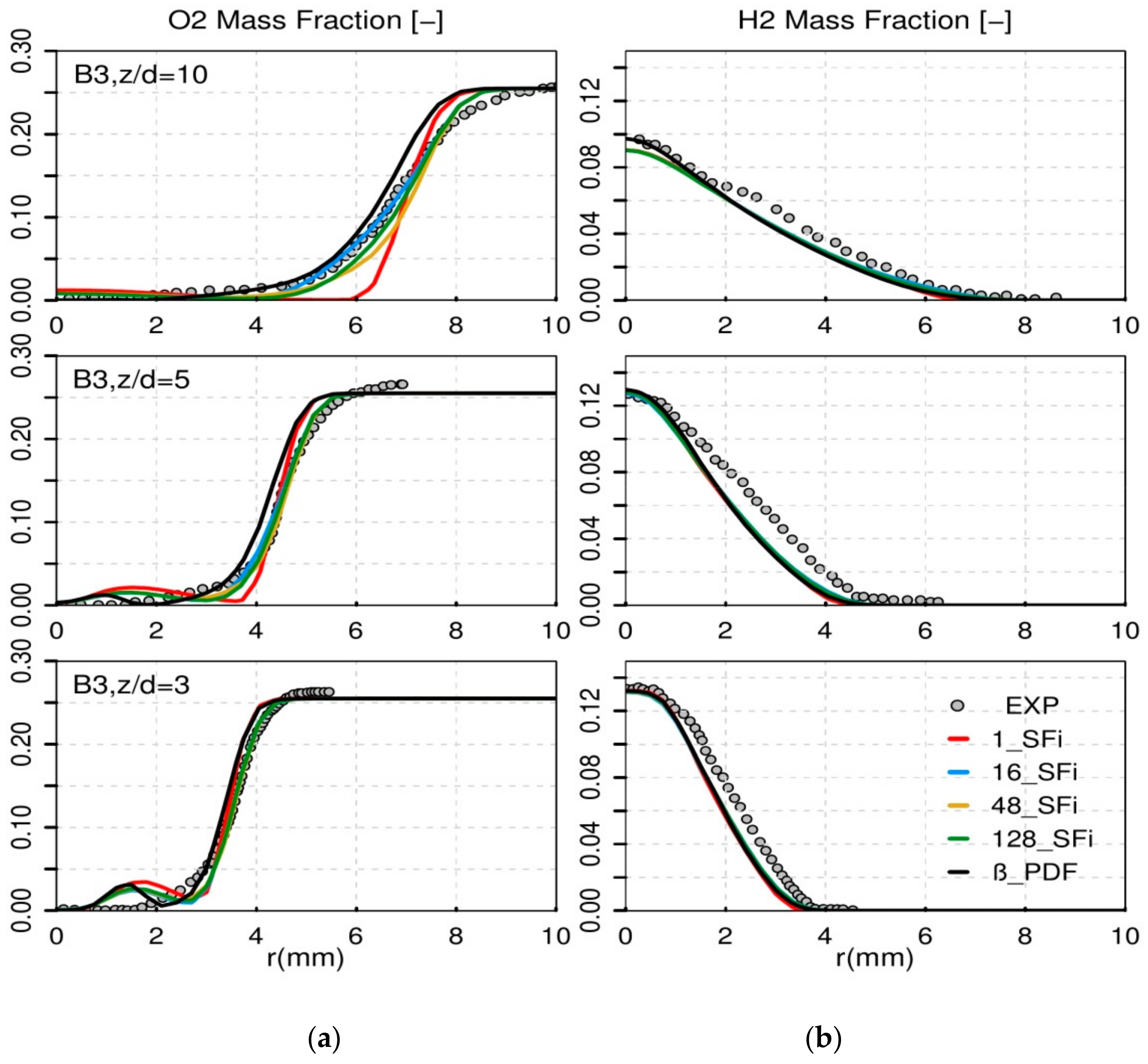
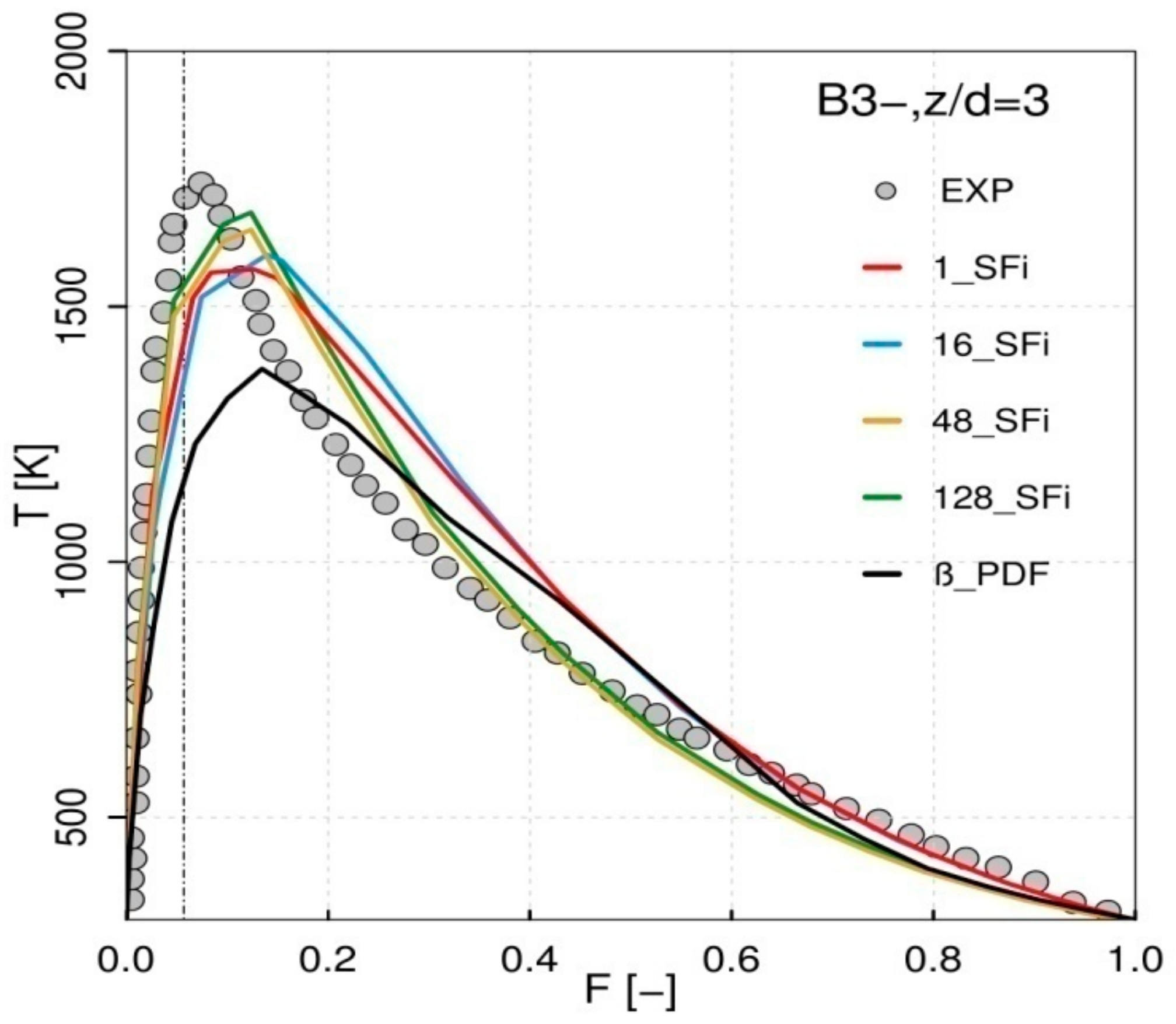
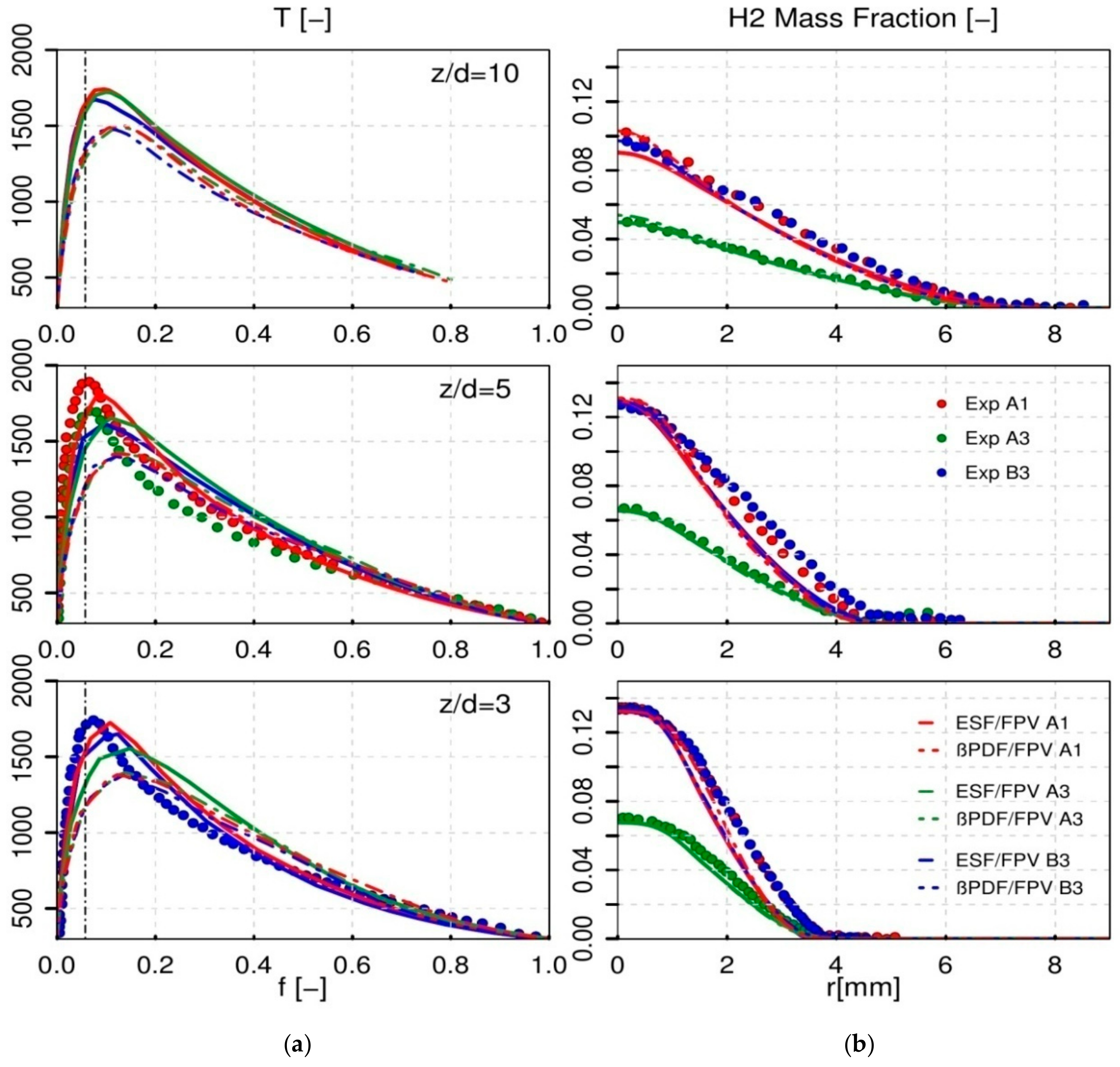
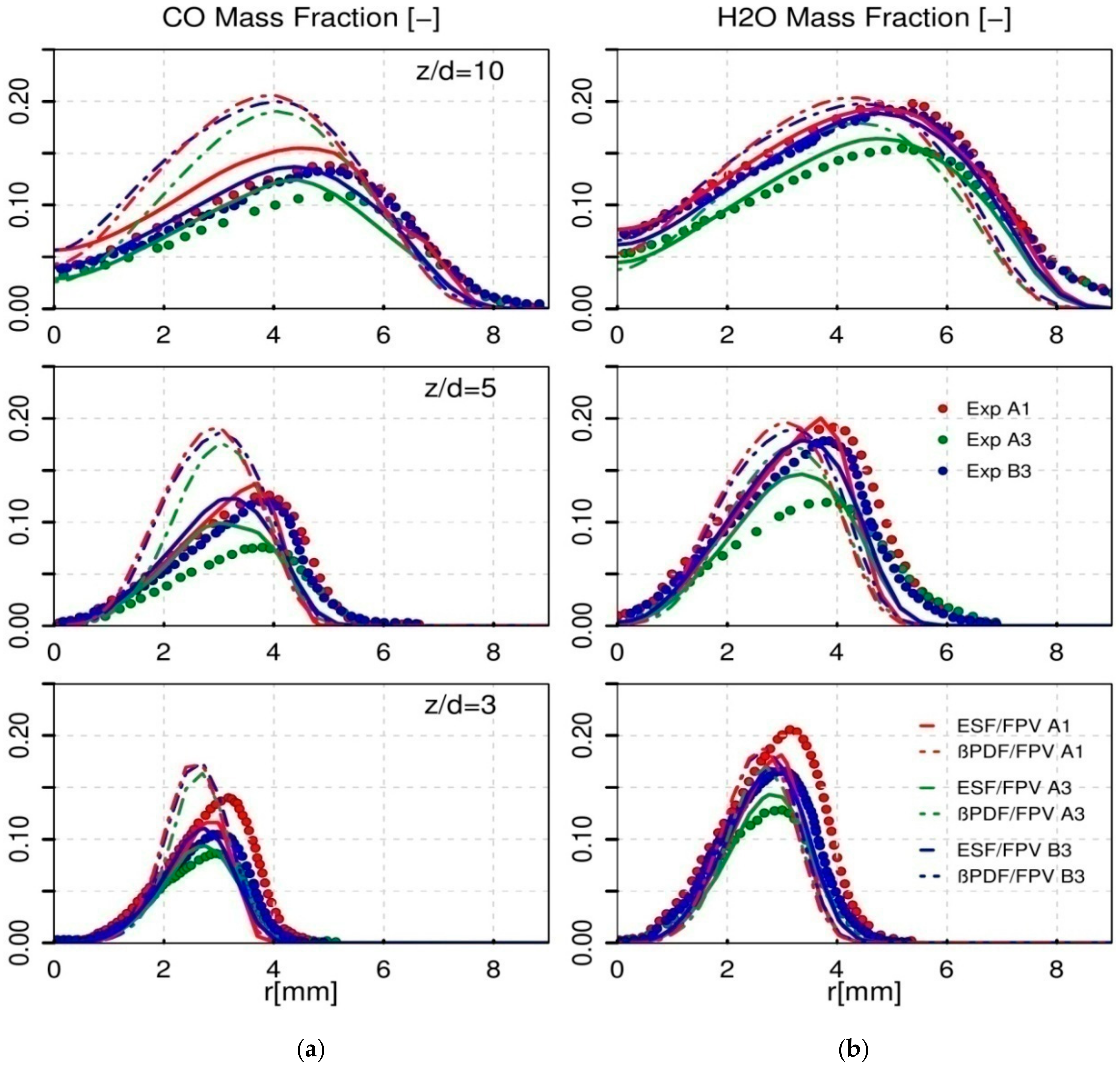
4.2.1. Oxyflame B3 and Combustion Modelling Comparison
4.2.2. H2% Enrichment in Fuel Side
4.2.3. CO2 Dilution in Oxidizer Side
4.2.4. Reynolds Number Effect
5. Conclusions
- A good prediction of different experimental and flow field variables, is reported by using the novel ESF/FPV approach.
- Related to the convergence of the stochastic field number (SFi), it turned out that starting the calculations with 48 SFi emerged as the compromise between accurate prediction and computational costs.
- Comparing the two different PDF-based combustion models, it turned out that the hybrid ESF/FPV clearly showed superiority in better predicting the temperature, H2O mass fraction and specially CO mass fraction, unlike the presumed β-PDF model which under-estimates the maximum adiabatic temperature and over-predicts the CO formation level at different positions above the nozzle downstream.
- With lower H2% enrichment in fuel side, fixed CO2/O2 ratio and constant Reynolds number, the maximum adiabatic temperature value decreases in a significant manner near the fuel nozzle and its location in the mixture fraction space is shifted toward the reach side of the fuel.
- With lower Reynolds number, constant CO2/O2 and CH4/H2 ratios, the CO formation is considerably intensified near the nozzle.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Model constant for mixture fraction variance | |
| Model constant in dissipation rate equation | |
| Model constant in dissipation rate equation | |
| Model constant | |
| Micro-mixing model coefficient | |
| Wiener term | |
| f | Mixture fraction |
| Joint probability density function | |
| Production of turbulence kinetic energy | |
| Turbulent kinetic energy | |
| Number of stochastic field | |
| Number of the chemical table controlling variables | |
| Pressure | |
| Probability density function | |
| Reynolds number | |
| Strain rate tensor | |
| Time | |
| Temperature | |
| Velocity component in ith direction | |
| Molar mass | |
| Positions coordinate in ith direction | |
| Mass fraction | |
| Time increment | |
| Kronecker-symbol | |
| Density | |
| Dynamic molecular viscosity | |
| Dynamic turbulent viscosity | |
| Schmidt number | |
| Turbulent Schmidt number | |
| Model constant | |
| Model constant | |
| Dissipation rate of turbulent kinetic energy | |
| Chemical source term | |
| General species variable | |
| Dirac delta function | |
| Composition space of species | |
| Referring to table controlling variable | |
| nth stochastic field of the variable | |
| Favre weighted quantity | |
| Mean quantity | |
| T-PDF | Transported probability density function |
| ESF | Eulerian Stochastic Field |
| PV | Progress Variable |
| FPV | Flamelet Progress Variable |
| P-PDF | Presumed probability density function |
| SDE | Stochastic differential equations |
| RANS | Reynolds averaged Navier–Stokes |
| CCS | Carbon Capture and Storage |
| FGM | Flamelet Generated Manifold |
| CMC | Conditional Moment Closure |
References
- Energy Agency. Available online: https://www.iea.org/newsroom/news/2015 (accessed on 1 October 2018).
- Zheng, L. Oxy-Fuel Combustion for Power Generation and Carbon Dioxide (CO2) Capture; Woodhead Publishing series in energy; Elsevier: Cambridge, UK, 2011. [Google Scholar]
- Jangi, M.; Li, C. Modelling of Methanol Combustion in a Direct Injection Compression Ignition Engine using an Accelerated Stochastic Fields Method. Energy Procedia 2017, 105, 1326–1331. [Google Scholar] [CrossRef]
- Hidouri, A.; Chrigui, M.; Boushaki, T.; Sadiki, A.; Janicka, J. Large eddy simulation of two isothermal and reacting turbulent separated oxy-fuel jets. Fuel 2017, 192, 108–120. [Google Scholar] [CrossRef]
- Pierce, C.D.; Moin, P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 2004, 504, 73–97. [Google Scholar] [CrossRef]
- Ihme, M.; Pitsch, H. Prediction of extinction and reignition in non-premixed turbulent flames using a flamelet/progress variable model 2. Application in LES of Sandia flames D. and E. Combust. Flame 2008, 155, 90–107. [Google Scholar] [CrossRef]
- Jordi, V.M. Numerical Simulation of Turbulent Diffusion Flames Using Flamelet Models on Unstructured Meshes. Ph.D.Thesis, Centre Tecnologic de Transferencia de Calor Departament de Maquinesi Motors Termics Universitat Politecnica de Catalunya, Terrassa, Spain, 2015. [Google Scholar]
- Ferraris, S.A.; Wen, J.X. LES of the Sandia Flame D Using Laminar Flamelet Decomposition for Conditional Source-Term Estimation. Flow Turbul. Combust. 2008, 81, 609–639. [Google Scholar] [CrossRef]
- Di Renzo, M. LES of the Sandia Flame D Using an FPV Combustion Model. Energy Procedia 2015, 82, 402–409. [Google Scholar] [CrossRef]
- Hunger, F.; Zulkifli, M.; Williams, B.; Beyrau, F.; Hasse, C. A combined experimental and numerical study of laminar and turbulent non-piloted Oxyfuel jet flames using a direct comparison of the Rayleigh signal. FlowTurbul. Combust. 2016, 97, 231–262. [Google Scholar] [CrossRef]
- Shahbazian, N.; Groth, C.P.T.; Gülder, O. Assessment of Presumed PDF Models for Large Eddy Simulation of Turbulent Premixed Flames. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Raman, V.; Pitsch, H. Eulerian transported probability density function sub-filter model for LES simulations of turbulent combustion. Combust. Theory Model. 2007, 10, 439–458. [Google Scholar] [CrossRef]
- Jones, W.P.; Prasad, V.N. Large Eddy Simulation of the Sandia Flame Series (D–F) using the Eulerian stochastic field method. Combust. Flame 2010, 157, 1621–1636. [Google Scholar] [CrossRef]
- Pope, S.B. PDF methods for turbulent reactive flows. Prog. Energy Combust. 1985, 11, 119–192. [Google Scholar] [CrossRef]
- Pope, S.B. A Monte Carlo Method for the PDF Equations of Turbulent Reactive Flow. J. Combust. Sci. Technol. 2008, 25, 159–174. [Google Scholar] [CrossRef]
- Valińo, L. A field Monte Carlo formulation for calculating the probability density functions of a single scalar in turbulent flow. Flow Turbul. Combust. 1998, 60, 157–172. [Google Scholar] [CrossRef]
- Haworth, D.C. Progress in the probability density function methods for turbulent reacting flows. Prog. Energy Combust. Sci. 2010, 36, 168–259. [Google Scholar] [CrossRef]
- Fox, R.O.; Raman, V. A multienvironment conditional probability density function model for turbulent reacting flows. Phys. Fluids 2004, 16, 4551–4565. [Google Scholar] [CrossRef]
- Sabelnikov, V.; Soulard, O. Rapidally decorrelating velocity-field model as tool for solving one-point Fokker-Planck equations for probability density functions of turbulent reactive scalars. Phys. Rev. 2005, 72. [Google Scholar] [CrossRef]
- Jones, W.P.; Marquis, A.; Prasad, V. LES of a turbulent premixed swirl burner using the Eulerian stochastic field method. Combst. Flame 2012, 159, 3079–3095. [Google Scholar] [CrossRef]
- Jones, W.P.; Navarro-Martinez, S. Numerical study of n-heptane auto-ignition using LES-PDF methods. Flow Turbul. Combust. 2009, 83, 407–423. [Google Scholar] [CrossRef]
- Jangi, M.; Lucchini, T.; Gong, C.; Bai, X.S. Effects of fuel cetane number on the structure of diesel spray combustion: An accelerated Eulerian stochastic fields method. Combust. Theory Model. 2015, 19, 549–567. [Google Scholar] [CrossRef]
- Gong, C.; Jangi, M.; Bai, X.S.; Liang, H.; Sun, M.B. Large eddy simulation of hydrogen combustion in supersonic flows using an Eulerian stochastic fields method. Int. J. Hydrogen Energy 2017, 42, 1264–1275. [Google Scholar] [CrossRef]
- Gong, C.; Jangi, M.; Bai, X.S. Diesel flame lift-off stabilization in the presence of laser-ignition: A numerical study. Combust. Theory Model. 2015, 19, 696–713. [Google Scholar] [CrossRef]
- Avdic, A.; Kuenne, G. DiMare, F.; Janicka, J. LES combustion modelling using the Eulerian stochastic field method coupled with tabulated chemistry. Combust. Flame 2017, 175, 201–219. [Google Scholar] [CrossRef]
- El-Asrag, H.A.; Graham, G. A comparison between two different Flamelet reduced order manifolds for non-premixed turbulent flames. Available online: https://www.google.com.tw/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=2ahUKEwjq9sa639DeAhUT97wKHeSeBGIQ7gEwAHoECAkQBw&url=https%3A%2F%2Ftranslate.google.com.tw%2Ftranslate%3Fhl%3Dzh-TW%26sl%3Den%26u%3Dhttps%3A%2F%2Fsutherland.che.utah.edu%2FUSCI2013%2FPAPERS%2F2E01-070LT-0182.pdf%26prev%3Dsearch&usg=AOvVaw2U7BugwRgM4neQCdg1UIsV (accessed on 1 October 2018).
- TNF Workshop. Available online: http://www.ca.sandia.gov/TNF (accessed on 1 October 2018).
- Sevault, A.; Dunn, M.; Barlow, R.S.; Ditaranto, M. On the Structure of the Near Field of Oxy-Fuel Jet Flames Using Raman/Rayleigh Laser Diagnostics. Conbust. Flame 2012, 159, 3342–3352. [Google Scholar] [CrossRef]
- Ditaranto, M.; Hals, J. Combustion instabilities in sudden expansion oxy–fuel flames. Combust. Flame 2006, 146, 493–512. [Google Scholar] [CrossRef]
- Coppens, F.H.V.; Konnov, A.A. The effects of enrichment by H2 on propagation speeds in adiabatic flat and cellular premixed flames of CH4 + O2 + CO2. Fuel 2008, 81, 2866–2870. [Google Scholar] [CrossRef]
- Garmory, A.; Mastorakos, E. Numerical simulation of oxy-fuel jet flames using unstructured LES-CMC. Proceed. Combust. Ins. 2014, 35, 1207–1214. [Google Scholar] [CrossRef]
- Launder, B.E.; Sharma, B.I. Application of the Energy-Dissipation Model of Turbulence to the Calculation of Flow Near a Spinning Disc. Lett. Heat Mass Trans. 1974, 1, 131–138. [Google Scholar] [CrossRef]
- Branley, N.; Jones, W.P. Large eddy simulation of a turbulent non-premixed flame. Combust. Flame 2001, 127, 1914–1934. [Google Scholar] [CrossRef]
- Cook, A.W.; Riley, J.J.; Kosály, G. A laminar flamelet approach to subgrid-scale chemistry in turbulent flows. Combus. Flame 1997, 109, 332–341. [Google Scholar] [CrossRef]
- De Bruyn Kops, S.M.; Riley, J.J. Direct numerical simulation of laboratory experiments in isotropic turbulence. Phys. Fluids 1998, 10, 2125–2127. [Google Scholar] [CrossRef]
- Kempf, A.; Sadiki, A.; Janicka, J. Prediction of finite chemistry effects using large eddy simulation. Proceed. Combust. Ins. 2003, 29, 1979–1985. [Google Scholar] [CrossRef]
- Bekdemir, C.; Somers, L.; Angelberger, C. Predicting diesel combustion characteristics with Large-Eddy simulations including tabulated chemical kinetics. Proceed. Combust. Ins. 2013, 34, 3067–3074. [Google Scholar] [CrossRef]
- Wehrfritz, W.; Kaario, O.; Vuorinen, V.; Somers, L. Large Eddy Simulation of ndodecane spray flames using Flamelet generated manifolds, combustion and flame. Combust. Flame 2016, 167, 113–131. [Google Scholar] [CrossRef]
- FlameMaster v3.3.10. Available online: https://web.stanford.edu/group/pitsch/FlameMaster.htm (accessed on 1 October 2018).
- Gri-Mesh3.0. Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 1 October 2018).
- Subramaniam, S.; Pope, S. A mixing model for turbulent reactive flows based on Euclidean minimum spanning trees. Combst. Flame 1998, 115, 487–517. [Google Scholar] [CrossRef]
- Gao, F.; O’Brien, E.E. A large eddy simulation scheme for turbulent reacting flows. Phys. Fluids 1993, 5, 1282–2184. [Google Scholar] [CrossRef]
- Jaberi, F.A.; Colucci, P.J. Large eddy simulation for heat and mass transport in turbulent flows. Part 2: Scalar field. Int. J. Heat Mass Trans. 2003, 46, 1827–1840. [Google Scholar] [CrossRef]
- Jaberi, F.A.; Colucci, P.J.; James, S.; Givi, P.; Pope, S. Filtered mass density functionfor Large eddy simulation of turbulent reacting flows. J. Fluid Mechan. 1999, 401, 85–121. [Google Scholar] [CrossRef]
- Dopazo, C. Probability density function approach for a turbulent axisymmetric heated jet. Centerline evolution. Phys. Fluids 1975, 18, 397–404. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods:For Physics, Chemistry and the Natural Science, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Landenfeld, T.; Sadiki, S.; Janicka, J. A turbulence-chemistry interaction model based on multivariable presumed Beta-PDF methods for turbulent flames. Flow Turbul. Combust. 2002, 68, 111–135. [Google Scholar] [CrossRef]
- Keeheon, I.Y. Investigation of the Scalar Variance and Scalar Dissipation Rate in URANS and LES. Ph.D.Thesis, University of Waterloo, Waterloo, ON, Canada, 2011. [Google Scholar]
- Greenshields, C.J. OpenFOAM Programmer’s Guide. Available online: http://foam.sourceforge.net/docs/Guides-a4/OpenFOAMUserGuide-A4.pdf (accessed on 1 October 2018).
- Ditaranto, M.; Sautet, J.C.; Samaniego, J.M. Structural aspects of coaxial oxy-fuel flames. Exp. Fluids 2001, 30, 253–261. [Google Scholar] [CrossRef]
- Masri, A.R.; Dibble, R.W.; Barlow, R.S. Chemical kinetic effects in non-premixed flames of H2/CO2 fuel. Combust. Flame 1992, 91, 285–309. [Google Scholar] [CrossRef]
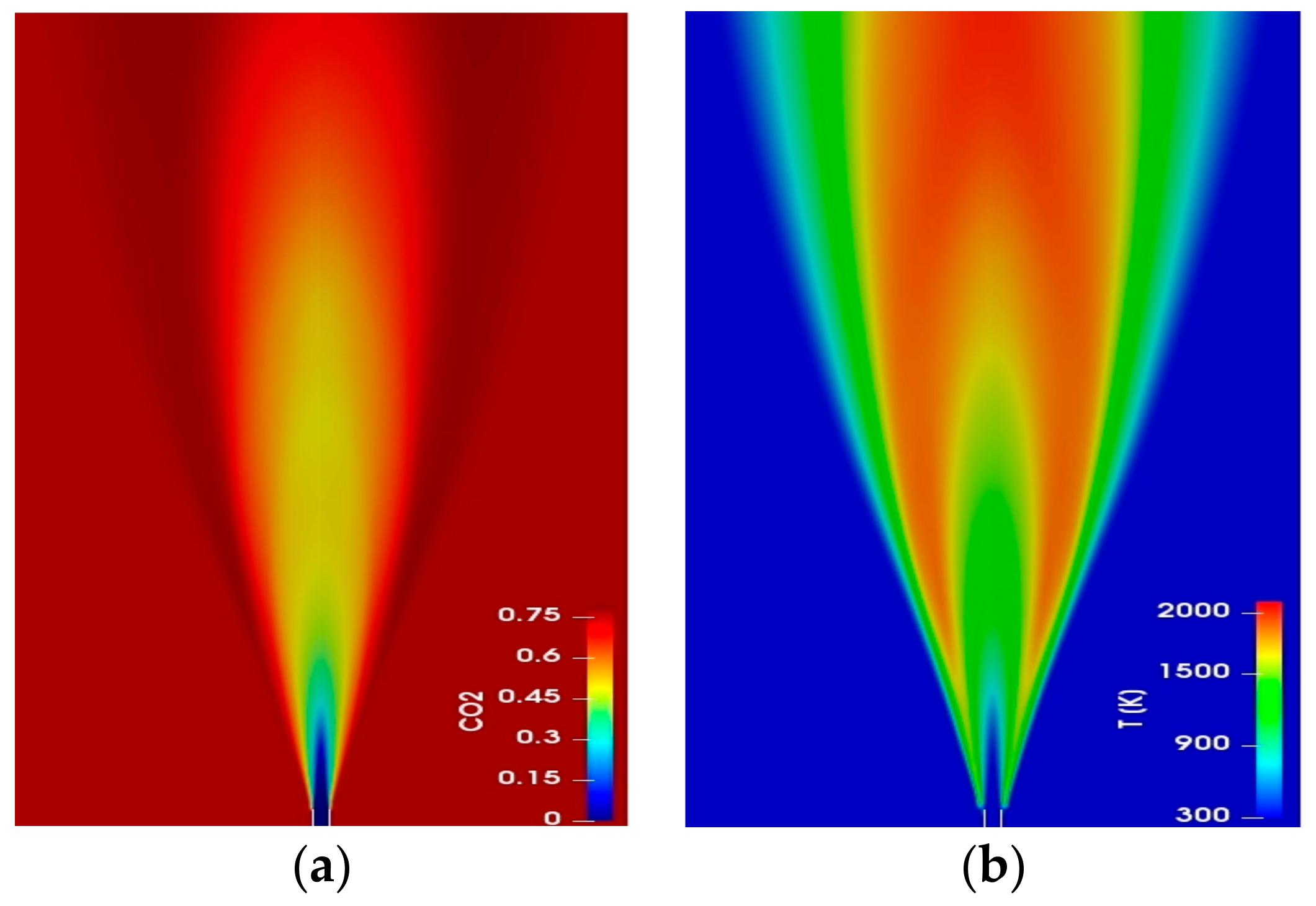
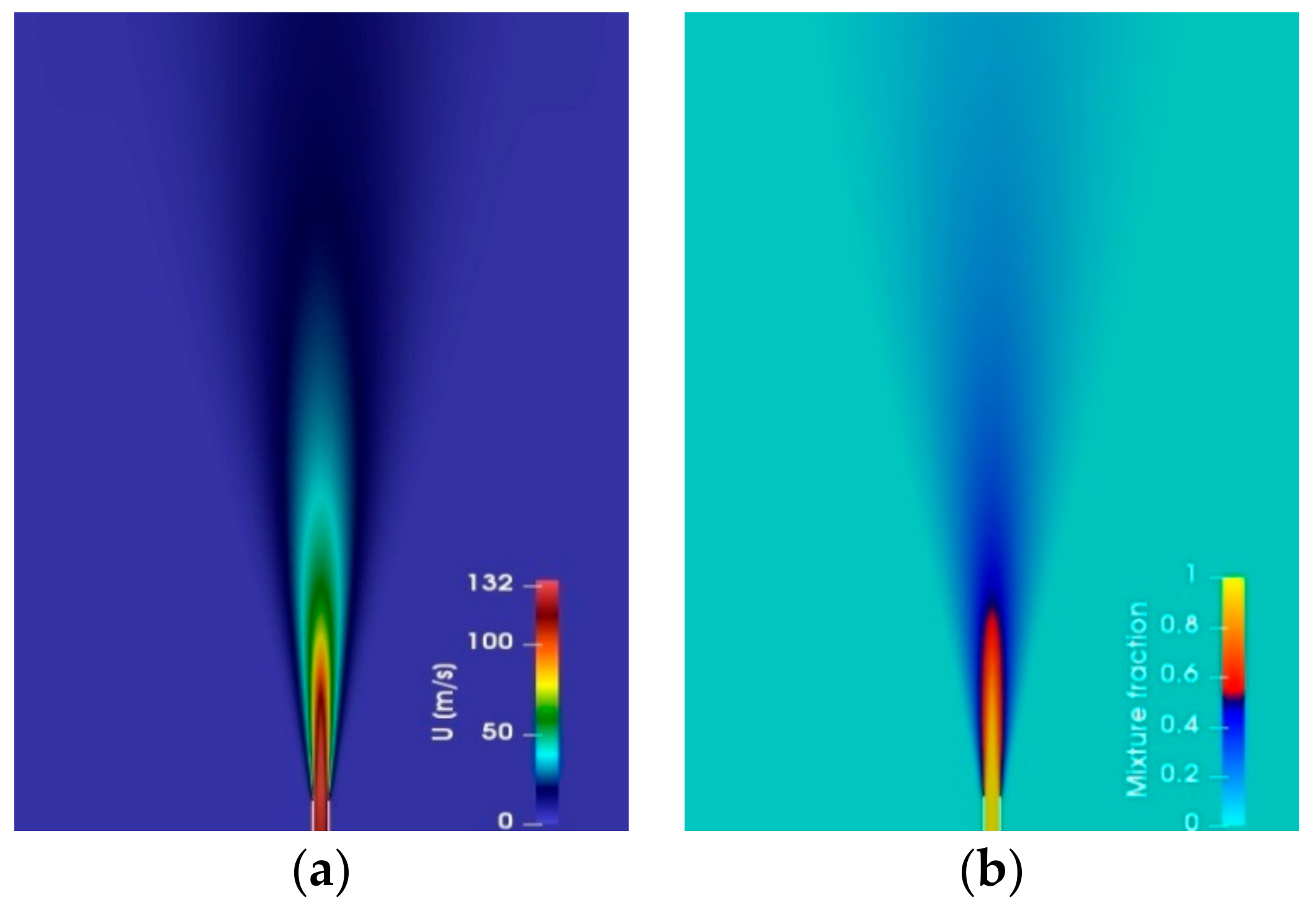

| Parameter | Fuel | Pilot | Co-Flow | Units |
|---|---|---|---|---|
| Mixture fraction | 0.156 | 0.043 | 0 | --- |
| Progress variable | 0 | 7 | 0 | --- |
| T | 294 | 1880 | 291 | K |
| Velocity | 49.6 | 11.4 | 0.9 | m/s |
| ν | 1.513 × 10−5 | m2/s | ||
| Reynolds Number | 22,000 | --- |
| Flame | %H2 in Fuel | Refuel | Vel. Fuel [m/s] | Vel. Oxy [m/s] | PVOxy | ν [m2/s] |
|---|---|---|---|---|---|---|
| A1 | 55 | 15,000 | 84.4 | 0.775 | 0 | 3.271 × 10−5 |
| A3 | 37 | 15,000 | 75.8 | 0.739 | 0 | 3.271 × 10−5 |
| B3 | 55 | 18,000 | 117.8 | 0.933 | 0 | 3.271 × 10−5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, R.; Jangi, M.; Fiorina, B.; Pfitzner, M.; Sadiki, A. Numerical Investigation of an OxyfuelNon-Premixed CombustionUsing a Hybrid Eulerian Stochastic Field/Flamelet Progress Variable Approach: Effects of H2/CO2 Enrichment and Reynolds Number. Energies 2018, 11, 3158. https://doi.org/10.3390/en11113158
Mahmoud R, Jangi M, Fiorina B, Pfitzner M, Sadiki A. Numerical Investigation of an OxyfuelNon-Premixed CombustionUsing a Hybrid Eulerian Stochastic Field/Flamelet Progress Variable Approach: Effects of H2/CO2 Enrichment and Reynolds Number. Energies. 2018; 11(11):3158. https://doi.org/10.3390/en11113158
Chicago/Turabian StyleMahmoud, Rihab, Mehdi Jangi, Benoit Fiorina, Michael Pfitzner, and Amsini Sadiki. 2018. "Numerical Investigation of an OxyfuelNon-Premixed CombustionUsing a Hybrid Eulerian Stochastic Field/Flamelet Progress Variable Approach: Effects of H2/CO2 Enrichment and Reynolds Number" Energies 11, no. 11: 3158. https://doi.org/10.3390/en11113158
APA StyleMahmoud, R., Jangi, M., Fiorina, B., Pfitzner, M., & Sadiki, A. (2018). Numerical Investigation of an OxyfuelNon-Premixed CombustionUsing a Hybrid Eulerian Stochastic Field/Flamelet Progress Variable Approach: Effects of H2/CO2 Enrichment and Reynolds Number. Energies, 11(11), 3158. https://doi.org/10.3390/en11113158







