Hybrid Approach for Detecting and Classifying Power Quality Disturbances Based on the Variational Mode Decomposition and Deep Stochastic Configuration Network
Abstract
1. Introduction
2. Variation Mode Decomposition
2.1. The Structure of VMD
- (i)
- Obtain the unilateral frequency spectrum of each mode by computing the associated analytic signal by means of Hilbert transform (in which ):
- (ii)
- Shift the frequency spectrum of each mode to baseband by multiplying an exponential tuned with estimated center frequency:
- (iii)
- Calculate the bandwidth of each mode by means of the squared -norm of the gradient. The constrained variational problem is as follows:where and are all the modes with short bandwidth properties and their center frequencies, respectively.
2.2. The Computation of VMD
- (i)
- Initialize the , , , and ;
- (ii)
- Update the and repeatedly according to (6), (7);
- (iii)
- Update dual ascent according to
- (iv)
- Repeat step (2), (3), until convergence: .
2.3. Determination of VMD Parameters
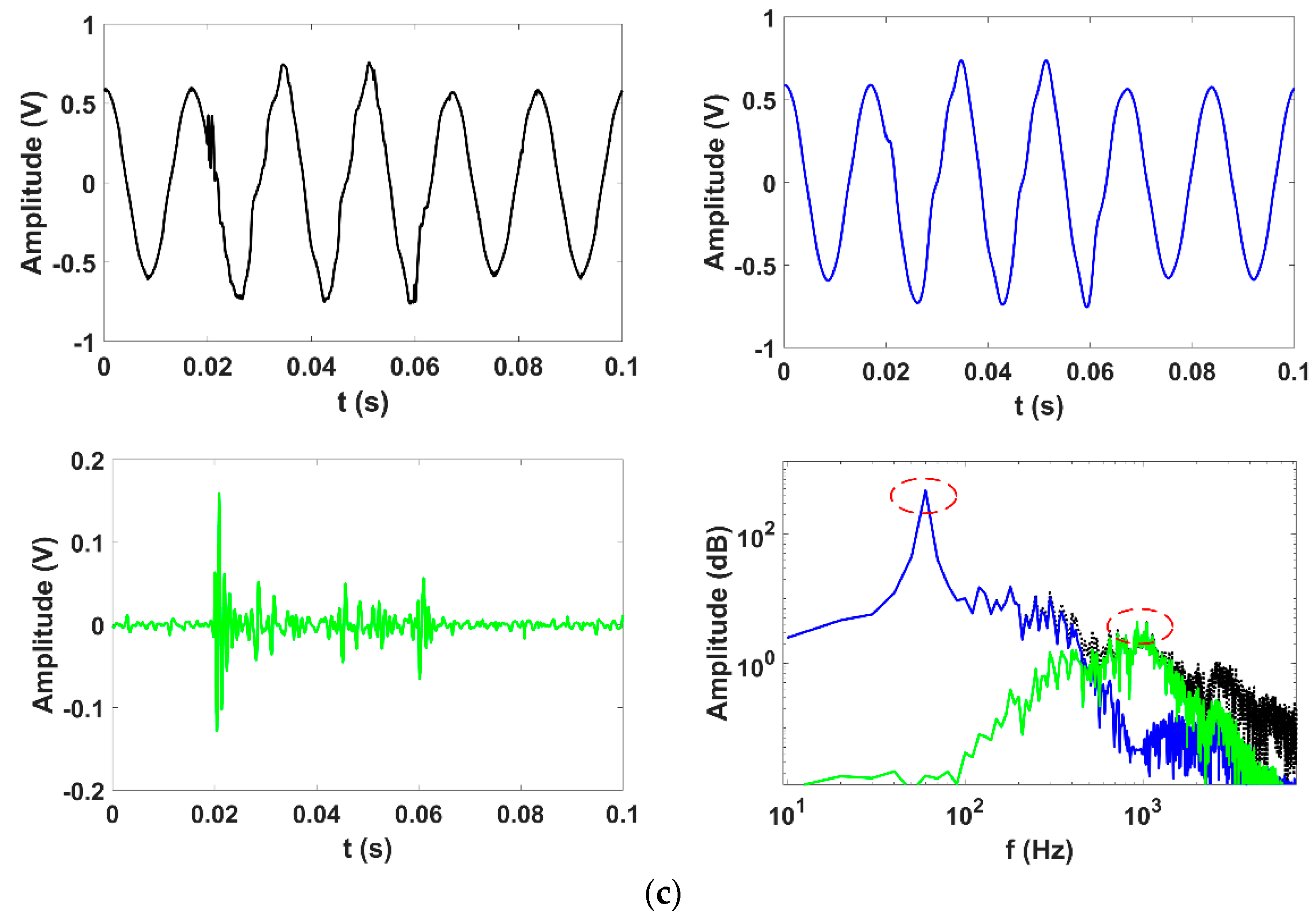
2.4. PQ Disturbances Analysis
2.5. Flicker Separation
3. Power Disturbance Detection and Classification based on VMD and DSCN
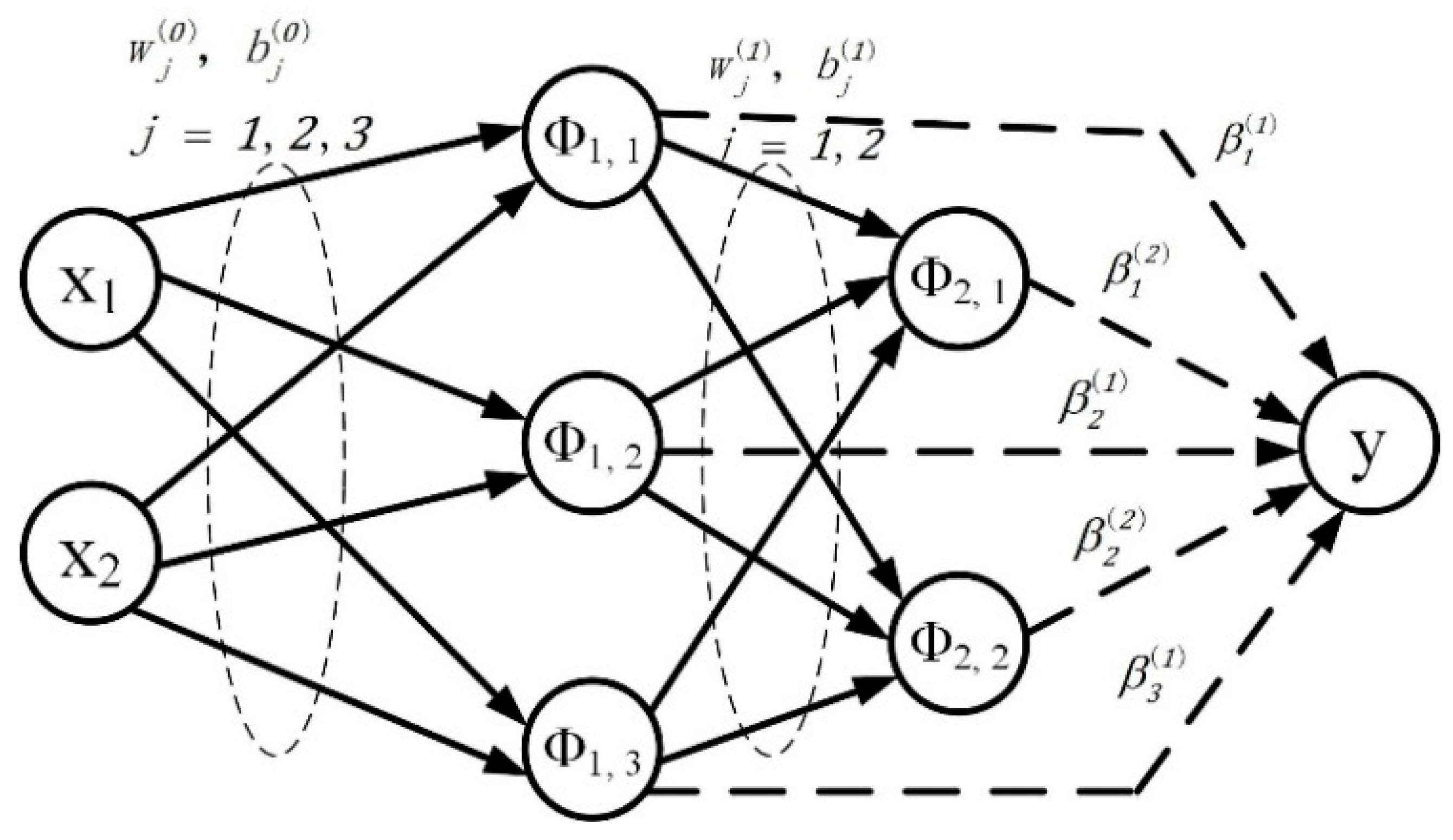
3.1. Deep Stochastic Configuration Networks Algorithm
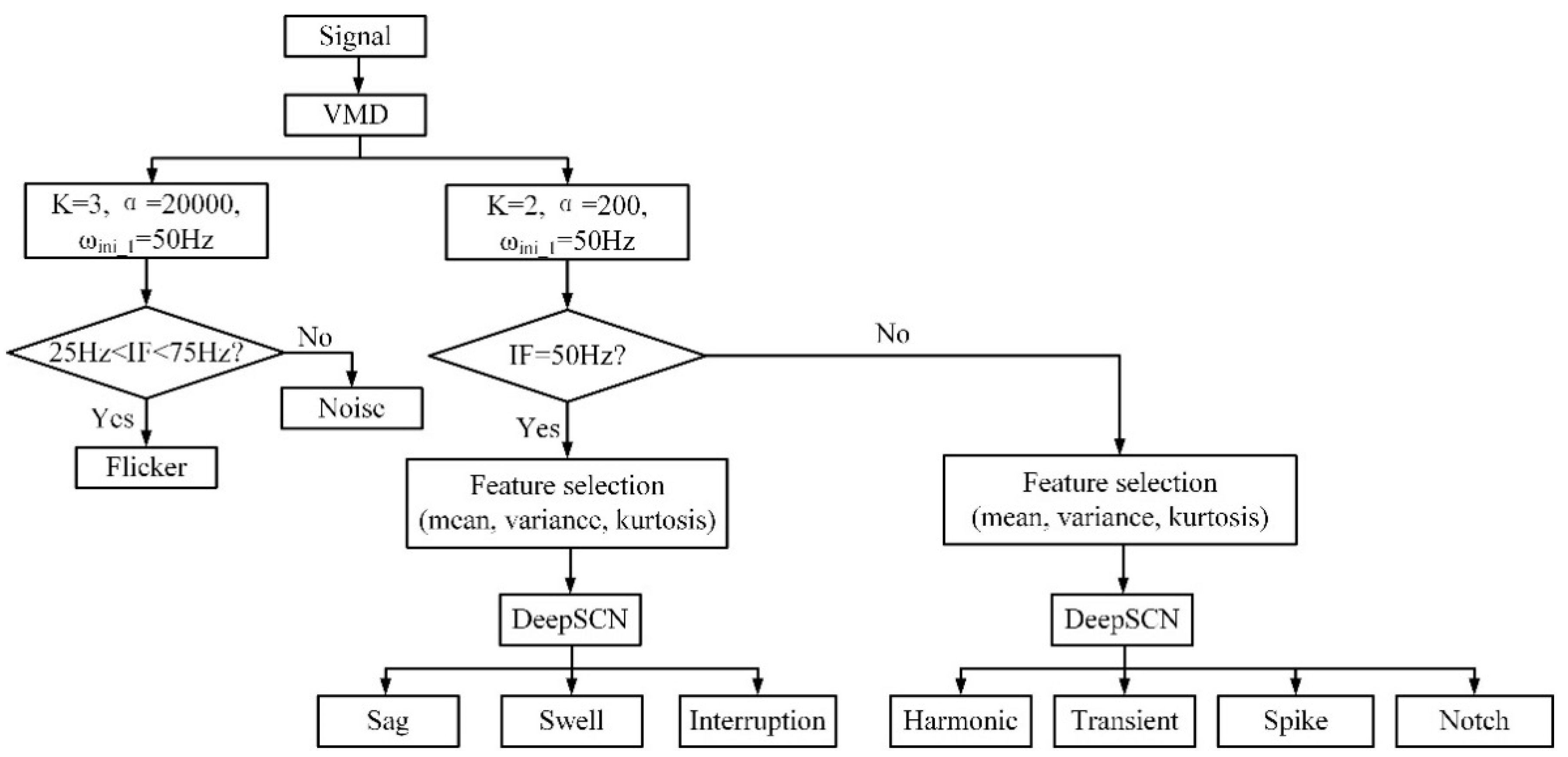
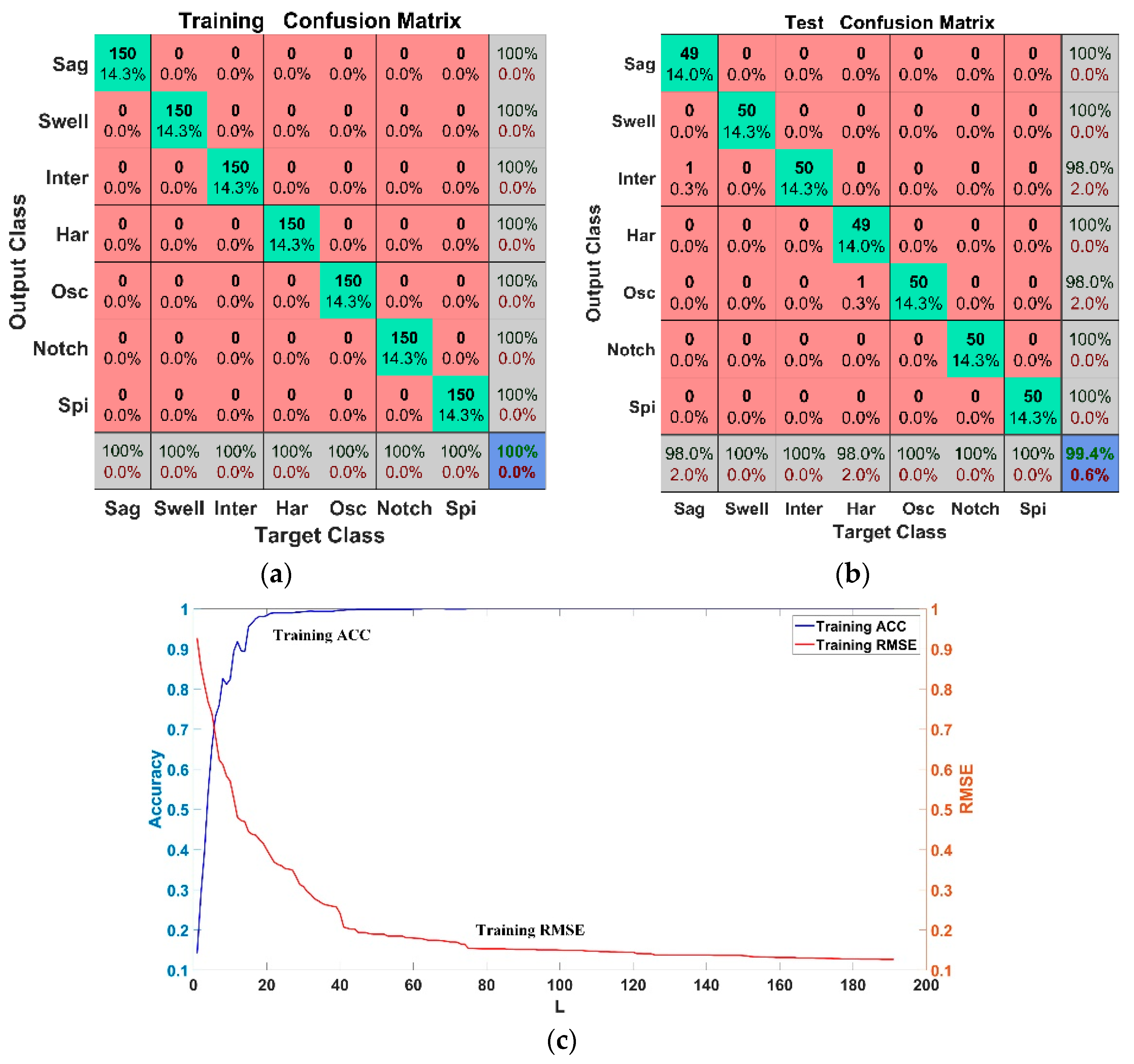
3.2. Disturbance Detection and Classification
4. Results and Discussion
4.1. Synthetic Signal
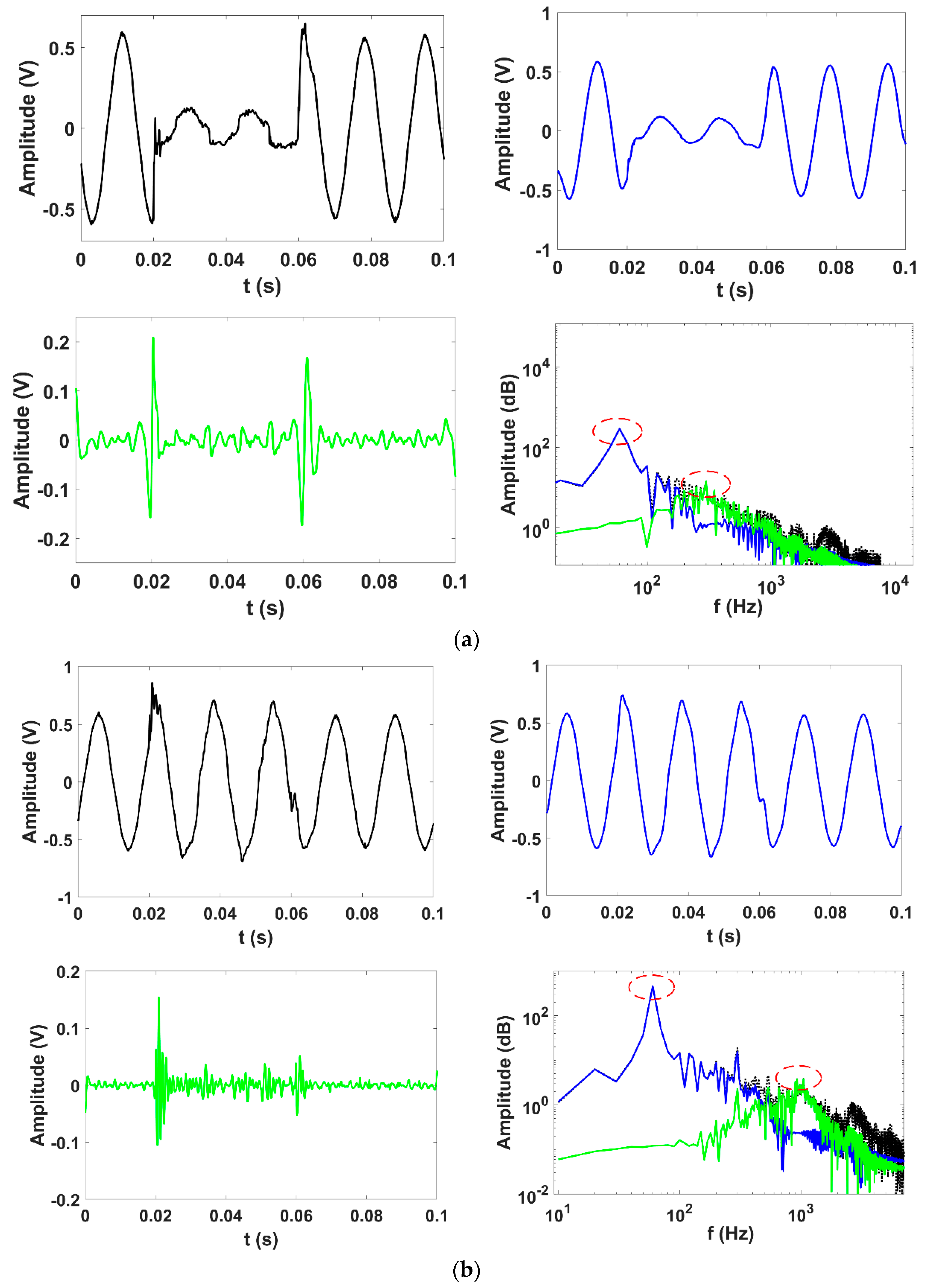
4.2. Real World Signal
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Díaz-Araujo, M.; Medina, A.; Cisneros-Magaña, R.; Ramírez, A. Periodic steady state assessment of microgrids with photovoltaic generation using limit cycle extrapolation and cubic splines. Energies 2018, 11, 2096. [Google Scholar] [CrossRef]
- Deng, C.H.; Chen, Y.H.; Tan, J.; Xia, P.; Liang, N.; Yao, W.W.; Zhang, Y.A. Distributed variable droop curve control strategies in smart microgrid. Energies 2017, 11, 24. [Google Scholar] [CrossRef]
- González-De-La-Rosa, J.J.; Agüera-Pérez, A.; Palomares-Salas, J.C.; Florencias-Oliveros, O.; Sierra-Fernández, J.M. A dual monitoring technique to detect power quality transients based on the fourth-order spectrogram. Energies 2018, 11, 503. [Google Scholar] [CrossRef]
- Rosa, J.J.G.; Sierra-Fernández, J.M.; Agüera-Pérez, A.; Palomares-Salas, J.C.; Moreno-Muñoz, A. An application of the spectral kurtosis to characterize power quality events. Int. J. Electr. Power Energy Syst. 2015, 49, 386–398. [Google Scholar] [CrossRef]
- Lucas, A.; Trentadue, G.; Scholz, H.; Otura, M. Power quality performance of fast-charging under extreme temperature conditions. Energies 2018, 11, 2635. [Google Scholar] [CrossRef]
- Voltage Characteristics of Electricity Supplied by Public Distribution Systems; Belgian Standards: Belgium, 1994.
- Testing and Measurement Techniques Power Quality Measurement Methods; IEC 61000-4-30; International Electrotechnical Commission: Geneva, Switzerland, 2003.
- IEEE Recommended Practice for Monitoring Electric Power Quality; IEEE Standard 1159–2009; IEEE: Piscataway, NI, USA, 2009.
- Javadi, A.; Al-Haddad, K. A single phase active device for power quality improvement of electric field transportation. IEEE Trans. Ind. Electron. 2015, 62, 3033–3041. [Google Scholar] [CrossRef]
- Xiao, H.; Wei, J.; Li, Q. Identification of combined power quality disturbances using singular value decomposition (SVD) and Total Least Squares-Estimation of Signal Parameters via Rotational Invariance Techniques (TLS-ESPRIT). Energies 2017, 10, 1809. [Google Scholar] [CrossRef]
- Pérez-Ortiz, M.; Jiménez-Fernández, S.; Gutiérrez, P.A.; Alexandre, E.; Hervás-Martínez, C.; Salcedo-Sanz, S. A review of classification problems and algorithms in renewable energy applications. Energies 2016, 9, 607. [Google Scholar] [CrossRef]
- Heydt, G.T.; Fjeld, P.S.; Liu, C.C.; Pierce, D.; Tu, L.; Hensley, G. Applications of the windowed FFT to electric power quality assessment. IEEE Trans. Power Deliv. 1999, 14, 1411–1416. [Google Scholar] [CrossRef]
- Gaouda, A.M.; Salama, M.M.A.; Sultan, M.R.; Chikhani, A.Y. Power quality detection and classification using wavelet-multiresolution signal decomposition. IEEE Trans. Power Deliv. 1999, 14, 1469–1476. [Google Scholar] [CrossRef]
- Gu, Y.H.; Bollen, M.H.J. Time-frequency and time-scale domain analysis of voltage disturbances. IEEE Trans Power Deliv. 2000, 15, 1279–1284. [Google Scholar] [CrossRef]
- Santoso, S.; Grady, W.M.; Powers, E.J.; Lamoree, J.; Bhatt, S.C. Characterization of distribution power quality events with Fourier and wavelet transforms. IEEE Trans. Power Deliv. 2000, 15, 247–254. [Google Scholar] [CrossRef]
- Barros, J.; Diego, R.I.; Apráiz, M. Applications of wavelets in electric power quality: Voltage events. Electr. Power Syst. Res. 2012, 88, 130–136. [Google Scholar] [CrossRef]
- Poisson, O.; Rioual, P.; Meunier, M. Detection and measurement of power quality disturbances using wavelet transform. IEEE Trans. Power Deliv. 2000, 15, 1039–1044. [Google Scholar] [CrossRef]
- Tarasiuk, T. Hybrid wavelet-fourier spectrum analysis. IEEE Trans. Power Deliv. 2004, 19, 957–964. [Google Scholar] [CrossRef]
- Wang, H.H.; Wang, P.; Liu, T. Power quality disturbance classification using the S-transform and probabilistic neural network. Energies 2017, 10, 107. [Google Scholar] [CrossRef]
- Biswal, B.; Biswal, M.; Mishra, S.; Jalaja, R. Automatic classification of power quality events using balanced neural tree. IEEE Trans. Ind. Electron. 2013, 61, 521–530. [Google Scholar] [CrossRef]
- Cai, K.W.; Wang, Z.Q.; Li, G.F.; He, D.G.; Song, J.Y. Harmonic separation from grid voltage using ensemble empirical-mode decomposition and independent component analysis. Int. Trans. Electr. Energy 2017, 11, e2405. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Zi, Y.; Pan, J. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive. Mech. Syst. Signal Process. 2017, 85, 512–529. [Google Scholar] [CrossRef]
- Yi, C.C.; Lv, Y.; Dang, Z. A fault diagnosis scheme for rolling bearing based on particle swarm optimization in variational mode decomposition. Shock Vib. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Aneesh, C.; Kumar, S.; Hisham, P.M.; Soman, K.P. Performance comparison of variational mode decomposition over empirical wavelet transform for the classification of power quality disturbances using support vector machine. Procedia Comput. Sci. 2015, 46, 372–380. [Google Scholar] [CrossRef]
- Zhao, C.; Li, K.C.; Li, Y.Z.; Wang, L.Y.; Luo, Y.; Xu, X.B.; Ding, X.J.; Meng, Q.X. Novel method based on variational mode decomposition and a random discriminative projectionextreme learning machine for multiple power quality disturbance recognition. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Li, J.; Teng, Z.; Tang, Q.; Song, J. Detection and classification of power quality disturbances using double resolution S-transform and DAG-SVMs. IEEE Trans. Instrum. Meas. 2016, 65, 2302–2312. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Samantaray, S.R.; Manikandan, M.S. Variational mode decomposition and decision tree based detection and classification of power quality disturbances in grid-connected distributed generation system. IEEE Trans. Smart Grid 2016, 9, 3122–3132. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M.; Romero-Troncoso, R.D.J.; Osornio-Rios, R.A.; Garcia-Perez, A. Detection and classification of single and combined power quality disturbances using neural networks. IEEE Trans. Ind. Electron. 2013, 61, 2473–2482. [Google Scholar] [CrossRef]
- Gaing, Z.L. Wavelet-based neural network for power disturbance recognition and classification. IEEE Trans. Power Deliv. 2004, 19, 1560–1568. [Google Scholar] [CrossRef]
- Wang, D.H.; Cui, C. Stochastic configuration networks ensemble with heterogeneous features for large-scale data analytics. Inf. Sci. 2017, 417, 55–71. [Google Scholar] [CrossRef]
- Wang, D.H.; Li, M. Deep stochastic configuration networks with universal approximation property. arXiv, 2017; arXiv:1702.05639. [Google Scholar]
- Wang, D.H.; Li, M. Stochastic configuration networks: Fundamentals and algorithms. IEEE Trans. Cybern. 2017, 47, 3466–3479. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Singh, B.; Shahani, D.T.; Chandra, A.; Al-Haddad, K. Recognition of power-quality disturbances using S-transform-based ANN classifier and rule-based decision tree. IEEE Trans. Ind. Appl. 2015, 51, 1249–1258. [Google Scholar] [CrossRef]
- Biswal, M.; Dash, P.K. Detection and characterization of multiple power quality disturbances with a fast S-transform and decision tree based classifier. Digit. Signal Process. 2013, 23, 1071–1083. [Google Scholar] [CrossRef]
- Masoum, M.A.S.; Jamali, S.; Ghaffarzadeh, N. Detection and classification of power quality disturbances using discrete wavelet transform and wavelet networks. IET Sci. Meas. Technol. 2010, 4, 193–205. [Google Scholar] [CrossRef]
- Biswal, M.; Dash, P.K. Measurement and classification of simultaneous power signal patterns with an S-transform variant and fuzzy decision tree. IEEE Trans. Ind. Inform. 2013, 9, 1819–1827. [Google Scholar] [CrossRef]
- He, S.; Li, K.; Zhang, M. A real-time power quality disturbances classification using hybrid method based on S-transform and dynamics. IEEE Trans. Instrum. Meas. 2013, 62, 2465–2475. [Google Scholar] [CrossRef]

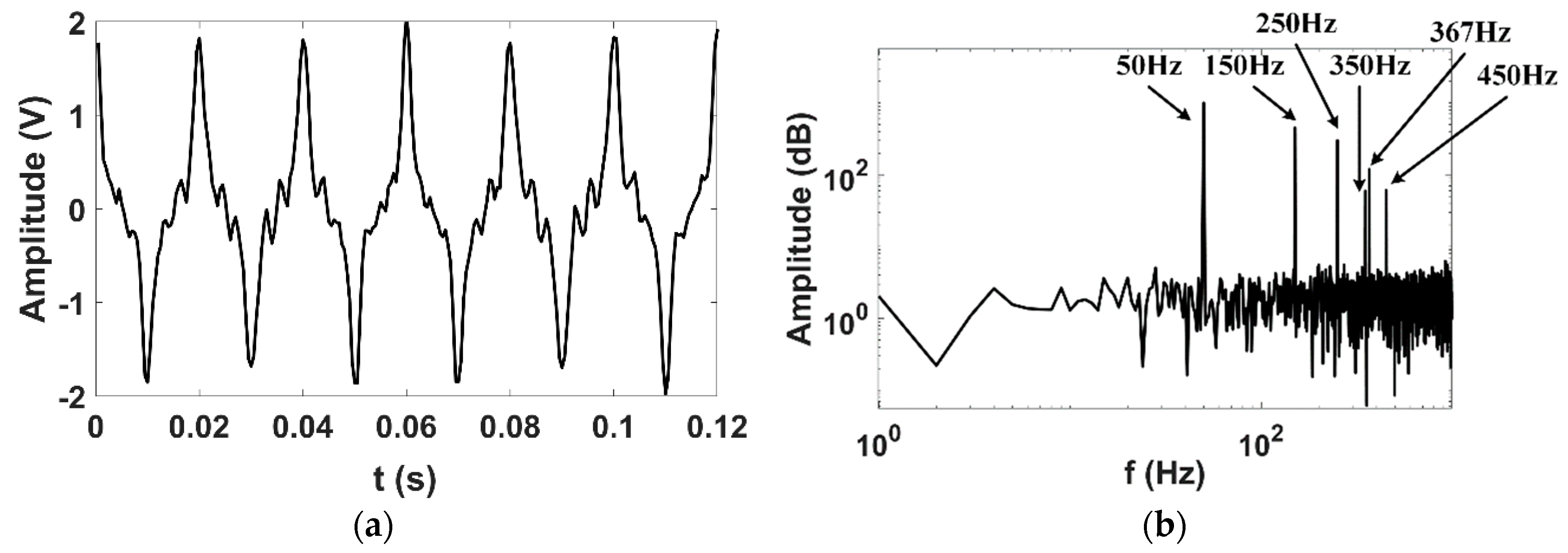
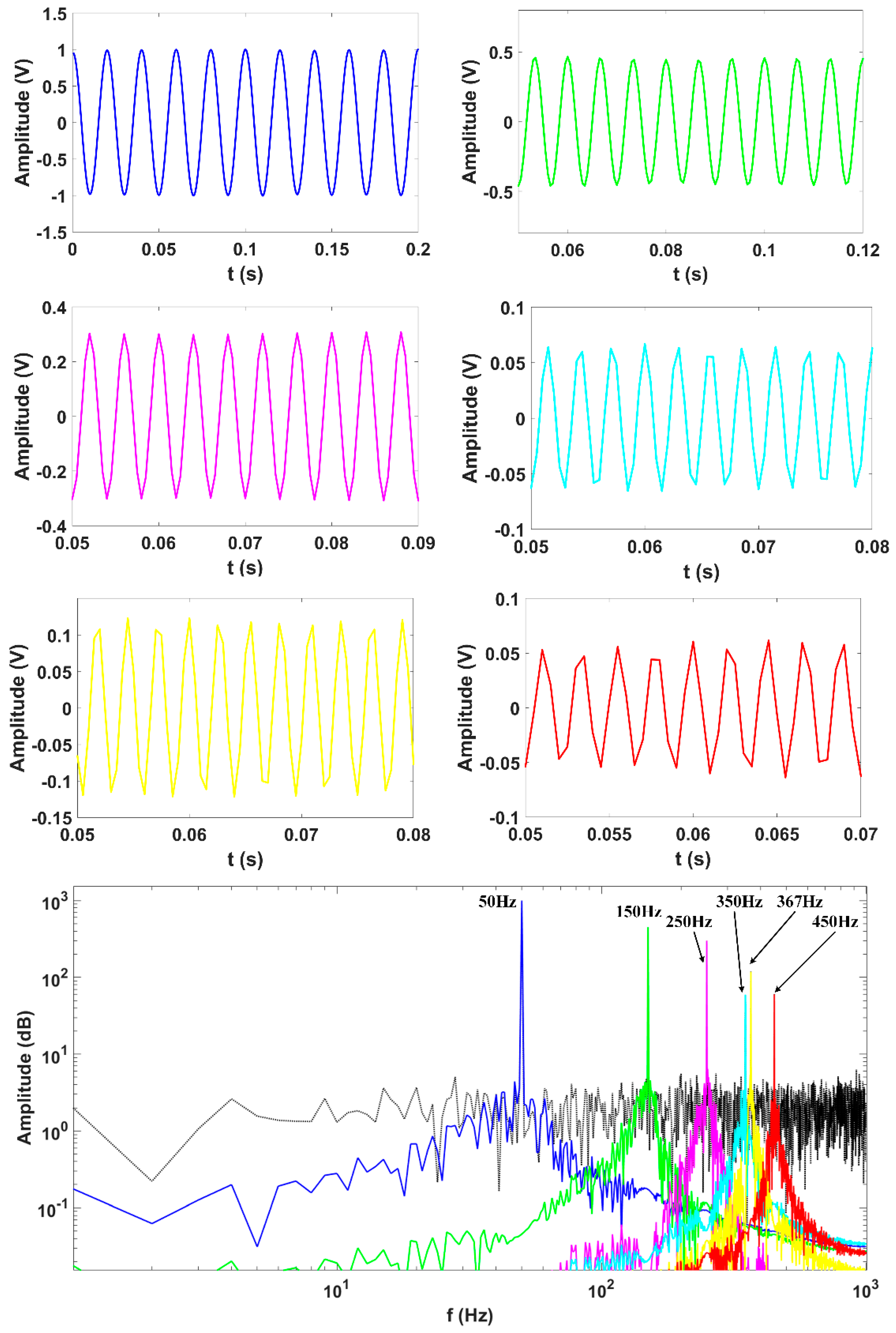


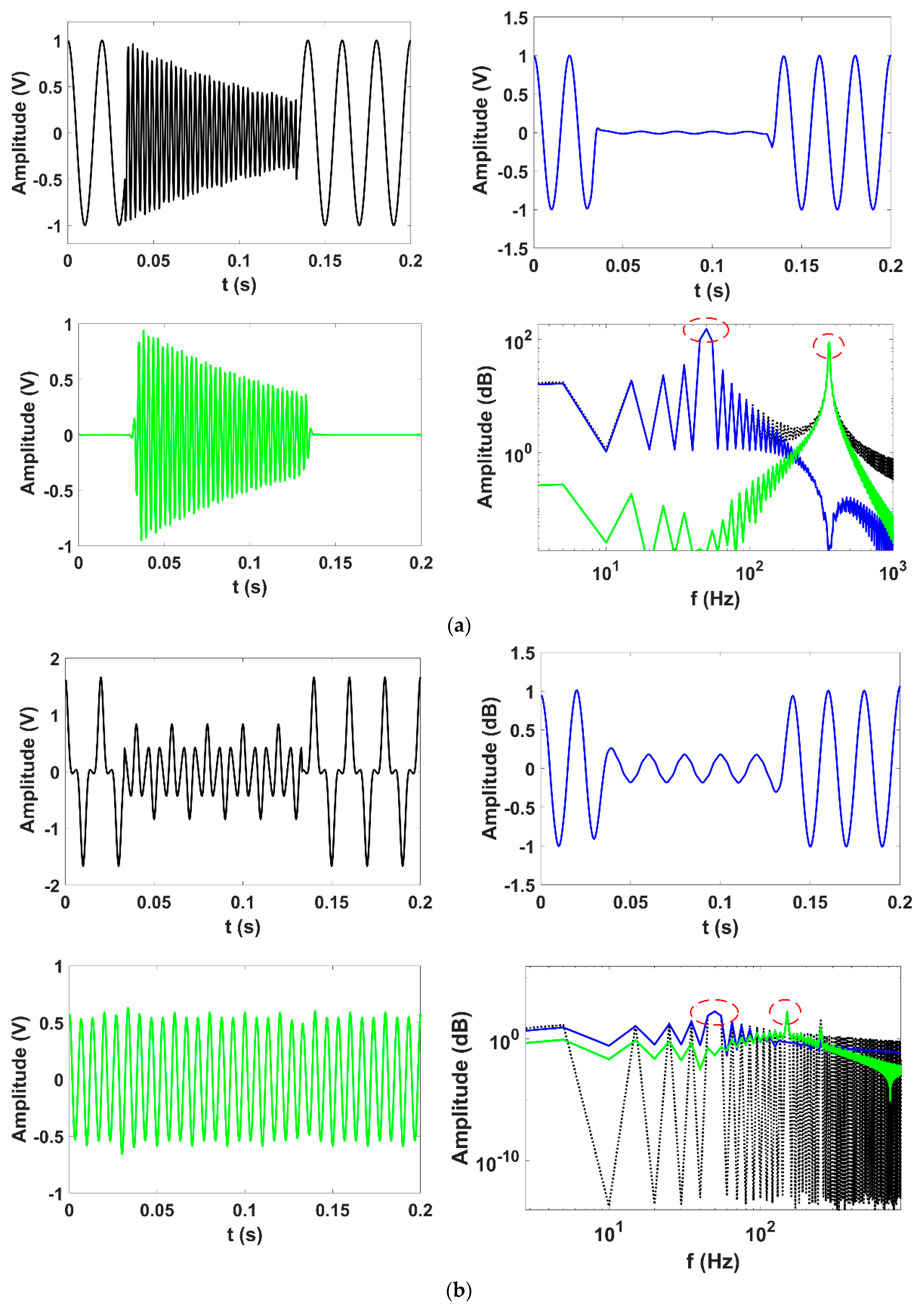
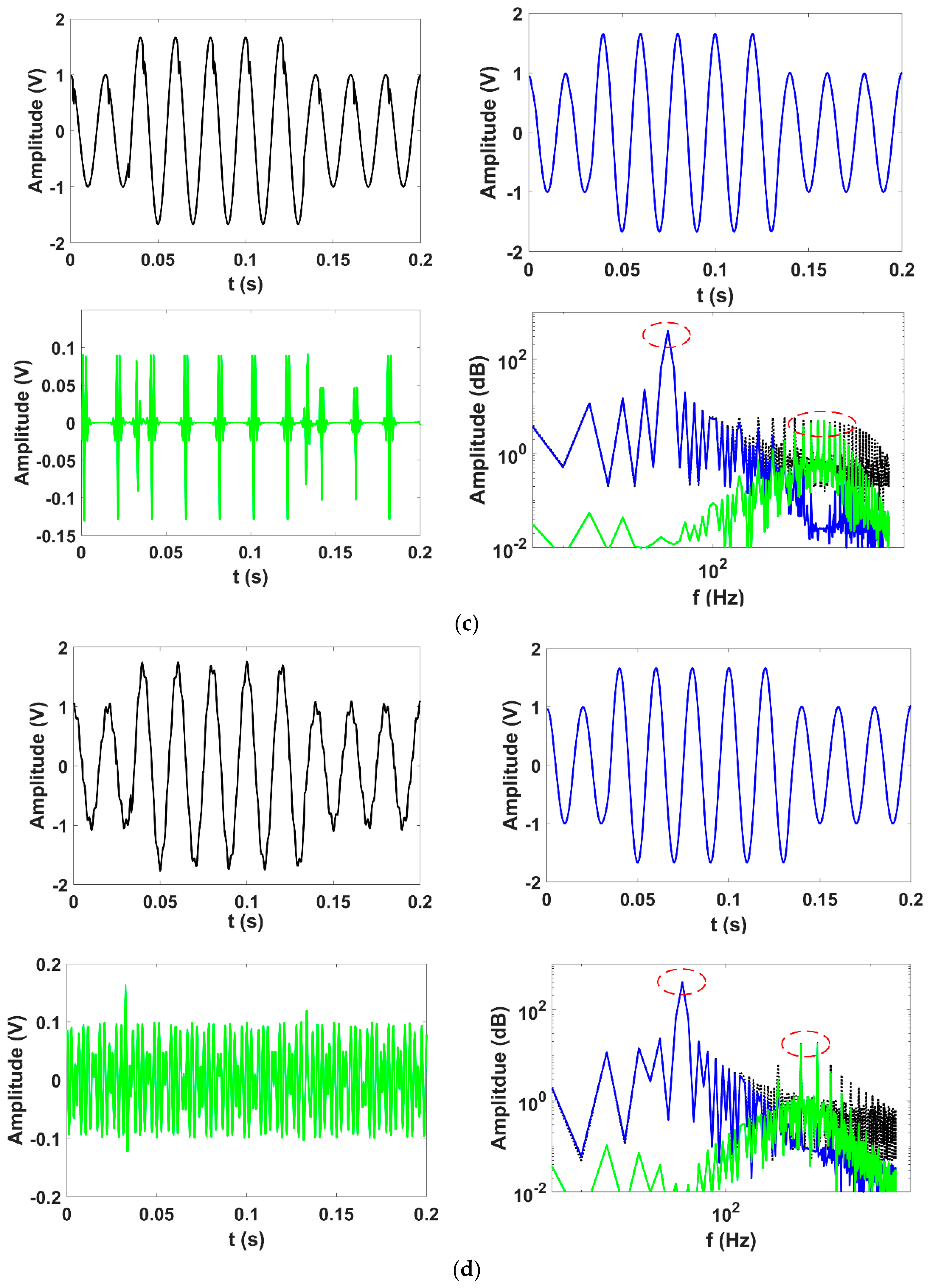
| Synthetic Signal | Results of VMD | ||
|---|---|---|---|
| Freq. (Hz) | Amp. (pu) | Freq. (Hz) | Amp. (pu) |
| 50 | 1 | 50.03 | 1.01 |
| 150 | 0.45 | 150.07 | 0.452 |
| 250 | 0.3 | 250 | 0.31 |
| 350 | 0.06 | 350.16 | 0.056 |
| 367 | 0.12 | 367.19 | 0.124 |
| 450 | 0.06 | 450.16 | 0.063 |
| Parameter | Synthetic Signal | Results of VMD |
|---|---|---|
| 1 | 0.999 | |
| (Hz) | 50 | 50.03 |
| 0.4 | 0.049 + 0.05 = 0.099 | |
| 41 | 41.02 | |
| 59 | 59.03 |
| Feature Extraction Method | Type of Classifier | No. of PQ Disturbance | Accuracy (%) | Ref. |
|---|---|---|---|---|
| EMD | Balanced Neural Tree | 8 | 97.9 | [20] |
| ST | NN+DT | 13 | 99.9 | [34] |
| Hybrid ST | DT | 11 | 94.36 | [35] |
| ADALINE | FNN | 12 | 90.58 | [29] |
| VMD | DSCN | 7 | 99.4 | Proposed method |
| PQ Disturbance | Wavelet Network [36] | Fuzzy & ST [37] | ADALINE & FFNN [29] | Dynamics & ST [38] | Proposed Method |
|---|---|---|---|---|---|
| Sag | 98.67% | 97.33% | 100% | 99% | 98% |
| Swell | 99.33% | 98.66% | 100% | 98% | 100% |
| Interruption | 98% | 96.66% | 100% | 96% | 100% |
| Harmonics | 99.33% | 100% | 98% | 99% | 98% |
| Oscillation | 98.67% | 94% | 98% | 99% | 100% |
| Notch | 97.33% | 96% | 97% | 98% | 100% |
| Spike | - | 100% | 97% | 97% | 100% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, K.; Alalibo, B.P.; Cao, W.; Liu, Z.; Wang, Z.; Li, G. Hybrid Approach for Detecting and Classifying Power Quality Disturbances Based on the Variational Mode Decomposition and Deep Stochastic Configuration Network. Energies 2018, 11, 3040. https://doi.org/10.3390/en11113040
Cai K, Alalibo BP, Cao W, Liu Z, Wang Z, Li G. Hybrid Approach for Detecting and Classifying Power Quality Disturbances Based on the Variational Mode Decomposition and Deep Stochastic Configuration Network. Energies. 2018; 11(11):3040. https://doi.org/10.3390/en11113040
Chicago/Turabian StyleCai, Kewei, Belema Prince Alalibo, Wenping Cao, Zheng Liu, Zhiqiang Wang, and Guofeng Li. 2018. "Hybrid Approach for Detecting and Classifying Power Quality Disturbances Based on the Variational Mode Decomposition and Deep Stochastic Configuration Network" Energies 11, no. 11: 3040. https://doi.org/10.3390/en11113040
APA StyleCai, K., Alalibo, B. P., Cao, W., Liu, Z., Wang, Z., & Li, G. (2018). Hybrid Approach for Detecting and Classifying Power Quality Disturbances Based on the Variational Mode Decomposition and Deep Stochastic Configuration Network. Energies, 11(11), 3040. https://doi.org/10.3390/en11113040






