Parallel Control Method Based on the Consensus Algorithm for the Non-Isolated AC/DC Charging Module
Abstract
1. Introduction
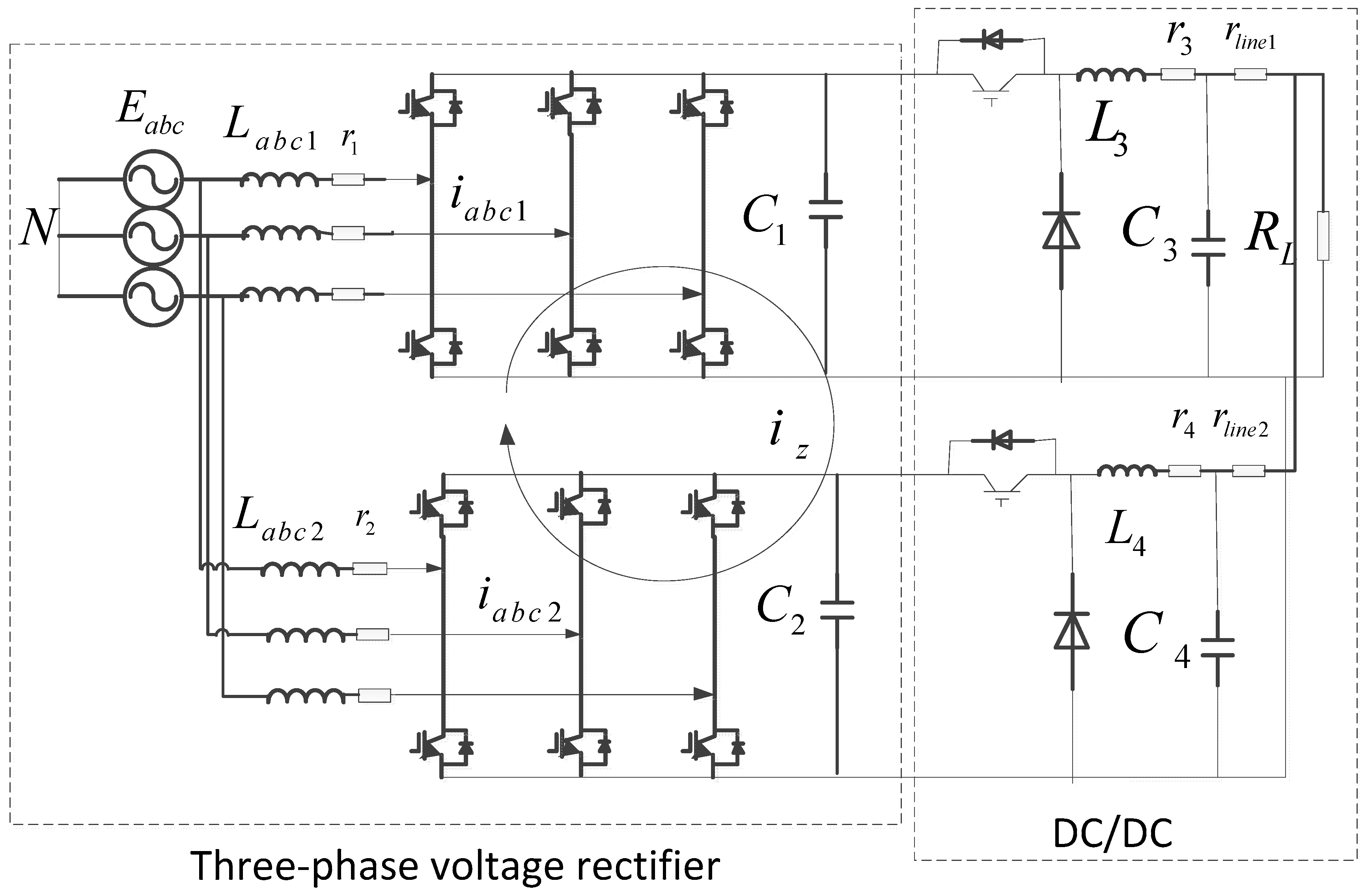
2. Parallel Connection of Non-Isolated AC/DC Charging Modules
2.1. Multi-Module Parallel Topology
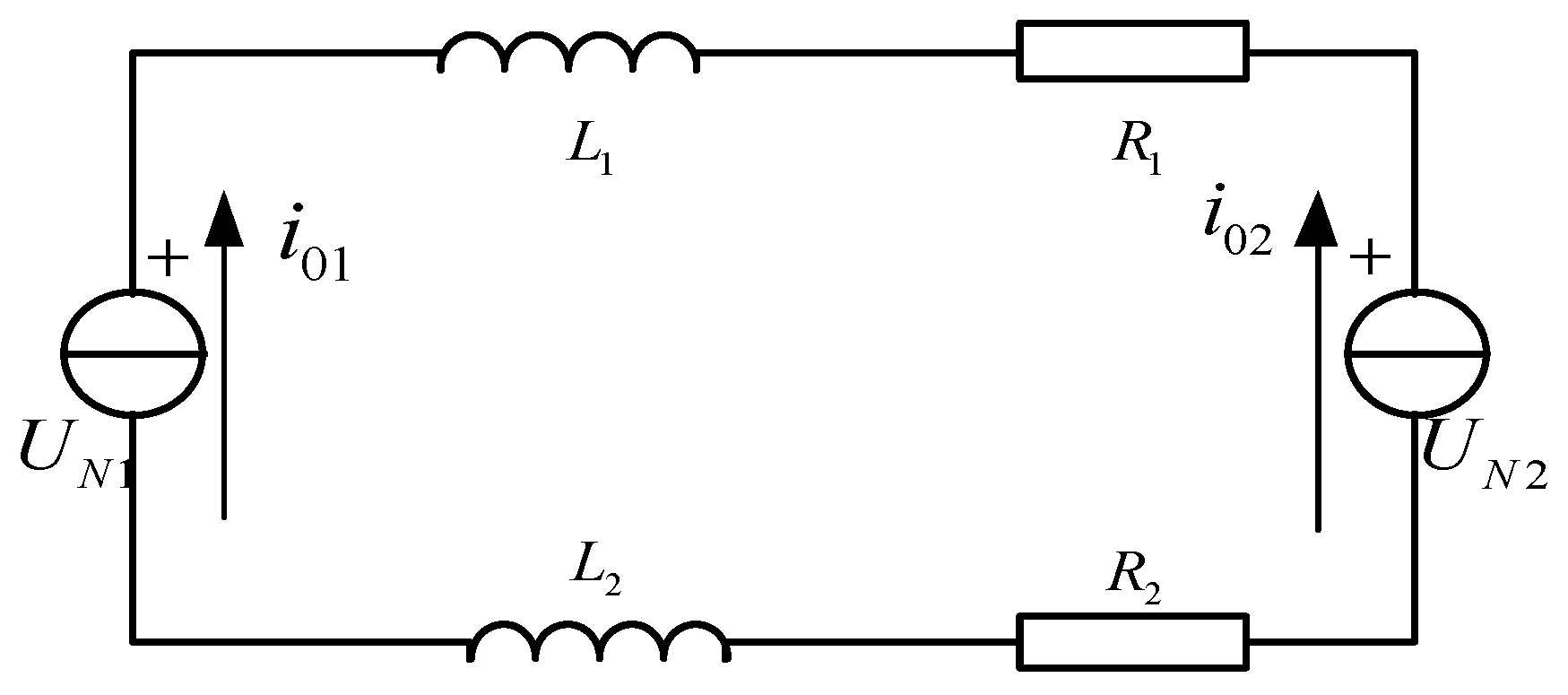
2.2. Mathematical Model Analysis of Zero-Sequence Circulation
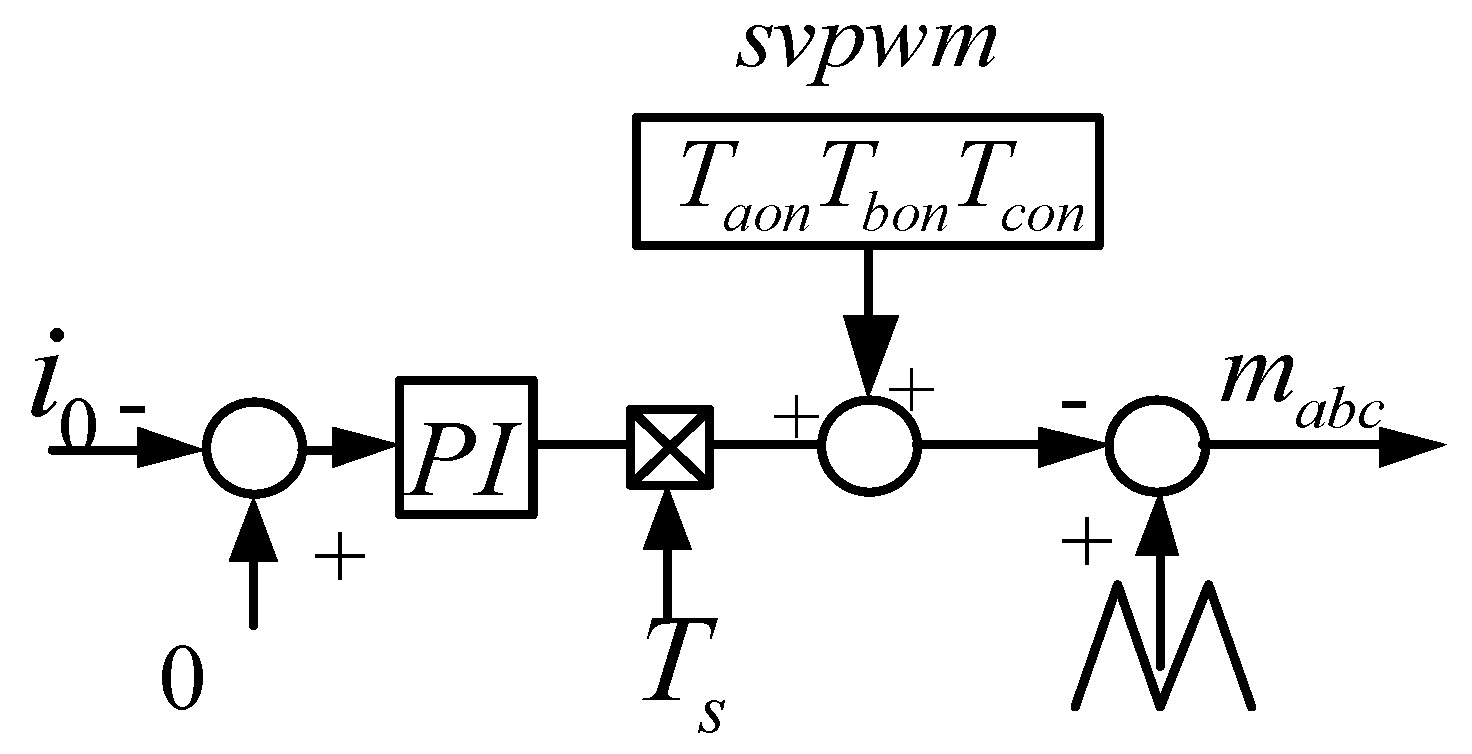
3. Improved SVPWM Suppression of Zero Sequence Circulation
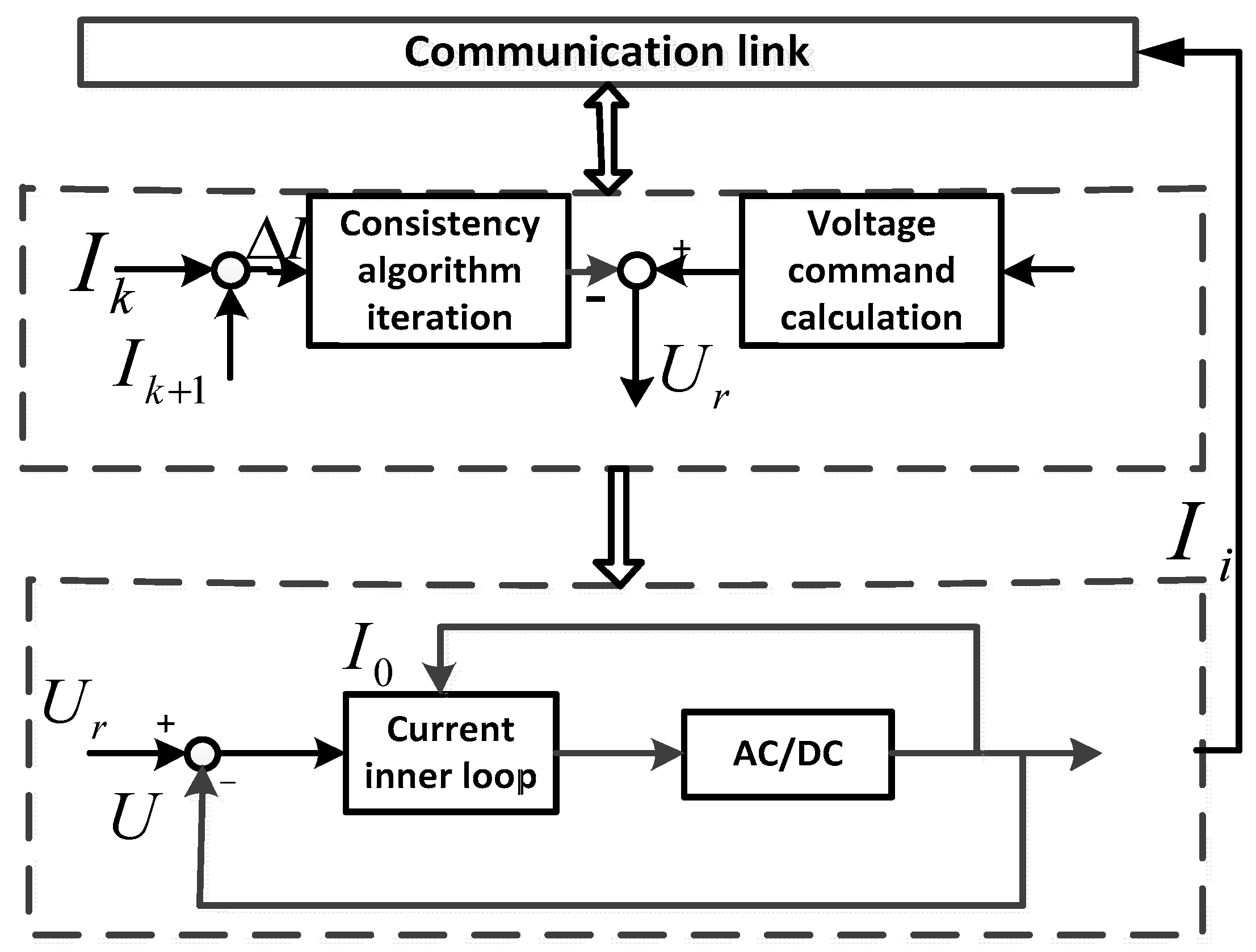
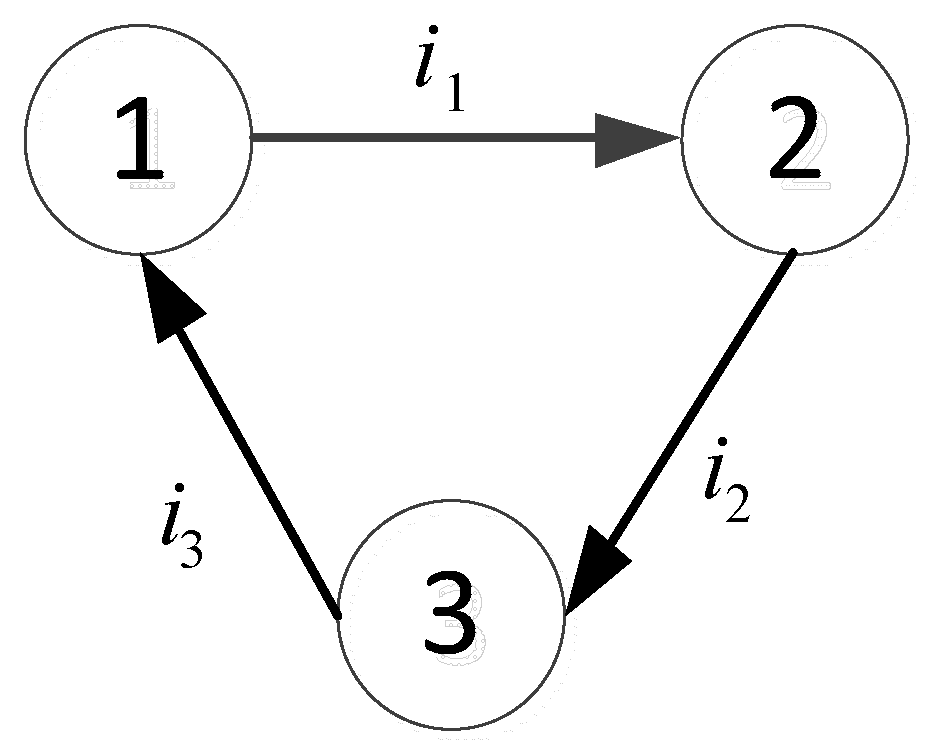
4. Consistency-Based Current Sharing Control
5. Simulation and Experiment
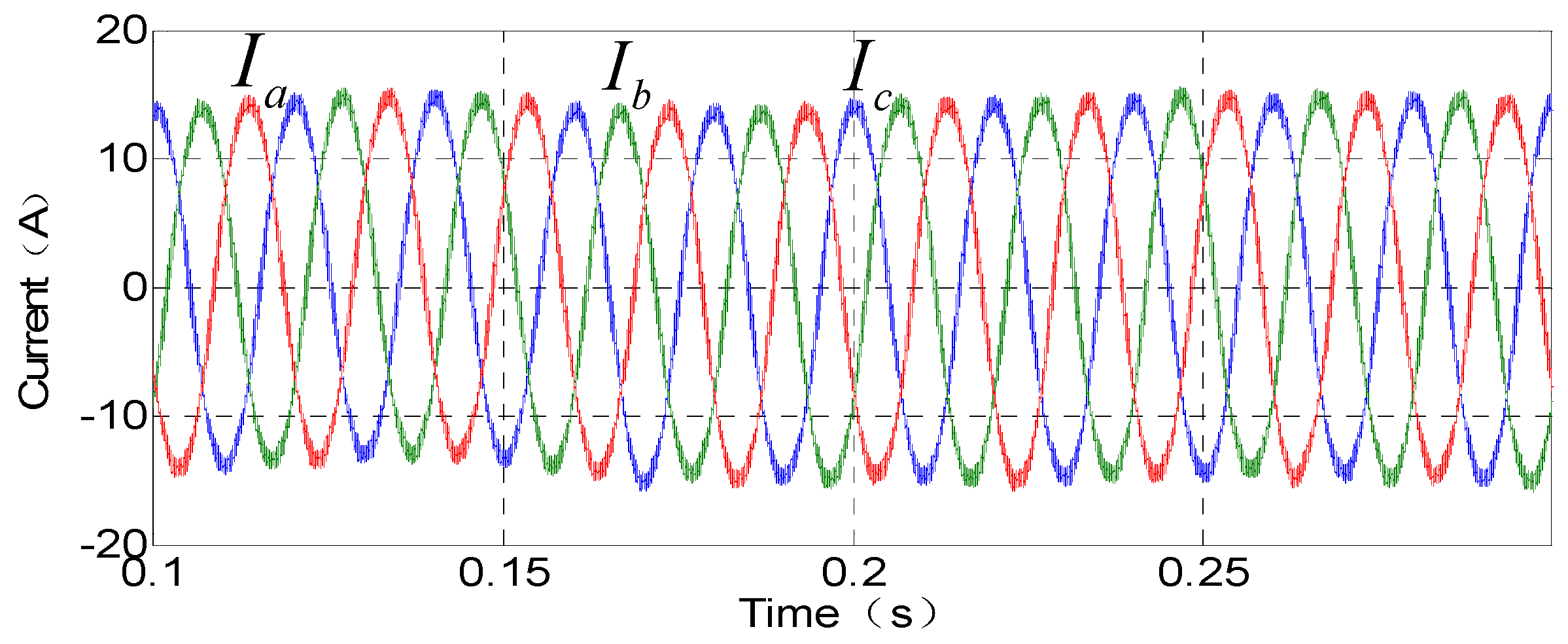
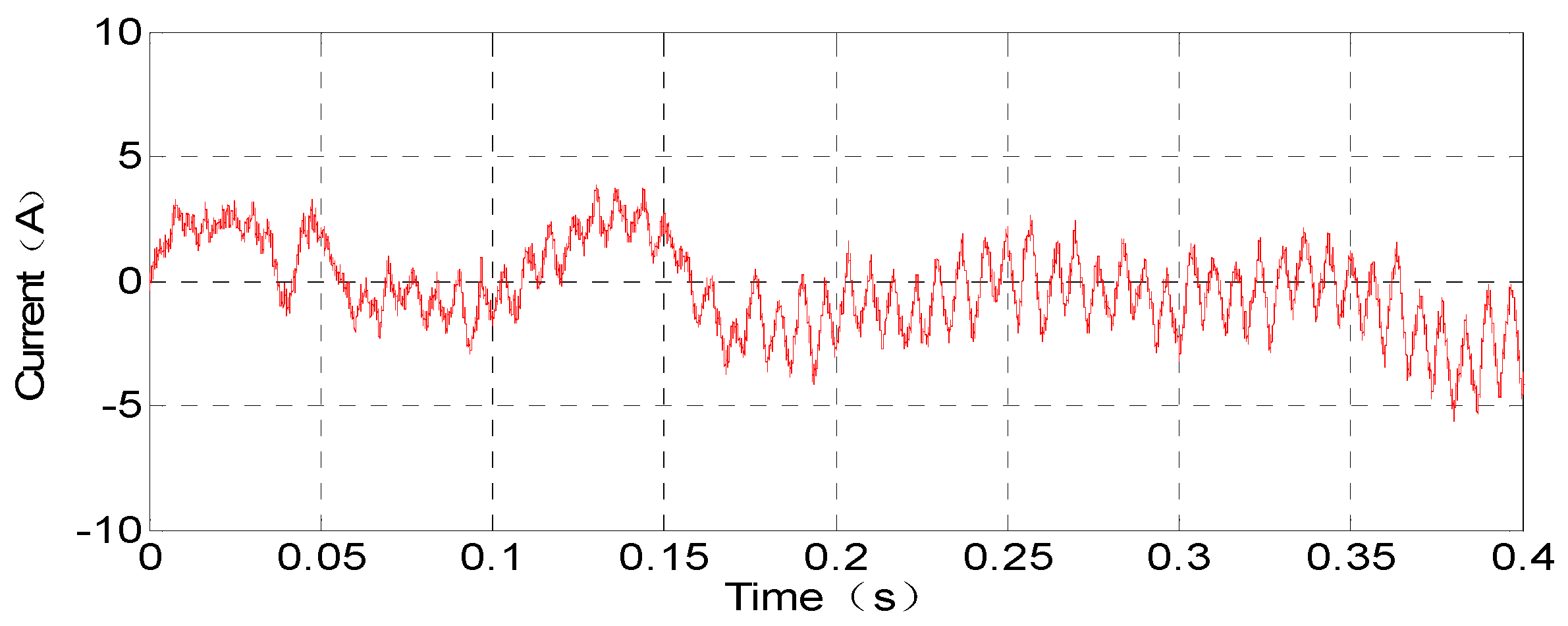
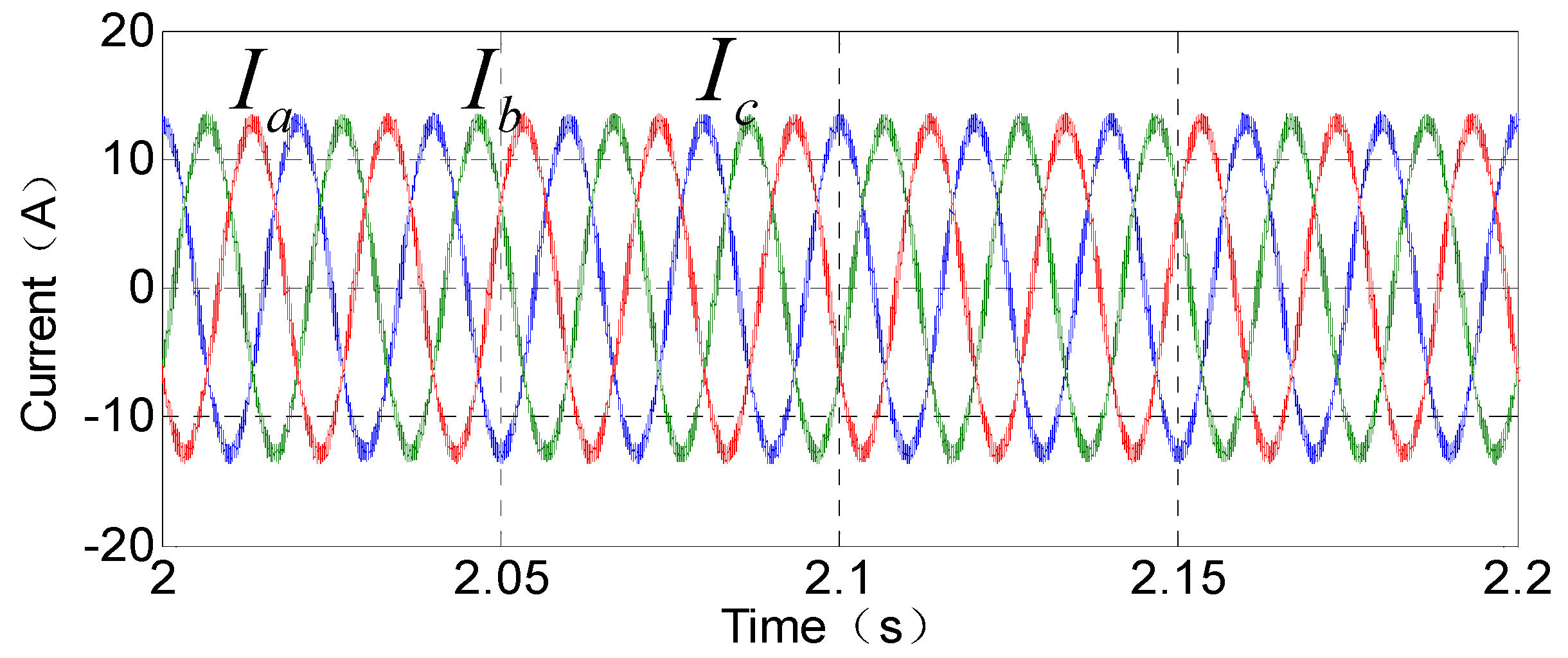
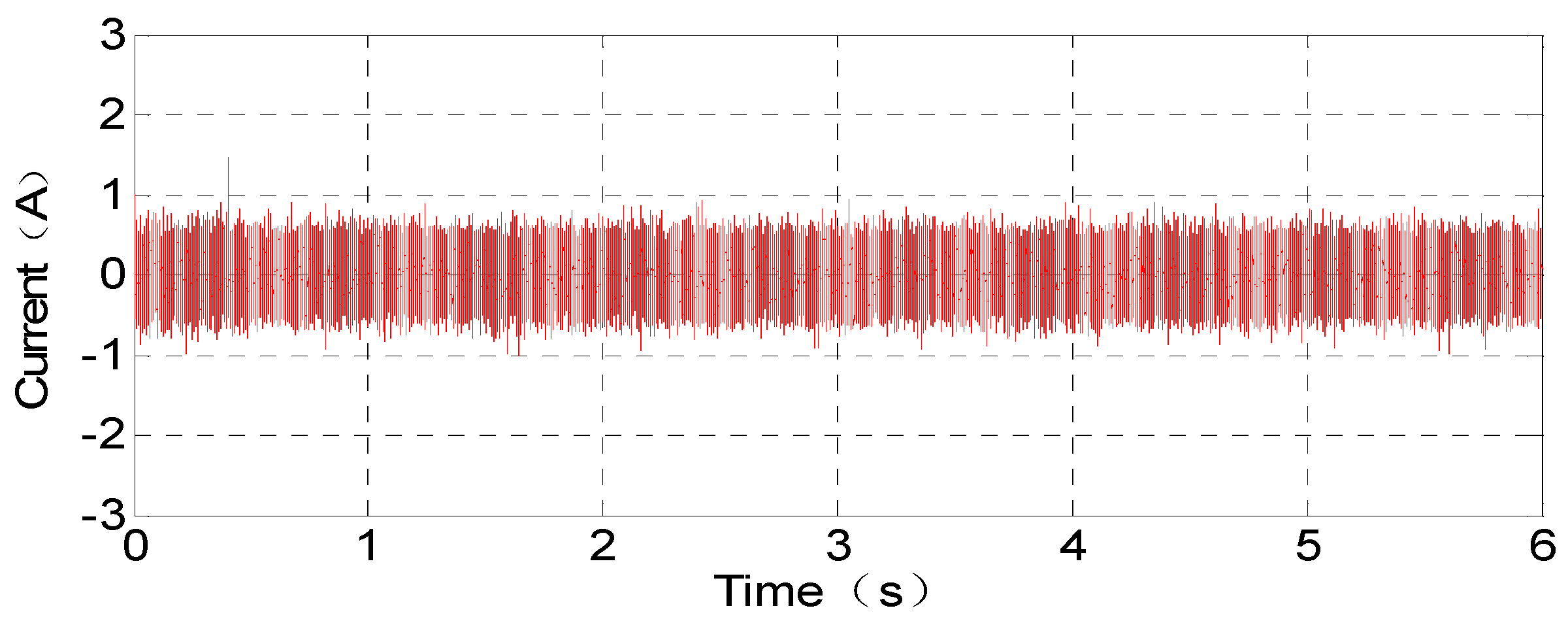
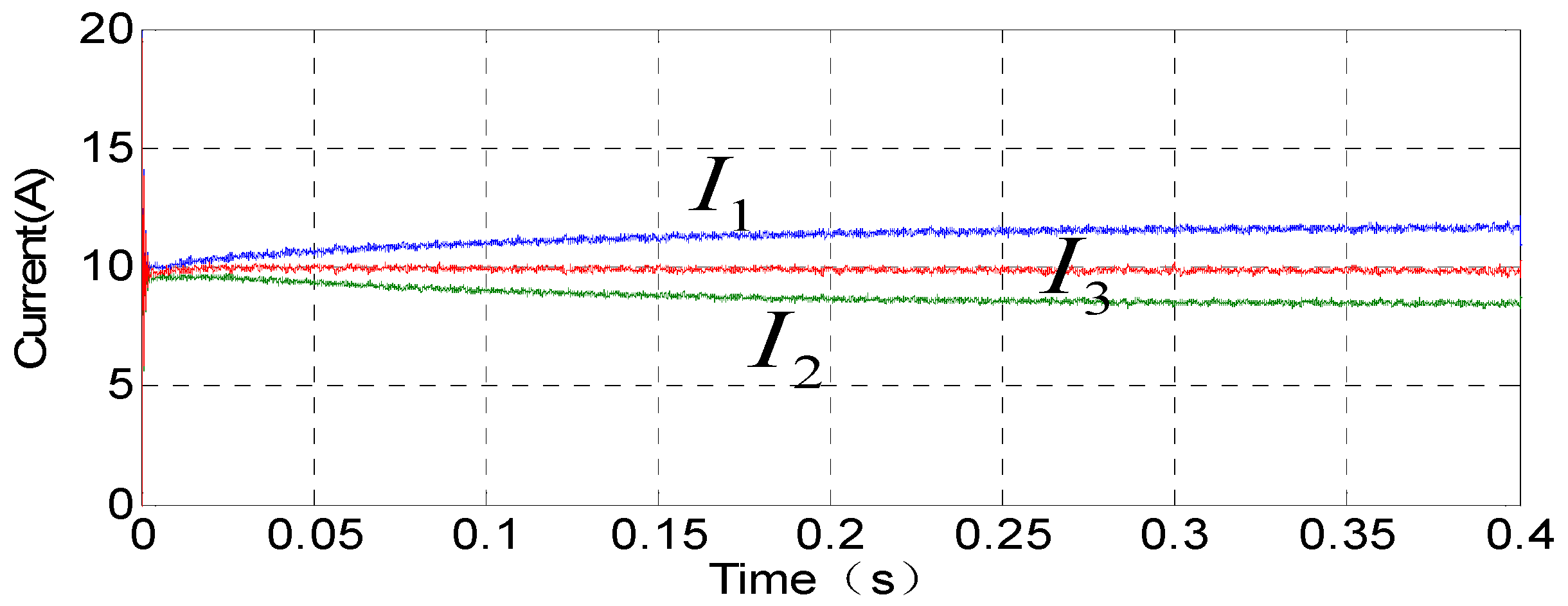
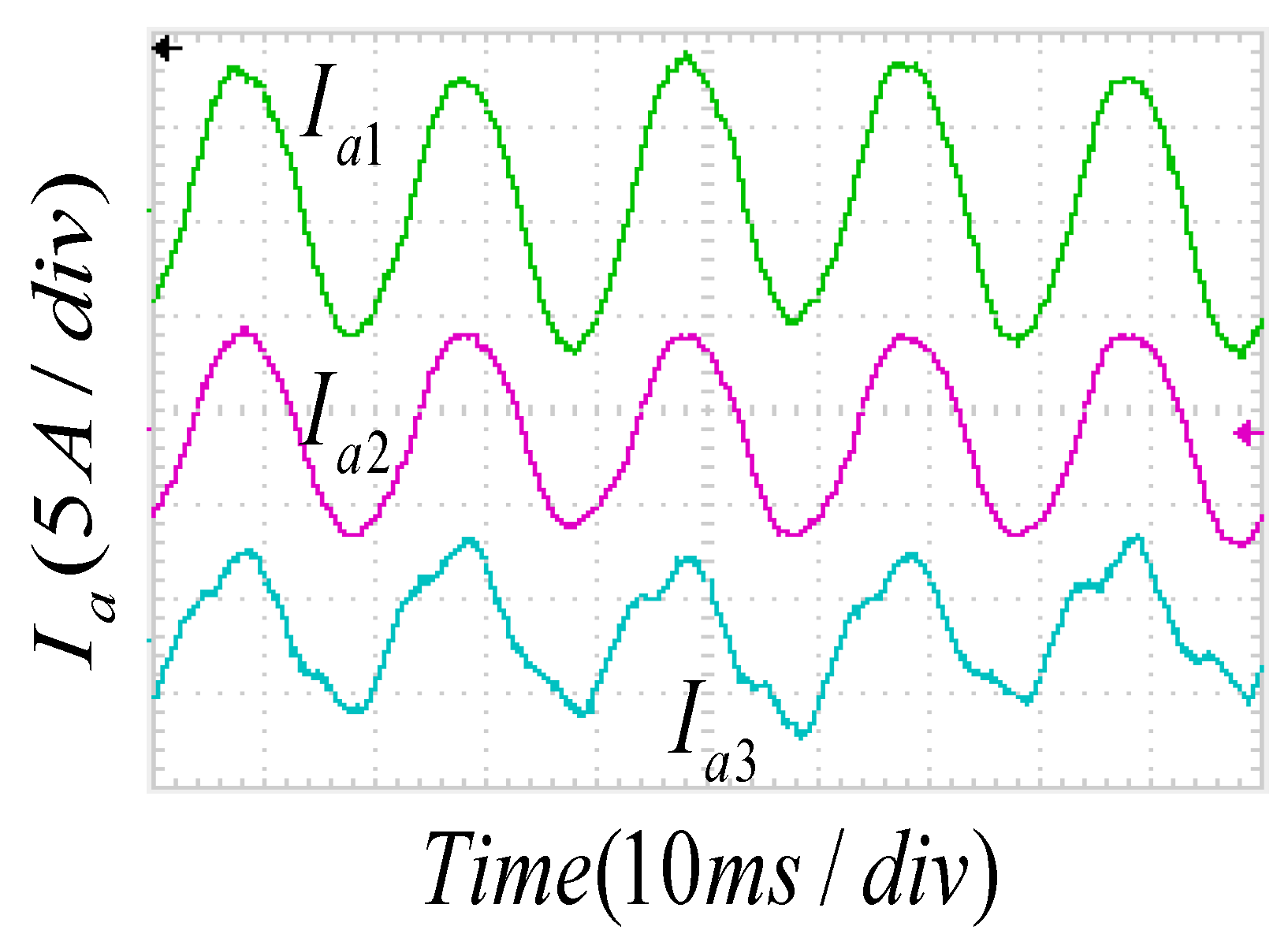
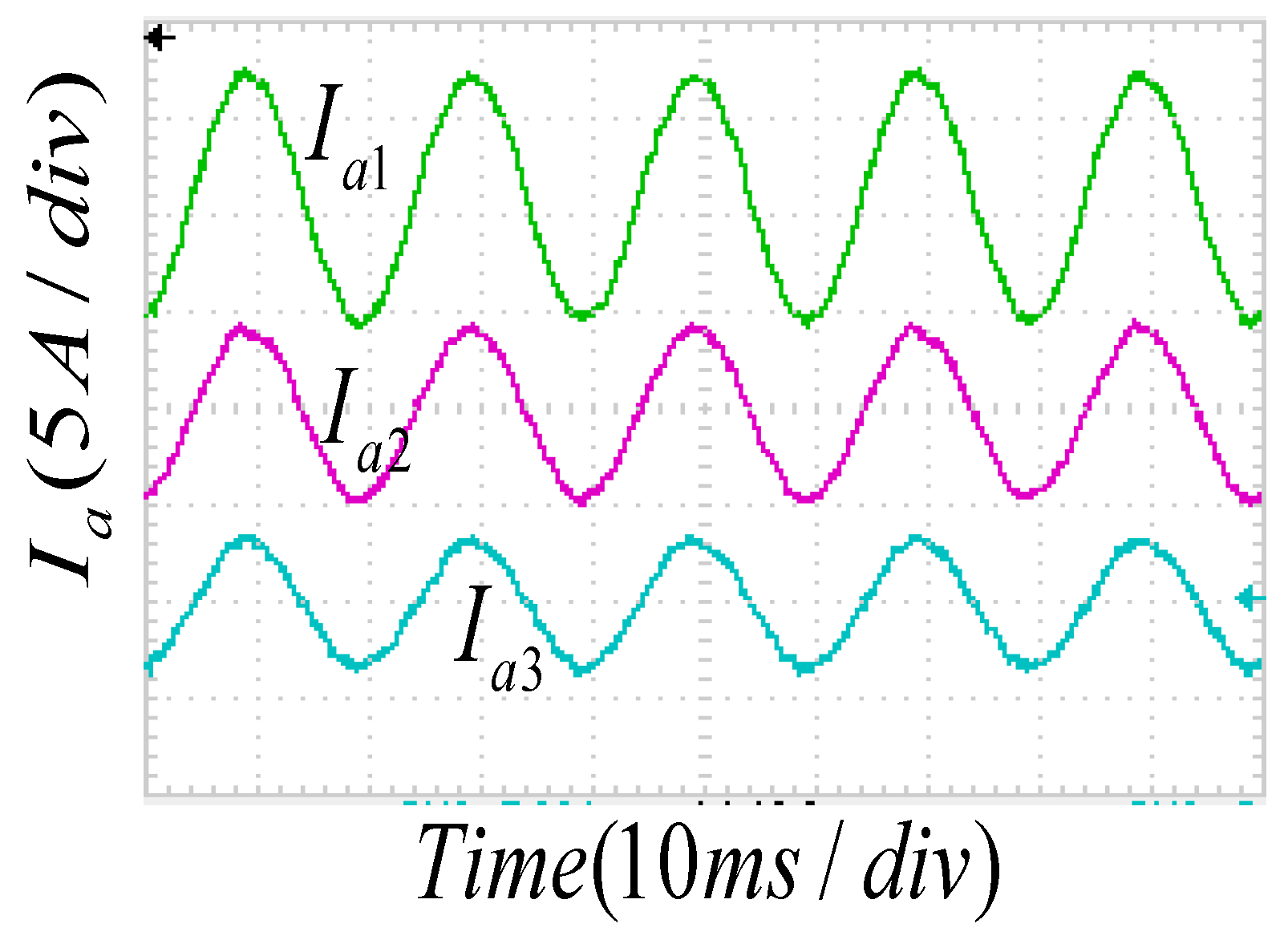
5.1. Zero-Sequence Circulation Suppression Simulation Results
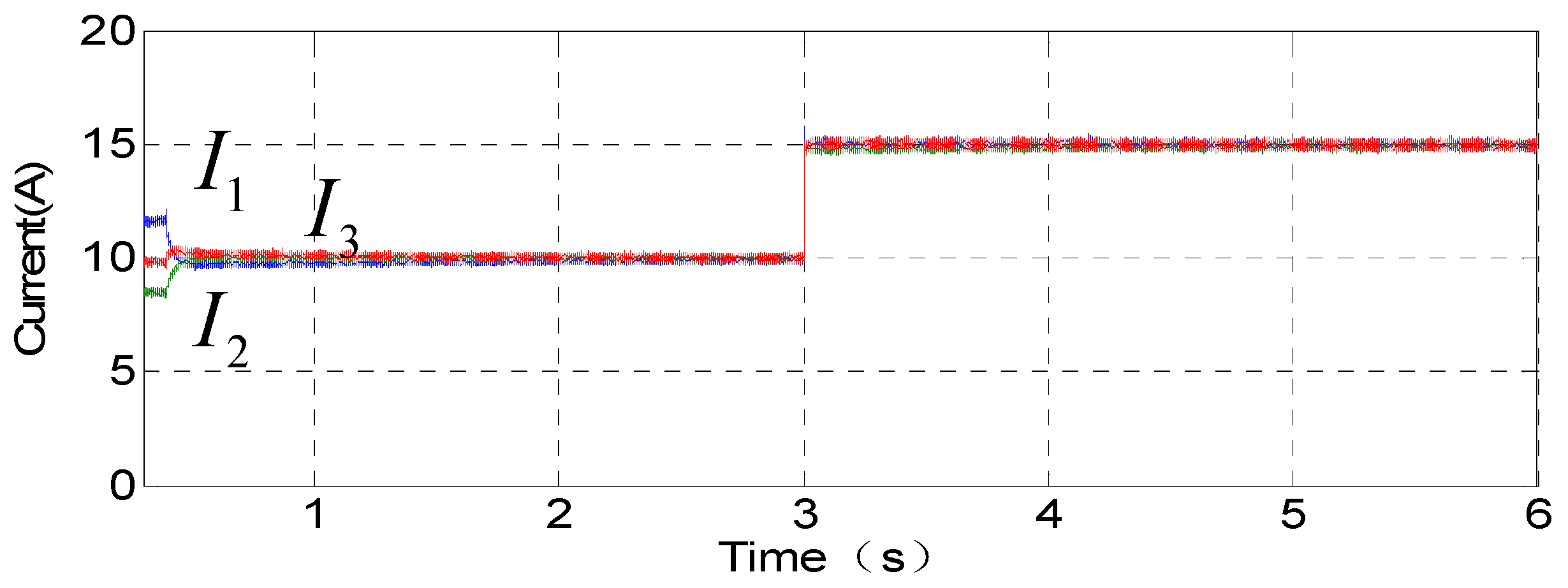
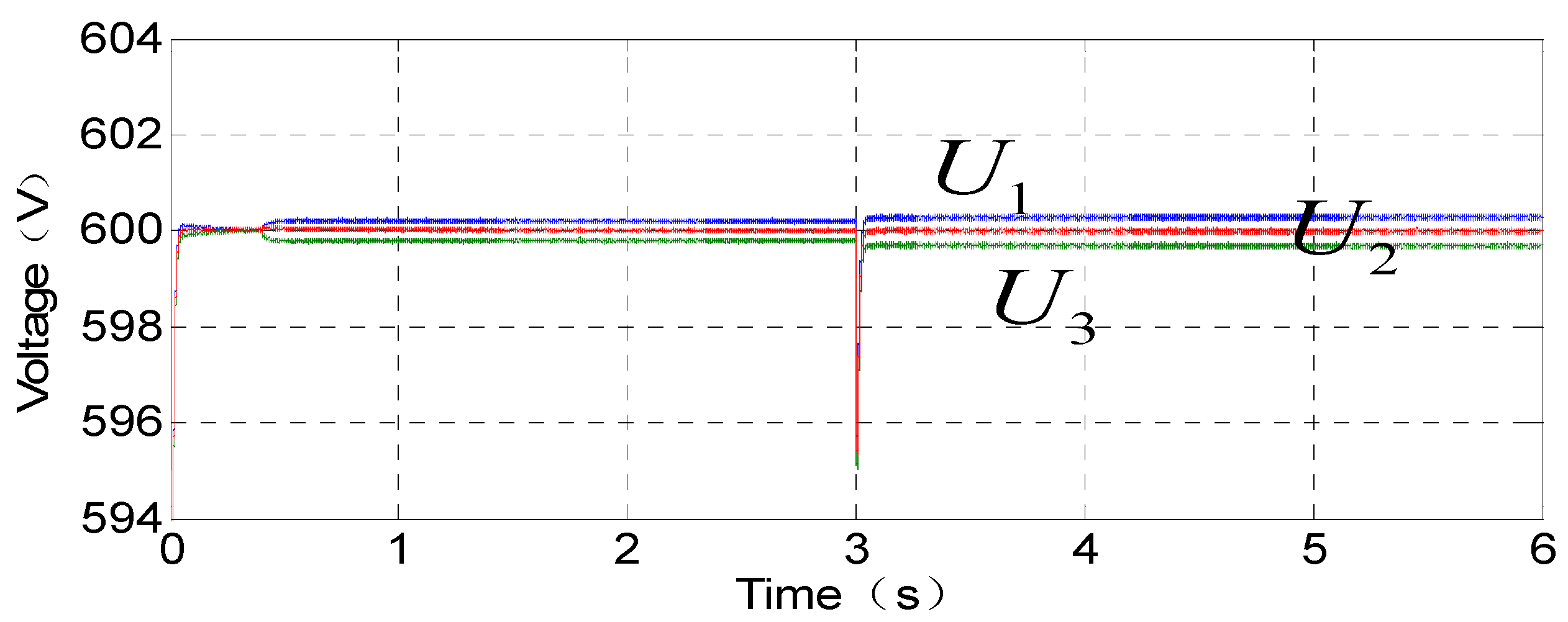
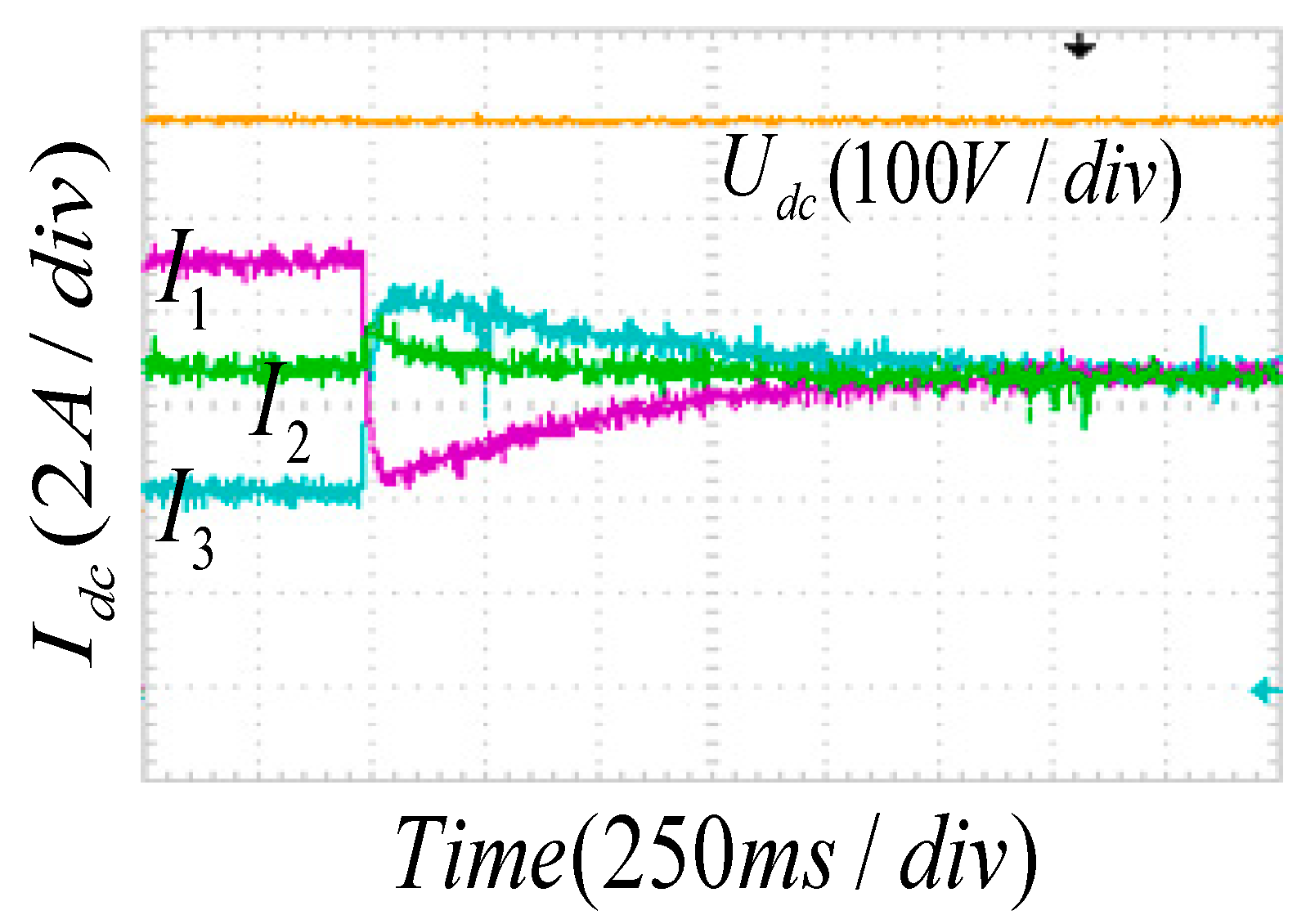
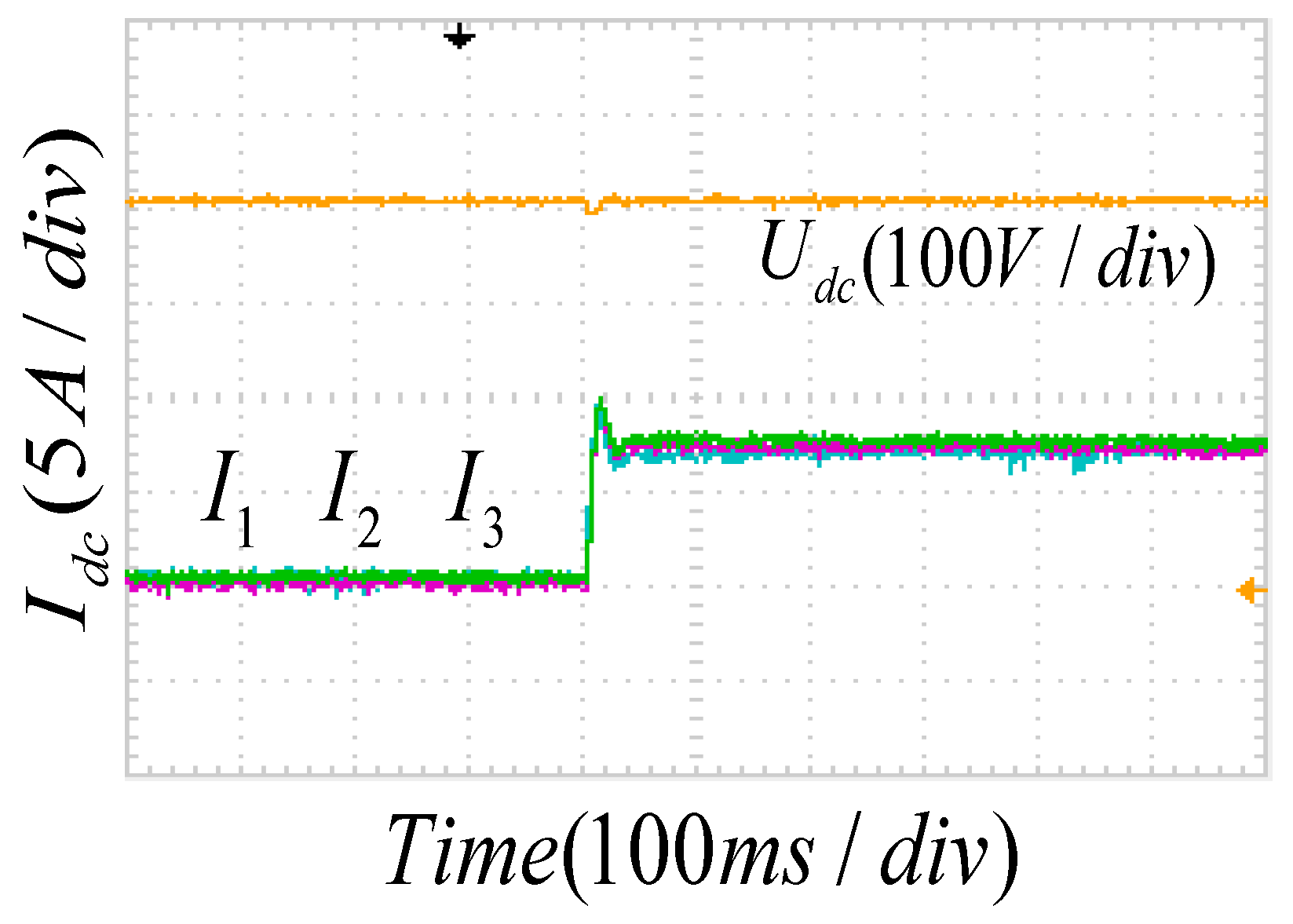
5.2. Current Sharing Simulation Results
6. Conclusions
- Only the zero-sequence circulation current is sampled for feedback control to inhibit circulation, which does not require complex calculation and no communication is required among modules, thus reducing the communication burden.
- Compared with the droop control method, the proposed current sharing control strategy can ensure the voltage accuracy while maintaining the current sharing accuracy.
- Compared with the master–slave control, the proposed current sharing control strategy has no master module or slave module, which greatly increases redundancy.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, X.G.; Wang, T.Y.; Wang, X.F.; Wang, G.L.; Chen, Z.; Xu, D.G. A Coordinate Control Strategy for Circulating Current Suppression in Multiparalleled Three-Phase Inverters. IEEE Trans. Ind. Electron. 2017, 64, 838–847. [Google Scholar] [CrossRef]
- Pan, C.T.; Liao, Y.H. Modeling and Control of Circulating Currents for Parallel Three-Phase Boost Rectifiers with Different Load Sharing. IEEE Trans. Ind. Electron. 2008, 55, 2776–2785. [Google Scholar]
- Chen, T.P. Circulating zero-sequence current control of parallel three-phase inverters. IEE Proc. Elec. Power Appl. 2006, 153, 282–288. [Google Scholar] [CrossRef]
- Komatsuzaki, Y. Cross current control for parallel operating three phase inverter. In Proceedings of the 1994 Power Electronics Specialist Conference-PESC’94 Record, Taipei, Taiwan, 20–25 June 1994; pp. 943–950. [Google Scholar]
- Zhang, Z.C.; Ooi, B.T. Multimodular current-source SPWM converters for superconducting a magnetic energy storage system. IEEE Trans. Power Electron. 1993, 8, 250–256. [Google Scholar] [CrossRef]
- Ge, B.G.; Lu, X.; Yu, X.H.; Zhan, M.S.; Peng, F.Z. Multiphase-Leg Coupling Current Balancer for Parallel Operation of Multiple MW Power Modules. IEEE Trans. Ind. Electron. 2014, 61, 1147–1157. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Z.Q.; Chen, Q.H. Research and simulation of circulation current control for grid tied inverters connected in parallel. In Proceedings of the Chinese Control and Decision Conference (CCDC) IEEE Conferences, Yinchuan, China, 28–30 May 2016; pp. 6036–6041. [Google Scholar]
- Ye, Z.H.; Boroyevich, D.; Choi, J.Y.; Lee, F.C. Control of circulating current in two parallel three-phase boost rectifiers. IEEE Trans. Power Electron. 2002, 17, 609–615. [Google Scholar]
- Xing, K.; Mazumder, S.K.; Ye, Z.; Lee, F.C.; Boroyevich, D. The circulating current in paralleled three-phase boost PFC rectifiers. In Proceedings of the PESC 98 Record, 29th Annual IEEE Power Electronics Specialists Conference (Cat. No.98CH36196), Fukuoka, Japan, 22 May 1998; pp. 783–789. [Google Scholar]
- Hou, C.C. A multicarrier PWM for parallel three-phase active front-end converters. IEEE Trans. Power Electron. 2013, 28, 2753–2759. [Google Scholar] [CrossRef]
- Wang, X.H.; Thu, T.; Hoang, G. Fractional-Order Modelling and Control for Two Parallel PWM Rectifiers. 2018 International Federation of Automatic Control. Available online: http://folk.ntnu.no/skoge/prost/proceedings/PID-2018/0004.PDF (accessed on 16 October 2018).
- Mazumder, S.K. A novel discrete control strategy for independent stabilization of parallel three-phase boost converters by combining spacevector modulation with variable-structure control. IEEE Trans. Power Electron. 2003, 18, 1070–1083. [Google Scholar] [CrossRef]
- Mazumder, S.K.; Acharya, K.; Tahir, M. Joint optimization of control performance and network resource utilization in homogeneous power networks. IEEE Trans. Ind. Electron. 2009, 56, 1736–1745. [Google Scholar] [CrossRef]
- Mazumder, S.K. Continuous and discrete variable-structure controls for parallel three-phase boost rectifier. IEEE Trans. Ind. Electron. 2005, 52, 340–354. [Google Scholar] [CrossRef]
- Meng, L.X.; Dragicevic, T.; Guerrero, J.M.; Vasquez, J.C.; Vasquez, J.C. Dynamic consensus algorithm base distributed global efficiency optimization of a droop controlled DC microgrid. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 1276–1283. [Google Scholar]
- Li, Y.; Fan, L.L. Stability Analysis of Two Parallel Converters with Voltage–Current Droop Control. IEEE Trans. Power Deliv. 2017, 32, 2389–2397. [Google Scholar] [CrossRef]
- Yang, J.; Jin, X.M.; Wu, X.Z.; Acuna, P.; Aguilera, R.P.; Morstyn, T.; Agelidis, V.G. Decentralised control method for DC microgrids with improved current sharing accuracy. IET Gener. Transm. Distrib. 2017, 11, 696–706. [Google Scholar] [CrossRef]
- Ao, J.H.; Wang, Z.; Chen, J.; Peng, L.; Chen, Y. The Cost-Efficient Gating Drivers with Master-Slave Current Sharing Control for Parallel SiC MOSFETs. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Bangkok, Thailand, 6–9 June 2018; pp. 1–5. [Google Scholar]
- Borrega, M.; Marroyo, L.; González, R.; Balda, J.L.; Agorreta, J.L. Modeling and Control of a Master–Slave PV Inverter With N-Paralleled Inverters and Three-Phase Three-Limb InductorsMikel Borrega. IEEE Trans. Power Electron. 2013, 28, 2842–2855. [Google Scholar] [CrossRef]
- Li, Q.-Q.; Liu, S.-L.; Xu, H.-S. Research on the maximum current automatic current-sharing control based on DSP. In Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA), Macau, China, 18–20 July 2017; pp. 1044–1049. [Google Scholar]
- Xiong, L.S.; Zhuo, F.; Wang, F.; Liu, X.K.; Chen, Y.; Zhu, M.H. Static Synchronous Generator Model: A New Perspective to Investigate Dynamic Characteristics and Stability Issues of Grid-tied PWM Inverter. IEEE Trans. Power Electron. 2016, 31, 6264–6280. [Google Scholar] [CrossRef]
- Zhang, H.G.; Kim, S.; Sun, Q.Y.; Zhou, J.G. Distributed adaptive virtual impedance control for accurate reactive power sharing based on consensus control in microgrids. IEEE Trans. Smart Grid. 2017, 8, 1749–1761. [Google Scholar] [CrossRef]
- Guo, F.H.; Wen, C.Y.; Mao, J.F.; Song, Y.D. Distributed secondary voltage and frequency restoration control of droop-controlled inverter-based microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4355–4364. [Google Scholar] [CrossRef]
- Schiffer, J.; Seel, T.; Raisch, J.; Sezi, T. Voltage Stability and Reactive Power Sharing in Inverter-Based Microgrids With Consensus-Based Distributed Voltage Control. IEEE Trans. Control Syst. Technol. 2016, 24, 96–109. [Google Scholar] [CrossRef]

| Grid line voltage | 380 |
| Grid frequency | 50 |
| Pre-stage rectifier inductor | 4 mH |
| Pre-stage rectifier capacitor | 3000 uF |
| Output DC voltage | 800 V |
| Post-buck circuit inductance | 6 mH |
| Post-buck circuit capacitor | 2 mF |
| The output voltage | 600 V |
| Load impedance | 20 Ω |
| Module 1 line impedance | 0.1 Ω |
| Module 2 line impedance | 0.14 Ω |
| Module 3 line impedance | 0.12 Ω |
| Zero axis Kp | 0.04 |
| Zero axis Ki | 0.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Wang, T.; Xiong, L.; Zhang, G.; Qian, X. Parallel Control Method Based on the Consensus Algorithm for the Non-Isolated AC/DC Charging Module. Energies 2018, 11, 2828. https://doi.org/10.3390/en11102828
Zhu Y, Wang T, Xiong L, Zhang G, Qian X. Parallel Control Method Based on the Consensus Algorithm for the Non-Isolated AC/DC Charging Module. Energies. 2018; 11(10):2828. https://doi.org/10.3390/en11102828
Chicago/Turabian StyleZhu, Yixin, Tao Wang, Liansong Xiong, Gaofeng Zhang, and Xin Qian. 2018. "Parallel Control Method Based on the Consensus Algorithm for the Non-Isolated AC/DC Charging Module" Energies 11, no. 10: 2828. https://doi.org/10.3390/en11102828
APA StyleZhu, Y., Wang, T., Xiong, L., Zhang, G., & Qian, X. (2018). Parallel Control Method Based on the Consensus Algorithm for the Non-Isolated AC/DC Charging Module. Energies, 11(10), 2828. https://doi.org/10.3390/en11102828




