A Novel Approach to Investigating Transport of Lost Circulation Materials in Rough Fracture
Abstract
:1. Introduction
2. Methodology
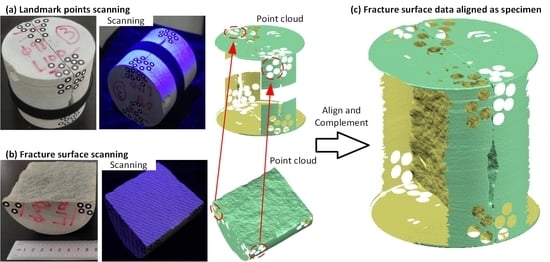
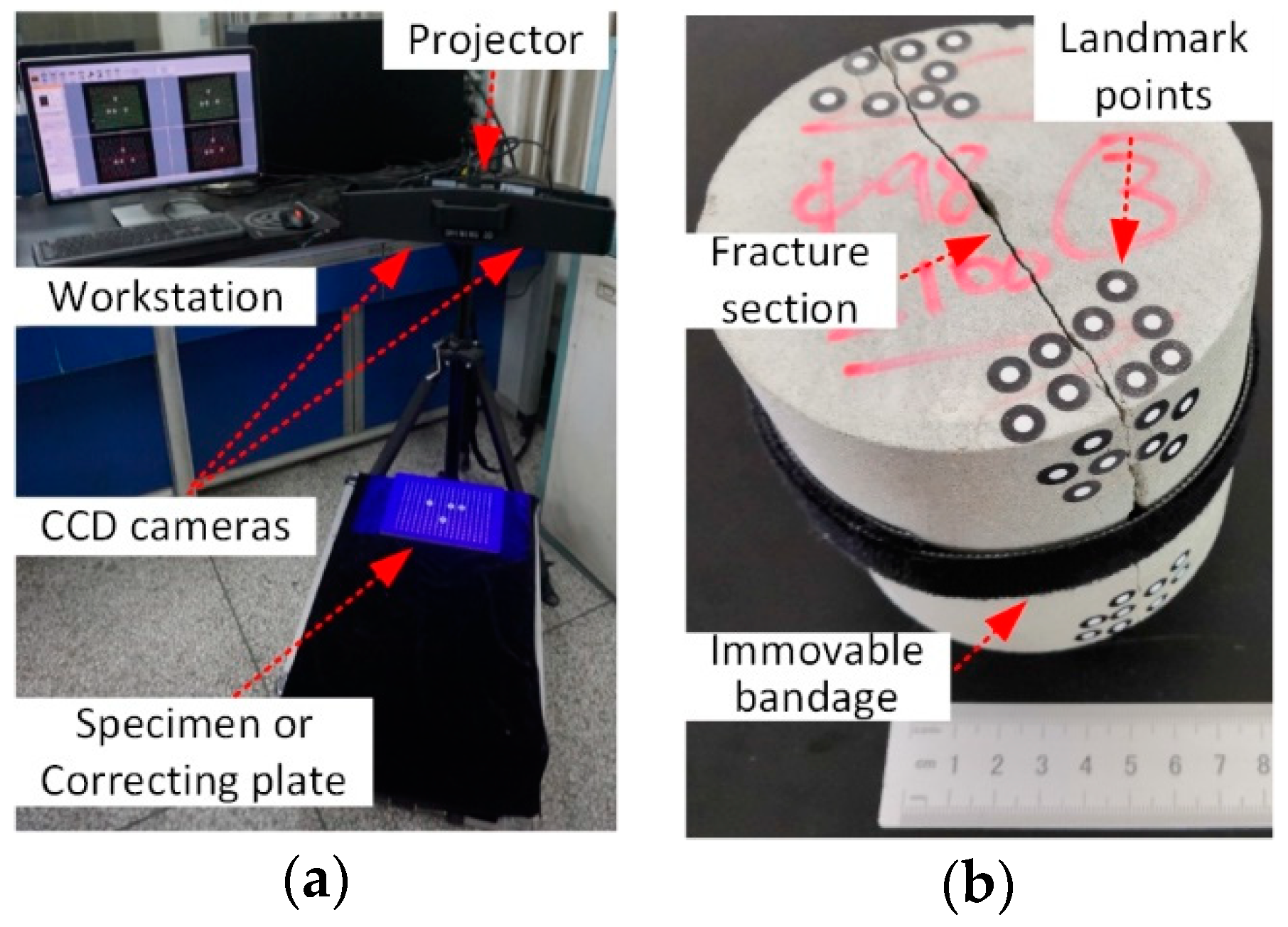
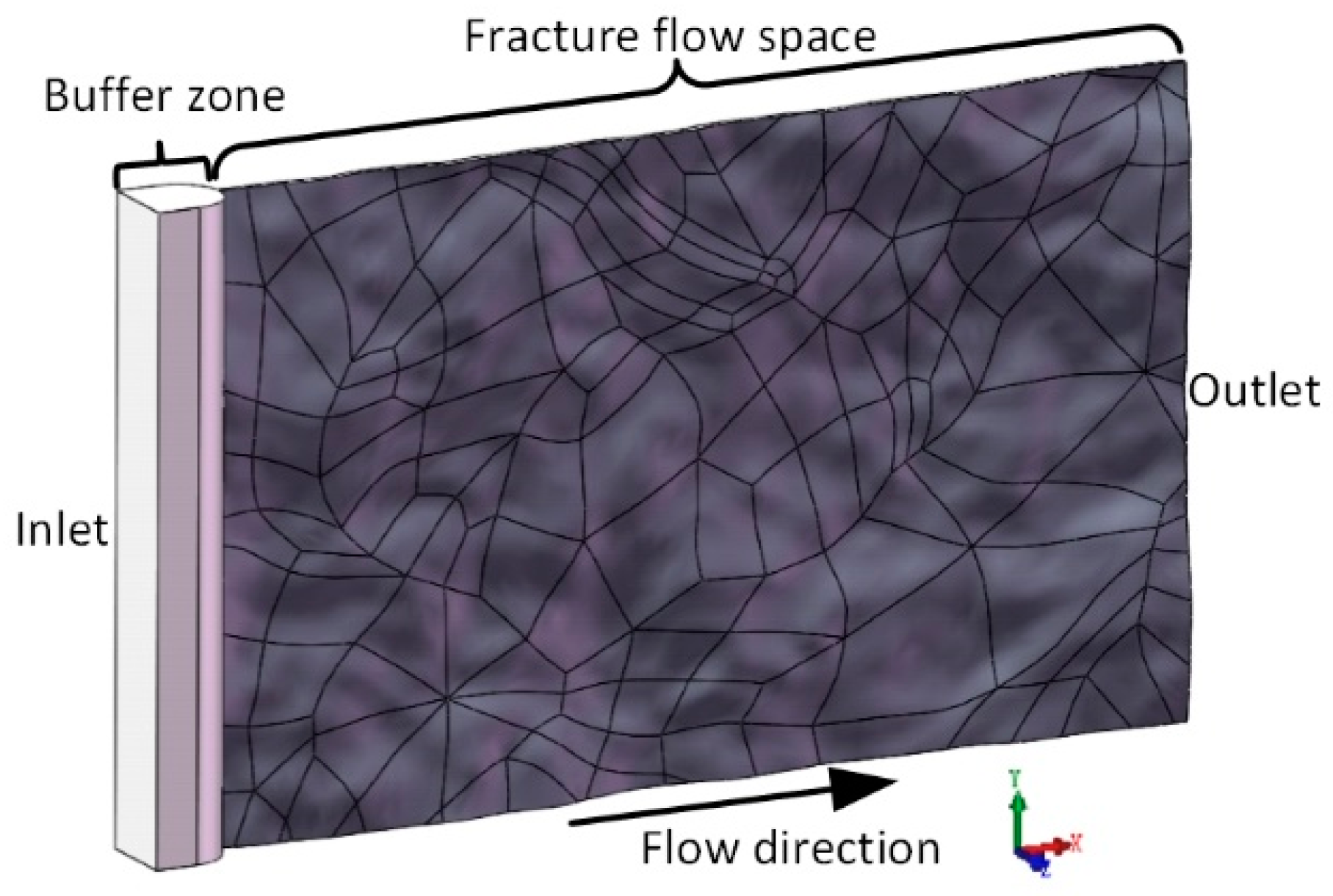
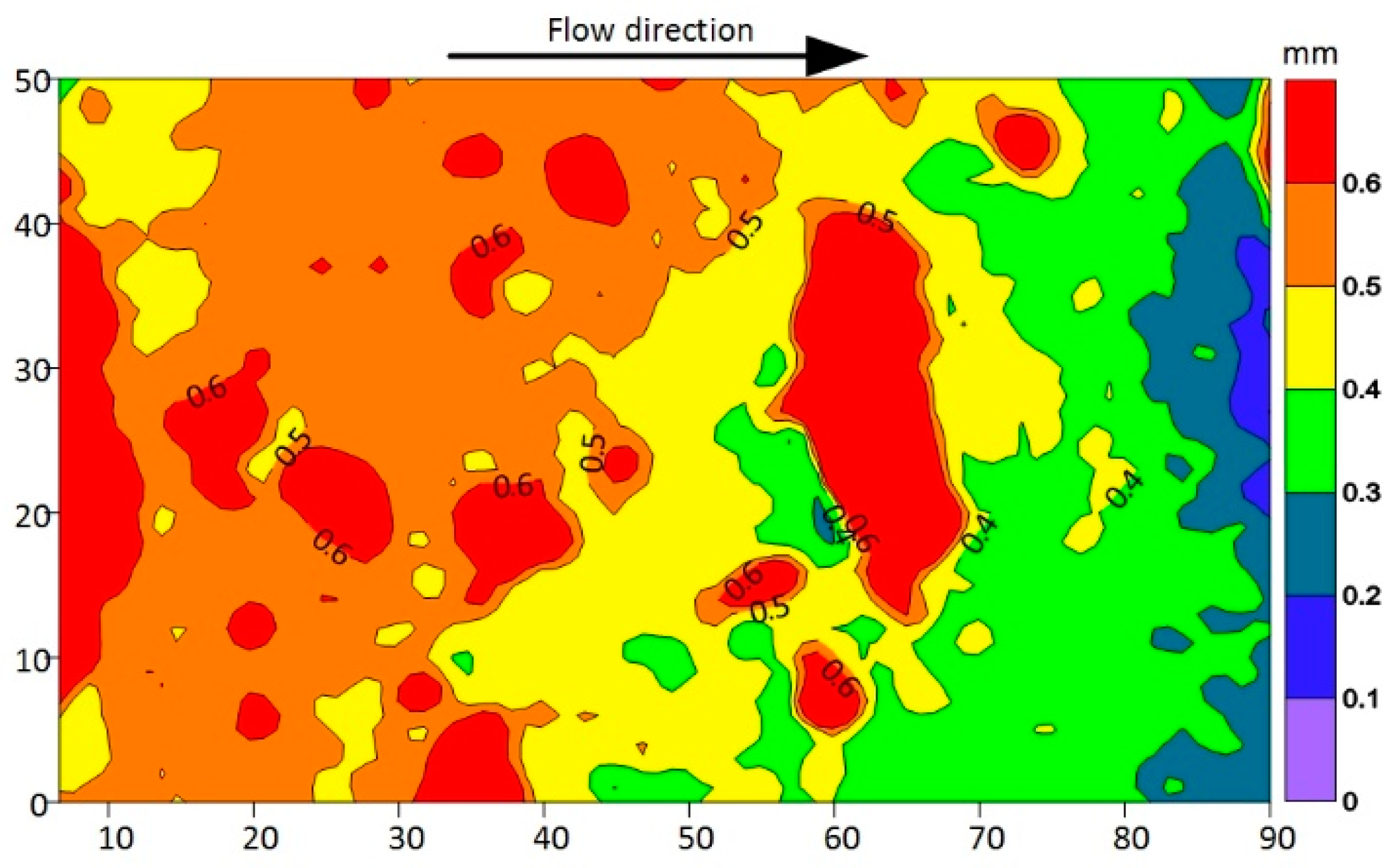
2.1. Modeling of Rock Fracture Flow Space
2.2. Basic Theory of CFD-DEM
2.3. Numerical Model Overview
3. Results
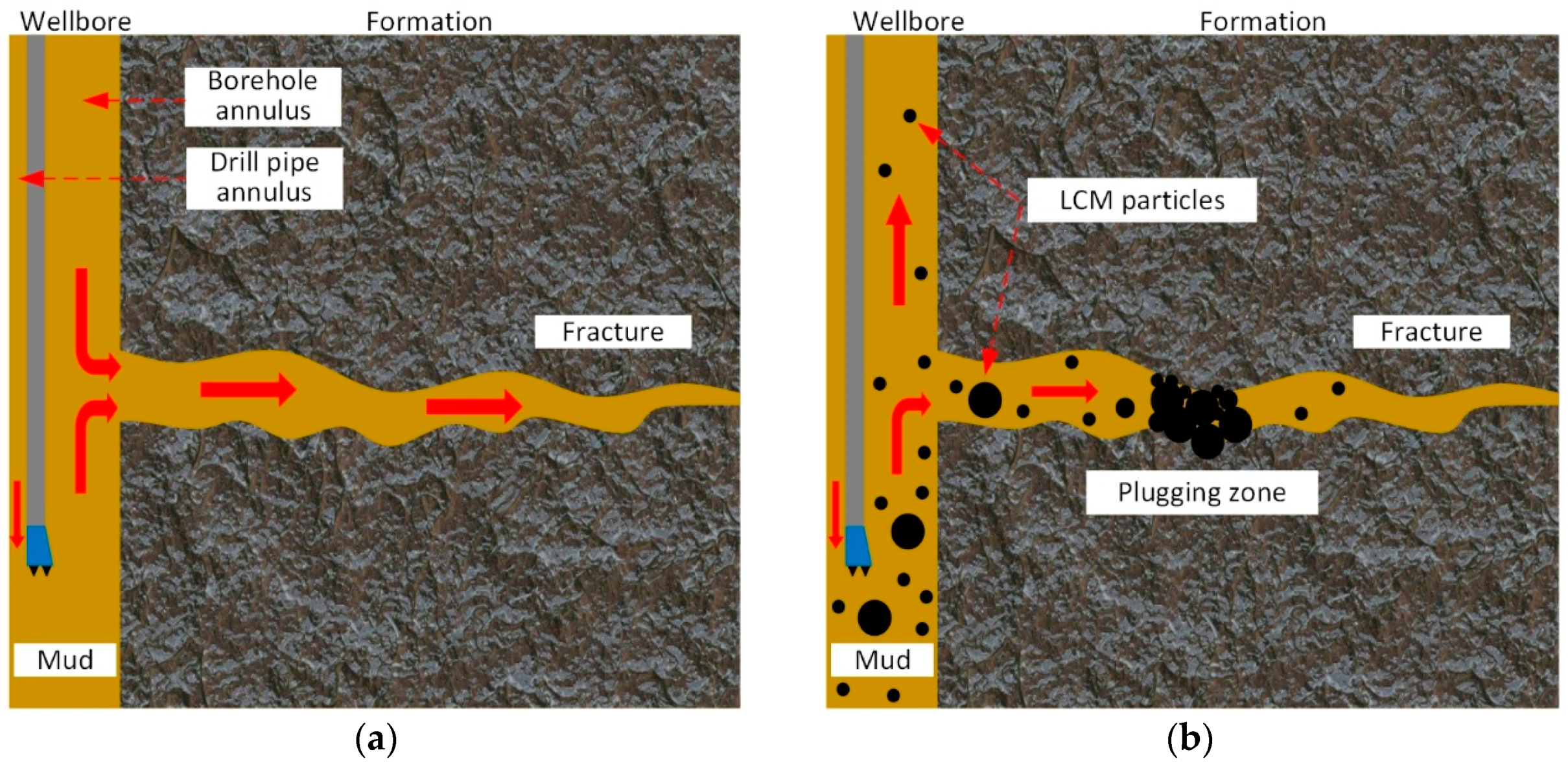
3.1. LCM Particle Transport and Plugging Process in Rough Fractures
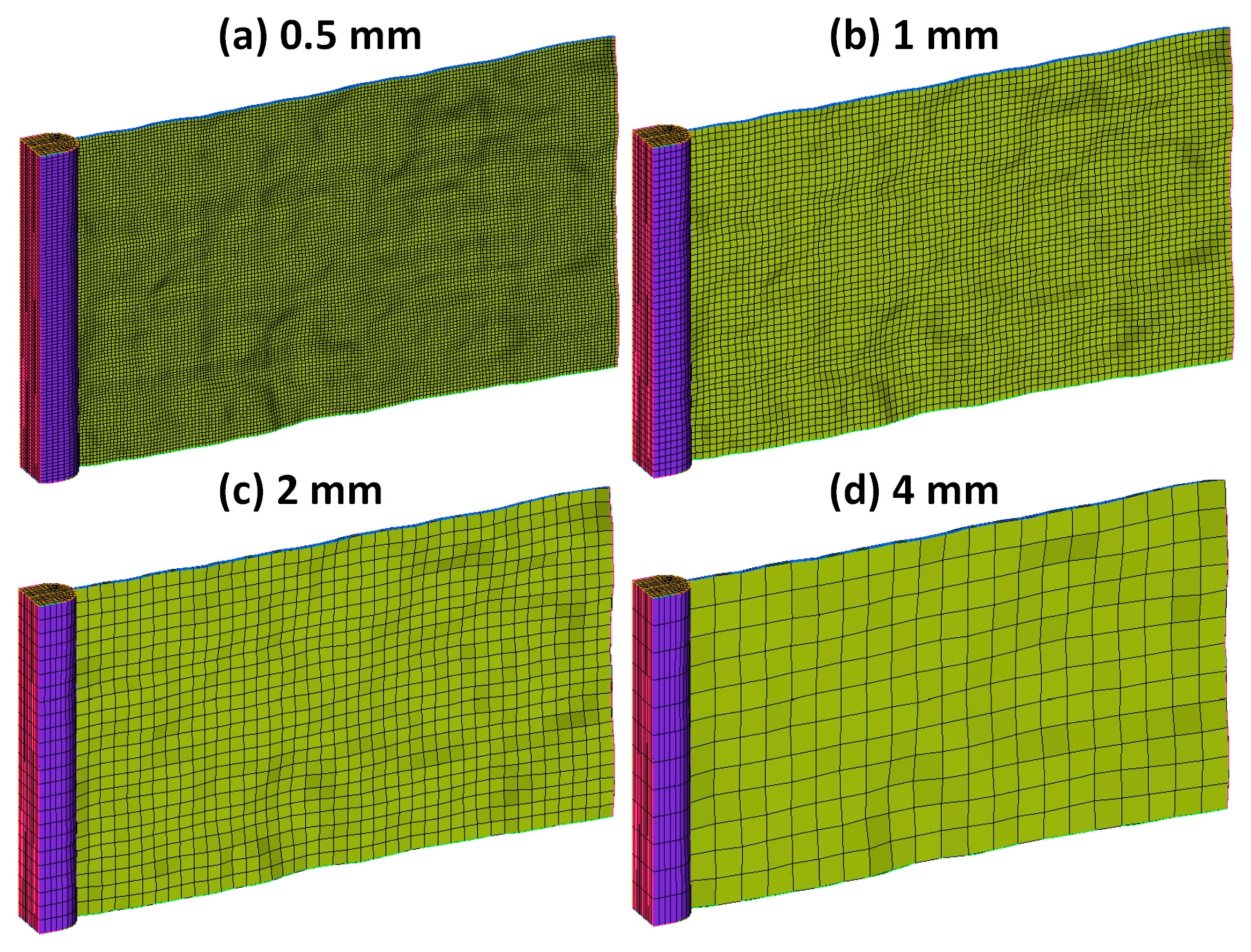
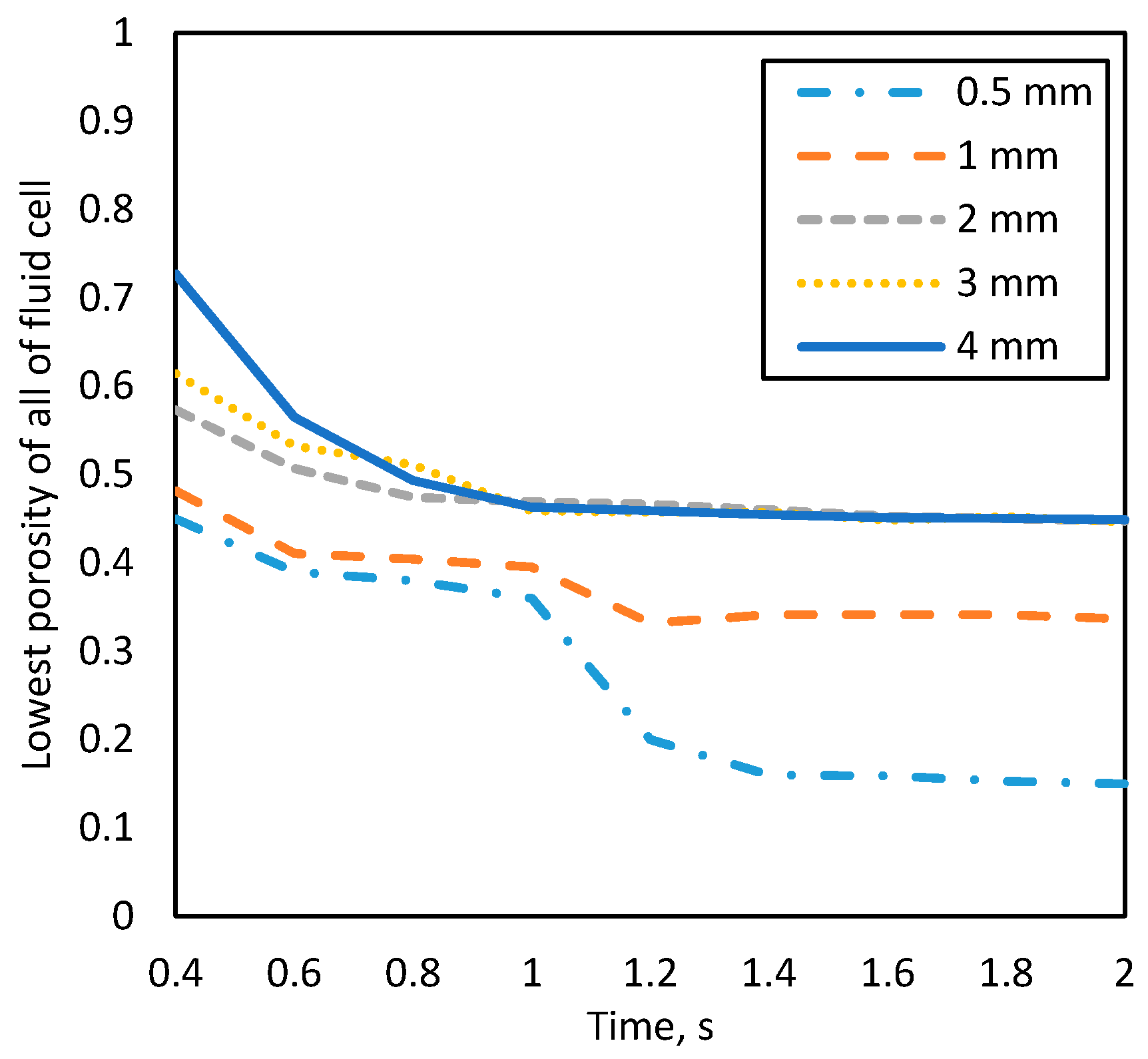
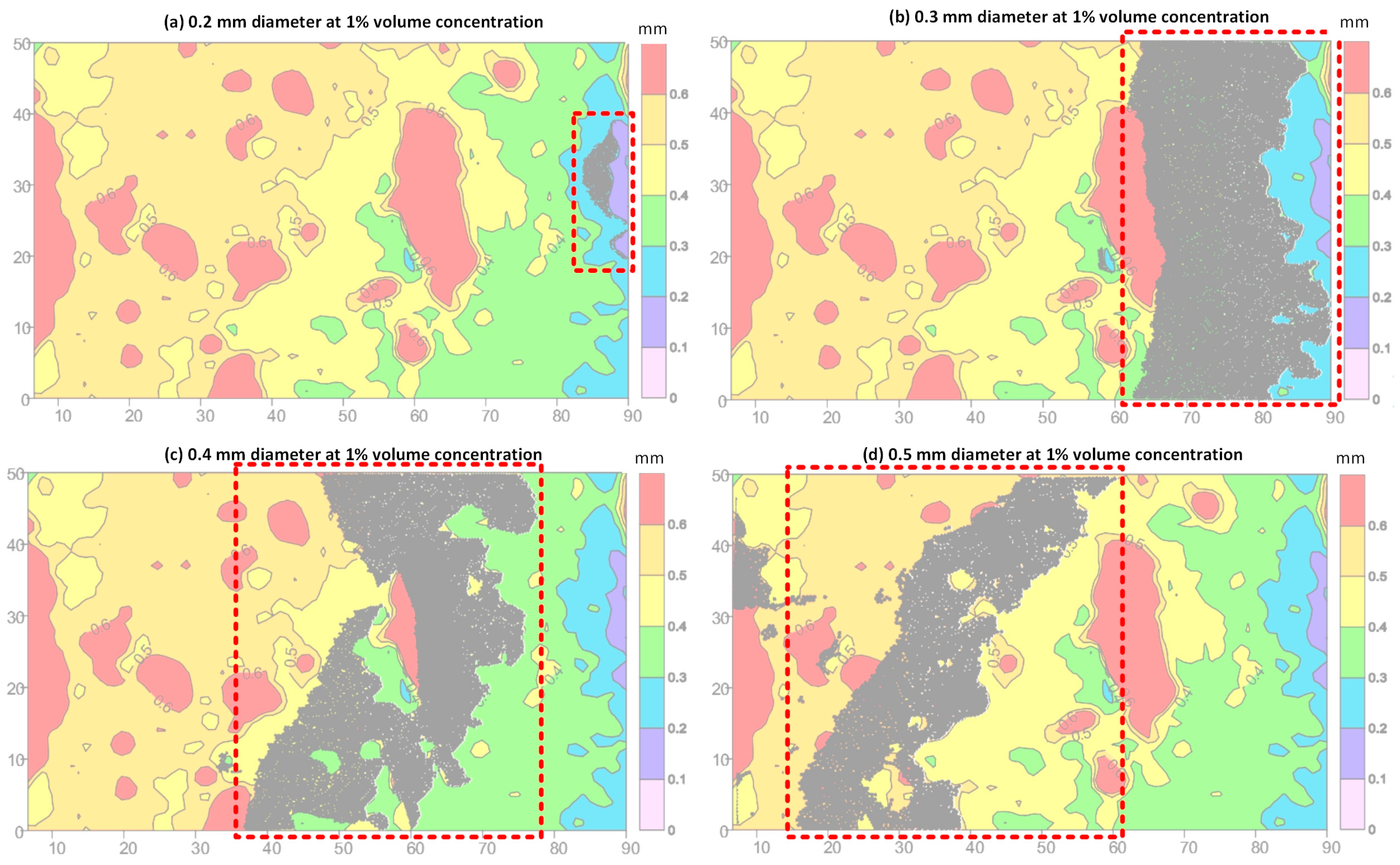
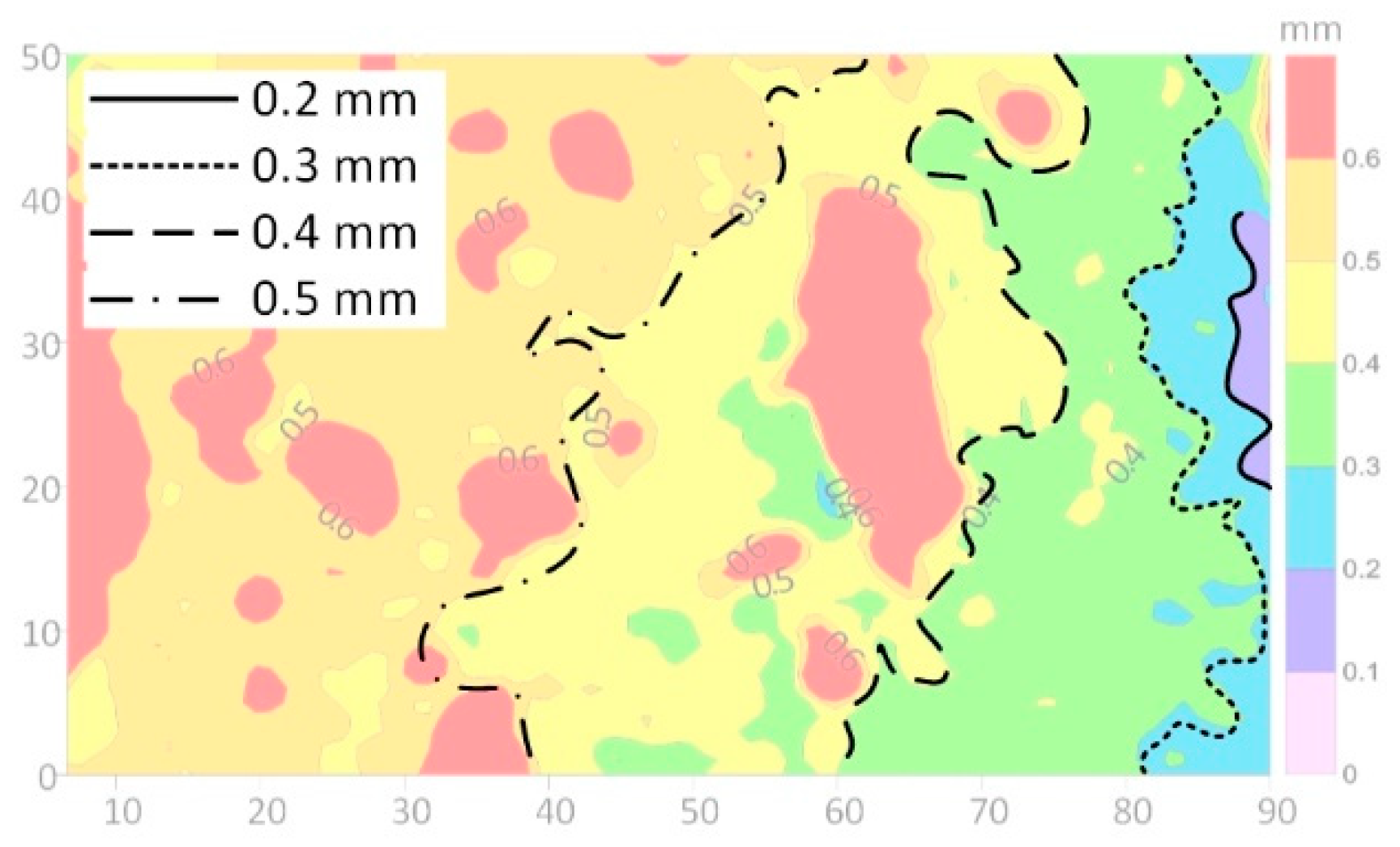
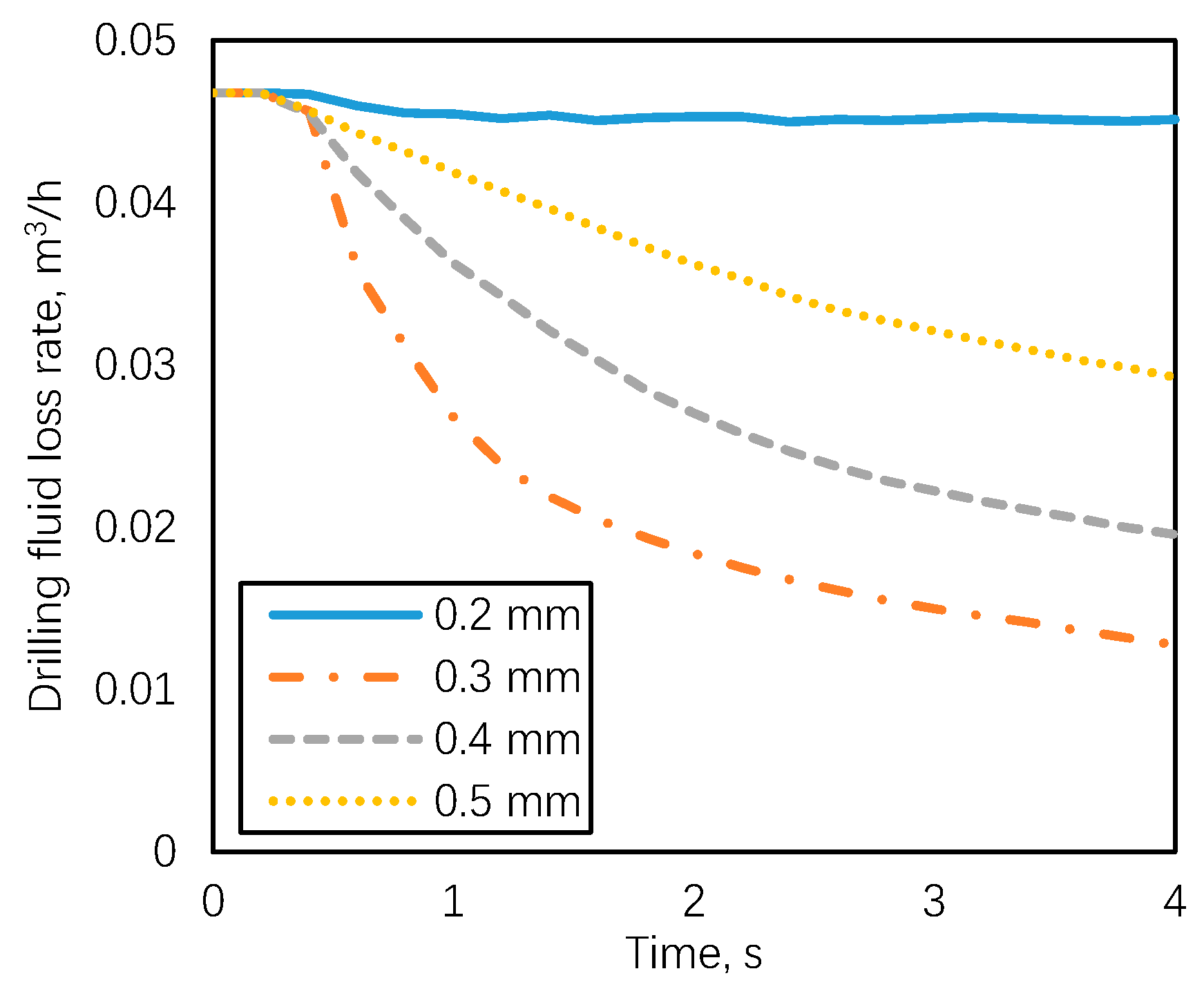
3.2. Effect of LCM Size
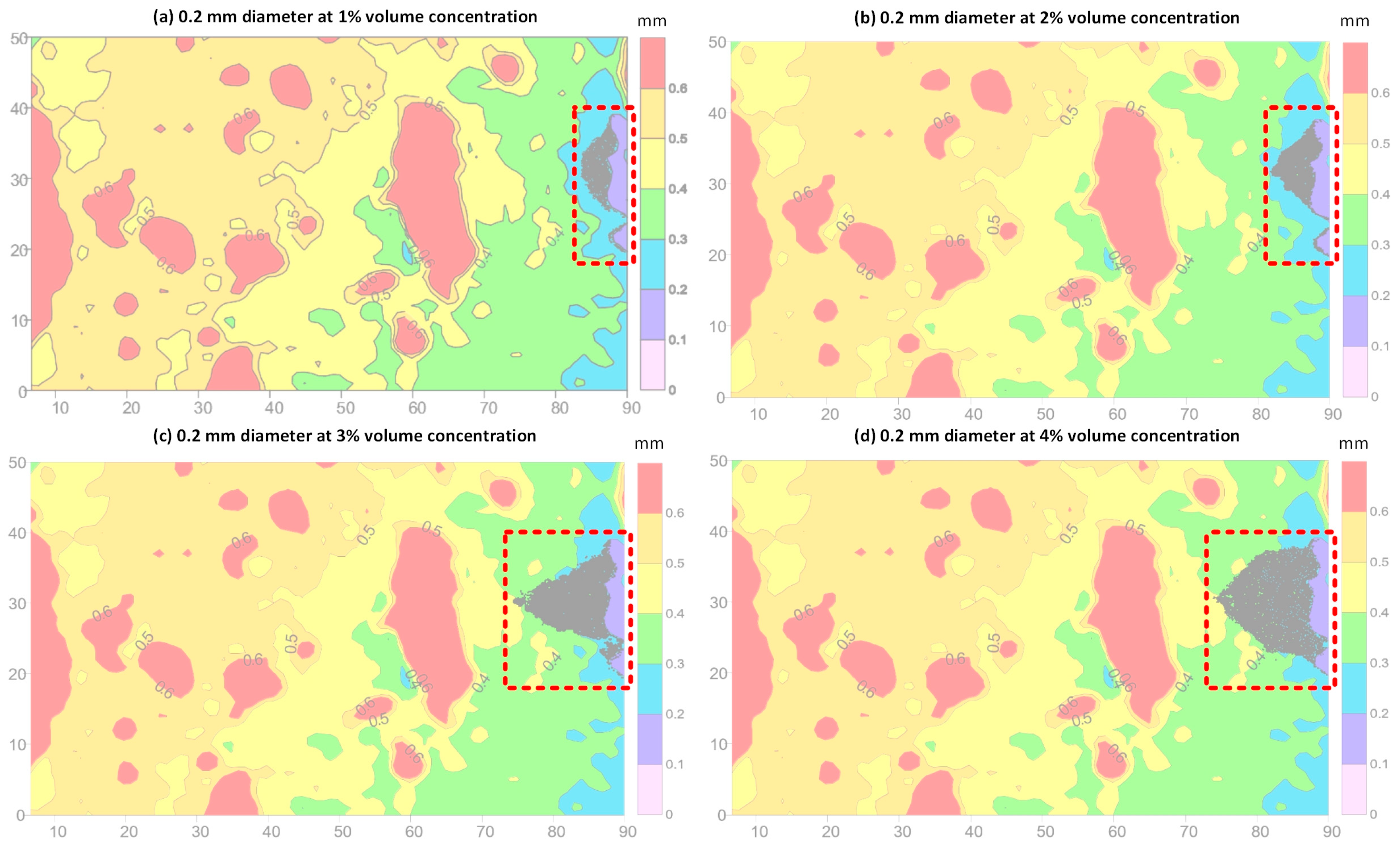
3.3. Effect of LCM Volume Concentration
3.4. The Effect of LCM Shape
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Savari, S.; Kulkarni, S.D.; Whitfill, D.L.; Jamison, D.E. ‘Engineering’ Design of Lost Circulation Materials (LCMs) is More than Adding a Word. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, London, UK, 17–19 March 2015. [Google Scholar]
- Growcock, F. How to Stabilize and Strengthen the Wellbore during Drilling Operation. Available online: http://www.spe.org/dl/docs/2010/FredGrowcock.pdf (accessed on 1 July 2018).
- Alberty, M.W.; McLean, M.R. A Physical Model for Stress Cages. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar]
- Dupriest, F.E. Fracture Closure Stress (FCS) and Lost Returns Practices. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 23–25 February 2005. [Google Scholar]
- Van Oort, E.; Friedheim, J.E.; Pierce, T.; Lee, J. Avoiding Losses in Depleted and Weak Zones by Constantly Strengthening Wellbores. SPE Drill. Complet. 2011, 26, 519–530. [Google Scholar] [CrossRef]
- Feng, Y.; Gray, K.E. Review of fundamental studies on lost circulation and wellbore strengthening. J. Petrol. Sci. Eng. 2017, 152, 511–522. [Google Scholar] [CrossRef]
- Salehi, S.; Hussmann, S.; Karimi, M.; Ezeakacha, C.P.; Tavanaei, A. Profiling Drilling Fluid’s Invasion Using Scanning Electron Microscopy: Implications for Bridging and Wellbore Strengthening Effects. In Proceedings of the SPE Deepwater Drilling and Completions Conference, Galveston, TX, USA, 10–11 September 2014. [Google Scholar]
- Hands, N.; Kowbel, K.; Maikranz, S.; Nouris, R. Drill-in fluid reduces formation damage, increases production rates. Oil Gas J. 1998, 96, 65–69. [Google Scholar]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Mollanouri Shamsi, M.; Farhadi Nia, S.; Jessen, K. Conductivity of Proppant-Packs under Variable Stress Conditions: An Integrated 3D Discrete Element and Lattice Boltzman Method Approach. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 27–30 April 2015. [Google Scholar]
- Blyton, C.A.J.; Gala, D.P.; Sharma, M.M. A Comprehensive Study of Proppant Transport in a Hydraulic Fracture. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015. [Google Scholar]
- Zeng, J.; Li, H.; Zhang, D. Numerical simulation of proppant transport in hydraulic fracture with the upscaling CFD-DEM method. J. Nat. Gas Sci. Eng. 2016, 33, 264–277. [Google Scholar] [CrossRef]
- Zhang, G.; Li, M.; Gutierrez, M. Numerical simulation of proppant distribution in hydraulic fractures in horizontal wells. J. Nat. Gas Sci. Eng. 2017, 48, 157–168. [Google Scholar] [CrossRef]
- Akhshik, S.; Rajabi, M. CFD-DEM modeling of cuttings transport in underbalanced drilling considering aerated mud effects and downhole conditions. J. Petrol. Sci. Eng. 2018, 160, 229–246. [Google Scholar] [CrossRef]
- Shi, X.; Prodanović, M.; Holder, J.; Gray, K.E.; DiCarlo, D. Coupled solid and fluid mechanics modeling of formation damage near wellbore. J. Petrol. Sci. Eng. 2013, 112, 88–96. [Google Scholar] [CrossRef]
- Mirabolghasemi, M.; Prodanović, M.; DiCarlo, D.; Ji, H. Prediction of empirical properties using direct pore-scale simulation of straining through 3D microtomography images of porous media. J. Hydrol. 2015, 529, 768–778. [Google Scholar] [CrossRef]
- Khan, H.J.; Mirabolghasemi, M.S.; Yang, H.; Prodanović, M.; DiCarlo, D.A.; Balhoff, M.T. Study of formation damage caused by retention of bi-dispersed particles using combined pore-scale simulations and particle flooding experiments. J. Petrol. Sci. Eng. 2017, 158, 293–308. [Google Scholar] [CrossRef]
- Wang, G.; Pu, X. Discrete element simulation of granular lost circulation material plugging a fracture. Particul. Sci. Technol. 2014, 32, 112–117. [Google Scholar] [CrossRef]
- Tatone, B.S.; Grasselli, G. Quantitative measurements of fracture aperture and directional roughness from rock cores. Rock Mech. Rock Eng. 2012, 45, 619–629. [Google Scholar] [CrossRef]
- Tatone, B.S.; Grasselli, G. An investigation of discontinuity roughness scale dependency using high-resolution surface measurements. Rock Mech. Rock Eng. 2013, 46, 657–681. [Google Scholar] [CrossRef]
- Hong, E.S.; Kwon, T.H.; Song, K.I.; Cho, G.C. Observation of the degradation characteristics and scale of unevenness on three-dimensional artificial rock joint surfaces subjected to shear. Rock Mech. Rock Eng. 2016, 49, 3–17. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD-DEM. Prog. Comput. Fluid Dyn. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Z.; Sun, Z.; An, S.; Zhang, W.; Liu, P.; Yao, J.; Ma, J. Research on Stress Sensitivity of Fractured Carbonate Reservoirs Based on CT Technology. Energies 2017, 10, 1833. [Google Scholar] [CrossRef]
- Chen, Y.; Naoi, M.; Tomonaga, Y.; Akai, T.; Tanaka, H.; Takagi, S.; Ishida, T. Method for Visualizing Fractures Induced by Laboratory-Based Hydraulic Fracturing and Its Application to Shale Samples. Energies 2018, 11, 1976. [Google Scholar] [CrossRef]
- Zhu, W.; Chang, X.; Wang, Y.; Zhai, H.; Yao, Z. Reconstruction of Hydraulic Fractures Using Passive Ultrasonic Travel-Time Tomography. Energies 2018, 11, 1321. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Basu, D.; Das, K.; Smart, K.; Ofoegbu, G. Comparison of Eulerian-Granular and discrete element models for simulation of proppant flows in fractured reservoirs. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Goniva, C.; Kloss, C.; Deen, N.G.; Kuipers, J.A.; Pirker, S. Influence of rolling friction on single spout fluidized bed simulation. Particuology 2012, 10, 582–591. [Google Scholar] [CrossRef]
- Jakub, P.; Bancewicz, M.; Koza, Z. Is Magnus effect relevant for proppant settling in narrow fractures? Energy Procedia 2017, 125, 443–449. [Google Scholar]
- Ai, J.; Chen, J.F.; Rotter, J.M.; Ooi, J.Y. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- van der Hoef, M.A.; van Sint Annaland, M.; Deen, N.G.; Kuipers, J.A.M. Numerical simulation of dense gas-solid fluidized beds: A multiscale modeling strategy. Annu. Rev. Fluid Mech. 2008, 40, 47–70. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, H.; Zhou, H. Discrete-Element-Method/Computational-Fluid-Dynamics Coupling Simulation of Proppant Embedment and Fracture Conductivity After Hydraulic Fracturing. SPE J. 2017, 22, 632–644. [Google Scholar] [CrossRef]
- Xu, C.; Kang, Y.; Chen, F.; You, Z. Fracture plugging optimization for drill-in fluid loss control and formation damage prevention in fractured tight reservoir. J. Nat. Gas Sci. Eng. 2016, 35, 1216–1227. [Google Scholar] [CrossRef]
- Bokkers, G.A.; Annaland, M.V.S.; Kuipers, J.A.M. Mixing and segregation in a bidisperse gas–solid fluidised bed: A numerical and experimental study. Powder Technol. 2004, 140, 176–186. [Google Scholar]
- van der Hoef, M.A.; Beetstra, R.; Kuipers, J.A.M. Lattice-boltzmann simulations of low-reynolds-number flow past mono- and bidisperse arrays of spheres: Results for the permeability and drag force. J. Fluid Mech. 2005, 528, 233–254. [Google Scholar] [CrossRef]
- Beetstra, R.; van der Hoef, M.A.; Kuipers, J.A.M. Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres. AIChE J. 2007, 53, 489–501. [Google Scholar] [CrossRef]
- Wang, G.; Cao, C.; Pu, X.; Zhao, Z. Experimental investigation on plugging behavior of granular lost circulation materials in fractured thief zone. Particul. Sci. Technol. 2016, 34, 392–396. [Google Scholar] [CrossRef]
- Al-Saba, M.T.; Nygaard, R.; Saasen, A.; Nes, O.M. Lost Circulation Materials Capability of Sealing Wide Fractures. In Proceedings of the SPE Deepwater Drilling and Completions Conference, Galveston, TX, USA, 10–11 September 2014. [Google Scholar]
- Al-Saba, M.T.; Nygaard, R.; Saasen, A.; Nes, O.M. Laboratory Evaluation of Sealing Wide Fractures Using Conventional Lost Circulation Materials. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar]
- Razavi, O.; Vajargah, A.K.; Oort, E.V. Optimum particle size distribution design for lost circulation control and wellbore strengthening. J. Nat. Gas Sci. Eng. 2016, 35, 836–850. [Google Scholar] [CrossRef]
- Lu, G.; Third, J.R.; Müller, C.R. Discrete element models for non-spherical particle systems: From theoretical developments to applications. Chem. Eng. Sci. 2015, 127, 425–465. [Google Scholar] [CrossRef]




| Drilling Fluid Density (Kg/m3) | Drilling Fluid Viscosity (mPa·s) | LCM Density (Kg/m3) | LCM Young’s Modulus (MPa) | LCM Poisson Ratio | LCM Friction Coefficient | LCM Restitution Coefficient | Gravity (m/s2) |
|---|---|---|---|---|---|---|---|
| 1640 | 30 | 2200 | 1000 | 0.25 | 0.3 | 0.5 | 9.8 |
| Literature | Experiment Description | Experiment Results | Simulation Results |
|---|---|---|---|
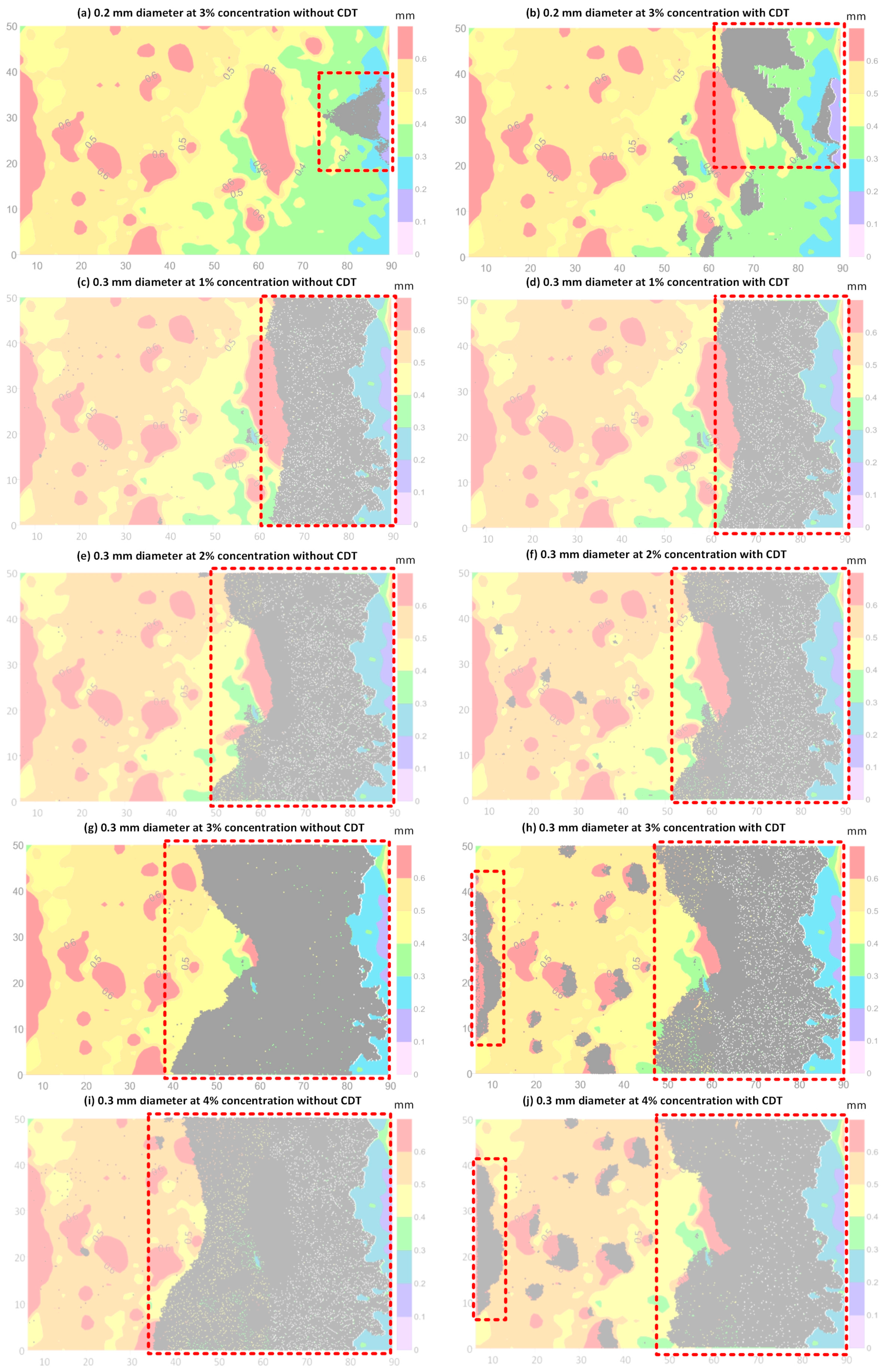
| Wang [39] | Tapered slots size: 2.3 mm at inlet and 1.1 mm at outlet; LCM size: 0.45–1.4 mm. | The plugging depth depends on the values of D50 and D90; the large D50 and D90 values result in a shallow plugging depth in the fracture. | As shown in Figure 13, the front edge of the plugging zone forms at the fracture aperture isopleth, which has the same value as the LCM particles’ diameter. |
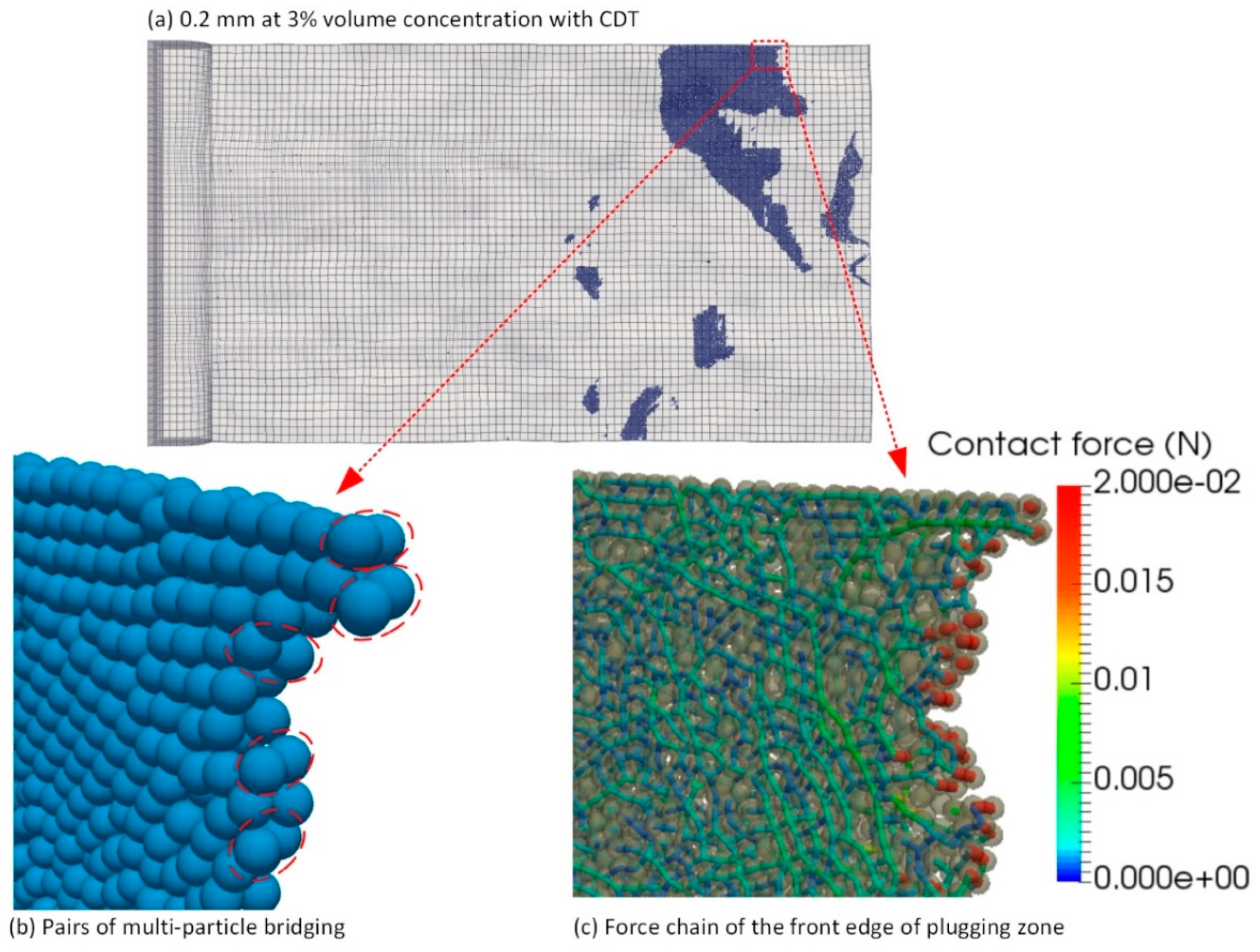
| Al-Saba [40] | Tapered slots size: 2.5–5 mm at inlet and 1–2 mm at outlet; LCM size (D50): 0.005–2.3 mm. | Irregular LCM such as nut shells are capable of sealing wide fractures. | As shown in Figure 16a,b, the irregularity of LCM particles result in LCM multi-particle bridging, where the fracture aperture is larger than the size of the LCM. |
| Al-Saba [41] | A high concentration of larger particles resulted in a screening out at the fracture. | As shown in Figure 16c–j, with the increase in LCM concentration, LCM piles up at the fracture inlet and makes it more difficult for LCM to enter the fracture. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Li, G.; Meng, Y.; Guo, B. A Novel Approach to Investigating Transport of Lost Circulation Materials in Rough Fracture. Energies 2018, 11, 2572. https://doi.org/10.3390/en11102572
Feng Y, Li G, Meng Y, Guo B. A Novel Approach to Investigating Transport of Lost Circulation Materials in Rough Fracture. Energies. 2018; 11(10):2572. https://doi.org/10.3390/en11102572
Chicago/Turabian StyleFeng, Yi, Gao Li, Yingfeng Meng, and Boyun Guo. 2018. "A Novel Approach to Investigating Transport of Lost Circulation Materials in Rough Fracture" Energies 11, no. 10: 2572. https://doi.org/10.3390/en11102572
APA StyleFeng, Y., Li, G., Meng, Y., & Guo, B. (2018). A Novel Approach to Investigating Transport of Lost Circulation Materials in Rough Fracture. Energies, 11(10), 2572. https://doi.org/10.3390/en11102572