Study and Application of Intelligent Sliding Mode Control for Voltage Source Inverters
Abstract
1. Introduction
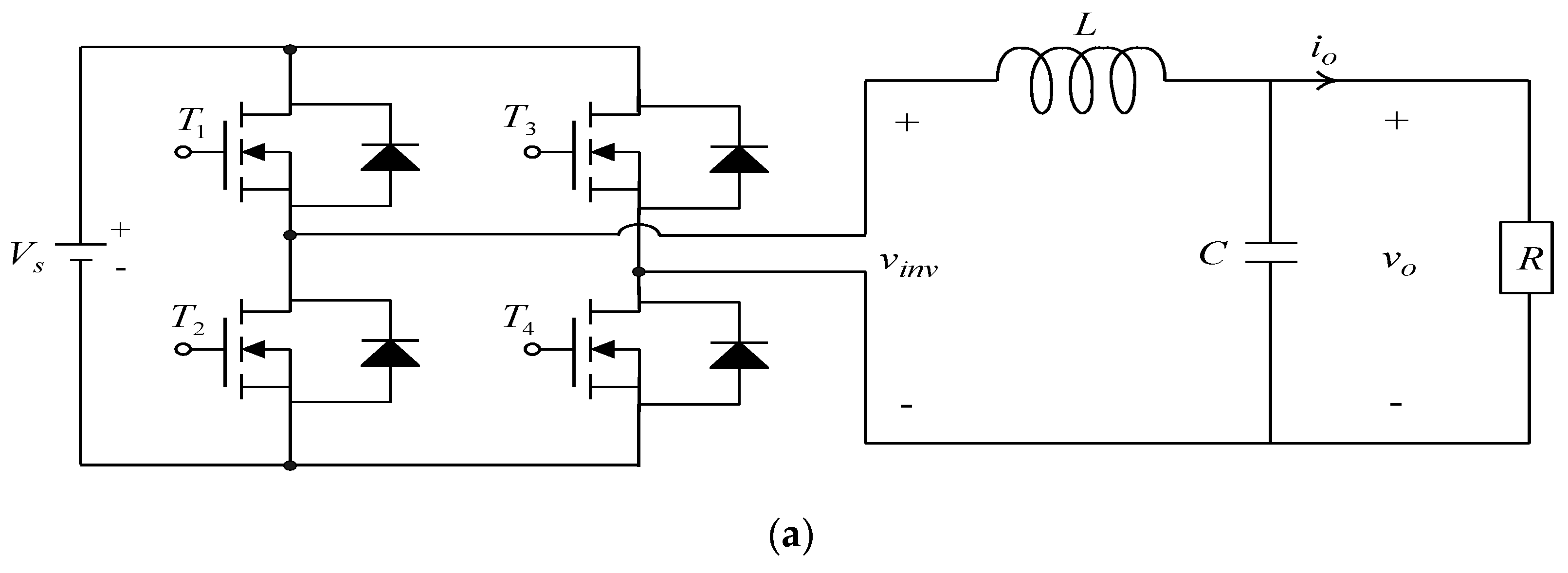
2. Mathematical Representation of VSI
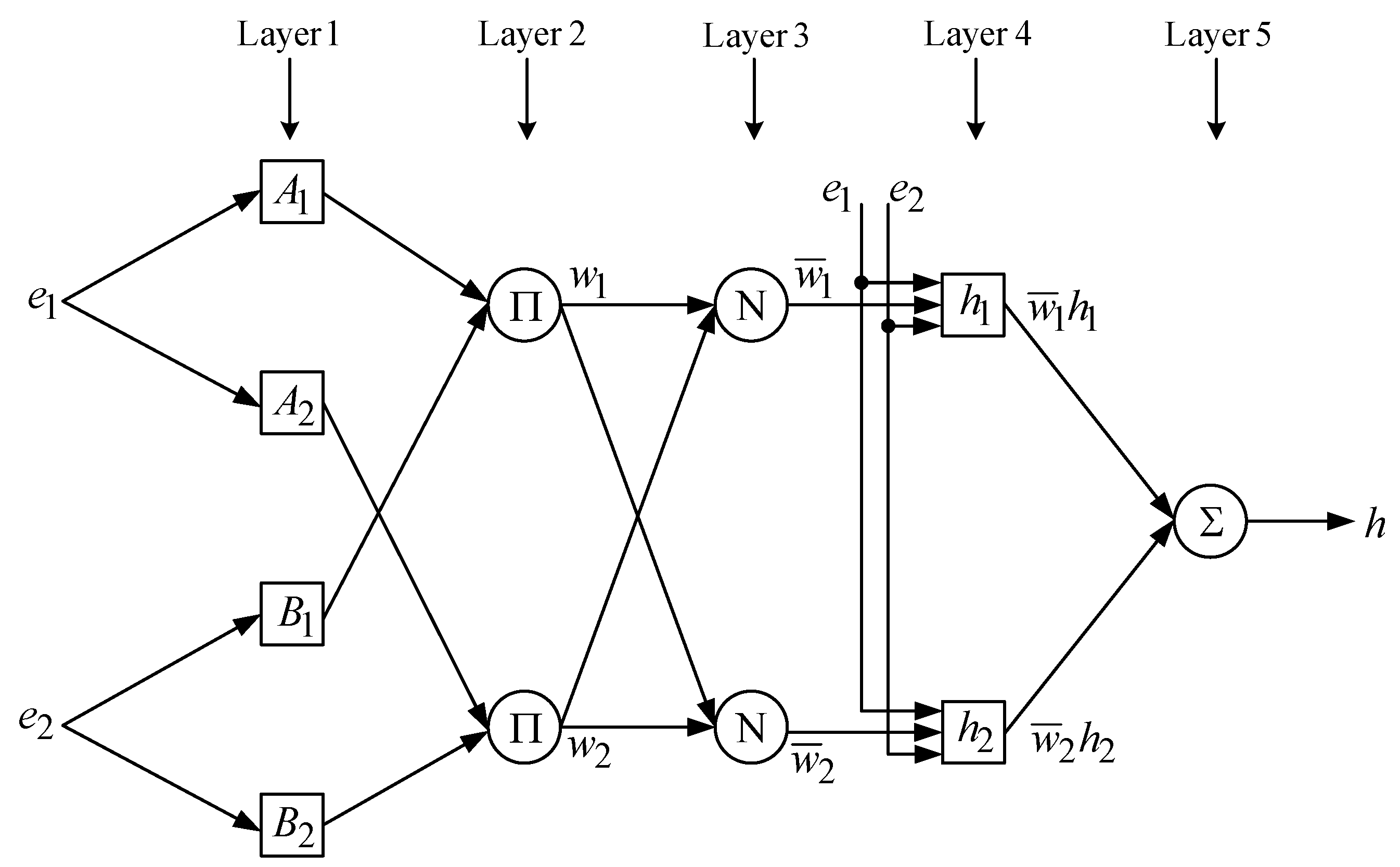
3. Proposed Control Approach of VSI
Problem Statement
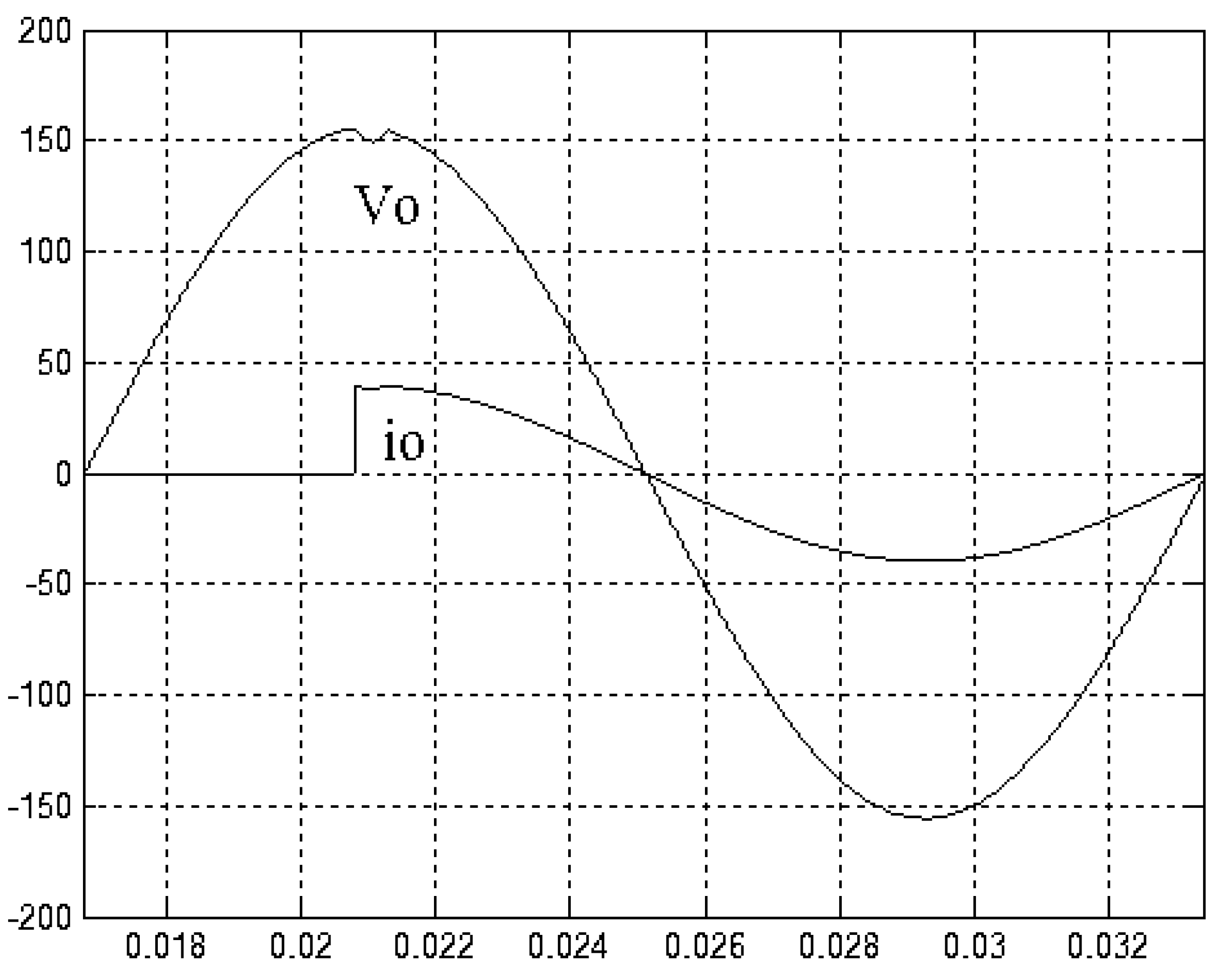
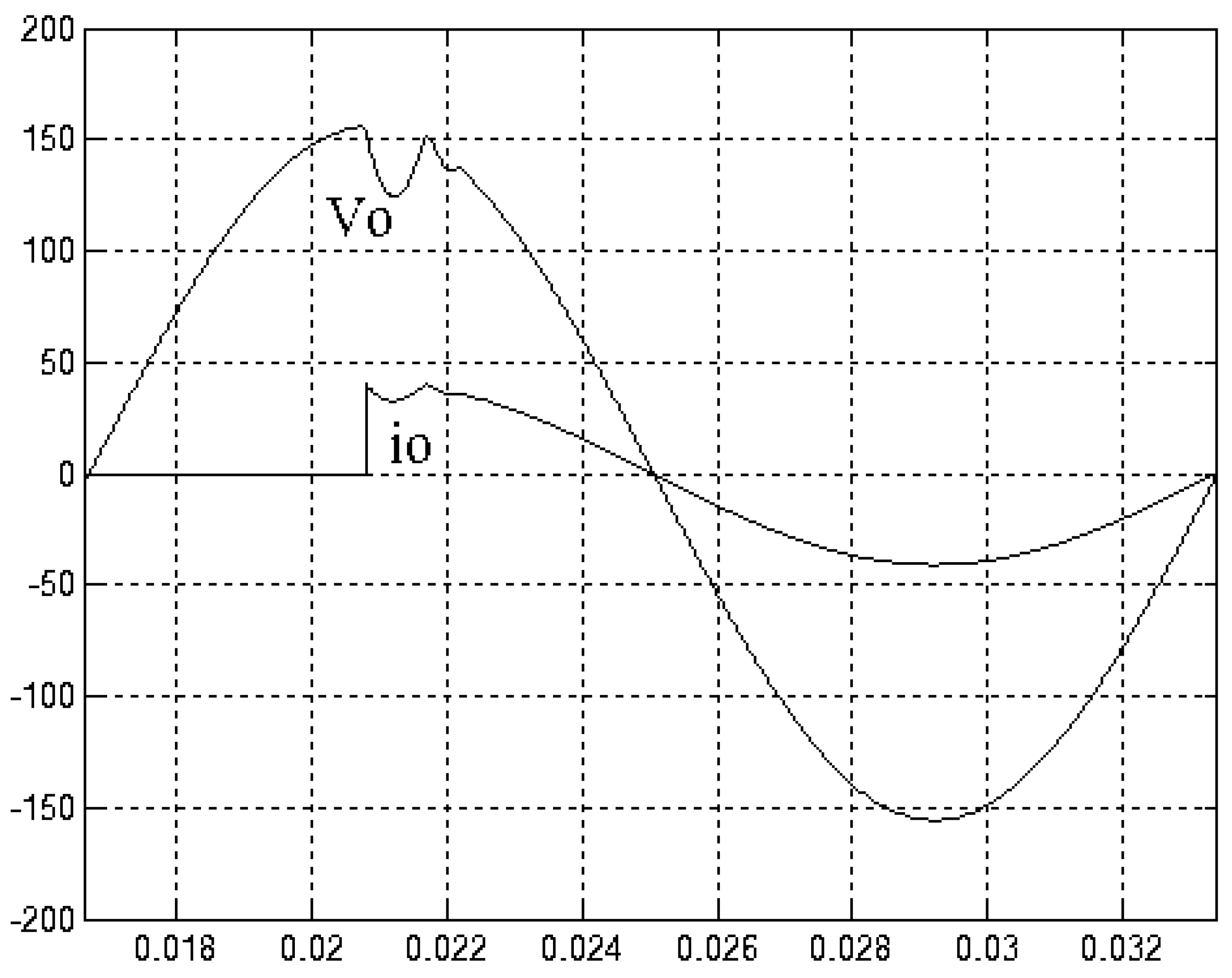
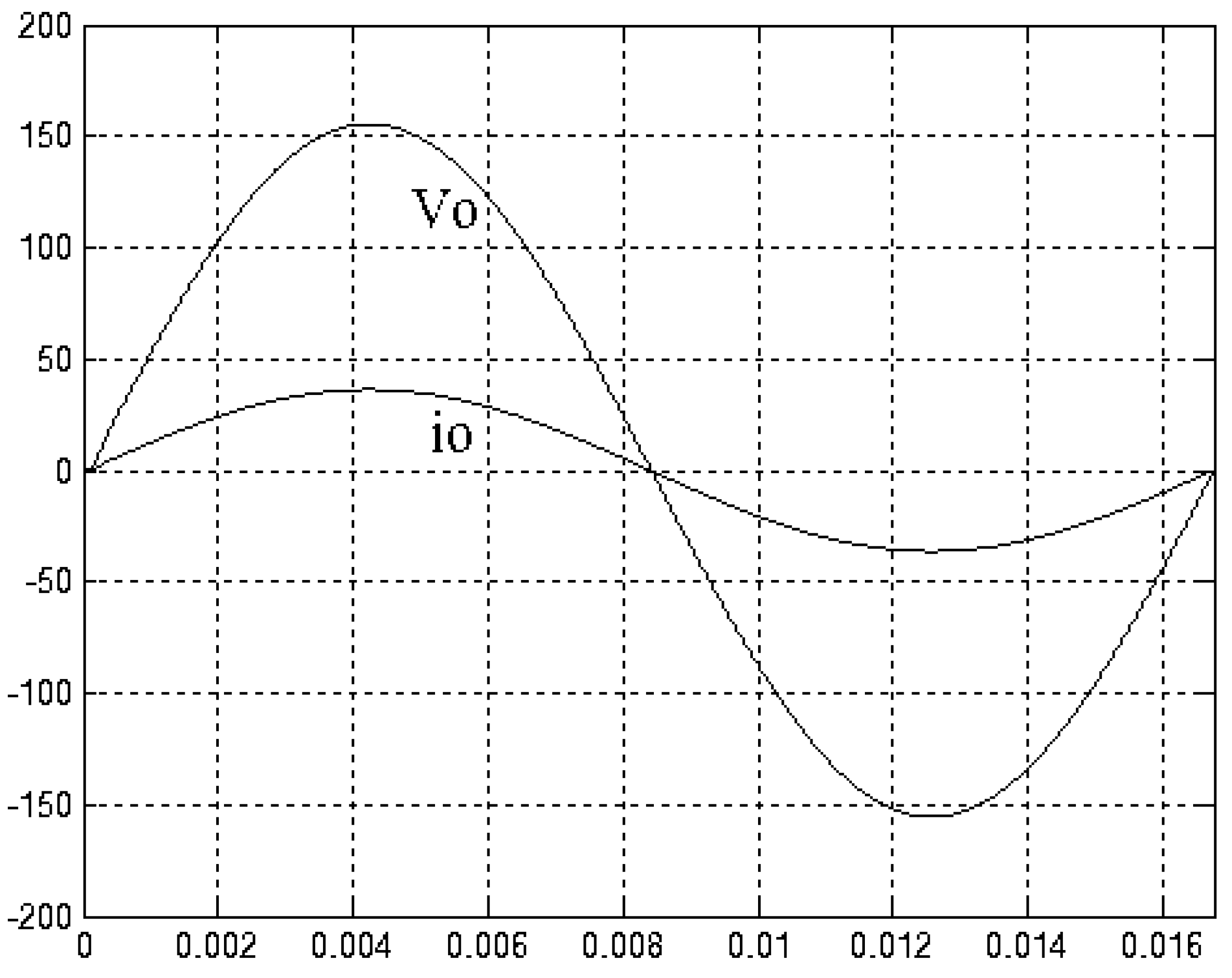
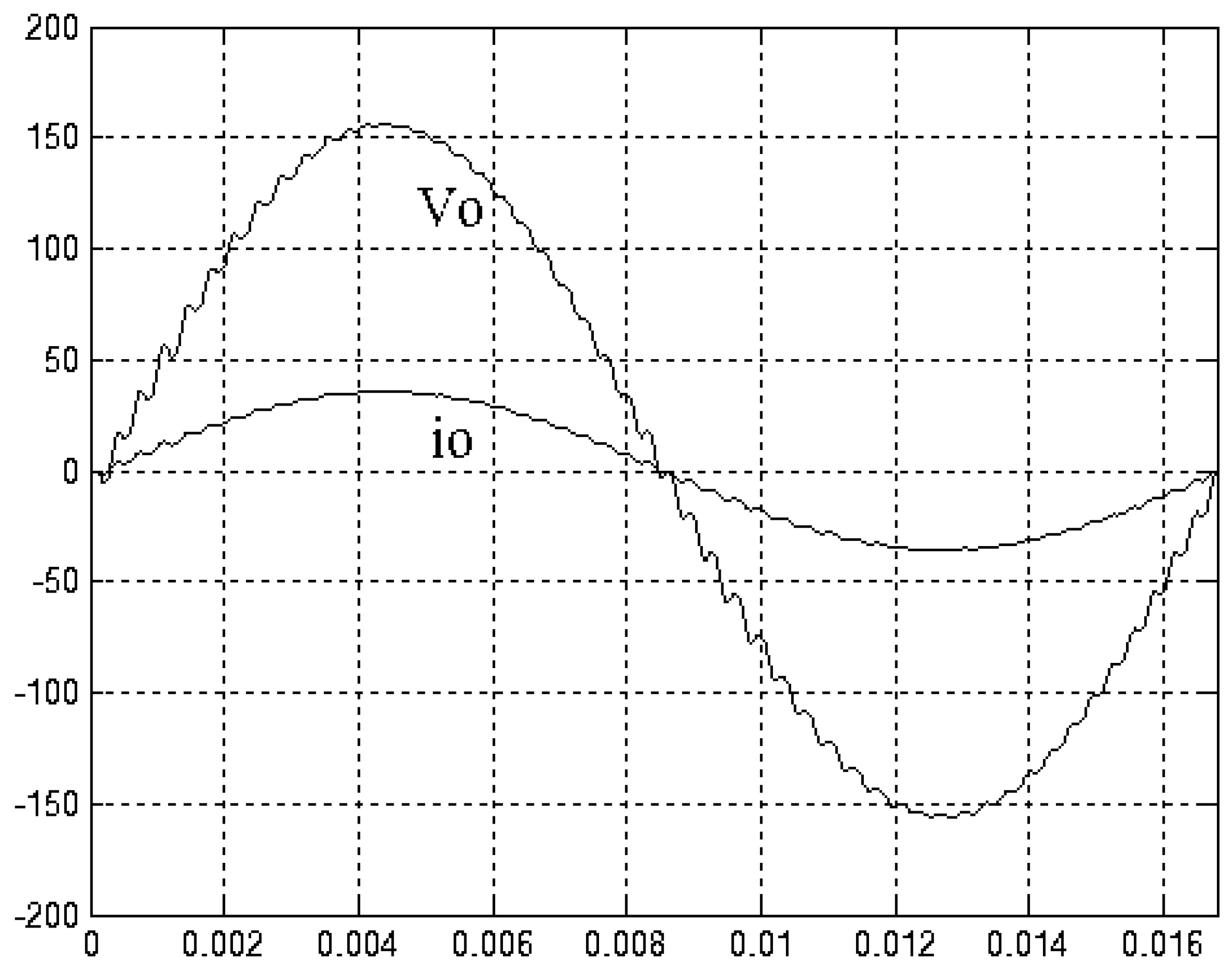
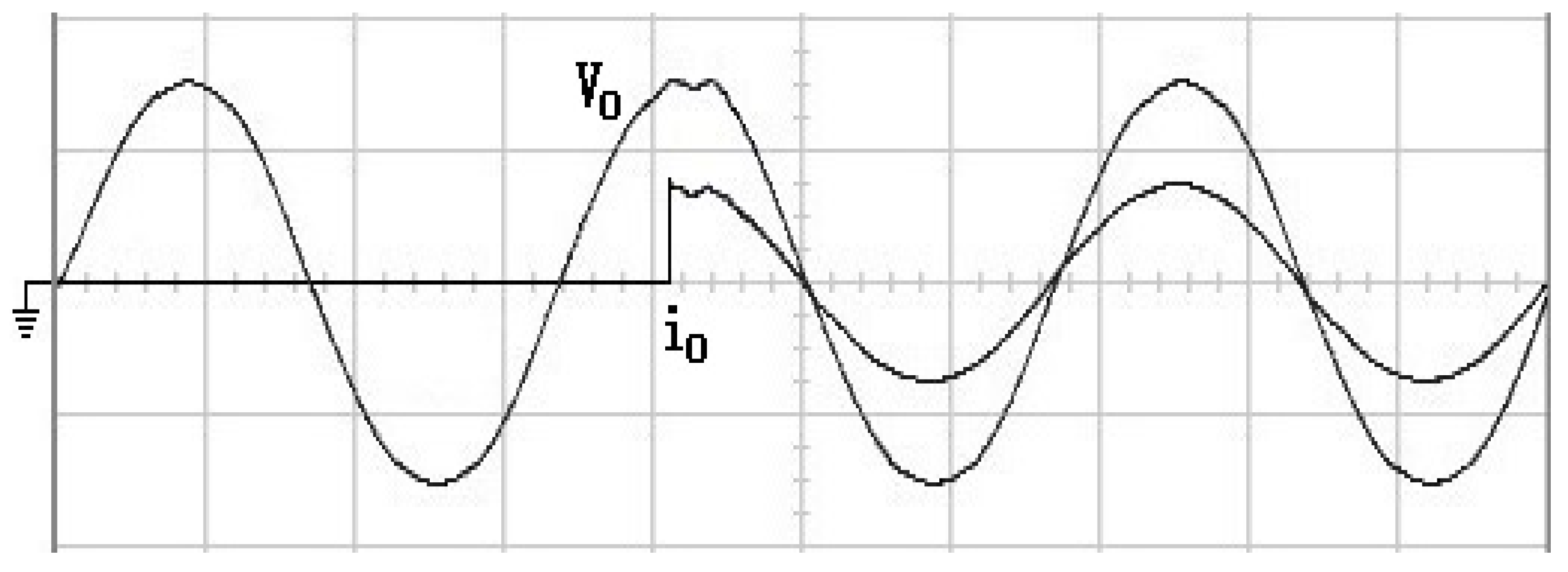
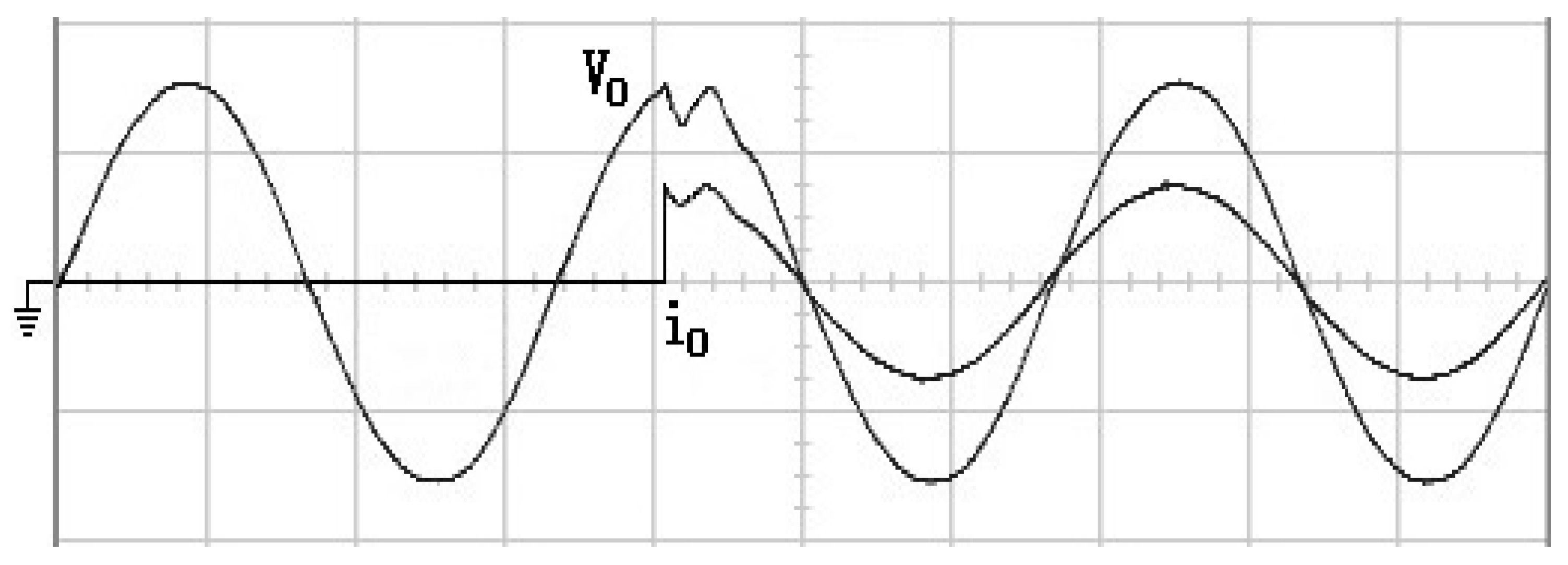
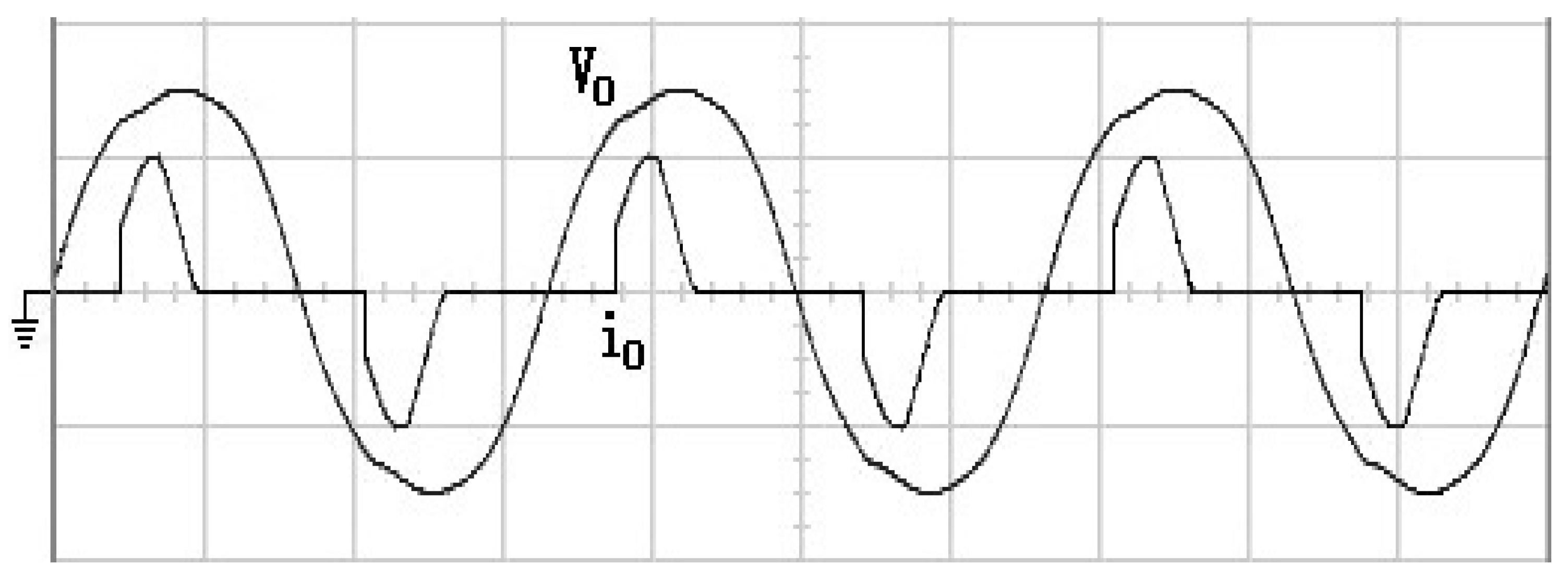
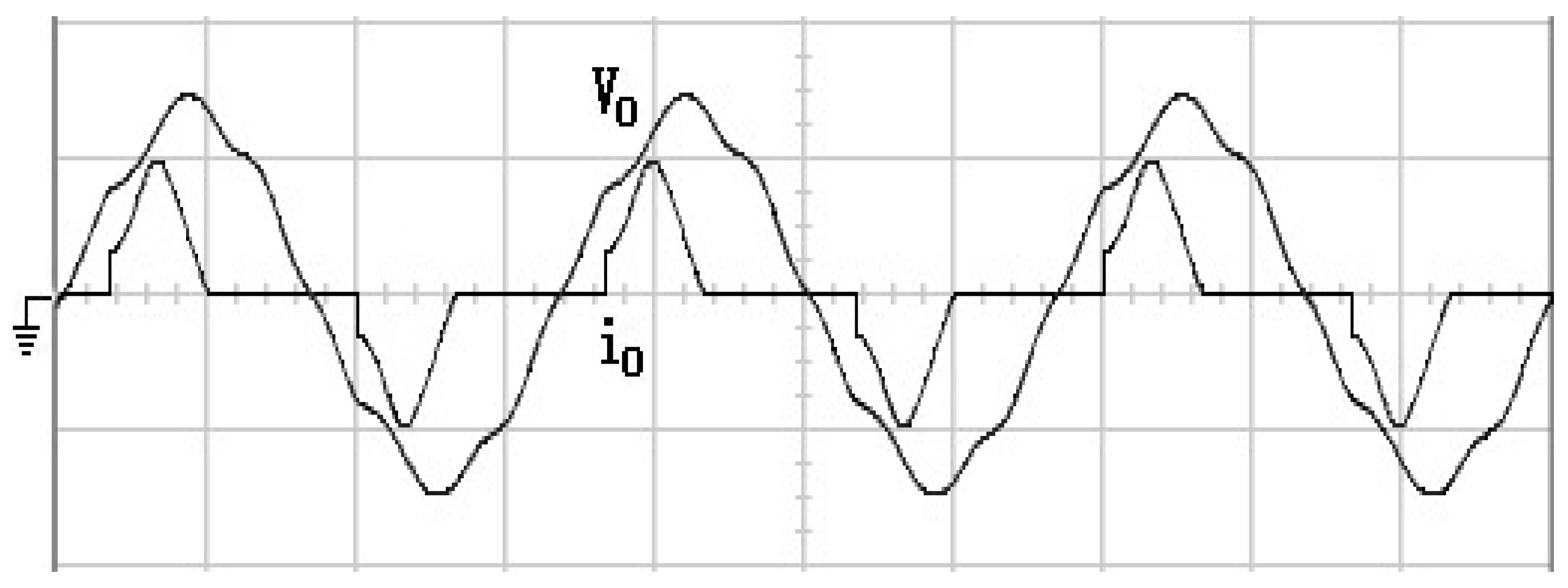
4. Simulation and Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bevrani, H.; Ise, T. Microgrid Dynamics and Control; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Sechilariu, M.; Locment, F. Urban DC Microgrid: Intelligent Control and Power Flow Optimization; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Mahmoud, M.S. Microgrid: Advanced Control Methods and Renewable Energy System Integration; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Blaabjerg, F. Control of Power Electronic Converters and Systems; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Sahoo, S.K. Harmonic Analysis of Voltage Source Inverter Using PWM Techniques: Performance Analysis of Three Phase Voltage Source Inverter Using PWM Techniques; LAP LAMBERT Academic Publishing: Riga, Latvia, 2012. [Google Scholar]
- Chen, C.; Xiong, R.; Shen, W.X. A Lithium-Ion Battery-in-the-Loop Approach to Test and Validate Multiscale Dual H Infinity Filters for State-of-Charge and Capacity Estimation. IEEE Trans. Power Electron. 2018, 33, 332–342. [Google Scholar] [CrossRef]
- He, Y.B.; Chung, S.H.; Ho, N.M.; Wu, W.M. Modified Cascaded Boundary-Deadbeat Control for a Virtually-Grounded Three-Phase Grid-Connected Inverter with LCL Filter. IEEE Trans. Power Electron. 2017, 32, 8163–8180. [Google Scholar] [CrossRef]
- Xie, C.A.; Zhao, X.; Savaghebi, M.; Meng, L.; Guerrero, J.M.; Vasquez, J.C. Multirate Fractional-Order Repetitive Control of Shunt Active Power Filter Suitable for Microgrid Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 809–819. [Google Scholar] [CrossRef]
- Utkin, V.I. Variable Structure Systems with Sliding Modes. IEEE Trans. Autom. Control 1977, AC-22, 212–222. [Google Scholar] [CrossRef]
- Sundarapandian, V.; Lien, C.H. Applications of Sliding Mode Control in Science and Engineering; Springer: Berlin, Germany, 2017. [Google Scholar]
- Nabil, D.; Jawhar, G.; Zhu, Q.M. Applications of Sliding Mode Control; Springer: Berlin, Germany, 2017. [Google Scholar]
- Bagheri, F.; Komurcugil, H.; Kukrer, O. Fixed switching frequency sliding-mode control methodology for single-phase LCL-filtered quasi-Z-source grid-tied inverters. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018; pp. 1–6. [Google Scholar]
- Abrishamifar, A.; Ahmad, A.; Mohamadian, M. Fixed Switching Frequency Sliding Mode Control for Single-Phase Unipolar Inverter. IEEE Trans. Power Electron. 2012, 27, 2507–2514. [Google Scholar] [CrossRef]
- Aamir, M.; Kalwar, K.A.; Mekhilef, S. Proportional-Resonant and Slide Mode Control for Single-Phase UPS Inverter. Electr. Power Compon. Syst. 2017, 45, 11–21. [Google Scholar] [CrossRef]
- Hao, X.; Yang, X.; Liu, T.; Huang, L.; Chen, W.J. A Sliding-Mode Controller with Multiresonant Sliding Surface for Single-Phase Grid-Connected VSI with an LCL Filter. IEEE Trans. Power Electron. 2013, 28, 2259–2268. [Google Scholar] [CrossRef]
- Khajeh-Shalaly, B.; Shahgholian, G. A Multi-Slope Sliding-Mode Control Approach for Single-Phase Inverters under Different Loads. Electronics 2016, 5, 68. [Google Scholar] [CrossRef]
- Lachichi, A.; Pierfederici, S.; Martin, J.P.; Davat, B. Study of a Hybrid Fixed Frequency Current Controller Suitable for DC–DC Applications. IEEE Trans. Power Electron. 2008, 23, 1437–1448. [Google Scholar] [CrossRef]
- Zakipour, A.; Shokri-Kojori, S.; Bina, M.T. Closed-loop control of the grid-connected Z-source inverter using hyper-plane MIMO sliding mode. IET Power Electron. 2017, 10, 2229–2241. [Google Scholar] [CrossRef]
- Knight, J.; Shirsavar, S.; Holderbaum, W. An improved reliability Cuk based solar inverter with sliding mode control. IEEE Trans. Power Electron. 2006, 21, 1107–1115. [Google Scholar] [CrossRef]
- Islam, G.; Muyeen, S.M.; Al-Durra, A.; Hasanien, H.M. RTDS implementation of an improved sliding mode based inverter controller for PV system. ISA Trans. 2016, 62, 50–59. [Google Scholar] [CrossRef] [PubMed]
- Montoya, D.G.; Paja, C.A.R.; Giral, R. Improved Design of Sliding-Mode Controllers Based on the Requirements of MPPT Techniques. IEEE Trans. Power Electron. 2016, 31, 235–247. [Google Scholar] [CrossRef]
- Yu, X.H.; Wang, B.; Batbayar, B.; Wang, L.P.; Man, Z.H. An improved training algorithm for feedforward neural network learning based on terminal attractors. J. Glob. Optim. 2011, 51, 271–284. [Google Scholar] [CrossRef]
- Xiong, J.J.; Zhang, G.B. Global fast dynamic terminal sliding mode control for a quadrotor UAV. ISA Trans. 2017, 66, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Mishra, J.; Yu, X.; Jalili, M.; Feng, Y. On fast terminal sliding-mode control design for higher order systems. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 252–257. [Google Scholar]
- Mobayen, S. Fast terminal sliding mode controller design for nonlinear second-order systems with time-varying uncertainties. Complexity 2015, 21, 239–244. [Google Scholar] [CrossRef]
- Veluvolu, K.C.; Defoort, M.; Soh, Y.C. High-gain observer with sliding mode for nonlinear state estimation and fault reconstruction. J. Frankl. Inst. 2014, 351, 1995–2014. [Google Scholar] [CrossRef]
- Guisser, M.; L-Jouni, A.E.; Abdelmounim, E.L.H. Robust Sliding Mode MPPT Controller Based on High Gain Observer of a Photovoltaic Water Pumping System. Int. Rev. Autom. Control 2014, 7, 225–232. [Google Scholar] [CrossRef]
- Vidal-Idiarte, E.; Martinez-Salamero, L.; Gispert, F.G.; Gomariz, S. Sliding and fuzzy control of a boost converter using a 8-bit microcontroller. IEE Proc. Electr. Power Appl. 2004, 151, 5–11. [Google Scholar] [CrossRef]
- Cao, J.B.; Cao, B.G. Fuzzy-Logic-Based Sliding-Mode Controller Design for Position-Sensorless Electric Vehicle. IEEE Trans. Power Electron. 2009, 24, 2368–2378. [Google Scholar] [CrossRef]
- Radu, S.M.; Tudoroiu, E.R.; Kecs, W.; Ilias, N.; Tudoroiu, N. Real Time Implementation of an Improved Hybrid Fuzzy Sliding Mode Observer Estimator. Adv. Sci. Technol. Eng. Syst. J. 2017, 2, 214–226. [Google Scholar] [CrossRef]
- Guzman, R.; Vicuna, L.G.; Morales, J.; Castilla, M.; Miret, J. Model-Based Active Damping Control for Three-Phase Voltage Source Inverters with LCL Filter. IEEE Trans. Power Electron. 2017, 32, 5637–5650. [Google Scholar] [CrossRef]
- Fei, J.T.; Zhu, Y.K. Adaptive fuzzy sliding control of single-phase PV grid-connected inverter. In Proceedings of the IEEE Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 1233–1238. [Google Scholar]
- Wai, R.J.; Lin, Y.F.; Liu, Y.K. Design of Adaptive Fuzzy-Neural-Network Control for a Single-Stage Boost Inverter. IEEE Trans. Power Electron. 2015, 30, 7282–7298. [Google Scholar] [CrossRef]
- Mohammad, M. Optimal Operation Management of a Typical Microgrid as Grid Connected in Power Systems Using Fuzzy Sliding-Mode Control (FSMC) Approach. World Appl. Sci. J. 2013, 28, 440–448. [Google Scholar]
- Leu, V.Q.; Choi, H.H.; Jung, J.W. Fuzzy Sliding Mode Speed Controller for PM Synchronous Motors with a Load Torque Observer. IEEE Trans. Power Electron. 2012, 27, 1530–1539. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence; Prentice-Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Vafaei, S.; Rezvani, A.; Gandomkar, M.; Izadbakhsh, M. Enhancement of grid-connected photovoltaic system using ANFIS-GA under different circumstances. Front. Energy 2015, 9, 322–334. [Google Scholar] [CrossRef]
- Abdulwahid, A.H.; Wang, S.R. A Novel Approach for Microgrid Protection Based upon Combined ANFIS and Hilbert Space-Based Power Setting. Energies 2016, 9, 1042. [Google Scholar] [CrossRef]
- Logeswaran, T.; Senthilkumar, A.; Karuppusamy, P. Adaptive neuro-fuzzy model for grid-connected photovoltaic system. Int. J. Fuzzy Syst. 2016, 17, 585–594. [Google Scholar] [CrossRef]
- Garcia, P.; Garcia, C.A.; Fernandez, L.M.; Llorens, F.; Jurado, F. ANFIS-Based Control of a Grid-Connected Hybrid System Integrating Renewable Energies, Hydrogen and Batteries. IEEE Trans. Ind. Inform. 2014, 10, 1107–1117. [Google Scholar] [CrossRef]
- Kabzinski, J. Advanced Control of Electrical Drives and Power Electronic Converters; Springer: Berlin, Germany, 2017. [Google Scholar]
- Mahdavi, J.; Emaadi, A.; Bellar, M.; Ehsani, M. Analysis of power electronic converters using the generalized state-space averaging approach. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 767–770. [Google Scholar] [CrossRef]
- Ang, S.; Oliva, A. Power-Switching Converters; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Noman, A.M.; Addoweesh, K.E.; Alolah, A.I. Simulation and Practical Implementation of ANFIS-Based MPPT Method for PV Applications Using Isolated Ćuk Converter. Int. J. Photoenergy 2017, 2017, 3106734. [Google Scholar] [CrossRef]
- Elagori, A.; Tacer, M. Implementation and Evaluation of Maximum Power Point Tracking (MPPT) Based on Adaptive Neuro-Fuzzy Inference System for Photovoltaic PV System. Int. J. Electron. Mech. Mechatron. Eng. 2017, 7, 1453–1474. [Google Scholar]
- Shabaan, S.; El-Sebah, I.A.; Bekhit, P. Maximum power point tracking for photovoltaic solar pump based on ANFIS tuning system. J. Electr. Syst. Inf. Technol. 2018, 1, 11–22. [Google Scholar] [CrossRef]
- Singh, M.; Chandra, A. Application of Adaptive Network-Based Fuzzy Inference System for Sensorless Control of PMSG-Based Wind Turbine with Nonlinear-Load-Compensation Capabilities. IEEE Trans. Power Electron. 2011, 26, 165–175. [Google Scholar] [CrossRef]
- Cheok, A.D.; Wang, Z.F. Fuzzy logic rotor position estimation based switched reluctance motor DSP drive with accuracy enhancement. IEEE Trans. Power Electron. 2005, 4, 908–921. [Google Scholar] [CrossRef]
- Senjyu, T.; Kashiwagi, T.; Uezato, K. Position control of ultrasonic motors using MRAC and dead-zone compensation with fuzzy inference. IEEE Trans. Power Electron. 2002, 2, 265–272. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S. Lithium–Sulfur Battery State-of-Charge Observability Analysis and Estimation. IEEE Trans. Power Electron. 2018, 33, 5847–5859. [Google Scholar] [CrossRef]
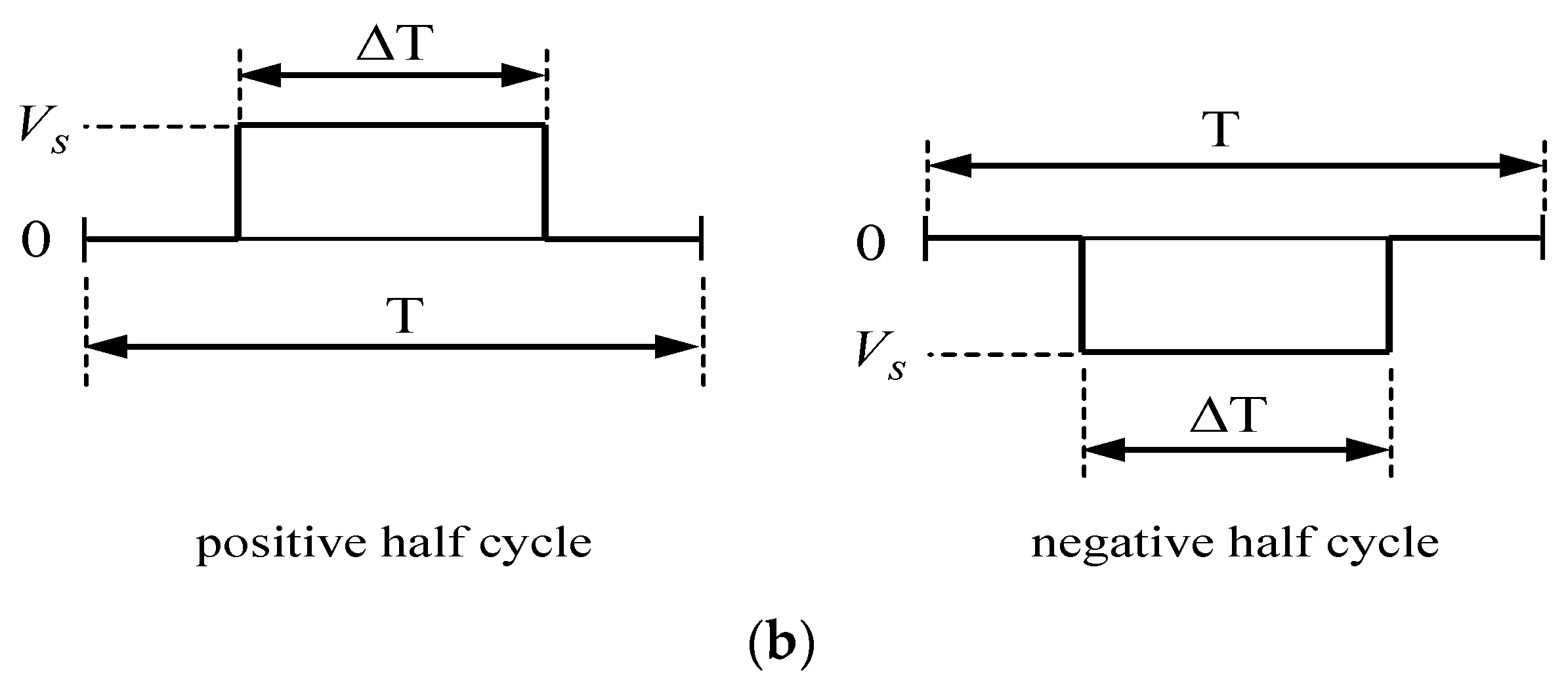

| Filter Inductor | |
| Filter Capacitor | |
| Resistive Load | |
| DC link Voltage | |
| Output Voltage and Frequency | |
| Switching Frequency |
| Proposed Approach | |
|---|---|
| Step-load changing | Filter parameter variations |
| Voltage drop | %THD |
| 4.6 Vrms | 0.02% |
| Conventional SMC | |
| Step-load changing | Filter parameter variations |
| Voltage drop | %THD |
| 22.9 Vrms | 14.32% |
| Proposed Approach | |
|---|---|
| Step-load changing | Rectifier load |
| Voltage drop | %THD |
| 6.5 Vrms | 1.82% |
| Conventional SMC | |
| Step-load changing | Rectifier load |
| Voltage drop | %THD |
| 24.5 Vrms | 10.21% |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, E.-C. Study and Application of Intelligent Sliding Mode Control for Voltage Source Inverters. Energies 2018, 11, 2544. https://doi.org/10.3390/en11102544
Chang E-C. Study and Application of Intelligent Sliding Mode Control for Voltage Source Inverters. Energies. 2018; 11(10):2544. https://doi.org/10.3390/en11102544
Chicago/Turabian StyleChang, En-Chih. 2018. "Study and Application of Intelligent Sliding Mode Control for Voltage Source Inverters" Energies 11, no. 10: 2544. https://doi.org/10.3390/en11102544
APA StyleChang, E.-C. (2018). Study and Application of Intelligent Sliding Mode Control for Voltage Source Inverters. Energies, 11(10), 2544. https://doi.org/10.3390/en11102544




