Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review
Abstract
1. Introduction
1.1. An Overview and Motivations
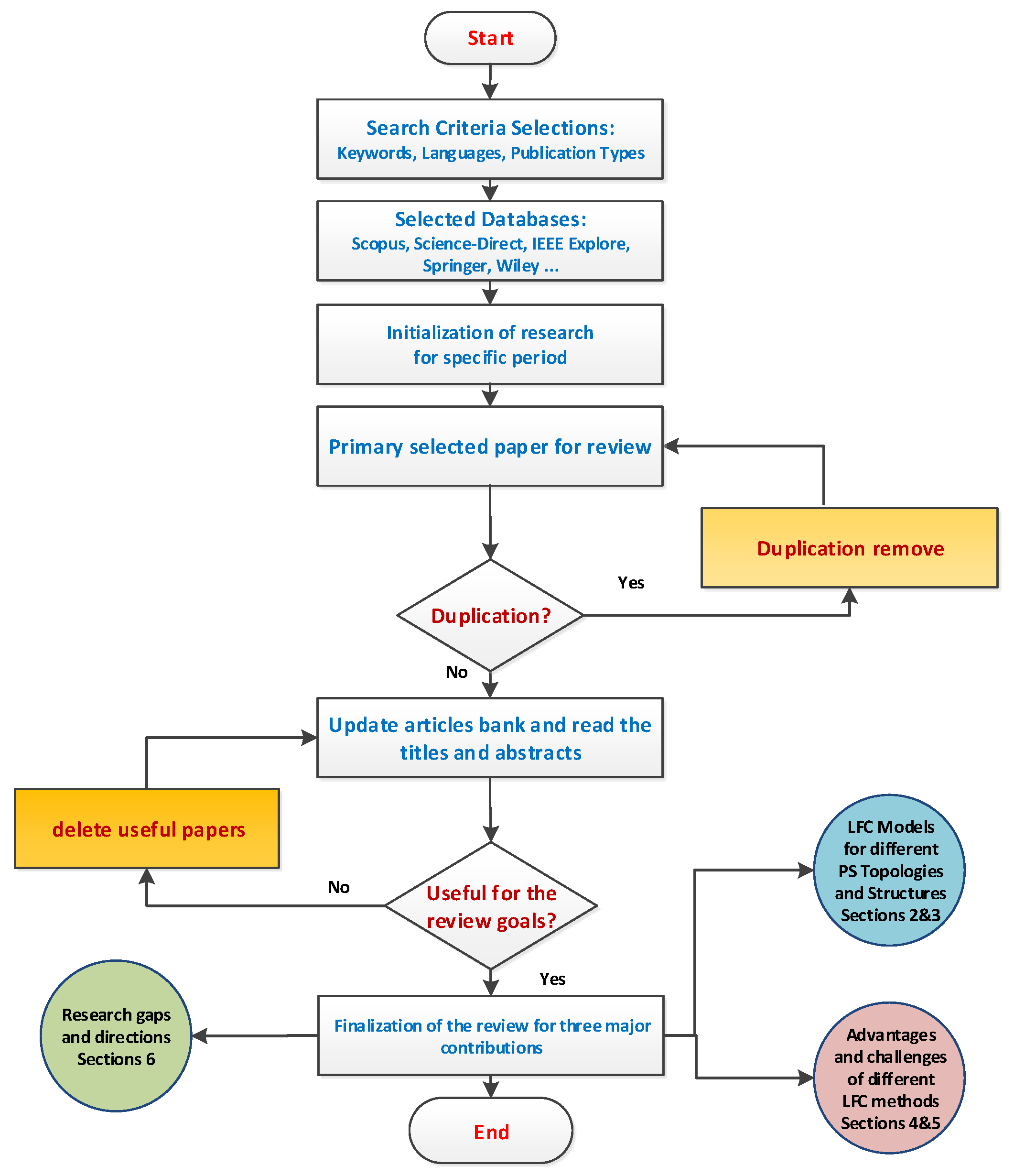
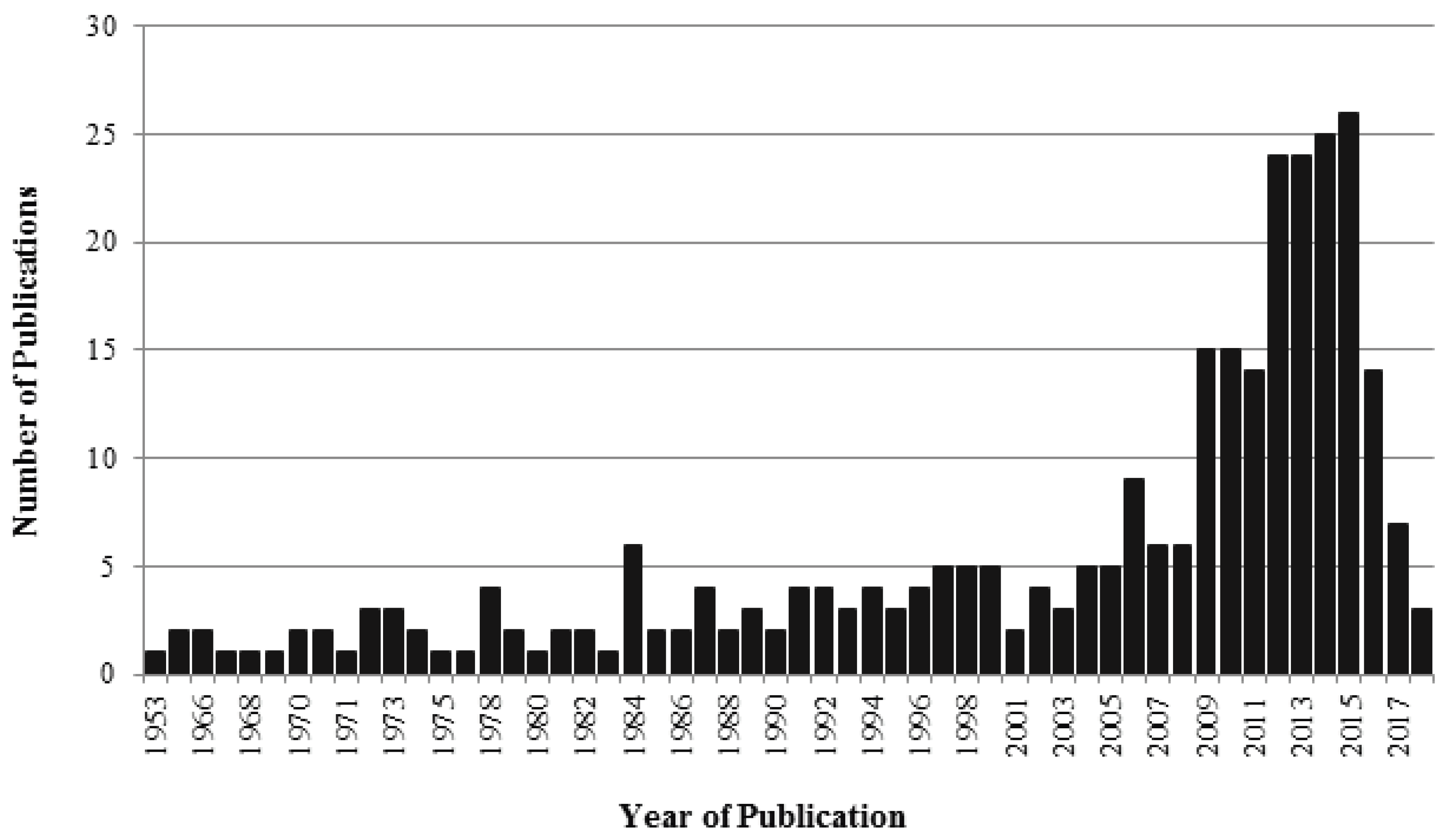
1.2. Survey Methodology
1.3. Contributions and Review Structure
2. Survey on Different Load Frequency Control (LFC) Topologies and Structures
2.1. Single-Area Power Systems
2.2. Dual-Area Power Systems
2.3. Three-Area Power Systems
2.4. Four-Area Power Systems
3. Survey on LFC Emerging Technologies and Concepts
3.1. Electric Power Systems with HVDC
3.2. Electric Power Systems under Deregulation
3.3. Power Systems with Distributed Generation and Renewable Energy Resources
3.4. Microgrids
3.5. Smart Grids
4. Taxonomy of Control Technique
4.1. Classical Control Methods
- The problem of optimally tuning the parameters of load frequency controllers needs more realistic methods.
- The robustness against parametric and nonparametric uncertainties need to be clearly-solved.
- These control approach should be developed to have tolerance against sensor and actuator faults.
- They need more investigation for their robustness against possible cyber-attack issues.
4.2. Optimal Control Methods
- The dynamic states of the power system need to be observed in real time.
- Cyber-attacks issues need to be considered in the designed dynamic estimators.
- The parametric uncertainties in the designed observers need to be considered.
- Dynamic observers that can eliminate the unknown input effects need to be developed.
4.3. Adaptive Schemes
4.4. Variable Structure Control Methods
- The performance of variable structure control methods for power systems with a high penetration level of highly variable sources such as renewable energy resources need to be investigated.
- This control is not optimally tuned in the above studies.
4.5. Robust Schemes
- They need a good knowledge of the system dynamic models which is not available in most power systems.
- They are usually designed for a band of uncertainties that is highly variable.
- Their applicability for power systems under some critical conditions such as cyber-attacks and unknown inputs are not investigated.
4.6. Centralized and Decentralized Control Methods
- All the above-mentioned studies present quasi-decentralized control approaches because the total power flow deviation through the tie-lines connected with other areas is requested for constructing the control signal. Since this measured signal is not locally measured, the proposed methods are not fully decentralized ones. However, it is a good research point to develop fully decentralized control approaches for LFC in power systems to improve the power system stability and security.
- It is important to consider cyber-attack issues in the future power system LFC.
- It is of great importance for future smart grids to design decentralized LFC based on wide-area measurement and control systems (WAMCS).
5. Soft Computing Based Control Schemes
5.1. Soft Computing Based Control Schemes
5.2. Objective Functions and Optimization Formulation
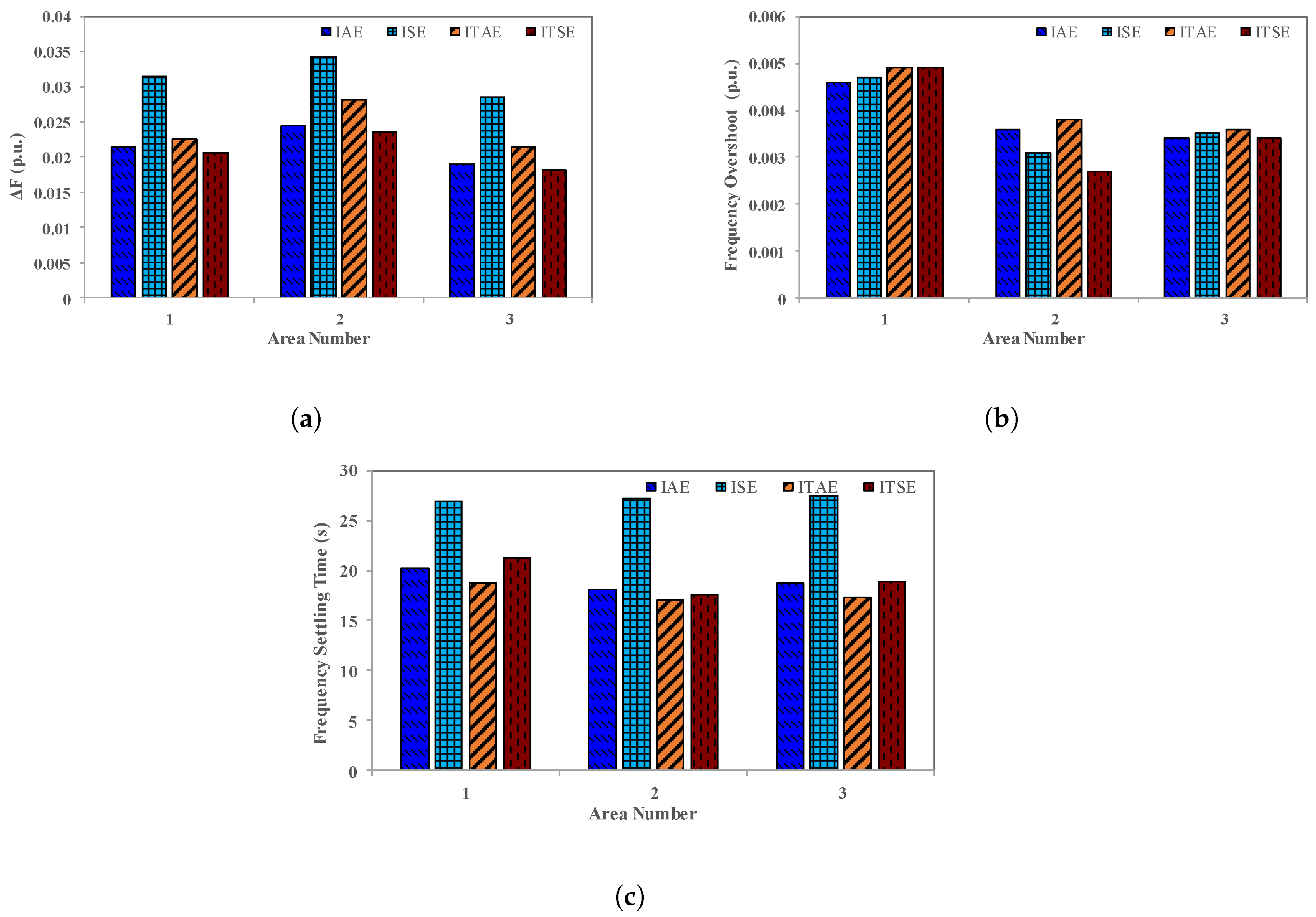
5.3. Comparison
6. Research Gaps and Directions
- Increasing the robustness of control methods applied to LFC
- Proposing optimal-robust control methods for LFC can handle both of the parameter and power production variations
- Proposing new objective functions for LFC that can improve the power system performance
- Investigating the reliability of LFC loops
- Increasing the ability of LFC system to handle cyber-attack issues
- Proposing suitable control methods that can detect and isolate sensor faults in LFC loops
- New fault diagnosis methods suitable for LFC are needed
- Designing control methods for power systems modeled without assumptions
- Considering the interactions between LFC and other control loops such as LFC and AVR control loops
- Proposing new control methods make use of WAMS
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ABC | Artificial bee colony |
| ACE | Area control error |
| AE | Aqua electrolyzer |
| AGC | Automatic generation control |
| BFO | Bacterial foraging optimization |
| BIA | Bat inspired algorithm |
| CS | Cuckoo search algorithm |
| DE | Differential evolution algorithm |
| DG | Distributed generation |
| DISCOs | Distribution companies |
| EVs | Electric vehicles |
| FA | Firefly algorithm |
| FACTS | Flexible AC transmission system |
| FC | Fuel cell |
| GDB | Governor dead band |
| GENCOs | Generation companies |
| GRC | Generation rate constraint |
| IAE | Integral of absolute error |
| ITAE | Integral of time multiplied by absolute error |
| ISE | Integral of squared error |
| ITSE | Integral of time multiplied by squared error |
| ID | Integral derivative |
| IDD | Integral plus double derivative |
| ISO | Independent system operator |
| PID | Proportional-integral-derivative |
| PIDD | Proportional-integral plus double derivative |
| PIDF | PID with filter |
| PSO | Particle swarm optimization |
| QO | Quasi oppositional |
| QOHS | Quasi-oppositional harmony search algorithm |
| SOA | Seeker optimization algorithm |
| STC | Self-tuning control |
| SOA | Seeker optimization algorithm |
| LFC | Load frequency control |
| LUSTLBO | hybrid local unimodal sampling and TLBO algorithm |
| MIMO-PID | Input-multiple output PID |
| TRANSCOs | Transmission companies |
| TLBO | Teaching-learning-based optimization |
| RERs | Renewable energy resources |
| PV | Photovoltaic |
| WAMCS | Wide-area measurement and control systems |
| WDO | Wind driven optimization algorithm |
| WTG | Wind turbine generator |
References
- Denyer, D.; Tranfield, D. Producing a systematic review. In The Sage Handbook of Organizational Research Methods; Sage Publications Ltd.: Thousand Oaks, CA, USA, 2009. [Google Scholar]
- Shamseer, L.; Moher, D.; Clarke, M.; Ghersi, D.; Liberati, A.; Petticrew, M.; Shekelle, P.; Stewart, L.A. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015: Elaboration and explanation. BMJ 2015, 349, g7647. [Google Scholar] [CrossRef] [PubMed]
- Moher, D.; Shamseer, L.; Clarke, M.; Ghersi, D.; Liberati, A.; Petticrew, M.; Shekelle, P.; Stewart, L.A. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015 statement. Syst. Rev. 2015, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Kirkham, J.J.; Dwan, K.M.; Altman, D.G.; Gamble, C.; Dodd, S.; Smyth, R.; Williamson, P.R. The impact of outcome reporting bias in randomised controlled trials on a cohort of systematic reviews. BMJ 2010, 340, c365. [Google Scholar] [CrossRef] [PubMed]
- Kirkham, J.J.; Altman, D.G.; Williamson, P.R. Bias due to changes in specified outcomes during the systematic review process. PLoS ONE 2010, 5, e9810. [Google Scholar] [CrossRef] [PubMed]
- Pandey, S.K.; Mohanty, S.R.; Kishor, N. A literature survey on load–frequency control for conventional and distribution generation power systems. Renew. Sustain. Energy Rev. 2013, 25, 318–334. [Google Scholar] [CrossRef]
- Jain, S.K.; Chakrabarti, S.; Singh, S. Review of load frequency control methods, Part-I: Introduction and pre-deregulation scenario. In Proceedings of the 2013 IEEE International Conference on Control, Automation, Robotics and Embedded Systems (CARE), Jabalpur, India, 16–18 December 2013; pp. 1–5. [Google Scholar]
- Ashmole, P.; Battlebury, D.; Bowdler, R. Power-system model for large frequency disturbances. Proc. Inst. Electr. Eng. 1974, 121, 601–608. [Google Scholar] [CrossRef]
- Pan, C.T.; Liaw, C.M. An adaptive controller for power system load-frequency control. IEEE Trans. Power Syst. 1989, 4, 122–128. [Google Scholar] [CrossRef]
- Rakhshani, E.; Rouzbehi, K.; Sadeh, S. A new combined model for simulation of mutual effects between LFC and AVR loops. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference (APPEEC 2009), Wuhan, China, 27–31 March 2009; pp. 1–5. [Google Scholar]
- Wang, Y.; Zhou, R.; Wen, C. Robust load-frequency controller design for power systems. IEE Proc. C Gener. Transm. Distrib. 1993, 140, 11–16. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, R.; Wen, C. New robust adaptive load-frequency control with system parametric uncertainties. IEE Proc. Gener. Transm. Distrib. 1994, 141, 184–190. [Google Scholar] [CrossRef]
- Jiang, L.; Yao, W.; Wu, Q.; Wen, J.; Cheng, S. Delay-dependent stability for load frequency control with constant and time-varying delays. IEEE Trans. Power Syst. 2012, 27, 932–941. [Google Scholar] [CrossRef]
- Doolla, S.; Bhatti, T. Load frequency control of an isolated small-hydro power plant with reduced dump load. IEEE Trans. Power Syst. 2006, 21, 1912–1919. [Google Scholar] [CrossRef]
- Kusic, G.; Sutterfield, J.; Caprez, A.; Haneline, J.; Bergman, B. Automatic generation control for hydro systems. IEEE Trans. Energy Convers. 1988, 3, 33–39. [Google Scholar] [CrossRef]
- Foord, T. Step response of a governed hydrogenerator. Proc. Inst. Electr. Eng. 1978, 125, 1247–1248. [Google Scholar] [CrossRef]
- Rakhshani, E.; Sadeh, J. Simulation of two-area AGC system in a competitive environment using reduced- order observer method. In Proceedings of the 5th International Conference on European Electricity Market (EEM 2008), Lisbon, Portugal, 28–30 May 2008; pp. 1–6. [Google Scholar]
- Singh, B.; Kasal, G.K. Voltage and frequency controller for a three-phase four-wire autonomous wind energy conversion system. IEEE Trans. Energy Convers. 2008, 23, 509–518. [Google Scholar] [CrossRef]
- Parmar, K.S.; Majhi, S.; Kothari, D. Multi-area load frequency control in a power system using optimal output feedback method. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems (PEDES) & 2010 Power India, New Delhi, India, 20–23 December 2010; pp. 1–5. [Google Scholar]
- Parmar, K.S.; Majhi, S.; Kothari, D. Load frequency control of a realistic power system with multi-source power generation. Int. J. Electr. Power Energy Syst. 2012, 42, 426–433. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Sarasúa, J.I. Failures during Load-Frequency Control Maneuvers in an Upgraded Hydropower Plant: Causes, Identification of Causes and Solution Proposals. Energies 2015, 8, 10584–10604. [Google Scholar] [CrossRef]
- Concordia, C.; Kirchmayer, L. Tie-line power and frequency control of electric power systems. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1953, 72, 562–572. [Google Scholar]
- Concordia, C.; Kirchmayer, L. Tie-line power and frequency control of electric power systems-Part II. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1954, 73, 133–146. [Google Scholar]
- Moorthi, V.; Aggarwal, R. Damping effects of excitation control in load-frequency control system. Proc. Inst. Electr. Eng. 1974, 121, 1409–1416. [Google Scholar] [CrossRef]
- Kumar, D.V. Intelligent controllers for automatic generation control. In Proceedings of the 1998 IEEE Region 10 International Conference on Global Connectivity in Energy, Computer, Communication and Control (TENCON’98), New Delhi, India, 17–19 December 1998; Volume 2, pp. 557–574. [Google Scholar]
- Chen, D.; Kumar, S.; York, M.; Wang, L. Smart automatic generation control. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Bose, A.; Atiyyah, I. Regulation error in load frequency control. IEEE Trans. Power Appar. Syst. 1980, 99, 650–657. [Google Scholar] [CrossRef]
- Kothari, M.; Nanda, J.; Kothari, D.; Das, D. Discrete-mode automatic generation control of a two-area reheat thermal system with new area control error. IEEE Trans. Power Syst. 1989, 4, 730–738. [Google Scholar] [CrossRef]
- Shirai, G. Load frequency sampled-data control via Lyapunov’s second method. Proc. IEEE 1981, 69, 129–130. [Google Scholar] [CrossRef]
- Hsu, Y.Y.; Chan, W.C. Coordinated frequency and voltage control of synchronous generators. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 2–10. [Google Scholar] [CrossRef]
- Kocaarslan, I.; Çam, E. Fuzzy logic controller in interconnected electrical power systems for load-frequency control. Int. J. Electr. Power Energy Syst. 2005, 27, 542–549. [Google Scholar] [CrossRef]
- Çam, E.; Kocaarslan, I. Load frequency control in two area power systems using fuzzy logic controller. Energy Convers. Manag. 2005, 46, 233–243. [Google Scholar] [CrossRef]
- Khodabakhshian, A.; Hooshmand, R. A new PID controller design for automatic generation control of hydro power systems. Int. J. Electr. Power Energy Syst. 2010, 32, 375–382. [Google Scholar] [CrossRef]
- Saikia, L.C.; Bharali, A.; Dixit, O.; Malakar, T.; Sharma, B.; Kouli, S. Automatic generation control of multi-area hydro system using classical controllers. In Proceedings of the 1st International Conference on Power and Energy in NERIST (ICPEN), Nirjuli, India, 28–29 December 2012; pp. 1–6. [Google Scholar]
- Bhatti, T. AGC of two area power system interconnected by AC/DC links with diverse sources in each area. Int. J. Electr. Power Energy Syst. 2014, 55, 297–304. [Google Scholar]
- Hore, D. An analysis of two area load frequency control with different types of feedback controllers. Int. J. Eng. Res. Technol. 2014, 3, 922–925. [Google Scholar]
- Kamboj, V.K.; Arora, K.; Khurana, P. Automatic generation control for interconnected hydro-thermal system with the help of conventional controllers. Int. J. Electr. Comput. Eng. 2012, 2, 547–552. [Google Scholar] [CrossRef]
- Verma, R.; Pal, S. Intelligent automatic generation control of two-area hydrothermal power system using ANN and fuzzy logic. In Proceedings of the 2013 International Conference on Communication Systems and Network Technologies (CSNT), Gwalior, India, 6–8 April 2013; pp. 552–556. [Google Scholar]
- Kumar, P.; Varshana, P.; Das, J. Two area LFC model reduction. In Proceedings of the 1998 IEEE Region 10 International Conference on Global Connectivity in Energy, Computer, Communication and Control (TENCON’98), New Delhi, India, 17–19 December 1998; Volume 1, pp. 186–188. [Google Scholar]
- Alhelou, H.H.; Golshan, M.H.; Askari-Marnani, J. Robust sensor fault detection and isolation scheme for interconnected smart power systems in presence of RER and EVs using unknown input observer. Int. J. Electr. Power Energy Syst. 2018, 99, 682–694. [Google Scholar] [CrossRef]
- Shankar, R.; Pradhan, S.; Chatterjee, K.; Mandal, R. A comprehensive state of the art literature survey on LFC mechanism for power system. Renew. Sustain. Energy Rev. 2017, 76, 1185–1207. [Google Scholar] [CrossRef]
- Bhatt, P.; Roy, R.; Ghoshal, S. Comparative performance evaluation of SMES–SMES, TCPS–SMES and SSSC–SMES controllers in automatic generation control for a two-area hydro–hydro system. Int. J. Electr. Power Energy Syst. 2011, 33, 1585–1597. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, K.; Yuan, K.; Teng, X. Tie-Line Bias Control Applicability to Load Frequency Control for Multi-Area Interconnected Power Systems of Complex Topology. Energies 2017, 10, 78. [Google Scholar] [CrossRef]
- Verma, R.; Pal, S. Fuzzy gain scheduled automatic generation control of two area multi unit power system. In Proceedings of the 2013 Students Conference on Engineering and Systems (SCES), Allahabad, India, 12–14 April 2013; pp. 1–6. [Google Scholar]
- Verma, Y.P.; Kumar, A. Load frequency control in deregulated power system with wind integrated system using fuzzy controller. Front. Energy 2013, 7, 245–254. [Google Scholar] [CrossRef]
- Tripathy, S.; Balasubramanian, R.; Chandramohanan Nair, P. Adaptive automatic generation control with superconducting magnetic energy storage in power systems. IEEE Trans. Energy Convers. 1992, 7, 434–441. [Google Scholar] [CrossRef]
- Lu, C.F.; Liu, C.C.; Wu, C.J. Effect of battery energy storage system on load frequency control considering governor deadband and generation rate constraint. IEEE Trans. Energy Convers. 1995, 10, 555–561. [Google Scholar]
- Ngamroo, I.; Mitani, Y.; Tsuji, K. Application of SMES coordinated with solid-state phase shifter to load frequency control. IEEE Trans. Appl. Superconduct. 1999, 9, 322–325. [Google Scholar] [CrossRef]
- Dutta, A.; Debbarma, S. Contribution of Electric Vehicles for Frequency Regulation in Presence of Diverse Power Sources and Transmission Links. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018. [Google Scholar]
- Davison, E.; Tripathi, N. The optimal decentralized control of a large power system: Load and frequency control. IEEE Trans. Autom. Control 1978, 23, 312–325. [Google Scholar] [CrossRef]
- Bevrani, H.; Daneshfar, F.; Daneshmand, P.R. Intelligent automatic generation control: Multi-agent Bayesian networks approach. In Proceedings of the 2010 IEEE International Symposium on Intelligent Control (ISIC), Yokohama, Japan, 8–10 September 2010; pp. 773–778. [Google Scholar]
- Yousef, H.A.; Khalfan, A.K.; Albadi, M.H.; Hosseinzadeh, N. Load frequency control of a multi-area power system: An adaptive fuzzy logic approach. IEEE Trans. Power Syst. 2014, 29, 1822–1830. [Google Scholar] [CrossRef]
- Saikia, L.C.; Paul, A.; Dash, P.; Choudhury, N.D. AGC of an interconnected multi-area hydrothermal system using a neuro-fuzzy controller. In Proceedings of the 2014 International Conference on Control, Instrumentation, Energy and Communication (CIEC), Calcutta, India, 31 January–2 February 2014; pp. 407–411. [Google Scholar]
- Shiva, C.K.; Mukherjee, V. A novel quasi-oppositional harmony search algorithm for automatic generation control of power system. Appl. Soft Comput. 2015, 35, 749–765. [Google Scholar] [CrossRef]
- Gondaliya, S.; Arora, K. Automatic generation control of multi area power plants with the help of advanced controller. IJERT 2015, 4, 470–474. [Google Scholar] [CrossRef]
- Adaryani, M.R.; Afrakhte, H. NARMA-L2 controller for three-area load frequency control. In Proceedings of the 19th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 17–19 May 2011; pp. 1–6. [Google Scholar]
- Rahmani, M.; Sadati, N. Hierarchical optimal robust load-frequency control for power systems. IET Gener. Transm. Distrib. 2012, 6, 303–312. [Google Scholar] [CrossRef]
- Shiroei, M.; Toulabi, M.R.; Ranjbar, A.M. Robust multivariable predictive based load frequency control considering generation rate constraint. Int. J. Electr. Power Energy Syst. 2013, 46, 405–413. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Anand, B. Automatic generation control of three area hydro-thermal power systems with electric and mechanical governor. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Coimbatore, India, 8–20 December 2014; pp. 1–6. [Google Scholar]
- Dong, L.; Zhang, Y.; Gao, Z. A robust decentralized load frequency controller for interconnected power systems. ISA Trans. 2012, 51, 410–419. [Google Scholar] [CrossRef] [PubMed]
- Bengiamin, N.; Chan, W. Multilevel load-frequency control of interconnected power systems. Proc. Inst. Electr. Eng. 1978, 125, 521–526. [Google Scholar] [CrossRef]
- Bevrani, H.; Mitani, Y.; Tsuji, K. Robust decentralised load-frequency control using an iterative linear matrix inequalities algorithm. IEE Proc. Gener. Transm. Distrib. 2004, 151, 347–354. [Google Scholar] [CrossRef]
- Ghoshal, S. Multi-area frequency and tie-line power flow control with fuzzy logic based integral gain scheduling. J. Inst. Eng. India Part El Electr. Eng. Div. 2003, 135–141. [Google Scholar]
- Bevrani, H.; Habibi, F.; Babahajyani, P.; Watanabe, M.; Mitani, Y. Intelligent frequency control in an AC microgrid: Online PSO-based fuzzy tuning approach. IEEE Trans. Smart Grid 2012, 3, 1935–1944. [Google Scholar] [CrossRef]
- Daneshfar, F.; Bevrani, H. Multiobjective design of load frequency control using genetic algorithms. Int. J. Electr. Power Energy Syst. 2012, 42, 257–263. [Google Scholar] [CrossRef]
- Yu, X.; Tomsovic, K. Application of linear matrix inequalities for load frequency control with communication delays. IEEE Trans. Power Syst. 2004, 19, 1508–1515. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Anand, B.; Dey, N.; Ashour, A.S. Artificial intelligence in performance analysis of load frequency control in thermal-wind-hydro power systems. Int. J. Adv. Comput. Sci. Appl. 2015, 6, 203–212. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Anand, B.; Dey, N. Evolutionary algorithm based LFC of single area thermal power system with different steam configurations and non-linearity. In Information Systems Design and Intelligent Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 185–194. [Google Scholar]
- Jagatheesan, K.; Anand, B.; Samanta, S.; Dey, N.; Santhi, V.; Ashour, A.S.; Balas, V.E. Application of flower pollination algorithm in load frequency control of multi-area interconnected power system with nonlinearity. Neural Comput. Appl. 2017, 28, 475–488. [Google Scholar] [CrossRef]
- Davison, E.; Tripathi, N. Decentralized tuning regulators: An application to solve the load and frequency control problem for a large power system. In Proceedings of the 18th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Fort Lauderdale, FL, USA, 12–14 December 1979; Volume 18, pp. 879–885. [Google Scholar]
- Mola, S.M.; Jahed-Motlagh, M.R. Robust decentralized load frequency control of multi-area power system via performance limitations using LMIs. In Proceedings of the Fifth International Conference on Intelligent Control and Information Processing (ICICIP), Dalian, China, 18–20 August 2014; pp. 108–114. [Google Scholar]
- Khooban, M.H.; Niknam, T. A new intelligent online fuzzy tuning approach for multi-area load frequency control: Self Adaptive Modified Bat Algorithm. Int. J. Electr. Power Energy Syst. 2015, 71, 254–261. [Google Scholar] [CrossRef]
- Malik, O.; Kumar, A.; Hope, G. A load frequency control algorithm based on a generalized approach. IEEE Trans. Power Syst. 1988, 3, 375–382. [Google Scholar] [CrossRef]
- Prakash, S.; Sinha, S. Four area Load Frequency Control of interconnected hydro-thermal power system by Intelligent PID control technique. In Proceedings of the 2012 Students Conference on Engineering and Systems (SCES), Allahabad, India, 16–18 March 2012; pp. 1–6. [Google Scholar]
- Prakash, S.; Bhardwaj, A.; Sinha, S. Neuro fuzzy hybrid intelligent approach for four-area load frequency control of interconnected power system. In Proceedings of the 2nd International Conference on Power, Control and Embedded Systems (ICPCES), Allahabad, India, 17–19 December 2012; pp. 1–7. [Google Scholar]
- Padhan, D.G.; Majhi, S. A new control scheme for PID load frequency controller of single-area and multi-area power systems. ISA Trans. 2013, 52, 242–251. [Google Scholar] [CrossRef] [PubMed]
- Vrdoljak, K.; Perić, N.; Petrović, I. Sliding mode based load-frequency control in power systems. Electr. Power Syst. Res. 2010, 80, 514–527. [Google Scholar] [CrossRef]
- Yang, T.; Cimen, H.; Zhu, Q. Decentralised load-frequency controller design based on structured singular values. IEE Proc. Gener. Transm. Distrib. 1998, 145, 7–14. [Google Scholar] [CrossRef]
- Kumar, A.; Malik, O.; Hope, G. Discrete variable structure controller for load frequency control of multiarea interconnected power systems. IEE Proc. C Gener. Transm. Distrib. 1987, 134, 116–122. [Google Scholar] [CrossRef]
- Du, X.; Li, P. Fuzzy logic control optimal realization using GA for multi-area AGC systems. Int. J. Inf. Technol. 2006, 12, 63–72. [Google Scholar]
- Tan, W. Unified tuning of PID load frequency controller for power systems via IMC. IEEE Trans. Power Syst. 2010, 25, 341–350. [Google Scholar] [CrossRef]
- Aggarwal, R.P.; Bergseth, F.R. Large Signal Dynamics of Load-Frequency Control Systems and Their Optimization Using Nonlinear Programming: I. IEEE Trans. Power Appar. Syst. 1968, 87, 527–532. [Google Scholar] [CrossRef]
- Ibraheem; Kumar, P. Current status of the Indian power system and dynamic performance enhancement of hydro power systems with asynchronous tie lines. Electr. Power Compon. Syst. 2003, 31, 605–626. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Umrao, R.; Malik, O.P. Adaptive polar fuzzy logic based load frequency controller. Int. J. Electr. Power Energy Syst. 2015, 66, 154–159. [Google Scholar] [CrossRef]
- Yoshida, Y.; Machida, T. Study of the effect of the DC link on frequency control in interconnected AC systems. IEEE Trans. Power Appar. Syst. 1969, 88, 1036–1042. [Google Scholar] [CrossRef]
- Bengiamin, N.; Chan, W. 3-Level load-frequency control of power systems interconnected by asynchronous tie lines. Proc. Inst. Electr. Eng. 1979, 126, 1198–1200. [Google Scholar] [CrossRef]
- Pham, T.N.; Trinh, H. Load frequency control of power systems with electric vehicles and diverse transmission links using distributed functional observers. IEEE Trans. Smart Grid 2016, 7, 238–252. [Google Scholar] [CrossRef]
- Abraham, R.J.; Das, D.; Patra, A. Load following in a bilateral market with local controllers. Int. J. Electr. Power Energy Syst. 2011, 33, 1648–1657. [Google Scholar] [CrossRef]
- Shayeghi, H. A robust decentralized power system load frequency control. J. Electr. Eng. 2008, 59, 281–293. [Google Scholar]
- Shayeghi, H.; Shayanfar, H.A.; Jalili, A. Multi stage fuzzy PID load frequency controller in a restructured power system. J. Electr. Eng. 2007, 58, 61–70. [Google Scholar]
- Shayeghi, H.; Shayanfar, H.A. Design of decentralized robust LFC in a competitive electricity environment. J. Electr. Eng. 2005, 56, 225–236. [Google Scholar]
- Delfino, B.; Fornari, F.; Massucco, S. Load-frequency control and inadvertent interchange evaluation in restructured power systems. IEE Proc. Gener. Transm. Distrib. 2002, 149, 607–614. [Google Scholar] [CrossRef]
- Donde, V.; Pai, M.; Hiskens, I.A. Simulation and optimization in an AGC system after deregulation. IEEE Trans. Power Syst. 2001, 16, 481–489. [Google Scholar] [CrossRef]
- Kumar, J.; Ng, K.H.; Sheble, G. AGC simulator for price-based operation. II. Case study results. IEEE Trans. Power Syst. 1997, 12, 533–538. [Google Scholar] [CrossRef]
- Kumar, J.; Ng, K.H.; Sheble, G. AGC simulator for price-based operation. I. A model. IEEE Trans. Power Syst. 1997, 12, 527–532. [Google Scholar] [CrossRef]
- Hosseini, S.; Etemadi, A. Adaptive neuro-fuzzy inference system based automatic generation control. Electr. Power Syst. Res. 2008, 78, 1230–1239. [Google Scholar] [CrossRef]
- Christie, R.D.; Bose, A. Load frequency control issues in power system operations after deregulation. IEEE Trans. Power Syst. 1996, 11, 1191–1200. [Google Scholar] [CrossRef]
- Debbarma, S.; Saikia, L.C.; Sinha, N. AGC of a multi-area thermal system under deregulated environment using a non-integer controller. Electr. Power Syst. Res. 2013, 95, 175–183. [Google Scholar] [CrossRef]
- Tan, W.; Zhang, H.; Yu, M. Decentralized load frequency control in deregulated environments. Int. J. Electr. Power Energy Syst. 2012, 41, 16–26. [Google Scholar] [CrossRef]
- Bhatt, P.; Roy, R.; Ghoshal, S. Optimized multi area AGC simulation in restructured power systems. Int. J. Electr. Power Energy Syst. 2010, 32, 311–322. [Google Scholar] [CrossRef]
- Sekhar, G.C.; Sahu, R.K.; Baliarsingh, A.; Panda, S. Load frequency control of power system under deregulated environment using optimal firefly algorithm. Int. J. Electr. Power Energy Syst. 2016, 74, 195–211. [Google Scholar] [CrossRef]
- Bevrani, H. Robust Power System Frequency Control; Springer: Berlin/Heidelberg, Germany, 2009; Volume 85. [Google Scholar]
- Parmar, K.S.; Majhi, S.; Kothari, D. LFC of an interconnected power system with multi-source power generation in deregulated power environment. Int. J. Electr. Power Energy Syst. 2014, 57, 277–286. [Google Scholar] [CrossRef]
- Chokpanyasuwan, C. Robot Fuzzy logic-PID Controller for Wind-Diesel Power System using Particle Swarm Optimization. In Proceedings of the GMSARN International Conference on Sustainable Development: Issues and Prospects for the GMS, Kunming, China, 12–14 November 2008. [Google Scholar]
- Katiraei, F.; Iravani, M.R. Power management strategies for a microgrid with multiple distributed generation units. IEEE Trans. Power Syst. 2006, 21, 1821–1831. [Google Scholar] [CrossRef]
- Hilloowala, R.M.; Sharaf, A.M. A rule-based fuzzy logic controller for a PWM inverter in a stand alone wind energy conversion scheme. In Proceedings of the Conference Record of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; pp. 2066–2073. [Google Scholar]
- Hilloowala, R.M.; Sharaf, A.M. A rule-based fuzzy logic controller for a PWM inverter in a stand alone wind energy conversion scheme. IEEE Trans. Ind. Appl. 1996, 32, 57–65. [Google Scholar] [CrossRef]
- Asano, H.; Yajima, K.; Kaya, Y. Influence of photovoltaic power generation on required capacity for load frequency control. IEEE Trans. Energy Convers. 1996, 11, 188–193. [Google Scholar] [CrossRef]
- Curtice, D.H.; Reddoch, T. An assessment of load frequency control impacts caused by small wind turbines. IEEE Trans. Power Appar. Syst. 1983, 102, 162–170. [Google Scholar] [CrossRef]
- Wrate, C.A.; Wozniak, L. Hydrogenerator system identification using a simple genetic algorithm. IEEE Trans. Energy Convers. 1997, 12, 60–65. [Google Scholar] [CrossRef]
- Jovanovic, S.; Hogg, B.; Fox, B. Intelligent adaptive turbine controller. IEEE Trans. Energy Convers. 1995, 10, 195–198. [Google Scholar] [CrossRef]
- Scott, G.; Wilreker, V.; Shaltens, R. Wind turbine generator interaction with diesel generators on an isolated power system. IEEE Trans. Power Appar. Syst. 1984, 103, 933–937. [Google Scholar] [CrossRef]
- Anaya-Lara, O.; Hughes, F.; Jenkins, N.; Strbac, G. Contribution of DFIG-based wind farms to power system short-term frequency regulation. IEE Proc. Gener. Transm. Distrib. 2006, 153, 164–170. [Google Scholar] [CrossRef]
- Ekanayake, J.; Jenkins, N. Comparison of the response of doubly fed and fixed-speed induction generator wind turbines to changes in network frequency. IEEE Trans. Energy Convers. 2004, 19, 800–802. [Google Scholar] [CrossRef]
- Ramtharan, G.; Jenkins, N.; Ekanayake, J. Frequency support from doubly fed induction generator wind turbines. IET Renew. Power Gener. 2007, 1, 3–9. [Google Scholar] [CrossRef]
- Chang-Chien, L.R.; Lin, W.T.; Yin, Y.C. Enhancing frequency response control by DFIGs in the high wind penetrated power systems. IEEE Trans. Power Syst. 2011, 26, 710–718. [Google Scholar] [CrossRef]
- Kayikçi, M.; Milanovic, J.V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances. IEEE Trans. Power Syst. 2009, 24, 859–867. [Google Scholar] [CrossRef]
- De Almeida, R.G.; Lopes, J.P. Participation of doubly fed induction wind generators in system frequency regulation. IEEE Trans. Power Syst. 2007, 22, 944–950. [Google Scholar] [CrossRef]
- Kanellos, F.; Hatziargyriou, N. Control of variable speed wind turbines equipped with synchronous or doubly fed induction generators supplying islanded power systems. IET Renew. Power Gener. 2009, 3, 96–108. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Wang, Y. Control of DFIG-based wind farms for power network frequency support. In Proceedings of the 2010 International Conference on Power System Technology (POWERCON), Hangzhou, China, 24–28 October 2010; pp. 1–6. [Google Scholar]
- Hughes, F.M.; Anaya-Lara, O.; Jenkins, N.; Strbac, G. Control of DFIG-based wind generation for power network support. IEEE Trans. Power Syst. 2005, 20, 1958–1966. [Google Scholar] [CrossRef]
- Ray, P.K.; Mohanty, S.R.; Kishor, N.; Mohanty, A. Small-signal analysis of hybrid distributed generation system with HVDC-link and energy storage elements. In Proceedings of the 2nd International Conference on Emerging Trends in Engineering and Technology (ICETET), Nagpur, India, 16–18 December 2009; pp. 1–6. [Google Scholar]
- Dhanalakshmi, R.; Palaniswami, S. ANFIS based neuro-fuzzy controller in LFC of wind-micro hydro-diesel hybrid power system. Int. J. Comput. Appl. 2012, 42, 28–35. [Google Scholar]
- Bhatti, T.; Al-Ademi, A.; Bansal, N. Load-frequency control of isolated wind-diesel microhydro hybrid power system (WDMHPS). Energy 1997, 22, 461–470. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T.; Yona, A.; Funabashi, T.; Kim, C.H. A coordinated control method for leveling PV output power fluctuations of PV–diesel hybrid systems connected to isolated power utility. IEEE Trans. Energy Convers. 2009, 24, 153–162. [Google Scholar] [CrossRef]
- Piagi, P.; Lasseter, R.H. Autonomous control of microgrids. In Proceedings of the Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 8. [Google Scholar] [CrossRef]
- Lasseter, R.H. Microgrids. In Proceedings of the Power Engineering Society Winter Meeting, New York, NY, USA, 27–31 January 2002; Volume 1, pp. 305–308. [Google Scholar]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Moreira, C.; Madureira, A.G.; Lopes, J.P. Defining control strategies for microgrids islanded operation. IEEE Trans. Power Syst. 2006, 21, 916–924. [Google Scholar]
- Madureira, A.; Moreira, C.; Lopes, J.P. Secondary load-frequency control for microgrids in islanded operation. In Proceedings of the International Conference on Renewable Energy and Power Quality, Malaga, Spain, 4–6 April 2005. [Google Scholar]
- Singh, A.K.; Yadav, N.K. Load frequency control in Microgrid. IJRCCT 2013, 2, 680–684. [Google Scholar]
- Alhelou, H.S.H.; Golshan, M.; Fini, M.H. Multi agent electric vehicle control based primary frequency support for future smart micro-grid. In Proceedings of the Smart Grid Conference (SGC), Tehran, Iran, 22–23 December 2015; pp. 22–27. [Google Scholar]
- Mohamad, F.; Teh, J.; Lai, C.M.; Chen, L.R. Development of Energy Storage Systems for Power Network Reliability: A Review. Energies 2018, 11, 2278. [Google Scholar] [CrossRef]
- Mohamad, F.; Teh, J. Impacts of Energy Storage System on Power System Reliability: A Systematic Review. Energies 2018, 11, 1749. [Google Scholar] [CrossRef]
- Yuen, C.; Oudalov, A.; Timbus, A. The provision of frequency control reserves from multiple microgrids. IEEE Trans. Ind. Electron. 2011, 58, 173–183. [Google Scholar] [CrossRef]
- Short, J.A.; Infield, D.G.; Freris, L.L. Stabilization of grid frequency through dynamic demand control. IEEE Trans. Power Syst. 2007, 22, 1284–1293. [Google Scholar] [CrossRef]
- Nandar, C.S.A. Robust PI control of smart controllable load for frequency stabilization of microgrid power system. Renew. Energy 2013, 56, 16–23. [Google Scholar] [CrossRef]
- Shimizu, K.; Masuta, T.; Ota, Y.; Yokoyama, A. Load frequency control in power system using vehicle-to-grid system considering the customer convenience of electric vehicles. In Proceedings of the 2010 International Conference on Power System Technology (POWERCON), Hangzhou, China, 24–28 October 2010; pp. 1–8. [Google Scholar]
- Samarakoon, K.; Ekanayake, J.; Jenkins, N. Investigation of domestic load control to provide primary frequency response using smart meters. IEEE Trans. Smart Grid 2012, 3, 282–292. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Vachirasricirikul, S.; Ngamroo, I. Robust LFC in a smart grid with wind power penetration by coordinated V2G control and frequency controller. IEEE Trans. Smart Grid 2014, 5, 371–380. [Google Scholar] [CrossRef]
- Masuta, T.; Yokoyama, A. Supplementary load frequency control by use of a number of both electric vehicles and heat pump water heaters. IEEE Trans. Smart Grid 2012, 3, 1253–1262. [Google Scholar] [CrossRef]
- Kanchev, H.; Lu, D.; Colas, F.; Lazarov, V.; Francois, B. Energy management and operational planning of a microgrid with a PV-based active generator for smart grid applications. IEEE Trans. Ind. Electron. 2011, 58, 4583–4592. [Google Scholar] [CrossRef]
- Sargolzaei, A.; Yen, K.; Abdelghani, M.N. Delayed inputs attack on load frequency control in smart grid. In Proceedings of the ISGT 2014, Washington, DC, USA, 19–22 February 2014. [Google Scholar]
- Liu, S.; Liu, X.P.; El Saddik, A. Denial-of-Service (DoS) attacks on load frequency control in smart grids. In Proceedings of the 2013 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 24–27 February 2013; pp. 1–6. [Google Scholar]
- Alhelou, H.H.; Golshan, M. Hierarchical plug-in EV control based on primary frequency response in interconnected smart grid. In Proceedings of the 24th Iranian Conference on Electrical Engineering (ICEE), Shiraz, Iran, 10–12 May 2016; pp. 561–566. [Google Scholar]
- Alhelou, H.H. Fault Detection and Isolation in Power Systems Using Unknown Input Observer. In Advanced Condition Monitoring and Fault Diagnosis of Electric Machines; IGI Global: Hershey, PA, USA, 2018; p. 38. [Google Scholar]
- Makdisie, C.; Haidar, B.; Alhelou, H.H. An Optimal Photovoltaic Conversion System for Future Smart Grids. In Handbook of Research on Power and Energy System Optimization; IGI Global: Hershey, PA, USA, 2018; pp. 601–657. [Google Scholar]
- Villena, J.; Vigueras-Rodríguez, A.; Gómez-Lázaro, E.; Fuentes-Moreno, J.Á.; Muñoz-Benavente, I.; Molina-García, Á. An Analysis of Decentralized Demand Response as Frequency Control Support under CriticalWind Power Oscillations. Energies 2015, 8, 12881–12897. [Google Scholar] [CrossRef]
- Izadkhast, S.; Garcia-Gonzalez, P.; Frías, P.; Ramirez-Elizondo, L.; Bauer, P. Aggregation of plug-in electric vehicles in distribution networks for primary frequency control. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–7. [Google Scholar]
- Das, D.; Nanda, J.; Kothari, M.; Kothari, D. Automatic generation control of a hydrothermal system with new area control error considering generation rate constraint. Electr. Mach. Power Syst. 1990, 18, 461–471. [Google Scholar] [CrossRef]
- Bechert, T.E.; Chen, N. Area automatic generation control by multi-pass dynamic programming. IEEE Trans. Power Appar. Syst. 1977, 96, 1460–1469. [Google Scholar] [CrossRef]
- Elgerd, O.I.; Fosha, C.E. Optimum megawatt-frequency control of multiarea electric energy systems. IEEE Trans. Power Appar. Syst. 1970, 89, 556–563. [Google Scholar] [CrossRef]
- Quazza, G. Noninteracting controls of interconnected electric power systems. IEEE Trans. Power Appar. Syst. 1966, 85, 727–741. [Google Scholar] [CrossRef]
- Kumari, N.; Jha, A. Particle Swarm Optimization and Gradient Descent Methods for Optimization of PI Controller for AGC of Multi-area Thermal-Wind-Hydro Power Plants. In Proceedings of the 2013 UKSim 15th International Conference on Computer Modelling and Simulation (UKSim), Cambridge, UK, 10–12 April 2013; pp. 536–541. [Google Scholar]
- Zhao, H.; Zhu, G.; Xu, C. A novel frequency control strategy of micro-source based on the secondary frequency regulation of power system. In Proceedings of the 2012 China International Conference on Electricity Distribution (CICED), Shanghai, China, 10–14 September 2012; pp. 1–6. [Google Scholar]
- Chatterjee, K. Design of dual mode PI controller for load frequency control. Int. J. Emerg. Electr. Power Syst. 2011, 11. [Google Scholar] [CrossRef]
- Vrdoljak, K.; Perić, N.; Šepac, D. Optimal distribution of load-frequency control signal to hydro power plants. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics (ISIE), Bari, Italy, 4–7 July 2010; pp. 286–291. [Google Scholar]
- Lakshmi, D.; Fathima, A.P.; Muthu, R. Pso based load frequency control for single area power system. Int. J. Sci. Eng. Res. 2014, 5, 12–17. [Google Scholar]
- Shiroei, M.; Ranjbar, A. Supervisory predictive control of power system load frequency control. Int. J. Electr. Power Energy Syst. 2014, 61, 70–80. [Google Scholar] [CrossRef]
- Suman, M.; Rao, M.V.G.; Kumar, G.N.; Sekhar, O.C. Load frequency control of three unit interconnected multimachine power system with PI and fuzzy controllers. In Proceedings of the 2014 International Conference on Advances in Electrical Engineering (ICAEE), Vellore, India, 9–11 January 2014; pp. 1–5. [Google Scholar]
- Bevrani, H.; Hiyama, T. On load–frequency regulation with time delays: Design and real-time implementation. IEEE Trans. Energy Convers. 2009, 24, 292–300. [Google Scholar] [CrossRef]
- Nanda, J.; Mishra, S.; Mishra, P.; Sajith, K. A novel classical controller for automatic generation control in thermal and hydrothermal systems. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems (PEDES) & 2010 Power India, New Delhi, India, 20–23 December 2010; pp. 1–6. [Google Scholar]
- Sahu, R.K.; Gorripotu, T.S.; Panda, S. A hybrid DE–PS algorithm for load frequency control under deregulated power system with UPFC and RFB. Ain Shams Eng. J. 2015, 6, 893–911. [Google Scholar] [CrossRef]
- Ray, P.K.; Mohanty, S.R.; Kishor, N. Proportional–integral controller based small-signal analysis of hybrid distributed generation systems. Energy Convers. Manag. 2011, 52, 1943–1954. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, A.; Chanana, S. Genetic fuzzy PID controller based on adaptive gain scheduling for load frequency control. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems (PEDES) & 2010 Power India, New Delhi, India, 20–23 December 2010; pp. 1–8. [Google Scholar]
- Daneshfar, F.; Bevrani, H.; Mansoori, F. Bayesian networks design of load-frequency control based on GA. In Proceedings of the 2nd International Conference on Control, Instrumentation and Automation (ICCIA), Shiraz, Iran, 27–29 December 2011; pp. 315–319. [Google Scholar]
- Yazdizadeh, A.; Ramezani, M.H.; Hamedrahmat, E. Decentralized load frequency control using a new robust optimal MISO PID controller. Int. J. Electr. Power Energy Syst. 2012, 35, 57–65. [Google Scholar] [CrossRef]
- Farahani, M.; Ganjefar, S.; Alizadeh, M. PID controller adjustment using chaotic optimisation algorithm for multi-area load frequency control. IET Control Theory Appl. 2012, 6, 1984–1992. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Rout, U.K. DE optimized parallel 2-DOF PID controller for load frequency control of power system with governor dead-band nonlinearity. Int. J. Electr. Power Energy Syst. 2013, 49, 19–33. [Google Scholar] [CrossRef]
- Debbarma, S.; Saikia, L.C.; Sinha, N. Automatic generation control of multi-area system using two degree of freedom fractional order PID controller: A preliminary study. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kowloon, China, 8–11 December 2013; pp. 1–6. [Google Scholar]
- Soheilirad, M.; Farzan, P.; Othman, M.; Karami, K.; Hojabri, M. PID controller adjustment for MA-LFC by using Imperialist Competitive Algorithm. In Proceedings of the 2013 IEEE 7th International Power Engineering and Optimization Conference (PEOCO), Langkawi, Malaysia, 3–4 June 2013; pp. 507–512. [Google Scholar]
- Dash, P.; Saikia, L.C.; Sinha, N. AGC of a multi-area interconnected system with FACTS and firefly optimized 2DOF PID controller. In Proceedings of the 2014 International Conference on Control, Instrumentation, Energy and Communication (CIEC), Calcutta, India, 31 January–2 February 2014; pp. 397–401. [Google Scholar]
- Naidu, K.; Mokhlis, H.; Bakar, A.A. Multiobjective optimization using weighted sum artificial bee colony algorithm for load frequency control. Int. J. Electr. Power Energy Syst. 2014, 55, 657–667. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Salem, F. LFC based adaptive PID controller using ANN and ANFIS techniques. J. Electr. Syst. Inf. Technol. 2014, 1, 212–222. [Google Scholar] [CrossRef]
- Agnihotri, S.; Waghmare, L.M. Regression model for tuning the PID controller with fractional order time delay system. Ain Shams Eng. J. 2014, 5, 1071–1081. [Google Scholar] [CrossRef]
- Sondhi, S.; Hote, Y.V. Fractional order PID controller for load frequency control. Energy Convers. Manag. 2014, 85, 343–353. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Padhan, S. A novel hybrid gravitational search and pattern search algorithm for load frequency control of nonlinear power system. Appl. Soft Comput. 2015, 29, 310–327. [Google Scholar] [CrossRef]
- Oliveira, E.J.; Honório, L.M.; Anzai, A.H.; Oliveira, L.W.; Costa, E.B. Optimal transient droop compensator and PID tuning for load frequency control in hydro power systems. Int. J. Electr. Power Energy Syst. 2015, 68, 345–355. [Google Scholar] [CrossRef]
- Kouba, N.E.Y.; Menaa, M.; Hasni, M.; Boudour, M. Optimal control of frequency and voltage variations using PID controller based on particle swarm optimization. In Proceedings of the 4th International Conference on Systems and Control (ICSC), Sousse, Tunisia, 18–20 April 2015; pp. 424–429. [Google Scholar]
- Dhillon, S.S.; Lather, J.S.; Marwaha, S. Multi area load frequency control using particle swarm optimization and fuzzy rules. Procedia Comput. Sci. 2015, 57, 460–472. [Google Scholar] [CrossRef]
- Saikia, L.C.; Das, S.K.; Dash, P.; Raju, M. Multi—Area AGC with AC/DC link and BES and Cuckoo Search optimized PID controller. In Proceedings of the Third International Conference on Computer, Communication, Control and Information Technology (C3IT), Hooghly, India, 7–8 February 2015; pp. 1–6. [Google Scholar]
- Thirunavukarasu, R.; Chidambaram, I. PI2 controller based coordinated control with Redox Flow Battery and Unified Power Flow Controller for improved Restoration Indices in a deregulated power system. Ain Shams Eng. J. 2016, 7, 1011–1027. [Google Scholar] [CrossRef]
- Bensenouci, A.; Ghany, A.A. Step-wise optimum adaptive variable-structure load-frequency control design using simulated annealing. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 318–323. [Google Scholar]
- Chandrakala, K.V.; Balamurugan, S.; Sankaranarayanan, K. Variable structure fuzzy gain scheduling based load frequency controller for multi source multi area hydro thermal system. Int. J. Electr. Power Energy Syst. 2013, 53, 375–381. [Google Scholar] [CrossRef]
- Haes Alhelou, H.; Golsha, M.; Heydarian-Forushani, E.; Al-Sumaiti, A.; Siano, P. Decentralized Fractional Order Control Scheme for LFC of Deregulated Nonlinear Power Systems in Presence of EVs and RER. In Proceedings of the IEEE International conference on Smart Energy Systems and Technology, Sevilla, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar]
- Cohn, N. Considerations in the regulation of interconnected areas. IEEE Trans. Power Appar. Syst. 1967, 86, 1527–1538. [Google Scholar] [CrossRef]
- Cohn, N. Techniques for improving the control of bulk power transfers on interconnected systems. IEEE Trans. Power Appar. Syst. 1971, 90, 2409–2419. [Google Scholar] [CrossRef]
- Fosha, C.E.; Elgerd, O.I. The megawatt-frequency control problem: A new approach via optimal control theory. IEEE Trans. Power Appar. Syst. 1970, 89, 563–577. [Google Scholar] [CrossRef]
- Hain, Y.; Kulessky, R.; Nudelman, G. Identification-based power unit model for load-frequency control purposes. IEEE Trans. Power Syst. 2000, 15, 1313–1321. [Google Scholar] [CrossRef]
- Velusami, S.; Romar, K. Design of observer-based decentralized load-frequency controllers for interconnected power systems. Int. J. Power Energy Syst. 1997, 17, 152–160. [Google Scholar]
- Rubaai, A.; Udo, V. An adaptive control scheme for load-frequency control of multiarea power systems Part I. Identification and functional design. Electr. Power Syst. Res. 1992, 24, 183–188. [Google Scholar] [CrossRef]
- Feliachi, A. Load frequency control using reduced order models and local observers. Int. J. Energy Syst. 1987, 7, 72–75. [Google Scholar]
- Yamashita, K.; Taniguchi, T. Optimal observer design for load-frequency control. Int. J. Electr. Power Energy Syst. 1986, 8, 93–100. [Google Scholar] [CrossRef]
- Bohn, E.; Miniesy, S.M. Optimum load-frequency sampled-data control with randomly varying system disturbances. IEEE Trans. Power Appar. Syst. 1972, 91, 1916–1923. [Google Scholar] [CrossRef]
- Tacker, E.; Lee, C.; Reddoch, T.; Tan, T.; Julich, P. Optimal control of interconnected, electric energy systems—A new formulation. Proc. IEEE 1972, 60, 1239–1241. [Google Scholar] [CrossRef]
- Calovic, M. Linear regulator design for a load and frequency control. IEEE Trans. Power Appar. Syst. 1972, 91, 2271–2285. [Google Scholar] [CrossRef]
- Barcelo, W.R. Effect of power plant response on optimum load frequency control system design. IEEE Trans. Power Appar. Syst. 1973, 92, 254–258. [Google Scholar] [CrossRef]
- Kwatny, H.; Kalnitsky, K.; Bhatt, A. An optimal tracking approach to load-frequency control. IEEE Trans. Power Appar. Syst. 1975, 94, 1635–1643. [Google Scholar] [CrossRef]
- Doraiswami, R. A nonlinear load-frequency control design. IEEE Trans. Power Appar. Syst. 1978, 97, 1278–1284. [Google Scholar] [CrossRef]
- Moorthi, V.; Aggarwal, R. Suboptimal and near-optimal control of a load-frequency-control system. Proc. Inst. Electr. Eng. 1972, 119, 1653–1660. [Google Scholar] [CrossRef]
- Aldeen, M.; Trinh, H. Load-frequency control of interconnected power systems via constrained feedback control schemes. Comput. Electr. Eng. 1994, 20, 71–88. [Google Scholar] [CrossRef]
- Choi, S.; Sim, H.; Tan, K. Load frequency control via constant limited-state feedback. Electr. Power Syst. Res. 1981, 4, 265–269. [Google Scholar] [CrossRef]
- Aldeen, M.; Trinh, H. Combined modal and singular perturbation approach to decentralized control. Int. J. Syst. Sci. 1992, 23, 741–764. [Google Scholar] [CrossRef]
- Hasan, N.; Kumar, P. Sub-optimal automatic generation control of interconnected power system using constrained feedback control strategy. Int. J. Electr. Power Energy Syst. 2012, 43, 295–303. [Google Scholar] [CrossRef]
- Ibraheem; Kumar, P.; Hasan, N.; Nizamuddin. Sub-optimal automatic generation control of interconnected power system using output vector feedback control strategy. Electr. Power Compon. Syst. 2012, 40, 977–994. [Google Scholar] [CrossRef]
- Shirai, G. Load frequency control using Lyapunov’s second method: Bang-bang control of speed changer position. Proc. IEEE 1979, 67, 1458–1459. [Google Scholar] [CrossRef]
- Vajk, I.; Vajta, M.; Keviczky, L.; Haber, R.; Hetthéssy, J.; Kovacs, K. Adaptive load-frequency control of the hungarian power system. Automatica 1985, 21, 129–137. [Google Scholar] [CrossRef]
- Ross, C. Error adaptive control computer for interconnected power systems. IEEE Trans. Power Appar. Syst. 1966, 85, 742–749. [Google Scholar] [CrossRef]
- Kanniah, J.; Tripathy, S.; Malik, O.; Hope, G. Microprocessor-based adaptive load-frequency control. IEE Proc. C Gener. Transm. Distrib. 1984, 131, 121–128. [Google Scholar] [CrossRef]
- Shoults, R.R.; Ibarra, J.J. Multi-area adaptive LFC developed for a comprehensive AGC simulator. IEEE Trans. Power Syst. 1993, 8, 541–547. [Google Scholar] [CrossRef]
- Liaw, C. Design of a reduced-order adaptive load-frequency controller for an interconnected hydrothermal power system. Int. J. Control 1994, 60, 1051–1063. [Google Scholar] [CrossRef]
- Rubaai, A.; Udo, V. Self-tuning load frequency control: Multilevel adaptive approach. IEE Proc. Gener. Transm. Distrib. 1994, 141, 285–290. [Google Scholar] [CrossRef]
- Lee, K.; Yee, H.; Teo, C. Self-tuning algorithm for automatic generation control in an interconnected power system. Electr. Power Syst. Res. 1991, 20, 157–165. [Google Scholar] [CrossRef]
- Yamashita, K.; Miyagi, H. Load frequency self-tuning regulator for interconnected power systems with unknown deterministic load disturbances. Int. J. Control 1989, 49, 1555–1568. [Google Scholar] [CrossRef]
- Sheirah, M.; Malik, O.; Hope, G. Minimum variance strategy for load-frequency control. Int. J. Electr. Power Energy Syst. 1986, 8, 120–126. [Google Scholar] [CrossRef]
- Sheirah, M.; Abd-El-Fattah, M. Improved load-frequency self-tuning regulator. Int. J. Control 1984, 39, 143–158. [Google Scholar] [CrossRef]
- Yamashita, K.; Miyagi, H. Multivariable self-tuning regulator for load frequency control system with interaction of voltage on load demand. IEE Proc. D Control Theory Appl. 1991, 138, 177–183. [Google Scholar] [CrossRef]
- Talaq, J.; Al-Basri, F. Adaptive fuzzy gain scheduling for load frequency control. IEEE Trans. Power Syst. 1999, 14, 145–150. [Google Scholar] [CrossRef]
- Siraj, S.; Ab Muin, M.; Nor, K.; Rahim, S.; Mohamad, M.; Mid, E.C. A robust adaptive predictive load frequency controller to compensate for model mismatch. In Proceedings of the 4th International Power Engineering and Optimization Conference (PEOCO), Shah Alam, Malaysia, 23–24 June 2010; pp. 33–37. [Google Scholar]
- Yousef, H. Adaptive fuzzy logic load frequency control of multi-area power system. Int. J. Electr. Power Energy Syst. 2015, 68, 384–395. [Google Scholar] [CrossRef]
- Rao, C.S. Adaptive Neuro Fuzzy based Load Frequency Control of multi area system under open market scenario. In Proceedings of the 2012 International Conference on Advances in Engineering, Science and Management (ICAESM), Nagapattinam, India, 30–31 March 2012; pp. 5–10. [Google Scholar]
- Hsu, Y.Y.; Chan, W. Optimal variable structure controller for the load-frequency control of interconnected hydrothermal power systems. Int. J. Electr. Power Energy Syst. 1984, 6, 221–229. [Google Scholar] [CrossRef]
- Ray, G.; Prasad, A.; Prasad, G. A new approach to the design of robust load-frequency controller for large scale power systems. Electr. Power Syst. Res. 1999, 51, 13–22. [Google Scholar] [CrossRef]
- Rosyiana Fitri, I.; Kim, J.S.; Song, H. High-Gain Disturbance Observer-Based Robust Load Frequency Control of Power Systems with Multiple Areas. Energies 2017, 10, 595. [Google Scholar] [CrossRef]
- Lim, K.; Wang, Y.; Zhou, R. Robust decentralised load–frequency control of multi-area power systems. IEE Proc. Gener. Transm. Distrib. 1996, 143, 377–386. [Google Scholar] [CrossRef]
- Stankovic, A.M.; Tadmor, G.; Sakharuk, T.A. On robust control analysis and design for load frequency regulation. IEEE Trans. Power Syst. 1998, 13, 449–455. [Google Scholar] [CrossRef]
- Karrari, M.; Shayeghi, H.; Abedi, M.; Menhaj, M. Design of H∞ controller load frequency control in electrical power systems. Amirkabir J. Sci. Technol. 1999, 11, 79–88. [Google Scholar]
- Bevrani, H. Robust load frequency controller in a deregulated environment: A/spl mu/-synthesis approach. In Proceedings of the 1999 IEEE International Conference on Control Applications, Kohala Coast, HI, USA, 22–27 August 1999; Volume 1, pp. 616–621. [Google Scholar]
- Chaudhuri, B.; Pal, B.C.; Zolotas, A.C.; Jaimoukha, I.M.; Green, T.C. Mixed-sensitivity approach to H/sub/spl infin//control of power system oscillations employing multiple FACTS devices. IEEE Trans. Power Syst. 2003, 18, 1149–1156. [Google Scholar] [CrossRef]
- Azzam, M.; Mohamed, Y.S. Robust controller design for automatic generation control based on Q-parameterization. Energy Convers. Manag. 2002, 43, 1663–1673. [Google Scholar] [CrossRef]
- Azzam, M. Robust automatic generation control. In Proceedings of the International Conference on Simulation, York, UK, 30 September–2 October 1998. [Google Scholar]
- Kazemi, A.; Andami, H. A decentralized fuzzy logic enhanced variable structure controller applied to load frequency control system. Iran. J. Sci. Technol. Trans. B 2004, 28, 295–303. [Google Scholar]
- Ha, Q.; Trinh, H. A variable structure-based controller with fuzzy tuning for load-frequency control. Int. J. Power Energy Syst. 2000, 20, 146–154. [Google Scholar]
- Ngamroo, I.; Tippayachai, J.; Dechanupaprittha, S. Robust decentralised frequency stabilisers design of static synchronous series compensators by taking system uncertainties into consideration. Int. J. Electr. Power Energy Syst. 2006, 28, 513–524. [Google Scholar] [CrossRef]
- Tan, W.; Xu, Z. Robust analysis and design of load frequency controller for power systems. Electr. Power Syst. Res. 2009, 79, 846–853. [Google Scholar] [CrossRef]
- Ishii, T.; Shirai, G.; Fujita, G. Decentralized load frequency based on H inf control. Electr. Eng. Jpn. 2001, 136, 28–38. [Google Scholar] [CrossRef]
- Bevrani, H.; Mitani, Y.; Tsuji, K. Sequential design of decentralized load frequency controllers using μ synthesis and analysis. Energy Convers. Manag. 2004, 45, 865–881. [Google Scholar] [CrossRef]
- Tan, W.; Zhou, H. Robust analysis of decentralized load frequency control for multi-area power systems. Int. J. Electr. Power Energy Syst. 2012, 43, 996–1005. [Google Scholar] [CrossRef]
- Bensenouci, A.; Ghany, A.A. Mixed H∞/H2 with pole-placement design of robust LMI-based output feedback controllers for multi-area load frequency control. In Proceedings of the International Conference on “Computer as a Tool” (EUROCON 2007), Warsaw, Poland, 9–12 September 2007; pp. 1561–1566. [Google Scholar]
- Ćalović, M.S. Automatic generation control: Decentralized area-wise optimal solution. Electr. Power Syst. Res. 1984, 7, 115–139. [Google Scholar] [CrossRef]
- Aldeen, M.; Marsh, J. Observability, controllability and decentralized control of interconnected power systems. Comput. Electr. Eng. 1990, 16, 207–220. [Google Scholar] [CrossRef]
- Yang, T.; Ding, Z.; Yu, H. Decentralised power system load frequency control beyond the limit of diagonal dominance. Int. J. Electr. Power Energy Syst. 2002, 24, 173–184. [Google Scholar] [CrossRef]
- Yang, M.S. Decentralized sliding mode stabilizer design for multi-area interconnected power systems. In Proceedings of the 2000 IEEE International Symposium on Industrial Electronics, Puebla, Mexico, 4–8 December 2000; Volume 1, pp. 185–190. [Google Scholar]
- Aldeen, M. Interaction modelling approach to distributed control with application to power systems. Int. J. Control 1991, 53, 1035–1054. [Google Scholar] [CrossRef]
- Aldeen, M.; Marsh, J. Decentralised proportional-plus-integral design method for interconnected power systems. IEE Proc. C Gener. Transm. Distrib. 1991, 138, 263–274. [Google Scholar] [CrossRef]
- Feliachi, A. Optimal decentralized load frequency control. IEEE Trans. Power Syst. 1987, 2, 379–385. [Google Scholar] [CrossRef]
- Park, Y.M.; Lee, K.Y. Optimal decentralized load frequency control. Electr. Power Syst. Res. 1984, 7, 279–288. [Google Scholar] [CrossRef]
- Kawabata, H.; Kido, M. A decentralized scheme of load frequency control of power system. Electr. Eng. Jpn. 1982, 102, 100–106. [Google Scholar] [CrossRef]
- Muñoz-Benavente, I.; Gómez-Lázaro, E.; García-Sánchez, T.; Vigueras-Rodríguez, A.; Molina-García, A. Implementation and assessment of a decentralized load frequency control: Application to power systems with high wind energy penetration. Energies 2017, 10, 151. [Google Scholar] [CrossRef]
- De Mello, F.; Mills, R.; B’Rells, W. Automatic generation control part II-Digital control techniques. IEEE Trans. Power Appar. Syst. 1973, 92, 716–724. [Google Scholar] [CrossRef]
- Mills, R.; B’Rells, W. Automatic generation control part I-Process modeling. IEEE Trans. Power Appar. Syst. 1973, 92, 710–715. [Google Scholar] [CrossRef]
- Geromel, J.; Peres, P. Decentralised load-frequency control. IEE Proc. D Control Theory Appl. 1985, 132, 225–230. [Google Scholar] [CrossRef]
- Shirai, G. Load frequency control using a governor and voltage controls vis a new approach. Proc. IEEE 1978, 66, 1293–1295. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Ismail, A. A decentralized reliable automatic generation control. In Proceedings of the International Conference on Electric Power and Energy Conversion Systems (EPECS’09), Sharjah, UAE, 10–12 November 2009; pp. 1–6. [Google Scholar]
- Xi, L.; Yu, T.; Yang, B.; Zhang, X. A novel multi-agent decentralized win or learn fast policy hill-climbing with eligibility trace algorithm for smart generation control of interconnected complex power grids. Energy Convers. Manag. 2015, 103, 82–93. [Google Scholar] [CrossRef]
- Yadaiah, N.; Srinivas, P.S. Intelligent decentralized controllers for multi area power systems. In Proceedings of the 1st IEEE Conference on Industrial Electronics and Applications, Singapore, 24–26 May 2006; pp. 1–6. [Google Scholar]
- Pandey, S.; Mohanty, S.R.; Kishor, N.; Payasi, R.P. Iterative linear matrix inequality algorithm based decentralized controller for load frequency control of two-area thermal power systems. In Proceedings of the 2013 International Conference on Power, Energy and Control (ICPEC), Sri Rangalatchum Dindigul, India, 6–8 February 2013; pp. 431–436. [Google Scholar]
- Ansarian, M.; Shakouri, G.; Nazarzadeh, J.; Sadeghzadeh, S. A Novel Neuro-Optimal Approach for Decentralized LFC Design in multi-area power system. In Proceedings of the IEEE International Power and Energy Conference (PECon’06), Putra Jaya, Malaysia, 28–29 November 2006; pp. 167–172. [Google Scholar]
- Rezvantalab, J.; Kazemi, M.; Seddigh, A.K. Multi-area robust decentralized Load Frequency Controller design in a restructured power system using Quantitative Feedback Theory. In Proceedings of the International Conference on Electric Power and Energy Conversion Systems (EPECS’09), Sharjah, UAE, 10–12 November 2009; pp. 1–6. [Google Scholar]
- Zhou, H.; Hao, Y.; Tan, W. Partially decentralized load frequency control of multi-area power systems in deregulated environments. In Proceedings of the 11th World Congress on Intelligent Control and Automation (WCICA), Shenyang, China, 29 June–4 July 2014; pp. 4704–4709. [Google Scholar]
- Toulabi, M.; Shiroei, M.; Ranjbar, A. Robust analysis and design of power system load frequency control using the Kharitonov’s theorem. Int. J. Electr. Power Energy Syst. 2014, 55, 51–58. [Google Scholar] [CrossRef]
- Sudha, K.; Santhi, R.V. Robust decentralized load frequency control of interconnected power system with generation rate constraint using type-2 fuzzy approach. Int. J. Electr. Power Energy Syst. 2011, 33, 699–707. [Google Scholar] [CrossRef]
- Mi, Y.; Fu, Y.; Wang, C.; Wang, P. Decentralized sliding mode load frequency control for multi-area power systems. IEEE Trans. Power Syst. 2013, 28, 4301–4309. [Google Scholar] [CrossRef]
- Hiyama, T. Design of decentralised load-frequency regulators for interconnected power systems. IEE Proc. C Gener. Transm. Distrib. 1982, 129, 17–23. [Google Scholar] [CrossRef]
- Taher, S.A.; Hematti, R.; Abdolalipour, A.; Tabei, S.H. Optimal decentralized load frequency control using HPSO algorithms in deregulated power systems. Am. J. Appl. Sci. 2008, 5, 1167–1174. [Google Scholar] [CrossRef]
- Ganapathy, S.; Velusami, S. Design of MOEA based Decentralized Load-Frequency Controllers for Interconnected Power Systems with AC-DC Parallel Tie-lines. Int. J. Recent Trends Eng. 2009, 2, 357–361. [Google Scholar] [CrossRef]
- Chidambaram, I.; Paramasivam, B. Genetic algorithm based decentralized controller for load-frequency control of interconnected power systems with RFB considering TCPS in the tie-line. Int. J. Electron. Eng. Res. 2009, 1, 299–312. [Google Scholar]
- Tan, W. Tuning of PID load frequency controller for power systems. Energy Convers. Manag. 2009, 50, 1465–1472. [Google Scholar] [CrossRef]
- Alrifai, M.T.; Hassan, M.F.; Zribi, M. Decentralized load frequency controller for a multi-area interconnected power system. Int. J. Electr. Power Energy Syst. 2011, 33, 198–209. [Google Scholar] [CrossRef]
- Abdel-Magid, Y.; Dawoud, M. Genetic algorithms applications in load frequency control. In Proceedings of the 1st International Conference on Genetic Algorithms in Engineering Systems: Innovations and Applications (GALESIA), Sheffield, UK, 12–14 September 1995. [Google Scholar]
- Gautam, S.K.; Goyal, N. Improved particle swarm optimization based load frequency control in a single area power system. In Proceedings of the 2010 Annual IEEE India Conference (INDICON), Kolkata, India, 17–19 December 2010; pp. 1–4. [Google Scholar]
- Bhatt, P.; Ghoshal, S.; Roy, R.; Ghosal, S. Load frequency control of interconnected restructured power system along with DFIG and coordinated operation of TCPS-SMES. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems (PEDES) & 2010 Power India, New Delhi, India, 20–23 December 2010; pp. 1–6. [Google Scholar]
- Kumari, N.; Jha, A. Frequency control of multi-area power system network using PSO based LQR. In Proceedings of the 6th IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014; pp. 1–6. [Google Scholar]
- Shayeghi, H.; Shayanfar, H.; Jalili, A. LFC design of a deregulated power system with TCPS using PSO. Int. J. Electr. Electron. Eng. 2009, 3, 632–640. [Google Scholar]
- Mohanty, B.; Panda, S.; Hota, P. Controller parameters tuning of differential evolution algorithm and its application to load frequency control of multi-source power system. Int. J. Electr. Power Energy Syst. 2014, 54, 77–85. [Google Scholar] [CrossRef]
- Rout, U.K.; Sahu, R.K.; Panda, S. Design and analysis of differential evolution algorithm based automatic generation control for interconnected power system. Ain Shams Eng. J. 2013, 4, 409–421. [Google Scholar] [CrossRef]
- Sahu, B.K.; Pati, S.; Panda, S. Hybrid differential evolution particle swarm optimisation optimised fuzzy proportional–integral derivative controller for automatic generation control of interconnected power system. IET Gener. Transm. Distrib. 2014, 8, 1789–1800. [Google Scholar] [CrossRef]
- Sahu, R.K.; Sekhar, G.C.; Panda, S. DE optimized fuzzy PID controller with derivative filter for LFC of multi source power system in deregulated environment. Ain Shams Eng. J. 2015, 6, 511–530. [Google Scholar] [CrossRef]
- Saikia, L.C.; Chowdhury, A.; Shakya, N.; Shukla, S.; Soni, P.K. AGC of a multi area gas-thermal system using firefly optimized IDF controller. In Proceedings of the 2013 Annual IEEE India Conference (INDICON), Mumbai, India, 13–15 December 2013; pp. 1–6. [Google Scholar]
- Naidu, K.; Mokhlis, H.; Bakar, A.; Terzija, V.; Illias, H. Application of firefly algorithm with online wavelet filter in automatic generation control of an interconnected reheat thermal power system. Int. J. Electr. Power Energy Syst. 2014, 63, 401–413. [Google Scholar] [CrossRef]
- Panda, S.; Swain, S.C.; Mahapatra, S. A hybrid BFOA–MOL approach for FACTS-based damping controller design using modified local input signal. Int. J. Electr. Power Energy Syst. 2015, 67, 238–251. [Google Scholar] [CrossRef]
- Ali, E.; Abd-Elazim, S. BFOA based design of PID controller for two area Load Frequency Control with nonlinearities. Int. J. Electr. Power Energy Syst. 2013, 51, 224–231. [Google Scholar] [CrossRef]
- Balasundaram, P.; Akilandam, C.I. ABC algorithm based load-frequency controller for an interconnected power system considering nonlinearities and coordinated with UPFC and RFB. Int. J. Eng. Innov. Technol. 2012, 1, 1–11. [Google Scholar]
- Ghatuari, I.; Mishra, N.; Sahu, B.K. Performance analysis of automatic generation control of a two area interconnected thermal system with nonlinear governor using PSO and DE algorithm. In Proceedings of the 2013 International Conference on Energy Efficient Technologies for Sustainability (ICEETS), Nagercoil, India, 10–12 April 2013; pp. 1262–1266. [Google Scholar]
- Guo, X.; Liu, X. Particle swarm optimization sliding mode control on interconnected power system. In Proceedings of the 33rd Chinese Control Conference (CCC), Nanjing, China, 28–30 July 2014; pp. 93–97. [Google Scholar]
- Kouba, N.E.Y.; Menaa, M.; Hasni, M.; Boudour, M. A novel robust automatic generation control in interconnected multi-area power system based on bat inspired algorithm. In Proceedings of the 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015; pp. 1–6. [Google Scholar]
- Shiva, C.K.; Mukherjee, V. Automatic generation control of interconnected power system for robust decentralized random load disturbances using a novel quasi-oppositional harmony search algorithm. Int. J. Electr. Power Energy Syst. 2015, 73, 991–1001. [Google Scholar] [CrossRef]
- Shiva, C.K.; Mukherjee, V. Design and analysis of multi-source multi-area deregulated power system for automatic generation control using quasi-oppositional harmony search algorithm. Int. J. Electr. Power Energy Syst. 2016, 80, 382–395. [Google Scholar] [CrossRef]
- Pati, T.K.; Nayak, J.R.; Sahu, B.K. Application of TLBO algorithm to study the performance of automatic generation control of a two-area multi-units interconnected power system. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems (SPICES), Kozhikode, India, 19–21 February 2015; pp. 1–5. [Google Scholar]
- Dash, P.; Saikia, L.C.; Sinha, N. Comparison of performances of several FACTS devices using Cuckoo search algorithm optimized 2DOF controllers in multi-area AGC. Int. J. Electr. Power Energy Syst. 2015, 65, 316–324. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Ali, E. Cuckoo search algorithm based load frequency controller design for nonlinear interconnected power system. Int. J. Electr. Power Energy Syst. 2015, 73, 632–643. [Google Scholar] [CrossRef]
- Gholipour, E.; Nosratabadi, S.M. A new coordination strategy of SSSC and PSS controllers in power system using SOA algorithm based on Pareto method. Int. J. Electr. Power Energy Syst. 2015, 67, 462–471. [Google Scholar] [CrossRef]
- Sharma, Y.; Saikia, L.C. Automatic generation control of a multi-area ST–Thermal power system using Grey Wolf Optimizer algorithm based classical controllers. Int. J. Electr. Power Energy Syst. 2015, 73, 853–862. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Golshan, M.; Fini, M.H. Wind Driven Optimization Algorithm Application to Load Frequency Control in Interconnected Power Systems Considering GRC and GDB Nonlinearities. Electr. Power Compon. Syst. 2018. [Google Scholar]
- Zare, K.; Hagh, M.T.; Morsali, J. Effective oscillation damping of an interconnected multi-source power system with automatic generation control and TCSC. Int. J. Electr. Power Energy Syst. 2015, 65, 220–230. [Google Scholar] [CrossRef]
- Panda, S.; Yegireddy, N.K. Automatic generation control of multi-area power system using multi-objective non-dominated sorting genetic algorithm-II. Int. J. Electr. Power Energy Syst. 2013, 53, 54–63. [Google Scholar] [CrossRef]
- Hota, P.; Mohanty, B. Automatic generation control of multi source power generation under deregulated environment. Int. J. Electr. Power Energy Syst. 2016, 75, 205–214. [Google Scholar] [CrossRef]
- Abraham, R.J.; Das, D.; Patra, A. AGC system after deregulation considering TCPS in series with the tie-line. Int. J. Emerg. Electr. Power Syst. 2015, 16, 281–295. [Google Scholar] [CrossRef]
- Morsali, J.; Zare, K.; Hagh, M.T. Performance comparison of TCSC with TCPS and SSSC controllers in AGC of realistic interconnected multi-source power system. Ain Shams Eng. J. 2016, 7, 143–158. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, V.; Tyagi, B. Multi area AGC scheme using imperialist competition algorithm in restructured power system. Appl. Soft Comput. 2016, 48, 160–168. [Google Scholar] [CrossRef]
- Liu, X.; Kong, X.; Lee, K.Y. Distributed model predictive control for load frequency control with dynamic fuzzy valve position modelling for hydro–thermal power system. IET Control Theory Appl. 2016, 10, 1653–1664. [Google Scholar] [CrossRef]
- Morsali, J.; Zare, K.; Hagh, M.T. Applying fractional order PID to design TCSC-based damping controller in coordination with automatic generation control of interconnected multi-source power system. Eng. Sci. Technol. 2017, 20, 1–17. [Google Scholar] [CrossRef]
- Ma, M.; Zhang, C.; Liu, X.; Chen, H. Distributed Model Predictive Load Frequency Control of the Multi-Area Power System After Deregulation. IEEE Trans. Ind. Electron. 2017, 64, 5129–5139. [Google Scholar] [CrossRef]
- Arya, Y.; Kumar, N. BFOA-scaled fractional order fuzzy PID controller applied to AGC of multi-area multi-source electric power generating systems. Swarm Evol. Comput. 2017, 32, 202–218. [Google Scholar] [CrossRef]
- Pappachen, A.; Fathima, A.P. Load frequency control in deregulated power system integrated with SMES–TCPS combination using ANFIS controller. Int. J. Electr. Power Energy Syst. 2016, 82, 519–534. [Google Scholar] [CrossRef]
- Farahani, M.; Ganjefar, S. Solving LFC problem in an interconnected power system using superconducting magnetic energy storage. Phys. C Supercond. 2013, 487, 60–66. [Google Scholar] [CrossRef]
- Chaine, S.; Tripathy, M. Design of an optimal SMES for automatic generation control of two-area thermal power system using cuckoo search algorithm. J. Electr. Syst. Inf. Technol. 2015, 2, 1–13. [Google Scholar] [CrossRef]
- Selvaraju, R.K.; Somaskandan, G. Impact of energy storage units on load frequency control of deregulated power systems. Energy 2016, 97, 214–228. [Google Scholar] [CrossRef]
- Chidambaram, I.; Paramasivam, B. Optimized load-frequency simulation in restructured power system with redox flow batteries and interline power flow controller. Int. J. Electr. Power Energy Syst. 2013, 50, 9–24. [Google Scholar] [CrossRef]
- Shankar, R.; Chatterjee, K.; Bhushan, R. Impact of energy storage system on load frequency control for diverse sources of interconnected power system in deregulated power environment. Int. J. Electr. Power Energy Syst. 2016, 79, 11–26. [Google Scholar] [CrossRef]
- Arya, Y. AGC performance enrichment of multi-source hydrothermal gas power systems using new optimized FOFPID controller and redox flow batteries. Energy 2017, 127, 704–715. [Google Scholar] [CrossRef]
- Bhatt, P.; Roy, R.; Ghoshal, S. GA/particle swarm intelligence based optimization of two specific varieties of controller devices applied to two-area multi-units automatic generation control. Int. J. Electr. Power Energy Syst. 2010, 32, 299–310. [Google Scholar] [CrossRef]
- Mukherjee, V.; Ghoshal, S. Application of capacitive energy storage for transient performance improvement of power system. Electr. Power Syst. Res. 2009, 79, 282–294. [Google Scholar] [CrossRef]
- Ponnusamy, M.; Banakara, B.; Dash, S.S.; Veerasamy, M. Design of integral controller for load frequency control of static synchronous series compensator and capacitive energy source based multi area system consisting of diverse sources of generation employing imperialistic competition algorithm. Int. J. Electr. Power Energy Syst. 2015, 73, 863–871. [Google Scholar] [CrossRef]
- Mahto, T.; Mukherjee, V. A novel scaling factor based fuzzy logic controller for frequency control of an isolated hybrid power system. Energy 2017, 130, 339–350. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P. Capacitive energy storage with optimized controller for frequency regulation in realistic multisource deregulated power system. Energy 2018, 147, 1108–1128. [Google Scholar] [CrossRef]
- Fini, M.H.; Yousefi, G.R.; Alhelou, H.H. Comparative study on the performance of many-objective and single-objective optimisation algorithms in tuning load frequency controllers of multi-area power systems. IET Gener. Transm. Distrib. 2016, 10, 2915–2923. [Google Scholar] [CrossRef]
- Kumar, T.A.; Ramana, N. Tuning of Sliding mode observer optimal parameters for load frequency control in coordination with frequency controllable HVDC link in multi area deregulated power system. In Proceedings of the 2015 International Conference on Electrical, Electronics, Signals, Communication and Optimization (EESCO), Visakhapatnam, India, 24–25 January 2015. [Google Scholar]
- Kalyani, S.; Nagalakshmi, S.; Marisha, R. Load frequency control using battery energy storage system in interconnected power system. In Proceedings of the Third International Conference on Computing Communication & Networking Technologies (ICCCNT), Coimbatore, India, 26–28 July 2012; pp. 1–6. [Google Scholar]
- Sahu, R.K.; Gorripotu, T.S.; Panda, S. Automatic generation control of multi-area power systems with diverse energy sources using teaching learning based optimization algorithm. Eng. Sci. Technol. 2016, 19, 113–134. [Google Scholar] [CrossRef]

| Issue | Criterion |
|---|---|
| Sector | Power System (PS) |
| General Topic | PS operation and control |
| Discipline | Frequency control |
| Very specific topic | Load frequency control (LFC) |
| Keywords I | Load frequency control, automatic generation control, secondary frequency control |
| Keywords II | LFC, AGC, frequency regulation, supplementary frequency control |
| Language | English |
| Availability | Online available |
| Databases | Scopus, IEEE, Springer, ScienceDirect, Taylor and Francis, and Wiley |
| Publication type | Research articles, Conference papers, Books, and Standards |
| Issue | Number | Percentage |
|---|---|---|
| Articles | 256 | 81.79 |
| Conference papers | 54 | 17.25 |
| Standards | - | - |
| Books and book chapters | 3 | 0.96 |
| Reference | System Type | Number of | Generation Source | Area Type | Other Used | Controllers | Optimization |
|---|---|---|---|---|---|---|---|
| No. | Trad./Dereg. | Areas | Type | Multi/Single Source | Devices | Type | Technique |
| [170] | 2 | Thermal | - | 2-DOF PID | DE | ||
| [45] | 2 | Hydro–Thermal | DFIGs | FLC | Fuzzy | ||
| [296] | 2 | Hydro–Thermal–Gas | TCSC | I | IPSO | ||
| [103] | 2 | Hydro–Thermal–Gas | - | OOFC | - | ||
| [297] | 2 | Hydro–Thermal–Wind–Diesel | - | PIDD | TLBO | ||
| [298] | 2 | Thermal–Gas | - | I,PI,ID,PID | DE | ||
| [101] | 4 | Thermal | - | Fuzzy PID | FA | ||
| [299] | 2 | Thermal | TCPS | I | - | ||
| [300] | 2 | Thermal–Hydro–Gas | TCPS, TCSC | I | IPSO | ||
| [301] | Hydro–Thermal | - | PID | ICA | |||
| [302] | 4 | Hydro–Thermal | - | DMPC | DMPC | ||
| [289] | Thermal–Hydro–Gas | - | PID | QOHS | |||
| [303] | 2 | Thermal–Hydro–Gas | TCSC | FOPID | IPSO | ||
| [304] | 3 | Thermal | - | DMPC | DMPC | ||
| [305] | 2 | Thermal–Gas–Hydro | - | FOFPID | BFOA | ||
| [306] | 2 | Hydro–Thermal | SMES + TCPS | ANFISC | ANFIS-PS | ||
| [307] | 2 | Thermal | SMES | PID | PSA | ||
| [308] | 1 | Thermal | SMES | CHB-I | - | ||
| [309] | 2 | Thermal | SMES | I | CSA | ||
| [310] | 2 | Thermal | IPFC + RFB | I + FLC | BFO | ||
| [311] | 2 | Thermal–Hydro–Gas | RFB | I | OHS | ||
| [312] | 2 | Thermal–Hydro–Gas | RFB | FOFPID | ICA | ||
| [313] | 2 | Thermal—Hydro–Diesels | TCPS + CES | I | CRPSO | ||
| [314] | Thermal–Hydro | CES | I | CRPSO | |||
| [315] | 2 | Thermal–Hydro | SSSC + CES | I | ICA | ||
| [316] | 2 | Isolated-wind–diesel–IHPS | CES | SFFLC + PID | QOHS | ||
| [317] | 2 | Thermal–Hydro–Gas | CES + TCPS | PI | PSO-SCA |
| Controller | Parameters | ISE | IAE | ITSE | ITAE |
|---|---|---|---|---|---|
| I | Kp | 1.11756 | −0.6620 | −1.0433 | −1.0073 |
| I | Ki | −0.37987 | −2 | −2 | −1.5207 |
| I | Kd | −0.23455 | −1.1824 | −1.1538 | −1.2774 |
| I | N | 221.73313 | 127.20 | 279.6893 | 300 |
| II | Kp | −1.87535 | −2 | −1.85951 | −0.71544 |
| II | Ki | −0.85221 | −1.8080 | −2 | −1.869451 |
| II | Kd | 2 | −0.3039 | −0.43109 | −0.097959 |
| II | N | 1 | 11.8381 | 199.292 | 99.57012 |
| III | Kp | −2 | −2 | −2 | −1.95772 |
| III | Ki | −1.84575 | −1.800 | −1.9165 | −1.67929 |
| III | Kd | −1.46660 | −1.4519 | −1.51080 | −1.62555 |
| III | N | 209.546920 | 130.8763 | 291.22717 | 148.485 |
| Index | Symbol | IAE | ISE | ITAE | ITSE |
|---|---|---|---|---|---|
| Settling time (s) | 20.1700 | 27 | 18.6900 | 21.2600 | |
| Settling time (s) | 18.1400 | 27.2400 | 17.0300 | 17.5500 | |
| Settling time (s) | 18.7700 | 27.4100 | 17.3500 | 18.9300 | |
| Settling time (s) | 12.9800 | 28.8100 | 12.2200 | 14.8200 | |
| Settling time (s) | 10.8700 | 21.0500 | 9.7600 | 7.5500 | |
| Settling time (s) | 8.6700 | 19.7700 | 7.5200 | 7.7800 | |
| Maximum deviation (p.u) | 0.0215 | 0.0316 | 0.0225 | 0.0206 | |
| Maximum deviation (p.u) | 0.0245 | 0.0344 | 0.0282 | 0.0236 | |
| Maximum deviation (p.u) | 0.0191 | 0.0285 | 0.0215 | 0.0182 | |
| Maximum deviation (p.u) | 0.0044 | 0.0211 | 0.0039 | 0.0035 | |
| Maximum deviation (p.u) | 0.0025 | 0.0047 | 0.0052 | 0.0024 | |
| Maximum deviation (p.u) | 0.0012 | 0.0011 | 0.0016 | 9.5292 | |
| Maximum overshoot (p.u) | 0.0046 | 0.0047 | 0.0049 | 0.0049 | |
| Maximum overshoot (p.u) | 0.0036 | 0.0031 | 0.0038 | 0.0027 | |
| Maximum overshoot (p.u) | 0.0034 | 0.0035 | 0.0036 | 0.0034 | |
| Maximum overshoot (p.u) | 0.0026 | 0.0029 | 0.0031 | 0.0018 | |
| Maximum overshoot (p.u) | 0.0032 | 0.0038 | 0.0043 | 0.0023 | |
| Maximum overshoot (p.u) | 0.0015 | 0.0019 | 0.0023 | 0.0013 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhelou, H.H.; Hamedani-Golshan, M.-E.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies 2018, 11, 2497. https://doi.org/10.3390/en11102497
Alhelou HH, Hamedani-Golshan M-E, Zamani R, Heydarian-Forushani E, Siano P. Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies. 2018; 11(10):2497. https://doi.org/10.3390/en11102497
Chicago/Turabian StyleAlhelou, Hassan Haes, Mohamad-Esmail Hamedani-Golshan, Reza Zamani, Ehsan Heydarian-Forushani, and Pierluigi Siano. 2018. "Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review" Energies 11, no. 10: 2497. https://doi.org/10.3390/en11102497
APA StyleAlhelou, H. H., Hamedani-Golshan, M.-E., Zamani, R., Heydarian-Forushani, E., & Siano, P. (2018). Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies, 11(10), 2497. https://doi.org/10.3390/en11102497






