Development of an Advanced Rule-Based Control Strategy for a PHEV Using Machine Learning
Abstract
:1. Introduction
2. PHEV Model for Backward Simulator
2.1. Vehicle Configuration and Specification
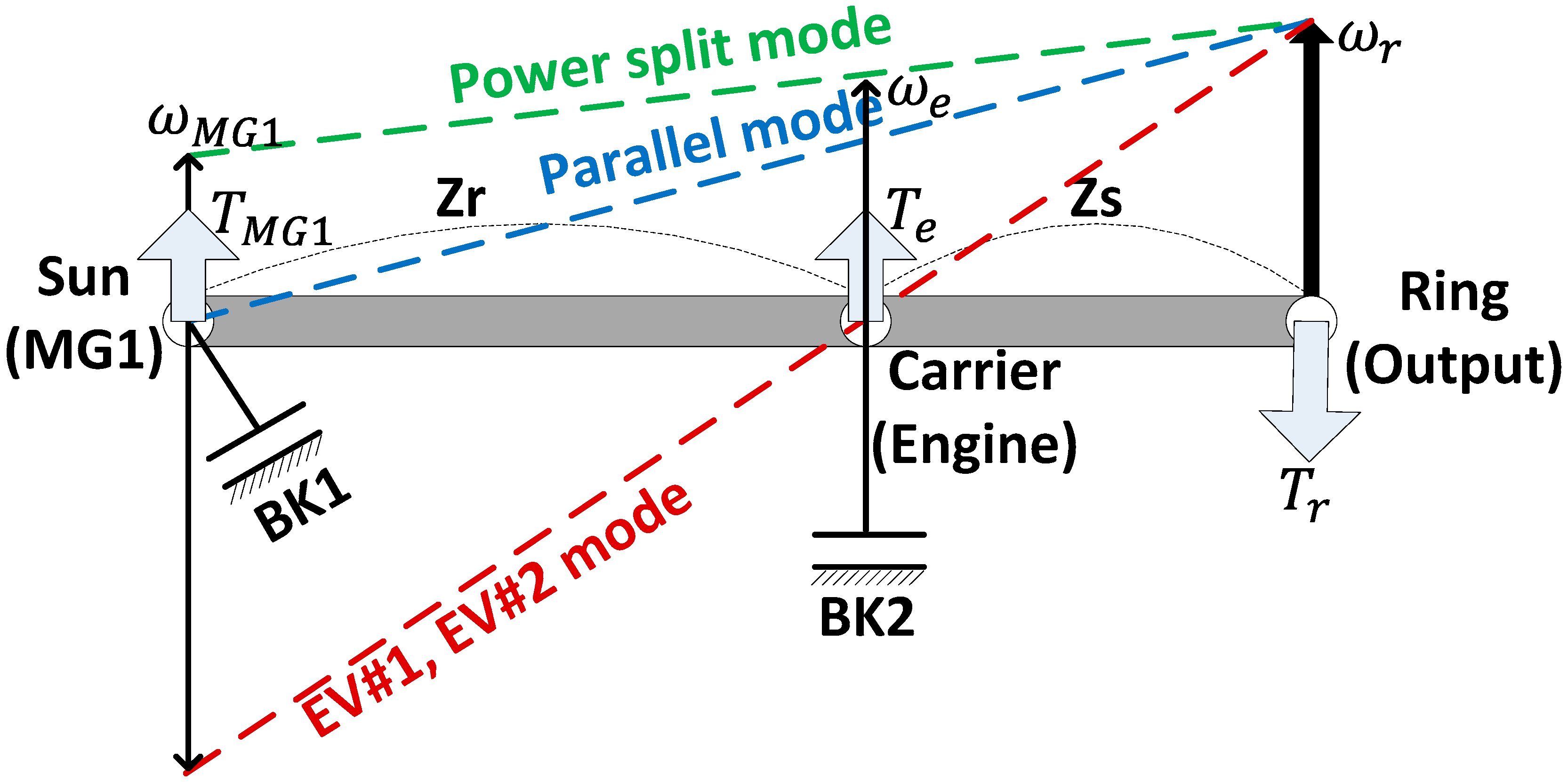
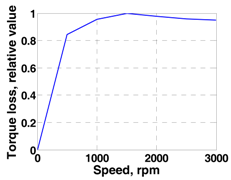
2.2. Speed and Torque Analysis
2.3. Backward Simulator with Component Losses
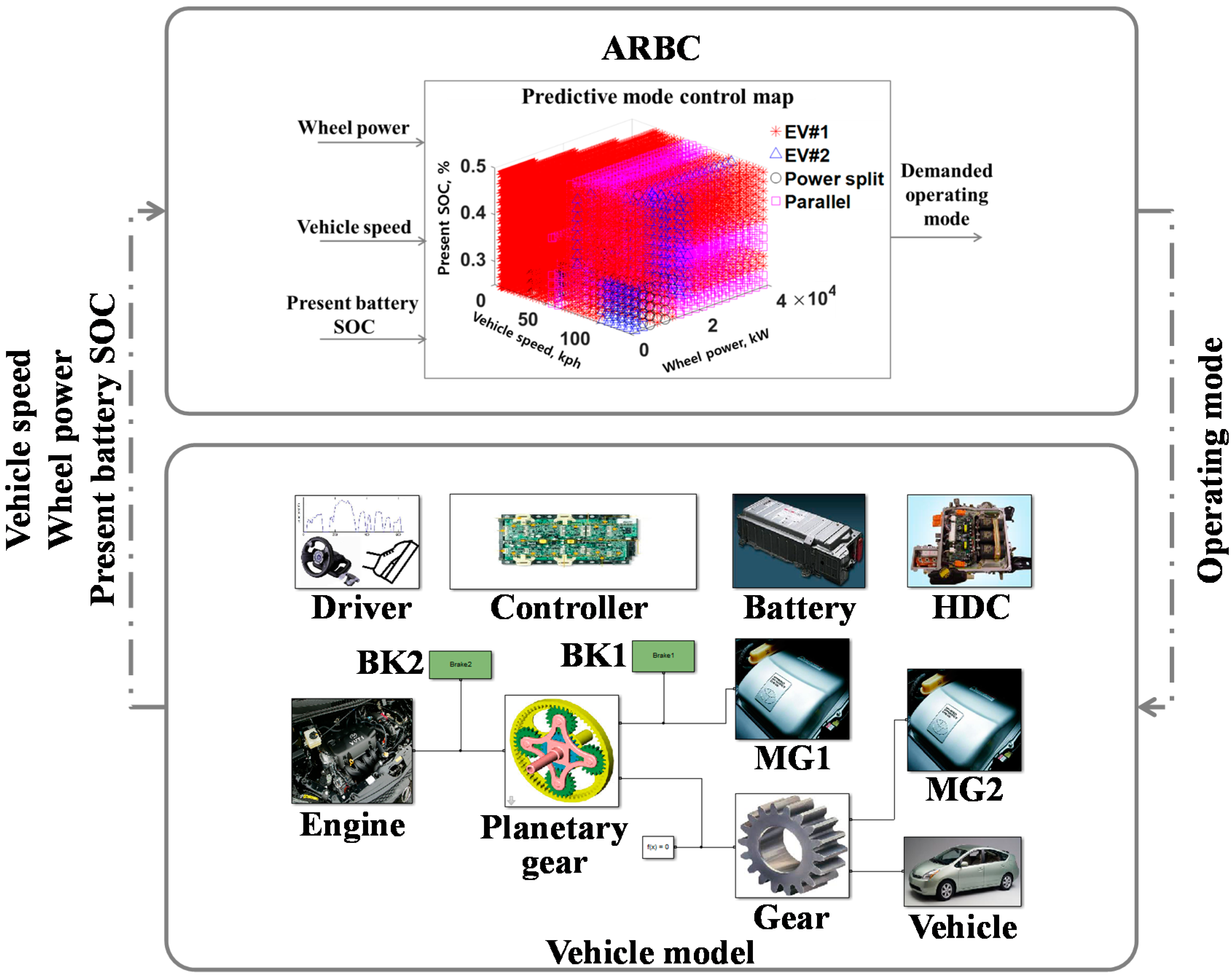
3. Advanced Rule-Based Mode Control Strategy
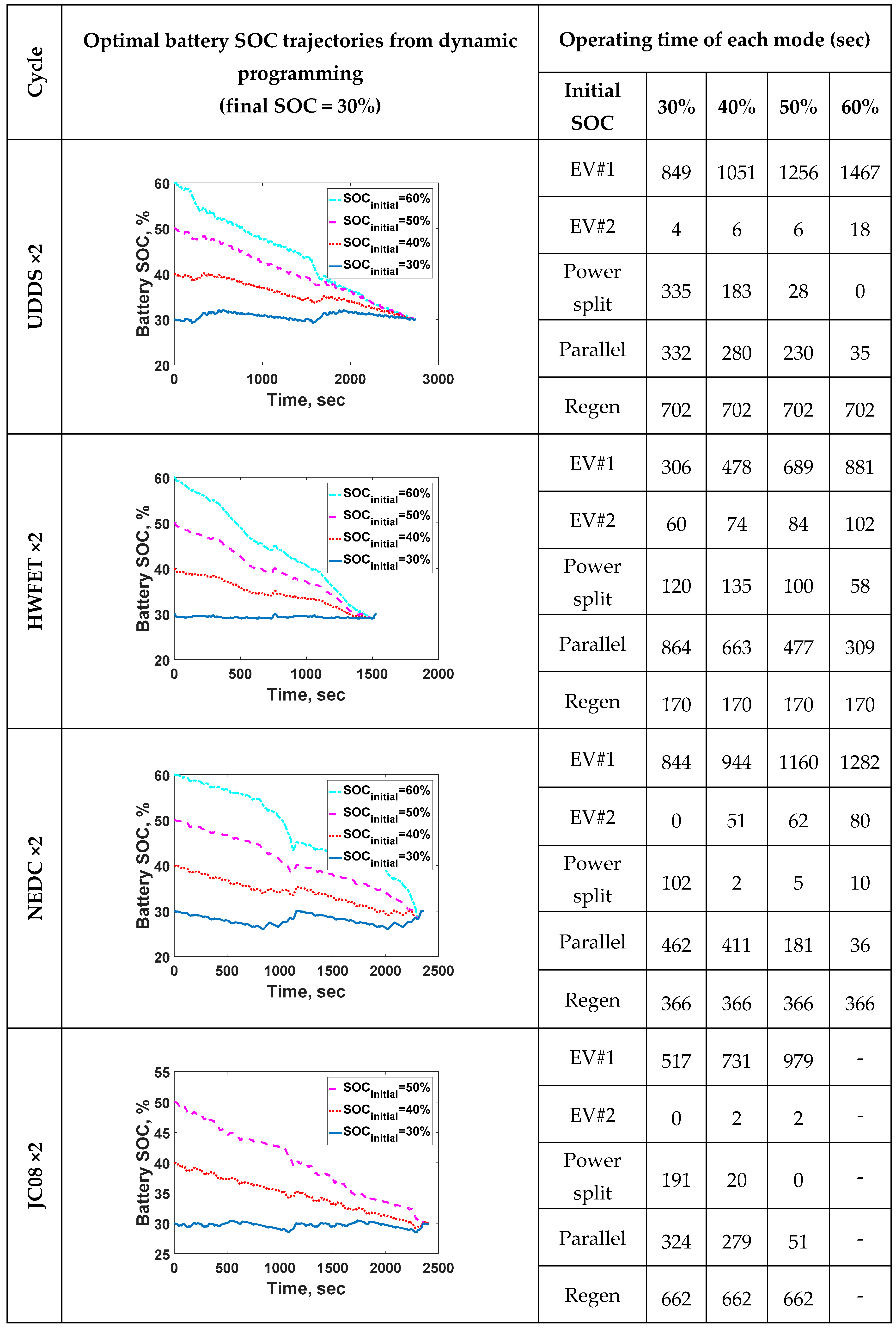
3.1. Dynamic Programming to Obtain the Optimal Operating Mode According to the Battery SOC and Driving Cycle Characteristics
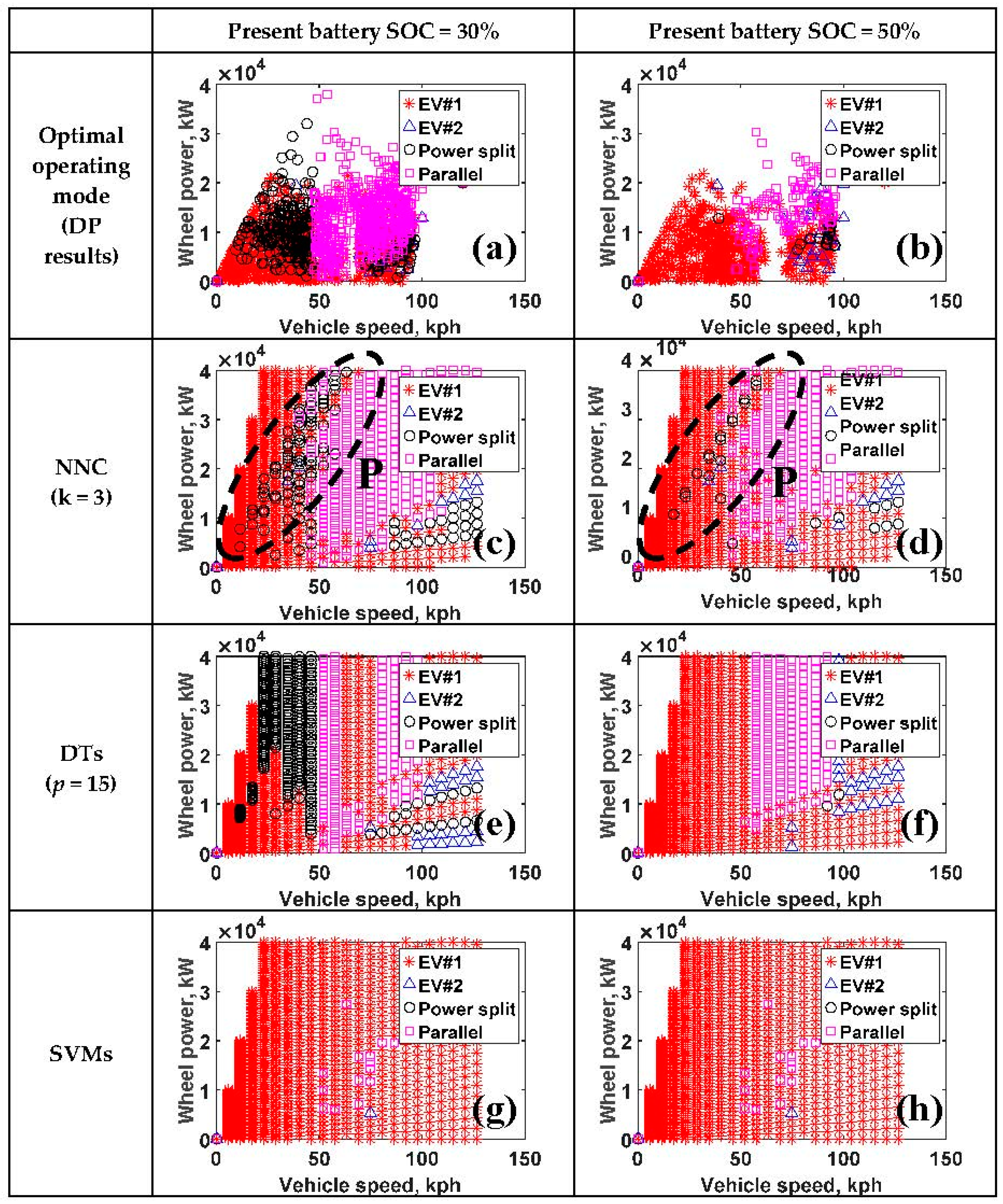
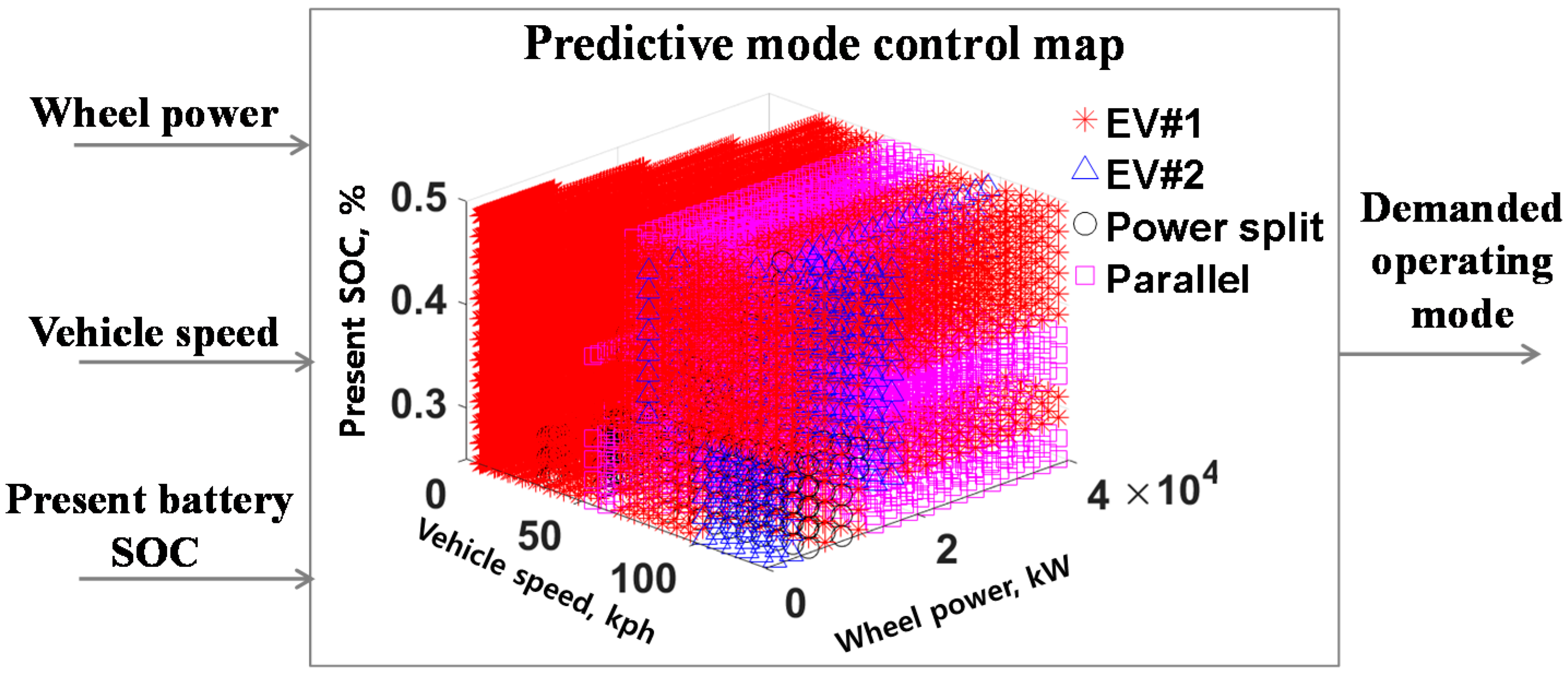
3.2. Advanced Rule-Based Mode Control Strategy Using a Predictive Mode Control Map
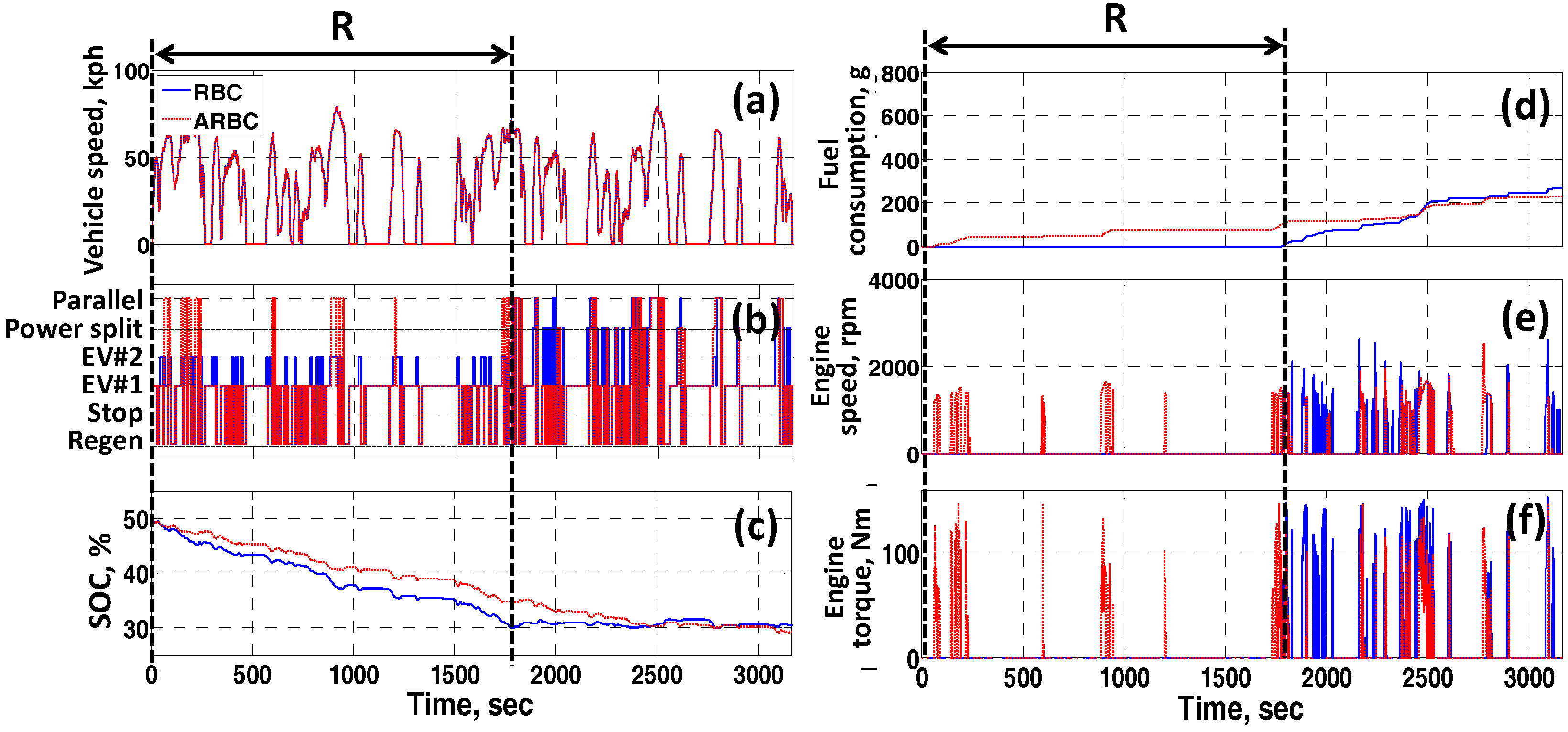
4. Performance of the Advanced Rule-Based Mode Control Strategy
4.1. Forward Simulator
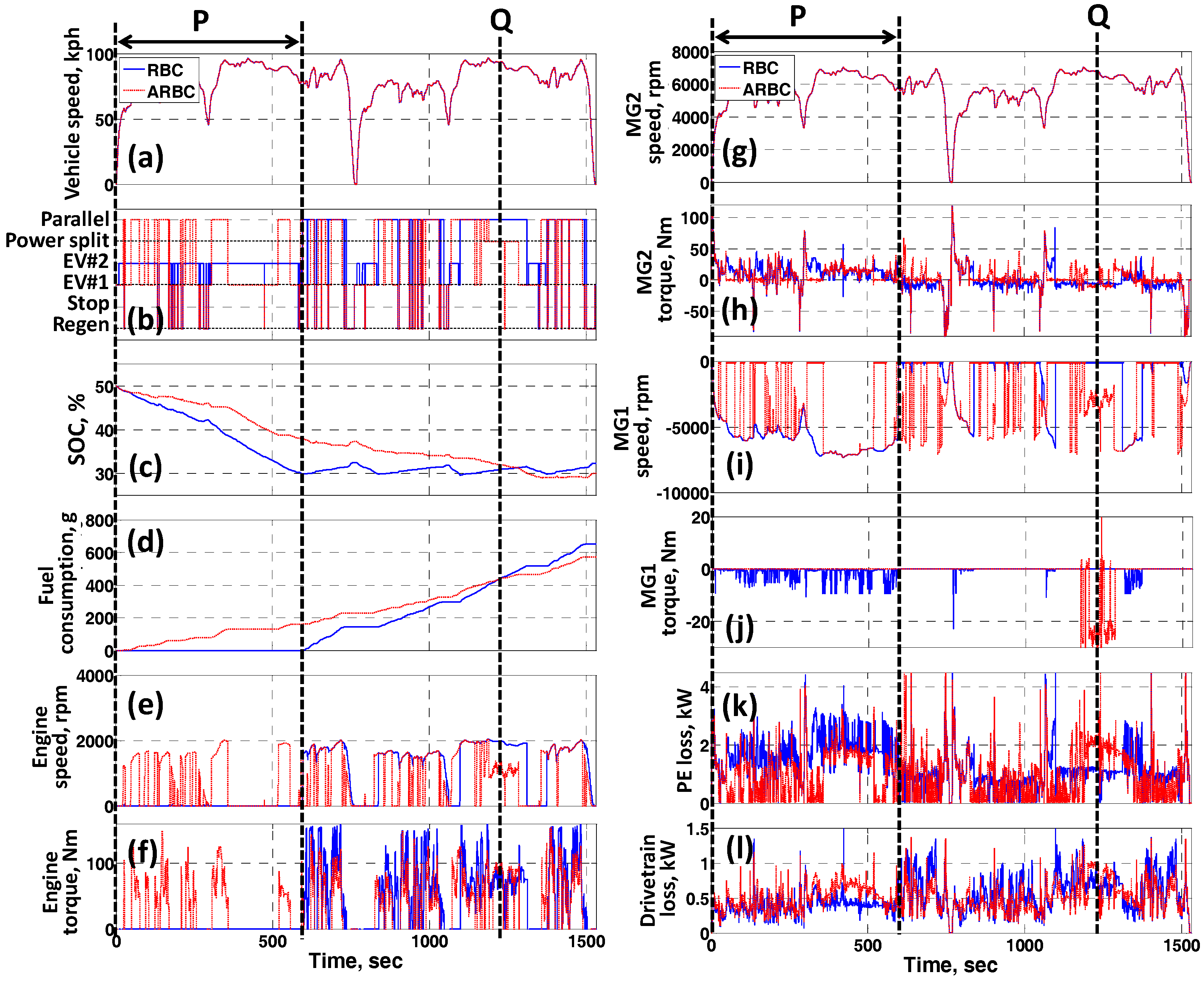
4.2. Performance of ARBC by Comparing with RBC
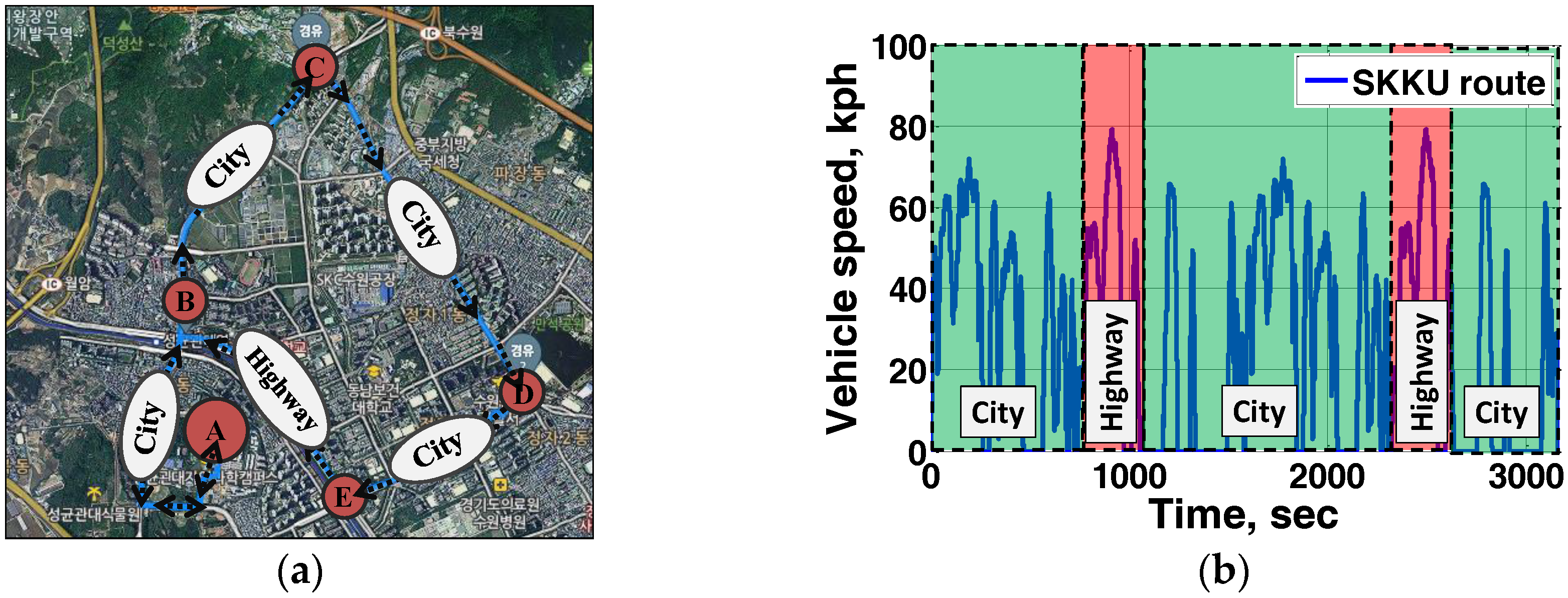
4.3. Performance of ARBC for a Real Driving Route
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, N.; Choi, S.; Jeong, J.; Vijayagopal, R.; Stutenberg, K.; Rousseau, A. Vehicle level control analysis for Voltec powertrain. In Proceedings of the EVS30 Conference, Stuttgart, Germany, 9–11 October 2017. [Google Scholar]
- Son, H.; Kim, H. Development of near optimal rule-based control for plug-in hybrid electric vehicles taking into account drivetrain component losses. Energies 2016, 9, 420. [Google Scholar] [CrossRef]
- Ma, C.; Kang, J.; Choi, W.; Song, M.; Ji, J.; Kim, H. A comparative study on the power characteristics and control strategies for plug-in hybrid electric vehicles. Int. J. Autom. Technol. 2012, 13, 505–516. [Google Scholar] [CrossRef]
- Kim, J.; Kim, N.; Hwang, S.; Hori, Y.; Kim, H. Motor control of input-split hybrid electric vehicles. Int. J. Autom. Technol. 2009, 10, 733–742. [Google Scholar] [CrossRef]
- Kang, J.; Choi, W.; Kim, H. Development of a control strategy based on the transmission efficiency with mechanical loss for a dual mode power split-type hybrid electric vehicle. Int. J. Autom. Technol. 2012, 13, 825–833. [Google Scholar] [CrossRef]
- Lee, H.; Jung, J.; Im, W; Cha, S. Optimization of rule-based power management control strategies of HEV based on dynamic programming. In Proceedings of the Korean Society of Automotive Engineers, Spring Conference, Gwang-ju, Korea, 28–29 May 2015; p. 953. [Google Scholar]
- Lin, C.; Peng, H.; Grizzle, J.W. Power management strategy for a parallel hybrid electric truck. IEEE Trans. Control Syst. Technol. 2003, 11, 839–849. [Google Scholar]
- Kim, N. Energy Management Strategy for Hybrid Electric Vehicles Based on Pontryagin’s Minimum Principle. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2009. [Google Scholar]
- Schouten, N.J.; Salman, M.A.; Kheir, N.A. Fuzzy logic control for parallel hybrid vehicles. IEEE Trans. Control Syst. Technol. 2002, 10, 460–468. [Google Scholar] [CrossRef]
- Li, S.G.; Sharkh, S.M.; Walsh, F.C.; Zhang, C.N. Energy and battery management of a plug-in series hybrid electric vehicle using fuzzy logic. IEEE Trans. Veh. Technol. 2011, 60, 3571–3585. [Google Scholar] [CrossRef]
- Paganelli, G.; Delprat, S.; Guerra, T.M.; Rimaux, J.; Santin, J.J. Equivalent consumption minimization strategy for parallel hybrid powertrains. In Proceedings of the Vehicular Technology Conference, Birmingham, AL, USA, 6–9 May 2002. [Google Scholar]
- Zhang, C.; Vahidi, A. Route preview in energy management of plug-in hybrid vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 546–553. [Google Scholar] [CrossRef]
- Yuan, Z.; Teng, L.; Fengchun, S.; Peng, H. Comparative study of dynamic programming and Pontryagin’s minimum principle on energy management for a parallel hybrid electric vehicle. Energies 2013, 6, 2305–2318. [Google Scholar] [CrossRef]
- He, H.; Tang, H.; Wang, X. Global optimal energy management strategy research for a plug-in series-parallel hybrid electric bus by using dynamic programming. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.; Peng, H. Optimal control of hybrid electric vehicles based on Pontryagin’s minimum principle. IEEE Trans. Control Syst. Technol. 2011, 19, 1279–1287. [Google Scholar]
- Kim, N.; Rousseau, A. Sufficient conditions of optimal control based on Pontryagin’s minimum principle for use in hybrid electric vehicles. J. Autom. Eng. 2012, 226, 1160–1170. [Google Scholar] [CrossRef]
- Onori, S.; Tribioli, L. Adaptive Pontryagin’s minimum principle supervisory controller design for the plug-in hybrid GM Chevrolet Volt. Appl. Energy 2015, 147, 224–234. [Google Scholar] [CrossRef]
- Finesso, R.; Spessa, E.; Venditti, M. An unsupervised machine-learning technique for the definition of a rule-based control strategy in a complex HEV. SAE Int. J. Altern. Powertrain 2016, 5, 308–327. [Google Scholar] [CrossRef]
- Jeon, S.; Jo, S.; Park, Y.; Lee, J. Multi-mode driving control of a parallel hybrid electric vehicle using driving pattern recognition. J. Dyn. Syst. Meas. Control 2002, 124, 141–149. [Google Scholar] [CrossRef]
- Son, H.; Park, K.; Hwang, S.; Kim, H. Design methodology of a power split type plug-in hybrid electric vehicle considering drivetrain losses. Energies 2017, 10, 437. [Google Scholar] [CrossRef]
- Benford, H.; Leising, M. The lever analogy: A new tool transmission analysis. SAE Pap. 1981, 810102. [Google Scholar] [CrossRef]
- Gears—Thermal Capacity—Part 2: Thermal Load-Carrying Capacity; ISO/TR 14179-2:2001; International Organization for Standardization: Geneva, Switzerland, 2001.
- Haka, R.J. Determination of efficiency (torque related losses) in planetary gearsets-generalized theory for simple and compound gearsets. In Proceedings of the ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2003; pp. 1085–1097. [Google Scholar]
- Chen, J.Y.; Borgerson, J.B. Analytical and test evaluation of planetary gear train efficiency (torque related losses) with multiple power flow arrangements. In Proceedings of the ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2003; pp. 1057–1065. [Google Scholar]
- SKF General Catalogue. Available online: http://www.worldcat.org/title/skf-general-catalogue/oclc/225258275 (accessed on 13 January 2016).
- Changenet, C.; Velex, P. A model for the prediction of churning losses in geared transmissions-preliminary results. J. Mech. Des. 2006, 129, 128–133. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Short, R.; Fukunaga, K. The optimal distance measure for nearest neighbor classification. IEEE Trans. Inf. Theory 1981, 27, 622–627. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Muralidharan, V.; Sugumaran, V. Feature extraction using wavelets and classification through decision tree algorithm for fault diagnosis of mono-block centrifugal pump. Energies 2013, 46, 353–359. [Google Scholar] [CrossRef]
- Hsu, C.; Lin, C. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar] [PubMed]
- Kilian, Q.W.; John, B.; Lawrence, K.S. Distance metric learning for large margin nearest neighbor classification. J. Mach. Learn. Res. 2009, 10, 207–244. [Google Scholar]
- Nadeau, C.; Bengio, Y. Inference for the generalization error. Mach. Learn. 2003, 52, 239–281. [Google Scholar] [CrossRef]
- Department of Energy, U.S. Electric and hybrid vehicle research, development, and demonstration program; petroleum-equivalent fuel economy calculation. Federal Regist. 2000, 65, 113. [Google Scholar]

| Operating mode | BK1 | BK2 | MG1 | MG2 | Engine |
| EV#1 | Disengaged | Disengaged | Off | On | Off |
| EV#2 | Disengaged | Engaged | On | On | Off |
| Power split | Disengaged | Disengaged | On | On | On |
| Parallel | Engaged | Disengaged | Off | On | On |
| Vehicle Specification | ||
|---|---|---|
| Engine | Max power/torque | 115 kW/185 Nm |
| MG1 | Max power/torque | 70 kW/50 Nm |
| MG2 | Max power/torque | 90 kW/270 Nm |
| Battery | Max power/capacity | 50 kW/25 Ah |
| Vehicle | Mass | 1800 kg |
| Tire radius | 0.32 m | |
| Gear ratio | PG/G1−G2/G3−G4/G5−G6 | 2.6/2.478/1.0/3.54 |
| Power electronics system | 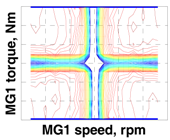 < MG1 > | 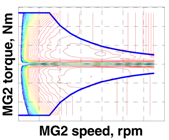 < MG2 > |  < HDC > | ||
| Drivetrain components | 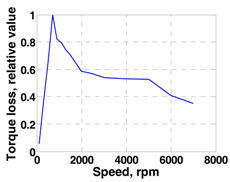 < Clutch > |  < MG1 unloaded > | |||
 < Seal ring > | 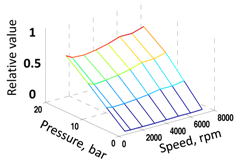 < Oil pump > | ||||
| Gear [22] | |||||
| Planetary gear (PG) [23,24] | |||||
| Bearing [22,25] | |||||
| Churning [26] | |||||
| Predictive Model (Classifier) | ||||||
|---|---|---|---|---|---|---|
| Training set | 70% | |||||
| Test set | 30% | |||||
| Resubstitution accuracy /Test accuracy [%] | Nearest neighbor classification (NNC) | Decision trees (DTs) | Support vector machine (SVMs) | |||
| k = 1 | 100% /93.3% | p = 0 | 97.3%/93.5% | Linear | 61.5% /61.6% | |
| k = 2 | 96.4% /93.2% | p = 5 | 97.2%/93.5% | Gaussian | 92.2% /90.2% | |
| k = 3 | 96.5% /92.4% | p = 10 | 97.0%/93.6% | |||
| k = 4 | 94.8% /92.7% | p = 15 | 96.5%/93.7% | |||
| k = 5 | 94.5% /92.5% | p = 20 | 95.9%/93.5% | |||
| k = 6 | 94.1% /92.6% | p = 25 | 95.1%/93.2% | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, H.; Kim, H.; Hwang, S.; Kim, H. Development of an Advanced Rule-Based Control Strategy for a PHEV Using Machine Learning. Energies 2018, 11, 89. https://doi.org/10.3390/en11010089
Son H, Kim H, Hwang S, Kim H. Development of an Advanced Rule-Based Control Strategy for a PHEV Using Machine Learning. Energies. 2018; 11(1):89. https://doi.org/10.3390/en11010089
Chicago/Turabian StyleSon, Hanho, Hyunhwa Kim, Sungho Hwang, and Hyunsoo Kim. 2018. "Development of an Advanced Rule-Based Control Strategy for a PHEV Using Machine Learning" Energies 11, no. 1: 89. https://doi.org/10.3390/en11010089
APA StyleSon, H., Kim, H., Hwang, S., & Kim, H. (2018). Development of an Advanced Rule-Based Control Strategy for a PHEV Using Machine Learning. Energies, 11(1), 89. https://doi.org/10.3390/en11010089





