1. Introduction
The increasing frequency of extreme weather events highlights the vulnerability of power systems to multiple outages [
1]. The consequent interest in assessing the power system response to these high impact low probability events and the growing amount of data coming e.g., from prediction systems favor the maturation of probabilistic risk based approaches. Thus, Transmission System Operators (TSOs) are shifting their focus from security analyses based on N − 1 credibility criterion to the evaluation of power system vulnerability to extreme N − k events. In this context, TSOs have recently discussed the opportunity to use risk concepts (a suitable combination of event probability and impact) to assess and assure power system security against multiple contingencies [
2,
3,
4,
5]. Probabilistic models of weather related threats can greatly benefit from spatial-temporal data concerning the evolution of the weather over the power system. In this context, big data analytics applications can be of great help in providing reasonable probabilistic models of a weather threat both in long term (through historical data series) and in medium-short term (through forecasts and quasi-real time data acquisition) [
2]. Big data analytics applications are raising more and more interest in the smart grid community, especially in the context of weather event alarming and management [
3,
4]. Reference [
5] proposes a big data driven tool for disaster management to support operators’ decisions in emergency conditions, while in [
6] a risk warning system is implemented based on big data. In order to plan strategies to relieve weather effects on distribution networks, in [
7] a fuzzy logic technique is proposed to support utility operators’ decisions in optimizing real time operation and maintenance scheduling. An innovative method for weather-driven risk framework is deployed to analyse data and generate risk maps to support decision makers. Among the potential threats, wet snow events are common in different countries e.g., Italy [
8], and they have been studied for many years. References [
8,
9] describe the activities carried out by the authors to propose and validate deterministic models aimed to forecast the amount of linear weight or thickness of snow sleeve accreted along the conductors of overhead lines (OHLs).
The goal of the paper is two-fold: (1) to propose a comprehensive methodology and platform which integrate a risk based security assessment tool for operational planning and quasi-real time operation [
10] with advanced forecasting systems providing large amount of geo-spatial data on the expected intensity and extension of the major weather threats (focusing on wet snow events), and (2) to thoroughly present the results of the application of the platform to a real-life case study.
The added value of the proposed integrated platform is to exploit the available forecasts on the weather threats in order to provide the list of most risky contingencies on an hourly basis over the whole forecasting period, thus supporting operators in preparing the power system operation for the near future hours (i.e., at an operational planning level). Linking the set of single and multiple contingencies to be studied to the forecast of the threat affecting the system is an important step forward with respect the approaches proposed in literature to screen the most dangerous multiple N − k contingencies, from optimization frameworks, aimed to identify dangerous multiple branch outages [
11,
12,
13] to rough set theory [
14], random chemistry [
15], graph theory [
16], and eigen-sensitivity and cutsets [
17], expert systems [
18] or fuzzy logic [
19] associated with neural networks. In fact, all these approaches have some limits, which are overcome by the contingency selection algorithm of the proposed methodology: (1) they usually screen the contingencies based on their impact, ignoring their probability; (2) common causes or dependent failures (e.g., busbar faults with protection misoperation) are neglected, while these events may initiate cascading outages and subsequent load disruptions; (3) most of the methods do not account for the current weather/environmental conditions.
The paper is organized as follows:
Section 2 describes the risk-based methodology which integrates the threat/vulnerability analysis with power system security analyses.
Section 3 discusses the data sources concerning the forecasts of extreme weather events with a focus on wet snow events, and the architecture of the risk based security assessment platform.
Section 4 presents the detailed wet snow threat model and the relevant vulnerability models for overhead lines.
Section 5 describes and discusses the results of the platform application to a realistic wet snow event scenario. Conclusions are drawn in
Section 6.
2. Probabilistic Risk Assessment Methodology and Tool
This section presents the rationale at the basis of the proposed risk based approach and an overview of the threat and vulnerability modeling framework.
2.1. The Rationale of the Approach
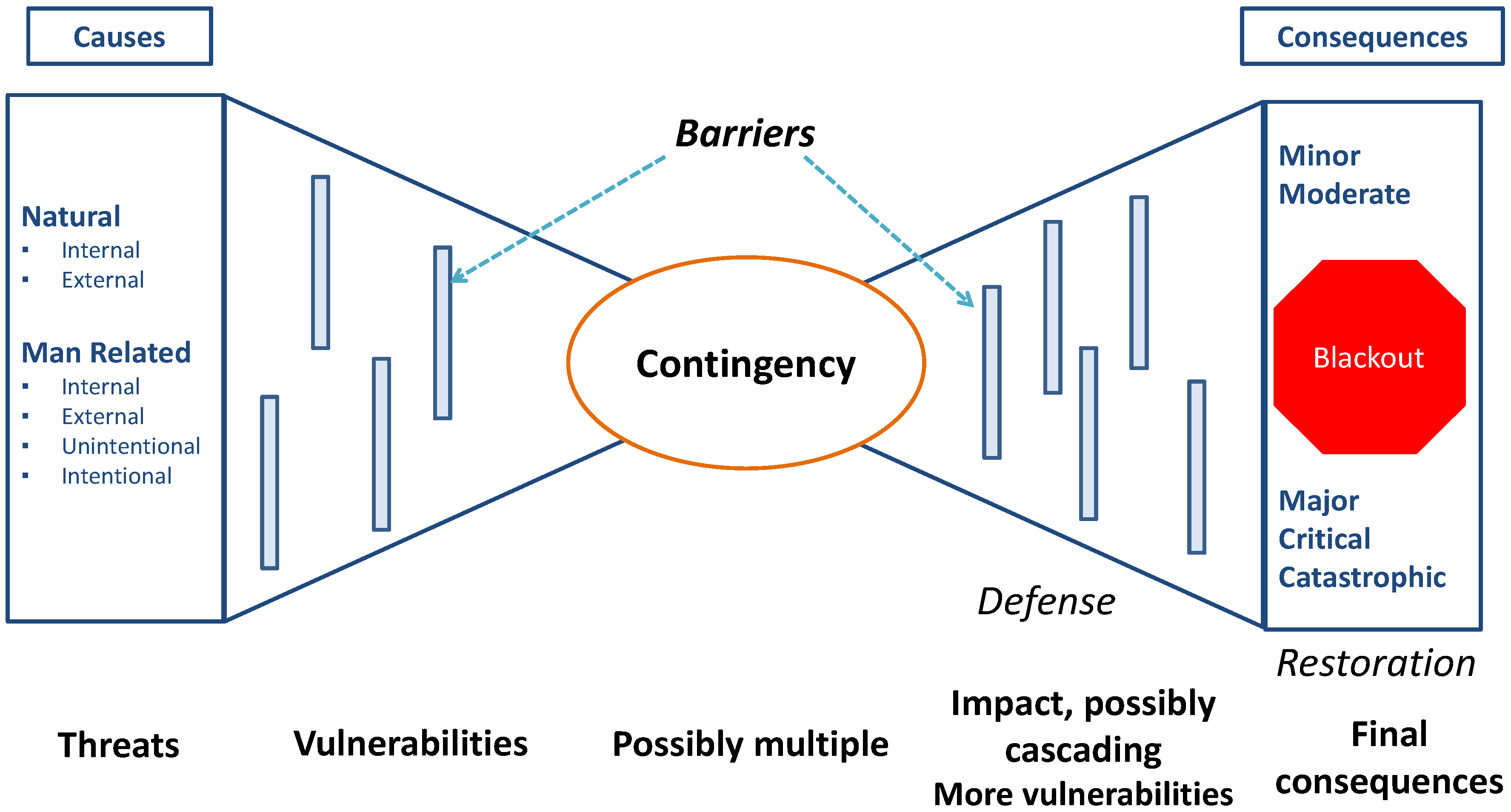
The proposed probabilistic risk assessment method is derived from the bow tie conceptual scheme visualizing the connections between the causes and consequences of undesired events:
Figure 1 illustrates an example where the disturbances consist in contingencies potentially provoking cascading outages and blackouts, i.e., with dangerous effects.
Threats are classified into natural threats and man-related threats (see the left side of bow tie), and further divided into internal or external to the power system. The man-related ones are also subdivided into intentional (e.g., sabotage) or unintentional (e.g., human errors). Threats may bring to a contingency via a set of causes which affect vulnerabilities; the contingency might provoke different impacts under several circumstances. These impacts may in turn act on other vulnerabilities, triggering cascading outages that finally lead to a blackout. To describe the deep connection between threats and contingencies, the conventional risk concept as a triple {contingency, probability, impact} [
20] is reconsidered and extended.
In the proposed modeling framework [
10] a threat can act on several vulnerabilities of power system components by triggering stress variables, consisting in the physical quantities exploited by the threat to influence the component vulnerabilities (e.g., a tornado may result in heavy mechanical forces on transmission line towers). This stress may provoke the component failure. The generic “contingency” at system level means the failure of one or more components. The methodology interprets the “vulnerability” as the conditional probability of a component failure given the occurrence of a specific threat. Also, any threat is modelled in probabilistic terms: e.g., the probability of a natural threat, like a wet snow event, depends on the weather situation at the time of the event itself. The sequel of the section will provide a description of the approach and of the relevant tool.
2.2. Modeling Component Failures
Given a single component with a vulnerability defined via a conditional probability function
[
21], the failure probability
PF of this component in the time interval
subjected to an individual threat described by a {stress, time} multivariate probability density function (pdf)
can be computed as in (1):
where
is the probability that the component in location
x fails between time instants
t0 and
t;
is the conditional probability distribution of the component failure at
t due to value
s of stress variable
S related to threat
Thr and applied at
τ. Also vulnerabilities are functions of time, e.g., because of ageing or maintenance;
is the pdf of threat
Thr applying value
s of stress variable
S in location
x, at time
τ. Term
is the probability to have stress
s at time
τ.
Random variables are represented via upper case letters (e.g.,
S), while their realizations or non- random variables via lower-case letters (e.g.,
s). Multivariate distributions in (1) must be adequately adjusted to model the specific component and threat under investigation. The tuning process may encounter some issues due to the reduced availability of statistical data from the historical series analyses or from prediction tools. If one considers an average model of stress variable
S in interval
, the previous formulation can be written as in (2):
where apex
(Δt) is related to the average (threat/vulnerability) model in time interval Δ
t. It’s worth noticing that Equation (2) can be used for different time frames, provided that an adequate average model is available on a Δ
t horizon. Next subsections and
Section 3 present respectively the models chosen for
and
, and the data sources to characterize the models.
Under the assumption of constant failure rates in Δt relevant for operation (e.g., from 15 min to 1 h), the probability of failure of more than one components, due to the same threat, is derived by combining the “time to failure” exponential distributions of all the affected components following the probability laws. The approach can model also the more general case of more than one components subjected to multiple threats, accounting for potential dependencies among threats.
Applying this formulation assures a general framework for the probabilistic modeling of power system contingencies. Short term models will be the focus of the present investigation, because the tool is mainly oriented to system operation. In the sequel, only single threat scenarios are investigated, without diminishing the generality of the proposed methodology.
2.3. Threat and Vulnerability Modeling
The threats modeled in the platform may range from natural disasters (ice and snow storms, pollution, lightning, earthquakes, sabotage, earthquake-induced landslides, floods, fires, tree contact, component aging) to deliberate acts of sabotage. Long term and short term probabilistic models for threats can be derived respectively from the elaboration of historical data series and from weather forecasting systems. The last term of (2) can be computed if the dependence of the stress variable pdf on location
x (
spatial dependence) is known. To this regard, the proposed methodology is general and it may incorporate an accurate representation of the geospatial distribution of the stress variable if data from prediction systems are available. Other references about long term threat models can be found in [
10]. Any component is described in terms of a vulnerability function with respect to each threat. The vulnerability models in (2) are derived from:
- (a)
Laboratory tests, like mechanical fragility curves, blast withstanding capacity curves, voltage withstanding capacity curves [
22] for insulating materials;
- (b)
Mathematical models which connect component properties to the exposure to specific threats, e.g., rolling sphere method for exposure to lightning [
23];
- (c)
Qualitative information from experts or specific drills, e.g., to define the vulnerability of a SCADA system, or of a substation to physical attacks.
Also ageing processes, e.g., Arrhenius’ law or combined electric-thermal stress [
24], can be included in vulnerability models.
Table 1 indicates the link between threats and stress variable(s).
2.4. Contingency Set Definition
The set of the contingencies to be analyzed in depth is detected via a two stage process:
An exhaustive set of single and multiple contingencies is generated by an enumeration technique, starting from critical components. Under the assumption of constant failure rates within Δ
t (valid hypothesis for time intervals up to 1 h), using probability theory and copula concept are used to combine the “time to failure” exponential distributions for all components involved in the contingency definition, in order to get the final distribution of the probability of contingency occurrence
PCTG(
t): in the contingency screening process, the adopted value for probability is the maximum value of
PCTG(
t) in the time interval Δ
t of study, henceforth named
probctg. Computing the probability for high order (N − k, k > 1) contingencies takes into account common mode and dependent events. Common mode events (e.g., outage of k branches subject to the same storm) are studied considering the available geo-spatial model (see
Section 3) of the threat affecting the grid area under investigation. Dependent events are: (a) busbar contingencies (also accounting for protection malfunctioning), (b) power plant contingencies and (c) double circuit line outages.
Contingencies are screened on the basis of ex-ante risk indicators, obtained by combining event probability with impact metrics i.e., the number of outaged components or topological metrics such as average inverse geodesic length [
27] and net-ability [
28]: their computation is very fast. The proposed screening algorithm offers several options to adjust the contingency set selection, e.g., maximum ex-ante risk threshold and the fraction of explained total failure probability.
For time domain simulations, each contingency is characterized not only by outaged components but also by the time sequence of the trippings themselves, which depend on the response of primary and backup protections.
2.5. Modeling Power System Response to Contingencies and Computing Impact and Risk Indicators
The impact of each retained contingency is computed using a quasi-static cascading outage simulator [
29] and/or a time domain simulator integrated in the platform.
The proposed approach introduces an extended risk concept: risk is defined as a quadruple {threat, vulnerability, contingency, impact} where the “probability” term of conventional triple {probability, contingency, impact} [
20] is replaced by the probability distributions associated to threats and vulnerabilities. This risk definition links Probabilistic Hazard Assessment (PHA) studies to Security Assessment (SA) analyses, focusing on the disturbance root causes. In particular, component vulnerability connects the probabilistic model of generic threat
Thrp with the probability of contingency
ctg, while the vulnerability in power system response connects contingency
ctg with the final consequences (impact) on the power system itself. The way how threats act on power system clearly depends also on the (current or forecast) power system operating conditions
OCj. The risk indicator adopted in the present paper is the expected value of the impact for the analysed contingencies, accounting for threats and component vulnerabilities. Term “operating condition” incorporates both strictly operational conditions, i.e., load pattern, generation dispatch and grid topology, and more general environmental conditions, e.g., ambient temperature, wind speed.
Anyway, risk can be associated to:
- (1)
A specific contingency, evaluated as dangerous in the specific OC subject to the given threat: contingency risk indicators help operators identify events with the highest risk (to plan suitable countermeasures);
- (2)
The operating condition and the set of dangerous contingencies: global indicators assess how system risk varies under changing threats.
The risk indicator related to a specific contingency
ctg—henceforth named
Contingency Risk CRctg—is given in (3):
where
and
are respectively the contingency impact and probability depending on operating conditions
OCj and threat
Thrp. The probabilistic threat and vulnerability analysis provides term
, while the simulation of power system response to contingency
ctg by means of the cascading outage simulator and time domain simulation allows to compute term
. In the sequel notation will be simplified substituting
with
and
with
.
The methodology can provide both static and dynamic impact and risk indicators [
10].
System risk indicators
R are computed as in (4):
where
is the number of dangerous contingencies selected by the screening algorithm and it depends on specific threat
Thrp and operating conditions
OCj.
Impact indicator impctg used in the present paper is the Loss of Load (LOL) at the end of the cascading path potentially activated by the contingency.
3. Data Sources and Platform Architecture
This section discusses the important topic of data sources for the tuning of short term probabilistic models of weather related threats and it describes the overall architecture of the integrated platform.
3.1. Data Issues for Model Tuning
Characterizing the probabilistic models is one of the main barriers for the application of probabilistic techniques in real world power system operation [
30]. Reliable data sources are required for a proper model tuning. In case of short term analyses (operational planning), the geospatial distribution of the stress variables (e.g., the mechanical tension on a conductor due to combined ice+wind load) which characterize each weather threat can be obtained starting from the geospatial distribution of the weather variables (temperature, wind speed, precipitation rate, etc.) by means of causal physical models (e.g., the Makkonen model for snow sleeve accretion, briefly described in
Section 4). The abovementioned weather variables are subject to forecast uncertainties, thus they must be treated as stochastic variables.
On the basis of the way these weather variable geospatial distributions are generated, the platform allows to characterize the threat probabilistic models via two modes:
In the operational planning mode, the platform integrates the k hour-ahead forecasts provided by numerical weather prediction systems to get an affordable probabilistic model for weather based threats (in particular, wet snow events which represent a major source of outages in specific zones of the Italian grid). In this mode the input data for the combined threat and contingency analysis platform define the so called threat/power system scenario and consist in:
For the sake of conciseness and clarity, the present paper will focus on the wet snow threat. The weather variables coming from two different high resolution NWP models, the WRF-ARW and RAMS dynamic cores [
8], constitute the input for wet snow hazard model. The simulations are done on two nested grids (d01, d02, see
Figure 2a) at a horizontal resolution of 0.125° (about 15 km) for the coarse domain (d01) and of 0.04° (about 5 km) for the finest grid (d02). The global model ECMWF provides the initial and boundary conditions for the simulation. Presently, the output of both weather models are used separately, but in the future the output will build up an outperforming Multi-Model Ensemble.
Wet snow condition has been identified when air temperature is in the range between −2 °C and +2 °C and, at the same time, the Snow Ratio of frozen precipitation is between 0.7 and 0.8, i.e., the Liquid Water Content of snowflakes is 20–30%.
The predictive system is based on several years of research activity and it is the core part of an alert system for wet snow formation on Overhead Lines (OHLs) in Italy. The system, named Wet snow Overload aLert and Forecasting (WOLF) [
8], is aimed to provide the wet snow loads forecast and the estimated anti-icing current for OHLs in the forecast horizon of +72 h.
Figure 2b shows an example of WRF-ARW simulation related to the accumulated daily precipitation (mm/24 h) for the wet snow event occurred in February 2015 in the North of Italy.
3.2. An Overview of the Platform
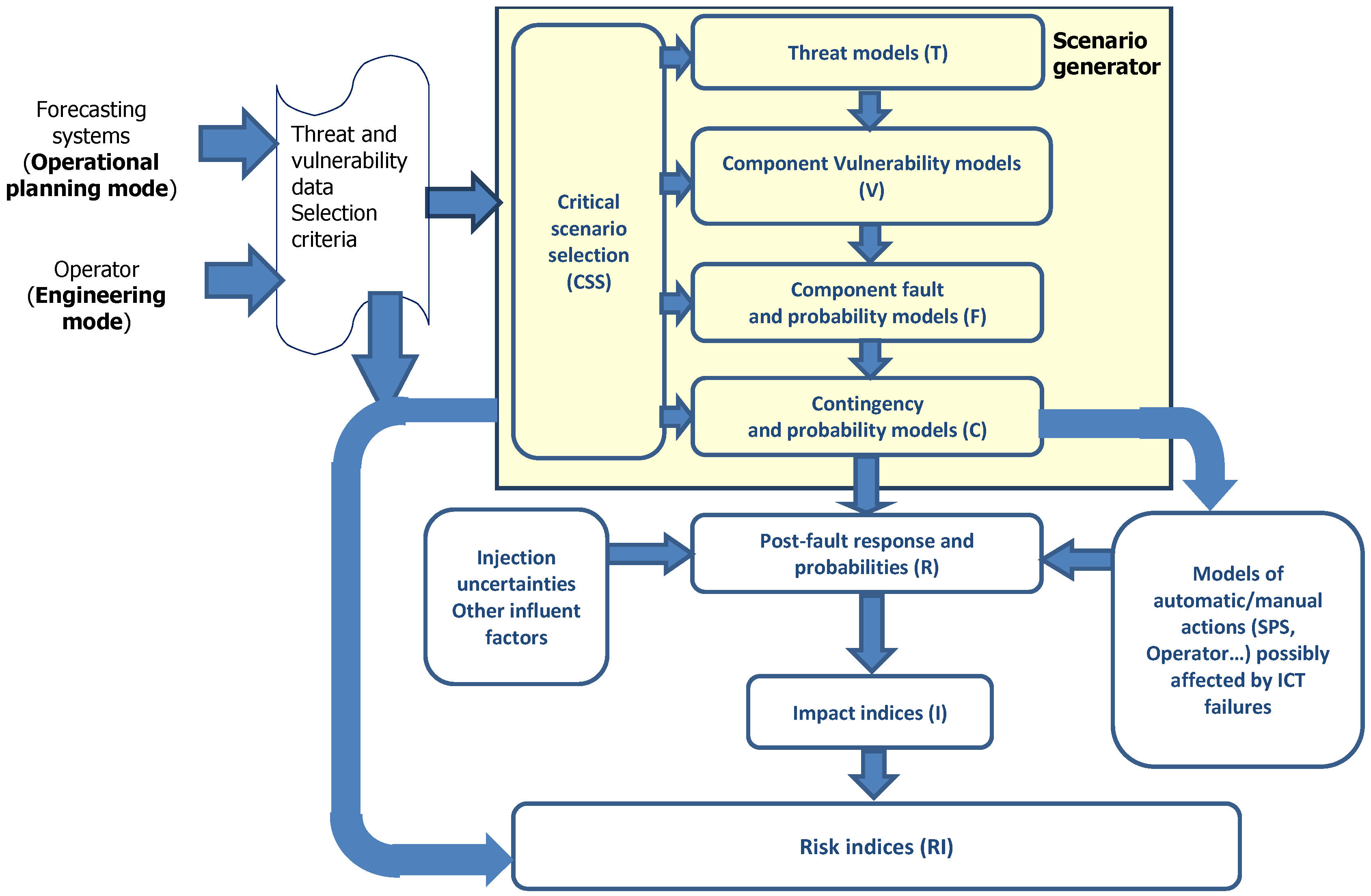
Figure 3 depicts the workflow of the tool for risk assessment: each module is identified via a specific letter put into brackets.
In the modules of scenario generator (top part of the diagram) the threat and power system component vulnerability are probabilistically modelled, evaluating the component failure probability [
10]. The data for short term probabilistic models for weather related threats may come from the user (engineering mode) or from a numerical prediction system (operational planning mode), as explained in
Section 3.1.
The cumulative sum screening method is run in module C: this allows to select the critical components (i.e., the ones which represent the largest fraction of explained total failure probability).
Then the enumeration technique is run still in module C in order to generate an exhaustive set of single and multiple also dependent contingencies, screened using fast algorithms. The response of power system to the retained contingencies is simulated by means of the time domain simulator and/or the cascading outage simulator in module R. Also influencing factors like forecast uncertainties on loads and renewables and uncertain response of defence/control systems are accounted for.
The impact of each contingency is assessed in module I, and risk indicators are computed by combining probability and impact in module RI. The final outcome consists in risk indicators to rank contingencies and track overall system security.
4. Wet Snow Threat Modeling
This section presents the probabilistic model of the wet snow threat, considering the physics of wet snow accretion. The wet snow affects OHLs via two stress variables:
The mechanical tension on the conductor section, due to the overall load including the wind load and the ice load produced by wet snow processes;
The surface conductivity of the insulator chains, which depends on the accumulation of wet snow and on the conductivity of the water content of the snow.
Thus, two separate threat probabilistic models are elaborated to account for the two phenomena. The relationship between the wet snow events and the surface conductivity on the insulators is being investigated in literature [
31]. However, in the study case of the present paper, the conductivity of the wet snow accretion on insulators in the area under investigation is negligible, thus the flashover model due to wet snow accretion is not considered henceforth.
4.1. The Physics of Wet Snow Accretion
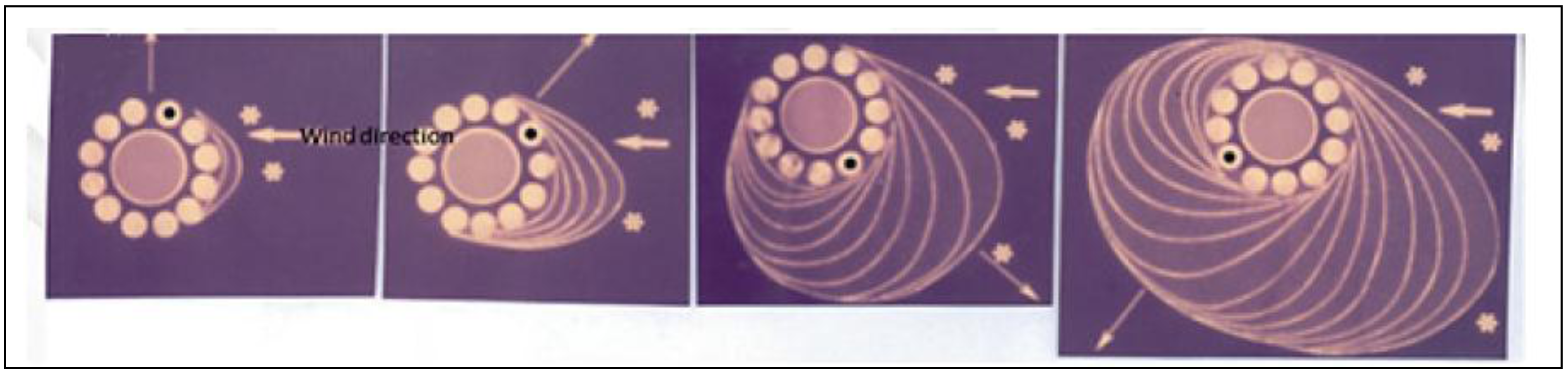
The most well-known temperature interval for wet snow conditions is −2 °C/+2 °C, also from the verification of many observations in different countries. In this range of temperature layer, the snowflakes can partially melt and their typical Liquid Water Content (LWC) varies from 20% to 30% of the total mass. In this situation the snowflakes deposit on the conductor and join together not only due to collision mechanism, but also due to the strong coalescence caused by the presence of LWC in the snowflakes which favors the growth of typically cylindrical sleeves around the wire (see in
Figure 4).
Wet snow events typically last for 18–24 h, generating snow sleeves up to 15 cm in diameter and causing an extra load on conductors up to 8–10 kg/m. The overload can produce severe damages to OHLs. Sometimes the conductor undergoes an extra load due to the intense wind blowing after the accretion process.
4.2. Threat Forecast Modeling
The model implemented in the platform [
10] to forecast the stress variables (i.e., the mechanical loads due to ice and wind) accounts for four main measurements concerning the wind speed intensity and direction, the ambient temperature and the precipitation rate.
All the models for wet snow accretion rest on Equation (5), which models the accretion of snow mass
M described in the ISO standard [
32] for icing of structures:
where
α1 is the collision efficiency;
α2 is the sticking efficiency, and
α3 is the accretion efficiency;
w is water content (kg/m
3);
A is the cross-sectional area (m
2) perpendicular to object;
V is the particle impact speed perpendicular to object (m/s).
For the wet snow precipitation, term w × A may be approximated by the precipitation flux. The terminal vertical velocity of snowflakes Vs is assumed to be 1.5 m/s, obtained by three-year measurements of a disdrometer during wet snowfall events at the icing station on the Italian Alps (WILD) 8. Sticking efficiency α2 may be inferred from some field observations. In particular, α2 depends on the liquid water content of snowflakes and the impact speed. The density of the snow sleeve ρs depends on wind intensity W because higher snowflake impact speeds tend to produce a more compact snow deposit.
Moreover the model assumes a cylindrical wet snow accretion on conductor without sleeve shedding phenomena (conservative accretion).
The empirical parameters have been deduced from measurements of icing station collected over the past three winters. The assumptions and the value ranges for the most important parameters used in the model are reported below:
Wet snow condition if air temperature is in the range of −2.0 to +2 °C;
SR (Snow Ratio) of frozen precipitation in the range 0.7–0.8;
Sticking coefficient α2 = 1/W1/3 if 1 m/s < W < 10 m/s; 0.1 if W > = 10 m/s; 1 if W ≤ 1 m/s;
Admirat approach [
31] suggests the following model for density of snow sleeve:
ρs = 300 + 20
W;
ρs = 500 kg/m
3 if
W > 10 m/s;
Vertical velocity of snowflakes Vs = 1.5 m/s.
For dry-snow condition, when the temperature is lower than −2.0 °C or the
SR > 0.8, the snow accretion is limited by empirical coefficient
α2 = 0.1 and
ρs = 100 kg/m
3. The angle
θ is equal to 90° to consider the worst conditions of accretion. More details can be found in [
9].
4.3. Modeling the Line Vulnerability
The vulnerability probabilistic model implemented for the OHLs in case of wet snow includes the vulnerability of:
- (1)
the phase conductors and the shielding wires which are affected by the mechanical tension due to the combined ice-wind load;
- (2)
the tower equipment (insulator chains, and bracings) subject to the combined force due to wind and ice loads.
As for item (1), a mechanical fragility curve is evaluated for each phase conductor Pmech_conductor and shielding wire Pmech_shieldwire consisting in a lognormal distribution of mechanical tension with a mean value equal to the expected tensile strength in kN for the conductor (e.g., 170 kN for phases in case of a 31.5 mm Aluminium Conductor Steel Reinforced (ACSR) conductors and a standard deviation equal to 2% of the expected value.
The mechanical failure probability of a single span of the line consists in (6):
where
Nphases and
Nshield_wires are respectively the number of phases (3 or 6 for a double circuit with common towers) and of shielding wires per span, and
Nconductors_per_phase is the number of conductors for each phase (typically from 1 to 3).
As for item (2), the vulnerability model of the equipment is composed by the mechanical fragility curve Pmech_equip consisting again in the lognormal distribution of the mechanical load, centered on the standard expected breaking strength of the weakest equipment, i.e., the bracings of the tower considering the typical design criteria followed by the TSO.
The mechanical failure probability of the tower due to equipment breakdown is given by (7):
where
Nequip_pertow represents the number of equipment per tower.
In the end, the failure probability of a line span
PFspan is given by (8):
The mechanical failure of the towers is neglected because lattice towers are much less vulnerable to ice and wind loads with respect to tower equipment like the bracings.
4.4. Modeling the Countermeasures at Component Level
Different countermeasures are being studied to reduce the wet snow sleeve. In particular, mechanical stabilizers of the conductors aim to avoid or at least to limit the conductor rotation which provokes sleeve accretion; moreover, ice-phobic coatings can delay the formation of the sleeve by reducing the sticking capability of the wet snow on the conductor or favor the sleeve shedding process. Further studies are required to model these countermeasures under a probabilistic point of view.
Presently a rough model of the ice-phobic coatings is provided to demonstrate the potentialities of the combined threat and contingency analysis tool. In particular, one property of the ice-phobic coatings is that they reduce the capability of the wet snow to stick to the conductor. This is modeled by limiting the sticking coefficient to 0.5 also for low wind speeds in the Makkonen model, thus using (9) to compute the sticking coefficient:
5. Study Case and Simulations
The study case refers to an emergency scenario due to a severe wet snow event really occurred in the North of Italy in 5–7 February 2015. In fact, the Italian High Voltage (HV) and Extra High Voltage (EHV) grid has been affected by a significant number of wet snow events in the last few years (2015–2017).
The wet snow storm affected both Medium/Low Voltage (MV/LV) distribution and HV/EHV transmission networks, but the focus of the present paper is on the transmission system. The adopted realistic model of the Italian HV (132/150 kV) and EHV (220/400 kV) grid includes 5500 electric nodes, 8000 lines, 800 generators.
The mechanical rated tensile strengths for the conductors are assumed equal to 170 and 100 kN respectively for ACSR conductors with cross-sectional areas of 585 and 308 mm2 (typical values for phase conductors respectively for 220/400 kV and 132 kV overhead lines). The shielding wires are steel conductors with a diameter equal to 11.5 mm.
Parameter
δ, fraction of total failure probability, adopted for the selection of critical components (see
Section 2.4) is set to 0.9, which means that the critical components contribute to the 90% of the total sum of failure probabilities over the whole system. The exploited big data consist in the forecasts of weather variables (ambient temperature, wind speed intensity and direction, precipitation rate) elaborated on 4 February 2015 for the subsequent 72 h (3-day ahead forecast). A total amount of 11,381 geospatial mesh points are considered for each forecast hour (from 1 to 72). The performed simulations and their goals are reported in
Table 2.
On the basis of public information [
33] the wet snow events affected a total equivalent length of 500 km of HV lines in the provinces of Bologna, Parma and Modena, with ice thicknesses up to 150–200 mm [
33].
5.1. Validation of the Platform: Scenario SC 1
In scenario SC 1 the geospatial data of weather forecasts are applied to the grid model thus obtaining the resulting geospatial distributions of the stress variables of interest, i.e., the mechanical tension on the phase conductors and the mechanical load on tower equipment, for each hour belonging to the 72 h forecasting period. By combining these stress variable distributions with the vulnerability curves of the components, the set of critical components can be identified for each forecast hour.
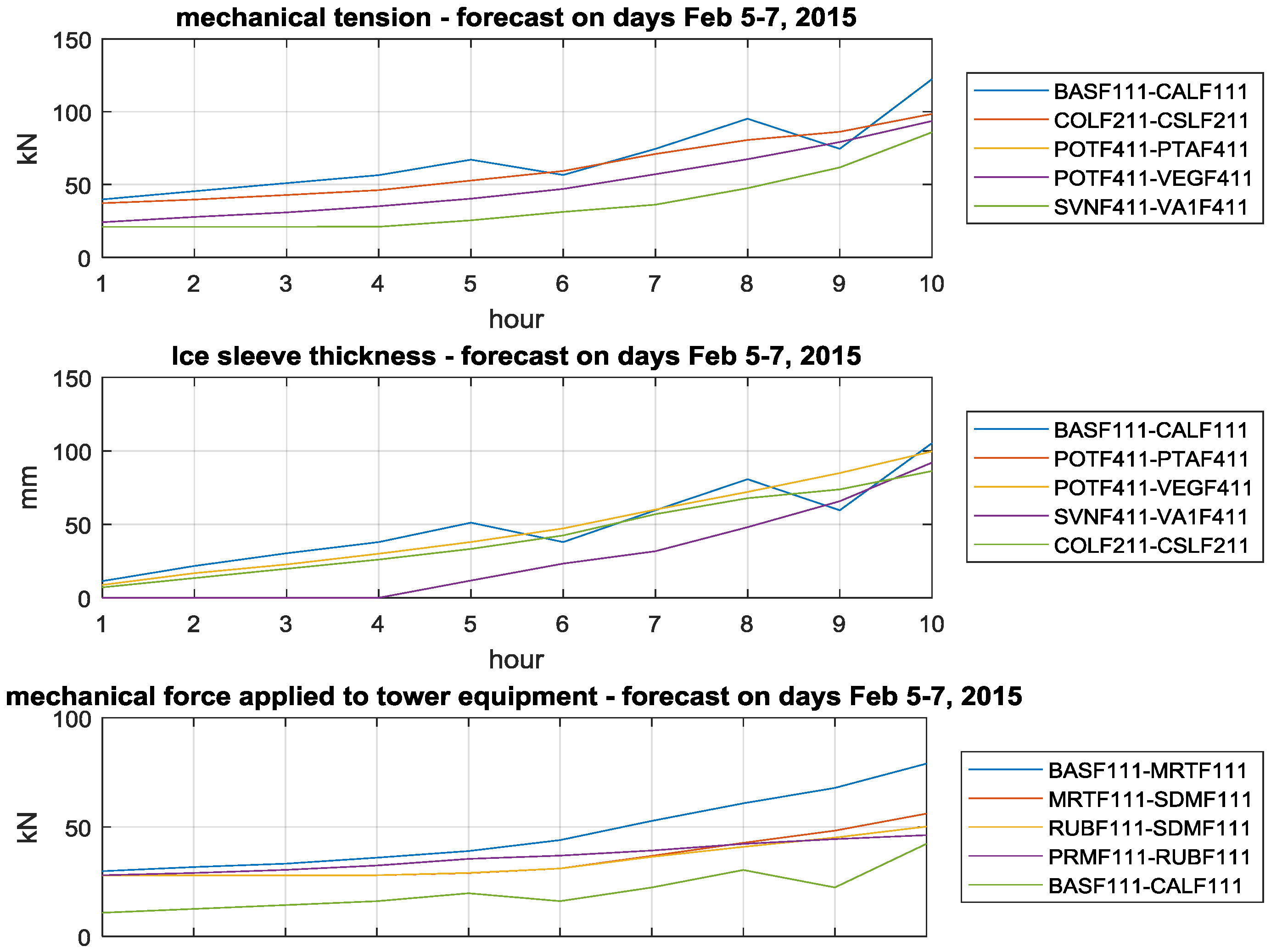
Figure 5 shows the expected values of the mechanical tension, the sleeve thickness and the load on tower equipment for the first 10 h of forecast, with focus on the OHL spans with the highest values of stress variables over the first 10 h in the area subject to the wet snow event.
It can be noticed that after just 10 h the ice sleeve reaches around 100 mm thicknesses, causing a mechanical tension on some OHLs approaching 100 kN which is the rated tensile strength of 132 kV OHLs. The comparison of simulations against the available information on recorded line outages during the event confirms the good performance of the tool, as the first line outages affected the 132 kV network at hour 12, thus close to hour 10. By comparing the results over the whole 72 h with the available data it’s worth noticing that:
- -
There is a good match between the maximum ice sleeve thickness recorded in the event (150–200 mm) and the ice thickness forecasted by the tool;
- -
There is also a good match between the portion of the grid with the largest number of collapsed lines (areas of Parma, Modena, Bologna) and the localization of the lines in
Table 3 which reports the list of the critical lines (i.e., the ones which most contribute to the total failure probability) with their failure probabilities at hours 8, 10, 15 and 28. The choice of a 28-h interval is justified by the fact that the majority of the line outages took place between hour 32 and hour 35 (on 6 February): using an interval of 28 h (just before hour 32) allows to test the prediction capability of the tool with respect to the actual outages recorded during the event.
In the first hours (8 and 10) the lines with the highest failure probabilities are in the rural area south of Bologna city. In hour 15 the affected lines still south of Bologna get closer to the city. The persistence of adverse weather conditions determine a large sleeve thickness on the conductor and values of tension close to the rated tensile strength around hours 30–40, which is confirmed by the records during Emilia Romagna events. In fact, during the event under study, after hour 35 (6 February) several 132 kV lines connected to substations in the provinces of Bologna, Parma and Modena suffered from mechanical damage with a repair time higher than 3 h. The list of critical lines for hour 28 confirms that the lines with very high failure probabilities are located in the area of Parma (substations FARF and FIOF) and between Modena and Bologna (substations MOVF, SDMF, MRTF and VIGF in
Table 3).
Figure 6 shows the geographical visualization of the set of critical lines respectively at hour 15 (in
Figure 6a) and 28 (in
Figure 6b).
Other causes of line damages, such as the fall of trees on conductors, reported in public sources [
33], and possible contacts among phases or small clearance between the phases and the ground due to sleeve loads, are not currently modeled inside the tool and will be considered in future activities.
On the basis of the lists of critical components at hour 15 in
Table 3 the power system tool described in [
10] and [
26] elaborates a set of 71 single and multiple contingencies which most contribute to the total risk of operating the system under such an extreme event. This set includes 6 “N−1” branch outages, 15 “N−2”, 20 “N−3”, 15 “N−4”, 6 “N−5” and 1 “N−6” common mode multiple branch contingencies, and 8 (multiple dependent) busbar contingencies.
Table 4 and
Table 5 report respectively the list of the ten most probable and the most risky contingencies with their probability of occurrence. It’s worth noticing that all the most risky contingencies and seven out of the ten most probable outages are N-k common mode contingencies (indicated with label “N−k” with k > 1): in fact, under extreme weather conditions multiple outages are more probable than single outages and contribute to the majority of the loss of load risk, which clearly highlights the limits of a conventional contingency analysis based on N−1 criterion.
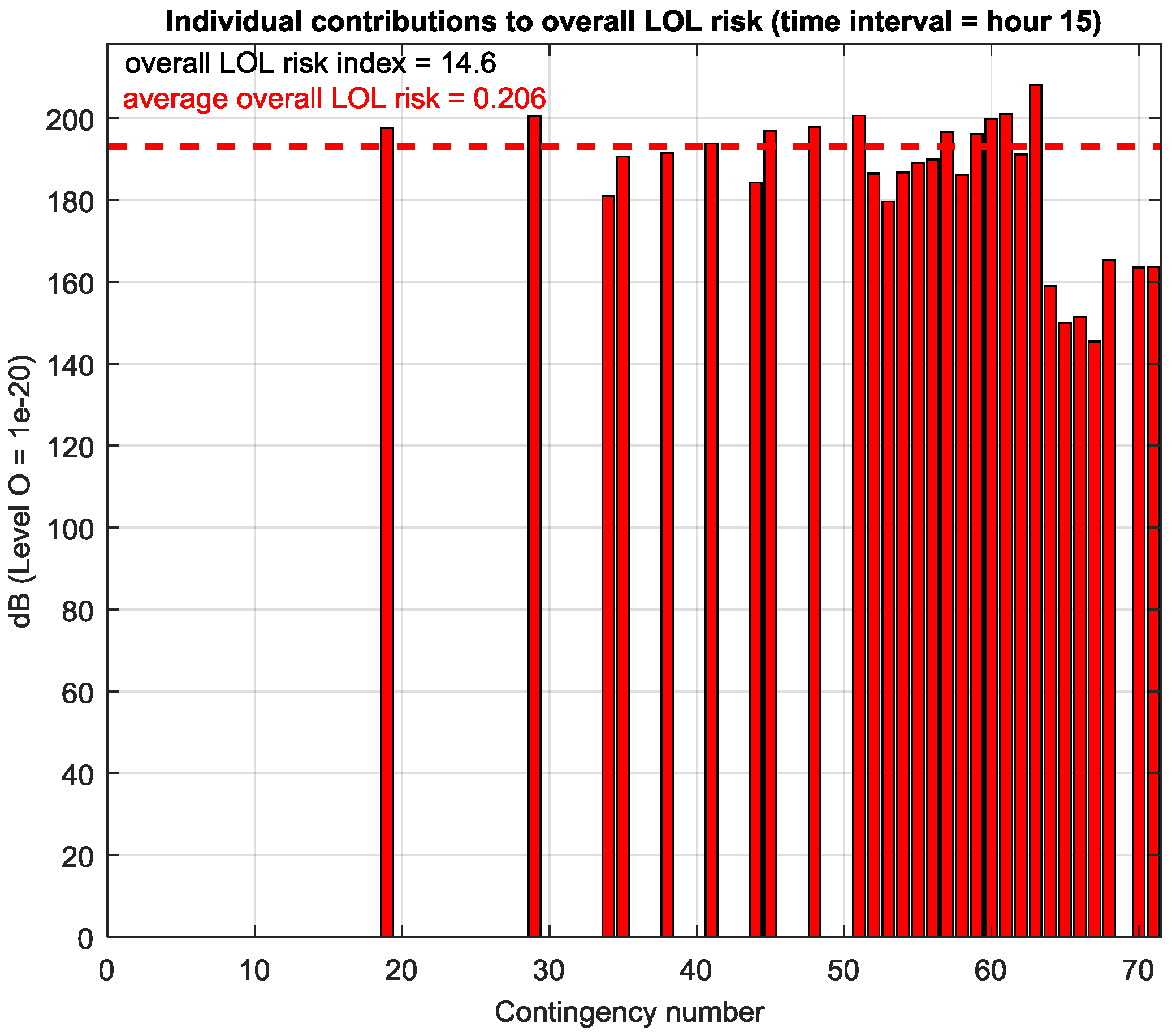
Figure 7 reports the loss of load risk indicators for the set of contingencies with an indication of the total risk of loss of load at hour 15 (equal to 14.6 expected lost MW).
5.2. A “What If” Scenario: Effect of Ice-Phobic Coatings
In scenario SC 2 the same forecast variables are applied to a grid model where the asset data related to OHLs have been modified by considering the ice-phobic coatings on all the critical lines.
The analysis detects only one critical line (POTF-VEGF 132 kV line) which is already in the set of critical lines in scenario SC 1. Its failure probability is drastically reduced from >0.9 to 4.66 × 10−2. The relevant set of risky contingencies is limited to three contingencies, consisting in 1 “N−1” line contingency, two “N−k” busbar dependent contingencies affecting 132 kV substations POTF and VEGF. After running the quasi static cascading outage simulator on the contingency set, it can be noticed that the use of ice-phobic coatings determines a substantial reduction of the total loss of load risk which passes from 14.6 expected lost MW’s in SC 1 to 5.3 × 10−5 expected lost MW’s in SC 2.
6. Conclusions
The paper has introduced an extended risk concept, a general approach for probabilistic risk based security assessment and a tool adequate for operation and operational planning contexts. The proposed holistic approach can adjust the set of single and multiple (also common mode and dependent) contingencies to be studied in security assessment sessions, on the basis of short term evolution of the actual threats, and it can rank the contingencies by means of risk indexes. In particular, the paper has focused on the integration of the risk-based security assessment tool with a weather forecasting system which provides 3-day ahead forecasts of weather variables characterizing the threats. The wet snow threat model is used to demonstrate the capability of the proposed tool: the integrated risk-based tool is thus applied to a real wet snow threat scenario occurred in February 2015 in the North of Italy. The simulations performed on a realistic model of the HV Italian grid confirm the effectiveness of the tool in forecasting critical conditions which occurred according to the historical records of line collapses during specific wet snow events. The mismatches between the real event recordings and the critical lines identified of the platform can be due to the fact that some of the outages were not provoked by snow sleeves but by other causes (e.g., fall of trees, contacts among phases or to the ground) currently not modelled in the platform.
The tool can bring different potential benefits to the TSOs. In fact, the selection of contingencies as a function of the environmental/weather threats, forecasted via available numerical prediction systems, permits operators to select the most risky disruption scenarios in the forecast period (up to few hours), and to prepare suitable preventive/corrective actions to cope with them, in case these scenarios really occur. Furthermore, the methodology represents a step forward with respect to conventional N−1 security assessment: first, the proposed contingency selection criterion, based on a risk concept, complements the N−1 credibility criterion including also multiple common mode and dependent events, potentially leading to large load disruptions. Secondly, the two-stage contingency screening process is able to select the subset of most significant multiple contingencies, which permits to reduce the computational burden in an operation context.
Besides predicting risky situations, the platform can also evaluate the benefits brought by potential countermeasures. Next steps will consist in a finer tuning of the vulnerability models of the grid components and the simulation of further indirect effects of weather threats (e.g., fall of trees).
Acknowledgments
This work has been financed by the Research Fund for the Italian Electrical System under the Contract Agreement between RSE S.p.A. and the Ministry of Economic Development—General Directorate for Nuclear Energy, Renewable Energy and Energy Efficiency in compliance with the Decree of 8 March 2006.
Author Contributions
Emanuele Ciapessoni, Diego Cirio and Andrea Pitto conceived and designed the methodology and the case study; Pietro Marcacci, Matteo Lacavalla and Andrea Pitto performed the simulations; Federico Silvestro, Stefano Massucco and Marino Sforna discussed the results; all the authors wrote and revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Panteli, M.; Mancarella, P. Influence of extreme weather and climate change on the resilience of power systems: Impacts and possible mitigation strategies. Electr. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
- Kezunovic, M.; Obradovic, Z.; Dokic, T.; Zhang, B.; Stojanovic, J.; Dehghanian, P.; Chen, P.C. Predicating Spatiotemporal Impacts of Weather on Power Systems using Big Data Science. In Data Science and Big Data: An Environment of Computational Intelligence; Springer: Berlin, Germany, 2017; ISBN 978-3-319-53474-9. [Google Scholar]
- Tin, P.; Zin, T.T.; Toriu, T.; Hama, H. An Integrated Framework for Disaster Event Analysis in Big Data Environments. In Proceedings of the Ninth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Beijing, China, 16–18 October 2013; pp. 255–258. [Google Scholar]
- Grolinger, K.; Capretz, M.A.M.; Mezghani, E.; Exposito, E. Knowledge as a Service Framework for Disaster Data Management. In Proceedings of the Workshop on Enabling Technologies: Infrastructure for Collaborative Enterprises, Hammamet, Tunisia, 17–20 June 2013; pp. 313–318. [Google Scholar]
- Wang, Y.F.; Deng, M.H.; Bao, Y.K.; Zhang, H.; Chen, J.Y.; Qian, J.; Guo, C.X. Power system disaster-mitigating dispatch platform based on big data. In Proceedings of the International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 1014–1019. [Google Scholar]
- Chen, L.; Chao, Y.; Ma, Y. Risk Warning System Based on Big Data Applied in the Power Informatization of State Grid. In Proceedings of the 2016 3rd International Conference on Information Science and Control Engineering (ICISCE), Beijing, China, 8–10 July 2016; pp. 578–582. [Google Scholar]
- Chen, P.C.; Kezunovic, M. Fuzzy Logic Approach to Predictive Risk Analysis in Distribution Outage Management. IEEE Trans. Smart Grid 2016, 7, 2827–2836. [Google Scholar] [CrossRef]
- Bonelli, P.; Lacavalla, M.; Marcacci, P.; Mariani, G.; Stella, G. Wet snow threat for power lines: A forecast and alert system applied in Italy. Nat. Hazards Earth Syst. Sci. 2010, 11, 2419–2431. [Google Scholar] [CrossRef]
- Lacavalla, M.; Marcacci, P.; Frigerio, A. Forecasting and monitoring wet snow sleeve on overhead power lines in Italy. In Proceedings of the 2015 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS), Trento, Italy, 9–10 July 2015; pp. 78–83. [Google Scholar]
- Ciapessoni, E.; Cirio, D.; Kjølle, G.; Massucco, S.; Pitto, A.; Sforna, M. Probabilistic Risk-Based Security Assessment of Power Systems Considering Incumbent Threats and Uncertainties. IEEE Trans. Smart Grid 2016, 7, 2890–2903. [Google Scholar] [CrossRef]
- Donde, V.; López, V.; Lesieutre, B.; Pinar, A.; Yang, C.; Meza, J. Severe Multiple Contingency Screening in Electric Power Systems. IEEE Trans. Power Syst. 2008, 23, 406–417. [Google Scholar] [CrossRef]
- Jiang, Q.; Huang, Z.; Xu, K. Contingency filtering technique for transient stability constrained optimal power flow. IET Gener. Transm. Distrib. 2013, 7, 1536–1546. [Google Scholar] [CrossRef]
- Genesi, C.; Granelli, G.; Innorta, M.; Marannino, P.; Montagna, M.; Zanellini, F. Identification of Critical Outages Leading to Cascading Failures in Electrical Power Systems. In Proceedings of the 2007 Powertech, Lausanne, Switzerland, 1–5 July 2007. [Google Scholar]
- Faustino Agreira, C.I.; Machado Ferreira, C.M.; Maciel Barbosa, F.P. Electric Power System Multiple Contingencies Analysis Using the Rough Set Theory. In Proceedings of the 2003 UPEC, Thessalonica, Greece, 1–3 September 2003. [Google Scholar]
- Eppstein, M.J.; Hines, P.D.H. A “Random Chemistry” Algorithm for Identifying Collections of Multiple Contingencies That Initiate Cascading Failure. IEEE Trans. Power Syst. 2012, 27, 1698–1705. [Google Scholar] [CrossRef]
- Lesieutre, B.; Roy, S.; Donde, V.; Pinar, A. Power System Extreme Event Screening Using Graph Partitioning. In Proceedings of the North American Power Symposium, Carbondale, IL, USA, 17–19 September 2006. [Google Scholar]
- Liu, X.; Joos, G. Transmission Grid Vulnerability Assessment by Eigen-Sensitivity and Cut-Set Screening. In Proceedings of the 2010 T&D Conference and Exposition, New Orleans, LA, USA, 19–22 April 2010. [Google Scholar]
- Yan, H.H.; Chow, J.-C.; Kam, M.; Fischl, R.; Sepich, C.R. Hybrid Expert System/Neural Network Hierarchical Architecture For Classifying Power System Contingencies. In Proceedings of the 1st International Forum on Applications of Neural Networks to Power Systems, Seattle, WA, USA, 23–26 July 1991. [Google Scholar]
- Kamwa, I.; Grondin, R.; Loud, L. Time-Varying Contingency Screening for Dynamic Security Assessment Using Intelligent-Systems Techniques. IEEE Trans. Power Syst. 2001, 16, 196–200. [Google Scholar] [CrossRef]
- Ni, M.; McCalley, J.D.; Vittal, V.; Tayyib, T. Online Risk-Based Security Assessment. IEEE Trans. Power Syst. 2003, 18, 258–265. [Google Scholar] [CrossRef]
- Vecchia, A.V. A Unified Approach to Probabilistic Risk Assessments for Earthquakes, Floods, Landslides, and Volcanoes. In Proceedings of the Multidisciplinary Workshop, Golden, CO, USA, 16–17 November 1999. [Google Scholar]
- Engelbrecht, C.S.; Hartings, R.; Lundquist, J. Statistical dimensioning of insulators with respect to polluted conditions. IEE Proc.-Gener. Transm. Distrib. 2004, 151, 321–326. [Google Scholar] [CrossRef]
- IEEE. IEEE Guide for Direct Lightning Stroke Shielding of Substations; Standard Std. 998-1996; IEEE: Piscataway, NJ, USA, 1996. [Google Scholar]
- Mamdouh Abd El Aziz, M.; Khalil Ibrahim, D.; Araby Kamel, H. Estimation of the Lifetime of Electrical Components in Distribution Networks. Online J. Electron. Electr. Eng. 2010, 2, 269–273. [Google Scholar]
- Barben, R. Vulnerability Assessment of Electric Power Supply under Extreme Weather Conditions. EPFL Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2010. [Google Scholar]
- Ciapessoni, E.; Cirio, D.; Pitto, A.; Kjølle, G.; Jakobsen, S.H.; Sforna, M. Contingency screening starting from probabilistic models of threats and component vulnerabilities. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–8. [Google Scholar]
- Hines, P.; Cotilla Sanchez, E.; Barrows, C. The Topological and Electrical Structure of Power Grids. In Proceedings of the 43rd Hawaii International Conference on System Sciences, Honolulu, HI, USA, 5–8 January 2010. [Google Scholar]
- Bompard, E.; Wu, D. Analysis of the structural vulnerability of the interconnected power grid of continental Europe with the Integrated Power System and Unified Power System based on extended topological approach. Int. Trans. Electr. Energy Syst. 2013, 23, 630–637. [Google Scholar] [CrossRef]
- Ciapessoni, E.; Cirio, D.; Pitto, A. Cascadings in large power systems: Benchmarking static vs. time domain simulation. In Proceedings of the 2014 IEEE PES General Meeting Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- GARPUR Consortium. Current Practices, Drivers and Barriers for New Reliability Standards; GARPUR FP7 EU Project; Deliverable 1.2; June 2014; European Union: Brussels, Belgium, 2014. [Google Scholar]
- Admirat, P.; Sakamoto, Y. Calibration of a wet-snow model on real cases in Japan and France. In Proceedings of the Fourth International Workshop on Atmospheric Icing of Structures (IWAIS), Paris, France, 5–7 September 1988. [Google Scholar]
- ISO Std. Atmospheric Icing of Structures; 12494; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- AEEGSI (Italian Regulatory Authority). Chiusura dell’indagine conoscitiva, avviata con Deliberazione dell’autorità 96/2015/e/eel, in relazione alle interruzioni del servizio elettrico occorse, nei giorni 6 Febbraio 2015 e seguenti, in vaste aree delle regioni Emilia Romagna e Lombardia; Deliberation Nr. 644; 22 December 2015; Italian Regulatory Authority: Rome, Italy, 2015. (In Italian)
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).