Calibration of Mine Ventilation Network Models Using the Non-Linear Optimization Algorithm
Abstract
:1. Introduction
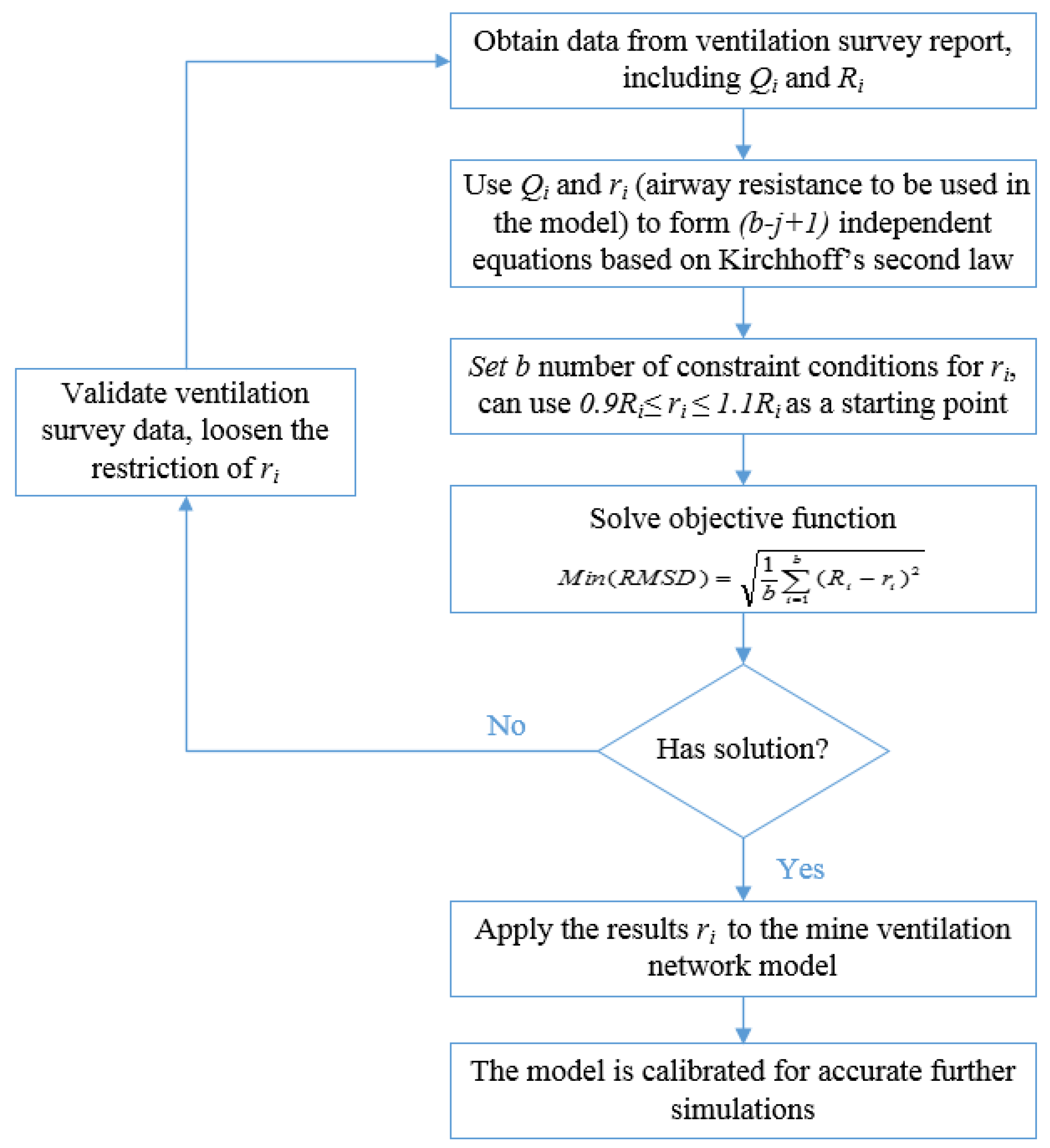
2. Methods
3. Numerical Model Validation
3.1. Ventilation Survey
3.2. MVN Model Establishment
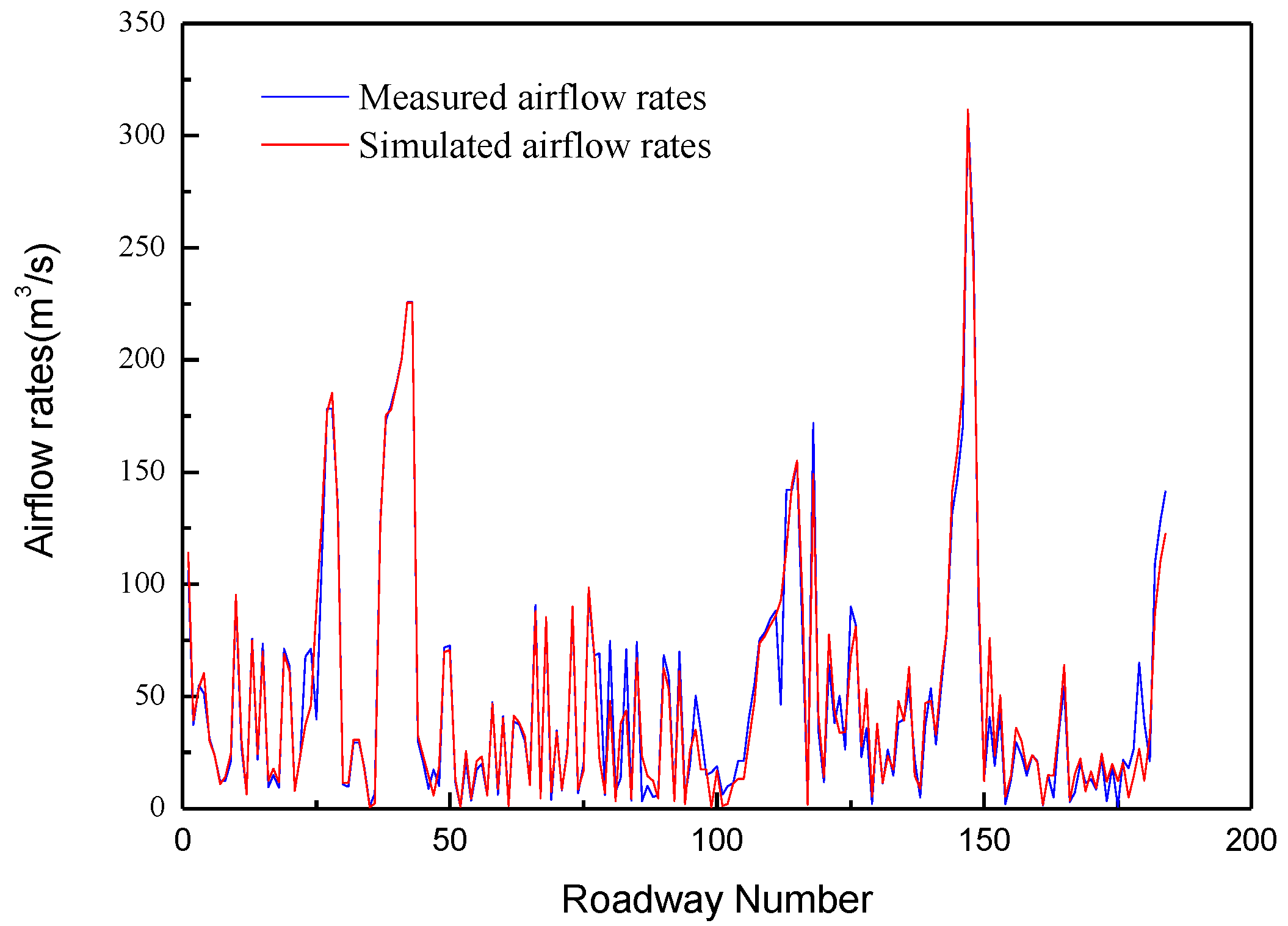
3.3. Model Calibration
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cheng, J.; Yang, S. Data mining applications in evaluating mine ventilation system. Saf. Sci. 2012, 50, 918–922. [Google Scholar] [CrossRef]
- Parra, M.T.; Villafruela, J.M.; Castro, F.; Mendez, C. Numerical and experimental analysis of different ventilation systems in deep mines. Build. Environ. 2006, 41, 87–93. [Google Scholar] [CrossRef]
- Zhou, F.; Wei, L.; Chen, K.; Cheng, J. Analyses of cascading failure in mine ventilation system and its effects in a serious mine gas explosion disaster. J. Fail. Anal. Prev. 2013, 13, 538–544. [Google Scholar] [CrossRef]
- Brodny, J.; Tutak, M. Determination of the zone endangered by methane explosion in goaf with caving of longwalls ventilated on „Y” system. Manag. Syst. Prod. Eng. 2016, 4, 247–251. [Google Scholar]
- Kurnia, J.C.; Sasmito, A.P.; Mujumdar, A.S. CFD simulation of methane dispersion and innovative methane management in underground mining faces. Appl. Math. Model. 2014, 38, 3467–3484. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, S.; Luo, Y. Mathematical models for optimizing and evaluating mine ventilation system. In Proceedings of the 13th United States/North American Mine Ventilation Symposium, Sudbury, ON, Canada, 13–16 June 2010; pp. 278–285. [Google Scholar]
- Widzyk-Capehart, E.; Watson, B. Agnew Gold Mine Expansion Mine Ventilation Evaluation Using Ventsim. In Proceedings of the 7th International Mine Ventilation Congress, Cracow, Poland, 17–22 June 2001; pp. 345–352. [Google Scholar]
- Feng, W.; Zhu, F.; Lv, H. The use of 3D simulation system in mine ventilation management. Procedia Eng. 2011, 26, 1370–1379. [Google Scholar]
- Şuvar, M.C.; Lupu, C.; Arad, V.; Cioclea, D.; Păsculescu, V.M.; Mija, N. Computerized simulation of mine ventilation networks for sustainable decision making process. Environ. Eng. Manag. J. 2014, 13, 1445–1451. [Google Scholar]
- Morar, M.S.; Radu, S.M.; Cioclea, D.; Gherghe, I. Use of IT equipment and specialized programs for solving ventilationnetworks. Calitatea 2017, 18, 121–126. [Google Scholar]
- Cheng, L.H.; Ueng, T.H.; Liu, C.W. Simulation of ventilation and fire in the underground facilities. Fire Saf. J. 2001, 36, 597–619. [Google Scholar] [CrossRef]
- Stefopoulos, E.K.; Damigos, D.G. Design of emergency ventilation system for an underground storage facility. Tunn. Undergr. Space Technol. 2007, 22, 209–302. [Google Scholar] [CrossRef]
- Kurnia, J.; Sasmito, A.; Mujumdar, A. Computational Study of Thermal Management in Underground Coal Mines: Effect of Operating Ventilation Parameters; National University of Singapore: Singapore, 2012. [Google Scholar]
- Dziurzyński, W.; Krach, A.; Pałka, T. A reliable method of completing and compensating the results of measurements of flow parameters in a network of headings/O pewnej metodzie uzupełniania I wyrównywania wyników pomiarów parametrów przepływu w sieci wyrobisk górniczych. Arch. Min. Sci. 2015, 60, 3–24. [Google Scholar] [CrossRef]
- Rowland, J.A. Ventilation Surveys and Modelling—Execution and Suggested Outputs. In Proceedings of the 11th Underground Coal Operator’s Conference, Wollongong, Australia, 10–11 February 2011; pp. 214–224. [Google Scholar]
- Wei, L.J.; Zhou, F.B.; Cheng, J.W.; Luo, X.R.; Li, X.L. Classification of structural complexity for mine ventilation networks. Complexity 2015, 21, 21–34. [Google Scholar] [CrossRef]
- Zhang, G. Ventilation Safety Science; China University of Mining & Technology Press: Xuzhou, China, 2011. [Google Scholar]
- Hu, Y.; Koroleva, O.I.; Krstić, M. Nonlinear control of mine ventilation networks. Syst. Control Lett. 2003, 49, 239–254. [Google Scholar] [CrossRef]
- McPherson, M.J. Subsurface Ventilation and Environmental Engineering; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Wang, Y.J.; Mutmansky, J.M. Modeling mine ventilation networks using five basic network elements. Min. Eng. 1997, 49, 65–69. [Google Scholar]
- Sui, J.; Yang, L.; Zhu, Z.; Fang, H.; Hua, Z. Mine ventilation optimization analysis and airflow control based on harmony annealing search. JCP 2011, 6, 1270–1277. [Google Scholar] [CrossRef]
- Nyaaba, W.; Frimpong, S.; El-Nagdy, K.A. Optimisation of mine ventilation networks using the Lagrangian algorithm for equality constraints. Int. J. Min. Reclam. Environ. 2015, 29, 201–212. [Google Scholar] [CrossRef]
- Ghaffari, S.; Aghajani, G.; Noruzi, A.; Hedayati Mehr, H. Optimal economic load dispatch based on wind energy and risk constrains through an intelligent algorithm. Complexity 2016, 21, 494–506. [Google Scholar] [CrossRef]
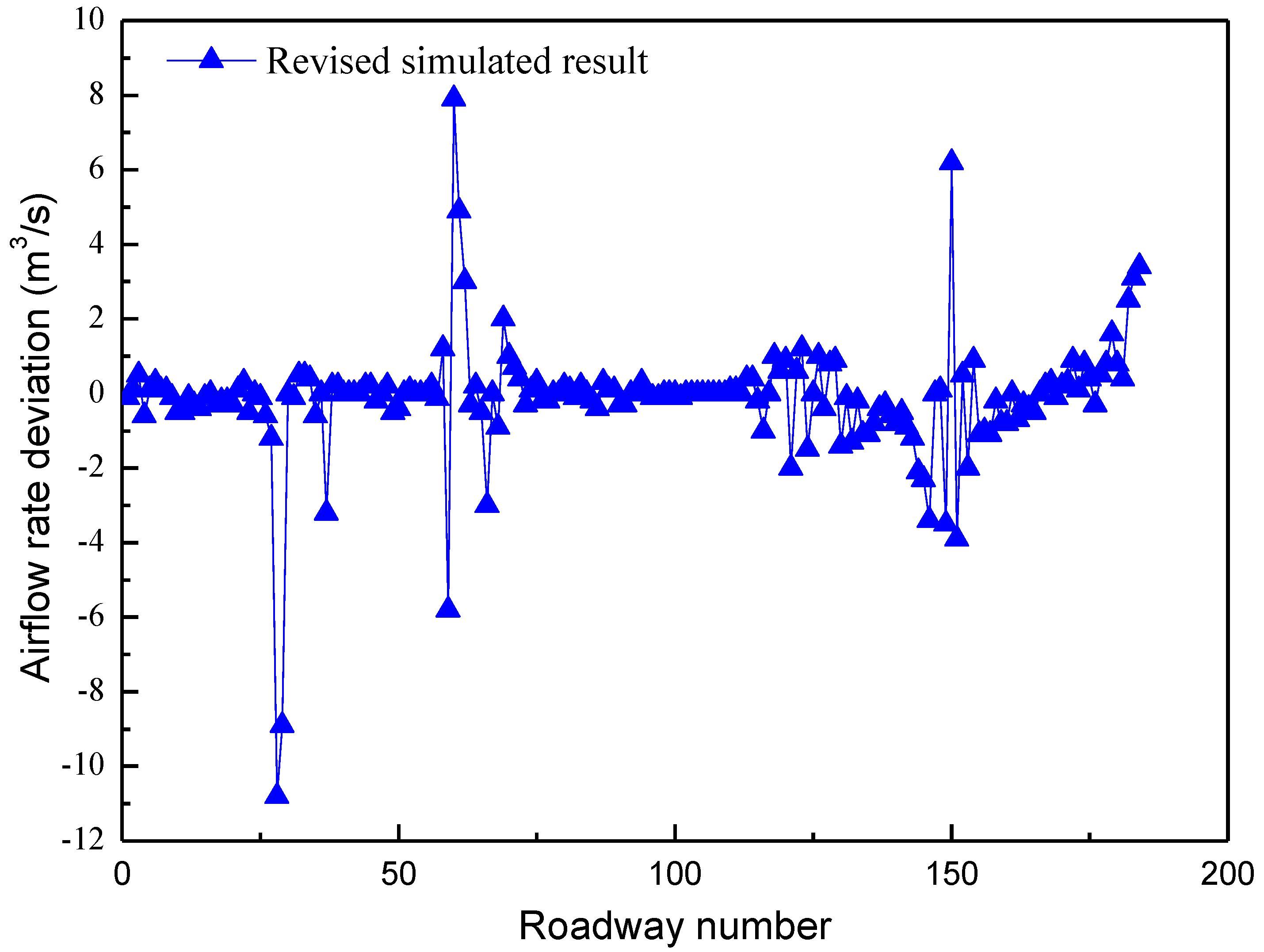
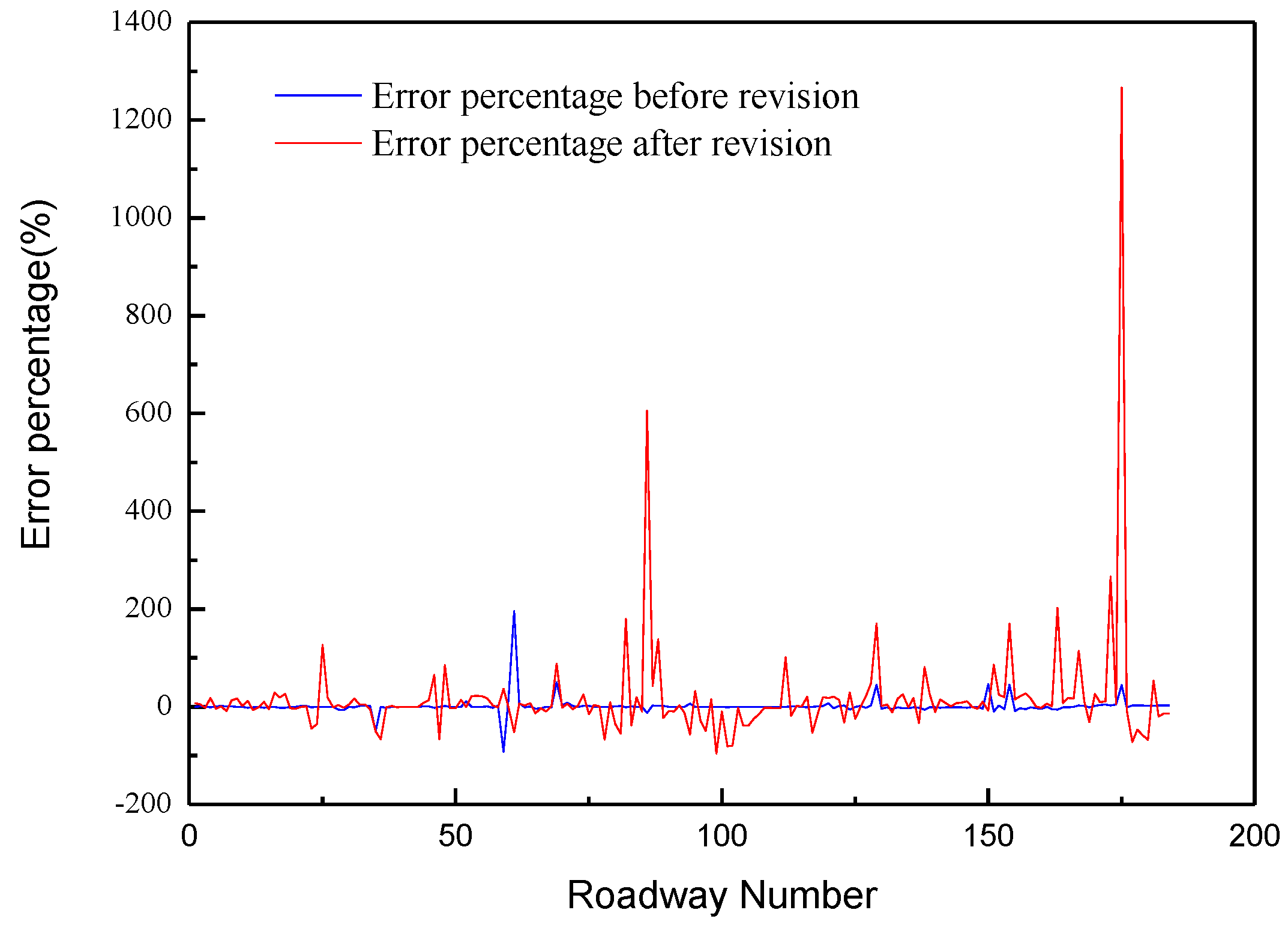
| Roadway Number | Measured Airflow Rate (m3/s) | Simulated Airflow Rate after Revision (m3/s) | Error Percentage |
|---|---|---|---|
| 35 | 1.2 | 0.6 | −50.00% |
| 52 | 0.9 | 1.0 | 11.11% |
| 59 | 6.3 | 0.5 | −92.06% |
| 61 | 2.5 | 7.4 | 196.00% |
| 69 | 4.0 | 6.0 | 50.00% |
| 86 | 3.3 | 2.9 | −12.12% |
| 129 | 2.0 | 2.9 | 45.00% |
| 150 | 13.3 | 19.5 | 46.62% |
| 154 | 2.0 | 2.9 | 45.00% |
| 175 | 0.9 | 1.3 | 44.44% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Huang, J.; Nie, B.; Chalmers, D.; Yang, Z. Calibration of Mine Ventilation Network Models Using the Non-Linear Optimization Algorithm. Energies 2018, 11, 31. https://doi.org/10.3390/en11010031
Xu G, Huang J, Nie B, Chalmers D, Yang Z. Calibration of Mine Ventilation Network Models Using the Non-Linear Optimization Algorithm. Energies. 2018; 11(1):31. https://doi.org/10.3390/en11010031
Chicago/Turabian StyleXu, Guang, Jinxin Huang, Baisheng Nie, Duncan Chalmers, and Zhuoming Yang. 2018. "Calibration of Mine Ventilation Network Models Using the Non-Linear Optimization Algorithm" Energies 11, no. 1: 31. https://doi.org/10.3390/en11010031
APA StyleXu, G., Huang, J., Nie, B., Chalmers, D., & Yang, Z. (2018). Calibration of Mine Ventilation Network Models Using the Non-Linear Optimization Algorithm. Energies, 11(1), 31. https://doi.org/10.3390/en11010031





