Optimal Operation of Interdependent Power Systems and Electrified Transportation Networks
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution of This Paper
- (1)
- We propose a novel framework for coupled electrified transportation and power networks to achieve optimal operation. We consider the shared variables between the interdependent networks to evaluate the interaction of two networks;
- (2)
- We develop a least cost routing strategy for electric vehicles to connect them with competing charging stations and their destinations: Our routing strategy considers charging costs, transportation cost, and traffic situation;
- (3)
- We analyze the cost benefits of the proposed framework by the simulations using a model of Shanghai transportation and power network. Although the proposed simulation framework captures the interdependent nature of power and transportation networks, there is still some future works to improve the practical aspect of this study. For instance, we use a snapshot of power system load demand for this study, however, future works can be extended to consider the problem in a real-time or near real-time fashion.
1.4. Organization of the Paper
2. Methodology
- EVs have stochastic nature on the transportation network and it is difficult to accurately estimate EV charging load for power network.
- Electric vehicle routing decisions are difficult considering limited energy storage, traffic conditions and multiple charging stations with different price alternatives.
- Linking the electrified transportation network with the power network is complex and it is difficult to optimize the operation of both networks.
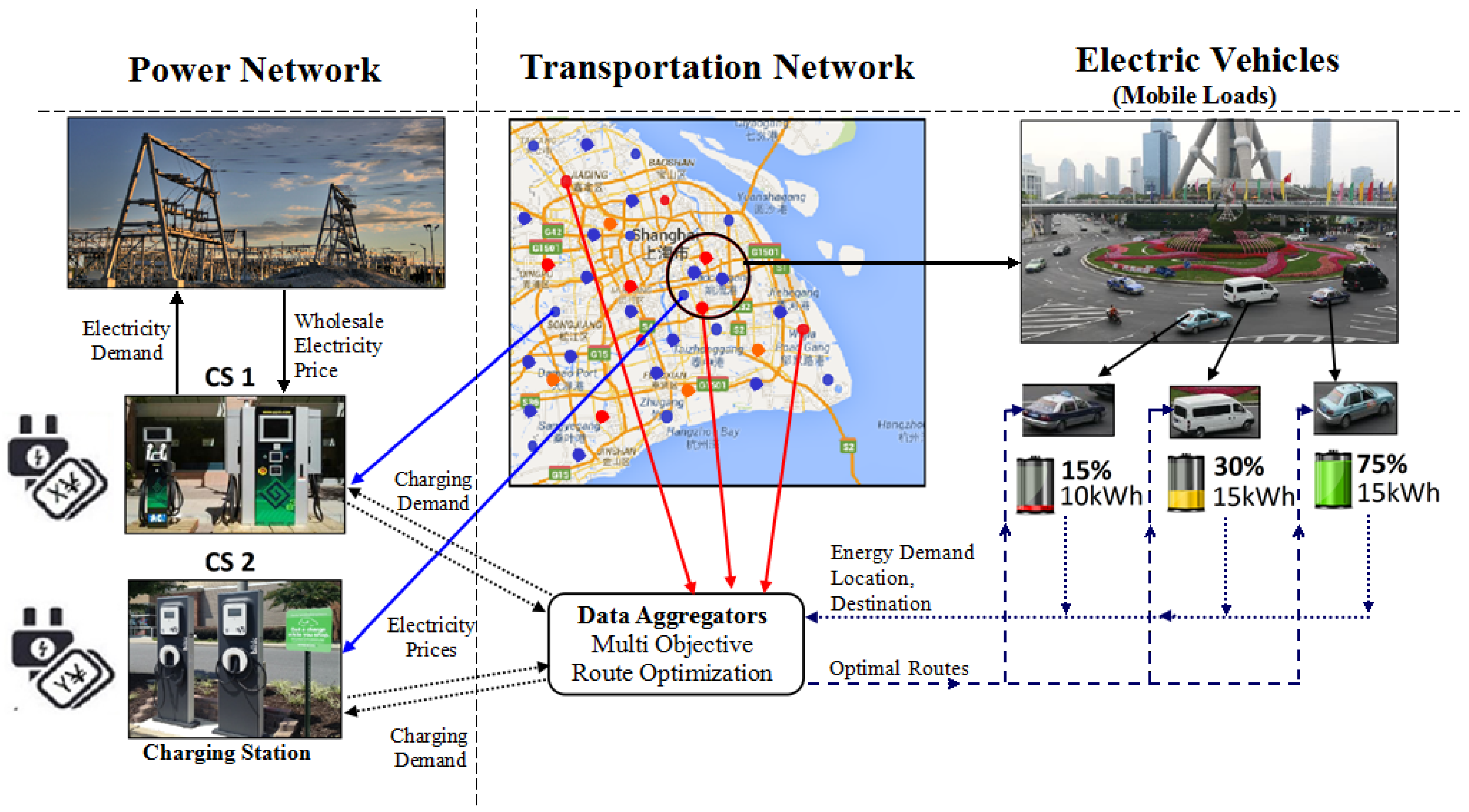
2.1. Integration of Interdependent Power and Transportation Networks
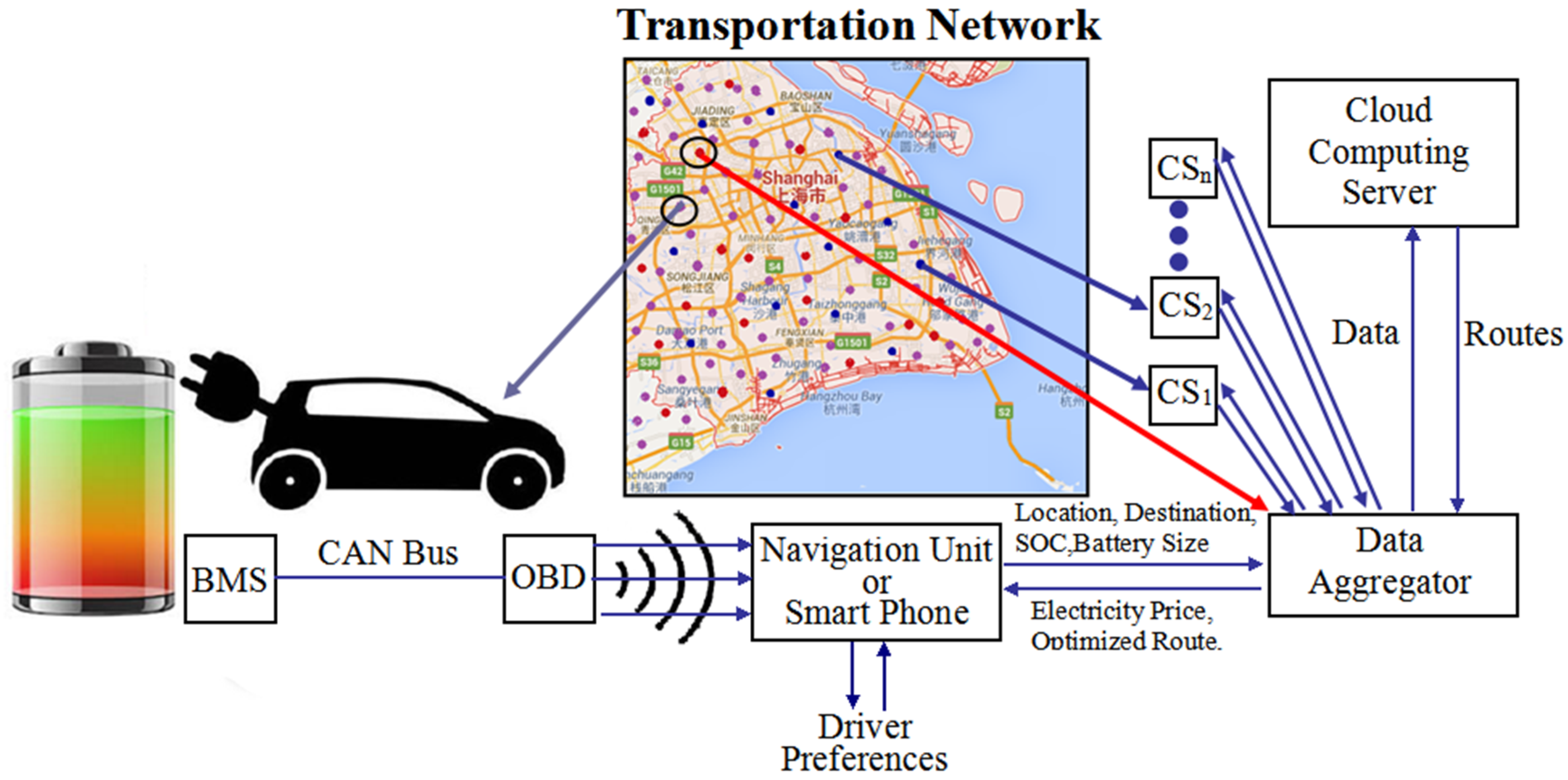
2.2. An Information Exchange Mechanism for EVs and Charging Stations
| Algorithm 1: Interaction of the charging stations with electric vehicles (EVs) to determine the price signals. |
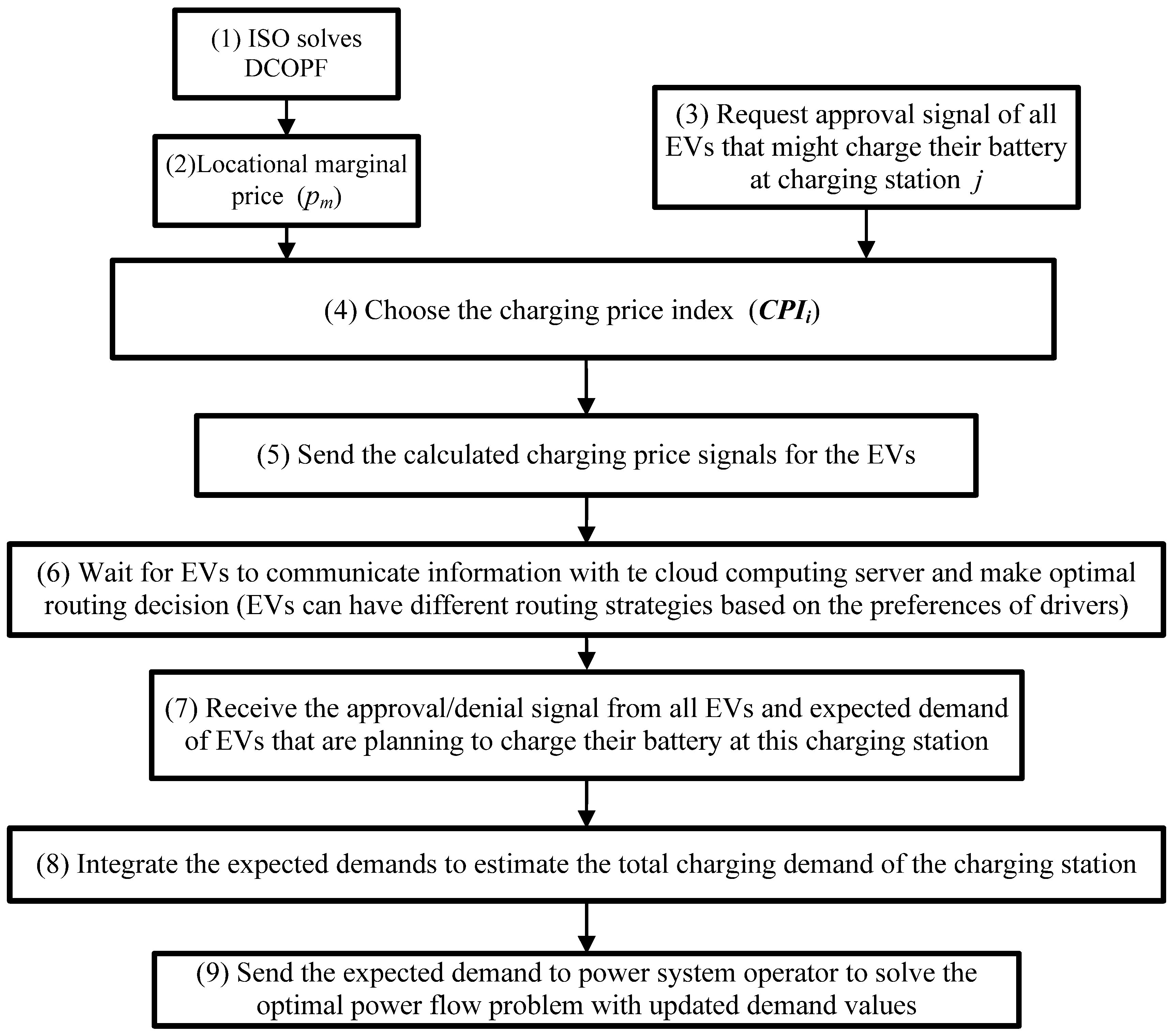
| 1. EV charging stations receive the locational marginal prices from the independent system operator (ISO) 2. EV charging stations receive the signal from each potential EV via cloud computing server whether the EV wants to potentially charge its battery at the charging station 3. EV charging station receives the expected duration, amount of charge required and distance from each EV 4. EV charging station determines the electricity price for each EV and communicates the price - go to {Algorithm 2} 5. Charging stations aggregate the expected EV charging demand based on the approved signals from EV to arrive at the charging station 6. Charging stations send their expected demands to the ISO for updating price signals for next time step 7. ISO solved DC Optimal Power Flow (DCOPF) to determine the nodal electricity prices 8. Go to step 1 |
| Algorithm 2: EVs to determine the optimal route utilizing bi-level routing scheme. |
| 1. EVs receive the price signals from all charging stations via cloud computing server 2. Optimal routing system receives the traffic data from transportation network database 3. Primary route optimization: EVs receive the optimal route and send a charging request signal to the candidate charging stations 4. EVs receive the approval signal from charging station 5. Secondary route optimization: EVs send the data set to the cloud computing server for the purposes of bi-level optimal routing from the starting point to charging station and from the charging station to the destination 6. EVs receive the suggested optimal routes from cloud computing server |
2.2.1. Electric Vehicle Module
2.2.2. Charging Station Module
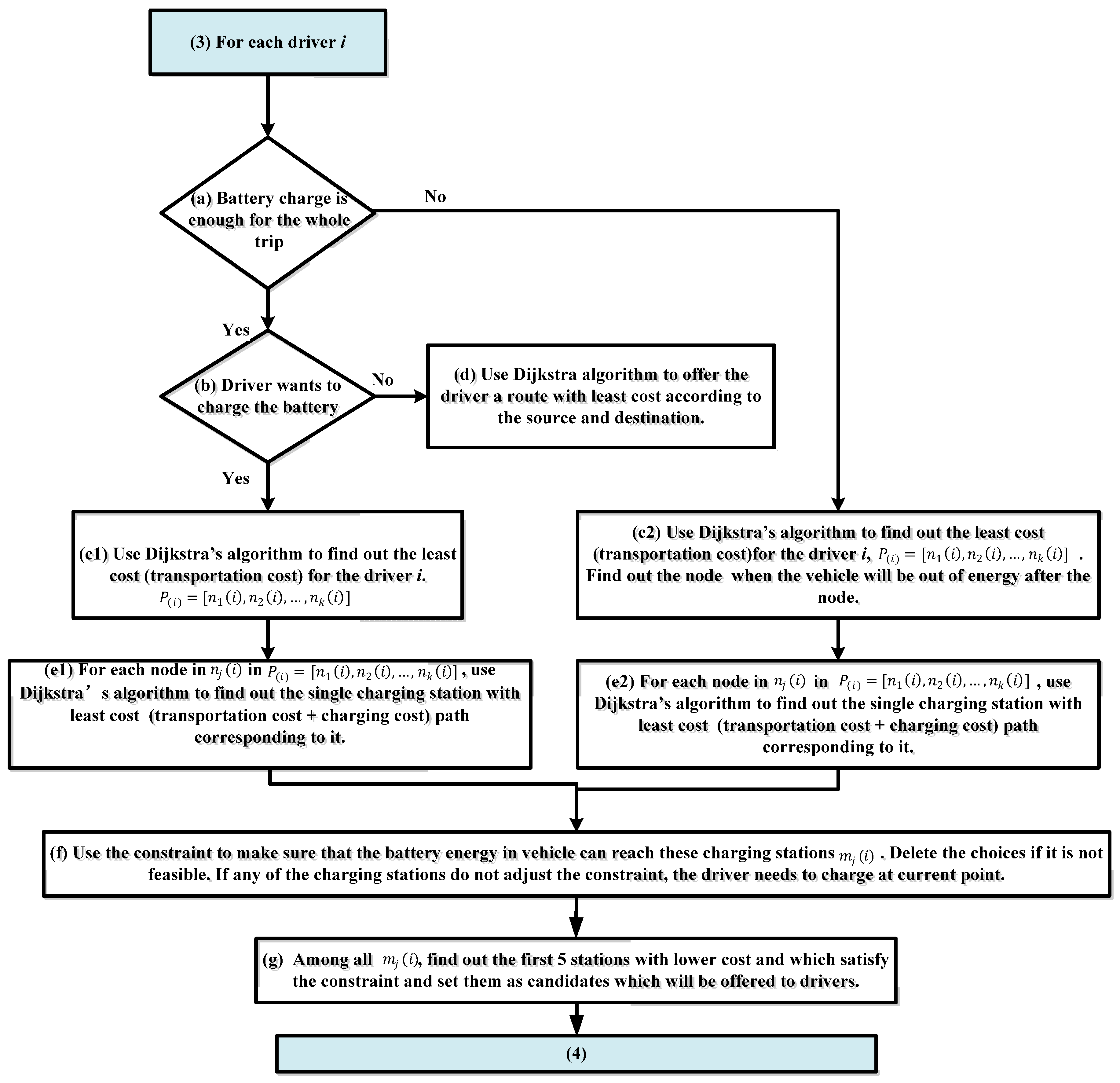
2.3. Vehicle Powertrain Connected Route Optimization Considering Charging Stations with Price Incentives
Breadth First Search Algorithm
2.4. Solving Optimal Power Flow Problem for Locational Marginal Electricity Prices
3. Case Study and Simulation Results
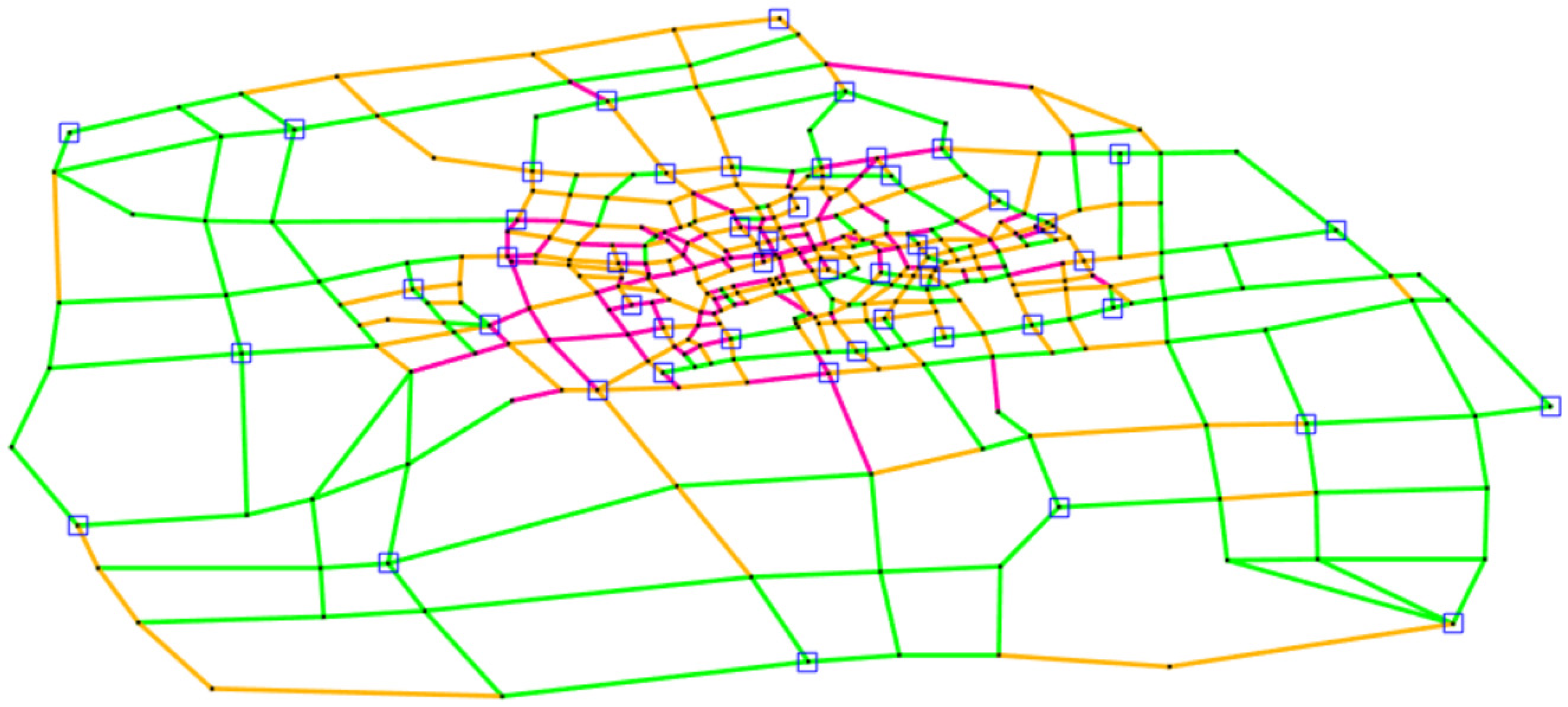
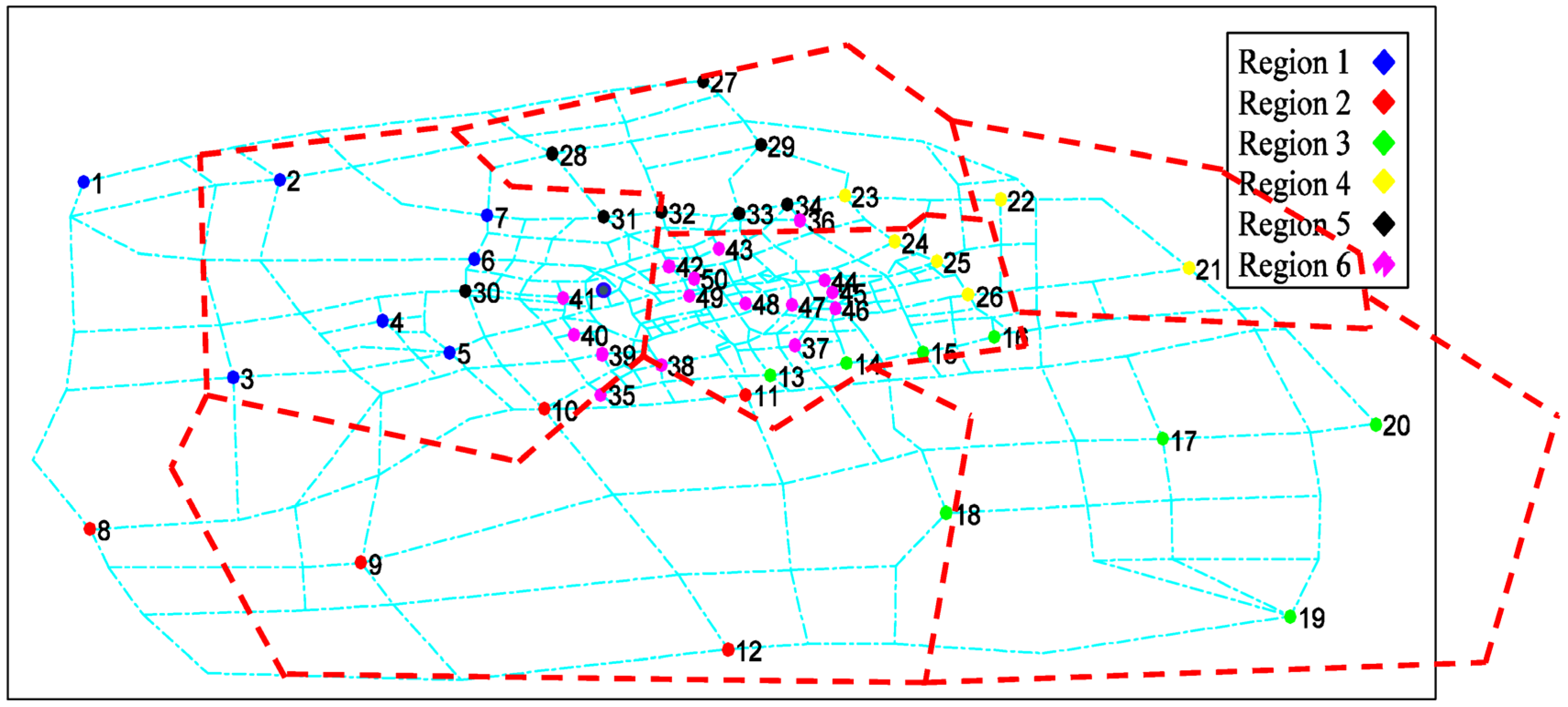
3.1. Proposed Power and Transportation Network Test Systems
3.2. Power Systems and Transportation Network Operation With and Without Using the Proposed Framework in Presence of PHEVs
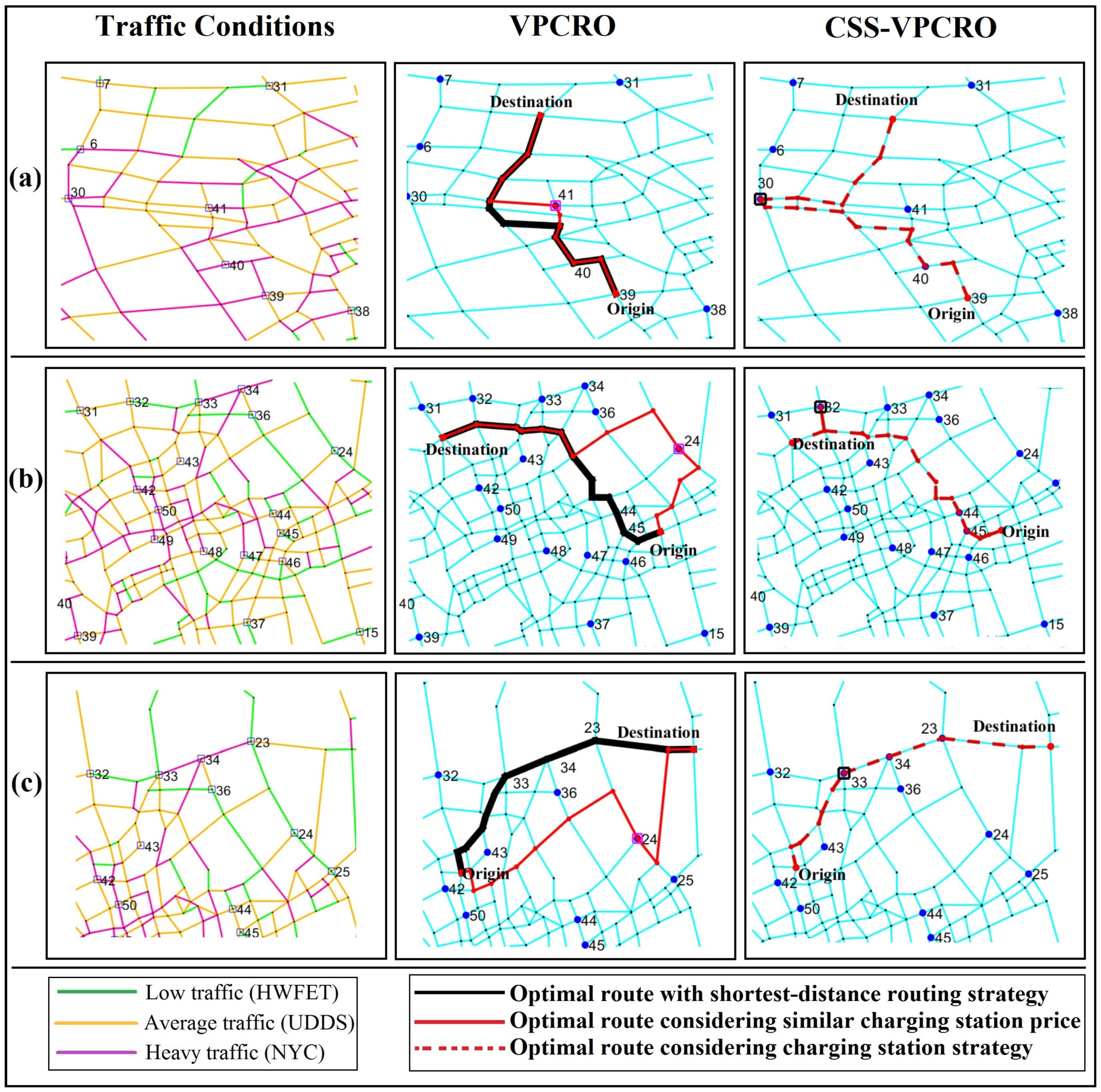
3.2.1. Impact of the Simultaneous Optimization on Vehicle Routing
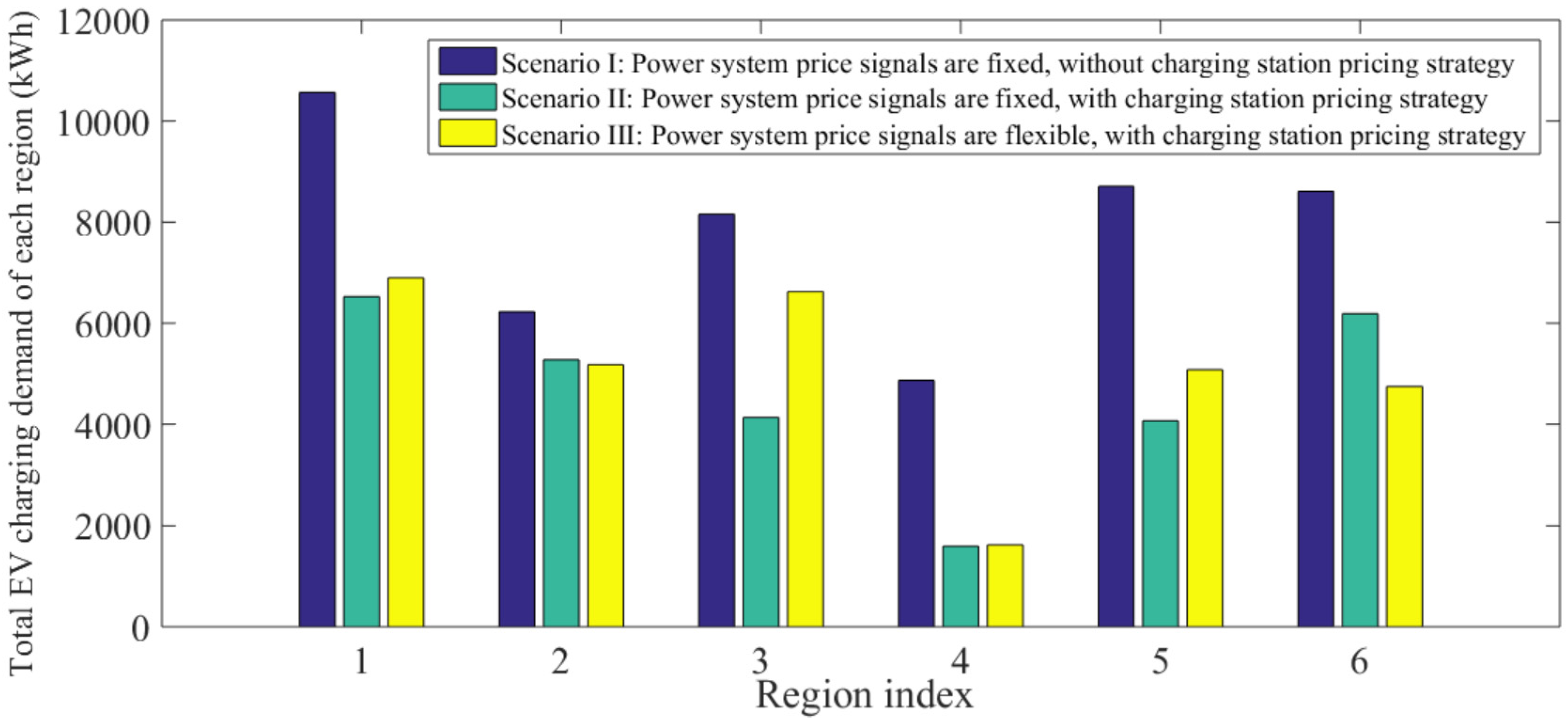
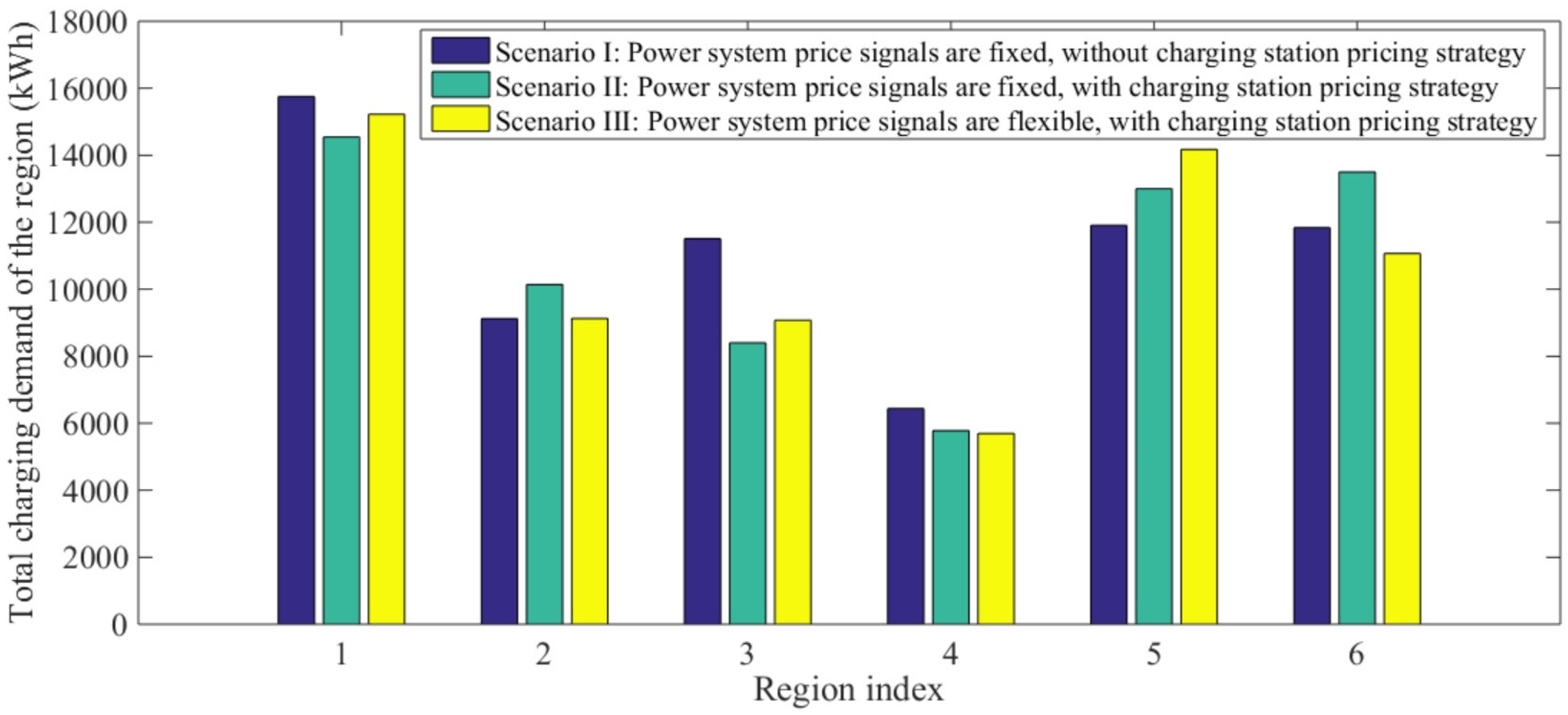
3.2.2. Impact of the Simultaneous Optimization on EV Charging Demand and Electricity Price
- (1)
- We consider the penetration level of PHEV20, PHEV40, PHEV60, and BEV100 to be 16%, 16%, 16%, and 52%, respectively. This will lead to more flexibility for the PHEVs, who are 48% of total cars in this study, to reduce their electricity consumption to optimize their transportation cost. In other words, 48% of the vehicles are capable of using fuel as an alternative for electricity if the offered charging electricity price from the charging stations is comparatively high.
- (2)
- Although the shortest path method only takes the distance into account, our CSS-VPCRO takes the traffic conditions into account as well. Consequently, it may choose a longer distance with light traffic condition which leads to energy saving, rather than a shorter distance with congested traffic which leads to higher energy consumption.
3.3. Power Systems and Transportation Network Operation With and Without Using the Proposed Framework in Absence of PHEVs
4. Conclusions
- Reducing the transportation cost by 40.9% for the analyzed electrified transportation network in the presence of PHEVs;
- Reducing the transportation cost by 8.6% for the analyzed electrified transportation network in the absence of PHEVs (in this case we only have battery-only EVs in the transportation network);
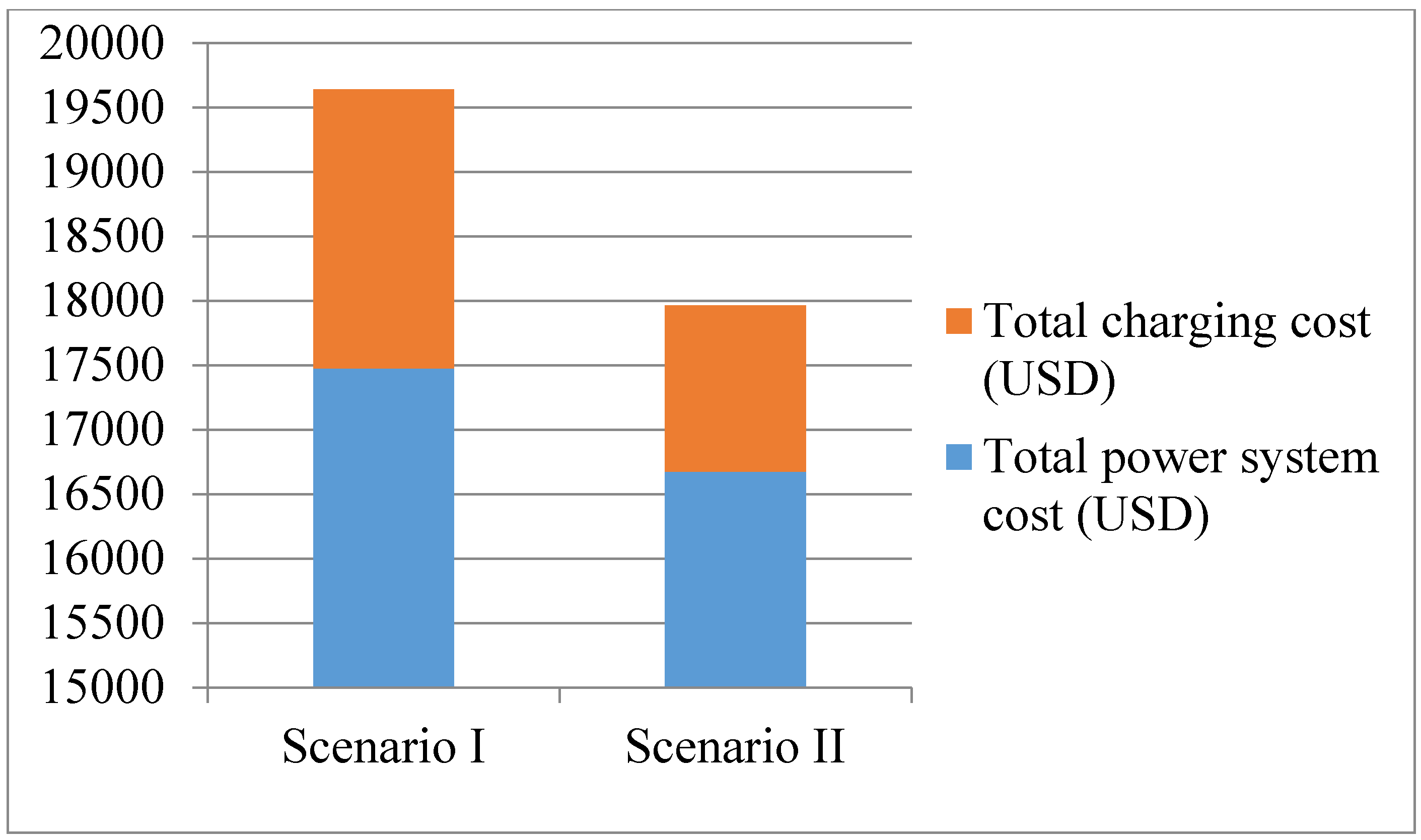
- Total power system cost is reduced: Our framework considers the locational marginal price of electricity to obtain the optimal route. However, in the conventional shortest path method the EVs only consider traffic conditions to find the optimal route.
- Real-time/near real-time simulation of the proposed interdependent power and transportation network framework
- Considering both inter-area and intra-area time resolutions for economic dispatch in power systems while performing the simulation results. This will make the study more realistic in terms of considering different time-scales from power systems perspective.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bradley, T.H.; Frank, A.A. Design, demonstrations and sustainability impact assessments for plug-in hybrid electric vehicles. Renew. Sustain. Energy Rev. 2009, 13, 115–128. [Google Scholar] [CrossRef]
- Samaras, C.; Meisterling, K. Life cycle assessment of greenhouse gas emissions from plug-in hybrid vehicles: Implications for policy. Environ. Sci. Technol. 2008, 42, 3170–3176. [Google Scholar] [CrossRef] [PubMed]
- Amini, M.H.; Moghaddam, M.P.; Karabasoglu, O. Simultaneous allocation of electric vehicles’ parking lots and distributed renewable resources in smart power distribution networks. Sustain. Cities Soc. 2017, 28, 332–342. [Google Scholar] [CrossRef]
- Zhou, G.; Ou, X.; Zhang, X. Development of electric vehicles use in China: A study from the perspective of life-cycle energy consumption and greenhouse gas emissions. Energy Policy 2013, 59, 875–884. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]
- Zhang, X.; Grijalva, S. An advanced data driven model for residential electric vehicle charging demand. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Alizadeh, M.; Scaglione, A.; Davies, J.; Kurani, K.S. A scalable stochastic model for the electricity demand of electric and plug-in hybrid vehicles. IEEE Trans. Smart Grid 2014, 5, 848–860. [Google Scholar] [CrossRef]
- Deilami, S.; Masoum, A.S.; Moses, P.S.; Masoum, M.A. Real-time coordination of plug-in electric vehicle charging in smart grids to minimize power losses and improve voltage profile. IEEE Trans. Smart Grid 2011, 2, 456–467. [Google Scholar] [CrossRef]
- Mingfei, B.A.N.; Jilai, Y.U. Procedural simulation method for aggregating charging load model of private electric vehicle cluster. J. Mod. Power Syst. Clean Energy 2015, 3, 170–179. [Google Scholar]
- Donadee, J.; Ilic, M.; Karabasoglu, O. Optimal autonomous charging of electric vehicles with stochastic driver behavior. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar]
- Amini, M.H.; McNamara, P.; Weng, P.; Karabasoglu, O.; Xu, Y. Hierarchical Electric Vehicle Charging Aggregator Strategy Using Dantzig-Wolfe Decomposition. IEEE Des. Test 2017. [Google Scholar] [CrossRef]
- Kempton, W.; Tomić, J. Vehicle-to-grid power fundamentals: Calculating capacity and net revenue. J. Power Sources 2005, 144, 268–279. [Google Scholar] [CrossRef]
- Lund, H.; Kempton, W. Integration of renewable energy into the transport and electricity sectors through V2G. Energy Policy 2008, 36, 3578–3587. [Google Scholar] [CrossRef]
- Yazdani-Damavandi, M.; Moghaddam, M.P.; Haghifam, M.R.; Shafie-khah, M.; Catalão, J.P. Modeling operational behavior of plug-in electric vehicles’ parking lot in multi energy systems. IEEE Trans. Smart Grid 2016, 7, 124–135. [Google Scholar] [CrossRef]
- Amini, M.H.; Kargarian, A.; Karabasoglu, O. ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation. Electric Power Syst. Res. 2016, 140, 378–390. [Google Scholar] [CrossRef]
- Amini, M.H.; Islam, A. Allocation of Electric Vehicles’ Parking Lots in Distribution Network. In Proceedings of the IEEE PES 5th Innovative Smart Grid Technologies Conference (ISGT 2014), Washington, DC, USA, 19–22 February 2014. [Google Scholar]
- Neyestani, N.; Damavandi, M.Y.; Shafie-khah, M.; Catalao, J.P. Modeling the PEV traffic pattern in an urban environment with parking lots and charging stations. In Proceedings of the 2015 IEEE Eindhoven Power Tech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Mohsenzadeh, A.; Pang, C.; Pazouki, S.; Haghifam, M. Optimal siting and sizing of electric vehicle public charging stations considering smart distribution network reliability. In Proceedings of the IEEE North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015. [Google Scholar]
- Chen, Q.; Liu, N. Optimal Power Utilizing Strategy for PV-based EV Charging Stations Considering Real-Time Price. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar]
- Eklund, P.W.; Kirkby, S.; Pollitt, S. A dynamic multi-source Dijkstra’s algorithm for vehicle routing. In Proceedings of the IEEE Australian and New Zealand Conference on Intelligent Information Systems, Adelaide, SA, Australia, 18–20 November 1996; pp. 329–333. [Google Scholar]
- Ahn, C.W.; Ramakrishna, R.S. A genetic algorithm for shortest path routing problem and the sizing of populations. IEEE Trans. Evolut. Comput. 2002, 6, 566–579. [Google Scholar]
- Goldberg, A.V.; Radzik, T. A heuristic improvement of the Bellman-Ford algorithm. Appl. Math. Lett. 1993, 6, 3–6. [Google Scholar] [CrossRef]
- Mohemmed, A.W.; Sahoo, N.C.; Geok, T.K. Solving shortest path problem using particle swarm optimization. Appl. Soft Comput. 2008, 8, 1643–1653. [Google Scholar] [CrossRef]
- Chabrier, A. Vehicle routing problem with elementary shortest path based column generation. Comput. Oper. Res. 2006, 33, 2972–2990. [Google Scholar] [CrossRef]
- Qiao, Z.; Karabasoglu, O. Vehicle Powertrain Connected Route Optimization for Conventional, Hybrid and Plug-in Electric Vehicles. arXiv, 2016; arXiv preprint. arXiv:1612.01243. [Google Scholar]
- Karabasoglu, O.; Michalek, J. Influence of driving patterns on life cycle cost and emissions of hybrid and plug-in electric vehicle powertrains. Energy Policy 2013, 60, 445–461. [Google Scholar] [CrossRef]
- Zhang, C.; Vahidi, A.; Pisu, P.; Li, X.; Tennant, K. Role of terrain preview in energy management of hybrid electric vehicles. IEEE Trans. Veh. Technol. 2010, 59, 1139–1147. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Tavares, G.; Zsigraiova, Z.; Semiao, V.; Carvalho, M. Optimisation of MSW collection routes for minimum fuel consumption using 3d GIS modelling. Waste Manag. 2009, 29, 1176–1185. [Google Scholar] [CrossRef] [PubMed]
- Artmeier, A.; Haselmayr, J.; Leucker, M.; Sachenbacher, M. The shortest path problem revisited: Optimal routing for electric vehicles. In Annual Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Yang, Z.; Long, K.; You, P.; Chow, M.Y. Joint scheduling of large-scale appliances and batteries via distributed mixed optimization. IEEE Trans. Power Syst. 2015, 30, 2031–2040. [Google Scholar] [CrossRef]
- You, P.; Yang, Z.; Zhang, Y.; Low, S.H. Optimal Charging Schedule for a Battery Switching Station Serving Electric Buses. IEEE Trans. Power Syst. 2016, 31, 3473–3483. [Google Scholar] [CrossRef]
- Bashash, S.; Moura, S.J.; Forman, J.C.; Fathy, H.K. Plug-in hybrid electric vehicle charge pattern optimization for energy cost and battery longevity. J. Power Sources 2011, 196, 541–549. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, K.; Guo, Y.; Su, W. Investigate the Impacts of PEV Charging Facilities on Integrated Electric Distribution System and Electrified Transportation System. IEEE Trans. Transp. Electr. 2015, 1, 178–187. [Google Scholar] [CrossRef]
- Allan, D.F.; Farid, A.M. A Benchmark Analysis of Open Source Transportation-Electrification Simulation Tools. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems (ITSC), Las Palmas, Spain, 15–18 September 2015; pp. 1202–1208. [Google Scholar]
- Viswanath, A.; Farid, A.M. A hybrid dynamic system model for the assessment of transportation electrification. In Proceedings of the IEEE American Control Conference, Portland, OR, USA, 4–6 June 2014. [Google Scholar]
- Farid, A.M. A Hybrid Dynamic System Model for Multimodal Transportation Electrification. IEEE Trans. Control Syst. Technol. 2016, 25, 940–951. [Google Scholar] [CrossRef]
- Farid, A.M. Symmetrica: Test case for transportation electrification research. Infrastruct. Complex. 2015, 2, 1–10. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Skiena, S. Dijkstra’s algorithm. In Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica; Addison-Wesley: Reading, MA, USA, 1990; pp. 225–227. [Google Scholar]
- Zhou, R.; Hansen, E.A. Breadth-first heuristic search. Artif. Intell. 2006, 170, 385–408. [Google Scholar] [CrossRef]
- Zhu, J. Optimization of Power System Operation; John Wiley & Sons: NJ, USA, 2015. [Google Scholar]
- Amini, M.H.; Jaddivada, R.; Mishra, S.; Karabasoglu, O. Distributed security constrained economic dispatch. In Proceedings of the IEEE Innovative Smart Grid Technologies-Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015. [Google Scholar]
- Mehrtash, M.; Kargarian, A.; Mohammadi, A. A partitioning-based bus renumbering effect on interior point-based OPF solution. In Proceedings of the IEEE Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018. [Google Scholar]
- Mohammadi, J.; Hug, G.; Kar, S. Agent-Based Distributed Security Constrained Optimal Power Flow. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Stott, B. Review of load-flow calculation methods. Proc. IEEE 1974, 62, 916–929. [Google Scholar] [CrossRef]
- Ott, A. PJM: A full service ISO market evolution (panel on evolution of electricity market structures). Power Eng. Soc. Summer Meet. IEEE 1999, 2, 746–748. [Google Scholar]
- Alvey, T.; Goodwin, D.; Ma, X.; Streiffert, D.; Sun, D. A security-constrained bid-clearing system for the New Zealand wholesale electricity market. IEEE Trans. Power Syst. 1998, 13, 340–346. [Google Scholar] [CrossRef]
- Shanghai Electric Vehicle Charging Infrastructure Special Plan (2016-2020). Available online: http://www.evpartner.com/news/12/detail-18938.html (accessed on September 2016).
- Tesla Model S Software Release Notes v6.0. Available online: https://www.tesla.com/sites/default/files/Tesla_Model_S_Software_6.0.pdf (accessed on January 2017).





| Vehicle Type | Symbol | Unit | HWFET | UDDS | NYC |
|---|---|---|---|---|---|
| PHEV20 | * | mi/kWh | 5.7 | 6.2 | 4.2 |
| mi/gal | 58.6 | 69.4 | 45.7 | ||
| PHEV40 | mi/kWh | 5.7 | 6.0 | 4.1 | |
| mi/gal | 58.2 | 68.0 | 43.1 | ||
| PHEV60 | mi/kWh | 5.6 | 5.7 | 3.8 | |
| mi/gal | 57.8 | 65.8 | 40.3 | ||
| BEV100 | mi/kWh | 4.8 | 5.2 | 3.1 |
| Bus Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Load demand (MWh) | 0 | 200 | 0 | 0 | 120 | 10 | 160 | 40 | 80 |
| Region index | NCS * | 1 | NCS | NCS | 2 | 3 | 4 | 5 | 6 |
| Max charging station capacity | NCS | 500 | NCS | NCS | 500 | 700 | 600 | 500 | 1500 |
| Number of charging stations | NCS | 7 | NCS | NCS | 5 | 8 | 6 | 8 | 16 |
| Scenario | I | II | III |
|---|---|---|---|
| Total power system cost (USD) | 17,476 | 165,68 | 16,677 |
| Total transportation network cost (USD) | 2165 | 1270 | 1287 |
| Additional power system cost (compared to the base case) | 14.14% | 8.30% | 8.36% |
| Scenario | I | II | III |
|---|---|---|---|
| Total power system cost (USD) | 18,720 | 18,530 | 18,427 |
| Total transportation network cost (USD) | 3409 | 3219 | 3116 |
| Additional power system cost (compared to the base case) | 22.27% | 21.02% | 20.35% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amini, M.H.; Karabasoglu, O. Optimal Operation of Interdependent Power Systems and Electrified Transportation Networks. Energies 2018, 11, 196. https://doi.org/10.3390/en11010196
Amini MH, Karabasoglu O. Optimal Operation of Interdependent Power Systems and Electrified Transportation Networks. Energies. 2018; 11(1):196. https://doi.org/10.3390/en11010196
Chicago/Turabian StyleAmini, M. Hadi, and Orkun Karabasoglu. 2018. "Optimal Operation of Interdependent Power Systems and Electrified Transportation Networks" Energies 11, no. 1: 196. https://doi.org/10.3390/en11010196
APA StyleAmini, M. H., & Karabasoglu, O. (2018). Optimal Operation of Interdependent Power Systems and Electrified Transportation Networks. Energies, 11(1), 196. https://doi.org/10.3390/en11010196






