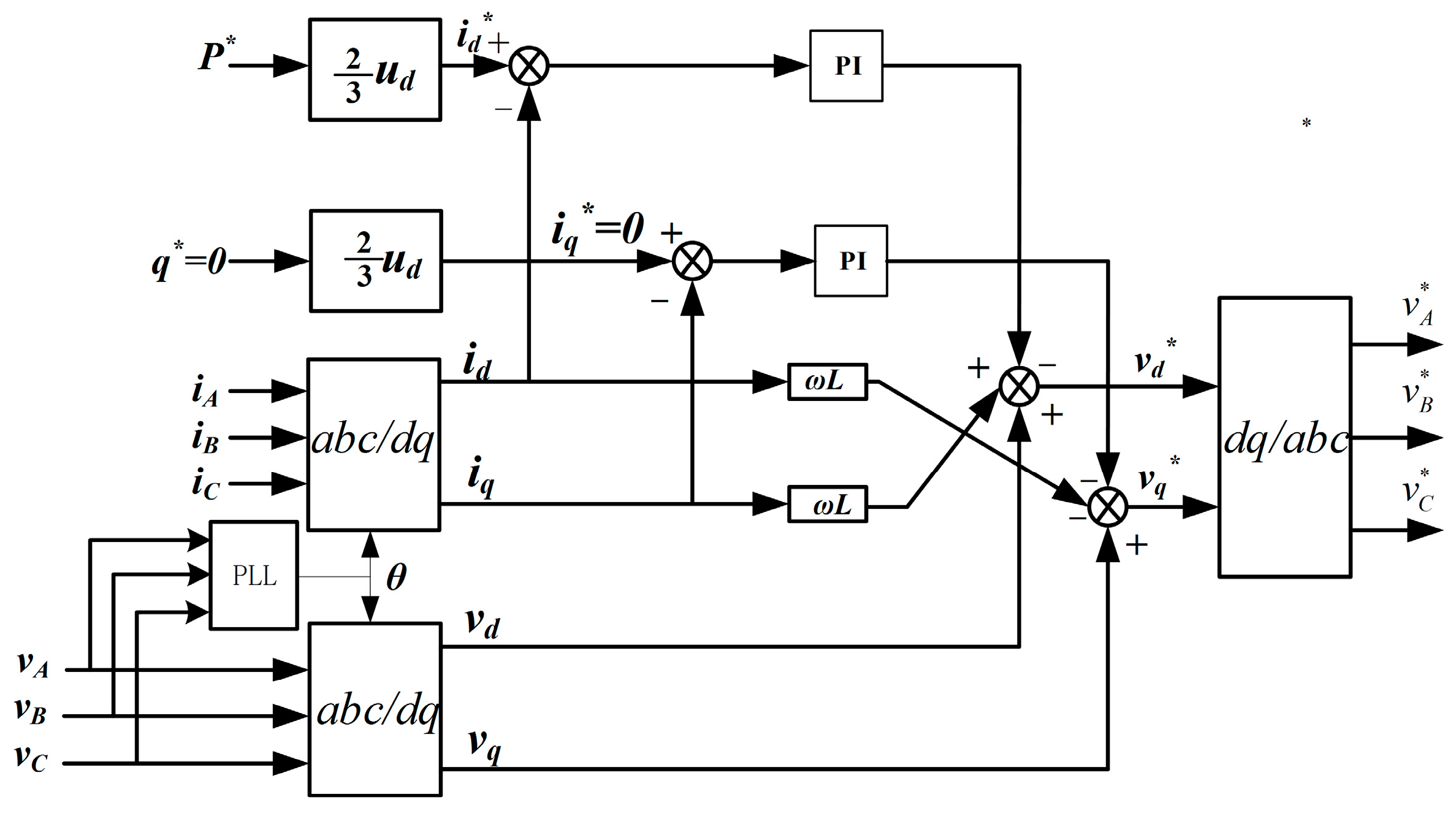
Since the faulty cells have been bypassed, the voltages of the remaining cells increase significantly, resulting in a higher probability of over-modulation. This causes larger THD in grid current and reduced grid power quality. To make a comparison of the effects of different control strategies under various fault conditions, a fault recovery gain (
km) is presented as
where
Vsp and
Vsf are the peak values of submodule voltage modulating signals under the fault condition and in normal operation, respectively. The peak voltage dominates the possibility of over-modulation in comparison with the nominal voltage.
km represents the voltage gain in each cell after a fault to fully recover the amplitude of output voltages in the normal condition. A smaller
km leads to a smaller increase in the peak voltage of each remaining cell, contributing to less probability of over-modulation and a better control effect.
The conventional fault-tolerant control strategy directly increases the voltage gain of the faulty phase to fully recover the amplitudes of output voltages to pre-fault condition. The fault recovery factor of the conventional control method is
where
N is the number of cascaded remaining cells in each phase (or cascaded number) in normal operation, and
M is that in the faulty phase. Although this method is simple, it leads to large voltage stress in the remaining cells in the faulty phase. Thus, considerable redundancy submodules are needed in the system to increase the faulty margin, coming at great financial cost to the company. Therefore, this paper presents three fault-tolerant control strategies for different fault situations in order to improve post-fault performance when a fault occurs with the lowest probability of over-modulation.
3.1. Fundamental Phase Shift Compensation
Fundamental phase shift compensation (FPSC) modifies phase angles of the converter phase voltage to generate balanced line-to-line voltages after a fault occurs [
23,
24,
25]. This is a suitable solution in some fault conditions in some fault conditions where faulty cells are mainly concentrated in one phase of the FGBESS. To obtain balanced line voltages, the following equations should be satisfied between phase voltages
Va,
Vb, and
Vc and phase angles
θab,
θbc, and
θca. The modified phase angles can be found from equations
Conventional FPSC only generates balanced line voltages after phase angles are modified. However, the system is not eventually restored to the exact parameters of the previous operation, as the amplitudes of the line voltages obtained are smaller. Therefore, a modified FPSC for fault-tolerant control in FGBESSs is proposed in this paper. After the line voltages are rebalanced, the submodule modulation index should also be appropriately enlarged using the fault recovery factor to thoroughly resume the converter operation. This is done with the equation
where
Vs is the peak phase voltage under normal operation,
MVs/
N and
VLf represent the phase and line voltages without
km, and
V’s and
VLp are the voltages after
km is added. M stands for the cascade number of remaining cells in each phase, which could also be separately expressed as
NA,
NB, and
NC if there is any difference in the cascaded number among these phases. The voltages after adjustment are calculated as
The phasor diagram of FPSC is shown in
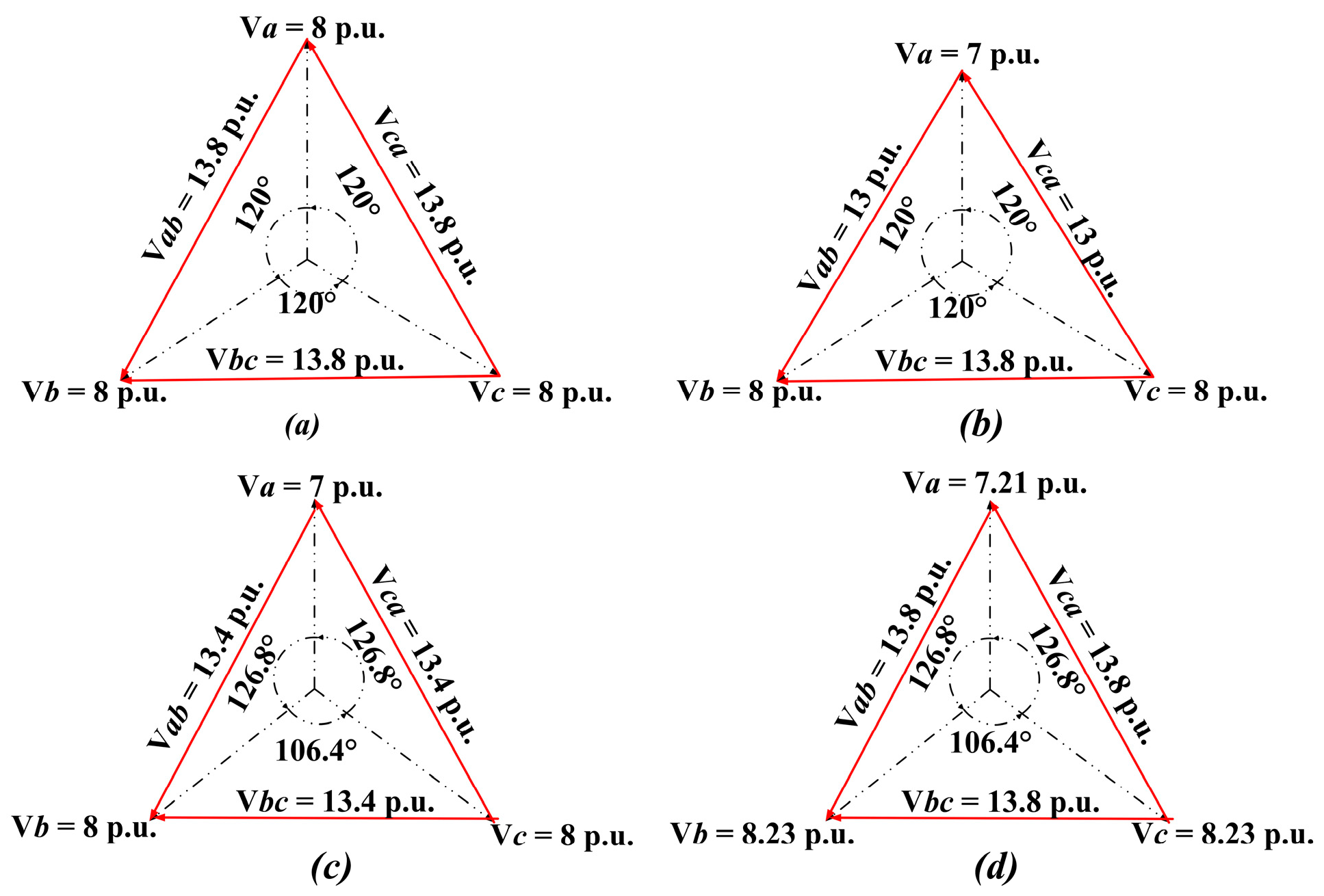
Figure 3. For a 17-level flexible group converter shown in
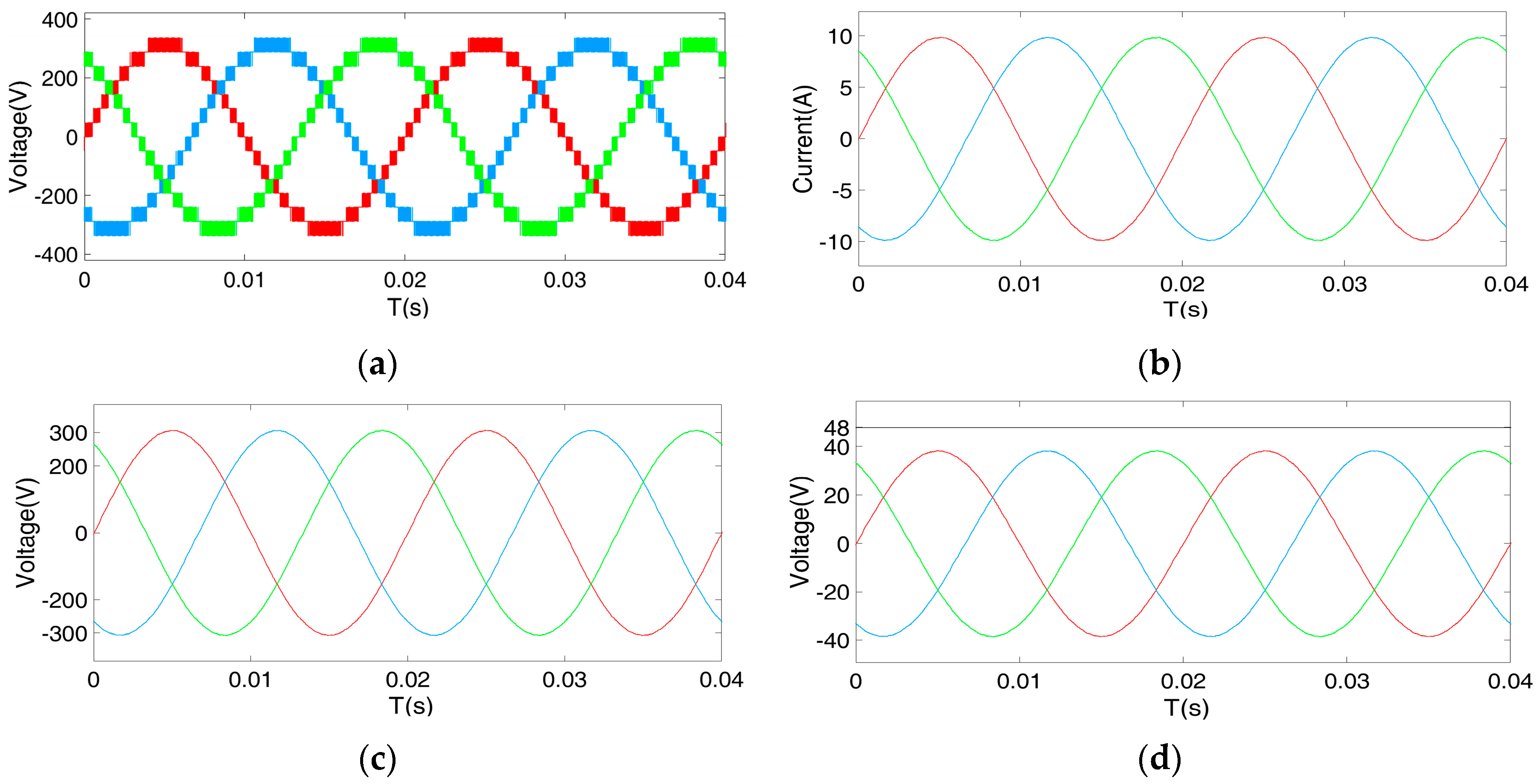
Figure 1, there are eight submodules cascaded in each phase during normal operation. Assuming that there is one bypassed cell in Phase A, the number of remaining cells in Phases A, B, and C would be seven, eight, and eight, respectively; this is called the “788” state in this paper.
Figure 3a shows that, in normal operation, the maximum amplitude of the line voltage is 13.8 p.u. (1 p.u. =
Vs/
N). After bypassing the faulty cell, as shown in
Figure 3b, the amplitude of
Vbc is still 13.8 p.u., while the magnitudes of
Vca and
Vab are reduced to 13
Vdc (13 p.u.). This means the line-to-line voltages are no longer balanced.
Figure 3c demonstrates how modifying the phase angle can lead to a balanced line voltage. According to
Figure 3, the phase angles should be adjusted as
θab = 126.8°,
θbc = 106.4°, and
θca = 126.8°. The line voltage is reduced to 13.4 p.u. after the application of the FPSC.
Figure 3d shows the voltage phasor diagram after adding a fault recovery factor. It can be concluded that line voltages are fully recovered to the pre-fault condition without generating unbalanced phase voltages by applying the proposed method.
Compared with the conventional strategy, this method has great significance for FGBESSs under fault conditions by evenly distributing the rise of voltage stress among all switches. It does this especially in conditions where faulty cells are mainly centered in a single phase, while large redundancy margins are available in the other two phases. The control strategy can generate rebalanced line voltages without any pollution to the power grid after a fault occurs, while totally restoring the system to normal operation after failure by adding a fault recovery factor. The proposed method has effectively lowered the risk of over-modulation in the faulty phase caused by directly increasing the modulation index.
3.2. Third Harmonic Injection Control
As mentioned above, FPSC is often used to obtain balanced three-phase line voltages via redundancy margin compensation. However, owing to the stochastic distribution of the remaining faulty cells in the FGBESS, FPSC provides limited improvement in conditions where the number of faulty cells located in each phase has significant differences, such as “668” and “678” states. This irregular distribution results in a greater phase angle offset, as well as a larger (km) for generating a balanced line voltage. This significantly increases the modulation ratio of each healthy cell and the probability of over-modulation. Thus, an alternative method is recommended for consideration in FGBESSs in these conditions.
A third harmonic injection (THI) is an effective way to improve DC voltage utilization in the above situations [
26]. Since the same third harmonic is injected in each phase voltage, there is zero average active power generated. The fundamental components of output current and voltage will not be changed. In a symmetrical system, a third harmonic injection with an amplitude 1/6th that of the fundamental frequency component achieves the highest output voltage without over-modulation [
27].
In this section, a fault redundancy strategy based on the third harmonic injection is proposed. After adding up different voltage gains to each phase based on their submodule cascaded amounts, a third harmonic with an amplitude 1/6th of the fundamental frequency is subsequently injected to bring down the phase voltage peak and, as a result, lower the modulation index while keeping a balanced line voltage. The output voltages after injection are as follows:
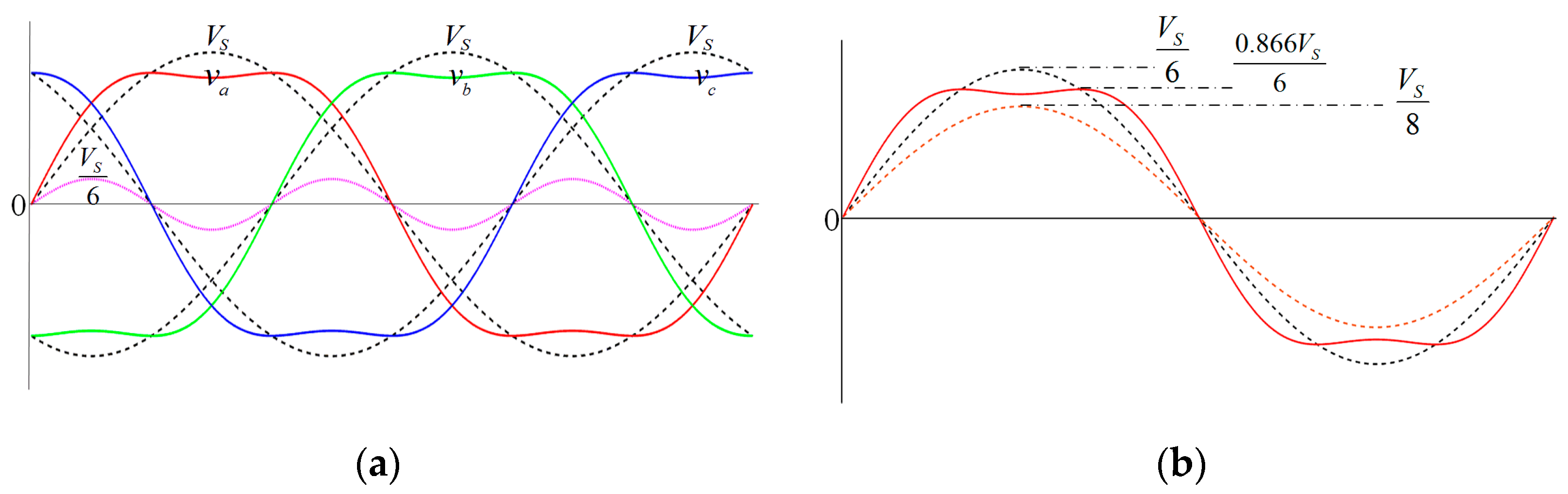
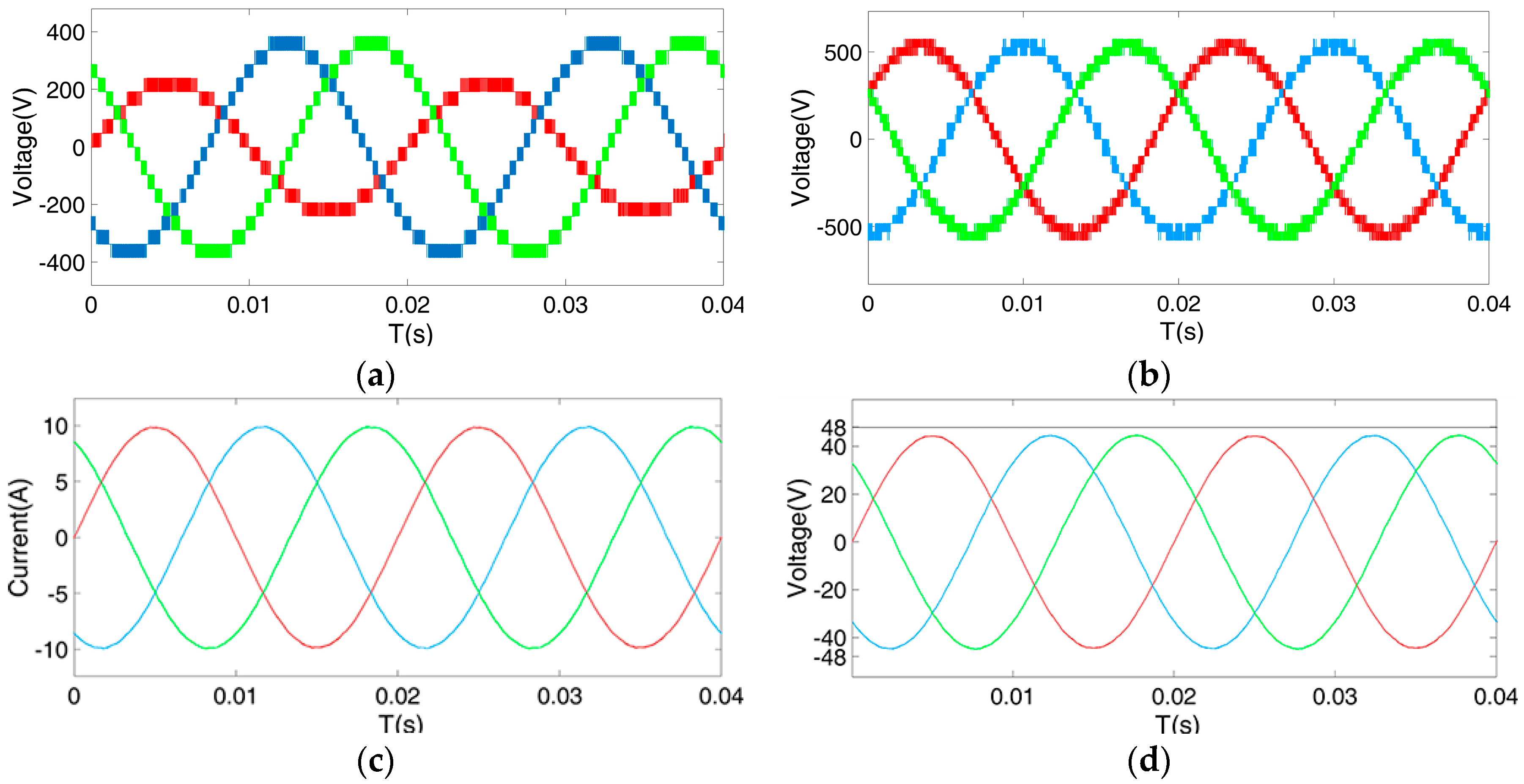
For example, in the abovementioned flexible group cascaded H-bridge (CHB) converter in “667” state, the peak voltage in the three-phase symmetric system becomes 0.866 times lower than the original value (or 0.866
Vs) after a third harmonic injection (
Figure 4a).
Figure 4b presents the voltage modulation waveform of a remaining submodule in Phase A. The amplitude is 1/8
VS during normal operation and increases sharply to 1/6
VS with the conventional fault strategy. This distributes the burden evenly to all remaining cells in the faulty phase. Similarly, after a THI, the amplitude of the modulation waveform in each cell shrinks to 1/6th of 0.866
VS. As mentioned above, for the system with
N modules cascaded in each phase,
where
Nmin equals the minimum value of the cascade number among Phases A, B, and C. Although the third harmonic varies due to the different numbers of remaining cells in each phase, the THI control presents a feasible solution to taking full advantage of battery capacity without generating any over-modulation. It does this while balancing line voltages to sustain a normal operation status under fault occurrence.
3.3. Hybrid Compensation Control
It is clear that FPSC generates a balanced voltage when faulty cells are mainly concentrated in a single phase. However, it lacks redundancy margins when there is a dispersed distribution of faulty cells. The THI method is greatly significant in improving post-fault performance and DC voltage utilization. However, when faulty cells are distributed among a wide range of groups, such as in the “557” state, the redundancy margin in the healthy phases is not enough to compensate for the losses as there are too many faulty cells in the system. Thus, the whole system suffers due to the high possibility of over-modulation.
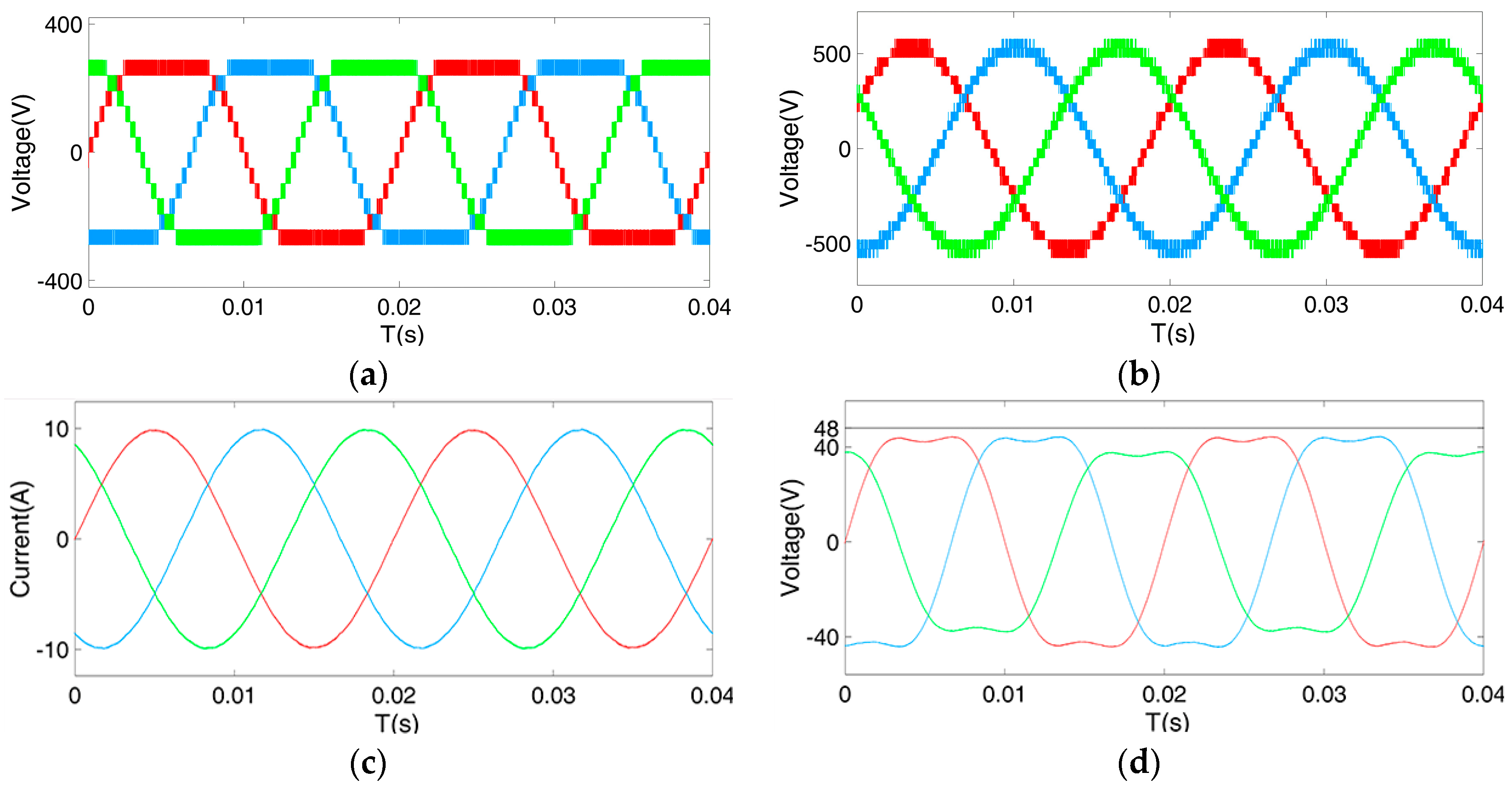
Therefore, a hybrid compensation strategy combining THI with FPSC is proposed in this section for intricate conditions where there are many faulty cells and a small redundancy margin for fault-tolerant control. After implementing the fundamental phase shift compensation under the fault condition, the third harmonic is injected. This method integrates the merits of the aforementioned two methods. It not only makes full use of the remaining modules but also effectively reduces the peak voltage of each phase and further expands the fault redundancy range.
As shown in
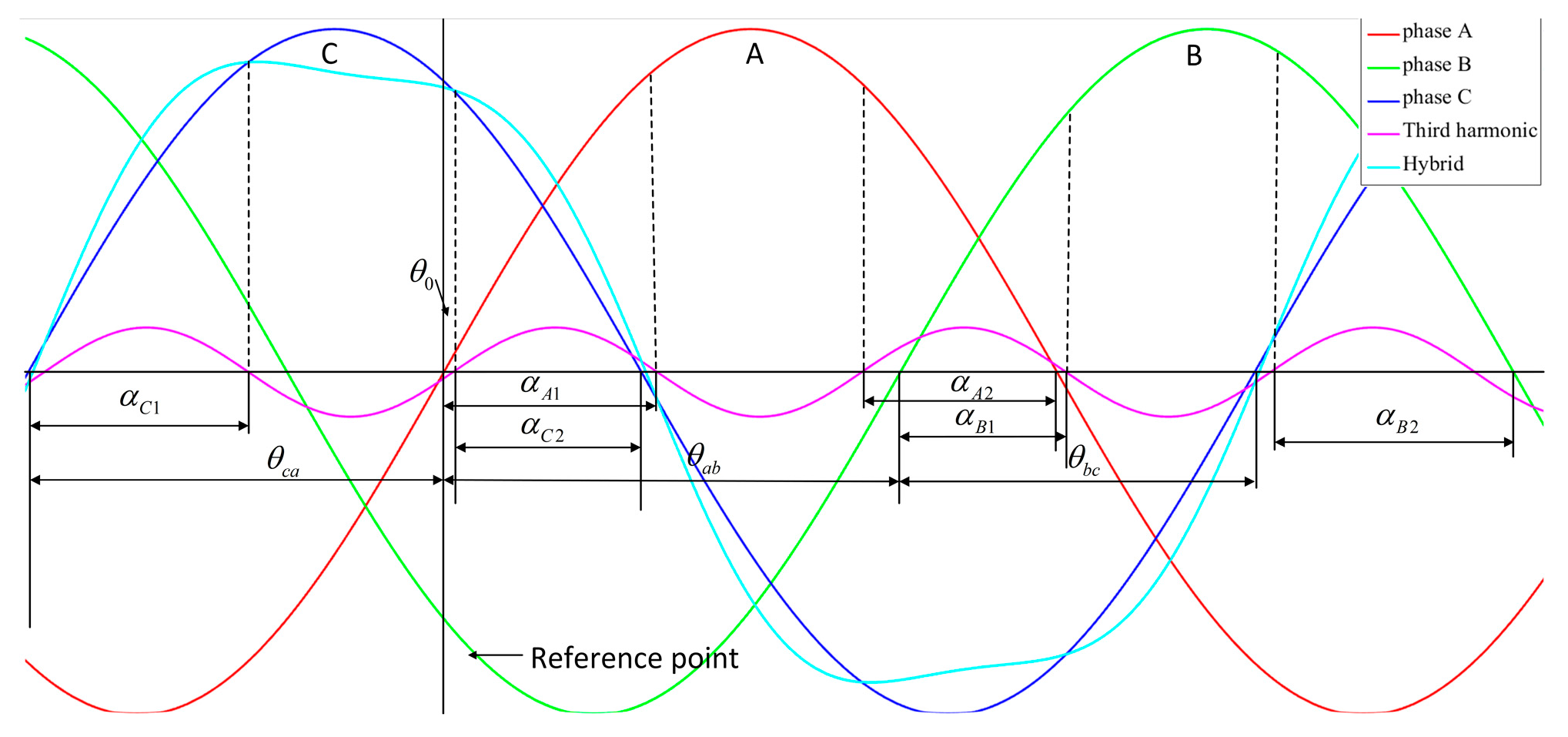
Section 3.2, the essence of the conventional THI method is to reduce the peak value of the synthetic voltage waveform. The synthetic voltage waveform has two extremums in each half-cycle. Each extremum value corresponds to a phase angle of a zero-crossing point in the third harmonic component waveform, which is called the pole angle. The two pole angles in Phase A are defined as
αA1 and
αA2, respectively, in
Figure 5. According to previous literature [
27,
28], the minimum peak voltage can be reached only if the two extremes are equal, which fully improves DC voltage utilization. In a conventional THI with three symmetrical phases, the extremes are equal, and corresponding pole angles are both 60°. That is, the peak voltages of the synthetic waveform are all matched with the phase angle of 60° in each phase. However, in the proposed hybrid control method, the simple conventional THI method is not suitable for an asymmetrical three-phase system. The amplitude and phase offset of the injected third harmonic component are different from previous values in the symmetrical system after FPSC. Thus, the proposed hybrid compensation strategy focuses on a novel method of modifying the phase offset and amplitude of the third harmonic injection component to fully improve the performance under post-fault operation.
Assuming the amplitude of the modified third harmonic component is
V3 and the initial phase shift is
θ0, the modified injected third harmonic (
vthi) is
In a period cycle of the fundamental waveform, there are six extremes in three positive half-wave periods. The possibility of over-modulation in the remaining cells is closely related to the maximum peak voltages among these six extremes in the three phases. Thus, to increase the amplitude fundamental component without any over-modulation, the maximum peak voltage should be reduced. After implementing FPSC, the phase shift is no longer symmetrical, so the extremes of each phase are influenced by their corresponding pole angles
αA1,
αA2,
αB1,
αB2,
αC1, and
αC2, as shown in
Figure 5.
Meanwhile, the pole angles in each phase are directly related to the initial phase angle of the third harmonic. The phase shifts between the three phases
θab,
θbc, and
θca are given by
According to previous literature [
28], a larger pole angle leads to a higher peak voltage. To generate the minimum peak voltage in three phases, the maximum pole angle needs to be reduced as much as possible. To find this maximum pole angle (
αp), the difference between each two pole angles are derived as follows:
Based on Equation (10), there are six different operations of these phase angles with different magnitudes. The following case, Case 1, illustrates the calculation of θ0.
In Case 1, assume that
θab > 120°,
θca > 120°, and
θbc < 120°. In this condition, the pole angle (α
C1) is always the largest among
αA1,
αB1, and
αC1, and
αB2 is the largest among the remaining angles. However, the relationship between
αC1 and
αB2 is closely related to
θ0. When
θ0 increases, the value of
αB2 increases while
αC1 reduces sharply, and vice versa. The only way to generate the minimum peak voltage is to minimize these two extremes at the same time, which leads to
αC1 =
αB2. The third harmonic injection then generates its optimal initial phase offset as
After substituting Equation (11) into Equation (9), the maximum pole angles are calculated as
As mentioned above, the optimal amplitude can be derived after
θ0 is generated. For example, in Case 1, since Phase C holds the maximum peak voltage in the three-phase, the amplitude of the third harmonic should be matched with the fundamental component of Phase C to minimize the peak voltages among the three phases. After hybrid compensation, the synthetic output voltage (
vc) is as shown below.
where
Vs is the amplitude of fundamental component waveform. The extreme of the above equation gives the calculation
When the synthetic output voltage reaches its peak voltage, the third harmonic waveform is just at its zero-crossing point (as seen in
Figure 5). Thus, the derivative amplitude of the injected third harmonic becomes −1. The phase angle corresponding to the maximum peak voltage is the same as the maximum pole angle. The amplitude of third harmonic can be derived as
Thus, it can be concluded that, for each fault condition, the optimal amplitude of the injected third harmonic is
By implementing the proposed method discussed above, the optimal initial phase offset and the corresponding pole angles under each operation can be obtained, as shown in
Table 1.
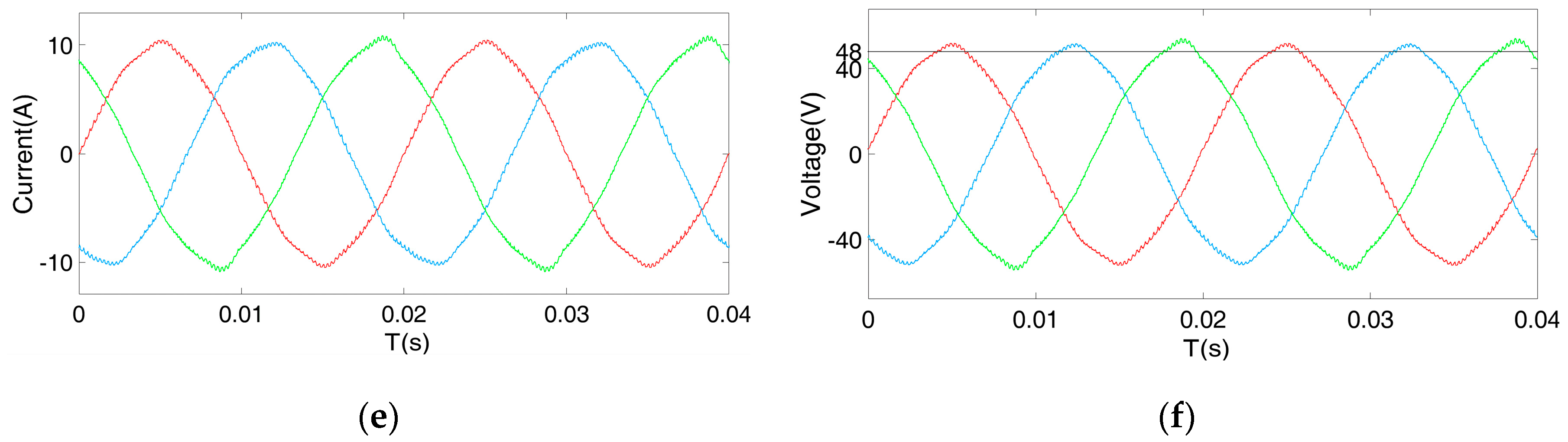
Through adjustments of the amplitude and phase of the third harmonic waveform under different fault conditions, an adjustable faulty recovery factor can range from 0.866 to 1 km. Hybrid compensation control is preferred for its advantages of obtaining a balanced grid current under fault conditions to meet grid requirements as well as fully improving the DC bus voltage utilization. This effectively utilizes the remaining margin to achieve control optimization in a quasi-fault mode. The method is suitable in a system with a large battery inconsistency and the irregular distribution of faulty cells.
3.4. Comparison
As mentioned above, the three proposed redundancy strategies would have different efficiencies in various fault operations. Thus,
km is used as a criterion in making comparisons and obtaining optimized solutions under conditions of fault occurrence.
Table 2 summarizes the phase voltages, the submodule modulation waveforms, and
km under different operation states.
The probability of over-modulation is related to the cascade number. In this paper, the modulation index in normal conditions is derived from the equation
where
Vpp and
Vgp represent the peak values of phase voltage and grid voltage, respectively. These are approximately equal when the inductive load is small enough. It is clear that
ma is closely determined by
N if
Vgp and
VB are constant. Thus,
ma mainly decides the limit of the fault recovery factor without over-modulation. For instance, in an FGBESS with eight modules cascaded in a phase,
ma equals 0.81 in normal operation with a standard grid of 380 V and a nominal battery pack voltage of 48 V. This means there is a large redundancy margin for fault-tolerant control. Assuming the modulation limit is 1, the highest value of
km without over-modulation is 1.23 (
km = 1/0.81 = 1.23). Thus, the optimal control strategy in each fault condition should be considered to keep
km less than 1.23. Based on the above parameters, the fault recovery factors for different control strategies in various failure modes are listed in
Table 3.
Based on the analysis of the fault recovery factors under different fault conditions listed above, implementing the hybrid comparison control method for every faulty operation to rebalance the line voltages and effectively utilize the battery capability in the remaining cells may appear to be wise. However, this simple idea comes with two major drawbacks. First, after the third harmonic is injected into the phase modulating voltages with the phase angles shifted in FPSC, the output voltages have great distortion because there is a phase angle offset between the fundamental component and the injected harmonic, as shown in
Figure 5. This results in an increased peak voltage and higher probability of over-modulation. A larger phase angle offset leads to a higher peak value, which generates considerable voltage gains in healthy phases and greater voltage stresses on the switching device. Second, in some conditions such as the “668” and “688” states, the other redundancy methods develop a better performance and higher battery utilization than the hybrid compensation control strategy. As a result, rather than only applying the hybrid compensation control method, the optimal redundancy strategy under each faulty operation should be derived to obtain the maximum available output voltage and effectively utilize the battery capacity in the remaining cells.
As depicted in
Table 3, the optimal control strategy in each fault condition is closely related to the number and distribution of the faulty cells and the implementation complexity of the strategy. In a 17-level system as described above, if
km is less than 1.23, which indicates a large margin for fault control, the simplest strategy is the best. If
km is larger than 1.23, the optimal strategy is the one with the smallest
km. For instance, in the “788” or “778” states, the conventional method is most feasible for its simple implementation. A third harmonic injection should be chosen for modes such as “678”, “668”, “667”, etc. for maximum DC voltage utilization. Fundamental phase shift control is more suitable in some conditions where faulty cells are concentrated in a single phase such as “688”, “588”, and “488”. In some complex operations, such as the “568” and “577” states, hybrid control has the best effect. Therefore, the system can restore normal operation and fully improve the battery energy utilization under multi-module failure through the choice of different fault-tolerant control strategies. This has great significance for the flexible group energy system and other high-power multi-module energy storage converters.