Magnet Shape Optimization of Two-Layer Spoke-Type Axial Flux Interior Permanent Magnet Machines
Abstract
:1. Introduction
2. Structure and Optimization Principle of TLST AFIPM Machines
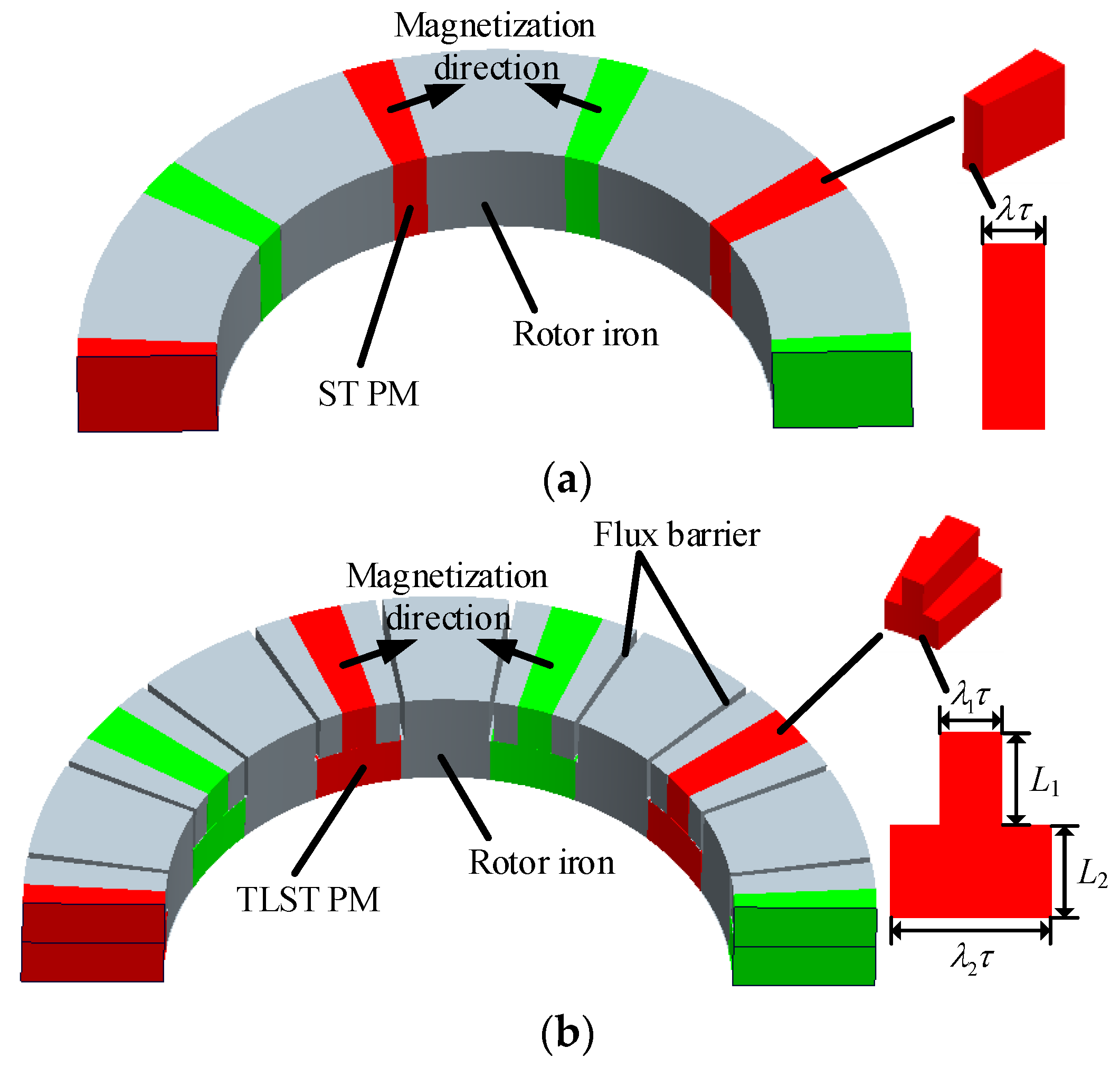
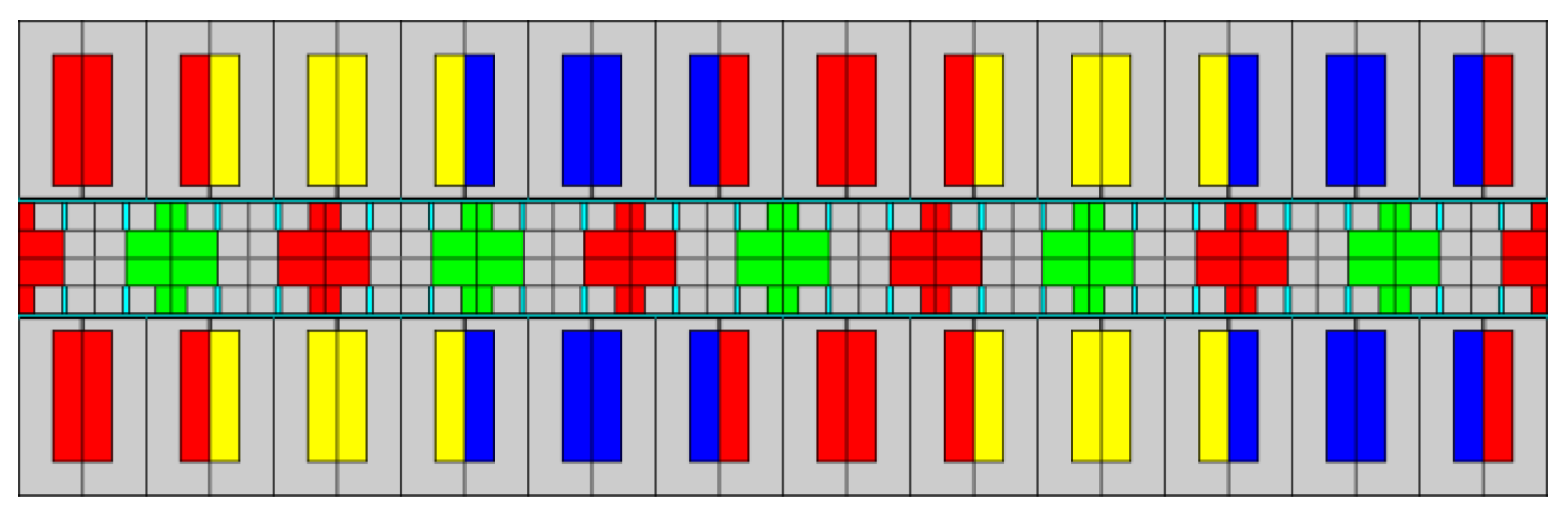
2.1. Structure of TLST AFIPM Machines
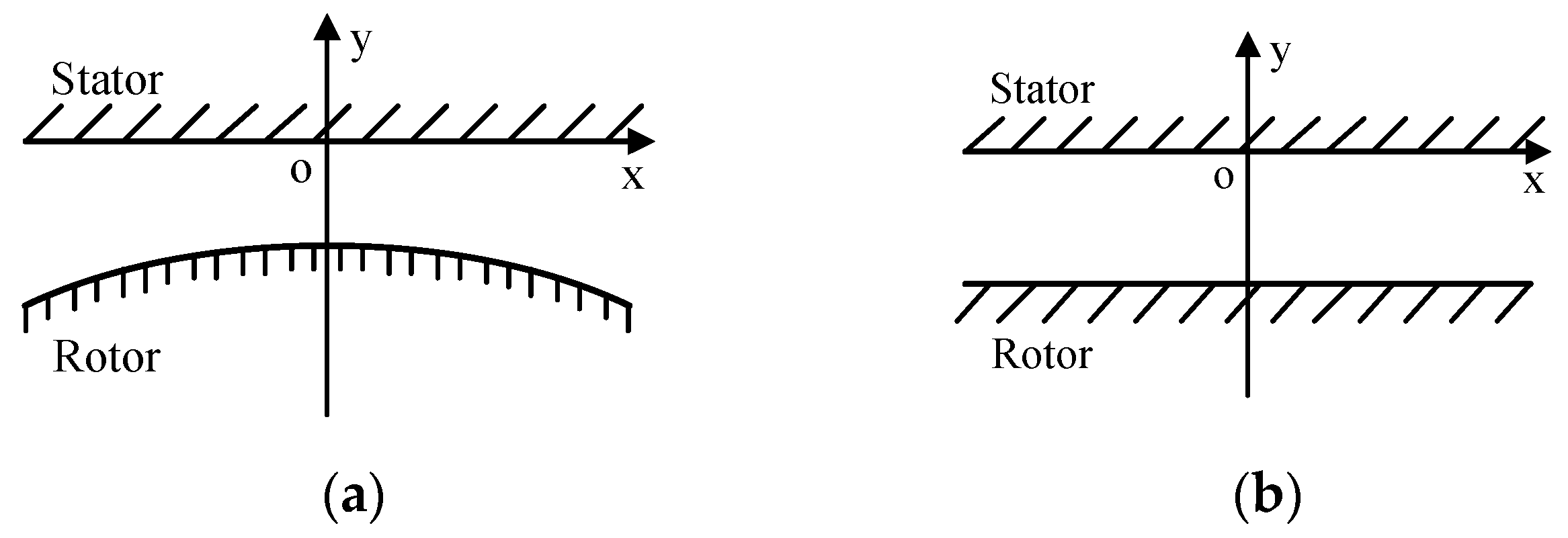
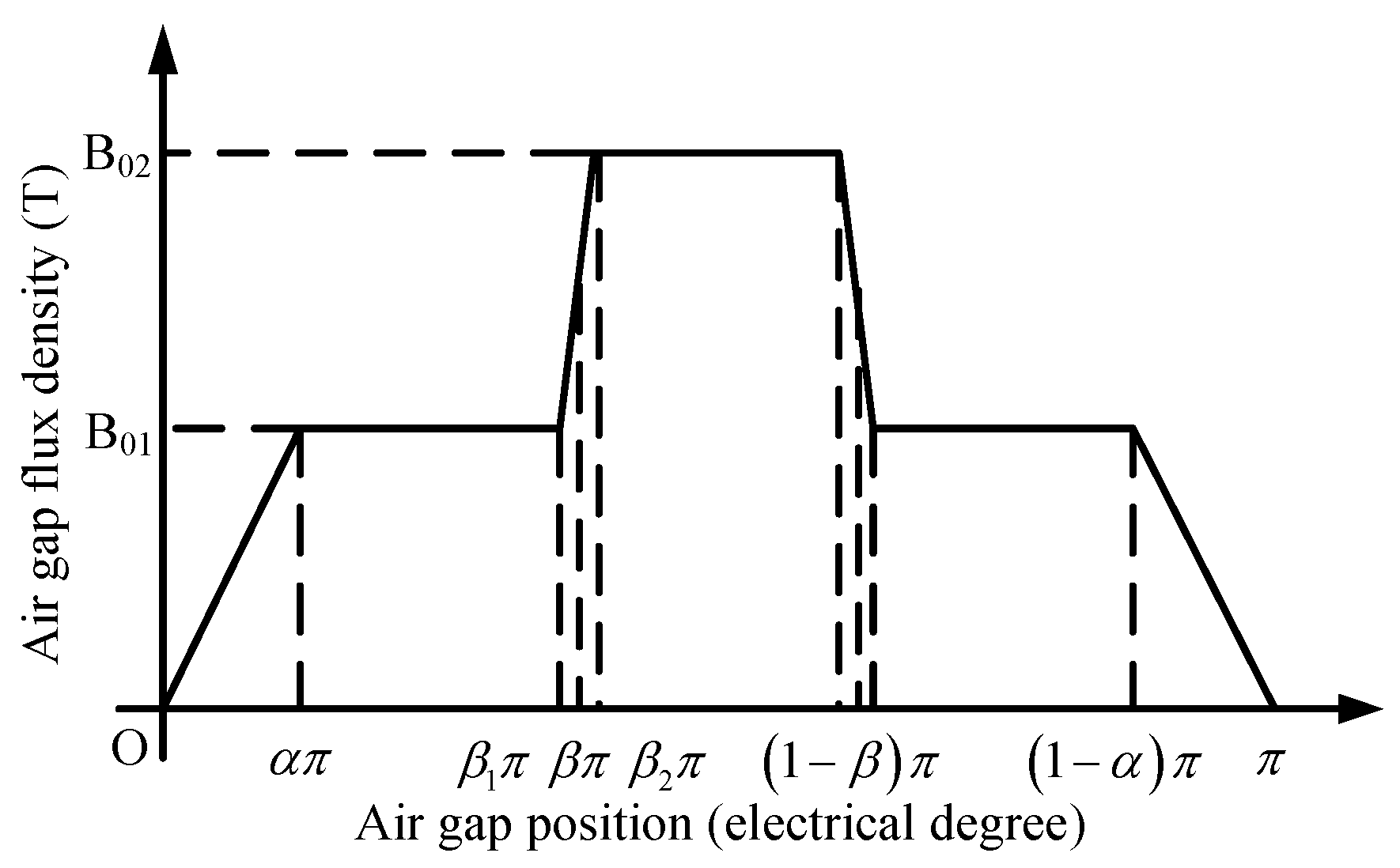
2.2. Air Gap Flux Density Optimization Principle of TLST AFIPM Machines
2.3. The Comparison between ST and TLST AFIPM Machine
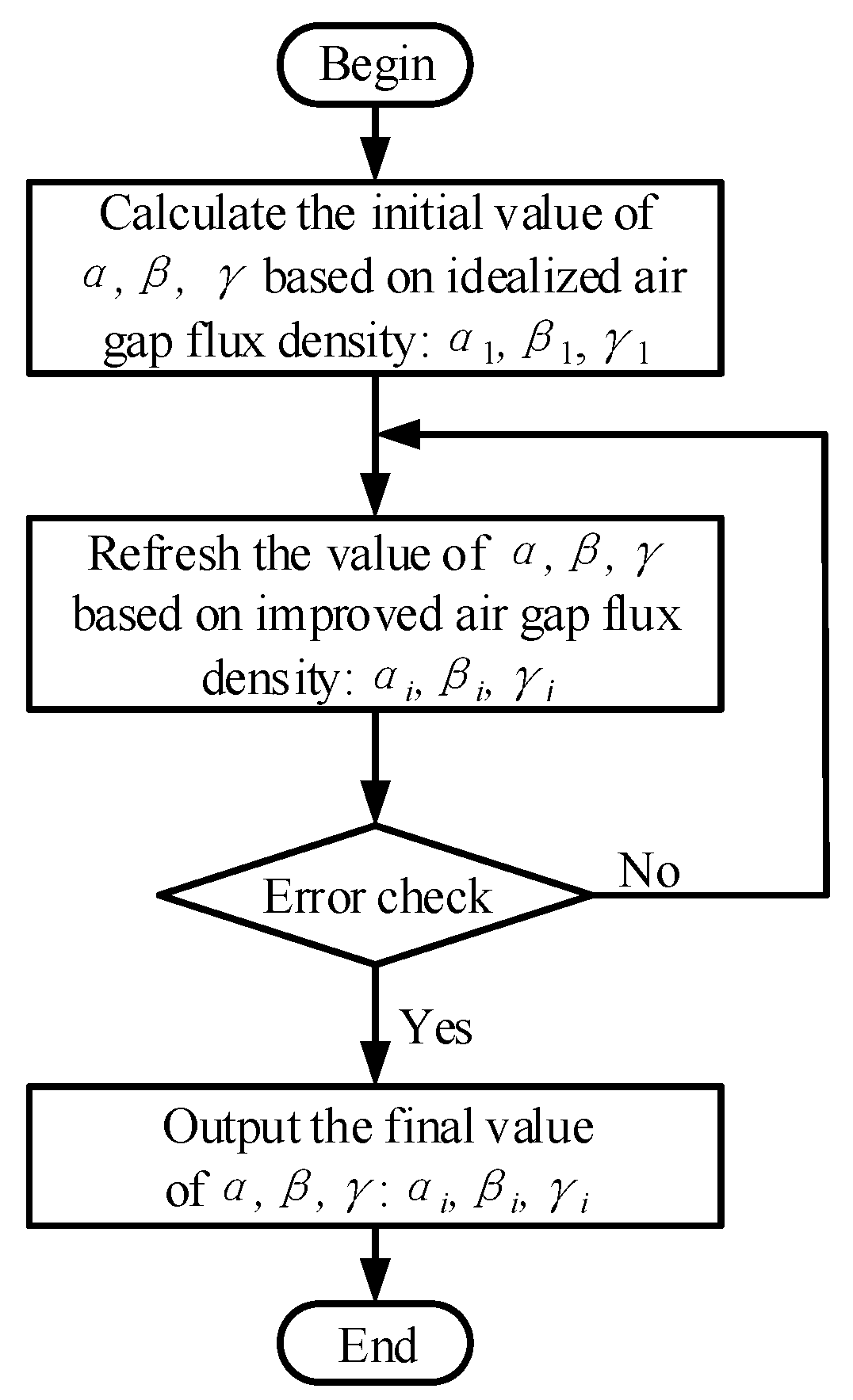
3. Optimization Design Process
3.1. Analysis Model
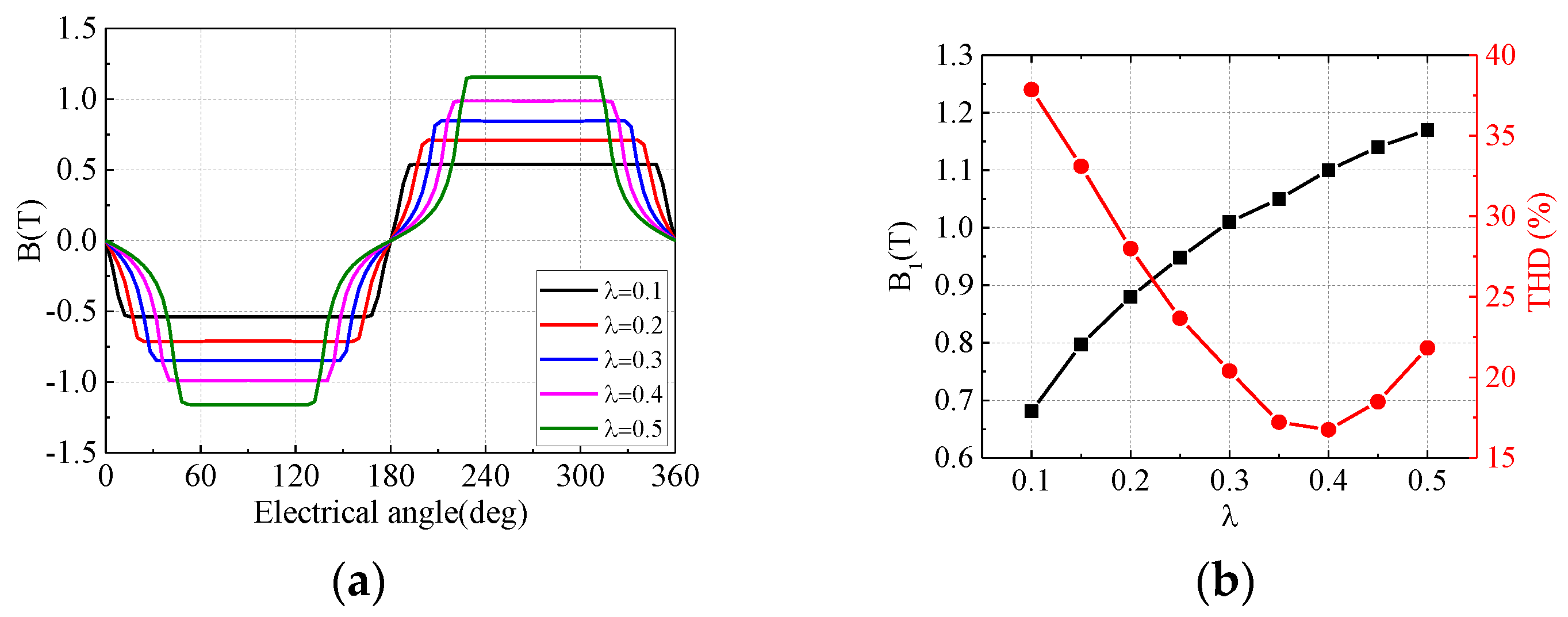
3.2. Determination of Initial Value
3.3. Iterative Computation
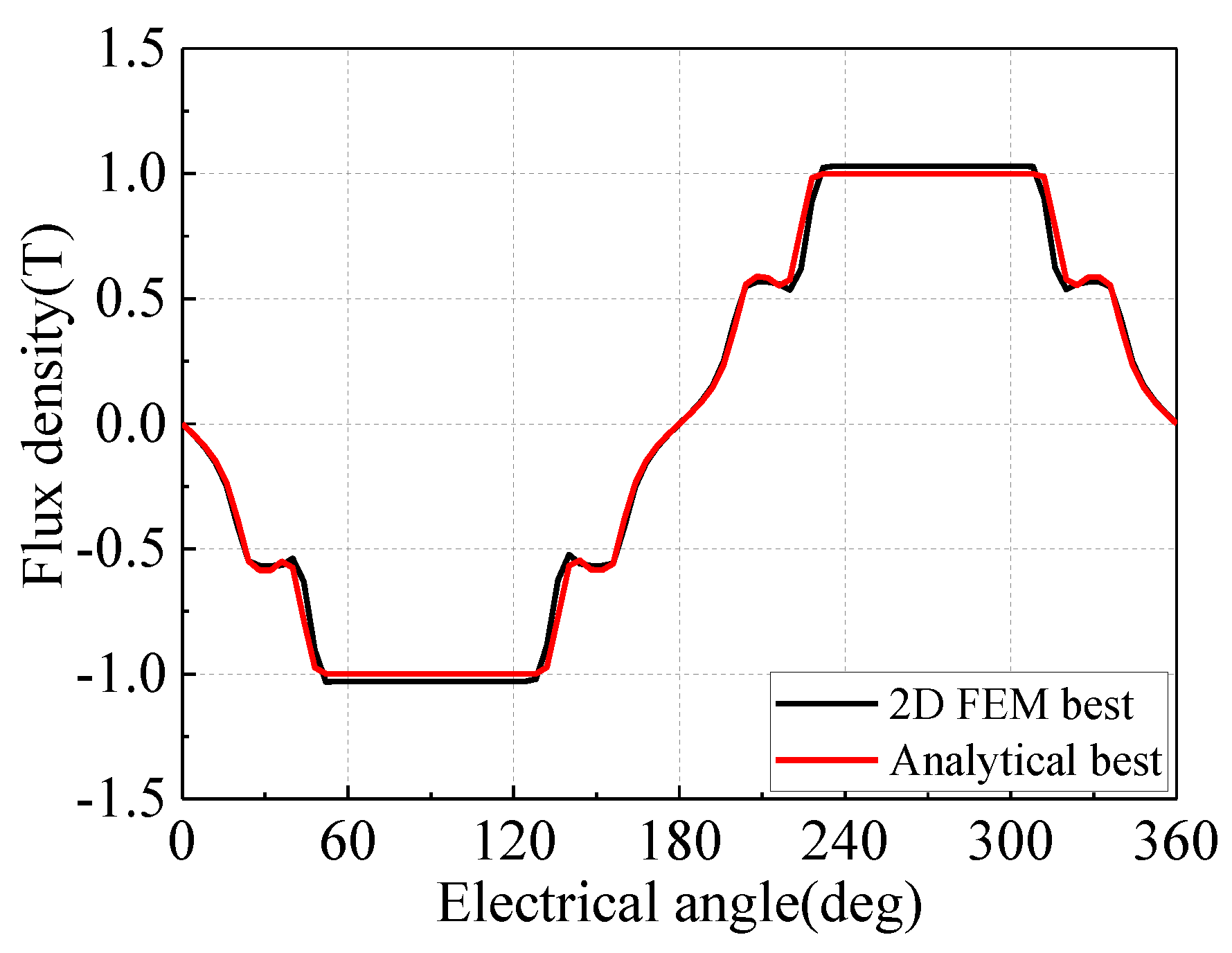
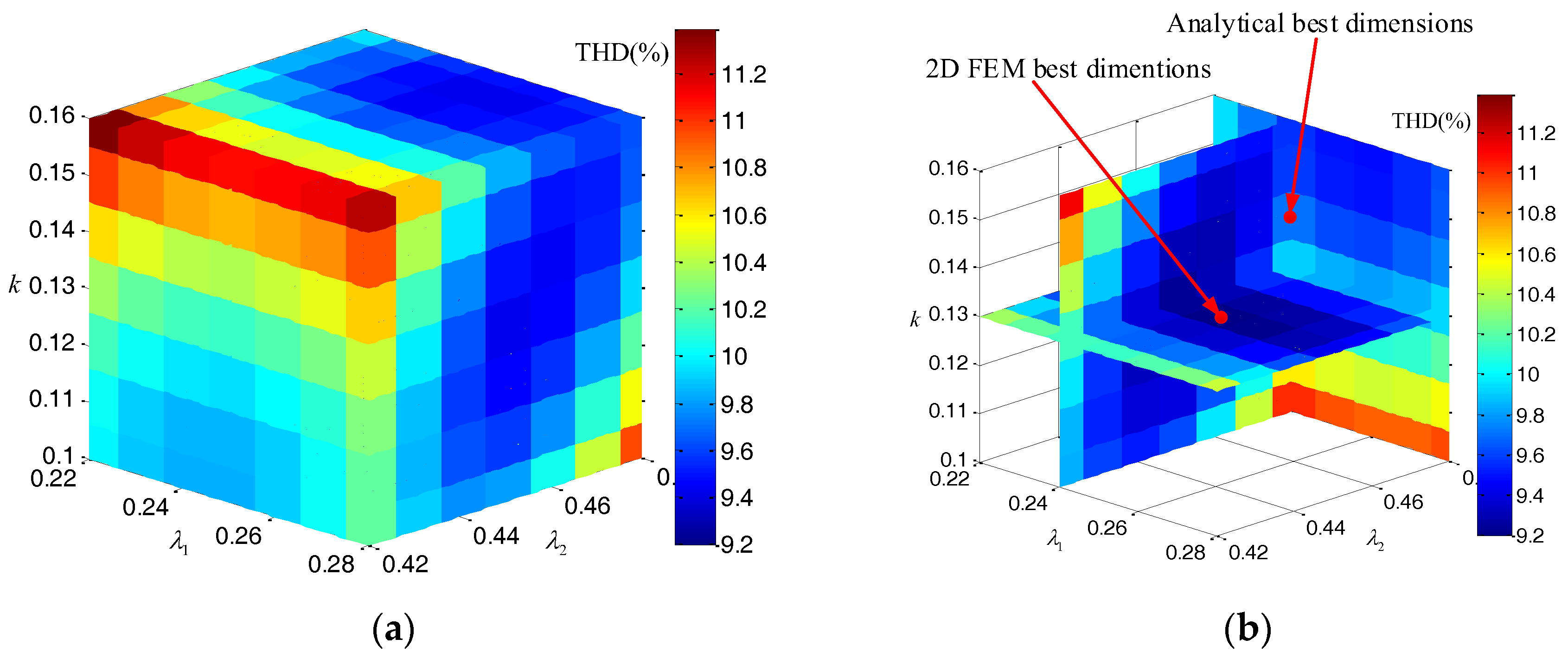
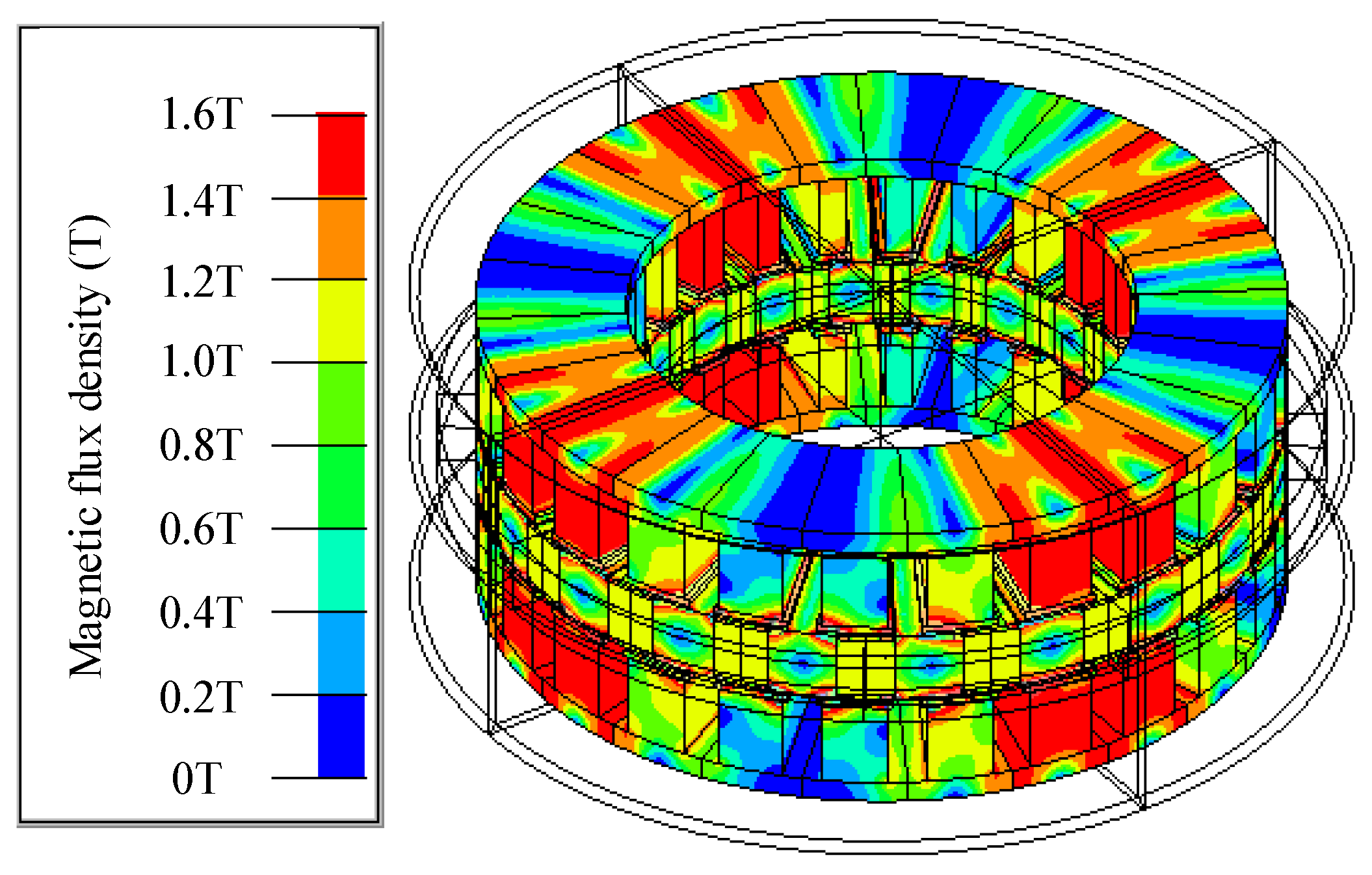
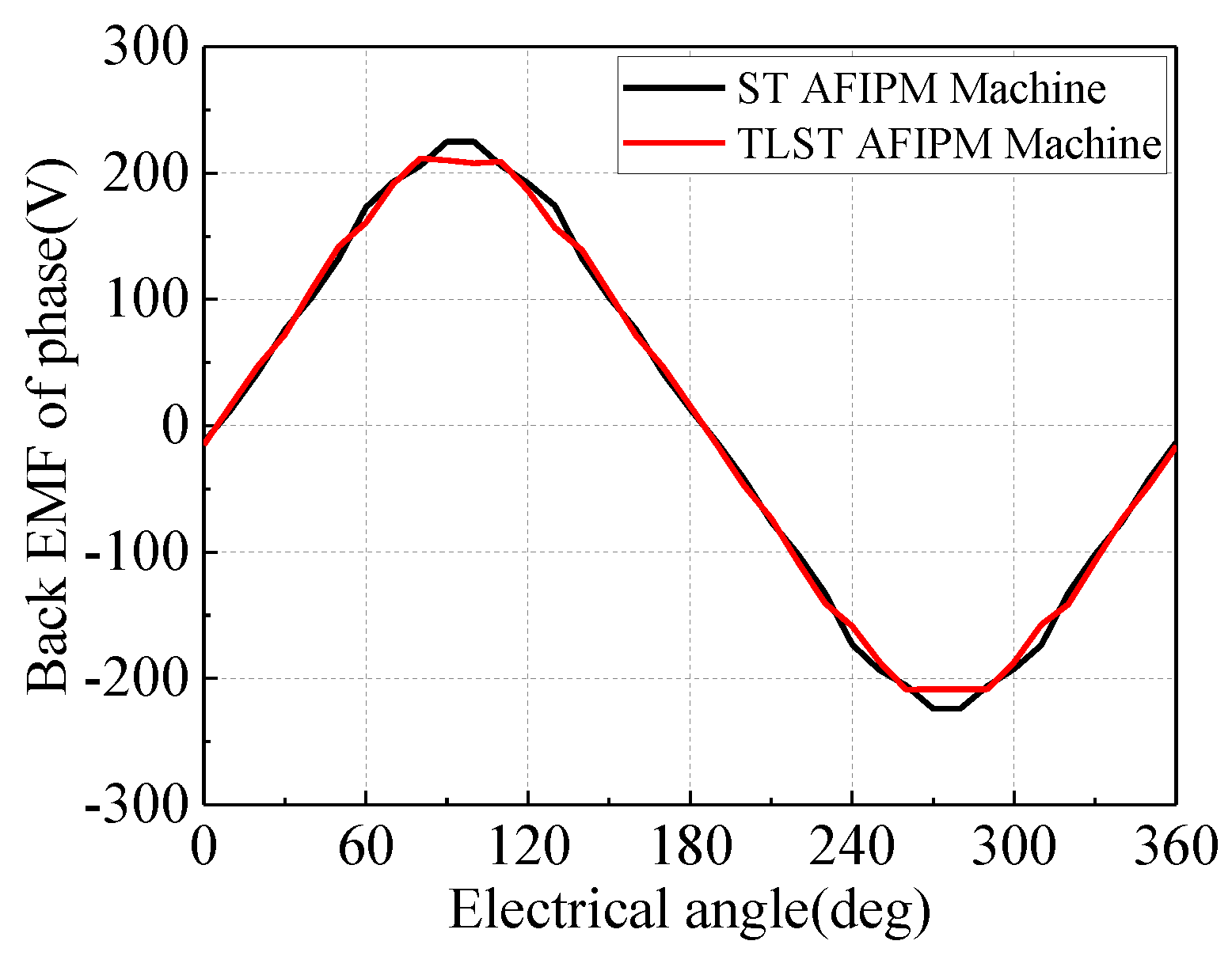
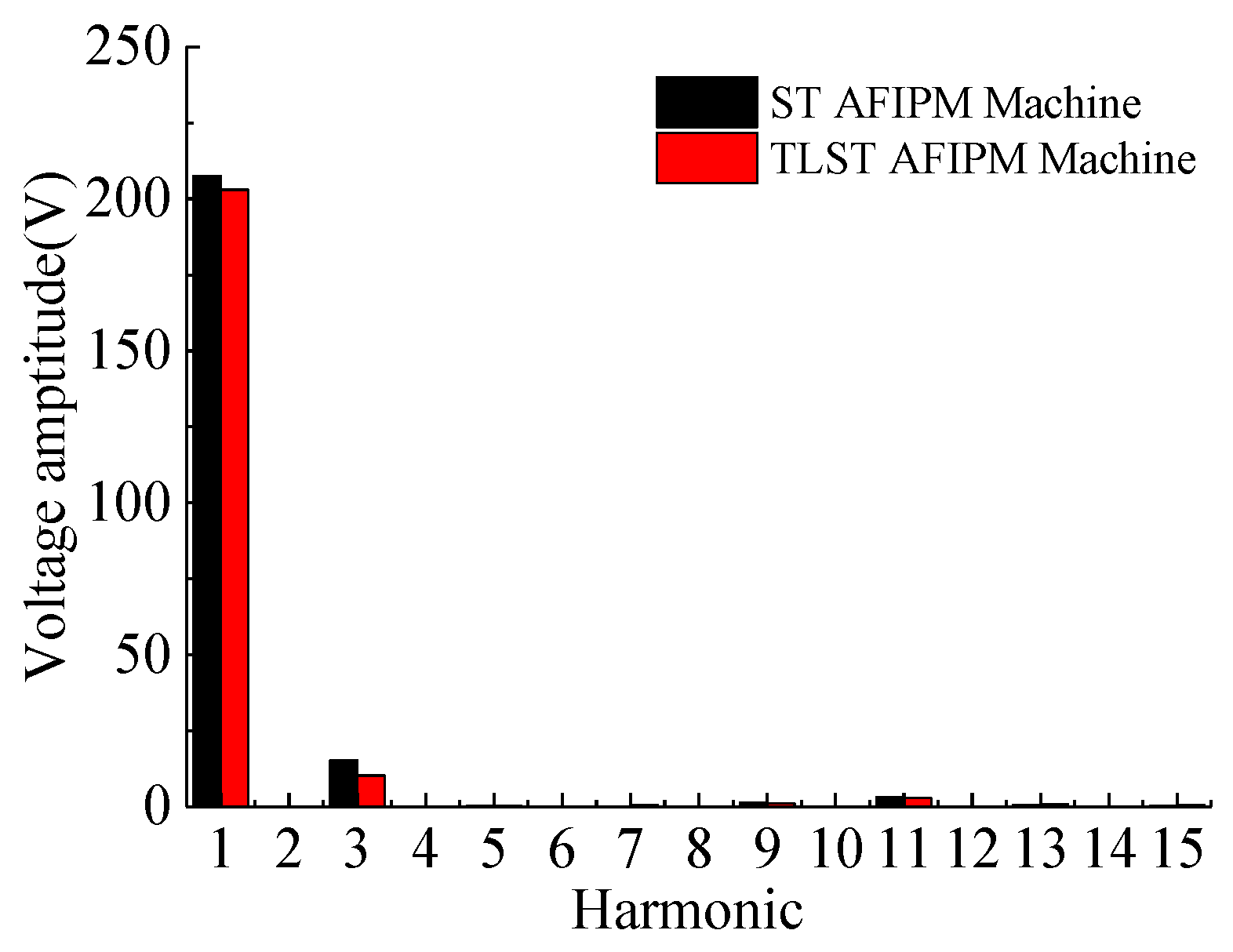
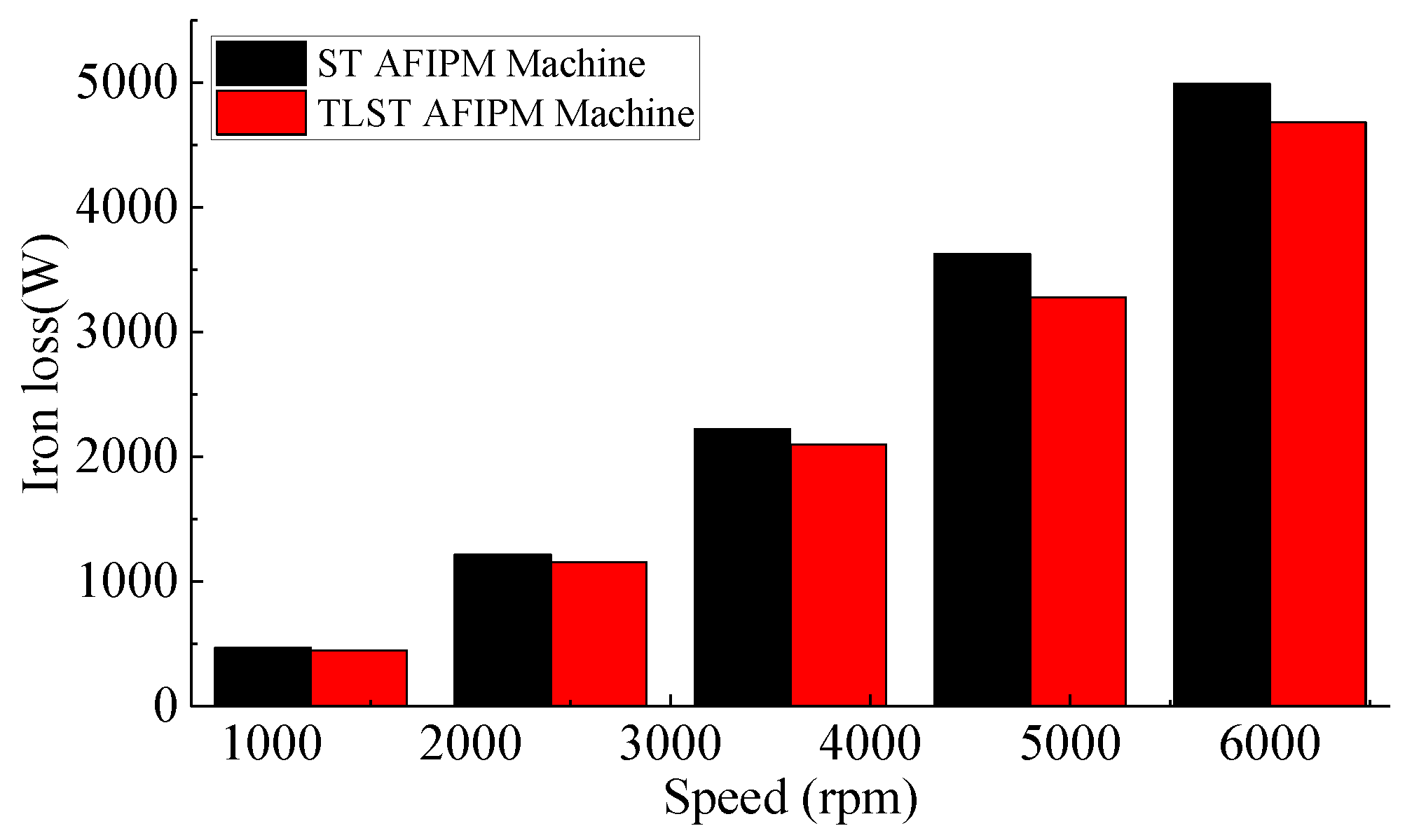
4. Optimal Design Result and Further Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kappatou, J.C.; Zalokostas, G.D.; Spyratos, D.A. 3-D FEM analysis, prototyping and tests of an axial flux permanent-magnet wind generator. Energies 2017, 10, 1269. [Google Scholar] [CrossRef]
- Huang, Y.; Guo, B.; Hemeida, A.; Sergeant, P. Analytical modeling of static eccentricities in axial flux permanent-magnet machines with concentrated windings. Energies 2016, 9, 892. [Google Scholar] [CrossRef]
- Wang, X.; Xu, S.; Li, C.; Li, X. Field-Weakening Performance Improvement of the Yokeless and Segmented Armature Axial Flux Motor for Electric Vehicles. Energies 2017, 10, 1492. [Google Scholar] [CrossRef]
- Yang, Y.P.; Shih, G.Y. Optimal Design of an Axial-Flux Permanent-Magnet Motor for an Electric Vehicle Based on Driving Scenarios. Energies 2016, 9, 285. [Google Scholar] [CrossRef]
- Zhao, J.; Li, B.; Gu, Z. Research on an axial flux PMSM with radially sliding permanent magnets. Energies 2015, 8, 1663–1684. [Google Scholar] [CrossRef]
- Laskaris, K.I.; Kladas, A.G. Permanent-magnet shape optimization effects on synchronous motor performance. IEEE Trans. Ind. Electron. 2011, 58, 3776–3783. [Google Scholar] [CrossRef]
- Chai, F.; Liang, P.; Pei, Y.; Cheng, S. Magnet Shape Optimization of Surface-Mounted Permanent-Magnet Motors to Reduce Harmonic Iron Losses. IEEE Trans. Mag. 2016, 52, 6301304. [Google Scholar] [CrossRef]
- Jin, P.; Yuan, Y.; Xu, Q.; Fang, S.; Lin, H.; Ho, S.L. Analysis of Axial-Flux Halbach Permanent-Magnet Machine. IEEE Trans. Mag. 2015, 51, 8207404. [Google Scholar] [CrossRef]
- Zhao, W.; Lipo, T.A.; Kwon, B.I. A Novel Dual-Rotor, Axial Field, Fault-Tolerant Flux-Switching Permanent Magnet Machine with High-Torque Performance. IEEE Trans. Mag. 2015, 51, 8112204. [Google Scholar] [CrossRef]
- Zhao, F.; Lipo, T.A.; Kwon, B.I. A novel dual-stator axial-flux spoke-type permanent magnet vernier machine for direct-drive applications. IEEE Trans. Mag. 2014, 50, 8104304. [Google Scholar] [CrossRef]
- Zhao, W.; Lipo, T.A.; Kwon, B.I. Comparative study on novel dual stator radial flux and axial flux permanent magnet motors with ferrite magnets for traction application. IEEE Trans. Mag. 2014, 50, 8104404. [Google Scholar] [CrossRef]
- Zhao, W.; Lipo, T.A.; Kwon, B.I. Design and analysis of a novel dual stator axial flux spoke-type ferrite permanent magnet machine. In Proceedings of the IEEE 39th Annual Conference Industral Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 2714–2719. [Google Scholar]
- Chirca, M.; Breban, S.; Oprea, C.; Radulescu, M. Comparative design analysis of ferrite-permanent-magnet micro-wind turbine generators. In Proceedings of the 2015 International Aegean Conference on Electrical machines and Power Electronics ACEMPOPTIM—ELECTROMOTION Joint Conference, Side, Turkey, 2–4 September 2015; pp. 687–692. [Google Scholar]
- Aydin, M.; Gulec, M. A New Coreless Axial Flux Interior Permanent Magnet Synchronous Motor with Sinusoidal Rotor Segments. IEEE Trans. Mag. 2016, 52, 8105204. [Google Scholar] [CrossRef]
- Hwang, K.Y.; Rhee, S.B.; Yang, B.Y.; Kwon, B.I. Rotor pole design in spoke-type brushless DC motor by response surface method. IEEE Trans. Mag. 2007, 43, 1833–1836. [Google Scholar] [CrossRef]
- Park, Y.U.; Cho, J.H.; Chung, D.H.; So, J.Y.; Kim, D.K. A rotor shape design of interior PM motor for reducing cogging torque in electric air-conditioning system of HEV. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Korea, 26–29 October 2013; pp. 1139–1143. [Google Scholar]
- Hwang, K.Y.; Jo, J.H.; Kwon, B.I. A study on optimal pole design of spoke-type IPMSM with concentrated winding for reducing the torque ripple by experiment design method. IEEE Trans. Mag. 2009, 45, 4712–4715. [Google Scholar] [CrossRef]
- Liu, M.; Han, Z.; Pei, Y.; Shi, P. Optimization of permanent magnet motor air-gap flux density based on the non-uniform air gap. In Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shengyang, China, 20–22 December 2013; pp. 3422–3426. [Google Scholar]
- Chai, F.; Liang, P.; Pei, Y.; Cheng, S. Analytical method for iron losses reduction in interior permanent magnet synchronous motor. IEEE Trans. Mag. 2015, 51, 6301404. [Google Scholar] [CrossRef]
- Chaithongsuk, S.; Nahid-Mobarakeh, B.; Caron, J.P.; Takorabet, N.; Meibody-Tabar, F. Optimal design of permanent magnet motors to improve field-weakening performances in variable speed drives. IEEE Trans. Ind. Electron. 2012, 59, 2484–2494. [Google Scholar] [CrossRef]
- Vansompel, H.; Sergeant, P.; Dupre, L. A multilayer 2-D–2-D coupled model for eddy current calculation in the rotor of an axial-flux PM machine. IEEE Trans. Energy Convers. 2012, 27, 784–791. [Google Scholar] [CrossRef]
- Jang, S.M.; Koo, M.M.; Park, Y.S.; Choi, J.Y.; Lee, S.H. Characteristic analysis on the influence of misaligned rotor position of double-sided axial flux permanent magnet machine and experimental verification. IEEE Trans. Mag. 2012, 48, 2941–2944. [Google Scholar] [CrossRef]
- Tiegna, H.; Amara, Y.; Barakat, G. A new quasi-3-D analytical model of axial flux permanent magnet machines. IEEE Trans. Mag. 2014, 50, 7020204. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, T.; Dong, J.; Lin, H.; Yang, H.; Cheng, M. Magnetic Equivalent Circuit Modeling of Yokeless Axial Flux Permanent Magnet Machine with Segmented Armature. IEEE Trans. Mag. 2014, 50, 8104204. [Google Scholar] [CrossRef]
- De Donato, G.; Giulii Capponi, F.; Caricchi, F. No-load performance of axial flux permanent magnet machines mounting magnetic wedges. IEEE Trans. Ind. Electron. 2012, 59, 3768–3779. [Google Scholar] [CrossRef]
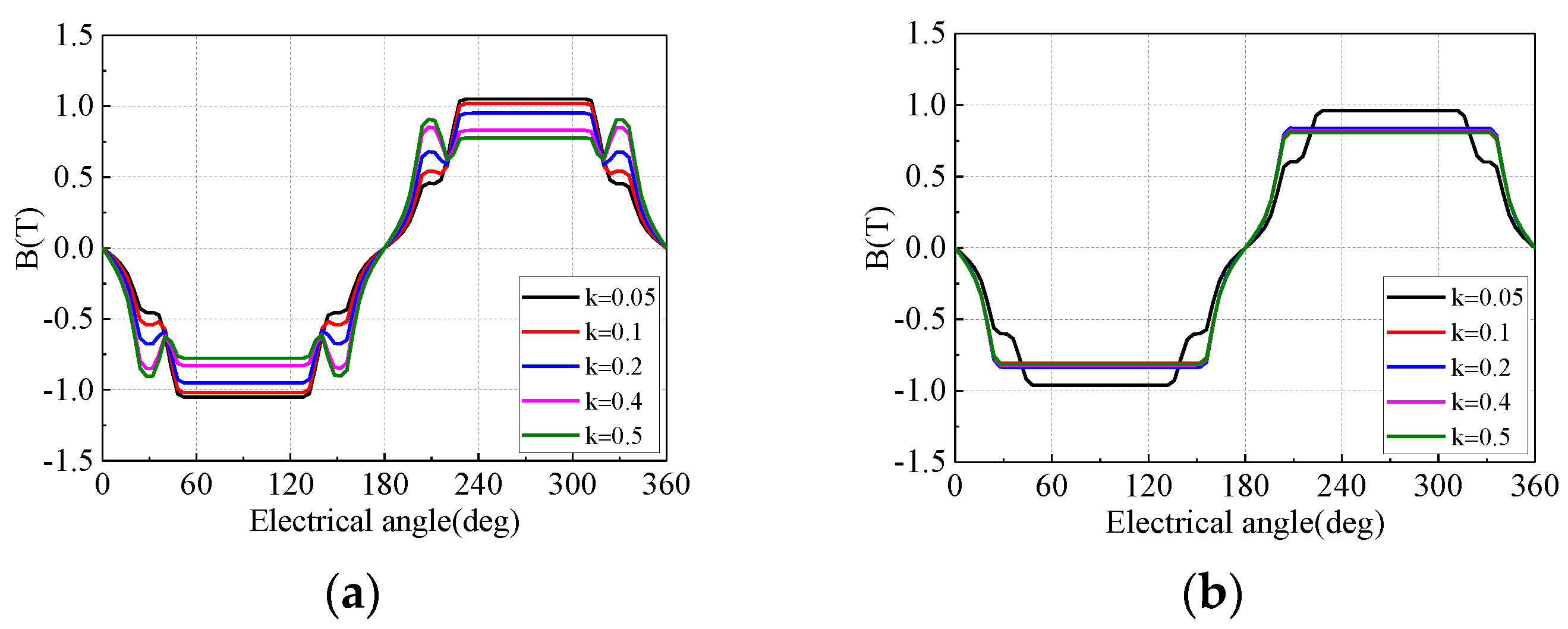
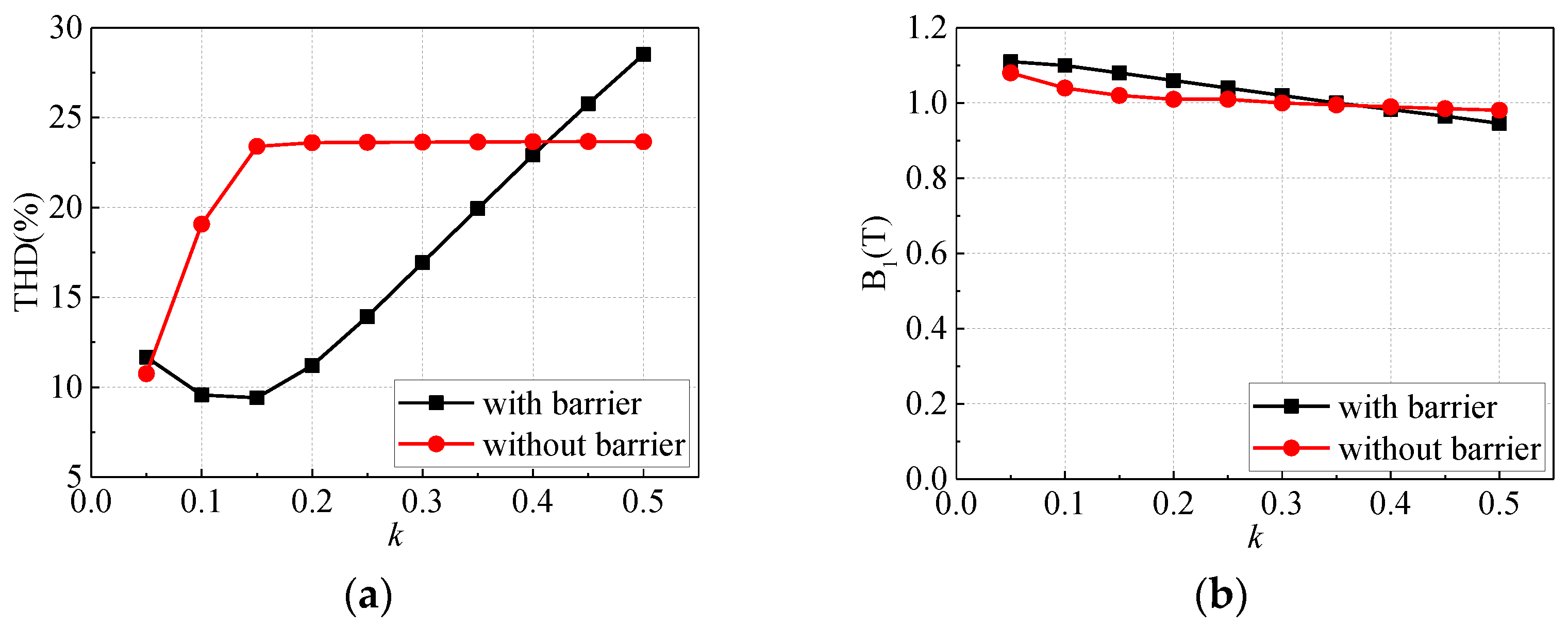
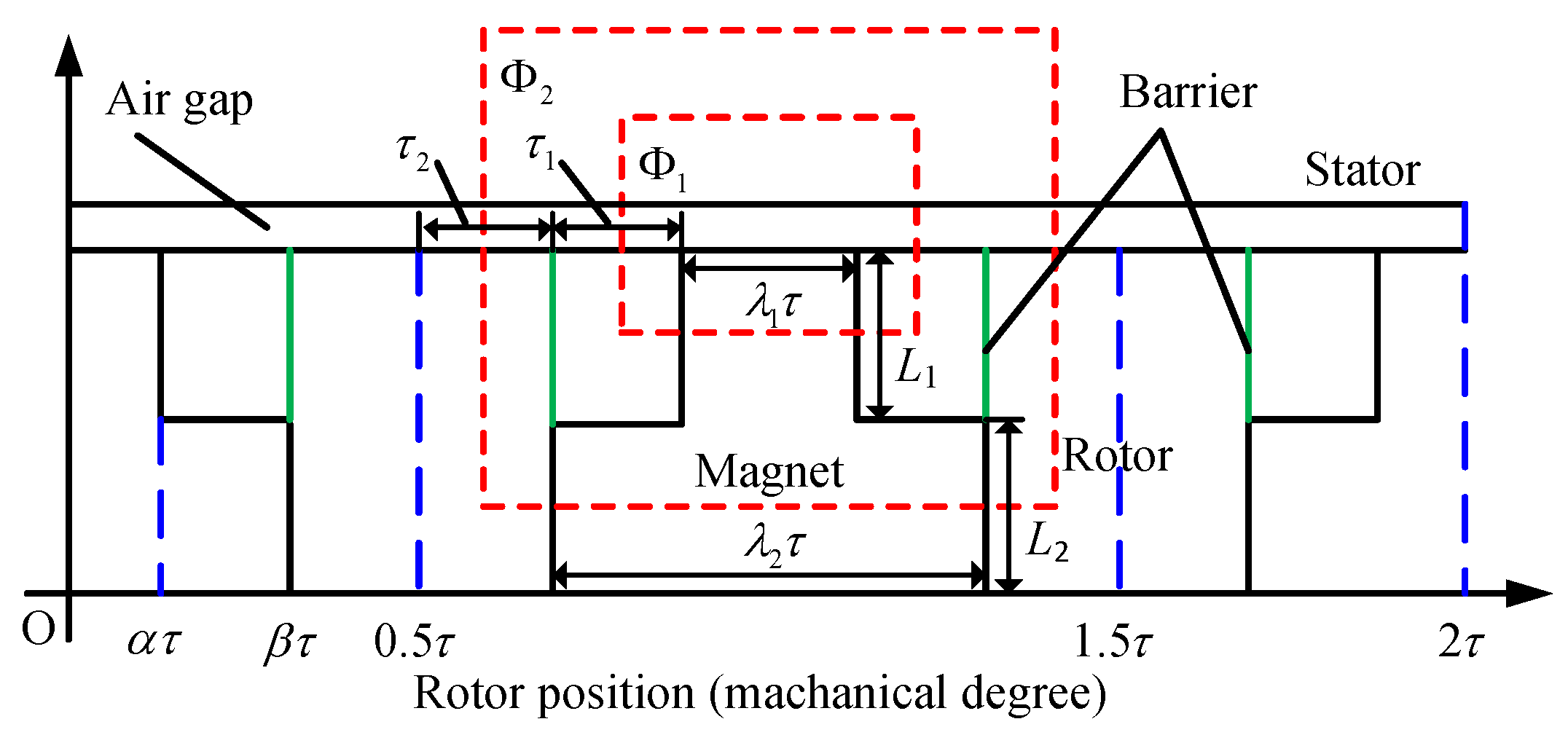

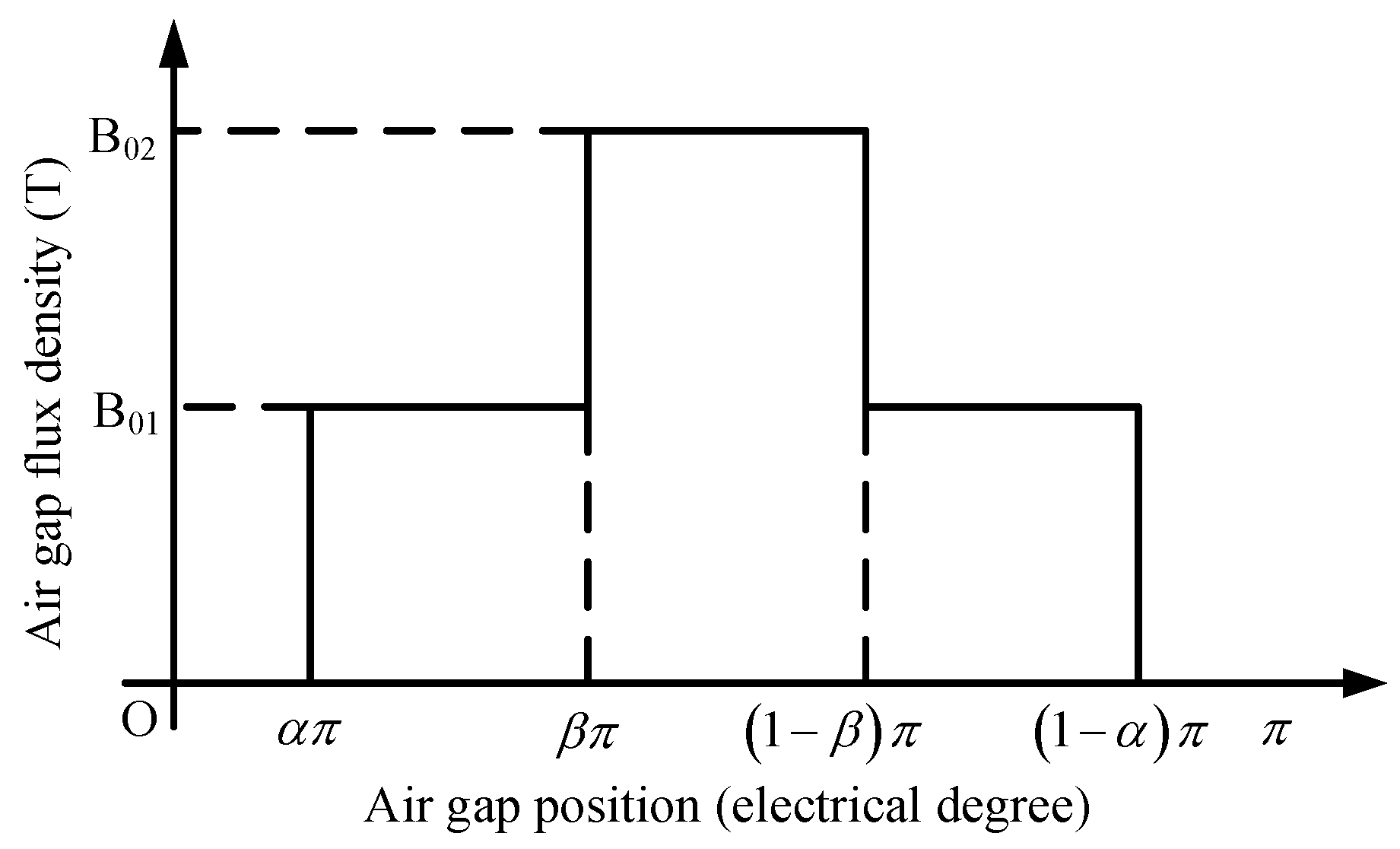
| Parameter | ST | TLST-1 | TLST-2 | TLST-3 |
|---|---|---|---|---|
| λ1(λ) | 0.38 | 0.30 | 0.25 | 0.20 |
| λ2 | -- | 0.392 | 0.400 | 0.407 |
| k | -- | 0.13 | 0.13 | 0.13 |
| V/VRPM | 1 | 1 | 1 | 1 |
| B1 | 1.08 | 1.070 | 1.058 | 1.045 |
| THD | 16.6% | 12.5% | 11.3% | 11.4% |
| Parameter | ST | TLST-4 | TLST-5 | TLST-6 |
|---|---|---|---|---|
| λ1(λ) | 0.38 | 0.30 | 0.25 | 0.20 |
| λ2 | -- | 0.41 | 0.45 | 0.48 |
| k | -- | 0.13 | 0.13 | 0.13 |
| V/VRPM | 1 | 1.04 | 1.116 | 1.167 |
| B1 | 1.08 | 1.08 | 1.08 | 1.08 |
| THD | 16.6% | 11.4% | 9.2% | 10.8% |
| Parameter | Value |
|---|---|
| Number of stator slots | 24 |
| Number of rotor poles | 20 |
| Pole pitch at average radius (mm) | 55 |
| Axial length of rotor(half side in axial direction) (mm) | 20 |
| Thickness of flux barrier (mm) | 3 |
| Air gap length (mm) | 2 |
| PM type | N38EH |
| Silicon steel sheet type | 35WW250 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, F.; Bi, Y.; Pei, Y. Magnet Shape Optimization of Two-Layer Spoke-Type Axial Flux Interior Permanent Magnet Machines. Energies 2018, 11, 15. https://doi.org/10.3390/en11010015
Chai F, Bi Y, Pei Y. Magnet Shape Optimization of Two-Layer Spoke-Type Axial Flux Interior Permanent Magnet Machines. Energies. 2018; 11(1):15. https://doi.org/10.3390/en11010015
Chicago/Turabian StyleChai, Feng, Yunlong Bi, and Yulong Pei. 2018. "Magnet Shape Optimization of Two-Layer Spoke-Type Axial Flux Interior Permanent Magnet Machines" Energies 11, no. 1: 15. https://doi.org/10.3390/en11010015
APA StyleChai, F., Bi, Y., & Pei, Y. (2018). Magnet Shape Optimization of Two-Layer Spoke-Type Axial Flux Interior Permanent Magnet Machines. Energies, 11(1), 15. https://doi.org/10.3390/en11010015





