Remaining Useful Life Estimation of Aircraft Engines Using a Modified Similarity and Supporting Vector Machine (SVM) Approach

Abstract

As the main power source for aircrafts, the reliability of an aero engine is critical for ensuring the safety of aircrafts. Prognostics and health management (PHM) on an aero engine can not only improve its safety, maintenance strategy and availability, but also reduce its operation and maintenance costs. Residual useful life (RUL) estimation is a key technology in the research of PHM. According to monitored performance data from the engine’s different positions, how to estimate RUL of an aircraft engine by utilizing these data is a challenge for ensuring the engine integrity and safety. In this paper, a framework for RUL estimation of an aircraft engine is proposed by using the whole lifecycle data and performance-deteriorated parameter data without failures based on the theory of similarity and supporting vector machine (SVM). Moreover, a new state of health indicator is introduced for the aircraft engine based on the preprocessing of raw data. Finally, the proposed method is validated by using 2008 PHM data challenge competition data, which shows its effectiveness and practicality.

1. Introduction

Recent developments of complex systems, such as aircraft engines, engineering machines, high-speed vehicles and computer numerical control (CNC) systems have been emphasized by the increasing requirements of on-line health monitoring for the purpose of maximizing its operational reliability and safety [1,2,3]. As the core part and power source of aircrafts, the reliable operation of an aero engine is critical for ensuring the reliability and safety of the aircraft, and to maintain its availability, and reduce its maintenance costs [4,5,6]. Among them, prognostics and health management (PHM) is an effective approach and one of the most commonly-used [7,8]. In particular, residual useful life (RUL) estimation is a key technology for PHM. In general, RUL estimation is to indicate the system/component lifetime before it can no longer perform its function, which is also an important way to reduce production loss, save maintenance costs and avoid fatal machine breakdowns of the equipment before its failure [9,10,11,12].

Since the aircraft engine is a complex system, there are various monitored performance data from different positions during its operation. How to estimate RUL of an aircraft engine by utilizing these data has become the focus of most engine industries. Until now, approaches to predict system lifetime can be broadly categorized into three types: physics-based models, data-driven approaches and hybrid approaches [12,13,14]. Generally, a physics-based model utilizes the failure physical model of the system/component to estimate its RUL, which is usually based on the system/component’s physics of failure or physics of dynamics deeply [15,16,17,18,19]. It can usually obtain reasonable and accurate predictions of RUL based on physical models with limited historical data [20]. However, it is usually different or too expensive to apply a physics-based model to a complex system. Besides, this approach has shown significant limitations due to the assumptions and simplifications of the adopted models [21]. The data-driven approach utilizes the monitored operational data relating to system health for RUL estimation [22,23], which is preferred when the system’s failure physics is complicated or unavailable but systems’ degradation procedure and degradation data are available. Note from [3] that the data-driven approach provides accurate RUL predictions for a complex system, which can be applied quickly and cheaply compared to the physics-based model. Furthermore, recent development of sensor technology and simulation capabilities enables us to continuously monitor the healthy situation of a complex system and obtain the related large amount of performance index data. In addition, data-driven approaches can be divided into three categories: statistical techniques and artificial intelligence (AI) techniques. The former includes regression methods such as the auto-regressive and moving average (ARMA) models, and the later includes neural networks and supporting vector machine (SVM), fuzzy logic, etc. The third approach, the so-called hybrid approach proposed by Hansen et al. [24], is the combination of physics-based and data-driven models, in which prognostics results are claimed to be more reliable and accurate, but few studies have been reported [20].

Data-driven RUL prediction models, which are most widely applied in the field of prognostics or PHM, mainly include extrapolation models and statistical models. The extrapolation model is usually used to fit a curve of a system degradation evolution by regression, extrapolate the curve to the failure threshold and obtain the RUL between the current moment and the predicted failure time [25]. The statistical model establishes the relationship between a system’s failure likelihood and its degradation indicator from collected CM (condition maintenance) and failure data [26]. The statistical model approach is classified into the models based on the direct CM data and indirect CM data. The models based on the direct CM data include the proportional hazards model [27,28], proportional covariate model (PCM) [29], Wiener processes, Gamma processes and Markovian-based models. The models based on the indirect CM data include stochastic filtering-based models, covariate-based hazard models and hidden Markov model (HMM) [30], hidden semi-Markov models (HSMM), etc. Statistical models are the most effective ones for RUL estimation when system failure procedure is invisible. Most research has been conducted in RUL estimation based on data-driven models. Stetter and Witczak [31] explored various degradation modeling techniques and how to select the degradation indicator to estimate the RUL. Lee et al. 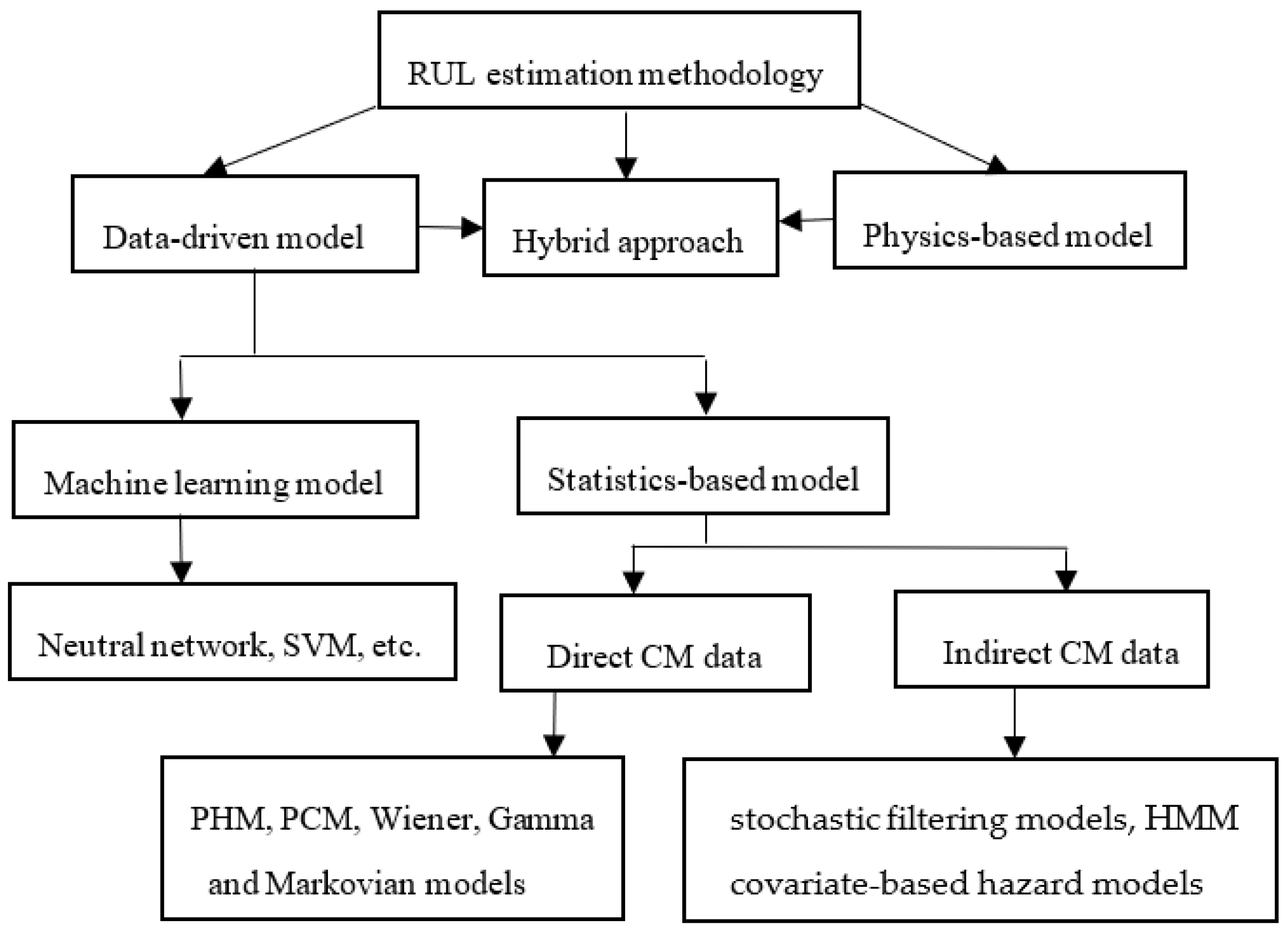[32] reviewed various methodologies and techniques in PHM research and proposed the systematic PHM design methodology, namely 5S methodology. Moreover, current methodologies of RUL estimation can be summarized as three classes as shown in Figure 1.

Referring to the previous literature and existing methods, a structured form of methodology for RUL prediction is expressed as shown in Figure 1.

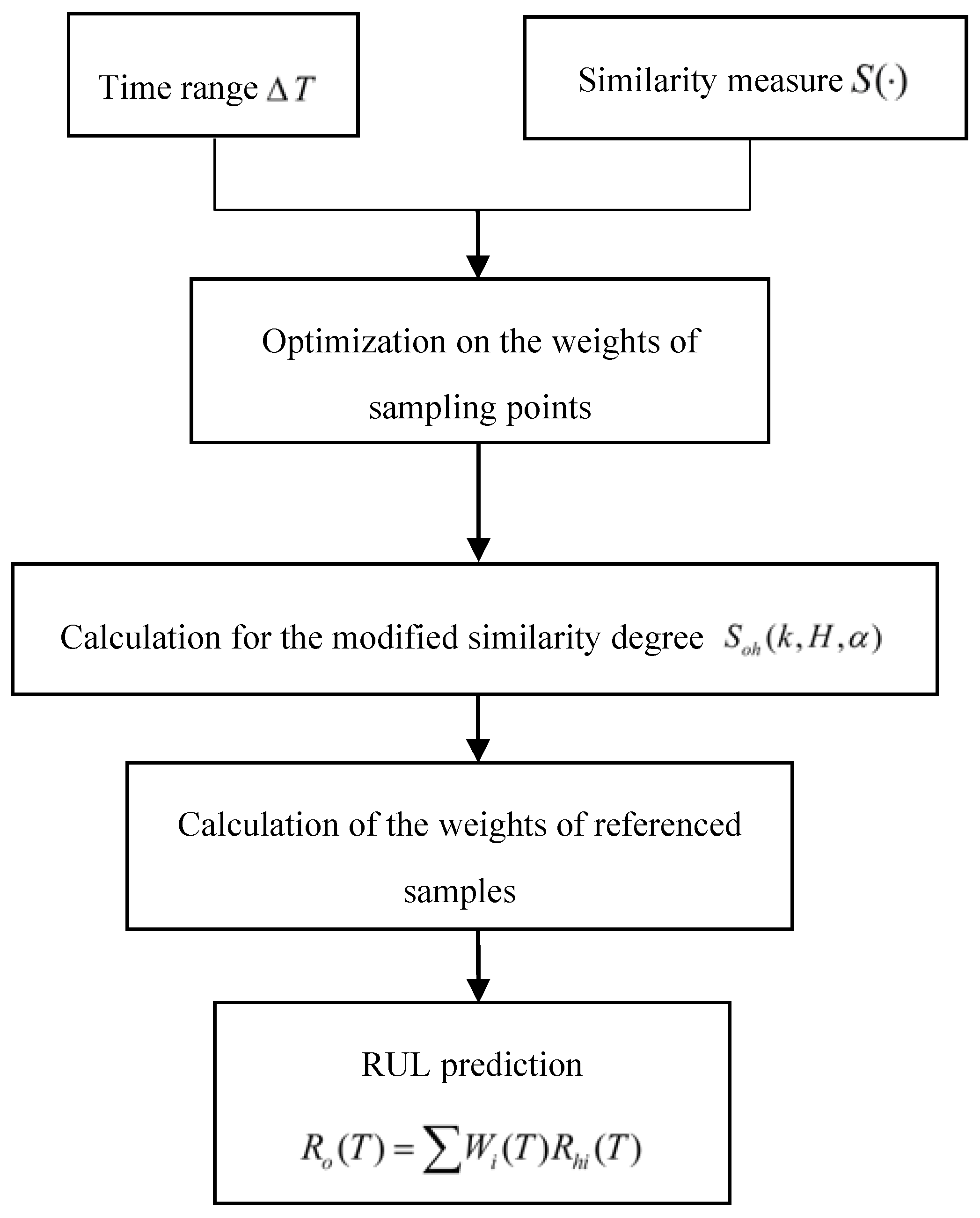
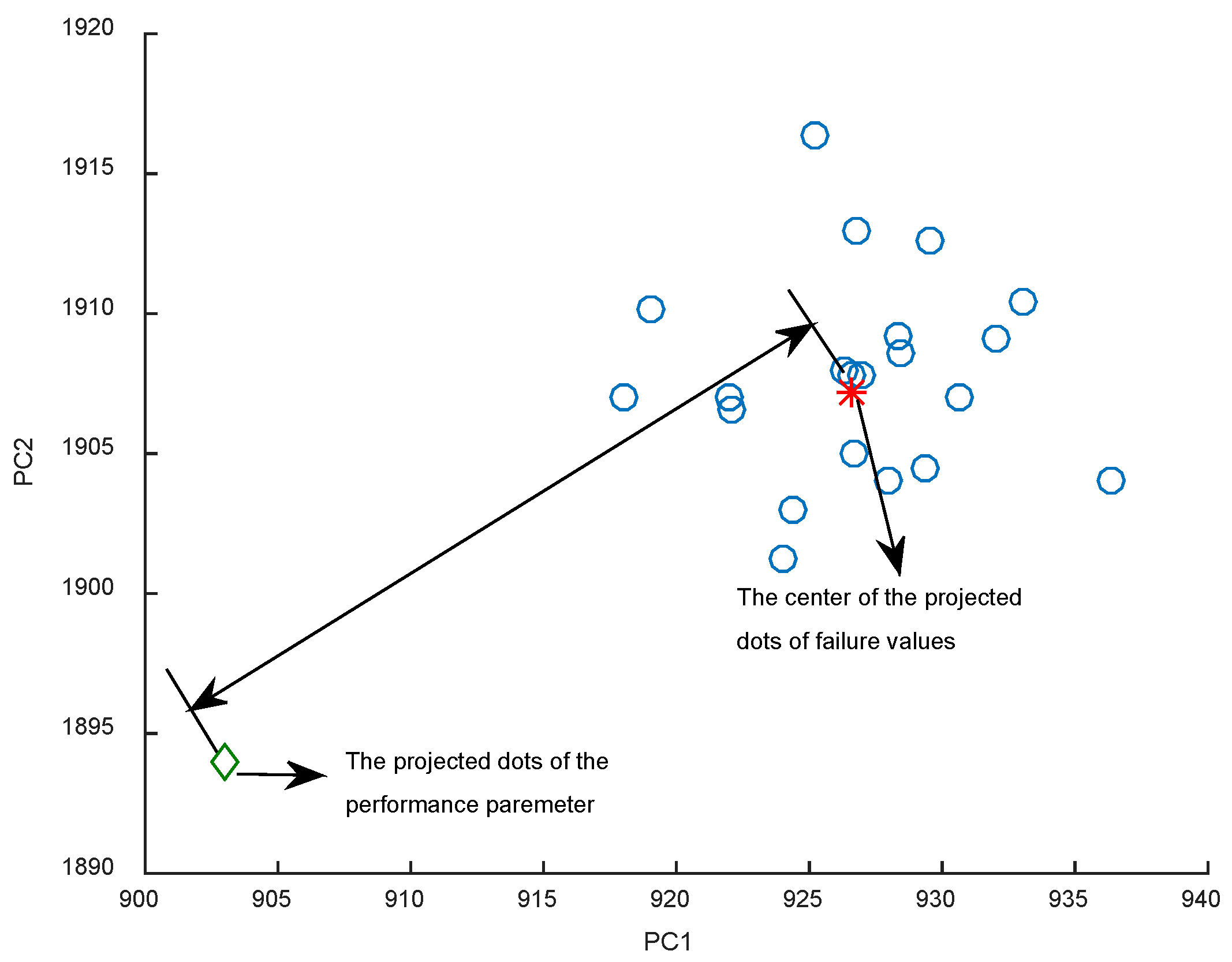
When utilizing the data-driven approach for RUL estimation, the whole run-to-failure data of systems are normally needed, but it is difficult to obtain enough run-to-failure data for the long-life systems with high reliability. Thus, it might lead to a large error if the available system history data are lacking. The same problem will arise when the ARMA model is employed. However, if there are some similar systems to the researched system, the failure and performance-deteriorated information of these similar systems are useful for RUL estimation of the researched system. In general, the principle of similarity-based RUL prediction approach is given as follows: if an operating system has similar performance to the reference system during a time range, then assume that they have a similar RUL. Because this reference system is an identical system with the operating system physically, moreover, they operate under the same working conditions and reference systems that have already failed. In addition, if there are more reference systems similar to the researched one, the similarity-based approach can be introduced through a weighted average of the reference systems’ RUL as the researched one’s RUL [33], while the weight is proportional to the similarity between the researched and reference systems. According to this, the similarity-based RUL prediction model gives more reasonable results without modeling the deteriorated process of the researched system. Besides, with the development of PHM, there are abundant historical deteriorated data before failure that could be utilized to perform PHM.

Zio et al. [21] developed a similarity-based approach to predict the RUL by comparing its evolution data to the trajectory patterns of reference samples through fuzzy similarity analysis, and aggregating their time to failure in a weighted sum, which accounts for their similarity to the developing pattern [21]. Gebraeel et al. [22] presents a stochastic process by combining with a data analysis method and deterioration modeling of the components for RUL prediction.

For the traditional similarity-based RUL prediction method, current and past degradation parameters of reference systems have an equal weight when calculating the similarity measure. However, as we all know, a system’s most recent performance to its current health/state is more relative than its earlier performance, and provides more information for its RUL than its earlier performance. Therefore, it is reasonable to assign more weight to a system’s most recent sampling point than its earlier sampling point of performance parameters when measuring its similarity with other systems. However, the traditional similarity-based method ignored this situation. Accordingly, this paper adopts a modified similar-based methodology which introduces a weight-adjusted coefficient $\mathsf{\alpha }$ to embody the different effect on the calculation of similarity degree from different time ranges while calculating the similarity measure. The more recent sampling point of performance, the bigger weight of the parameter is given. In addition, the earlier value of performance, the parameter is given smaller weight and this paper provides an approach to optimize the weight $\mathsf{\alpha }$.

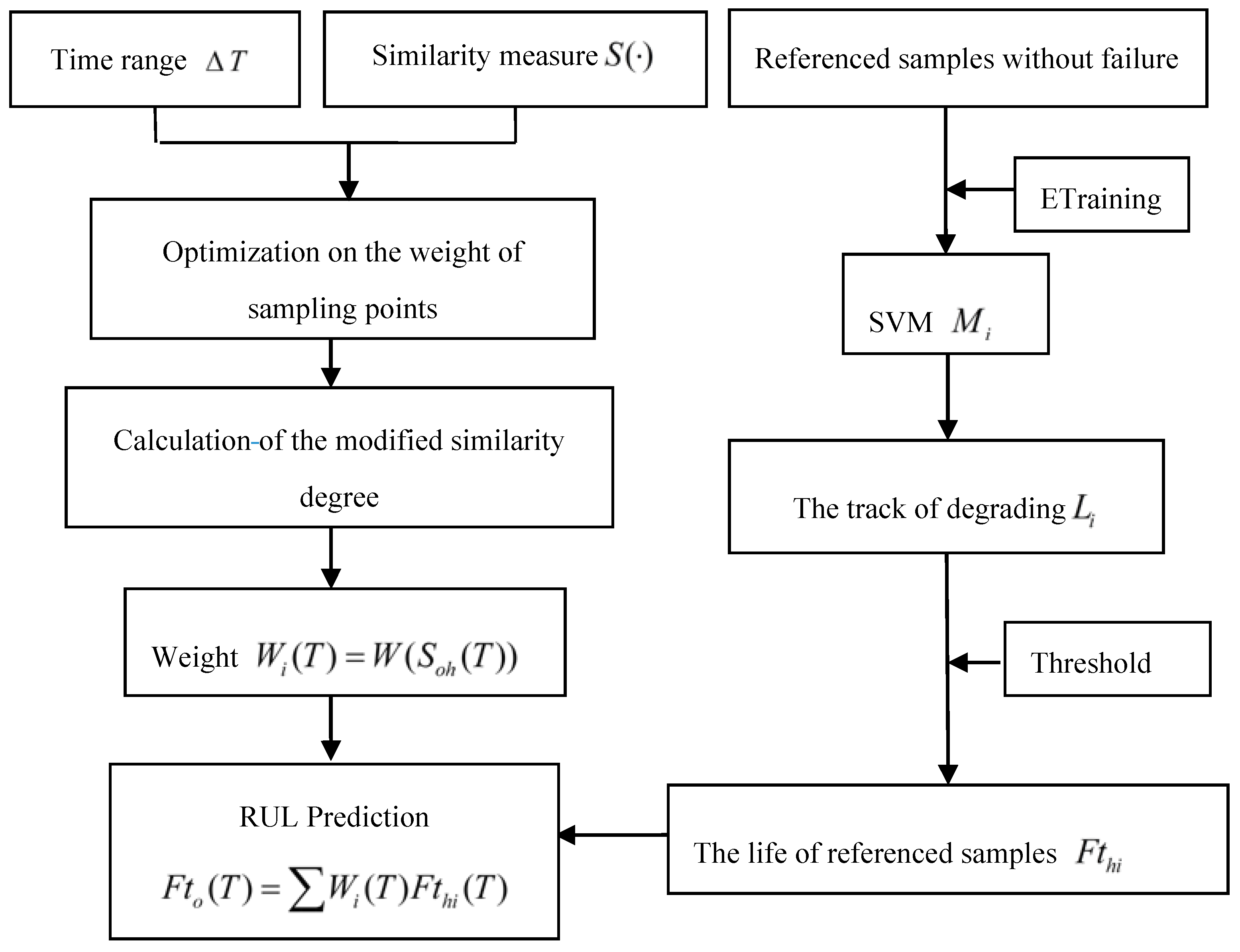
Until now, most research on the similarity-based model for RUL prediction are based on run-to-failure data, but sometimes there are only deteriorated performance data without run-to-failure data. How to utilize these deteriorated performance data, which do not work to failure, to estimate RUL of equipment by similarity-based method, is lacking and expected. Suspension history condition monitoring data usually contain useful information revealing the degradation situation of the system, including environmental factors and loading variations in actual situations, such as degradations and variations of stress amplitudes [10,11,12,34,35]. If these data are properly used, it is helpful to estimate RUL more accurately, particularly when the failure data are insufficient and unavailable in some cases [36,37]. Li et al. [38] used the suspension data to promote the prediction precision of a neural network. However, how to utilize these suspension data to predict RUL of the equipment has not been deeply studied.

This paper attempts to develop a modified similarity and SVM-based method to predict the RUL of an aircraft engine, including two schemes with different reference samples. The first scheme adopts a modified similarity-based method for estimating the RUL of the engine with abundant run-to-failure data of referenced samples, which is named as the modified similarity methodology based on run-to-failure data. The second scheme utilizes deteriorated data of samples without running to failure to estimate the RUL of the operating sample based on SVM and similarity methodology, named as the modified similarity and SVM methodology based on deteriorated data. The structure of this paper is as follows. Section 2 provides a detailed description of two approaches aimed for RUL estimation under two situations. Section 3 introduces how to utilize the proposed approaches to estimate the RUL of an aircraft engine. Section 4 concludes the current research.

2. Proposed Methodology for RUL Estimation

This section is devoted to introducing a similarity-based methodology including two schemes for RUL estimation. The first scheme is to estimate the RUL with abundant run-to-failure data of referenced samples. The other scheme is to estimate the RUL of aircraft engines with some deteriorated data of referenced samples which have no run-to-failure data.

2.1. The Scheme of the Modified Similarity Methodology Based on Run-to-Failure Data

The RUL of an operating sample is the weighted average of RUL of referenced samples. The weights are determined by the similarity degree between referenced samples and the operating one. In particular, the similarity degree is calculated by the weighted average of similarity degrees of sampling points between the reference and operating equipment. This subsection tends to introduce the framework of the modified similarity methodology based on run-to-failure data as shown in Figure 2.

2.1.1. Determination of Time Range for Similarity Measurement

In this analysis, the first step is to set up the time range $\Delta t$ for similarity measurement, namely, to determine the number of sampling points of the operating system for similarity measurement:

$$X\left(k,H\right)=\left[x\left(k·\Delta t\right),\cdots ,x\left(\left(k-H\right)·\Delta t\right)\right]$$

(1)

where H is the number of sampling points; $\Delta t$ represents the time range in which similarity degree between a referenced sample and the operating one; $x\left(k·\Delta t\right)$ denotes the degradation indicator of the operating sample at the kth sampling point since its operation.

Generally, most of the recent sampling points of the operating system represent its current state. In the traditional similarity-based method, any consecutive sampling points of the condition monitor a reference system before its failure can be used for similarity measurement [15]. In addition, a reasonably long time range can be determined based on operational experience in the lack of prior knowledge. The sampling points $X\left(k,H\right)$ in sampling time range are equally considered to be fully representative of the system’s RUL. In this paper, the sampling points of the reference system are confined in the same time range as the operating system, namely, $\left[k-H,k\right]$.

2.1.2. Calculation of the Similarity Measure

The second step is to define and calculate the similarity measure, which indicates the similarity degree between the operating and reference systems, and then quantify the degradation duration of the ith reference system that is most similar as the duration of the operating system. The similarity measure S is the function of degradation indicators of the system, which measures the similarity between referenced and operating systems. Note that it may be Euclidean distance, probability function [27] or membership function in fuzzy logic theory [26]. In this paper, the Euclidean distance of degradation indicators between the reference systems and the operating system is introduced as the similarity measure function. The traditional Euclidean distance is expressed as:

$$S_{ohi}\left(k,H,m\right)={\displaystyle \sum }_{\nu =0}^H{\left[X_0\left(\left(k-\nu \right)·\Delta t\right)-X_{hi}\left(\left(m-\nu \right)·\Delta t\right)\right]}^2/\left(H+1\right)$$

(2)

where $S_{ohi}\left(k,H,m\right)$ is the similarity measure between the operating system’s degradation process in the time range $\left[\left(k-H\right)\Delta t,k\Delta t\right]$ and reference system’s degradation process in the time range $\left[\left(m-H\right)\Delta t,m\Delta t\right]$; where $M_i\Delta t$ is the failure time of the ith reference system, and $H\le m\le M$. $X_0\left(\left(k-\nu \right)·\Delta t\right)$ denotes the degradation indicator of the operating system at the $vth$ sampling point from the $kth$ sampling point. $X_{hi}\left(\left(m-\nu \right)·\Delta t\right)$ denotes the degradation indicator of the ith reference system at the $vth$ sampling point from the $mth$ sampling point.

The similarity degree between the operating system and the ith reference system at time $T=k\Delta t$ is defined as:

$$S_{ohi}\left(k\right)=\frac{1}{\underset{H\le m\le M_i}{\min }S\left(k,H,m\right)}$$

(3)

In this analysis, more weights are assigned to the recent sampling point of degradation indicator than its former sampling points, thus, the Euclidean distance as the similarity measure for illustration is defined as:

$$S_{ohi}\left(k,H,\alpha \right)={\displaystyle \sum }_{\nu =0}^H\left\{{\alpha }^{\nu }{\left[X_0\left(\left(k-\nu \right)·\Delta t\right)-X_{hi}\left(\left(k-\nu \right)·\Delta t\right)\right]}^2\right\}/\left(H+1\right)$$

(4)

where $\alpha$ is a weight-adjusting coefficient ranging from 0 to 1. A smaller $\alpha$ corresponds to a smaller weight assigned to the former sampling point than recent sampling points of reference systems. $\alpha$ can be obtained by optimization for minimal predicting error of operating system’s RUL. An example to obtain $\alpha$ is elaborated in Section 3.1.

2.1.3. Definition of the Weight Function

The third step is to define the weight function based on the similarity measure. As aforementioned, the weight is a function of similarity-degree, which is assigned to the reference systems according similarity degree to calculate the RUL of the operating system. The weight of the ith reference system is given by

$$W_i\left(k\right)=\frac{S_{ohj}\left(k\right)}{{{\displaystyle \sum }}_{j=1}^n{S}_{ohj}\left(k\right)}$$

(5)

2.1.4. RUL Estimation of the Operating System

The last step is to estimate the RUL of the operating system. As aforementioned, the RUL of an operating sample at time $t=k\Delta t$ is the weighted mean value of reference systems at the kth sampling point, and can be obtained by

$$RUL\left(k\right)={\displaystyle \sum }_{i=1}^n{W}_i\left(k\right)RU{L}_i\left(k\right)$$

(6)

where n is the number of available reference systems.

The real RUL of the reference system at $t=k·\Delta t$ is $RU{L}_i\left(k\right)=\left(M_i-k\right)·\Delta t$, then the operating system’s RUL can be calculated by

$$SUL\left(k\right)={\displaystyle \sum }_{i=1}^n{W}_i\left(k\right)\left(M_i-k\right)·\Delta t$$

(7)

2.1.5. Optimization of the Weight-Adjust Coefficient $\alpha$

In order to embody different effects of sampling points of reference systems at different time on RUL estimation of the operating system, the weight-adjust coefficient $\alpha$ is introduced in this analysis. The weight-adjust coefficient $\alpha$ leads the recent sampling points of reference systems with more weights for the similarity degree calculation, which tends to provide more accurate prediction, specifically, $\alpha$ can be obtained by optimization under the goal function

$$MAP{E}_{\alpha }\left(k\right)=\min \left[{\displaystyle \sum }_{j=k_0}^{j=k-1}MAP{E}_{\alpha }\left(j\right)/\left(k-1-k_0\right)\right]$$

(8)

where $k_0$ denotes the first sampling point to deteriorate; $MAP{E}_{\alpha }\left(j\right)$ is the estimated percentage error at the value of $\alpha$.

2.2. The Scheme of the Similarity and SVM Methodology Based on Deteriorated Data

Research shows that the similarity-based method gives effective and accurate estimation under abundant run-to-failure data of reference samples. However, most equipment operates with high reliability and long life, especially in aerospace applications; the reference samples with enough run-to-failure data are seldom. For this limited or no run-to-failure reference samples, whether the similarity-based method can be used or not needs to be explored. In practices, there is abundant performance deteriorating data and maintenance data during its operating process. These suspension data include useful degradation information relating to the operating system. However, the degradation indicators after halting operating and lifetime of reference samples are unknown since they did not work until failure. Thus, the trend of the degradation indicators and the lifetime of reference samples need to be collected and analyzed. This methodology for RUL estimation consists two essential preprocessing procedures: performance assessment for reference samples and RUL estimation based on reference systems, and then the RUL of the operating system can be derived. In particular, the implementation flowchart is given in Figure 3.

Particularly, SVM is adopted to perform the degradation trend assessment of reference samples and estimate their lifetimes. As is well known, SVM has been commonly used for handling the data of small samples and multiple dimensions. The monitored degradation indicators of reference samples are used to train SVM and obtain the performance-deteriorated pattern of these samples, and fit their relation curve of degradation indicator with time. Based on the curve, the relation function is estimated by using the maximum likelihood estimation method. Once it reaches the failure threshold, the reference systems are considered as failure, so the lifetime of these reference samples can be estimated in this way. The estimated precision regarding the lifetime of these reference systems is the basis for calculating weights of similarity degree. When the estimated precision is higher, the weight assigned to this reference sample is higher. The rest steps are same as that of the modified similarity methodology based on run-to-failure data in Section 2.1.

3. Model Applications to an Aero Engine

This section provides two cases to illustrate the proposed two approaches for RUL estimation of an aero engine.

3.1. The Estimation of RUL for an Airplane Engine with Run-to-Failure Data Though the Modified Similarity Methodology

In this section, the similarity methodology based on run-to-failure data is applied to estimate the RUL of the aircraft engine with multidimensional degraded parameters. The 2008 PHM Data Challenge Competition is introduced for model validation and comparison. The data sets include 21 monitored parameters under 3 different operating modes at a sequence of time, in which three operating modes are flight height (Alt: 0–42 k feet), Mach number (M: 0–0.84) and throttle resolver angle (TRA: 20–100), which reflect the whole operational state of an aero engine. The 21 monitored parameters are different under different operating modes. The raw data of performance parameters from different parts of an aircraft engine is multiple and fluctuated largely without evident regular patterns. It is difficult to estimate the RUL based on these raw data. This paper puts forward a new indicator to characterize the health of the engine based on these raw data. The following section introduces the procedure to obtain the new health indicator.

Firstly, the 11 performance parameters that have shown evident changing trend with time are selected after inspecting 21 performance parameters. For the 11 performance parameters, a principal component analysis (PCA) is used to extract the main performance parameters that represent healthy state and degradation trend of the engine system from 11 performance parameters. PCA can reduce the data dimensions. Under different operating modes, the PCA result for 11 parameters is listed as shown in

Table 1. The detailed occupancy of the main two components in different modes.

Mode	Mode 1	Mode 2	Mode 3	Mode 4	Mode 5	Mode 6
PC1	0.6082	0.5892	0.7959	0.7185	0.6087	0.5363
PC2	0.3803	0.4005	0.1903	0.2641	0.3034	0.4329

. Through PCA, the main two-dimensional performance parameters, which occupy more than 98% in all 11 parameters, are derived. Then a new status indicator is established based on the residual two-dimensional performance parameters referring to [22]. The new status indicator is built using the Euclidean distance between the projection of two-dimensional performance parameters at a certain cycle on the failure space and the center of the failure space projection dot in an operating mode.

The detailed steps to construct this healthy status index are shown as follows:

(1)

Build the failure space (two-dimensional space) and calculate the projection of the failure values in the failure space, as shown as the hollow dots in Figure 3;

(2)

Calculate the center of these projection dots, as shown as star dot in Figure 3;

(3)

Calculate the projection dot of the performance parameters on the failure space at a certain cycle;

(4)

Calculate the Euclidean distance between the projection dot of the performance parameters in the failure space at a certain cycle and the center of the projected dots in the failure space in an operating mode, which is shown in Figure 4.

Further Euclidean distance means a healthier status of the engine, so this distance is defined as a new healthy status indicator, which represents the engine healthy state and degradation level.

Figure 4 plots the curve of the new health status index of the 196th reference sample. Though this healthy status index shows a certain changing trend, it is still fluctuated intensively. Accordingly, Karman filtering is utilized to further handle this healthy status index. Figure 5 reflects the compared curve of the 196th sample after and before Karman filtering. The red and thick curve is the new degradation indicator of the 196th sample after Karman filtering.

This paper predicted the RUL of five samples No. 196–200 at the 50th cycles, 30th cycles and 10th cycles before failures using the first scheme. An example prediction of the196th samples is given as

Table 2. The five-sample point of the degradation indicator values of the 196th sample.

Run Time	156 Cycles	161 Cycles	166 Cycles	171 Cycles	176 Cycles
RUL	2.5986	2.4292	2.3260	2.4667	2.3691

.

Firstly, the five sample values from the degradation indicator curve after Karman filtering at every 5 cycles before the 176th cycle are given in Table 2. Then the 10 samples which are most similar with the operated samples are selected as the reference samples according to the new degradation indicator in Equation (1). Time range is $\Delta T=5$, sampling interval is $\Delta T=1$. The weights of these reference samples are calculated by using Equation (4). The results and other information on these 10 reference samples are shown in

Table 3. Information of the reference samples.

Ranking	Sample Number	Sampling Interval	Lifetime	RUL	Weight
1	38	224–228	287	59	0.192924
2	82	193–197	223	26	0.164397
3	115	211–215	260	45	0.162683
4	12	120–124	242	118	0.093304
5	29	164–168	228	60	0.082048
6	103	219–223	243	20	0.080489
7	64	122–126	154	28	0.060018
8	53	205–209	259	50	0.058619
9	78	176–180	228	48	0.055197
10	34	244–248	286	38	0.050321

.

The predicted RUL of the 196th sample with its actual lifetime 226 cycles are based on these 10 reference samples is given in

Table 4. RUL estimation of the 196th sample.

Operating Time	Traditional Similarity Method		Modified Similarity Method
	Predicted RUL	Error (%)	Predicted RUL	Error (%)
176	225.69	0.1358	214.50	5.0871
177	238.11	5.3600	219.63	2.8201
178	213.58	5.4953	221.18	2.1310
179	209.86	7.1432	219.50	2.8742
180	203.53	9.9426	221.56	1.9642
…	…	…	…	…
196	197.23	12.7305	221.62	1.9388
197	200.43	11.3132	219.35	2.9427
198	205.42	9.1069	220.53	2.4208
199	200.55	11.2619	225.75	0.1121
200	194.23	14.0578	226.77	0.3401
…	…	…	…	…
216	188.03	16.8012	226.80	0.3558
217	184.37	18.4209	226.17	0.0741
218	182.68	19.1695	225.31	0.3036
219	183.04	19.0067	224.09	0.8448
220	181.41	19.7290	224.15	0.8169

. Meanwhile, the estimated RUL of the 196th sample by the traditional similarity method and modified similarity method are compared in Table 4. The weight-adjusted coefficient $\alpha$ is preliminarily set as 0.4 in this analysis.

As can be seen from Table 4, the modified method provides better predictions than the traditional one. Moreover, the error by the traditional method increases with time. The prediction precision by the modified method tends to be better when the time is closer to failure. Since the traditional method chooses reference samples that are most similar with the operating sample during a certain time interval in their whole life, the operating sample and this similar reference sample maybe are in different degradation epochs. The modified method constrains the same time range to seek the most similar reference samples. In addition, the modified method assigns larger weight to the more recent sampling point.

Finally, the weight-adjusting coefficient of sampling points is optimized. Through assigning different values to get different predicted precision, the optimized weight-adjusting coefficient value can be obtained at $\alpha =0.6$, as shown in Figure 6.

3.2. The Estimation of RUL for an Aero Engine with Deteriorated Data Though the Similarity and SVM Methodology

This methodology for RUL estimation includes two essential procedures: assessment for performance of reference samples and RUL estimation of reference samples. The assessment for performance of reference samples is implemented using SVM in this paper. The data are extracted from the same data sets as the previous case, but these whole life data of the original samples are cut off the rear part and only the front part data are applied in this scheme. The degradation indicator pattern of the No. 1 aircraft engine trained by SVM is shown in Figure 7.

The predicted lifetime of all the 20 reference samples by SVM are shown in

Table 5. The predicted lifetime of 20 trained samples.

Sample Number	Lifetime
$F{t}_1~F{t}_5$	231.12598	289.93651	214.7592	299.89567	372.86392
$F{t}_6~F{t}_{10}$	232.23493	174.22486	290.63039	183.51086	239.97266
$F{t}_{11}~F{t}_{15}$	214.47475	262.17492	215.14943	238.10682	297.89302
$F{t}_{15}~F{t}_{20}$	301.69223	236.68347	201.39653	243.82267	255.27005

. Chi-square test is used to measure the prediction precision, which are used for calculating the weights of reference samples. The No. 11, 13, 18, 17 and No. 3 samples with higher prediction precision are selected to calculate the operating sample’s lifetime as the reference samples. The calculated weights of the reference samples are given in

Table 6. The weights of the reference samples.

Reference Samples	W11	W13	W18	W17	W3
Weights	0.2526	0.2258	0.1957	0.1678	0.1581

. The lifetime of No. 196 sample is predicted as shown in

Table 7. Model predicted lifetime and error of the 196th sample.

Work Time	Predicted Failure Time	Error (%)
121–125	201.4377	10.86
126–130	189.9478	15.95
131–135	188.2144	16.71
136–140	187.5556	17.01
141–145	188.0059	16.81
146–150	192.7102	14.73
151–155	203.6575	9.88
156–160	227.415	0.62
161–165	227.8171	0.80
166–170	230.5832	2.02
171–175	219.4822	2.88
176–180	217.1443	3.91
181–185	220.0715	2.62
186–190	224.6852	0.58
191–195	219.9376	2.68
196–200	232.6292	2.93
201–205	231.4903	2.42
206–210	234.244	3.64
211–215	233.7521	3.43
216–220	230.2518	1.88
221–225	228.2501	0.99

.

It is worth noting from Table 7 that, the proposed methodology has shown better predictions than the traditional one. In particular, the prediction precision is higher when the operational time is closer to the failure point.

4. Conclusions

The RUL prediction of an aircraft engine can not only improve its safety, maintenance, and availability, but also reduce its operation and maintenance costs. This paper presents two schemes to estimate the RUL of an aircraft engine under different situations. The first scheme adopts a modified similarity-based method for estimating the RUL of the aero engine with abundant run-to-failure data of referenced samples. The second scheme utilizes deteriorated data of samples without up-to-failure data to estimate the RUL of the operating sample with less deteriorated performance data than the reference systems. The two schemes are utilized for RUL estimation of an aircraft engine. The model prediction precision shows these two schemes are effective and suitable for RUL estimation of aero engines. More specifically, it is suitable to adopt the modified similarity-based methodology when failed historical samples are abundant and the similarity and SVM methodology is suitable under limited historical samples conditions.