Switched Polytopic Controller Applied on a Positive Reconfigurable Power Electronic Converter
Abstract
:1. Introduction
- Internet of things (IoT): An RPEC focused on low cost and low size power supply was reported on [41].
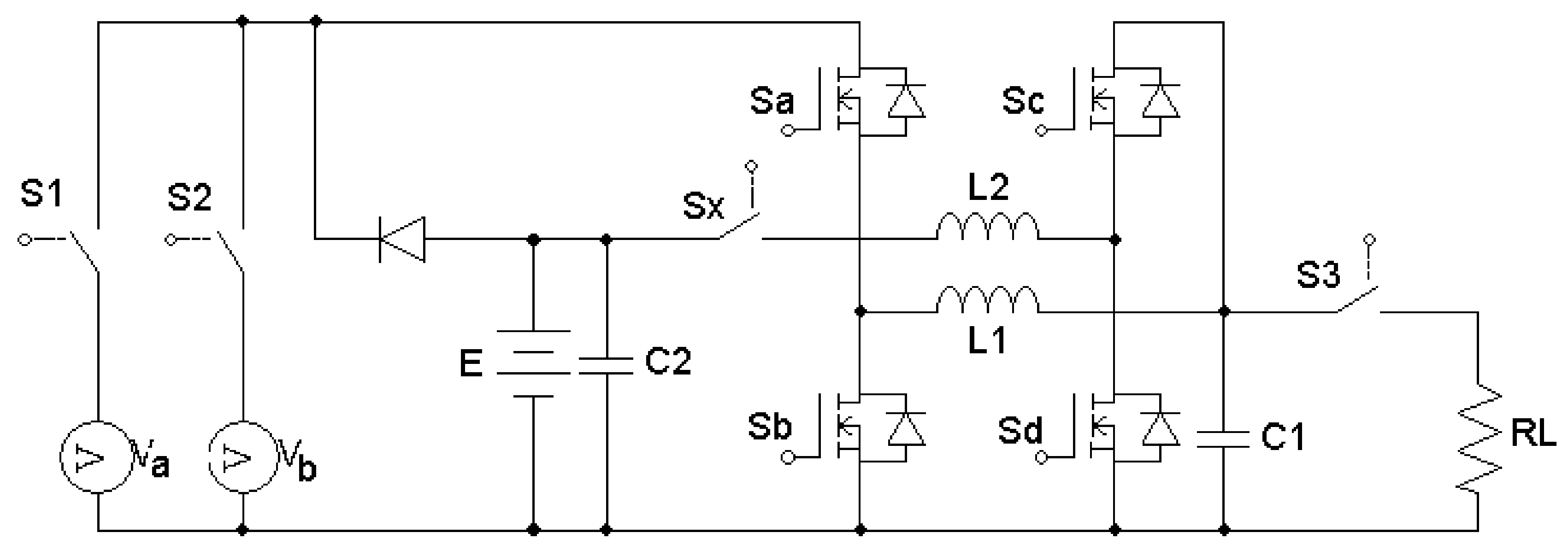
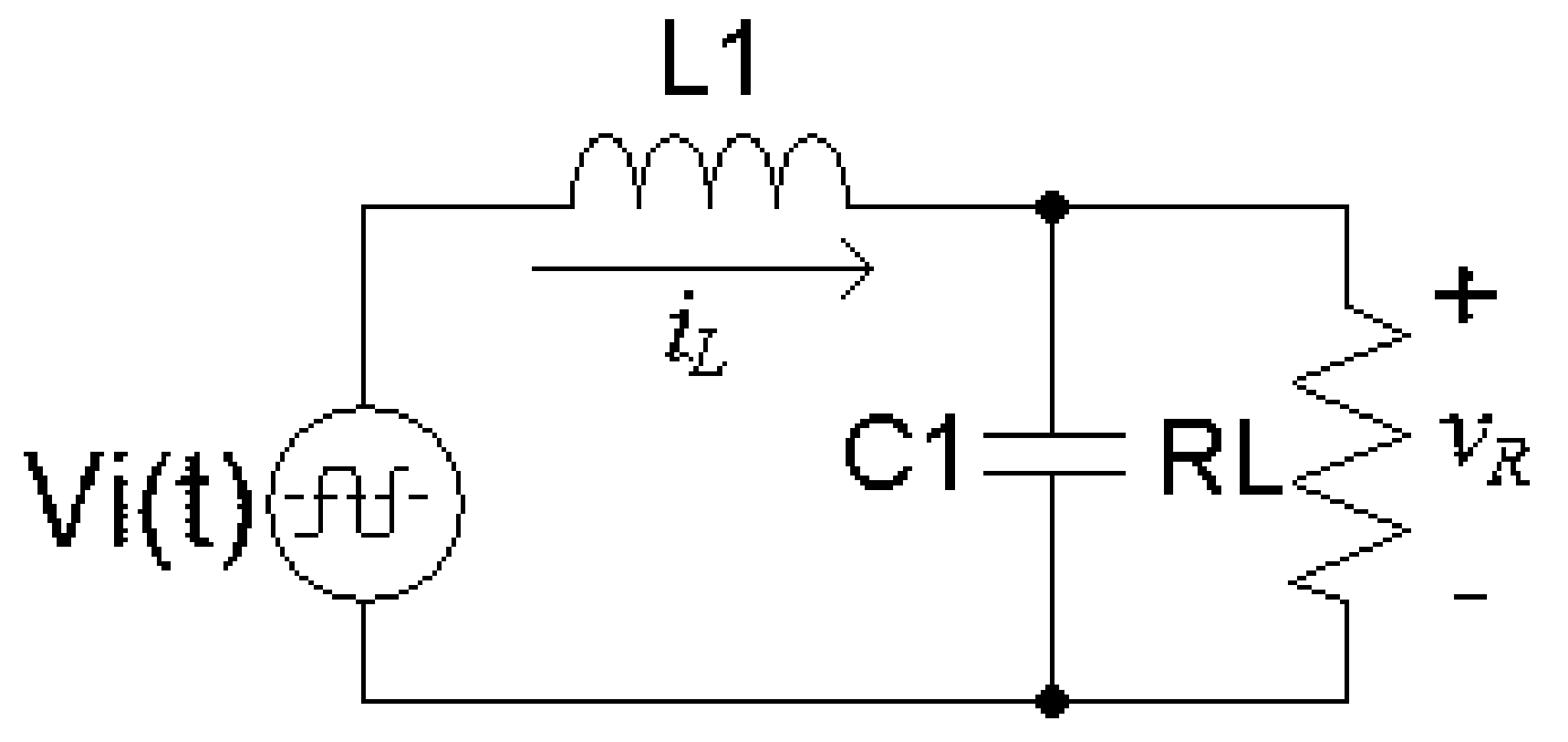
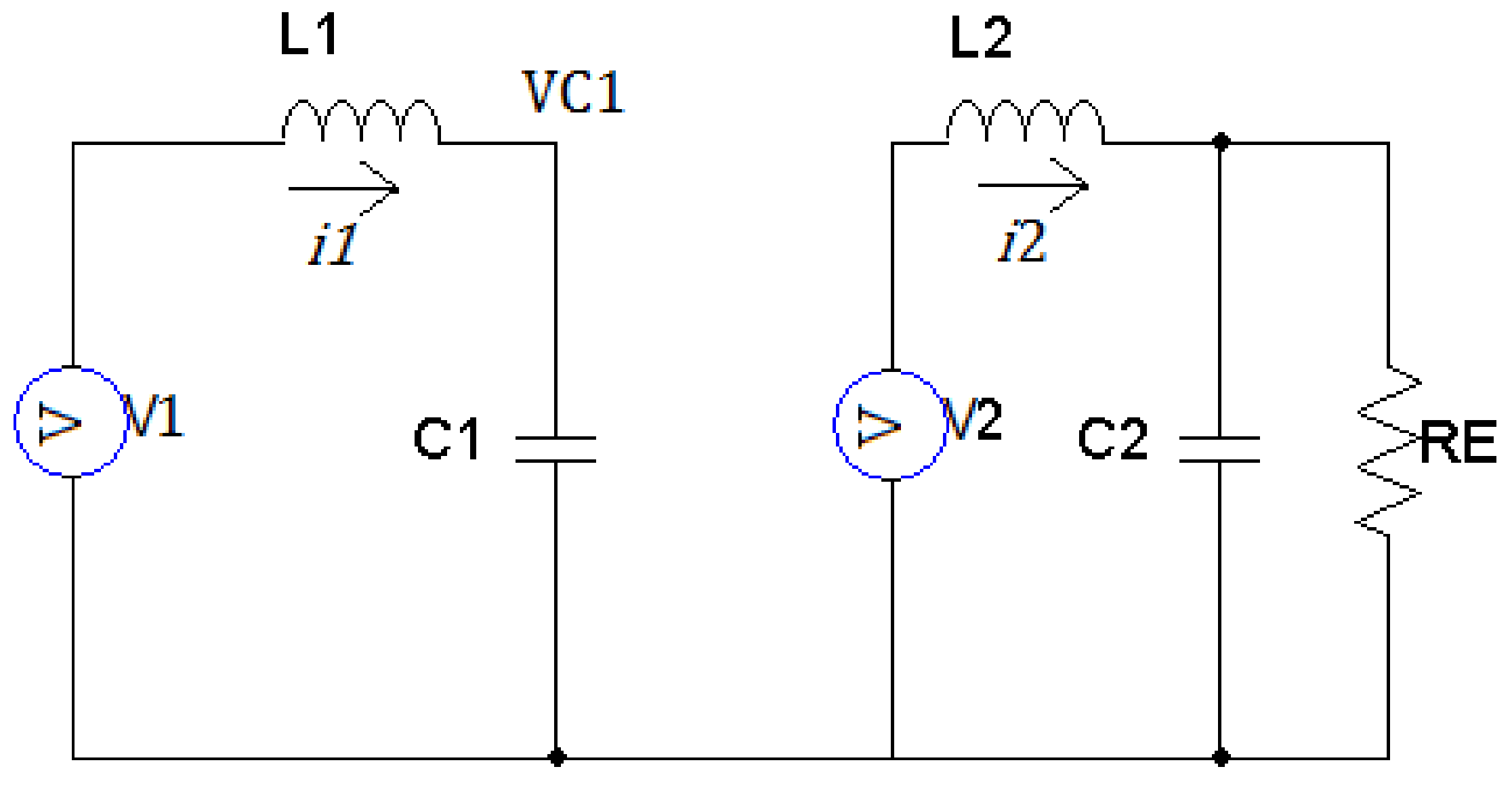
2. Modeling
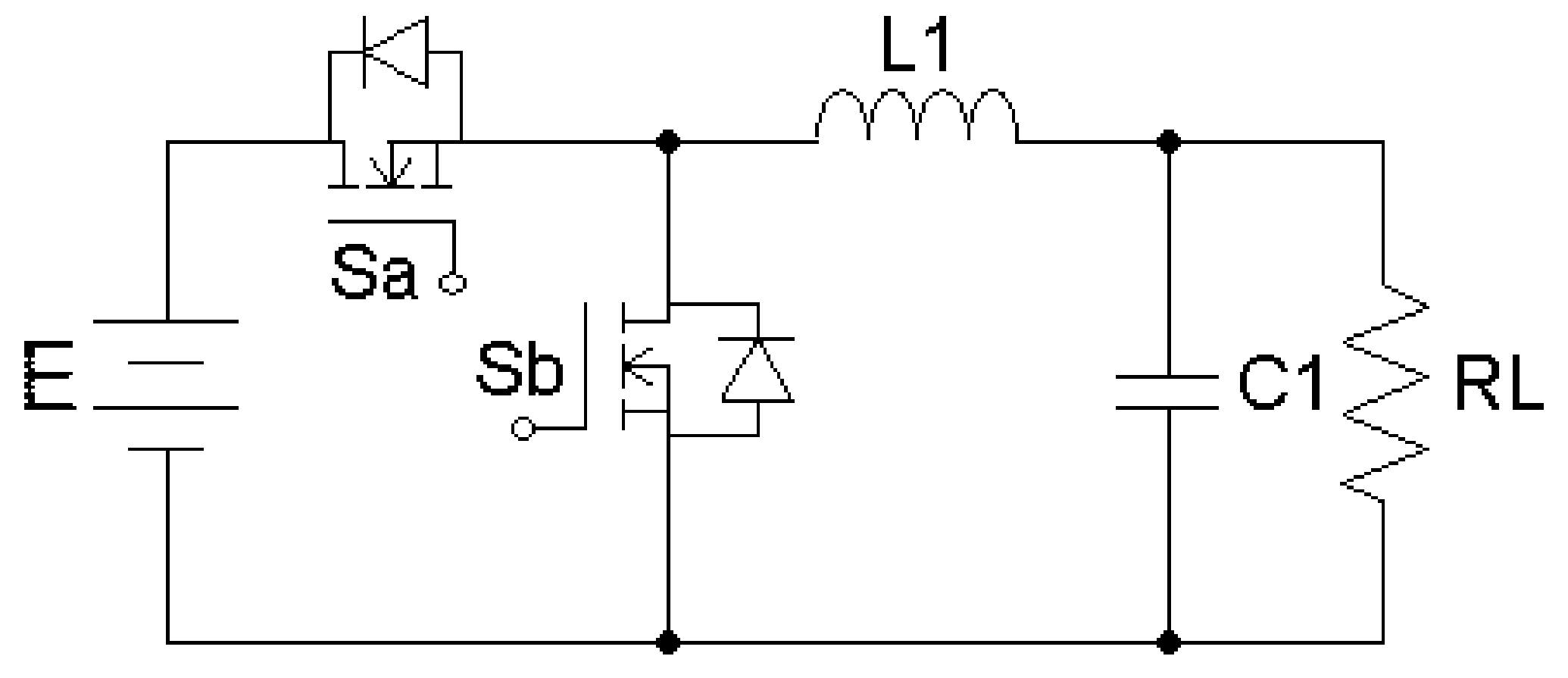
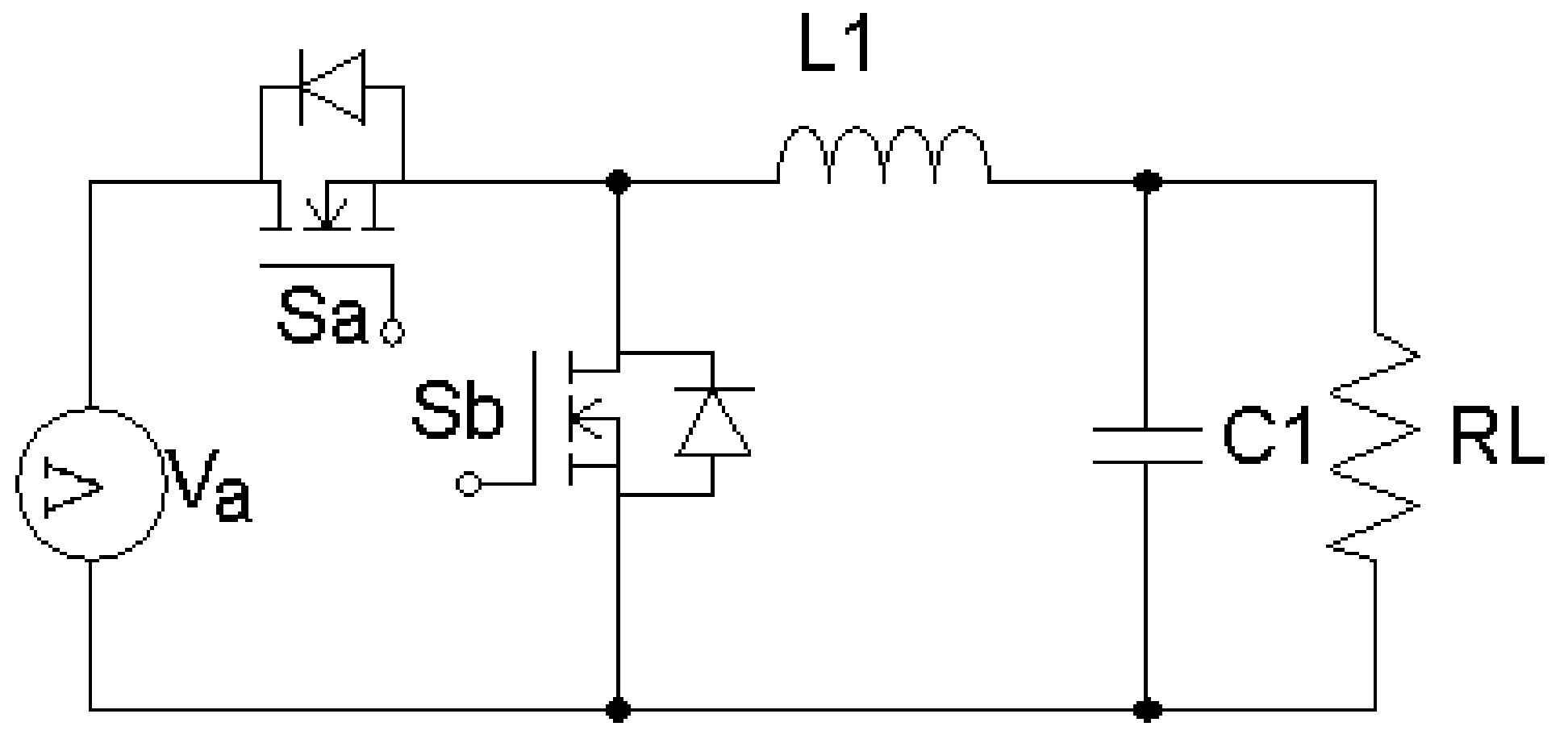
2.1. Mode I (Buck)
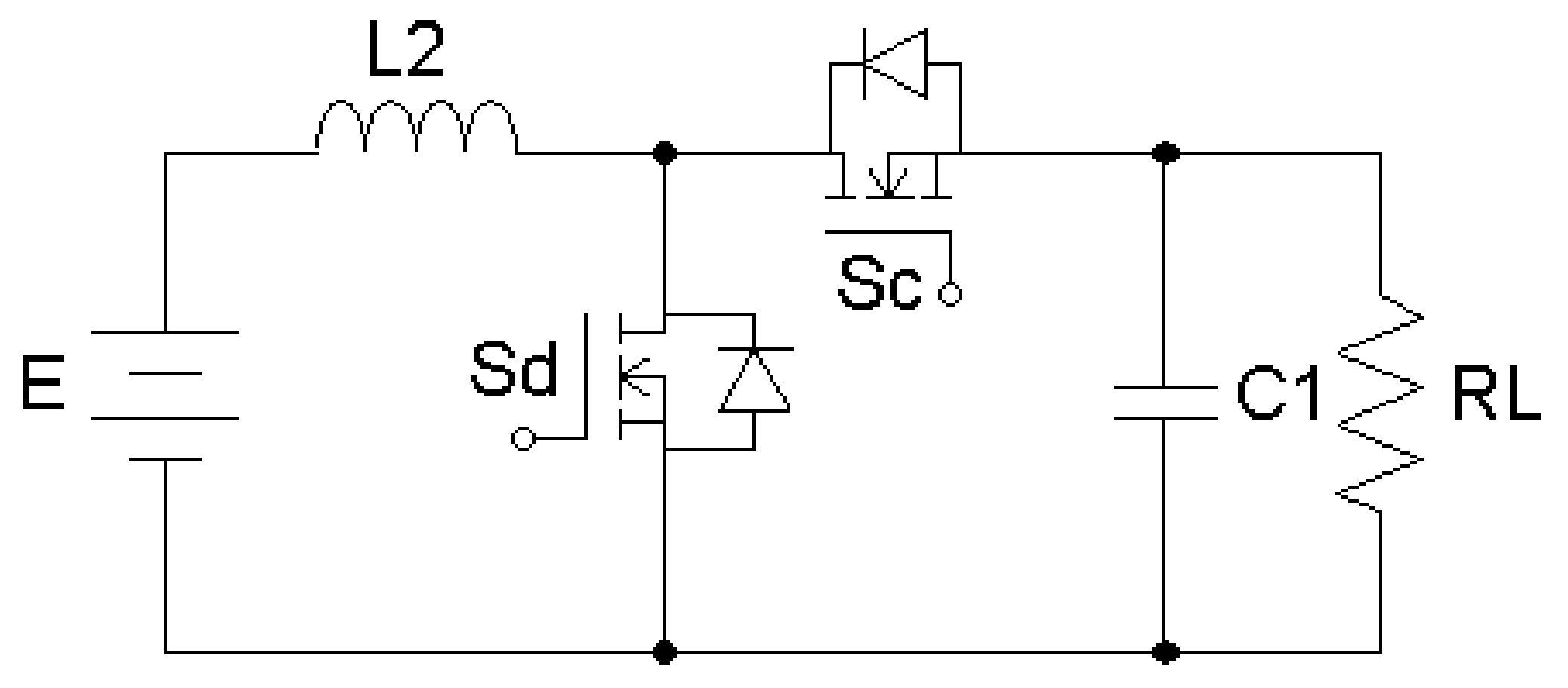
2.2. Mode II (Boost)
2.3. Mode III (Buck)
2.4. Mode IV (Buck)
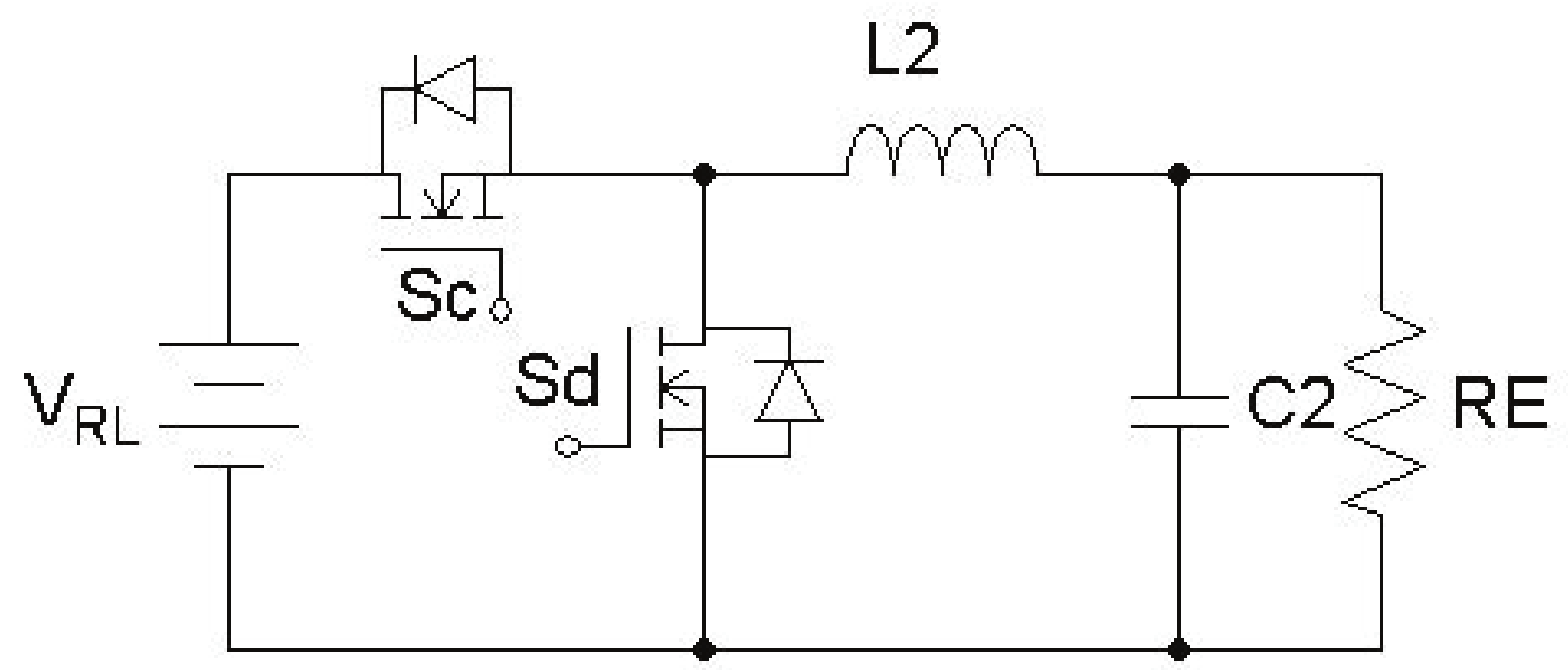
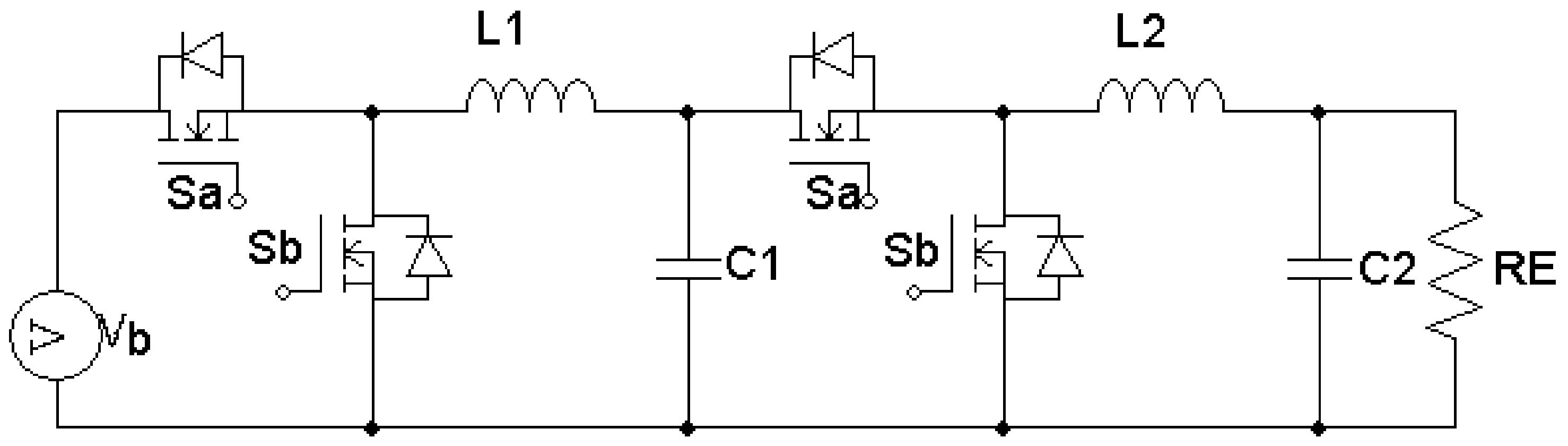
2.5. Mode V (Cascade Buck)
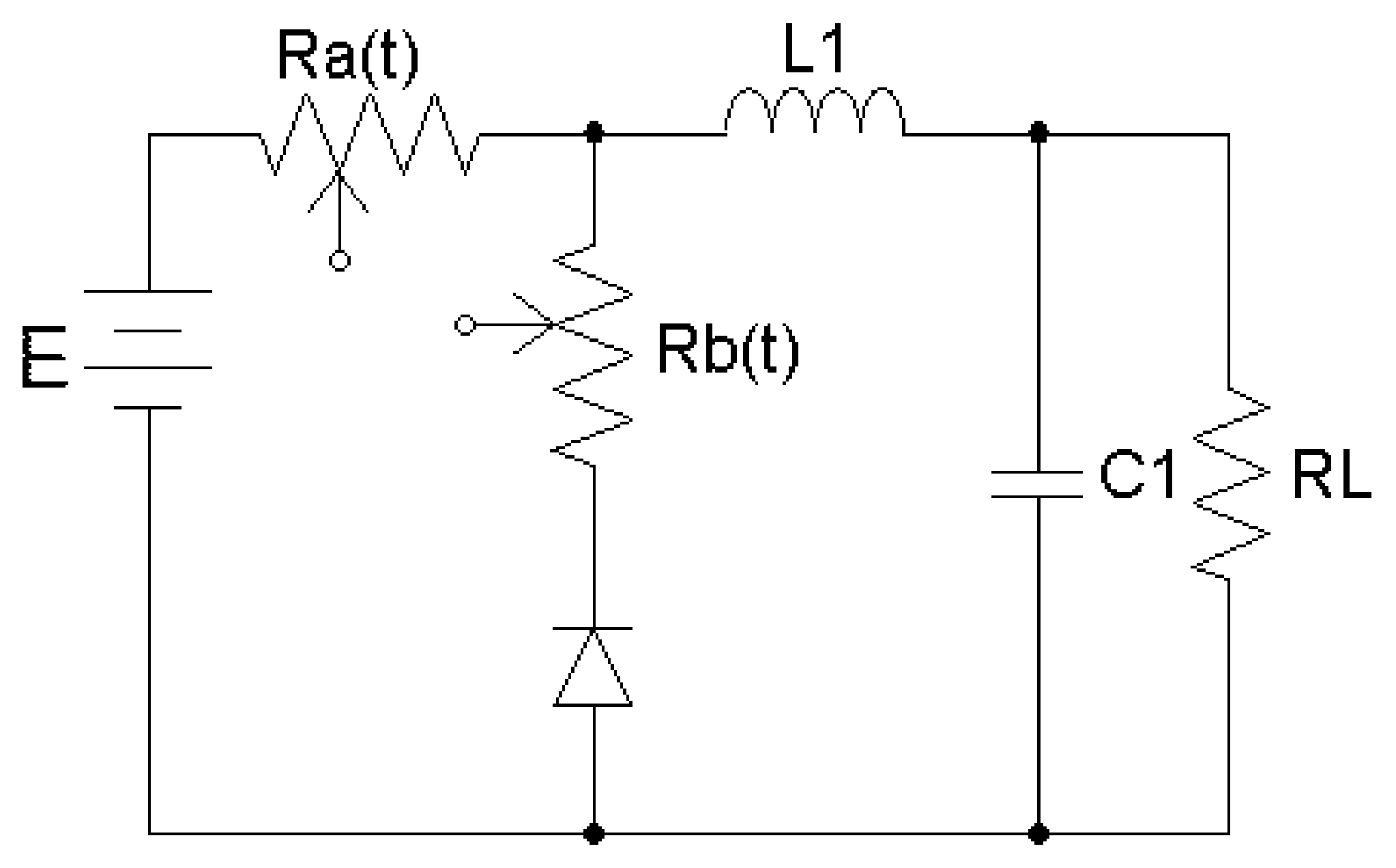
3. Controller Design
3.1. Controller Design for the Mode I (Buck)
3.2. Controller Design for the Mode II (Boost)
3.3. Controller Design for the Mode III (Buck)
3.4. Controller Design for the Mode IV (Buck)
3.5. Controller Design for the Mode V (Cascade Buck)
3.6. Global Stability
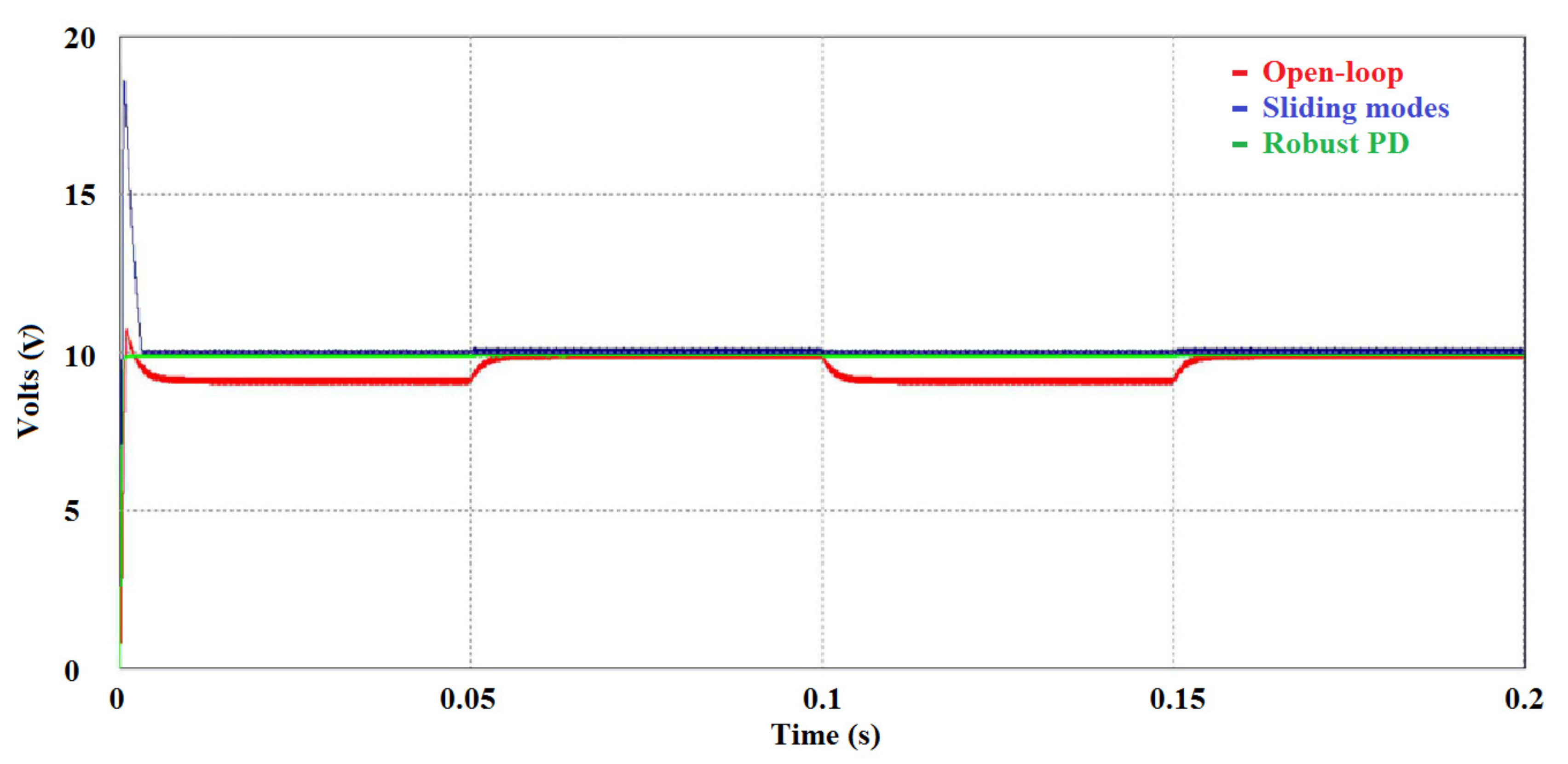
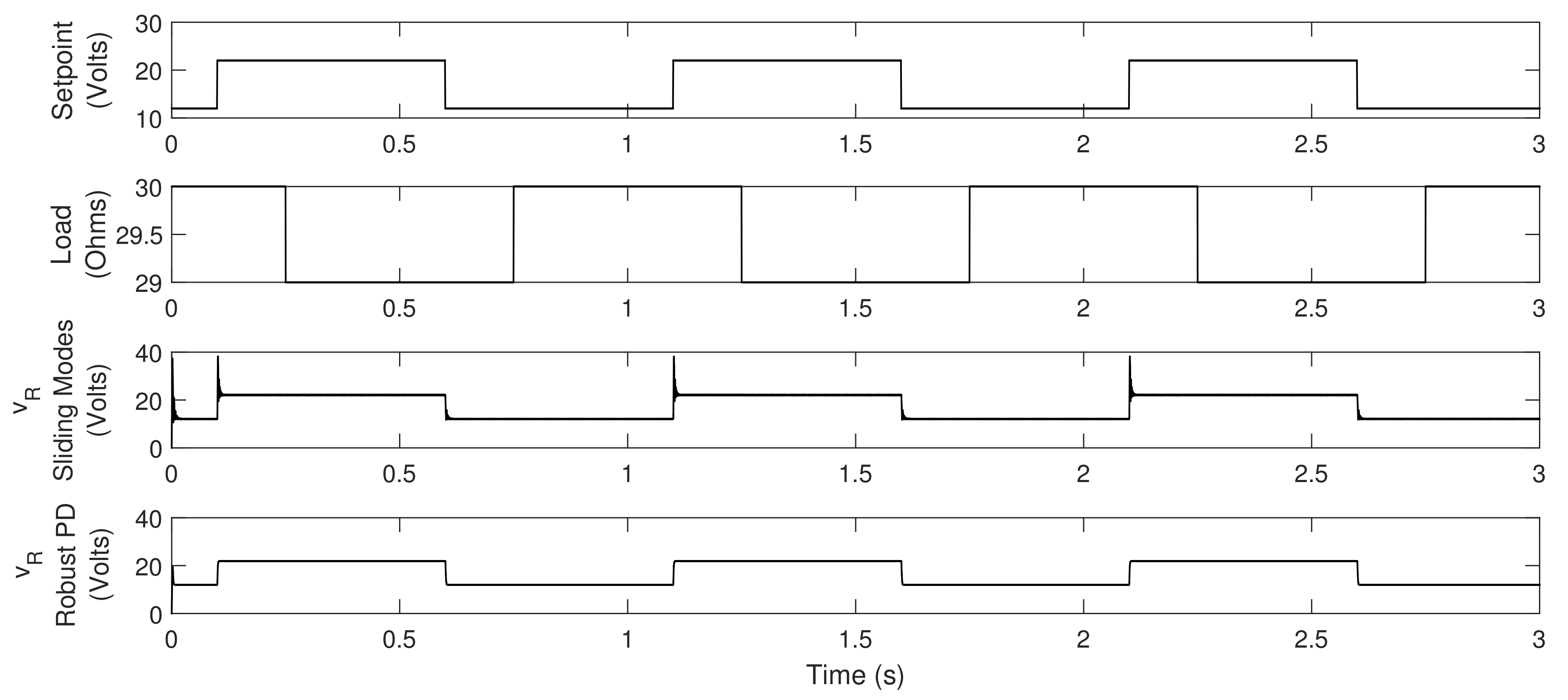
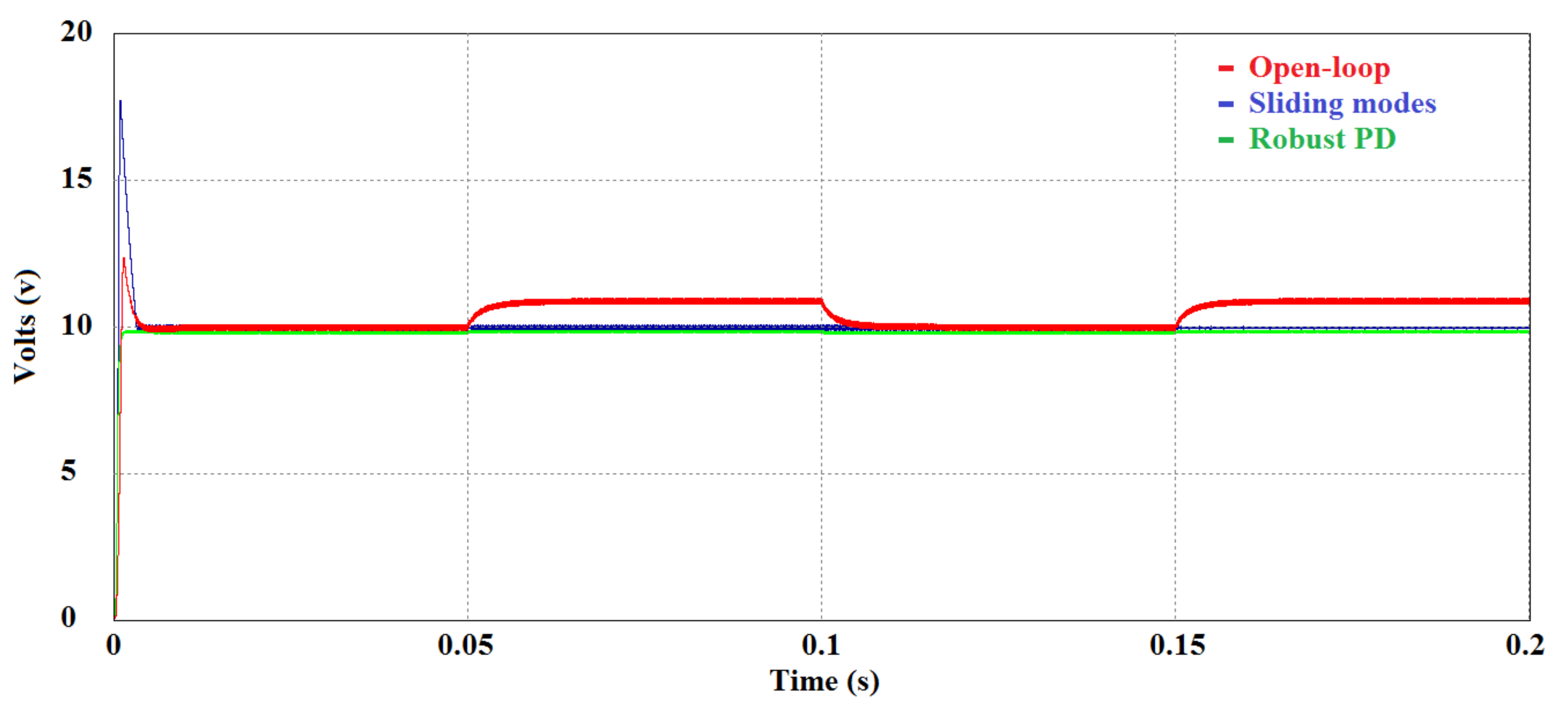
4. Simulations
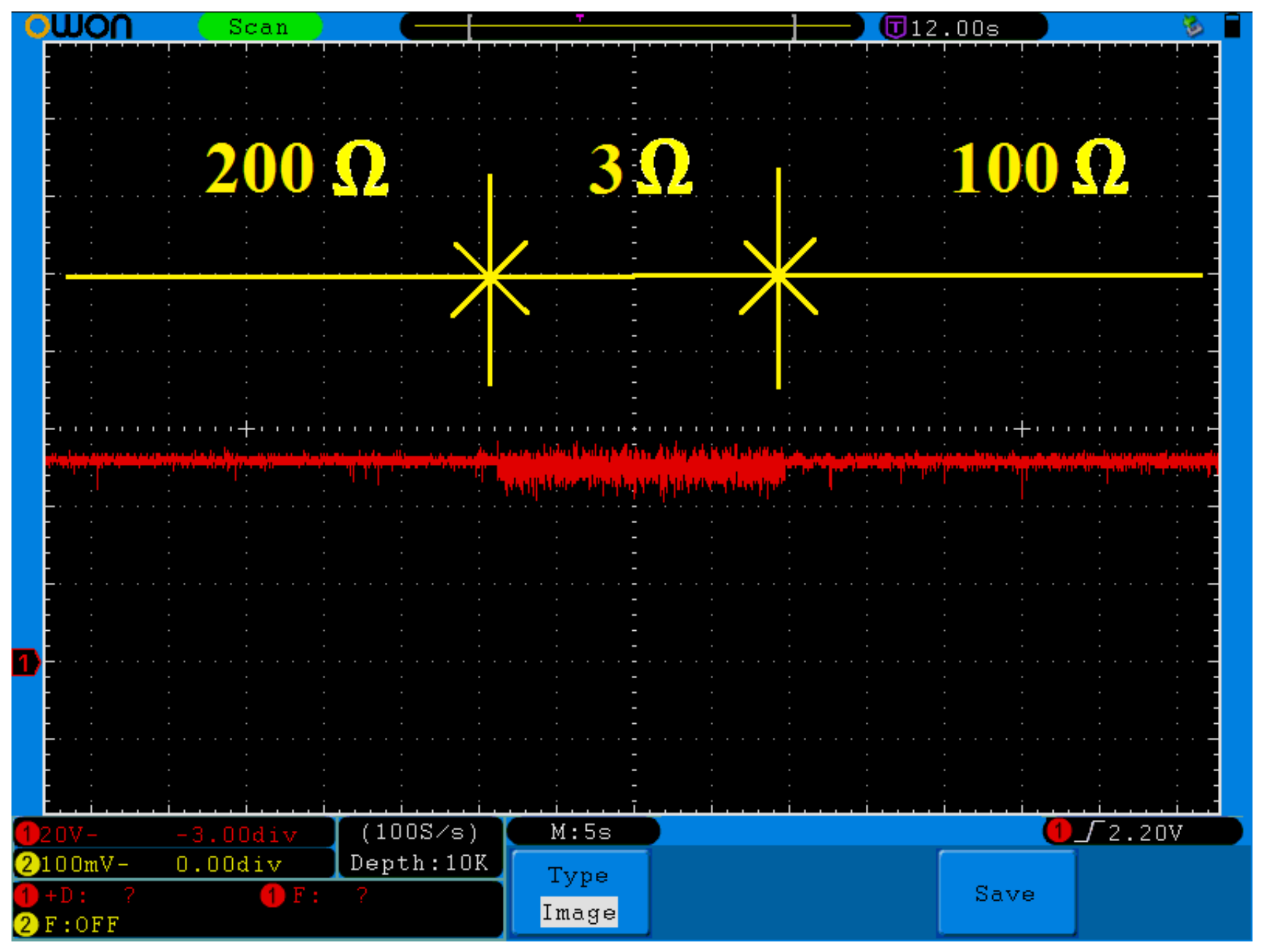
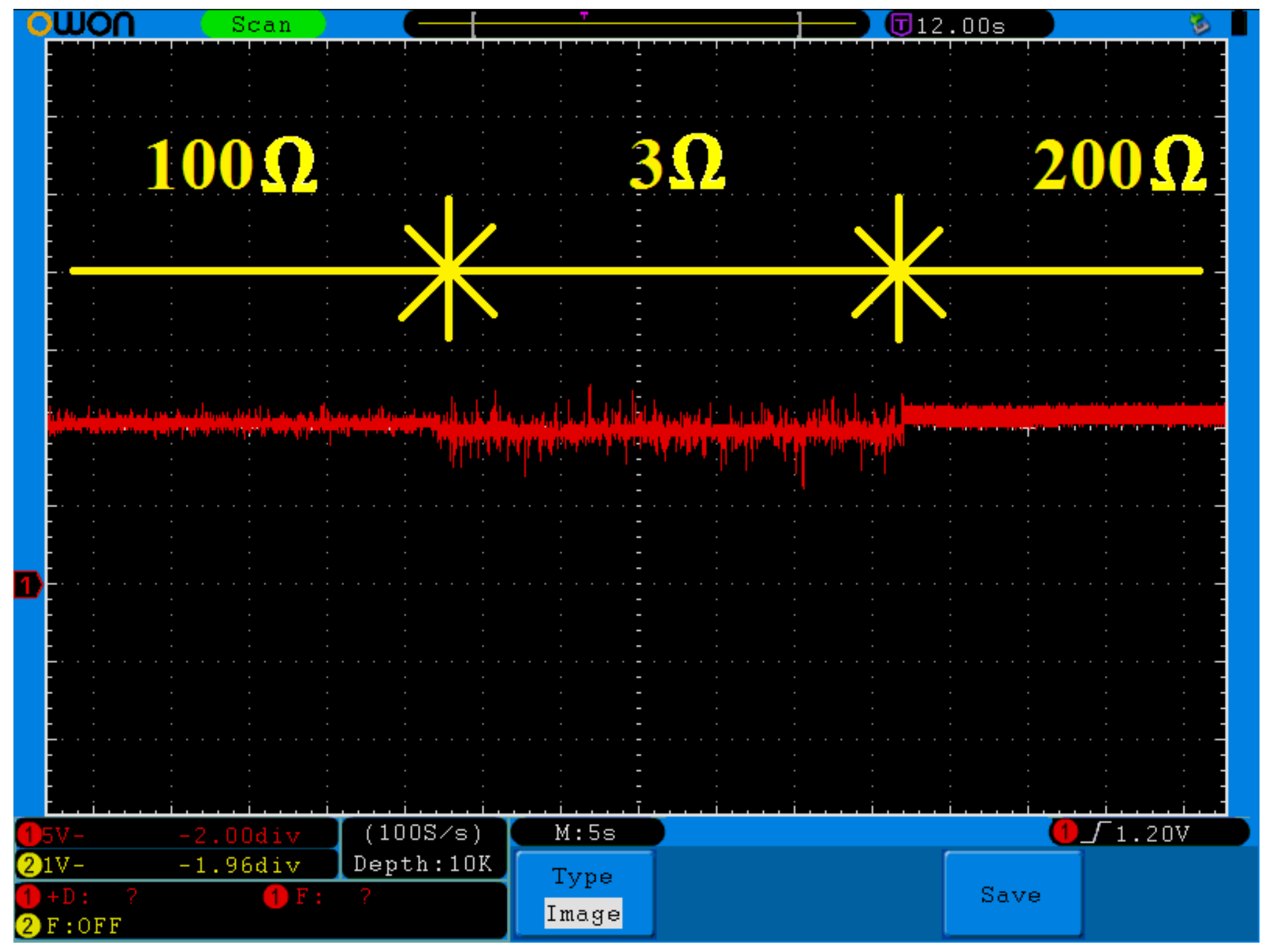
5. Experimental Behavior
6. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| CLF | Common Lyapunov function |
| DC | Direct Current |
| HPS | High-pressure sodium |
| IoT | Internet of things |
| LED | Light Emitting Diode |
| LPV | Linear Parameter Variant |
| PEC | Power electronic converters |
| PSS | Polytopic Switched System |
| RE | Renewable energy |
| RLC | Resistance-Inductor-Capacitor |
| RPEC | Reconfigurable power electronic converters |
| SLPV | Switched linear parameter varying |
| SPC | Switched polytopic controller |
| TE | Transport electrification |
References
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Ang, S.; Oliva, A. Power-Switching Converters; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Lee, S.W.; Do, H.L. Boost Integrated Two-Switch Forward AC-DC LED Driver with High Power Factor and Ripple-Free Output Inductor Current. IEEE Trans. Ind. Electron. 2017, 64, 5789–5796. [Google Scholar] [CrossRef]
- Cheng, H.L.; Cheng, C.A.; Chang, Y.N.; Tsai, K.M. Analysis and implementation of an integrated electronic ballast for high-intensity-discharge lamps featuring high-power factor. IET Power Electron. 2013, 6, 1010–1018. [Google Scholar] [CrossRef]
- Alonso, J.M.; Viña, J.; Vaquero, D.G.; Martínez, G.; Osorio, R. Analysis and design of the integrated double buck–boost converter as a high-power-factor driver for power-LED lamps. IEEE Trans. Ind. Electron. 2012, 59, 1689–1697. [Google Scholar] [CrossRef]
- Dalla Costa, M.A.; Marchesan, T.B.; da Silveira, J.S.; Seidel, Á.R.; do Prado, R.N.; Álvarez, J.M.A. Integrated power topologies to supply HPS lamps: A comparative study. IEEE Trans. Power Electron. 2010, 25, 2124–2132. [Google Scholar] [CrossRef]
- Kim, D.H.; Kim, M.J.; Lee, B.K. An Integrated Battery Charger With High Power Density and Efficiency for Electric Vehicles. IEEE Trans. Power Electron. 2017, 32, 4553–4565. [Google Scholar] [CrossRef]
- Ashique, R.H.; Salam, Z.; Aziz, M.J.B.A.; Bhatti, A.R. Integrated photovoltaic-grid dc fast charging system for electric vehicle: A review of the architecture and control. Renew. Sustain. Energy Rev. 2017, 69, 1243–1257. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Akbari, R.; Tahami, F.; Oraee, H. An Isolated Bidirectional Integrated Plug-in Hybrid Electric Vehicle Battery Charger with Resonant Converters. Electr. Power Compon. Syst. 2016, 44, 1371–1383. [Google Scholar] [CrossRef]
- Dusmez, S.; Khaligh, A. A compact and integrated multifunctional power electronic interface for plug-in electric vehicles. IEEE Trans. Power Electron. 2013, 28, 5690–5701. [Google Scholar] [CrossRef]
- Hegazy, O.; Barrero, R.; Van Mierlo, J.; Lataire, P.; Omar, N.; Coosemans, T. An advanced power electronics interface for electric vehicles applications. IEEE Trans. Power Electron. 2013, 28, 5508–5521. [Google Scholar] [CrossRef]
- Saponara, S.; Tisserand, P.; Chassard, P.; Ton, D.M. Design and Measurement of Integrated Converters for Belt-Driven Starter-Generator in 48 V Micro/Mild Hybrid Vehicles. IEEE Trans. Ind. Appl. 2017, 53, 3936–3949. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. PWM converter integrating switched capacitor converter and series-resonant voltage multiplier as equalizers for photovoltaic modules and series-connected energy storage cells for exploration rovers. IEEE Trans. Power Electron. 2017, 32, 8500–8513. [Google Scholar] [CrossRef]
- Chen, G.; Deng, Y.; Wang, K.; Hu, Y.; Jiang, L.; Wen, H.; He, X. Topology Derivation and Analysis of Integrated Multiple Output Isolated DC-DC Converters with Stacked Configuration for Low-Cost Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 2207–2218. [Google Scholar] [CrossRef]
- Sulligoi, G.; Vicenzutti, A.; Arcidiacono, V.; Khersonsky, Y. Voltage stability in large marine-integrated electrical and electronic power systems. IEEE Trans. Ind. Appl. 2016, 52, 3584–3594. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, C. An Integrated Multifunctional Bidirectional AC/DC and DC/DC Converter for Electric Vehicles Applications. Energies 2016, 9, 493. [Google Scholar] [CrossRef]
- McCoy, T.J. Integrated power systems—An outline of requirements and functionalities for ships. Proc. IEEE 2015, 103, 2276–2284. [Google Scholar] [CrossRef]
- Kim, S.Y.; Choe, S.; Ko, S.; Sul, S.K. A Naval Integrated Power System with a Battery Energy Storage System: Fuel efficiency, reliability, and quality of power. IEEE Electr. Mag. 2015, 3, 22–33. [Google Scholar] [CrossRef]
- Hsieh, C.Y.; Moallem, M.; Golnaraghi, F. A Bidirectional Boost Converter With Application to a Regenerative Suspension System. IEEE Trans. Veh. Technol. 2016, 65, 4301–4311. [Google Scholar] [CrossRef]
- Abebe, R.; Vakil, G.; Calzo, G.L.; Cox, T.; Lambert, S.; Johnson, M.; Gerada, C.; Mecrow, B. Integrated motor drives: State of the art and future trends. IET Electr. Power Appl. 2016, 10, 757–771. [Google Scholar] [CrossRef]
- Sulligoi, G.; Vicenzutti, A.; Menis, R. All-Electric Ship Design: From Electrical Propulsion to Integrated Electrical and Electronic Power Systems. IEEE Trans. Transp. Electr. 2016, 2, 507–521. [Google Scholar] [CrossRef]
- Emadi, A.; Williamson, S.S.; Khaligh, A. Power electronics intensive solutions for advanced electric, hybrid electric, and fuel cell vehicular power systems. IEEE Trans. Power Electron. 2006, 21, 567–577. [Google Scholar] [CrossRef]
- Leuenberger, D.; Biela, J. PV-Module-Integrated AC Inverters (AC Modules) with Subpanel MPP Tracking. IEEE Trans. Power Electron. 2017, 32, 6105–6118. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Blaabjerg, F.; Cecati, C. Power-Electronics-Enabled Autonomous Power Systems. IEEE Trans. Ind. Electron. 2017, 64, 5904–5906. [Google Scholar] [CrossRef]
- Chub, A.; Vinnikov, D.; Kosenko, R.; Liivik, E. Wide Input Voltage Range Photovoltaic Microconverter with Reconfigurable Buck–Boost Switching Stage. IEEE Trans. Ind. Electron. 2017, 64, 5974–5983. [Google Scholar] [CrossRef]
- Chatterjee, A.; Mohanty, K.; Kommukuri, V.S.; Thakre, K. Design and experimental investigation of digital model predictive current controller for single phase grid integrated photovoltaic systems. Renew. Energy 2017, 108, 438–448. [Google Scholar] [CrossRef]
- Li, F.; Liu, H. A Cascaded Coupled Inductor-Reverse High Step-Up Converter Integrating Three-Winding Coupled Inductor and Diode–Capacitor Technique. IEEE Trans. Ind. Inform. 2017, 13, 1121–1130. [Google Scholar] [CrossRef]
- Zhang, N.; Sutanto, D.; Muttaqi, K.M. A review of topologies of three-port DC-DC converters for the integration of renewable energy and energy storage system. Renew. Sustain. Energy Rev. 2016, 56, 388–401. [Google Scholar] [CrossRef]
- Verma, A.K.; Singh, B.; Shahani, D.T.; Jain, C. Grid-interfaced Solar Photovoltaic Smart Building with Bidirectional Power Flow Between Grid and Electric Vehicle with Improved Power Quality. Electr. Power Compon. Syst. 2016, 44, 480–494. [Google Scholar] [CrossRef]
- Maity, S.; Sahu, P.K. Modeling and analysis of a fast and robust module-integrated analog photovoltaic MPP tracker. IEEE Trans. Power Electron. 2016, 31, 280–291. [Google Scholar] [CrossRef]
- Li, Y.R.; Hurley, W.G. Editorial Special Issue on Sustainable Energy Systems Integration. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 854–857. [Google Scholar] [CrossRef]
- Novakovic, B.; Nasiri, A. Modular Multilevel Converter for Wind Energy Storage Applications. IEEE Trans. Ind. Electron. 2017, 64, 8867–8876. [Google Scholar] [CrossRef]
- Li, Y.; Han, Y. A module-integrated distributed battery energy storage and management system. IEEE Trans. Power Electron. 2016, 31, 8260–8270. [Google Scholar] [CrossRef]
- Dusmez, S.; Li, X.; Akin, B. A new multiinput three-level DC/DC converter. IEEE Trans. Power Electron. 2016, 31, 1230–1240. [Google Scholar] [CrossRef]
- Aguilar, C.; Vazquez, A.; Canales, F.; Gordillo, J. Integrated DC-AC Converter as Power Conditioner for Fuel Cell Based System. IEEE Lat. Am. Trans. 2016, 14, 2107–2113. [Google Scholar] [CrossRef]
- Adly, M.; Strunz, K. Irradiance-adaptive PV Module Integrated Converter for High Efficiency and Power Quality in Standalone and DC Microgrid Applications. IEEE Trans. Ind. Electron. 2017, 65, 436–446. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Blaabjerg, F. Single Switch Nonisolated Ultra-Step-Up DC-DC Converter with an Integrated Coupled Inductor for High Boost Applications. IEEE Trans. Power Electron. 2017, 32, 8544–8558. [Google Scholar] [CrossRef]
- Cecati, C.; Khalid, H.A.; Tinari, M.; Adinolfi, G.; Graditi, G. DC nanogrid for renewable sources with modular DC/DC LLC converter building block. IET Power Electron. 2016, 10, 536–544. [Google Scholar] [CrossRef]
- Qin, S.; Barth, C.B.; Pilawa-Podgurski, R.C. Enhancing microinverter energy capture with submodule differential power processing. IEEE Trans. Power Electron. 2016, 31, 3575–3585. [Google Scholar] [CrossRef]
- Strunz, K.; Abbasi, E.; Huu, D.N. DC microgrid for wind and solar power integration. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 115–126. [Google Scholar] [CrossRef]
- Gutierrez, F. Fully-Integrated Converter for Low-Cost and Low-Size Power Supply in Internet-of-Things Applications. Electronics 2017, 6, 38. [Google Scholar] [CrossRef]
- Almer, S.; Fujioka, H.; Jonsson, U.; Kao, C.Y.; Patino, D.; Riedinger, P.; Geyer, T.; Beccuti, A.; Papafotiou, G.; Morari, M.; et al. Hybrid control techniques for switched-mode DC-DC converters Part I: The step-down topology. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 5450–5457. [Google Scholar]
- Orłowska-Kowalska, T.; Blaabjerg, F.; Rodríguez, J. Advanced and Intelligent Control in Power Electronics and Drives; Springer: Berlin/Heidelberg, Germany, 2014; Volume 531. [Google Scholar]
- Vlad, C.; Rodriguez-Ayerbe, P.; Godoy, E.; Lefranc, P. Advanced control laws of DC-DC converters based on piecewise affine modelling. Application to a step-down converter. IET Power Electron. 2014, 7, 1482–1498. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, Z.; Qiao, W. An interconnection and damping assignment passivity-based controller for a DC-DC boost converter with a constant power load. IEEE Trans. Ind. Appl. 2014, 50, 2314–2322. [Google Scholar] [CrossRef]
- Khaligh, A.; Rahimi, A.M.; Emadi, A. Modified pulse-adjustment technique to control DC/DC converters driving variable constant-power loads. IEEE Trans. Ind. Electron. 2008, 55, 1133–1146. [Google Scholar] [CrossRef]
- Cervantes, I.; Perez-Pinal, F.J.; Mendoza-Torres, A. Hybrid Control of DC-DC power converters. In Renewable Energy; InTech: Chattanooga, TN, USA, 2009. [Google Scholar]
- Johansen, T.A.; De Molengraft, R.; Nijmeijer, H. Switched, piecewise and polytopic linear systems. Int. J. Control 2002, 75, 1241–1242. [Google Scholar] [CrossRef]
- Bengea, S.; DeCarlo, R.; Corless, M.; Rizzoni, G.; Yurkovich, S. A Polytopic System Approach for Gain Scheduled Control of a Diesel Engine. IFAC Proc. Vol. 2002, 35, 349–354. [Google Scholar] [CrossRef]
- Andrade-Da Silva, J.M.; Edwards, C.; Spurgeon, S.K. Sliding-mode output-feedback control based on LMIs for plants with mismatched uncertainties. IEEE Trans. Ind. Electron. 2009, 56, 3675–3683. [Google Scholar] [CrossRef]
- Donkers, M.; Heemels, W.; Van de Wouw, N.; Hetel, L. Stability analysis of networked control systems using a switched linear systems approach. IEEE Trans. Autom. Control 2011, 56, 2101–2115. [Google Scholar] [CrossRef]
- Huang, Y.; Changyin, Q.; Chengshan, Z.; Jingmei, W. Polytopic LPV modeling and gain-scheduled switching control for a flexible air-breathing hypersonic vehicle. J. Syst. Eng. Electron. 2013, 2, 118–127. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Dong, C. Asynchronous H infinite control for unmanned aerial vehicles: Switched polytopic system approach. IEEE/CAA J. Autom. Sin. 2015, 2, 207–216. [Google Scholar]
- Yang, T.; Li, A.; Niu, E. Robust dynamic output feedback control for switched polytopic systems under asynchronous switching. Chin. J. Aeronaut. 2015, 28, 1226–1235. [Google Scholar] [CrossRef]
- Dong, C.; Ma, A.; Wang, Q.; Wang, Z. Robust fault-tolerant tracking control for nonlinear networked control system: Asynchronous switched polytopic approach. Math. Probl. Eng. 2015, 2015, 903058. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Karimi, H.R.; Jasra, A. Robust finite-time control of switched linear systems and application to a class of servomechanism systems. IEEE/ASME Trans. Mechatron. 2015, 20, 2476–2485. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, J.; Li, C. Robust finite-time stability and stabilisation for switched linear parameter-varying systems and its application to bank-to-turn missiles. IET Control Theory Appl. 2015, 9, 2171–2179. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, K.; Pang, G.; Wei, H. Robust stabilisation for constrained discrete-time switched positive linear systems with uncertainties. IET Control Theory Appl. 2015, 9, 2598–2605. [Google Scholar] [CrossRef]
- Glover, S.F. Modeling and Stability Analysis of a Power Electronics Based Systems. Ph.D. Thesis, Department of Electrical Engineering, Purdue University, Lafayette, IN, USA, 2003. [Google Scholar]
- Arnedo, L.; Boroyevich, D.; Burgos, R.; Wang, F. Polytopic black-box modeling of DC-DC converters. In Proceedings of the Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1015–1021. [Google Scholar]
- Francés, A.; Asensi, R.; García, O.; Uceda, J. A blackbox large signal Lyapunov-based stability analysis method for power converter-based systems. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Francés, A.; Asensi, R.; García, O.; Prieto, R.; Uceda, J. A black-box modeling approach for DC nanogrids. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1624–1631. [Google Scholar]
- Francés, A.; Asensi, R.; García, O.; Prieto, R.; Uceda, J. The performance of polytopic models in smart DC microgrids. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–8. [Google Scholar]
- Aguilar-Najar, R.; Perez-Pinal, F.J.; Herrera-Ramirez, C.; Barranco-Gutiérrez, A. Novel positive integrated converter. In Proceedings of the 2016 13th International Conference on Power Electronics (CIEP), Guanajuato, Mexico, 20–23 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 41–46. [Google Scholar]
- Sira-Ramírez, H.; Silva-Ortigoza, R. Control Design Techniques in Power Electronics Devices; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Nehrir, M.H.; Wang, C. Modeling and Control of Fuel Cells: Distributed Generation Applications; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 41. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Khalil, H.K. Noninear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Licea, M.R.; Cervantes, I. Robust indirect-defined envelope control for rollover and lateral skid prevention. Control Eng. Pract. 2017, 61, 149–162. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Licea, M.-A.; Perez-Pinal, F.-J.; Barranco-Gutiérrez, A.-I.; Nuñez-Perez, J.-C. Switched Polytopic Controller Applied on a Positive Reconfigurable Power Electronic Converter. Energies 2018, 11, 116. https://doi.org/10.3390/en11010116
Rodríguez-Licea M-A, Perez-Pinal F-J, Barranco-Gutiérrez A-I, Nuñez-Perez J-C. Switched Polytopic Controller Applied on a Positive Reconfigurable Power Electronic Converter. Energies. 2018; 11(1):116. https://doi.org/10.3390/en11010116
Chicago/Turabian StyleRodríguez-Licea, Martín-A., Francisco-J. Perez-Pinal, Alejandro-I. Barranco-Gutiérrez, and Jose-C. Nuñez-Perez. 2018. "Switched Polytopic Controller Applied on a Positive Reconfigurable Power Electronic Converter" Energies 11, no. 1: 116. https://doi.org/10.3390/en11010116
APA StyleRodríguez-Licea, M.-A., Perez-Pinal, F.-J., Barranco-Gutiérrez, A.-I., & Nuñez-Perez, J.-C. (2018). Switched Polytopic Controller Applied on a Positive Reconfigurable Power Electronic Converter. Energies, 11(1), 116. https://doi.org/10.3390/en11010116







