Thermal Impact Assessment of Groundwater Heat Pumps (GWHPs): Rigorous vs. Simplified Models
Abstract
:1. Introduction
2. Methods
2.1. Flow and Heat-Transport in Porous Media
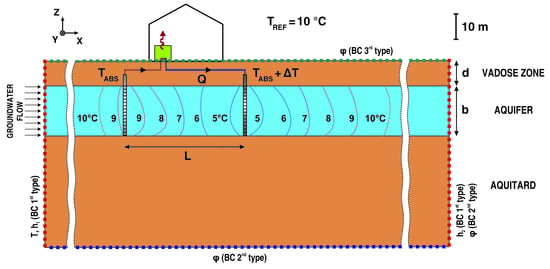
2.2. Model Setup
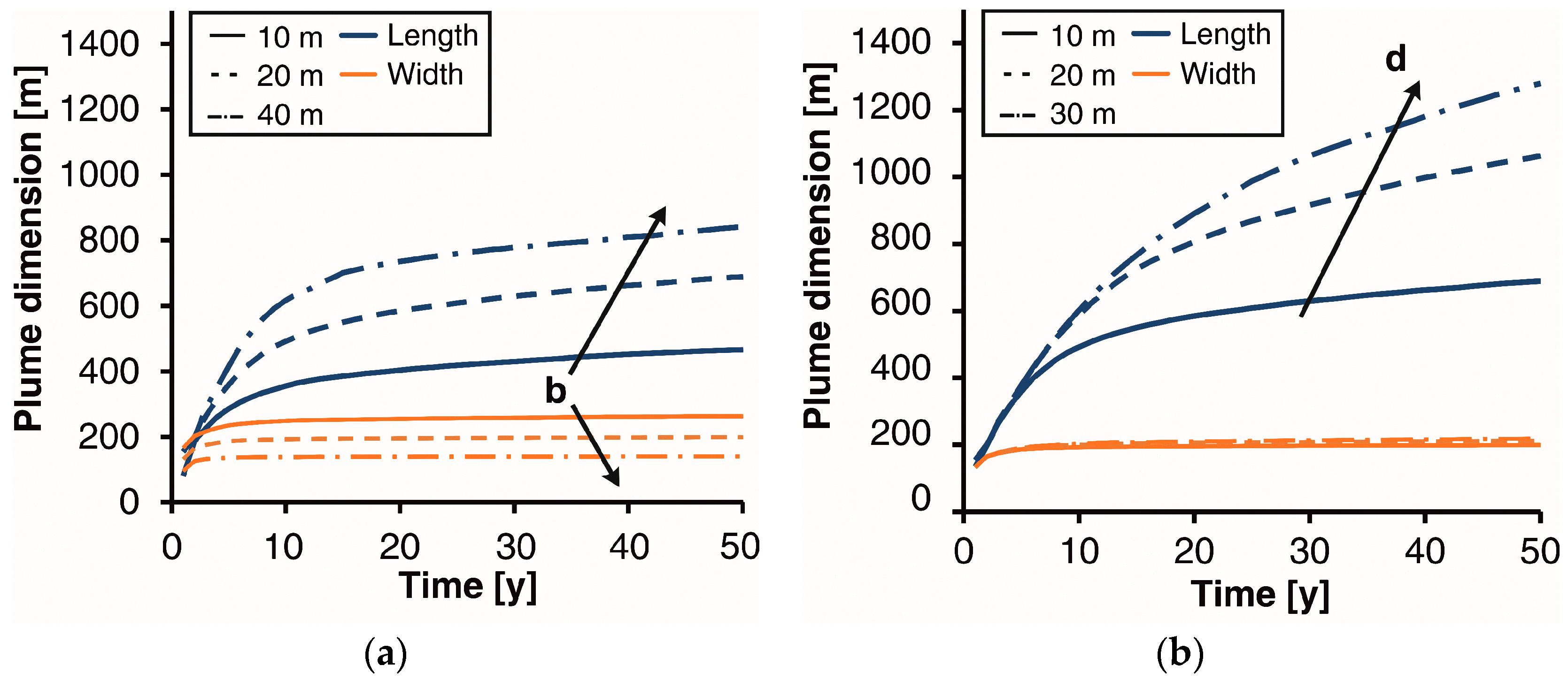
3. Results and Discussion
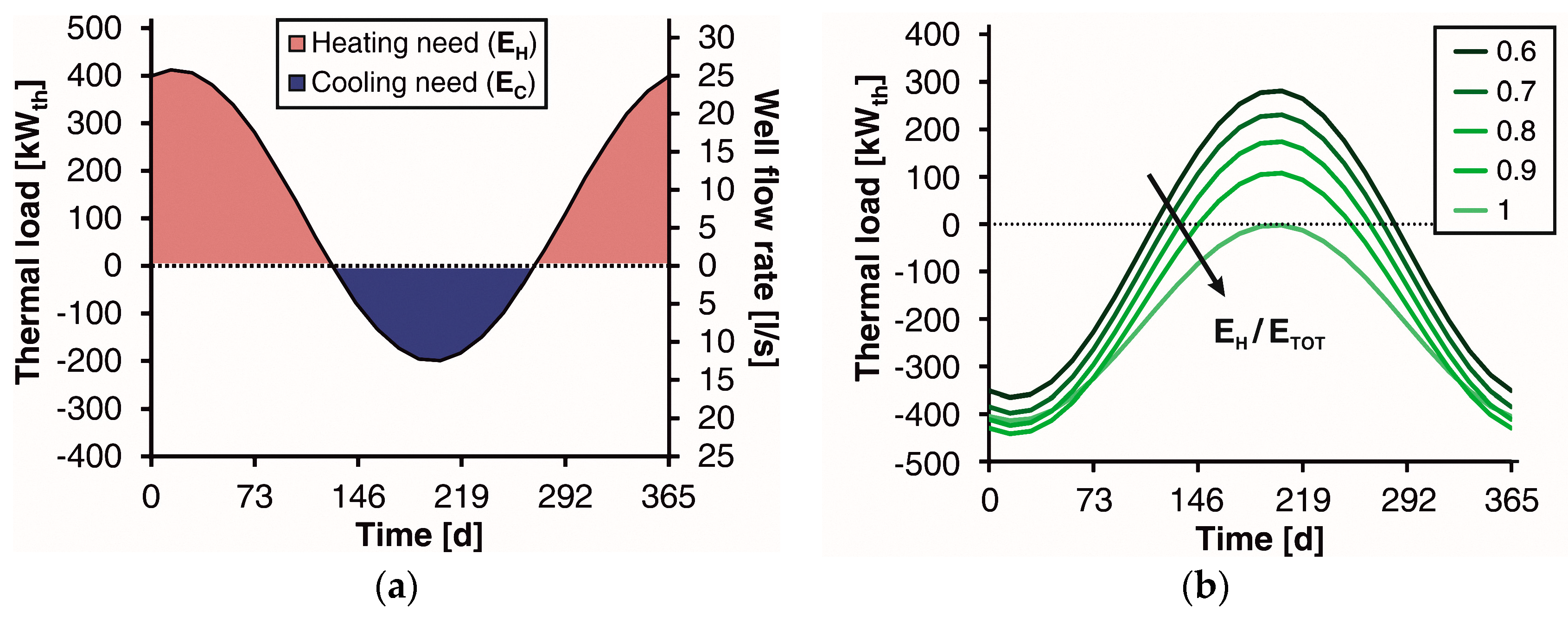
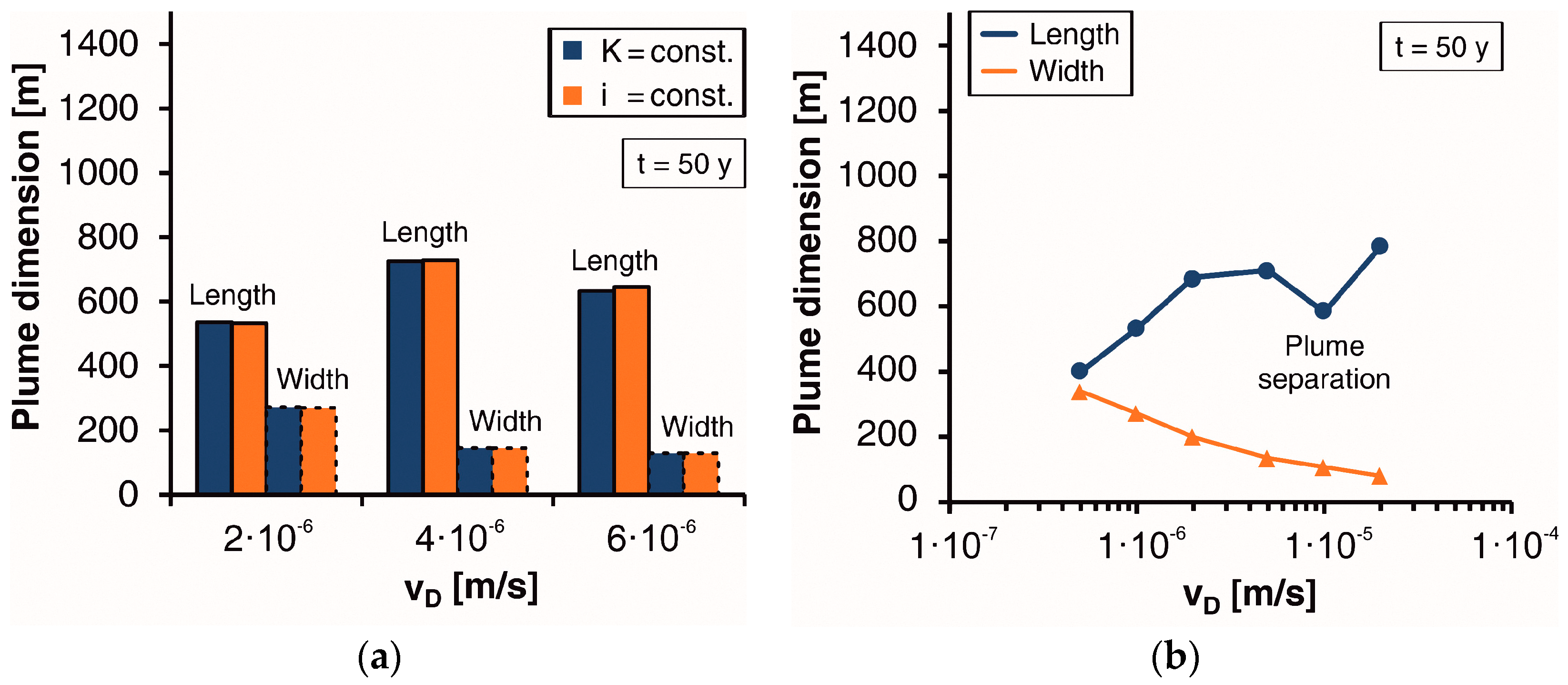
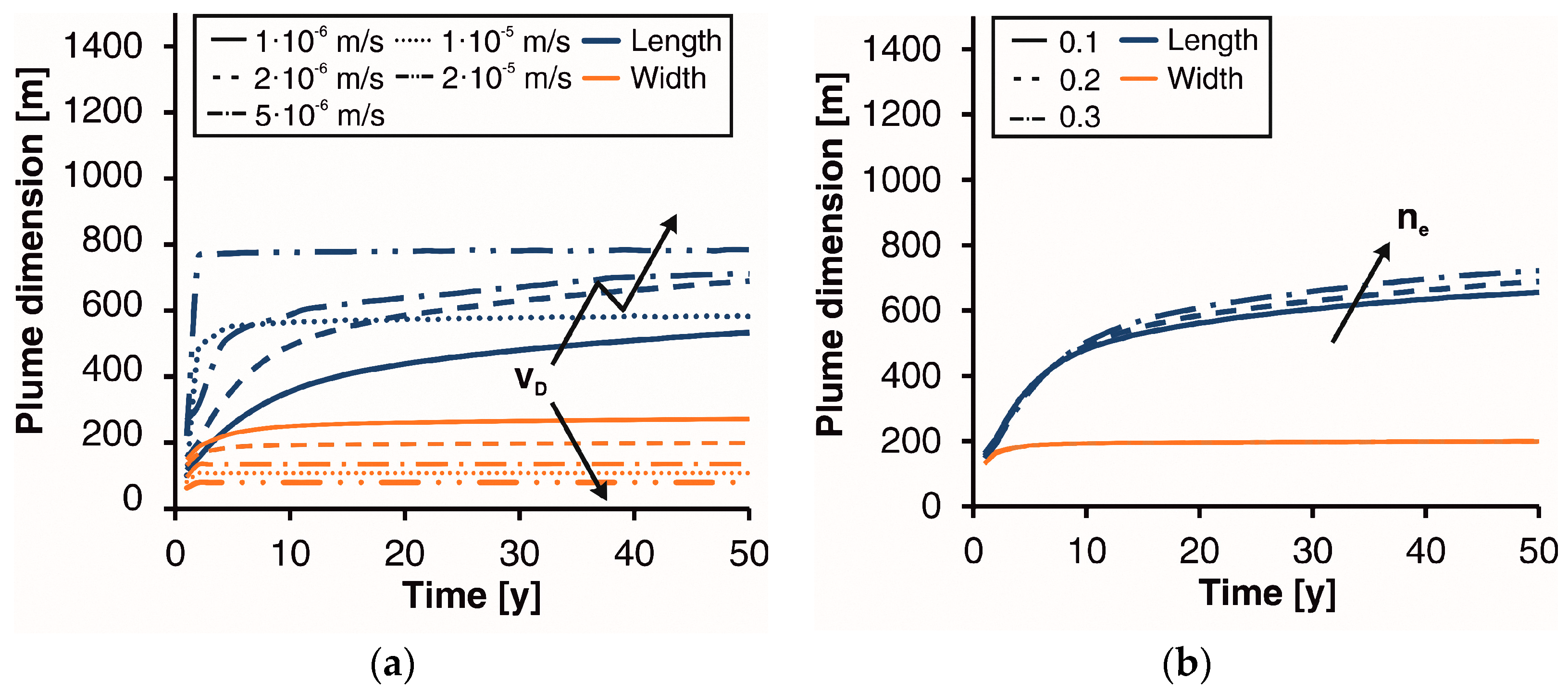
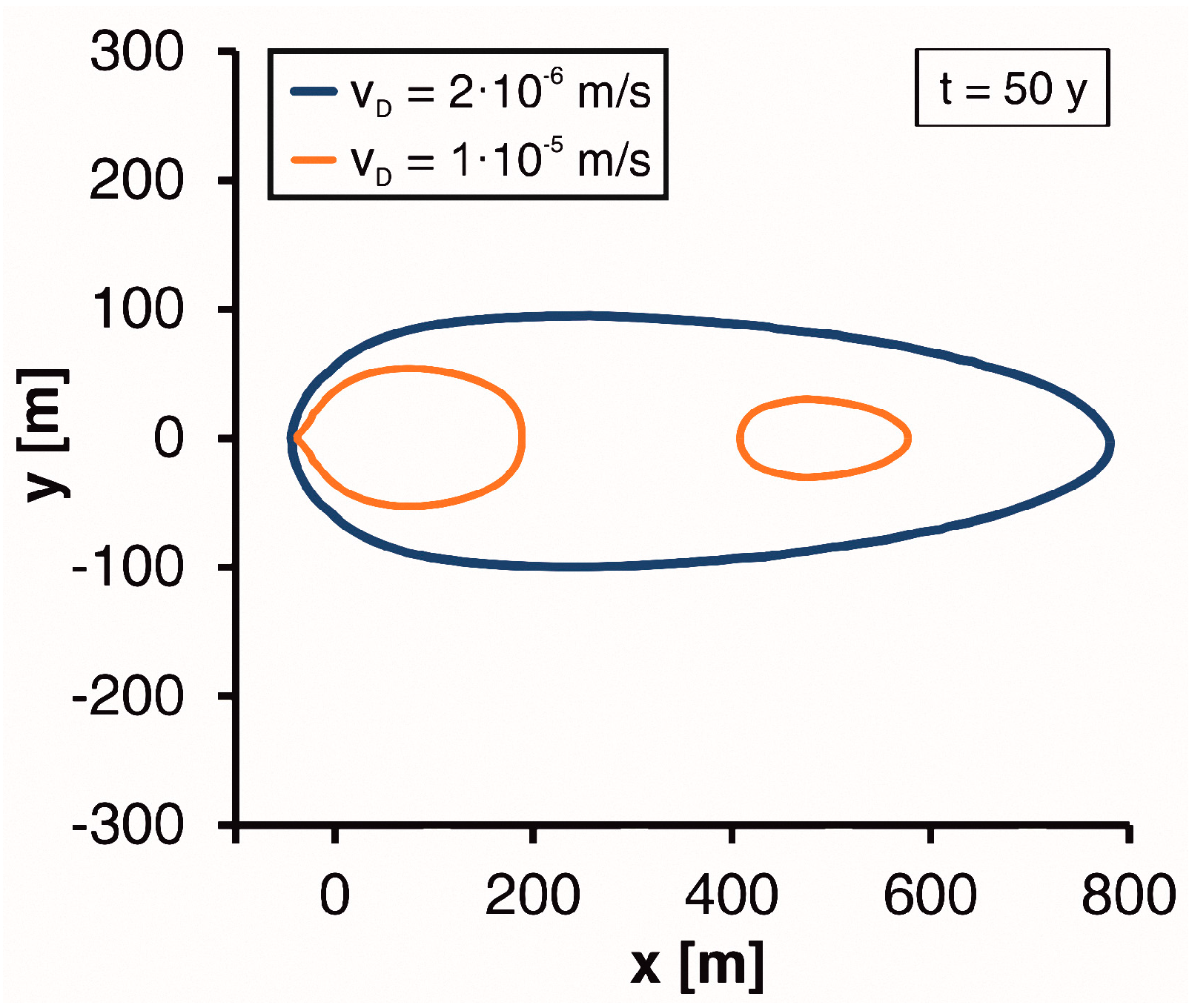
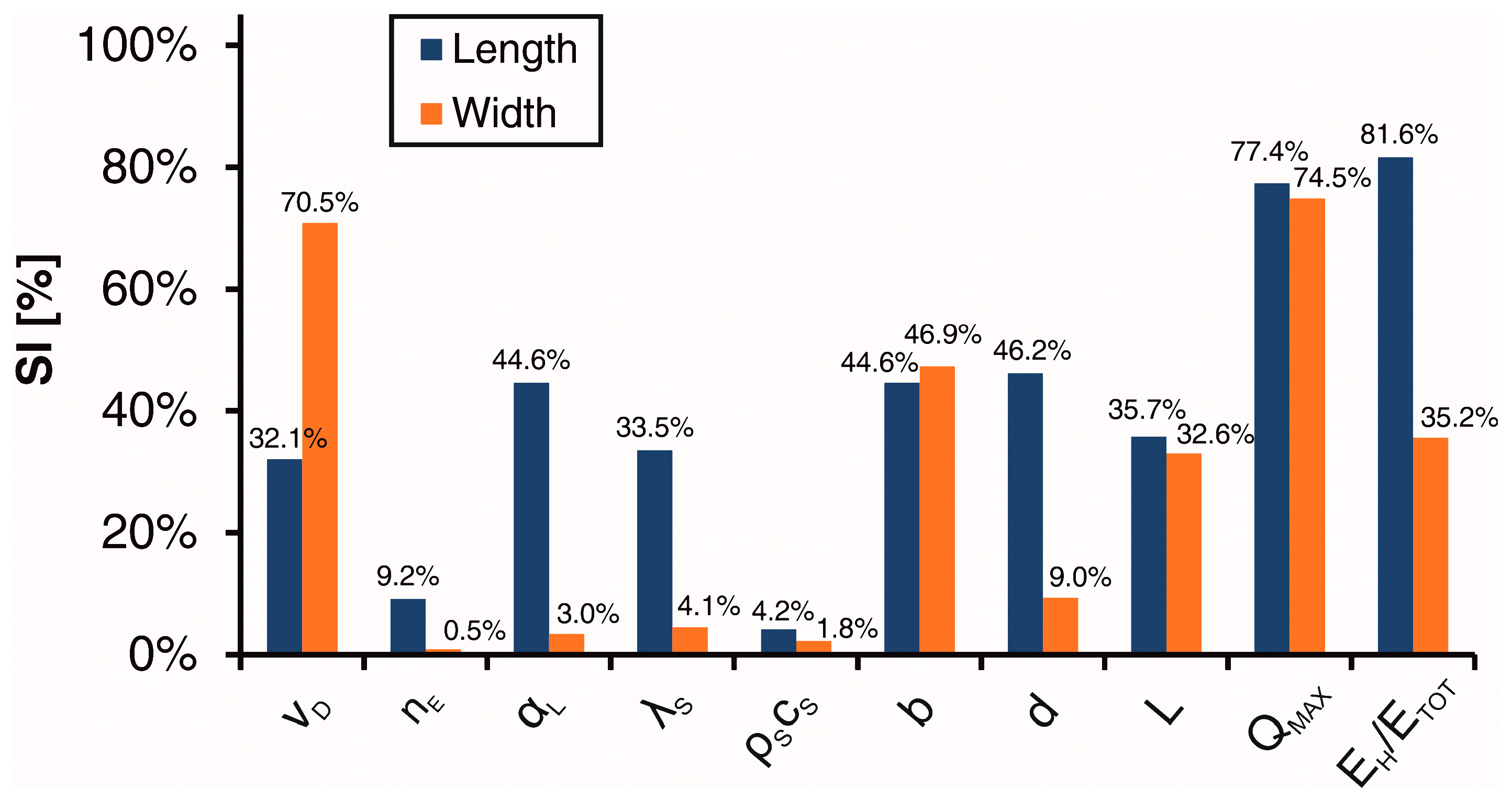
3.1. Sensitivity Analysis
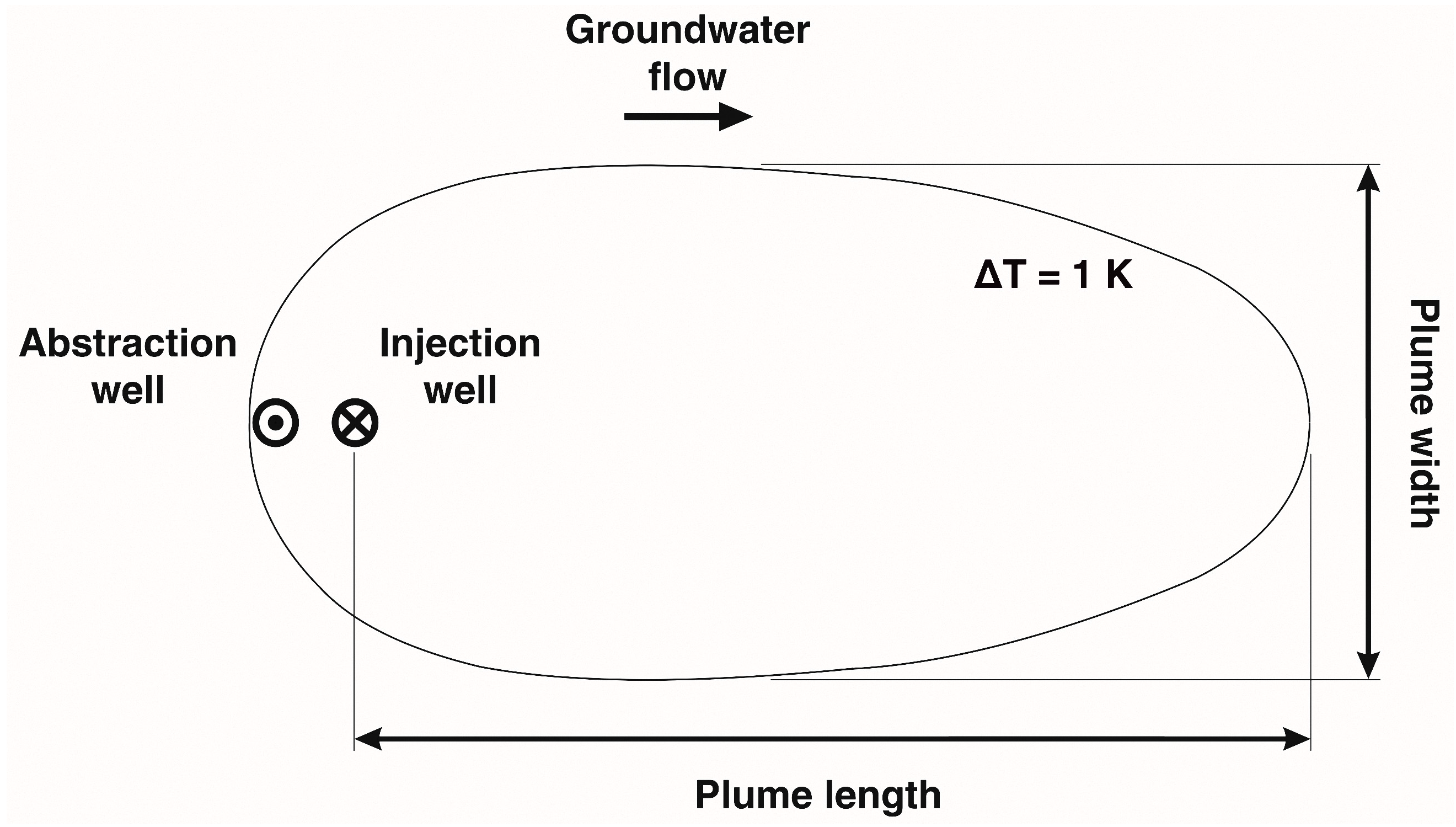
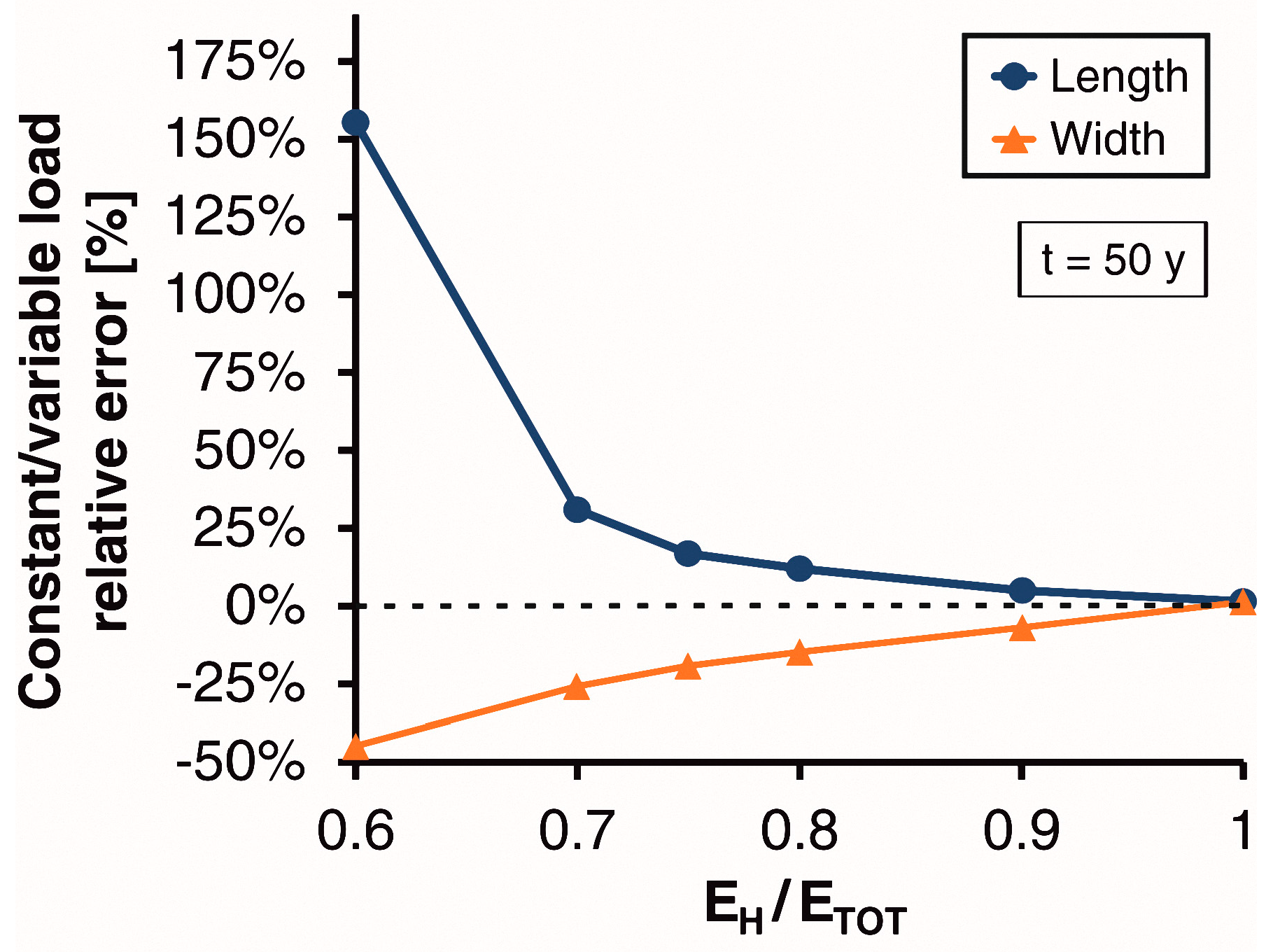
3.2. Comparison with Simplified Models
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Glossary
| Acronyms | |
| ASHP | Air Source Heat pump |
| ATES | Aquifer Thermal Energy Storage |
| BC | Boundary condition |
| COP | Coefficient of Performance |
| GED | Groundwater Energy Designer |
| GSHP | Ground Source Heat Pump |
| GWHP | Groundwater Heat Pump |
| SI | Sensitivity Index |
| Latin Letters | |
| b | saturated thickness of the aquifer (m) |
| , , | thermal dispersion coefficient, respectively in the , , direction (m2/s) |
| d | thickness of the vadose zone—water table depth (m) |
| , | annual heat exchanged with the aquifer for heating and cooling, respectively (MWh·y−1) |
| total annual heat exchanged with the aquifer (MWh·y−1) | |
| H | heat source/sink (W·m−3) |
| h | hydraulic head (m) |
| i | hydraulic gradient (dimensionless) |
| , , | hydraulic conductivity of the aquifer, respectively in the , , direction (m·s−1) |
| L | well spacing (m) |
| effective porosity (dimensionless) | |
| P | thermal power exchanged with the ground—negative for extraction, positive for injection (W) |
| Q | abstracted/injected water flow rate (m3·s−1) |
| max. annual abstracted/injected water flow rate (m3·s−1) | |
| fraction of max. annual abstracted/injected water flow rate traveling down-gradient (m3·s−1) | |
| thermal retardation factor (dimensionless) | |
| T | temperature (K) |
| temperature of water at the abstraction well (K) | |
| temperature of water at the injection well (K) | |
| t | time (s) |
| Darcy velocity of groundwater flow (m·s−1) | |
| effective velocity of groundwater (m·s−1) | |
| thermal velocity (m·s−1) | |
| X | thermal short-circuit parameter (dimensionless) |
| , | maximum and minimum value, respectively, of the output variable considered in the sensitivity analysis |
| Greek Letters | |
| longitudinal thermal dispersivity (m) | |
| transverse thermal dispersivity (m) | |
| thermal conductivity of the porous medium (W·m−1·K−1) | |
| thermal conductivity of the solid phase (W·m−1·K−1) | |
| thermal conductivity of water (W·m−1·K−1) | |
| thermal capacity of the porous medium (J·kg−1·K−1) | |
| thermal capacity of the solid phase (J·kg−1·K−1) | |
| thermal capacity of water (J·kg−1·K−1) | |
References
- Ouzzane, M.; Eslami-Nejad, P.; Badache, M.; Aidoun, Z. New correlations for the prediction of the undisturbed ground temperature. Geothermics 2015, 53, 379–384. [Google Scholar] [CrossRef]
- Omer, A.M. Ground-source heat pumps systems and applications. Renew. Sustain. Energy Rev. 2008, 12, 344–371. [Google Scholar] [CrossRef]
- Bayer, P.; Saner, D.; Bolay, S.; Rybach, L.; Blum, P. Greenhouse gas emission savings of ground source heat pump systems in Europe: A review. Renew. Sustain. Energy Rev. 2012, 16, 1256–1267. [Google Scholar] [CrossRef]
- Chung, J.T.; Choi, J.M. Design and performance study of the ground-coupled heat pump system with an operating parameter. Renew. Energy 2012, 42, 118–124. [Google Scholar] [CrossRef]
- Dehkordi, S.E.; Schincariol, R. Effect of thermal-hydrogeological and borehole heat exchanger properties on performance and impact of vertical closed-loop geothermal heat pump systems. Hydrogeol. J. 2014, 22, 189–203. [Google Scholar] [CrossRef]
- Casasso, A.; Sethi, R. G.POT: A quantitative method for the assessment and mapping of the shallow geothermal potential. Energy 2016, 106, 765–773. [Google Scholar] [CrossRef]
- Casasso, A.; Sethi, R. Sensitivity Analysis on the Performance of a Ground Source Heat Pump Equipped with a Double U-pipe Borehole Heat Exchanger. Energy Procedia 2014, 59, 301–308. [Google Scholar] [CrossRef]
- Casasso, A.; Sethi, R. Territorial Analysis for the Implementation of Geothermal Heat Pumps in the Province of Cuneo (NW Italy). Energy Procedia 2015, 78, 1159–1164. [Google Scholar] [CrossRef]
- Casasso, A.; Sethi, R. Modelling thermal recycling occurring in groundwater heat pumps (GWHPs). Renew. Energy 2015, 77, 86–93. [Google Scholar] [CrossRef]
- Galgaro, A.; Cultrera, M. Thermal short circuit on groundwater heat pump. Appl. Therm. Eng. 2013, 57, 107–115. [Google Scholar] [CrossRef]
- Stauffer, F.; Bayer, P.; Blum, P.; Molina-Giraldo, N.; Kinzelbach, W. Thermal Use of Shallow Groundwater; CRC Press—Taylor and Francis Group: Boca Raton, FL, USA, 2013; p. 250. [Google Scholar]
- Di Molfetta, A.; Sethi, R. Ingegneria Degli Acquiferi; Springer: Berlin, Germany, 2012; p. 370. [Google Scholar]
- Ampofo, F.; Maidment, G.G.; Missenden, J.F. Review of groundwater cooling systems in London. Appl. Therm. Eng. 2006, 26, 2055–2062. [Google Scholar] [CrossRef]
- Beretta, G.P.; Coppola, G.; Pona, L.D. Solute and heat transport in groundwater similarity: Model application of a high capacity open-loop heat pump. Geothermics 2014, 51, 63–70. [Google Scholar] [CrossRef]
- De Santoli, L.; Mancini, F.; Rossetti, S. The energy sustainability of Palazzo Italia at EXPO 2015: Analysis of an nZEB building. Energy Build. 2014, 82, 534–539. [Google Scholar] [CrossRef]
- Piemonte, C.; Porro, A. Palazzo Lombardia—Geothermal Heat Pump Capacity World Record for a Single Building Conditioning. In Proceedings of the European Geothermal Conference, Pisa, Italy, 3–7 June 2013; pp. 1–4. [Google Scholar]
- Bouwer, H. Artificial recharge of groundwater: Hydrogeology and engineering. Hydrogeol. J. 2002, 10, 121–142. [Google Scholar] [CrossRef]
- Banks, D. Thermogeological assessment of open-loop well-doublet schemes: A review and synthesis of analytical approaches. Hydrogeol. J. 2009, 17, 1149–1155. [Google Scholar] [CrossRef]
- Banks, D. An Introduction to Thermogeology: Ground Source Heating and Cooling; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 526. [Google Scholar]
- Gringarten, A.C.; Sauty, J.P. A theoretical study of heat extraction from aquifers with uniform regional flow. J. Geophys. Res. 1975, 80, 4956–4962. [Google Scholar] [CrossRef]
- Lippmann, M.J.; Tsang, C.F. Ground-Water Use for Cooling: Associated Aquifer Temperature Changes. Ground Water 1980, 18, 452–458. [Google Scholar] [CrossRef]
- Banks, D. The application of analytical solutions to the thermal plume from a well doublet ground source heating or cooling scheme. Q. J. Eng. Geol. Hydrogeol. 2011, 44, 191–197. [Google Scholar] [CrossRef]
- Shan, C. An analytical solution for the capture zone of two arbitrarily located wells. J. Hydrol. 1999, 222, 123–128. [Google Scholar] [CrossRef]
- Luo, J.; Kitanidis, P.K. Fluid residence times within a recirculation zone created by an extraction–injection well pair. J. Hydrol. 2004, 295, 149–162. [Google Scholar] [CrossRef]
- Milnes, E.; Perrochet, P. Assessing the impact of thermal feedback and recycling in open-loop groundwater heat pump (GWHP) systems: A complementary design tool. Hydrogeol. J. 2013, 21, 505–514. [Google Scholar] [CrossRef]
- Bridger, D.W.; Allen, D.M. Heat transport simulations in a heterogeneous aquifer used for aquifer thermal energy storage (ATES). Can. Geotech. J. 2010, 47, 96–115. [Google Scholar] [CrossRef]
- Bridger, D.W.; Allen, D.M. Influence of geologic layering on heat transport and storage in an aquifer thermal energy storage system. Hydrogeol. J. 2014, 22, 233–250. [Google Scholar] [CrossRef]
- Nam, Y.; Ooka, R. Numerical simulation of ground heat and water transfer for groundwater heat pump system based on real-scale experiment. Energy Build. 2010, 42, 69–75. [Google Scholar] [CrossRef]
- Ferguson, G.; Woodbury, A.D. Observed thermal pollution and post-development simulations of low-temperature geothermal systems in Winnipeg, Canada. Hydrogeol. J. 2006, 14, 1206–1215. [Google Scholar] [CrossRef]
- Fry, V.A. Lessons from London: Regulation of open-loop ground source heat pumps in central London. Q. J. Eng. Geol. Hydrogeol. 2009, 42, 325–334. [Google Scholar] [CrossRef]
- García-Gil, A.; Vázquez-Suñe, E.; Schneider, E.G.; Sánchez-Navarro, J.Á.; Mateo-Lázaro, J. The thermal consequences of river-level variations in an urban groundwater body highly affected by groundwater heat pumps. Sci. Total Environ. 2014, 485–486, 575–587. [Google Scholar]
- Lo Russo, S.; Gnavi, L.; Roccia, E.; Taddia, G.; Verda, V. Groundwater Heat Pump (GWHP) system modeling and Thermal Affected Zone (TAZ) prediction reliability: Influence of temporal variations in flow discharge and injection temperature. Geothermics 2014, 51, 103–112. [Google Scholar] [CrossRef]
- Poppei, J.; Mayer, G.; Schwarz, R. Groundwater Energy Designer (GED)—Computergestütztes Auslegungstool zur Wärme und Kältenutzung von Grundwasser [Computer Assisted Design Tool for the Use of Heat and Cold from Groundwater]; Bundesamt für Energie BFE: Ittigen, Switzerland, 2006; pp. 1–71. [Google Scholar]
- Diersch, H.J.G. FEFLOW. Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer: Berlin/Heidelberg, Germany, 2014; p. 996. [Google Scholar]
- Epting, J.; Huggenberger, P. Unraveling the heat island effect observed in urban groundwater bodies—Definition of a potential natural state. J. Hydrol. 2013, 501, 193–204. [Google Scholar] [CrossRef]
- Kim, K.Y.; Chon, C.M.; Park, K.H.; Park, Y.S.; Woo, N.C. Multi-depth monitoring of electrical conductivity and temperature of groundwater at a multilayered coastal aquifer: Jeju Island, Korea. Hydrol. Process. 2008, 22, 3724–3733. [Google Scholar] [CrossRef]
- Lee, J.-Y. Characteristics of ground and groundwater temperatures in a metropolitan city, Korea: Considerations for geothermal heat pumps. Geosci. J. 2006, 10, 165–175. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Hahn, J.-S. Characterization of groundwater temperature obtained from the Korean national groundwater monitoring stations: Implications for heat pumps. J. Hydrol. 2006, 329, 514–526. [Google Scholar] [CrossRef]
- Bense, V.; Kooi, H. Temporal and spatial variations of shallow subsurface temperature as a record of lateral variations in groundwater flow. J. Geophys. Res. Solid Earth 2004, 109, B4. [Google Scholar] [CrossRef]
- Heiselberg, P.; Brohus, H.; Hesselholt, A.; Rasmussen, H.; Seinre, E.; Thomas, S. Application of sensitivity analysis in design of sustainable buildings. Renew. Energy 2009, 34, 2030–2036. [Google Scholar] [CrossRef]
- De Marsily, G. Quantitative Hydrogeology; Academic Press: San Diego, CA, USA, 1986; p. 464. [Google Scholar]
- Schulze-Makuch, D. Longitudinal dispersivity data and implications for scaling behavior. Ground Water 2005, 43, 443–456. [Google Scholar] [CrossRef] [PubMed]
- Molina-Giraldo, N.; Blum, P.; Zhu, K.; Bayer, P.; Fang, Z. A moving finite line source model to simulate borehole heat exchangers with groundwater advection. Int. J. Therm. Sci. 2011, 50, 2506–2513. [Google Scholar] [CrossRef]
- Lo Russo, S.; Taddia, G.; Verda, V. Development of the thermally affected zone (TAZ) around a groundwater heat pump (GWHP) system: A sensitivity analysis. Geothermics 2012, 43, 66–74. [Google Scholar] [CrossRef]
- Böttcher, F. Estimation of Characteristic Heat Flow Current Extents in the North of Münchener Schotterebene; TUM: Munich, Germany, 2014. [Google Scholar]
- Park, B.-H.; Bae, G.-O.; Lee, K.-K. Importance of thermal dispersivity in designing groundwater heat pump (GWHP) system: Field and numerical study. Renew. Energy 2015, 83, 270–279. [Google Scholar] [CrossRef]
- Angelotti, A.; Alberti, L.; La Licata, I.; Antelmi, M. Energy performance and thermal impact of a Borehole Heat Exchanger in a sandy aquifer: Influence of the groundwater velocity. Energy Convers. Manag. 2014, 77, 700–708. [Google Scholar] [CrossRef]
- Butler, J.J., Jr.; Healey, J.M. Relationship between pumping-test and slug-test parameters: Scale effect or artifact? Ground Water 1998, 36, 305–313. [Google Scholar] [CrossRef]
- Vandenbohede, A.; Lebbe, L. Parameter estimation based on vertical heat transport in the surficial zone. Hydrogeol. J. 2010, 18, 931–943. [Google Scholar] [CrossRef]
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A critical review of data on field-scale dispersion in aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Ferguson, G. Heterogeneity and thermal modeling of ground water. Groundwater 2007, 45, 485–490. [Google Scholar] [CrossRef] [PubMed]
- Barends, F. Complete solution for transient heat transport in porous media, following Lauwerier. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Tan, H.; Cheng, X.; Guo, H. Closed Solutions for Transient Heat Transport in Geological Media: New Development, Comparisons, and Validations. Transp. Porous Media 2012, 93, 737–752. [Google Scholar] [CrossRef]

| Parameter | Symbol | Unit | Adopted Values | Default Value |
|---|---|---|---|---|
| Aquifer hydraulic conductivity | m·s−1 | 5 × 10−4, 10−3, 5 × 10−3, 10−2 | 10−3 | |
| 5 × 10−5, 10−4, 5 × 10−4, 10−3 | 10−4 | |||
| Hydraulic gradient | 10−3 | 1, 2, 4, 6, 10 | 2 | |
| Darcy velocity | m·s−1 | 10−6, 2 × 10−6, 5 × 10−6, 10−5, 2 × 10−6 | 2 × 10−6 | |
| Effective porosity | - | 0.1, 0.2, 0.3 | 0.2 | |
| Thermal dispersivity | m | 0.5, 2, 10, 50 | 10 | |
| 0.05, 0.2, 1, 5 | ||||
| Solid phase thermal conductivity | s | W·m−1·K−1 | 1.5, 2, 2.5, 3 | 3 |
| Solid phase volumetric heat capacity | 106·J·m−3·K−1 | 1.5, 2, 2.5 | 2 | |
| Aquifer thickness | m | 10, 20, 40 | 20 | |
| Vadose zone thickness | m | 10, 20, 30 | 10 | |
| Well distance | m | 20, 50, 100 | 50 | |
| Annual maximum injected water flow rate | l/s | 50, 25, 12, 5 | 25 | |
| Ratio of heating over total energy demand | - | 0.6, 0.7, 0.75, 0.8, 0.9, 1 | 0.75 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piga, B.; Casasso, A.; Pace, F.; Godio, A.; Sethi, R. Thermal Impact Assessment of Groundwater Heat Pumps (GWHPs): Rigorous vs. Simplified Models. Energies 2017, 10, 1385. https://doi.org/10.3390/en10091385
Piga B, Casasso A, Pace F, Godio A, Sethi R. Thermal Impact Assessment of Groundwater Heat Pumps (GWHPs): Rigorous vs. Simplified Models. Energies. 2017; 10(9):1385. https://doi.org/10.3390/en10091385
Chicago/Turabian StylePiga, Bruno, Alessandro Casasso, Francesca Pace, Alberto Godio, and Rajandrea Sethi. 2017. "Thermal Impact Assessment of Groundwater Heat Pumps (GWHPs): Rigorous vs. Simplified Models" Energies 10, no. 9: 1385. https://doi.org/10.3390/en10091385
APA StylePiga, B., Casasso, A., Pace, F., Godio, A., & Sethi, R. (2017). Thermal Impact Assessment of Groundwater Heat Pumps (GWHPs): Rigorous vs. Simplified Models. Energies, 10(9), 1385. https://doi.org/10.3390/en10091385