An Adaptive Square Root Unscented Kalman Filter Approach for State of Charge Estimation of Lithium-Ion Batteries
Abstract
:1. Introduction
2. Lithium-Ion Battery Modelling and Parameter Identification
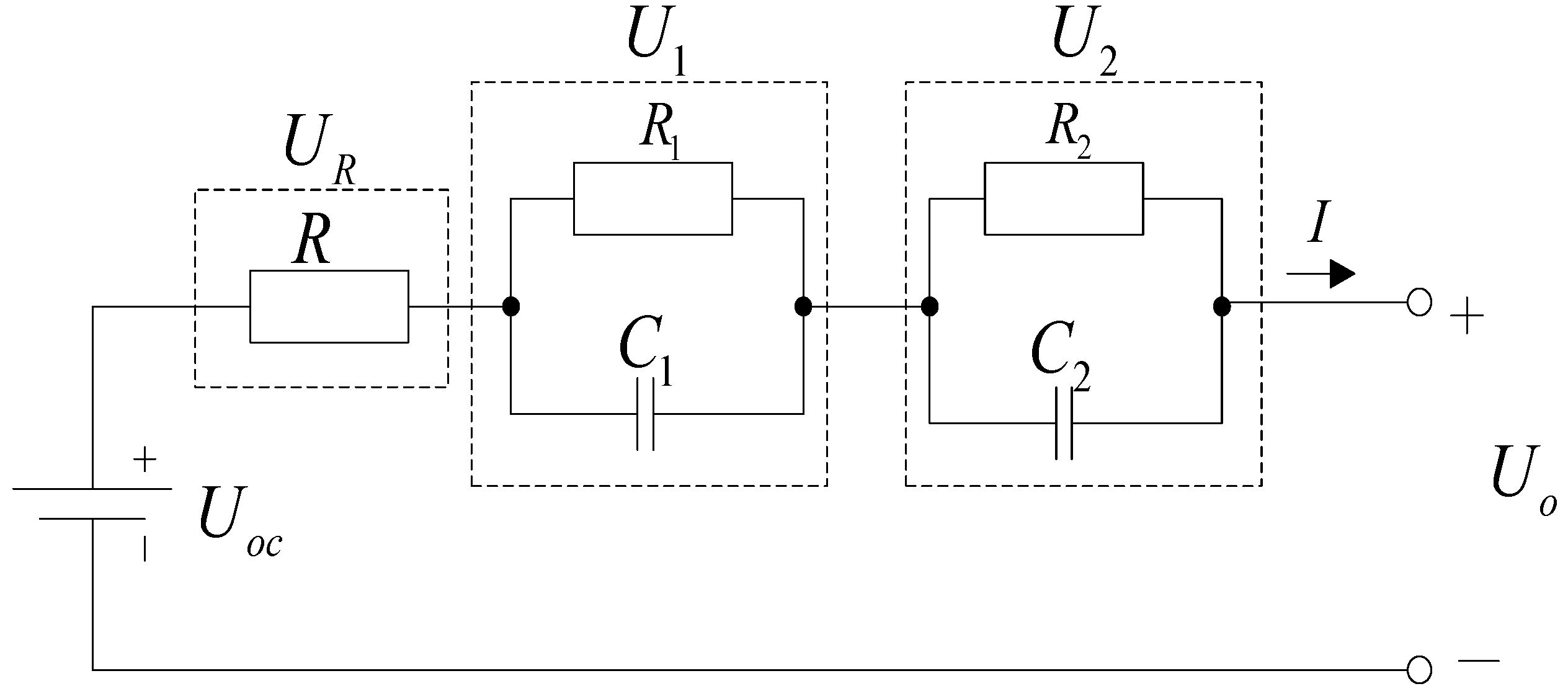
2.1. Lithium-Ion Battery Modelling
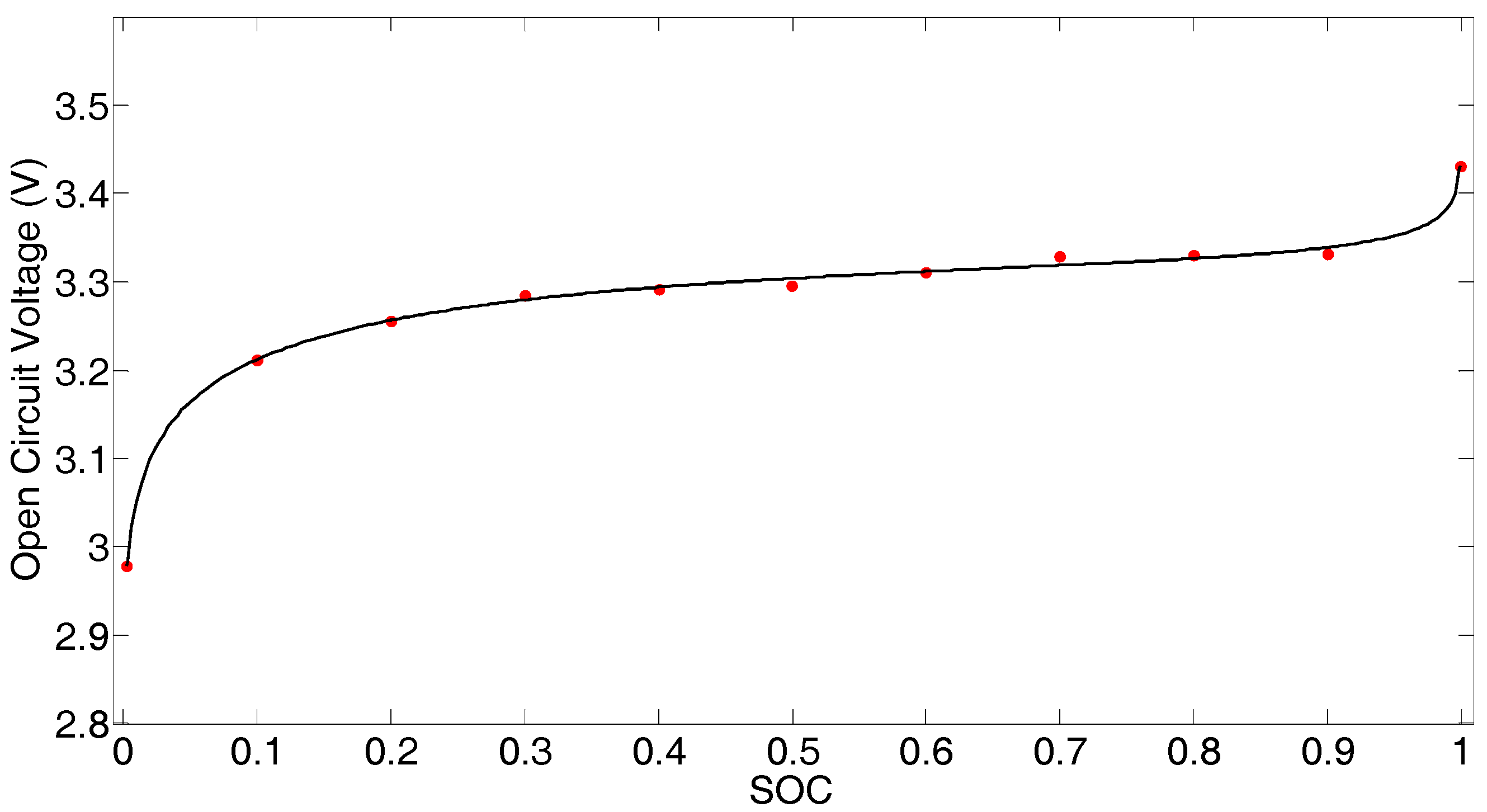
2.2. Parameter Identification
3. Adaptive Square Root Unscented Kalman Filter
4. Experimental Verification and Analysis
4.1. Experimental Platform
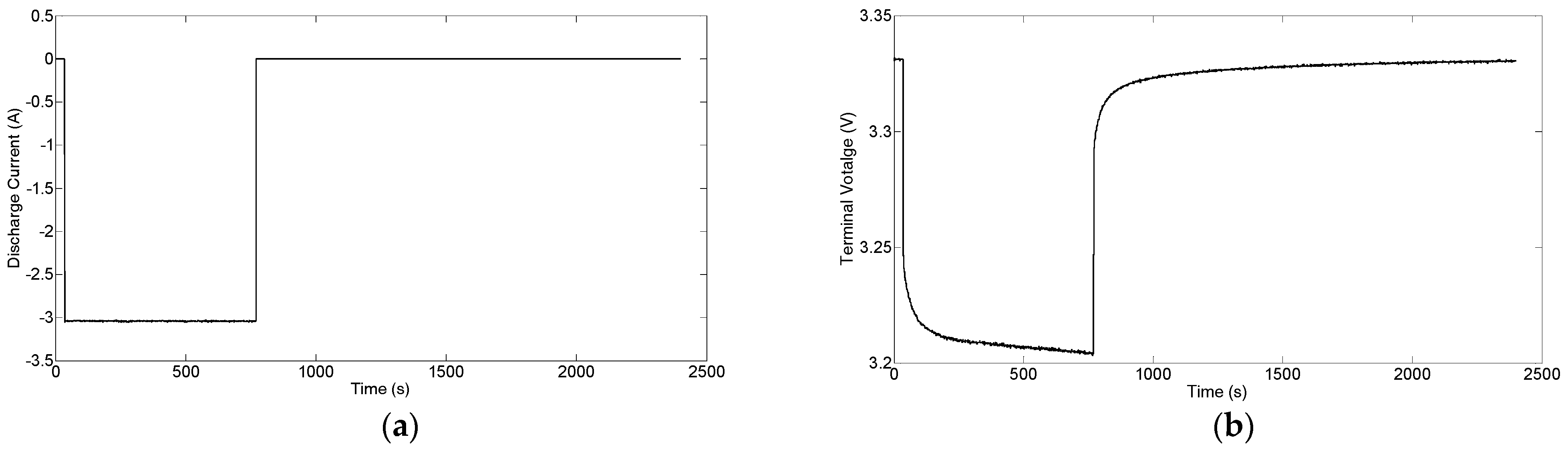
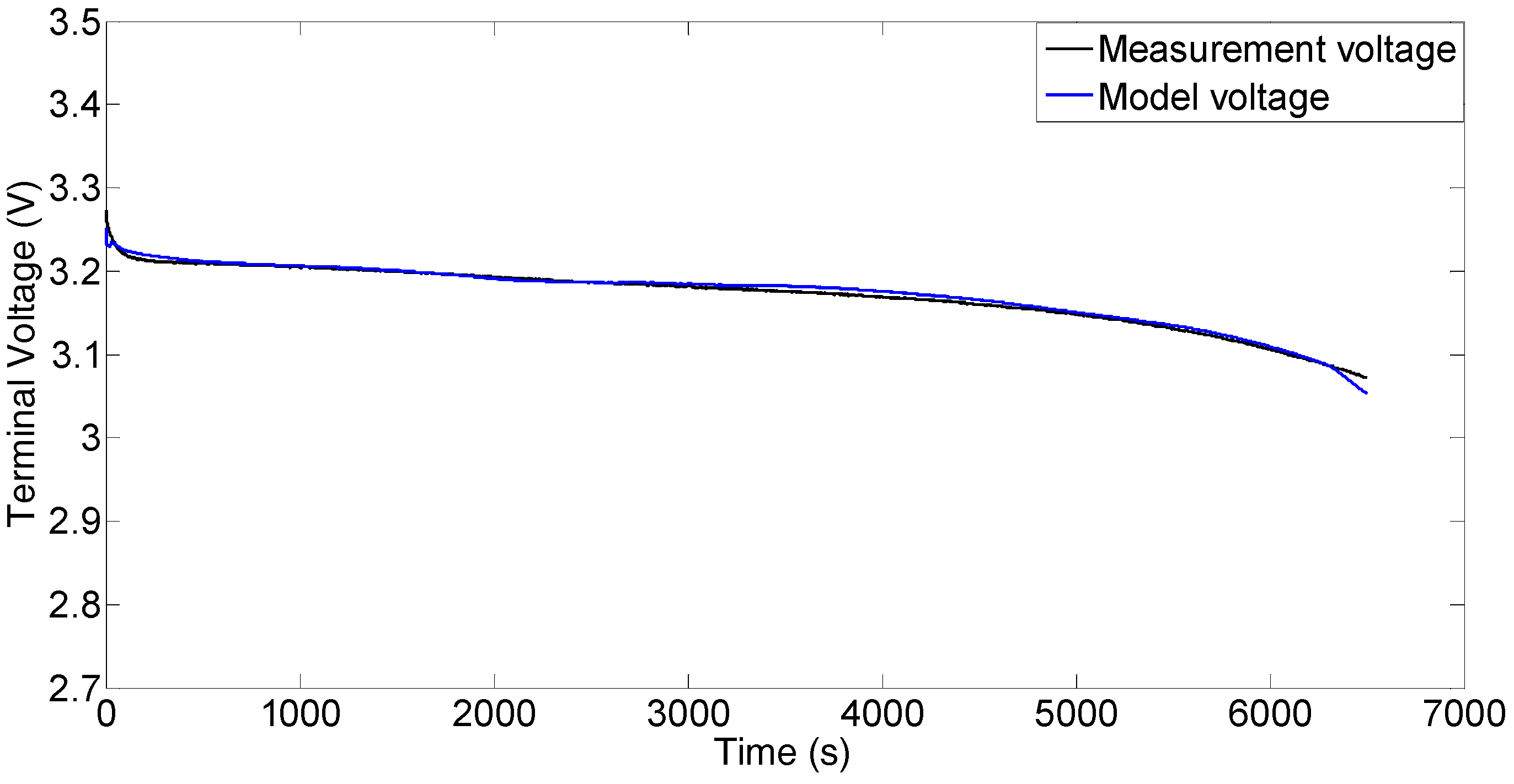
4.2. Battery Model Validation
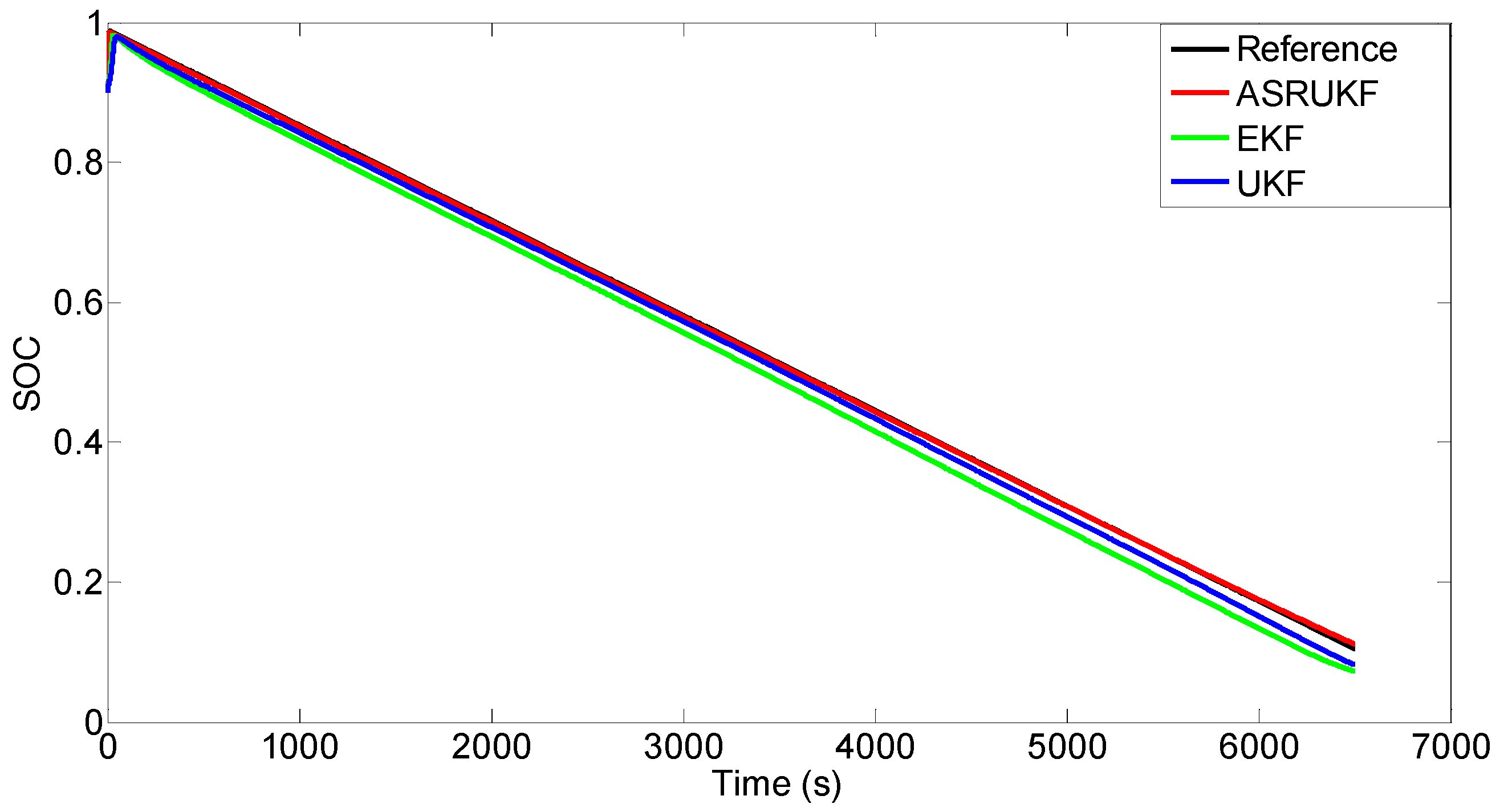
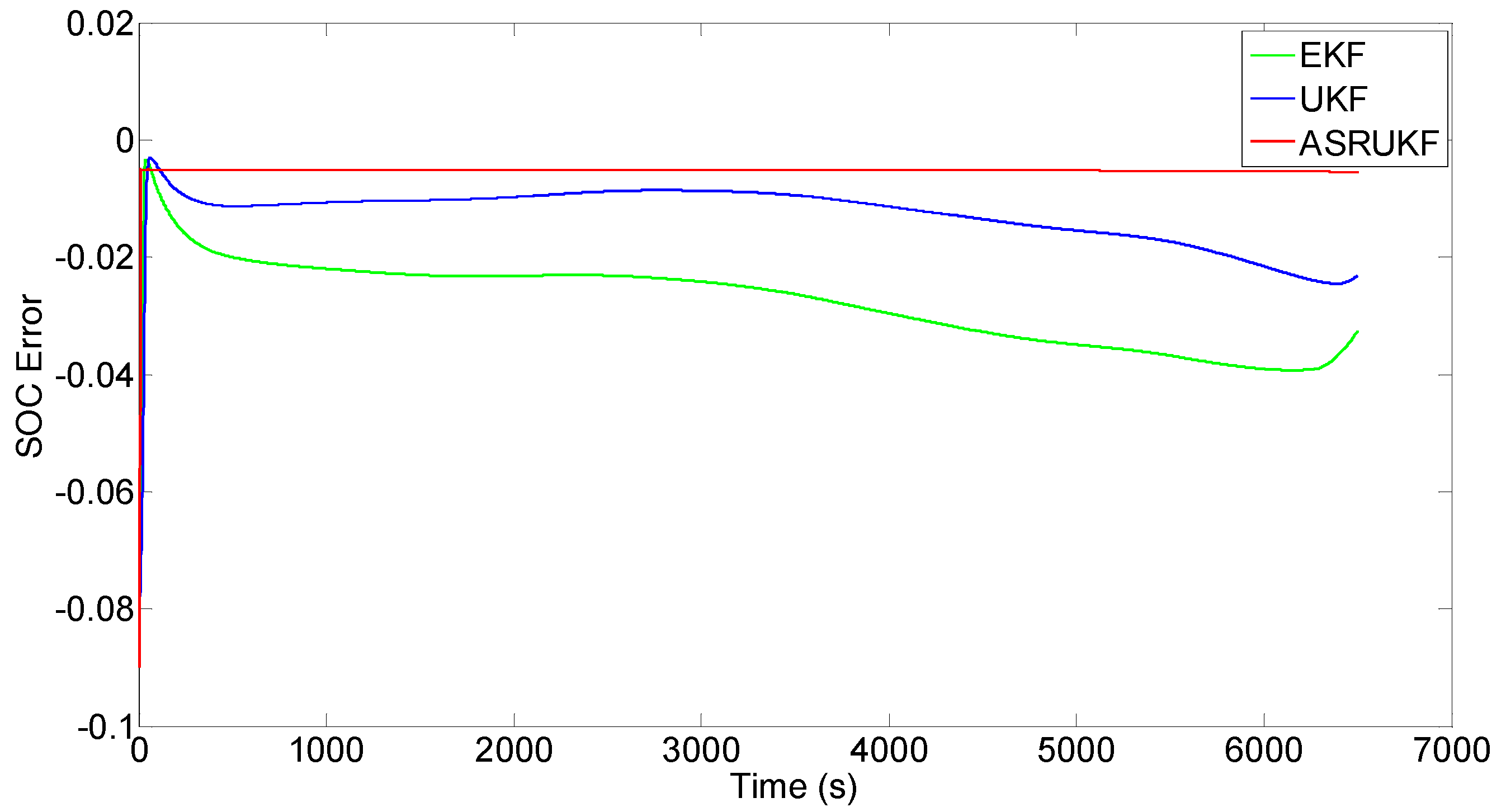
4.3. SOC Estimation Validation
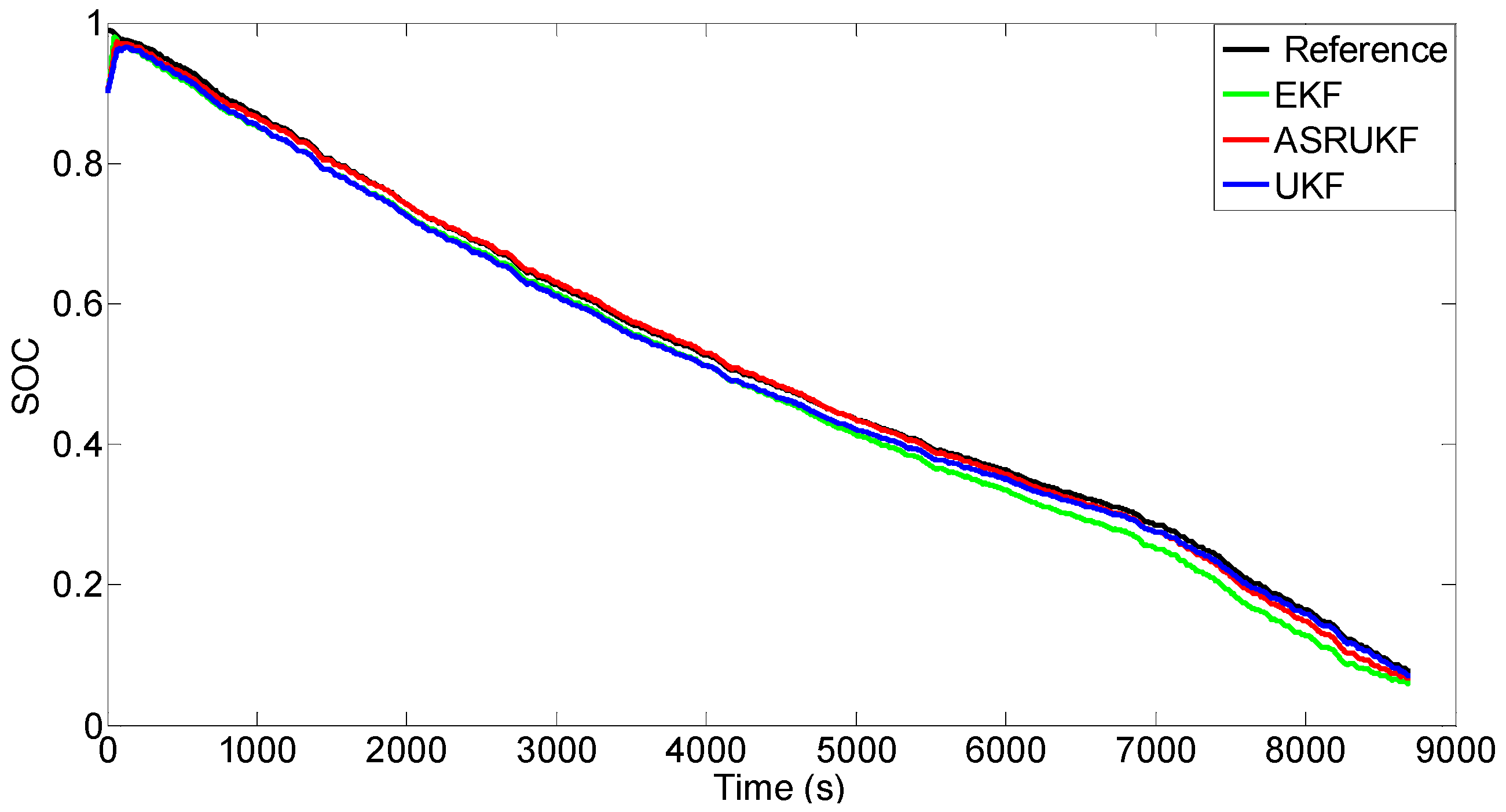
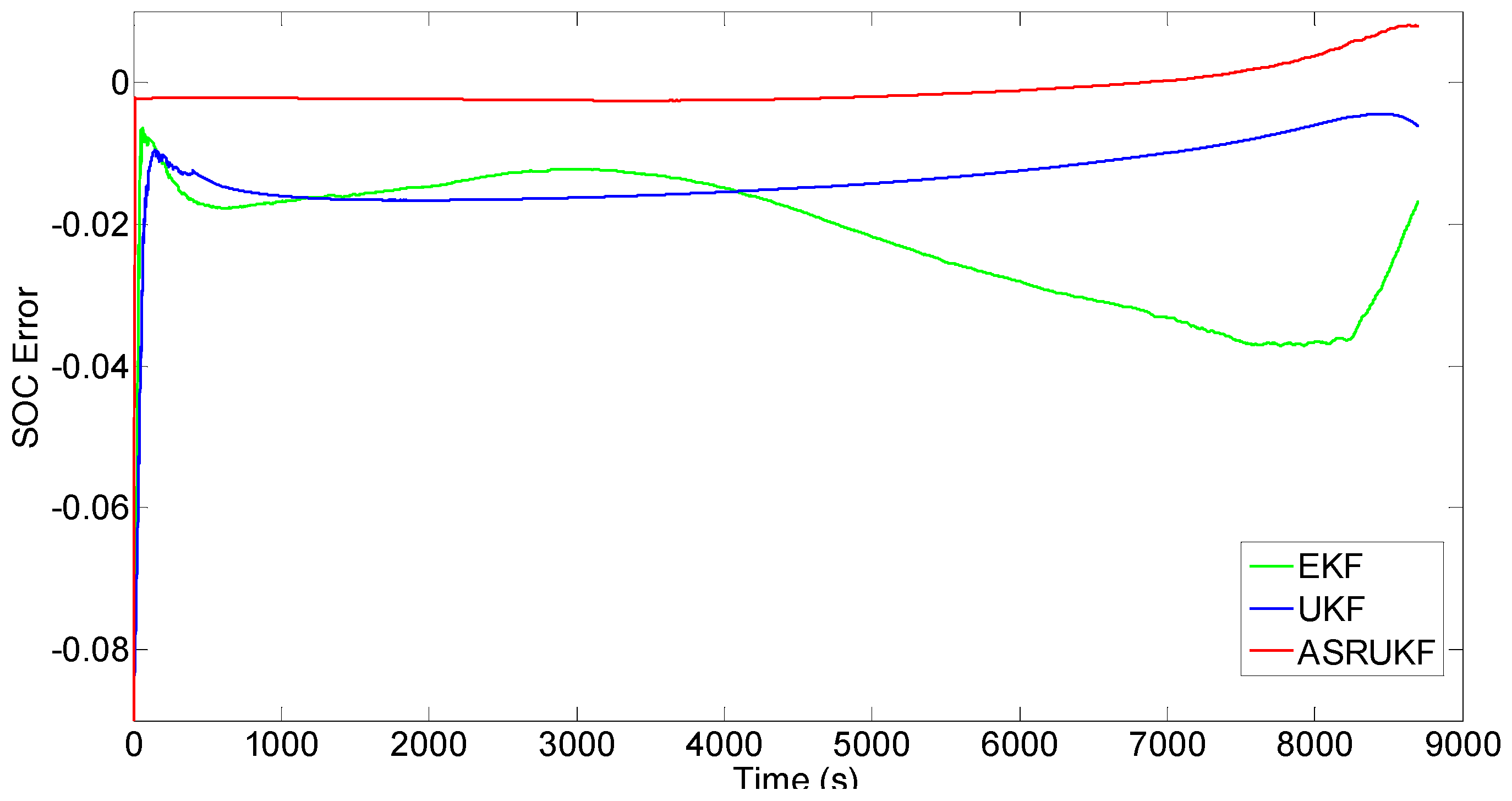
4.3.1. SOC Estimation Experimental Results under a Constant-Current Discharge
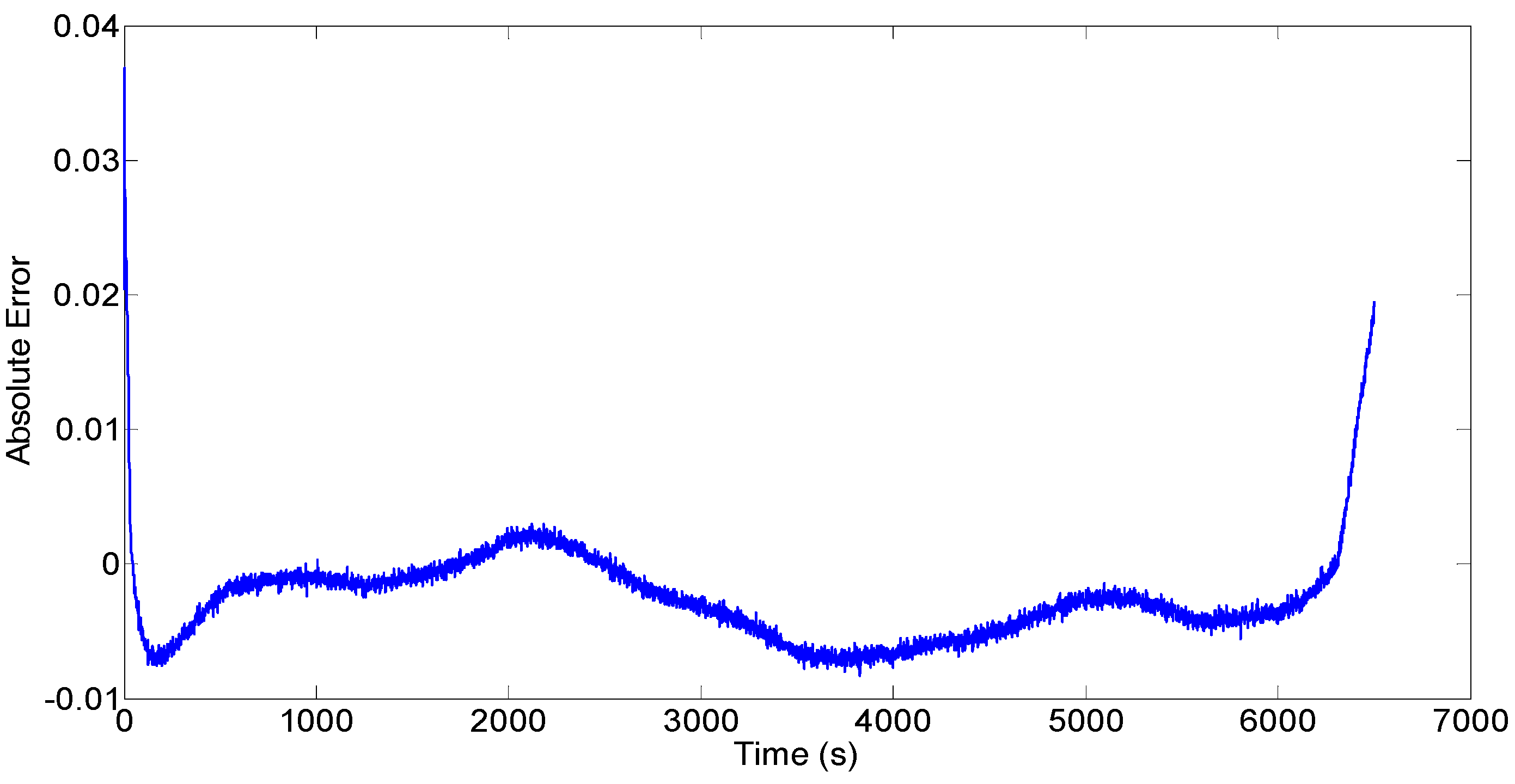
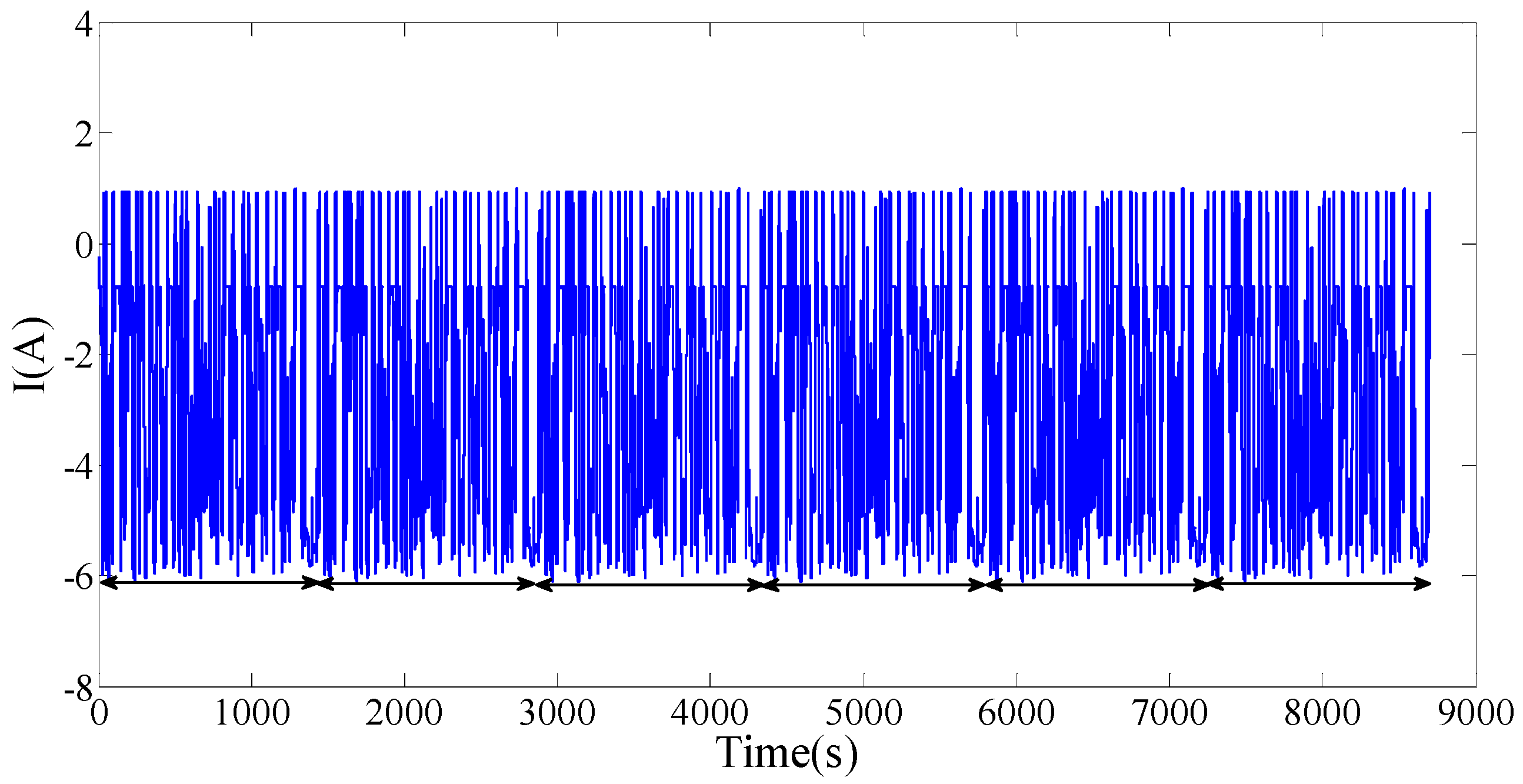
4.3.2. SOC Estimation by UDDS Test
4.3.3. Estimation Results Compared with References
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xiong, R.; Sun, F.; Gong, X.; Gao, C. A Data-Driven Based Adaptive State of Charge Estimator of Lithium-Ion Polymer Battery Used in Electric Vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-In Electric and Hybrid Vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Ng, K.; Moo, C.-S.; Chen, Y.-P.; Hsieh, Y.-C. Enhanced Coulomb Counting Method for Estimating State-of-Charge and State-of-Health Of Lithium-Ion Batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Wei, G.; Zhu, C. Online Estimation of Model Parameters and State of Charge of LiFePO4 Batteries Using a Novel Open-Circuit Voltage at Various Ambient Temperatures. Energies 2015, 8, 2950–2976. [Google Scholar] [CrossRef]
- Tong, S.; Klein, M.P.; Park, J.W. On-line Optimization of Battery Open Circuit Voltage for Improved State-of-Charge and State-of-Health Estimation. J. Power Sources 2015, 293, 416–428. [Google Scholar] [CrossRef]
- Tong, S.; Lacap, J.H.; Park, J. Battery State of Charge Estimation Using a Load-Classifying Neural Network. J. Energy Storage 2016, 7, 236–243. [Google Scholar] [CrossRef]
- Charkhgard, M.; Farrokhi, M. State-of-Charge Estimation for Lithium-Ion Batteries Using Neural Networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Guo, Y.F.; Zhao, Z.S.; Huang, L.M. SOC Estimation of Lithium Battery Based on Improved BP Neural Network. Energy Procedia 2017, 105, 4153–4158. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-circuit Voltage-Based State of Charge Estimation of Lithium-ion Battery Using Dual Neural Network Fusion Battery Model. Electrochim. Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Shen, Y.Q. Adaptive Online State-of-Charge Determination Based on Neuro-controller and Neural Network. Energy Convers. Manag. 2010, 51, 1093–1098. [Google Scholar] [CrossRef]
- Pérez, G.; Garmendia, M.; Reynaud, J.F.; Crego, J.; Viscarret, U. Enhanced closed loop State of Charge estimator for lithium-ion batteries based on Extended Kalman Filter. Appl. Energy 2015, 155, 834–845. [Google Scholar] [CrossRef]
- Pavković, D.; Krznar, M.; Komljenović, A.; Hrgetić, M.; Zorc, D. Dual EKF-Based State and Parameter Estimator for a LiFePO4 Battery Cell. J. Power Electron. 2017, 17, 398–410. [Google Scholar] [CrossRef]
- Paschero, M.; Storti, G.L.; Rizzi, A.; Mascioli, F.M.F.; Rizzoni, G. A Novel Mechanical Analogy-Based Battery Model for SOC Estimation Using a Multicell EKF. IEEE Trans. Sustain. Energy 2016, 7, 1695–1702. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Cho, B.H. Complementary Cooperation Algorithm Based on DEKF Combined with Pattern Recognition for SOC/Capacity Estimation and SOH Prediction. IEEE Trans. Power Electron. 2012, 27, 436–451. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on State of Charge Estimation of Batteries with Adaptive Extended Kalman Filter by Experiment Approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Mi, C.C. State of Charge Estimation of Lithium-Ion Batteries in Electric Drive Vehicles Using Extended Kalman Filter. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030. [Google Scholar] [CrossRef]
- Du, J.; Liu, Z.; Wang, Y.; Wen, C. An Adaptive Sliding Mode Observer for Lithium-Ion Battery State of Charge and State of Health Estimation in Electric Vehicles. Control Eng. Pract. 2016, 54, 81–90. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, J.; Liu, S.; Zhang, C. A Novel Sliding Mode Observer for State of Charge Estimation of EV Lithium Batteries. J. Power Electron. 2016, 16, 1131–1140. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Cao, Z.; Kapoor, A. A Novel Approach for State of Charge Estimation Based on Adaptive Switching Gain Sliding Mode Observer in Electric Vehicles. J. Power Sources 2014, 246, 667–678. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, J.; Ruan, H.; Zhang, C. Simply Designed and Universal Sliding Mode Observer for the SOC Estimation of Lithium-Ion Batteries. IET Power Electron. 2017, 10, 697–705. [Google Scholar] [CrossRef]
- He, Z.; Chen, D.; Pan, C.; Chen, L.; Wang, S. State of Charge Estimation of Power Li-Ion Batteries Using a Hybrid Estimation Algorithm Based on UKF. Electrochim. Acta 2016, 211, 101–109. [Google Scholar]
- He, H.; Xiong, R.; Peng, J. Real-time Estimation of Battery State-of-Charge with Unscented Kalman Filter and RTOS μCOS-II Platform. Appl. Energy 2016, 162, 1410–1418. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.; Sun, W.; Xu, Z.; Zheng, W. A Modified Model Based State of Charge Estimation of Power Lithium-Ion Batteries Using Unscented Kalman Filter. J. Power Sources 2014, 270, 619–626. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman Filter for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Gao, F. Lithium Polymer Battery State-of-Charge Estimation Based on Adaptive Unscented Kalman Filter and Support Vector Machine. IEEE Trans. Power Electron. 2015, 31, 2226–2238. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Xia, B.; Wang, H.; Tian, Y.; Wang, M.; Sun, W.; Xu, Z. State of Charge Estimation of Lithium-Ion Batteries Using an Adaptive Cubature Kalman filter. Energies 2015, 8, 5916–5936. [Google Scholar] [CrossRef]
- Aung, H.; Soon Low, K.; Ting Goh, S. State-of-Charge Estimation of Lithium-Ion Battery Using Square Root Spherical Unscented Kalman Filter (Sqrt-UKFST) in Nanosatellite. IEEE Trans. Power Electron. 2014, 30, 4774–4783. [Google Scholar] [CrossRef]
- Micea, M.V.; Ungurean, L.; Carstoiu, G.N.; Groza, V. Online State-of-Health Assessment for Battery Management Systems. IEEE Trans. Instrum. Meas. 2011, 60, 1997–2006. [Google Scholar] [CrossRef]
- Haykin, S. Kalman Filter and Neural Networks; John Wiley & Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Van der Merwe, R.; Wan, E.A. The Square-Root Unscented Kalman Filter for State and Parameter-Estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; Volume 6, pp. 3461–3464. [Google Scholar]


| K0 | K1 | K2 | K3 | K4 |
|---|---|---|---|---|
| 3.3893 | 0.0688 | −0.00592 | 0.0002 | −0.0707 |
| SOC | R (mΩ) | R1 (mΩ) | C1 (F) | R2 (mΩ) | C2 (F) |
|---|---|---|---|---|---|
| 0.1 | 29.44 | 5.76 | 87,318.81 | 8.88 | 3661.89 |
| 0.2 | 29.24 | 6.45 | 85,260.83 | 7.66 | 4956.27 |
| 0.3 | 29.29 | 7.66 | 73,577.30 | 7.20 | 5678.10 |
| 0.4 | 28.83 | 4.74 | 102,356.69 | 6.97 | 5755.12 |
| 0.5 | 28.68 | 3.98 | 141,531.77 | 6.15 | 5529.76 |
| 0.6 | 28.14 | 7.04 | 108,991.73 | 6.22 | 6196.12 |
| 0.7 | 27.78 | 8.49 | 53,941.98 | 7.30 | 5513.29 |
| 0.8 | 28.61 | 4.08 | 115,293.37 | 7.80 | 4613.10 |
| 0.9 | 28.56 | 3.42 | 166,961.48 | 6.18 | 5174.26 |
| 1 | 28.56 | 3.42 | 166,961.48 | 6.18 | 5174.26 |
| Methods | Mean Error | Maximum Error | RMSE |
|---|---|---|---|
| EKF | 2.8% | 3.9% | 3.2% |
| UKF | 1.2% | 2.4% | 1.5% |
| ASRUKF | 0.5% | 0.54% | 0.5% |
| Methods | Mean Error | Maximum Error | RMSE |
|---|---|---|---|
| EKF | 2.1% | 3.7% | 3.1% |
| UKF | 1.3% | 1.6% | 1.5% |
| ASRUKF | 0.2% | 0.8% | 0.4% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Cui, N.; Zhang, C. An Adaptive Square Root Unscented Kalman Filter Approach for State of Charge Estimation of Lithium-Ion Batteries. Energies 2017, 10, 1345. https://doi.org/10.3390/en10091345
Liu S, Cui N, Zhang C. An Adaptive Square Root Unscented Kalman Filter Approach for State of Charge Estimation of Lithium-Ion Batteries. Energies. 2017; 10(9):1345. https://doi.org/10.3390/en10091345
Chicago/Turabian StyleLiu, Shulin, Naxin Cui, and Chenghui Zhang. 2017. "An Adaptive Square Root Unscented Kalman Filter Approach for State of Charge Estimation of Lithium-Ion Batteries" Energies 10, no. 9: 1345. https://doi.org/10.3390/en10091345
APA StyleLiu, S., Cui, N., & Zhang, C. (2017). An Adaptive Square Root Unscented Kalman Filter Approach for State of Charge Estimation of Lithium-Ion Batteries. Energies, 10(9), 1345. https://doi.org/10.3390/en10091345





