Peak Forces on Wave Energy Linear Generators in Tsunami and Extreme Waves
Abstract
:1. Introduction
2. Method
2.1. Governing Equations
2.2. Numerical Implementation
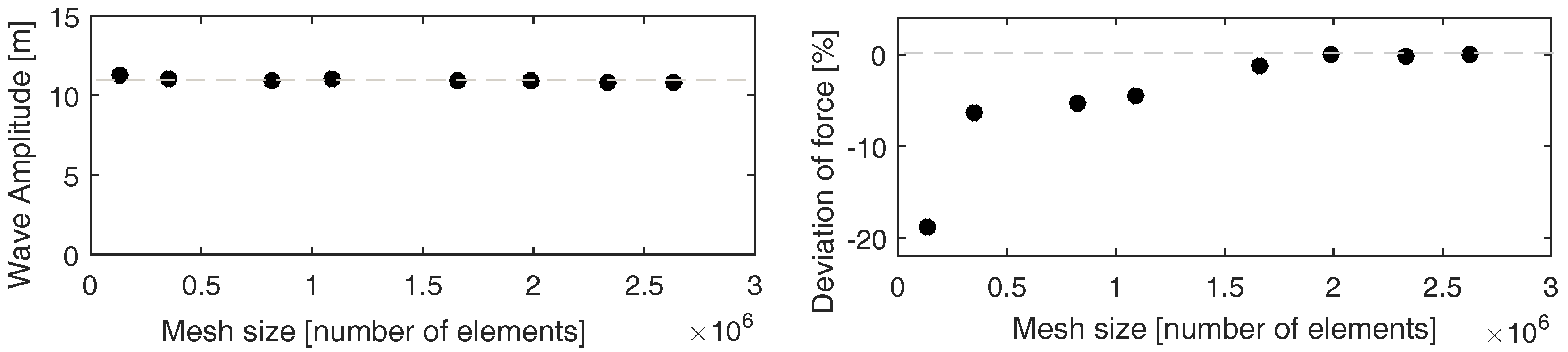
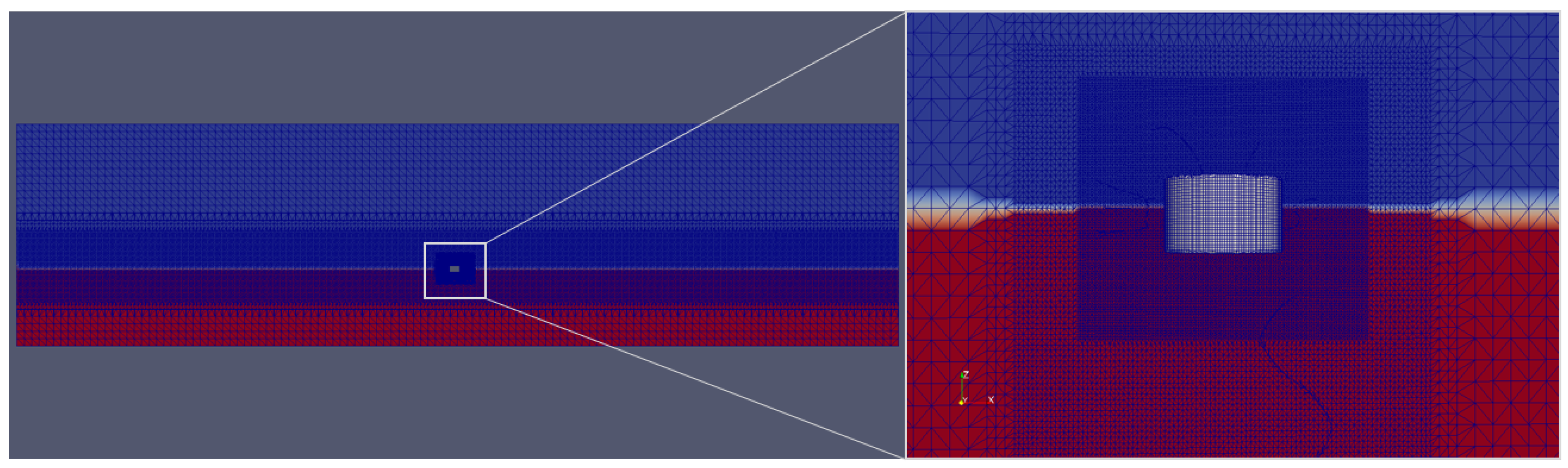
2.2.1. Numerical Wavetank
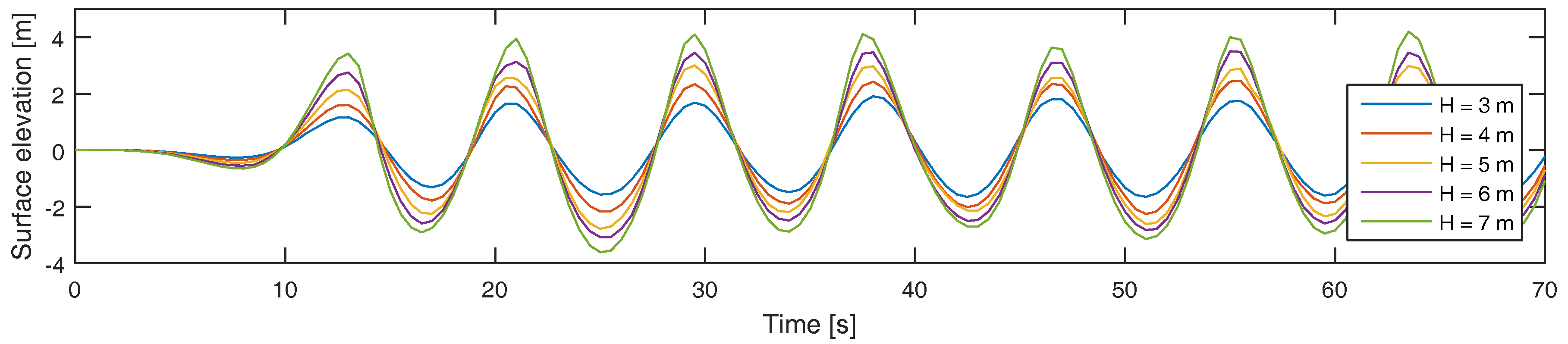
2.2.2. Incident Regular Wave
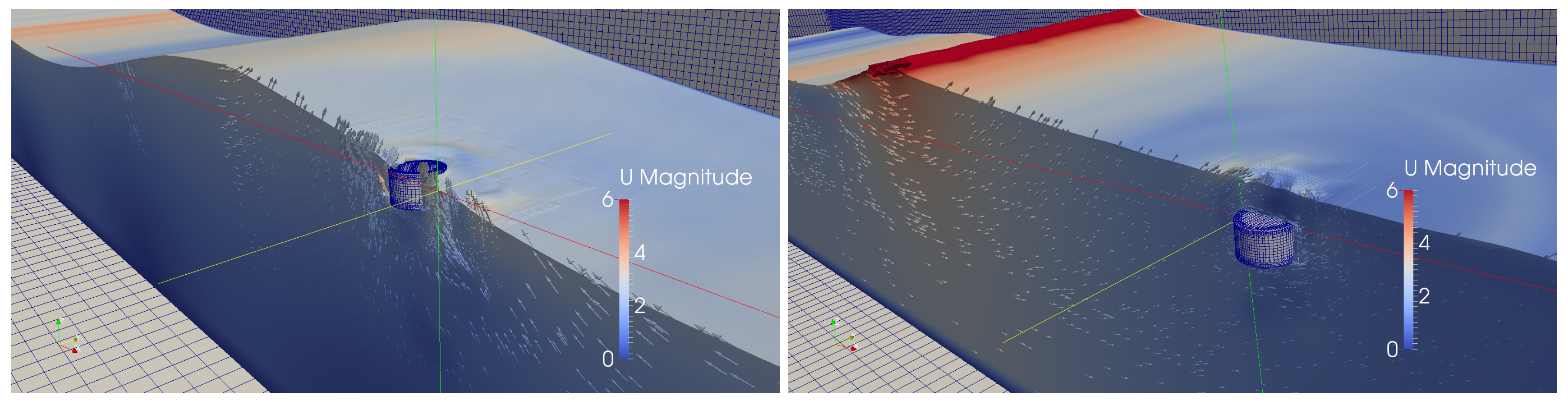
2.2.3. Incident Tsunami Wave
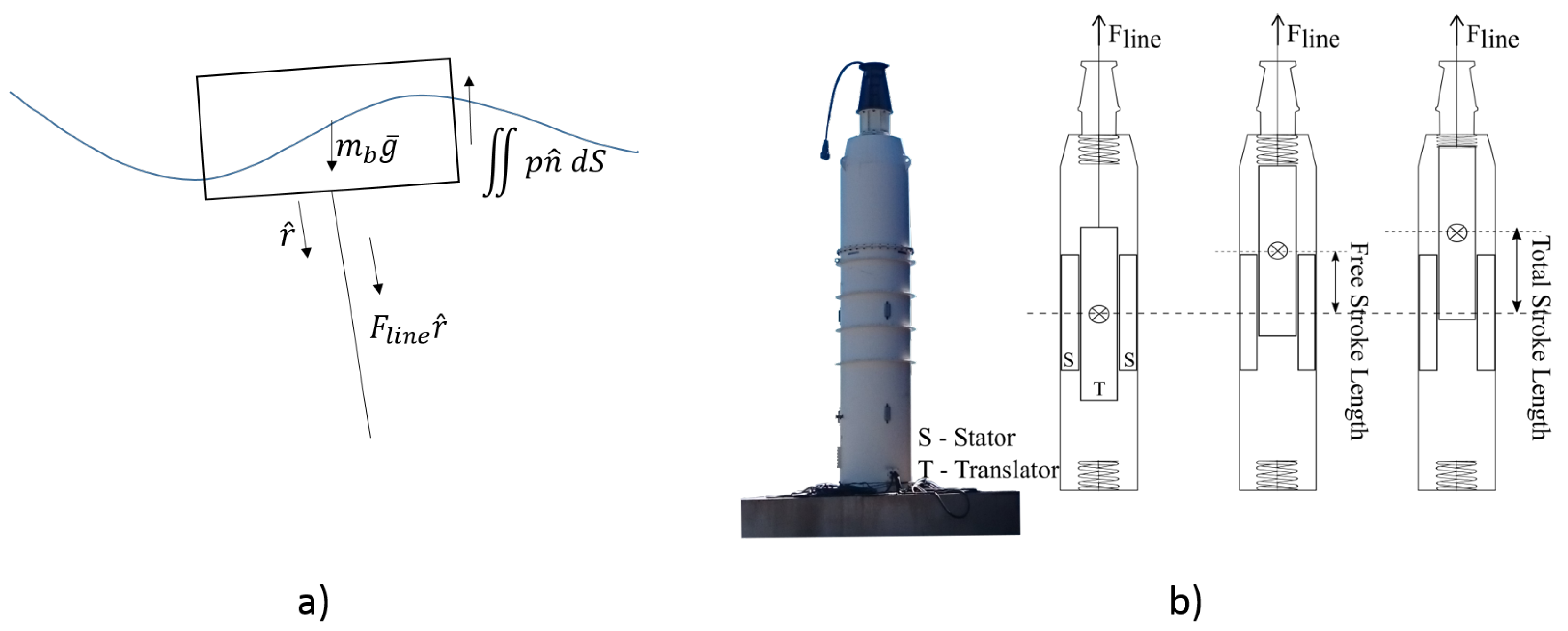
2.3. The WEC Model
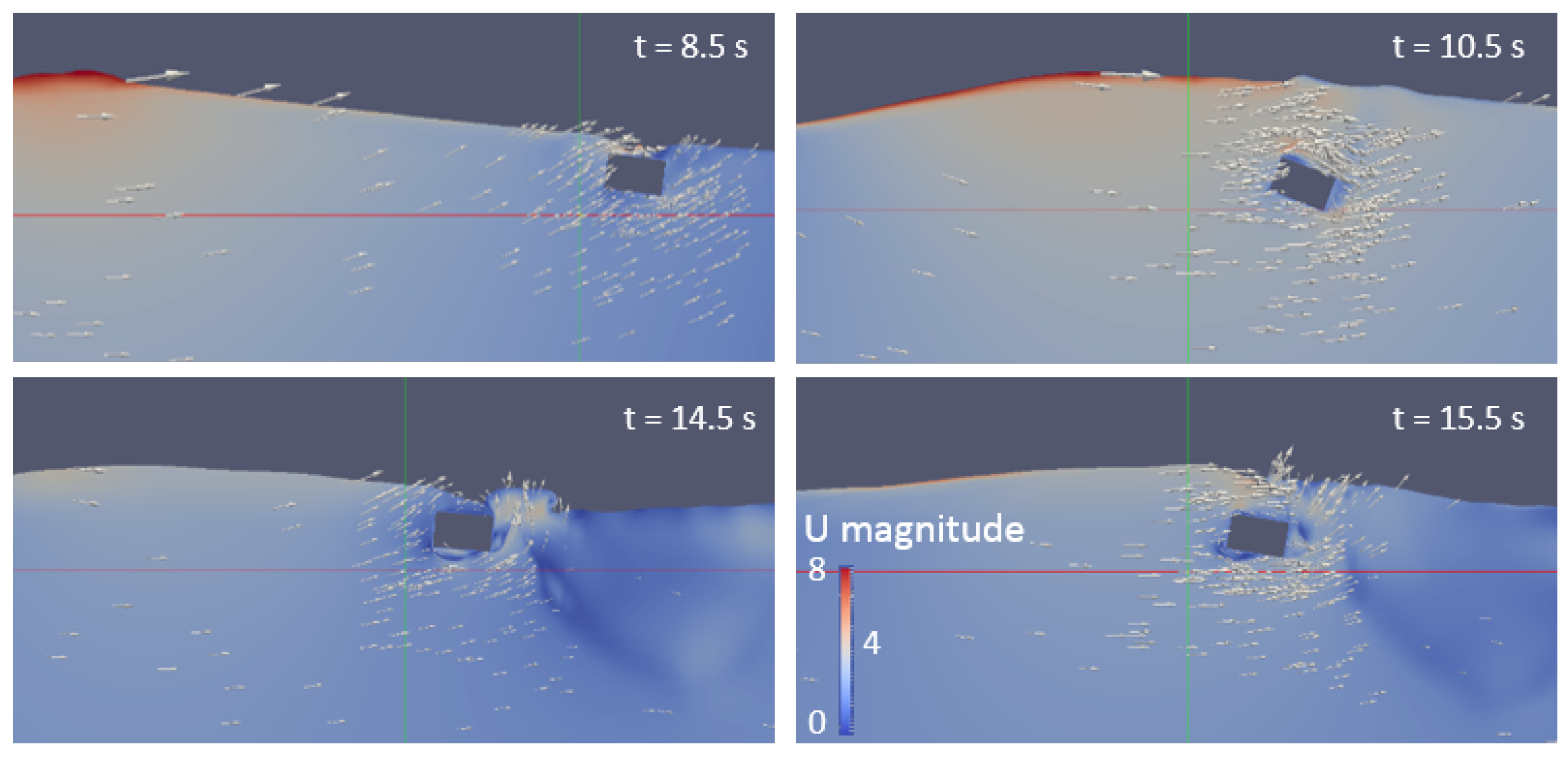
3. Results
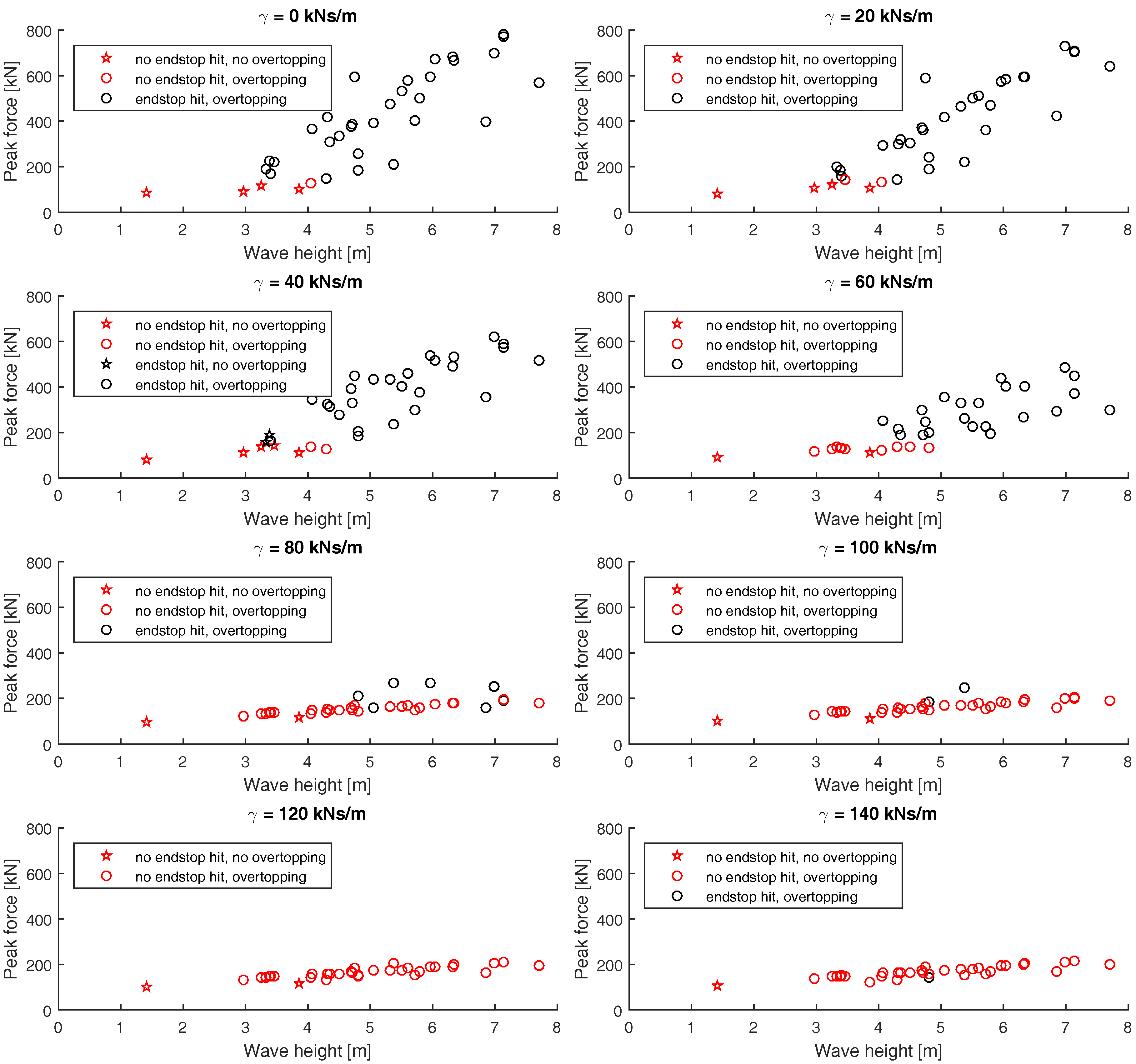
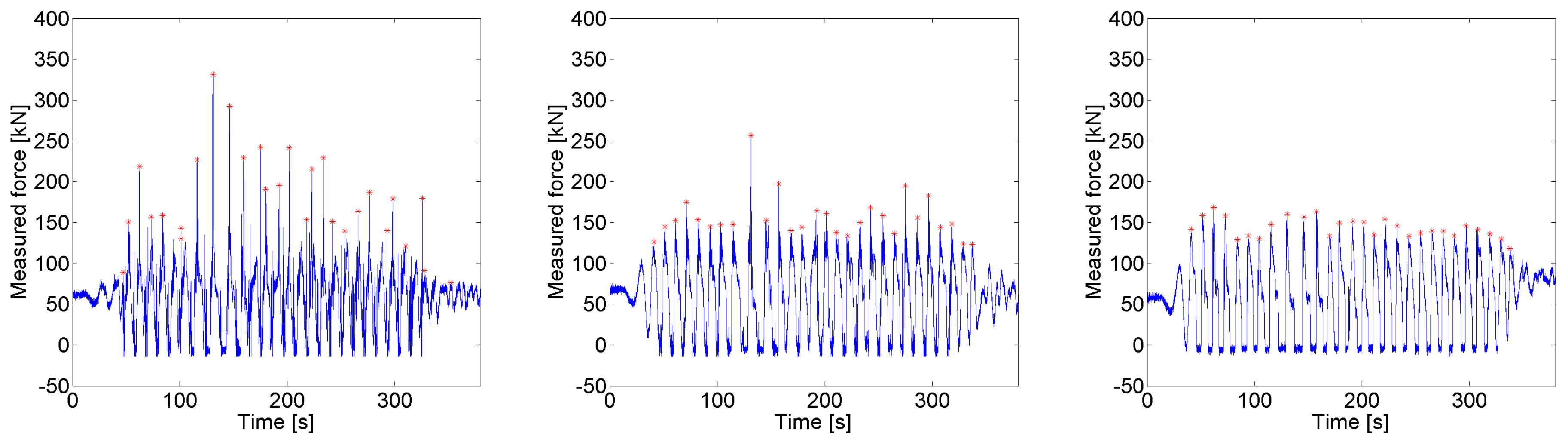
3.1. Peak Forces as a Function of Wave Height
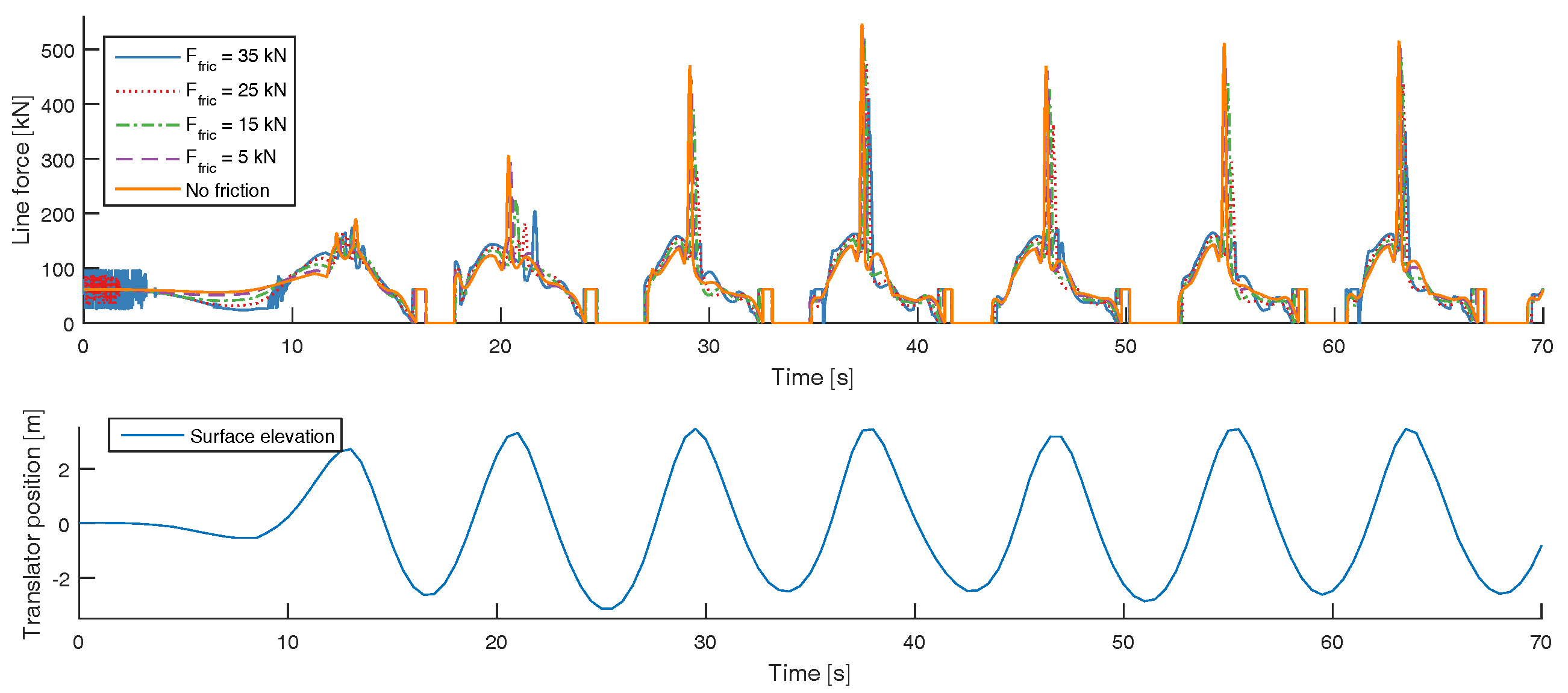
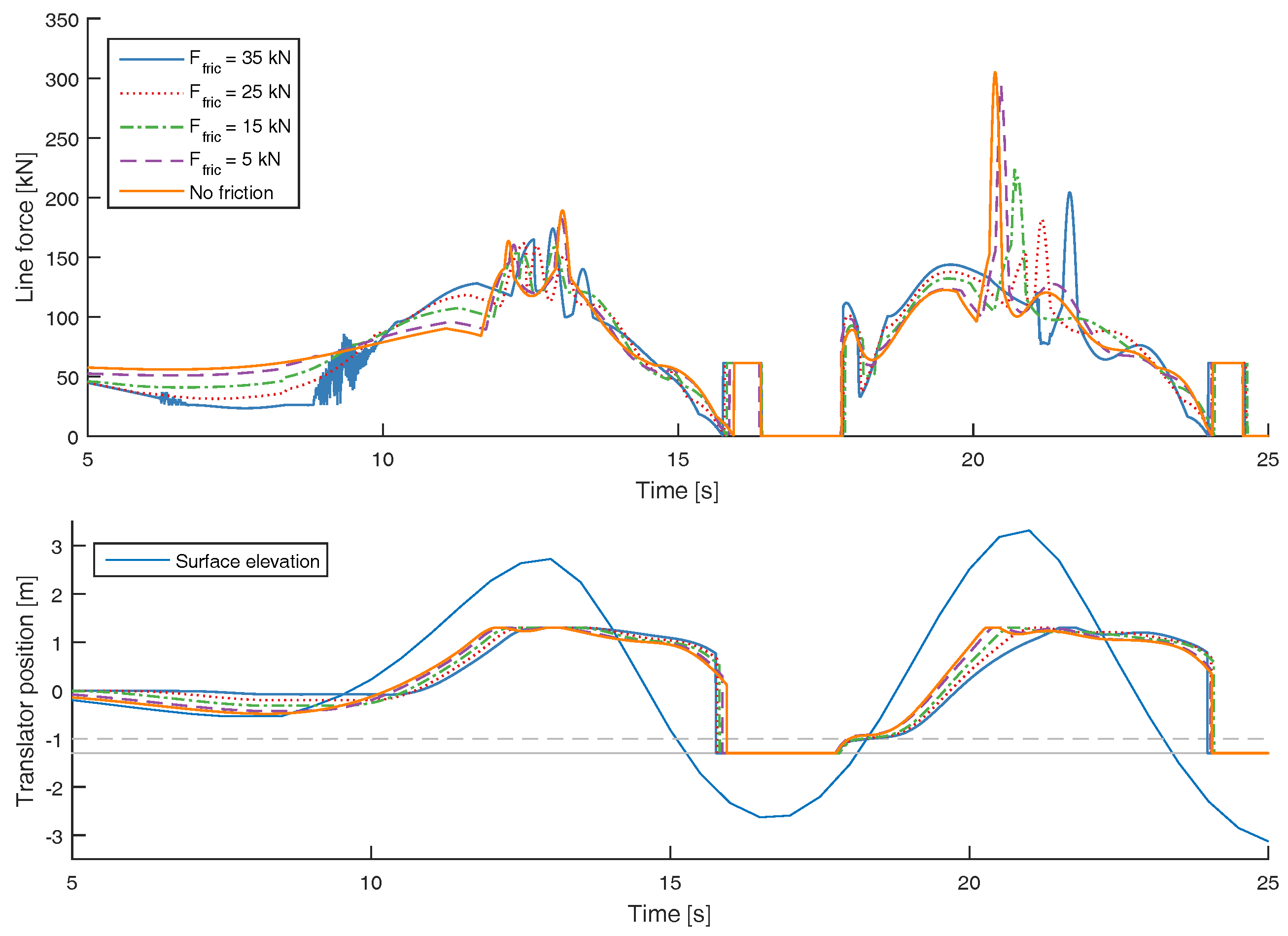
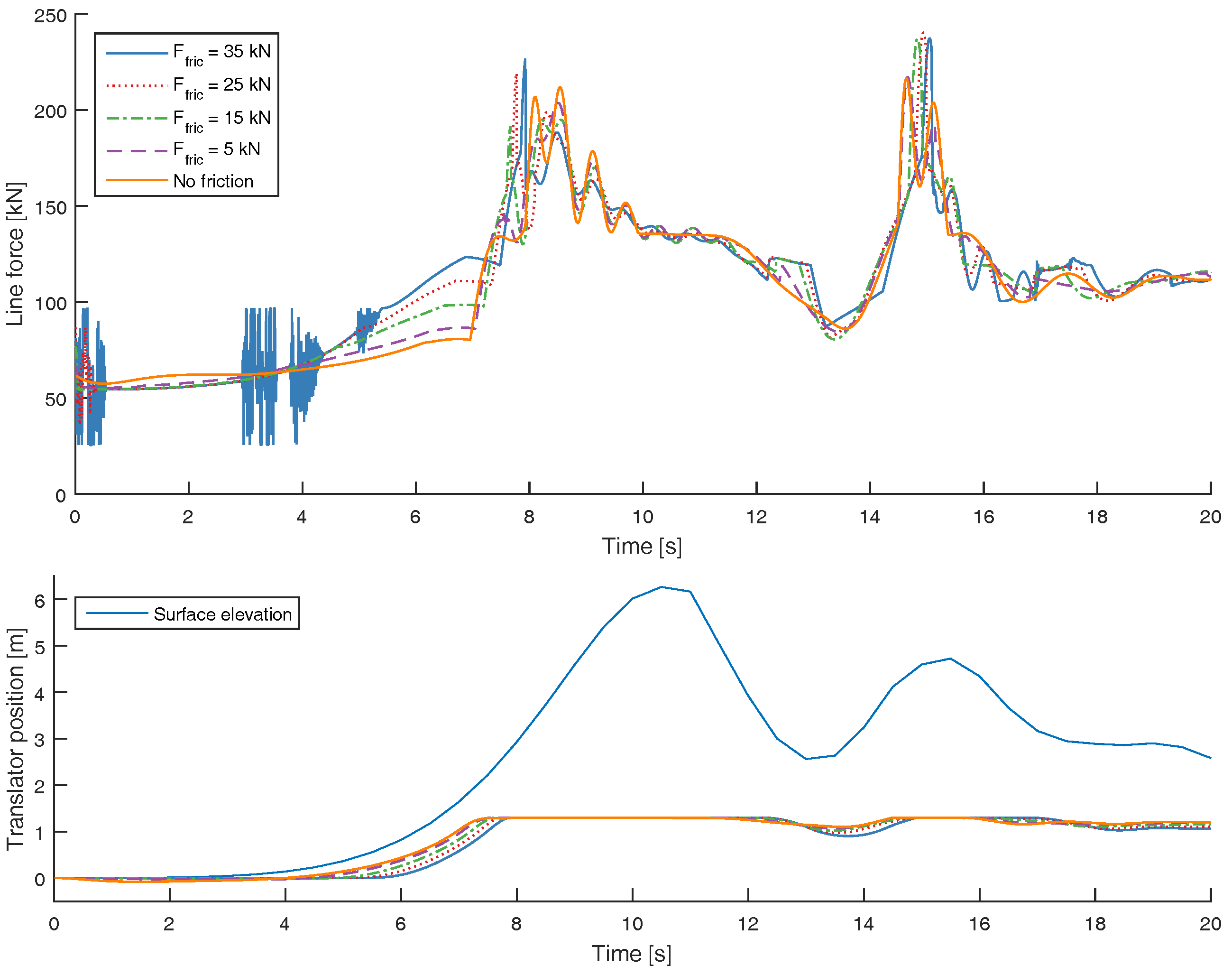
3.2. The Impact of Friction on the Survivability in Extreme Waves
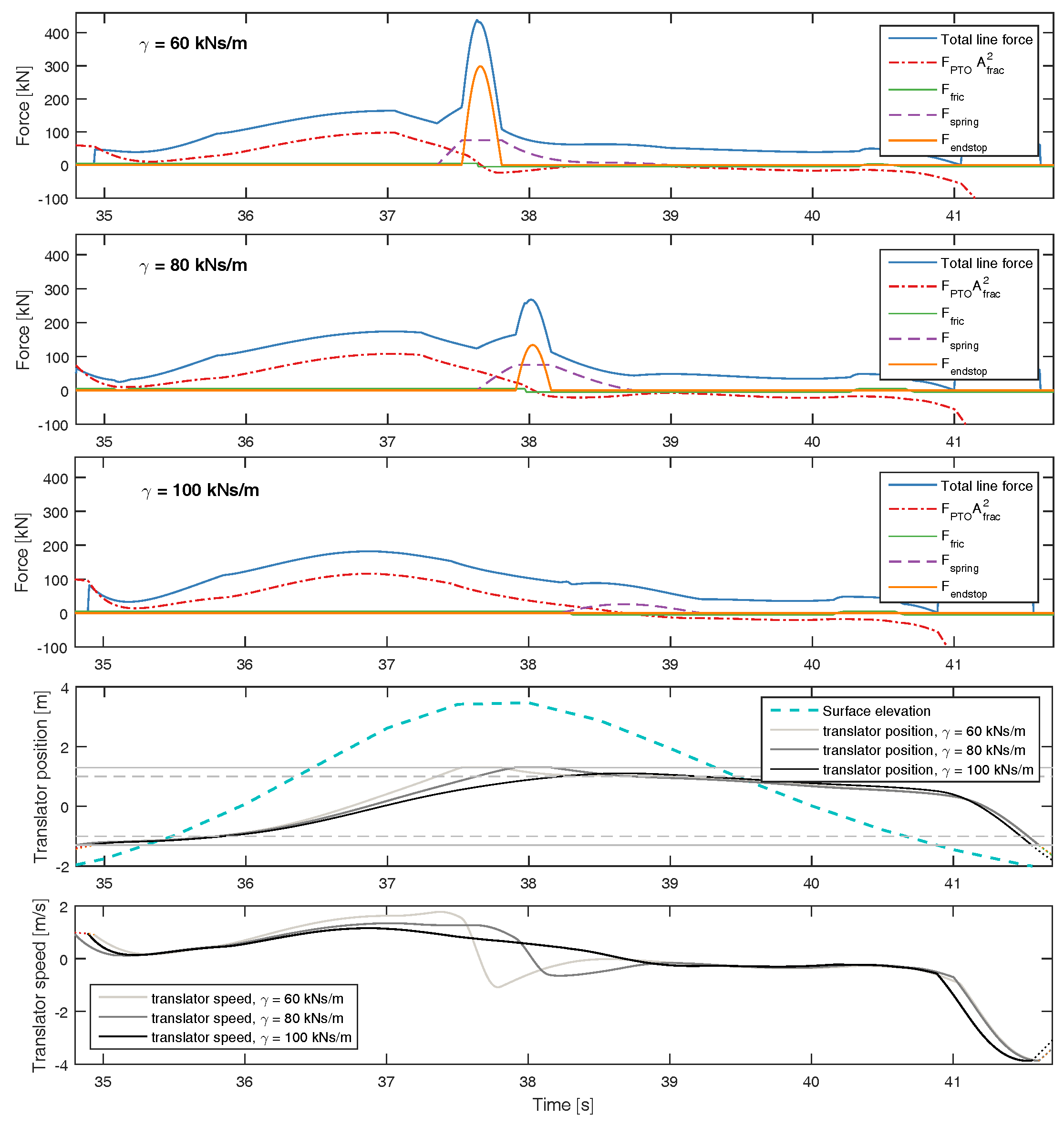
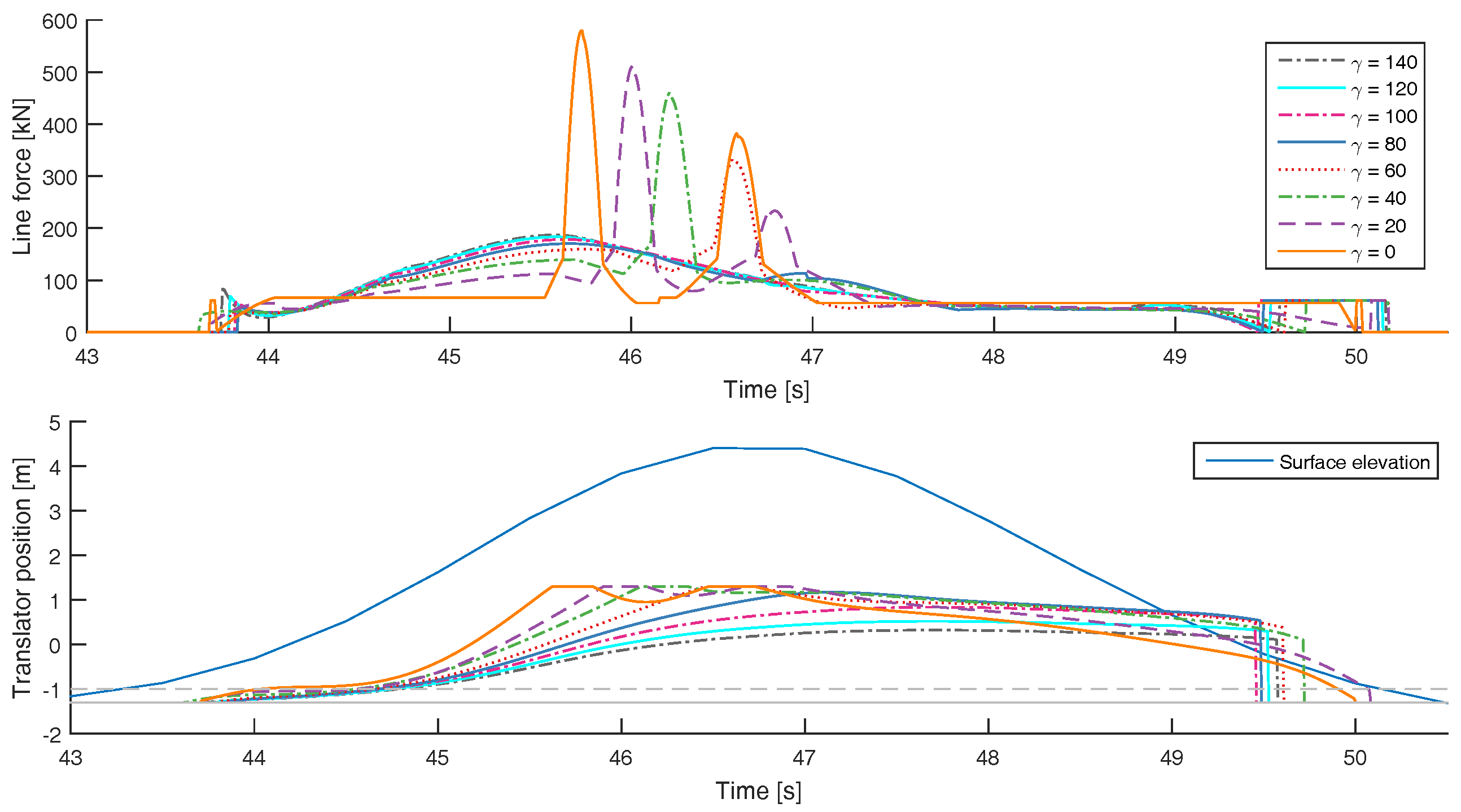
3.3. Endstop Forces Decrease with Increased Damping for Periodic Waves
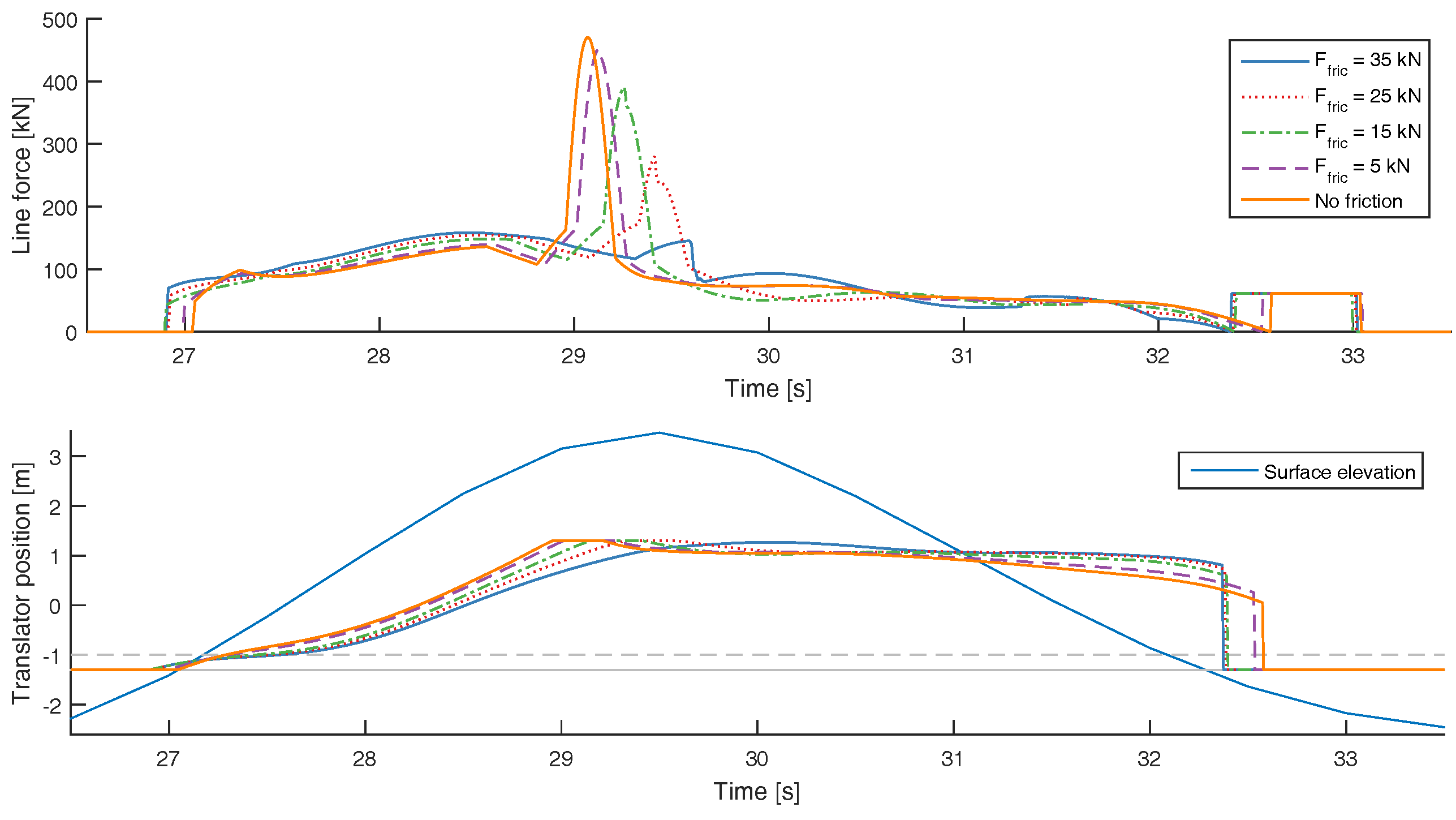
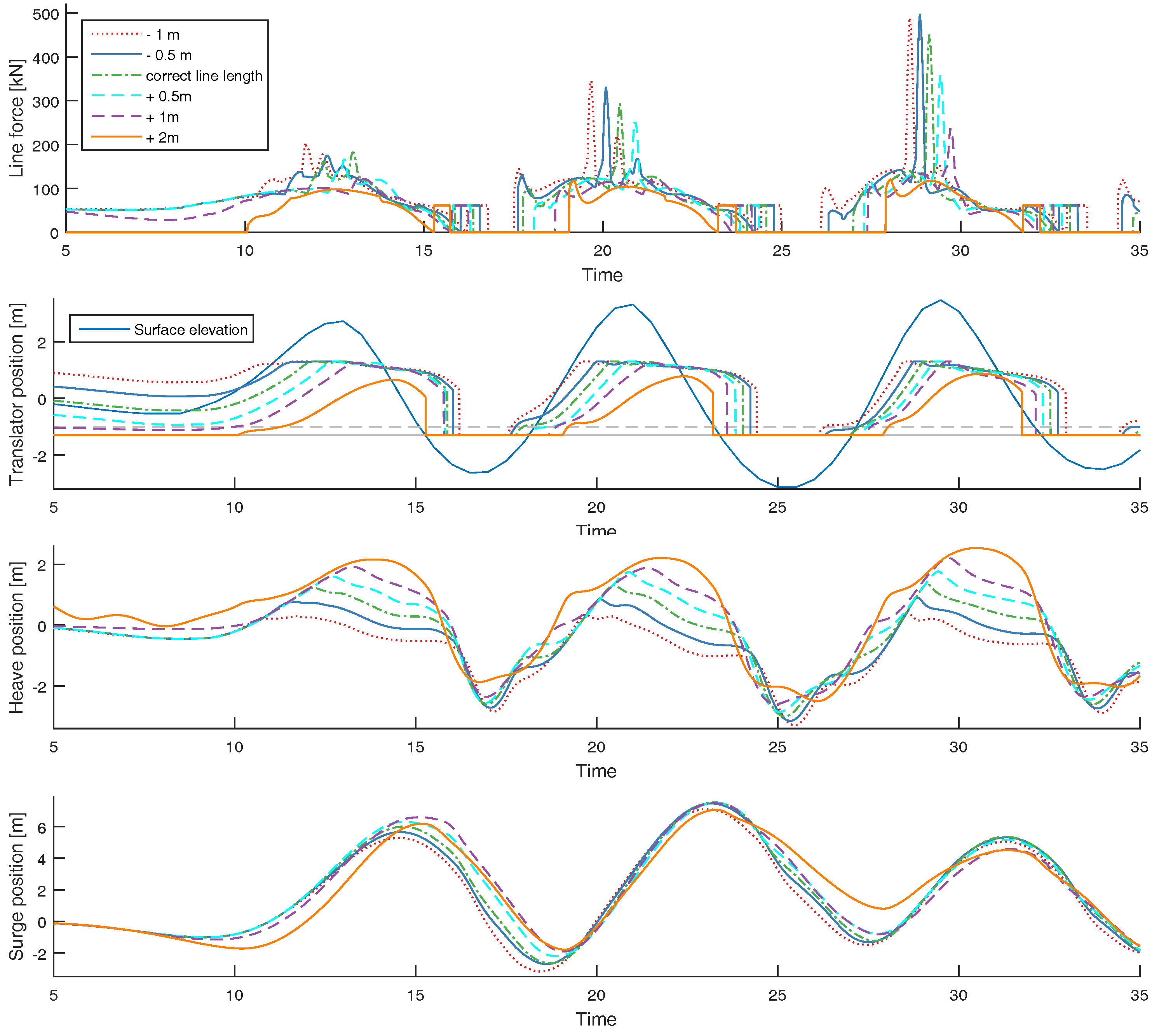
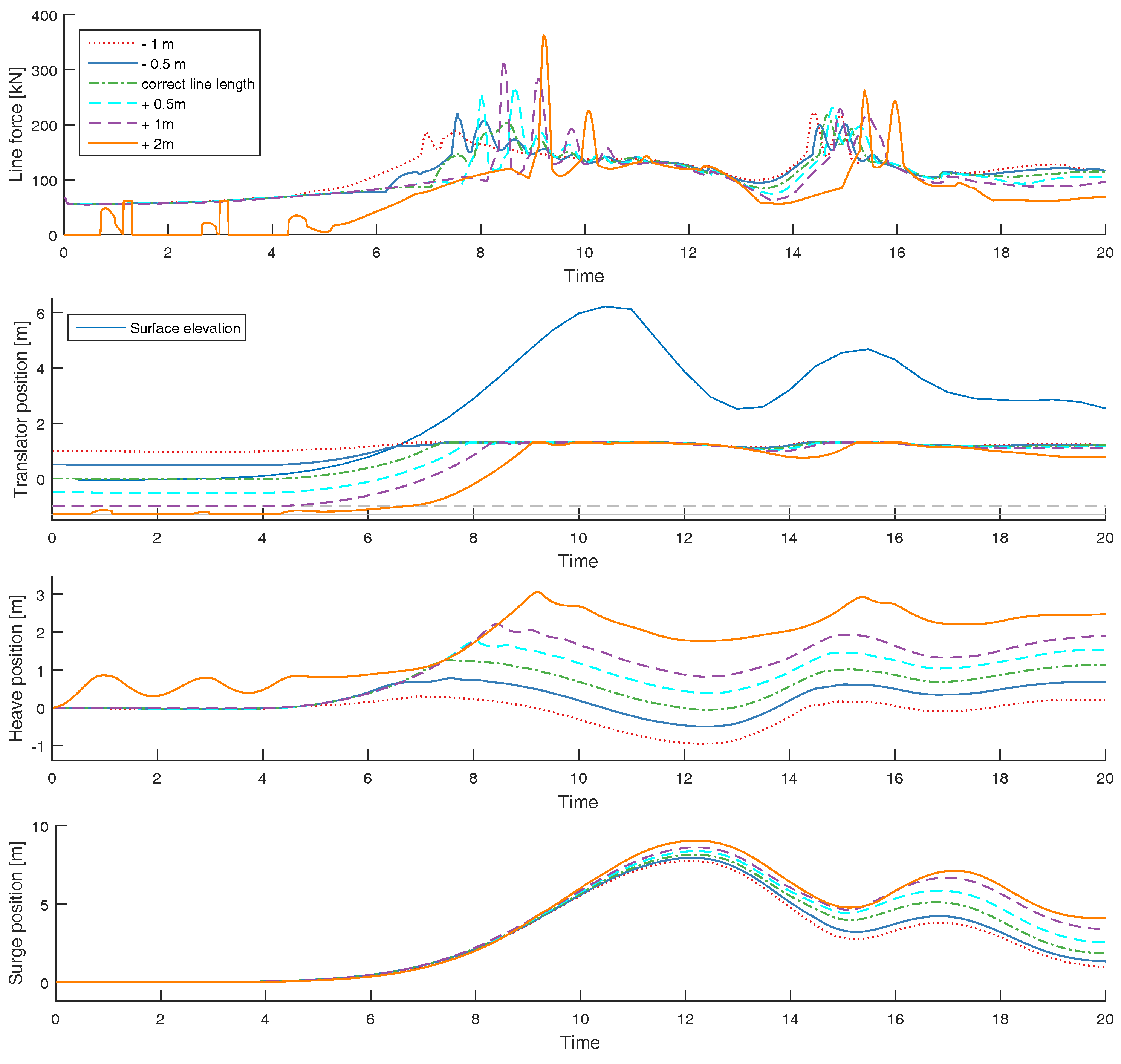
3.4. Influence of Line Length on Endstop Peak Force
4. Discussion
5. Conclusions
- For periodic waves, it was seen that both increased linear damping, , and increased constant damping , decreased the force of the endstop hits. This corresponds well with established experimental results.
- If the incident wave was not periodic, for the tsunami event or the transient waves at the front of the regular wave train, it was seen that increased friction could result in a latching effect and actually increase the force of the endstop hit instead of decreasing it. It is possible that this effect could also occur for irregular waves during normal operating conditions.
- Due to the differences in fluid velocity fields, the WEC was more vulnerable to a too long line length when impacted by a tsunami wave than by a regular wave. For a regular wave, an increased line length resulted in lower endstop forces and decreased surge motion. For the tsunami wave on the other hand, an increased line length resulted in significantly higher endstop forces.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| WEC | Wave Energy Converter |
| CFD | Computational Fluid Dynamics |
| RANS | Reynolds Average Navier-Stokes |
| VOF | Volume of Fluid |
| PTO | Power Take Off |
References
- Wolgamot, H.; Fitzgerald, C. Nonlinear hydrodynamic and real fluid effects on wave energy converters. Proc. IMechE Part A J. Power Energy 2015, 229, 772–794. [Google Scholar] [CrossRef]
- Day, A.; Babarit, A.; Fontaine, A.; He, Y.; Kraskowski, M.; Murai, M.; Penesis, I.; Salvatore, F.; Shin, H. Hydrodynamic modeling of marine renewable energy devices: A state of the art review. Ocean Eng. 2015, 108, 46–69. [Google Scholar] [CrossRef] [Green Version]
- Palm, J.; Eskilsson, C.; Paredes, G.; Bergdahl, L. Coupled mooring Analysis for Floating Wave Energy Converters Using CFD: Formulation and Validation. Int. J. Mar. Energy 2016, 16, 83–99. [Google Scholar] [CrossRef]
- Buccino, M.; Vicinanza, D.; Salerno, D.; Banfi, D.; Calabrese, M. Nature and magnitude of wave loadings at Seawave Slotcone Generators. Ocean Eng. 2015, 95, 34–58. [Google Scholar] [CrossRef]
- Buccino, M.; Dentale, F.; Salerno, D.; Contestabile, P.; Calabrese, M. The use of CFD in the analysis of wave loadings acting on Seawave Slotcone Generators. Sustainability 2017, 8, 1255. [Google Scholar] [CrossRef]
- Ransley, E. Survivability of Wave Energy Converter and Mooring Coupled 525 System Using CFD. Ph.D. Thesis, Plymouth University, Plymouth, UK, 2015. [Google Scholar]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Hann, M. Survivability of wave energy converters using CFD. Renew. Energy 2017, 109, 235–247. [Google Scholar] [CrossRef]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Hann, M.; Jakobsen, M.; Kramer, M. RANS-VOF modelling of the wavestar point absorber. Renew. Energy 2017, 109, 49–65. [Google Scholar] [CrossRef]
- Chen, W.; Dolguntseva, I.; Savin, A.; Zhang, Y.; Li, W.; Svensson, O.; Leijon, M. Numerical modelling of a point-absorbing wave energy converter in irregular and extreme waves. Appl. Ocean Res. 2017, 63, 90–105. [Google Scholar] [CrossRef]
- Sjökvist, L.; Wu, J.; Ransley, E.; Engström, J.; Eriksson, M.; Göteman, M. Numerical models for the motion and forces of point-absorbing wave energy converters in extreme waves. Ocean Eng. 2017. accepted. [Google Scholar]
- Hann, M.; Greaves, D.; Raby, A. Snatch loading of a single taut moored floating wave energy converter due to focussed wave groups. Ocean Eng. 2015, 96, 258–271. [Google Scholar] [CrossRef]
- Waters, R.; Stålberg, M.; Danielsson, O.; Svensson, O.; Gustafsson, S.; Strömstedt, E.; Eriksson, M.; Leijon, M. Experimental Results from Sea Trials of an Offshore Wave Energy System. Appl. Phys. Lett. 2007, 90, 034105. [Google Scholar] [CrossRef]
- Engström, E. Hydrodynamic Modelling for a Point Absorbing Wave Energy Converter. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2011. [Google Scholar]
- Eriksson, M.; Isberg, J.; Leijon, M. Hydrodynamic modelling of a direct drive wave energy converter. Int. J. Eng. Sci. 2005, 43, 1377–1387. [Google Scholar] [CrossRef]
- Pastor, J.; Liu, Y. Power absorption modeling and optimization of a point absorbing wave energy converter using numerical method. ASME J. Energy Resour. Technol. 2014, 136, 021207. [Google Scholar] [CrossRef]
- Pastor, J.; Liu, Y. Wave climate resource analysis for deployment of wave energy conversion technology. Sustainability 2016, 8, 1321. [Google Scholar] [CrossRef]
- Waters, R. Energy from Ocean Waves. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2008. [Google Scholar]
- Rahm, M. Ocean Wave Energy. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2010. [Google Scholar]
- Ekström, R. Offshore Marine Substation for Grid-Connection of Wave Power Farms—An Experimental Approach. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2010. [Google Scholar]
- Stålberg, M.; Waters, R.; Danielsson, O.; Leijon, M. Influence of Generator Damping on Peak Power for a Direct Drive Wave Energy Converter. J. Offshore Mech. Arct. Eng. 2008, 130. [Google Scholar] [CrossRef]
- Sjökvist, L.; Krishna, R.; Castellucci, V.; Hagnestål, A.; Rahm, M.; Leijon, M. On the optimization of point absorber buoys. J. Mar. Sci. Eng. 2014, 2, 477–492. [Google Scholar] [CrossRef]
- Hong, Y. Numerical Modelling and Mechanical Studies on a Point Absorber Type Wave Energy Converter. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2016. [Google Scholar]
- Li, W.; Isberg, J.; Engström, J.; Waters, R.; Leijon, M. Parametric Study of tge Power Absorbtion for a Linear Generator Wave Energy Converter. J. Ocean Wind Energy 2015, 2, 248–252. [Google Scholar] [CrossRef]
- Göteman, M.; Engström, J.; Eriksson, M.; Leijon, M.; Hann, M.; Ransley, E.; Greaves, D. Wave loads on a point-absorbing wave energy device in extreme waves. J. Ocean Wind Energy 2015, 2, 176–181. [Google Scholar] [CrossRef]
- Sjökvist, L.; Göteman, M. The effect of overtopping waves on peak forces on a point absorbing WEC. In Proceedings of the Asian Wave and Tidal Energy Conference Series AWTEC, Singapore, 24–28 October 2016. [Google Scholar]
- Ulvgård, L.; Sjökvist, L.; Göteman, M.; Leijon, M. Line Force and Damping at Full and Partial Stator Overlap in a Linear Generator for Wave Power. J. Mar. Sci. Eng. 2016, 4, 81. [Google Scholar] [CrossRef]
- Frost, A.; Ulvgård, L.; Sjökvist, L.; Leijon, M. Experimental study of generator damping at partial stator overlap in a linear generator for wave power. In Proceedings of the European Wave and Tidal Energy Conference Series EWTEC, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Sjökvist, L.; Göteman, M. Peak Forces on a Point Absorbing Wave Energy Converter Induced by Tsunami Waves. Renew. Energy 2017. under review. [Google Scholar]
- Jacobsen, N.G.; Fuhrman, D.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFOAM. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Waters, R.; Engström, J.; Isberg, J.; Leijon, M. Wave Climate off the Swedish West Coast. Renew. Energy 2009, 34, 1600–1606. [Google Scholar] [CrossRef]
- Mei, C.; Stiassnie, M.; Yue, D. Theory and Applications of Ocean Surface Waves, Part 1: Linear Aspects; World Scientific Publishing Co., Pte. Ltd.: Singapore, 2005. [Google Scholar]
- Douglas, S.; Nistor, I. On the effect of bed condition on the development of tsunami-induces loading on structures using OpenFOAM. Nat. Hazards 2015, 76, 1335–1356. [Google Scholar] [CrossRef]
- Madsen, P.; Furman, D.; Shäffer, H. On the solitary wave paradigm for tsunamis. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]

| Parameter | Abbrevation | Value |
|---|---|---|
| Buoy radius | 1.7 m | |
| Buoy height | 2.1 m | |
| Buoy mass | 5700 kg | |
| Translator mass | 6500 kg | |
| Translator height | 3 m | |
| Stator height | 2 m | |
| Free stroke length up/down | 1 m | |
| Total stroke length up/down | 1.25 m | |
| Endstop spring constant | 250 kN/m | |
| Spring constant corresponding to line elasticity | 2600 kN/m |
| Wave Height | 3 m | 4 m | 5 m | 6 m | 7 m |
| Wave Steepness (kA) | 0.08 | 0.11 | 0.14 | 0.17 | 0.19 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sjökvist, L.; Göteman, M. Peak Forces on Wave Energy Linear Generators in Tsunami and Extreme Waves. Energies 2017, 10, 1323. https://doi.org/10.3390/en10091323
Sjökvist L, Göteman M. Peak Forces on Wave Energy Linear Generators in Tsunami and Extreme Waves. Energies. 2017; 10(9):1323. https://doi.org/10.3390/en10091323
Chicago/Turabian StyleSjökvist, Linnea, and Malin Göteman. 2017. "Peak Forces on Wave Energy Linear Generators in Tsunami and Extreme Waves" Energies 10, no. 9: 1323. https://doi.org/10.3390/en10091323
APA StyleSjökvist, L., & Göteman, M. (2017). Peak Forces on Wave Energy Linear Generators in Tsunami and Extreme Waves. Energies, 10(9), 1323. https://doi.org/10.3390/en10091323





